2025年山东省济南历下区八年级第二学期数学期中考试试题(含答案)
文档属性
| 名称 | 2025年山东省济南历下区八年级第二学期数学期中考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 536.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 20:06:21 | ||
图片预览

文档简介
2024 - 2025 学年第二学期八年级期中教学质量检测数学试题(2025.4)
考试时间 120 分钟 满分 150 分
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
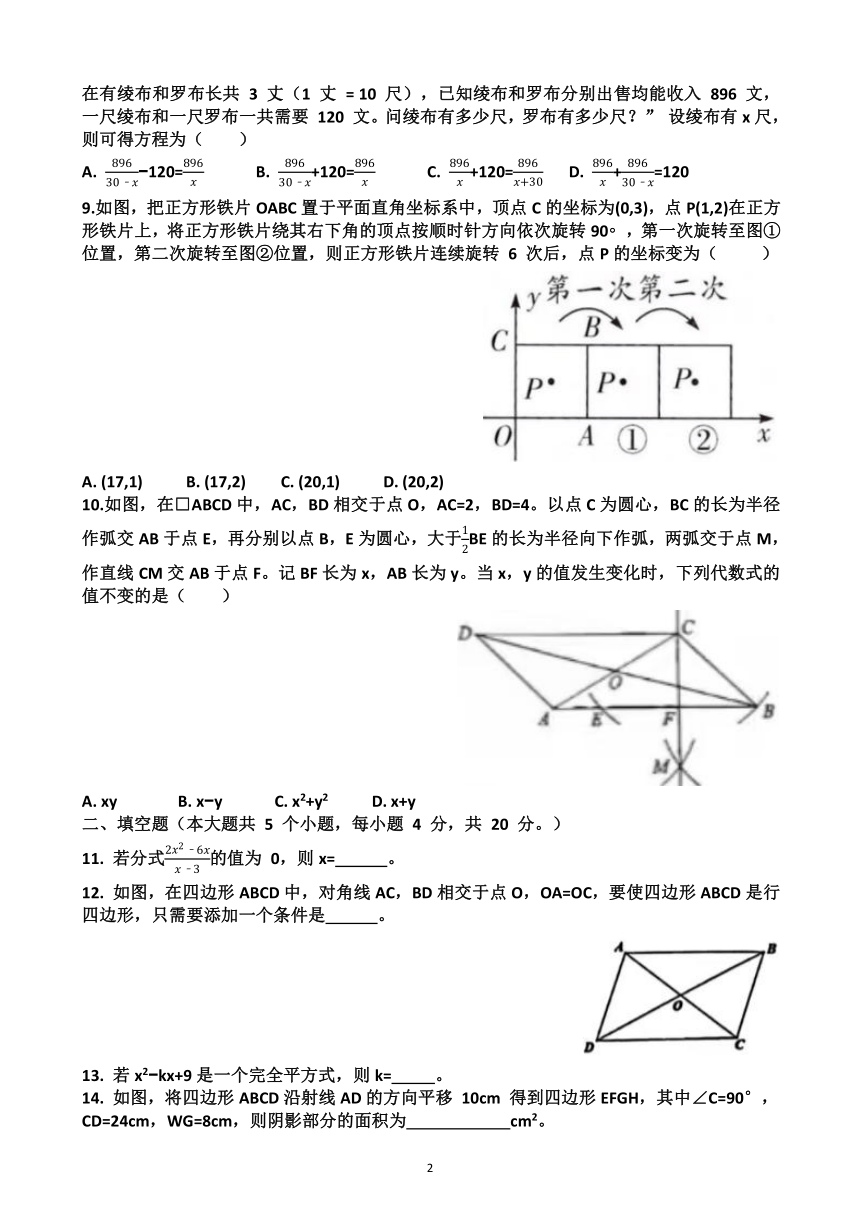
1.春晚主标识通过视觉元素传达出春晚的主题和寓意。下列主标识中,是中心对称图形的是( )
D.
2.下列等式从左到右的变形中,属于因式分解的是( )
A. (x+2)(x 2)=x2 4 B. x2 x 2=(x+1)(x 2) C. x2 x+1=x(x 1)+1 D. x2 1=(x 1)2
3.在平面直角坐标系中,将点E( 2,0)先向左平移 2 个单位长度,再向上平移 4 个单位长度,得到点E′,则点E′的坐标是( )
A. (0,4) B. (0, 4) C. ( 4, 4) D. ( 4,4)
4.关于平行四边形的性质,下列说法错误的是( )
A. 对角线互相平分 B. 对边平行且相等 C. 对角线相等 D. 对角相等
5.若分式 是最简分式,则Δ表示的整式可能是( )
A. 2a+2b B. a2+b2 C. a2+2ab+b2 D. (a b)2
6.图 1 是装满了液体的高脚杯(数据如图所示),图 2 是用去部分液体后的高脚杯(数据如图所示),则图 2 中液面AB的宽度为( )
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
7.如图,△ABC是边长为 4 的等边三角形,点D在边BC的延长线上且CD=1,连接AD,将线段AD绕点D顺时针旋转60 得到线段DE,连接AE,则DE的长为( )
A. B. 3 C. D.2
8.我国明代《永乐大典》中记载了 “绫罗尺价” 问题:“今有绫、罗共三丈,各值钱八百九十六文,只云绫、罗各一尺共值钱一百二十文。问绫、罗尺价各几何?” 其大意为:“现在有绫布和罗布长共 3 丈(1 丈 = 10 尺),已知绫布和罗布分别出售均能收入 896 文,一尺绫布和一尺罗布一共需要 120 文。问绫布有多少尺,罗布有多少尺?” 设绫布有x尺,则可得方程为( )
A. 120= B. +120= C. +120= D. +=120
9.如图,把正方形铁片OABC置于平面直角坐标系中,顶点C的坐标为(0,3),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90 ,第一次旋转至图①位置,第二次旋转至图②位置,则正方形铁片连续旋转 6 次后,点P的坐标变为( )
A. (17,1) B. (17,2) C. (20,1) D. (20,2)
10.如图,在□ABCD中,AC,BD相交于点O,AC=2,BD=4。以点C为圆心,BC的长为半径作弧交AB于点E,再分别以点B,E为圆心,大于BE的长为半径向下作弧,两弧交于点M,作直线CM交AB于点F。记BF长为x,AB长为y。当x,y的值发生变化时,下列代数式的值不变的是( )
A. xy B. x y C. x2+y2 D. x+y
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11. 若分式的值为 0,则x= 。
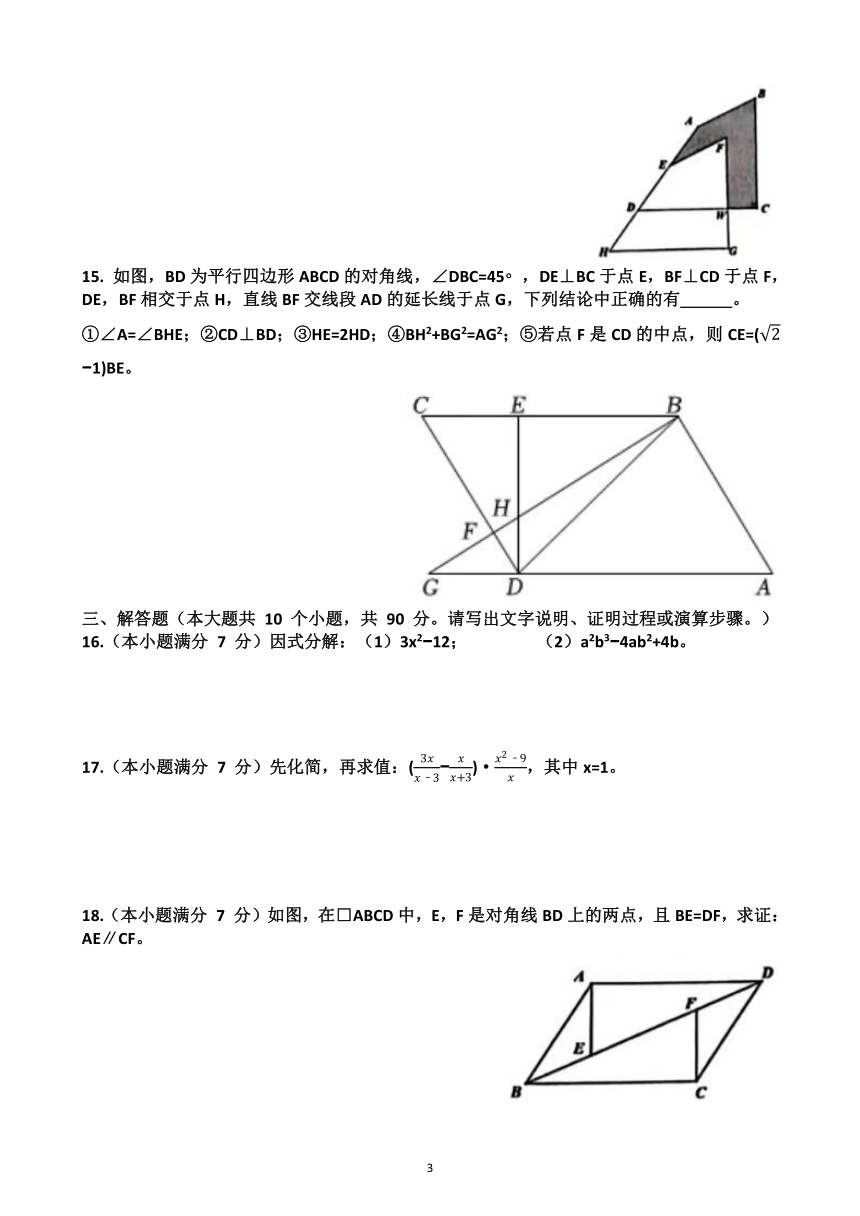
12. 如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,要使四边形ABCD是行四边形,只需要添加一个条件是 。
13. 若x2 kx+9是一个完全平方式,则k= 。
14. 如图,将四边形ABCD沿射线AD的方向平移 10cm 得到四边形EFGH,其中∠C=90°,
CD=24cm,WG=8cm,则阴影部分的面积为 cm2。
15. 如图,BD为平行四边形ABCD的对角线,∠DBC=45 ,DE⊥BC于点E,BF⊥CD于点F,DE,BF相交于点H,直线BF交线段AD的延长线于点G,下列结论中正确的有 。
①∠A=∠BHE;②CD⊥BD;③HE=2HD;④BH2+BG2=AG2;⑤若点F是CD的中点,则CE=( 1)BE。
三、解答题(本大题共 10 个小题,共 90 分。请写出文字说明、证明过程或演算步骤。)
16.(本小题满分 7 分)因式分解:(1)3x2 12; (2)a2b3 4ab2+4b。
17.(本小题满分 7 分)先化简,再求值:( )·,其中x=1。
18.(本小题满分 7 分)如图,在□ABCD中,E,F是对角线BD上的两点,且BE=DF,求证:AE∥CF。
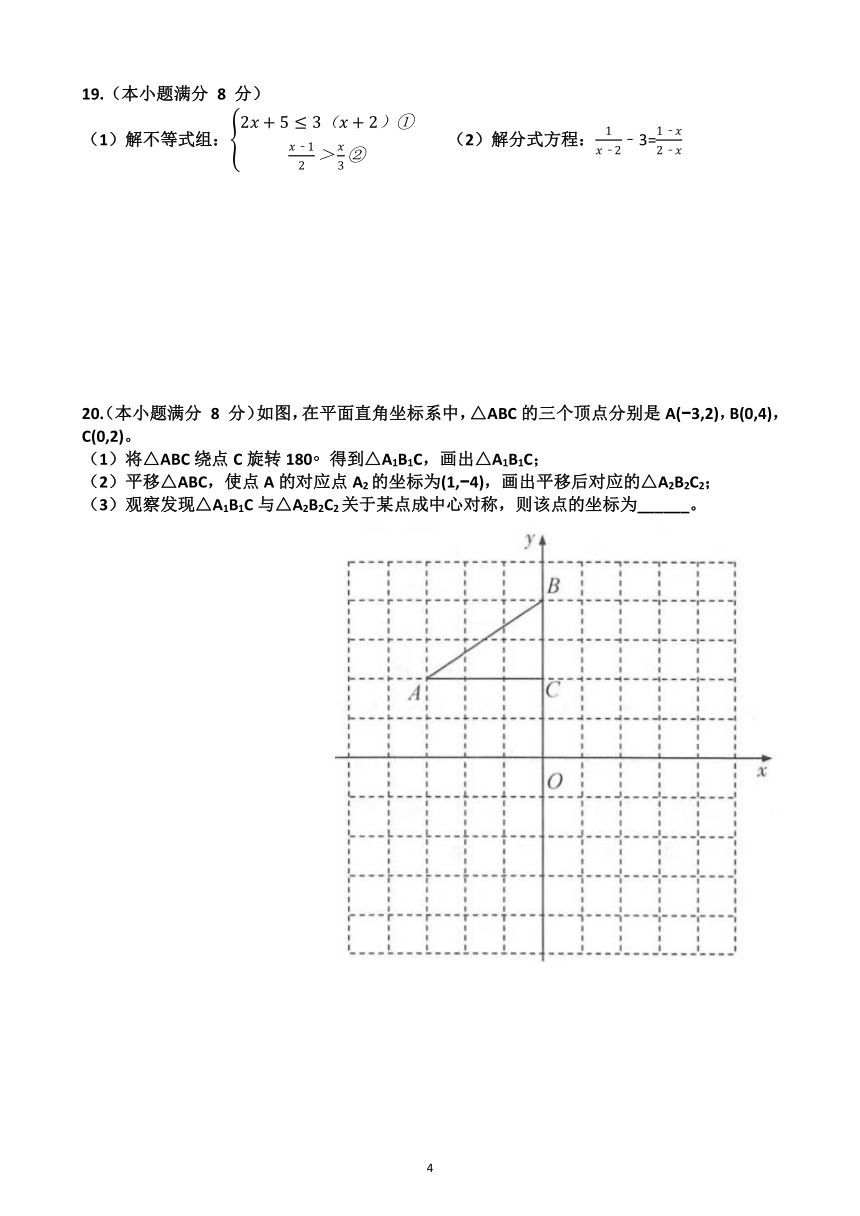
19.(本小题满分 8 分)
(1)解不等式组: (2)解分式方程:﹣3=
20.(本小题满分 8 分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A( 3,2),B(0,4),C(0,2)。
(1)将△ABC绕点C旋转180 得到△A1B1C,画出△A1B1C;
(2)平移△ABC,使点A的对应点A2的坐标为(1, 4),画出平移后对应的△A2B2C2;
(3)观察发现△A1B1C与△A2B2C2关于某点成中心对称,则该点的坐标为______。
21.(本小题满分 9 分)请根据材料中的信息,解决相关问题:
背景知识 为了健全分时电价机制,引导电动汽车在用电低谷时段充电,某市实施峰谷分时电价制度。
相关素材 素材一:用电高峰时段(简称峰时)为 7:00 - 23:00,用电低谷时段(简称谷时)为 23:00 - 次日 7:00,峰时电价比谷时电价高 0.2 元 / 度; 素材二:小明家的电动汽车用家用充电桩充电,三月份的峰时电费为 50 元,谷时电费为 30 元,并且峰时用电量与谷时用电量相等; 素材三:李老师家的电动汽车用家用充电桩充电,三月份的充电量为 180 度,电费不超过 64 元。
问题解决 问题 1:求该市峰时电价与谷时电价; 问题 2:三月份李老师家的谷时用电量至少为多少度?
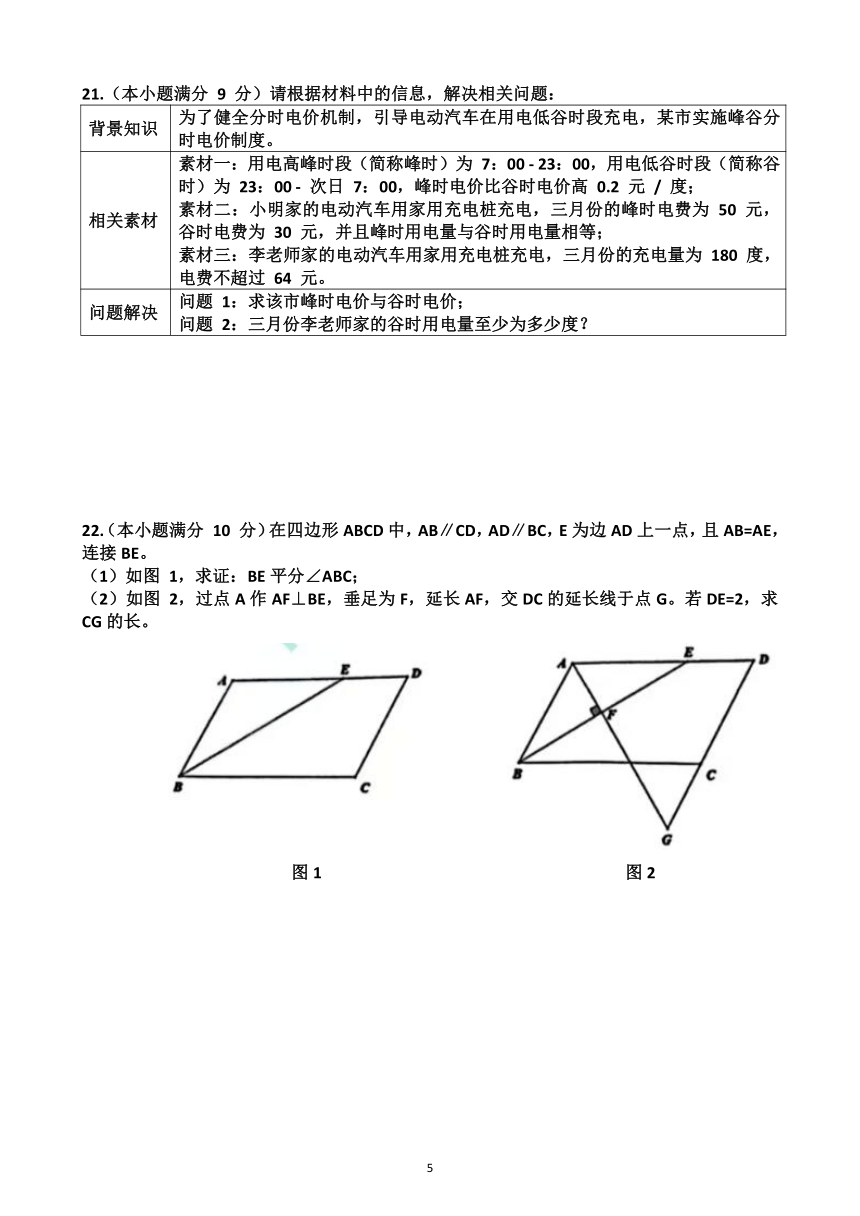
22.(本小题满分 10 分)在四边形ABCD中,AB∥CD,AD∥BC,E为边AD上一点,且AB=AE,连接BE。
(1)如图 1,求证:BE平分∠ABC;
(2)如图 2,过点A作AF⊥BE,垂足为F,延长AF,交DC的延长线于点G。若DE=2,求CG的长。
图1 图2
23.(本小题满分 10 分)【阅读材料】
类比分数学分式
将分式拆分成一个整式与一个真分式的和(差)的形式,有助于我们解决分式中的整除问题。
通过阅读上述材料,解决下列问题:
【理解知识】
(1)假分式可以写成带分式的形式为______。
【掌握知识】
(2)已知x是正整数,当分式的值为整数时,求x的值;
【应用知识】
(3)已知M=是一个四位数,且为正数,由M的前两位数字所组成的两位数记为,由M的后两位数字组成的两位数记为,若比小 5,且的平方能被整除,求这个四位数。
24.(本小题满分 12 分)在平面直角坐标系中,点A,B的坐标分别为A( 2,5),B( 2,0),将线段AB向右平移t个单位长度(t>0),再向下平移 1 个单位长度,得到线段CD,其中点A与点C是对应点,点B与点D是对应点,连接AC,BD。
(1)判断四边形ABDC的形状,并说明理由;
(2)分别连接AD,BC,交点为M,
①如图,连接OM,当OM⊥AD时,求t的值;
②作与△ABM关于点O成中心对称的△A1B1M1,当点D位于△A1B1M1的内部或边上时,直接写出t的取值范围。
25.(本小题满分 12 分)
(一)类比探究已知△ABC是等腰直角三角形,AB=AC,∠BAC=90 ,点D为平面内一动点,连接AD,将线段AD绕点A逆时针旋转90 得到线段AE,连接CE。
(1)如图 1,当点D在斜边BC上时,线段BD与线段CE的数量关系是______,BD与CE的位置关系是______;
(2)如图 2,当点D为△ABC的边AB左侧一点时,延长CE,BD交于点M,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由;
(二)学以致用
(3)如图 3,已知△ABC是等腰直角三角形,AB=AC,∠BAC=90 ,点D为△ABC的边BC下方一点,连接AD,BD,CD,若∠BDC=90°,AD=4,求△BDC面积的最大值。
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.春晚主标识通过视觉元素传达出春晚的主题和寓意。下列主标识中,是中心对称图形的是( D )
D.
2.下列等式从左到右的变形中,属于因式分解的是( B )
A. (x+2)(x 2)=x2 4 B. x2 x 2=(x+1)(x 2) C. x2 x+1=x(x 1)+1 D. x2 1=(x 1)2
3.在平面直角坐标系中,将点E( 2,0)先向左平移 2 个单位长度,再向上平移 4 个单位长度,得到点E′,则点E′的坐标是( D )
A. (0,4) B. (0, 4) C. ( 4, 4) D. ( 4,4)
4.关于平行四边形的性质,下列说法错误的是( C )
A. 对角线互相平分 B. 对边平行且相等 C. 对角线相等 D. 对角相等
5.若分式 是最简分式,则Δ表示的整式可能是( B )
A. 2a+2b B. a2+b2 C. a2+2ab+b2 D. (a b)2
6.图 1 是装满了液体的高脚杯(数据如图所示),图 2 是用去部分液体后的高脚杯(数据如图所示),则图 2 中液面AB的宽度为( C )
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
7.如图,△ABC是边长为 4 的等边三角形,点D在边BC的延长线上且CD=1,连接AD,将线段AD绕点D顺时针旋转60 得到线段DE,连接AE,则DE的长为( A )
A. B. 3 C. D.2
8.我国明代《永乐大典》中记载了 “绫罗尺价” 问题:“今有绫、罗共三丈,各值钱八百九十六文,只云绫、罗各一尺共值钱一百二十文。问绫、罗尺价各几何?” 其大意为:“现在有绫布和罗布长共 3 丈(1 丈 = 10 尺),已知绫布和罗布分别出售均能收入 896 文,一尺绫布和一尺罗布一共需要 120 文。问绫布有多少尺,罗布有多少尺?” 设绫布有x尺,则可得方程为( D )
A. 120= B. +120= C. +120= D. +=120
9.如图,把正方形铁片OABC置于平面直角坐标系中,顶点C的坐标为(0,3),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90 ,第一次旋转至图①位置,第二次旋转至图②位置,则正方形铁片连续旋转 6 次后,点P的坐标变为( C )
A. (17,1) B. (17,2) C. (20,1) D. (20,2)
10.如图,在□ABCD中,AC,BD相交于点O,AC=2,BD=4。以点C为圆心,BC的长为半径作弧交AB于点E,再分别以点B,E为圆心,大于BE的长为半径向下作弧,两弧交于点M,作直线CM交AB于点F。记BF长为x,AB长为y。当x,y的值发生变化时,下列代数式的值不变的是( A )
A. xy B. x y C. x2+y2 D. x+y
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11. 若分式的值为 0,则x= 0 。
12. 如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,要使四边形ABCD是行四边形,只需要添加一个条件是 OB=OD 。
13. 若x2 kx+9是一个完全平方式,则k= ±6 。
14. 如图,将四边形ABCD沿射线AD的方向平移 10cm 得到四边形EFGH,其中∠C=90°,
CD=24cm,WG=8cm,则阴影部分的面积为 168 cm2。
15. 如图,BD为平行四边形ABCD的对角线,∠DBC=45 ,DE⊥BC于点E,BF⊥CD于点F,DE,BF相交于点H,直线BF交线段AD的延长线于点G,下列结论中正确的有 ①④⑤ 。
①∠A=∠BHE;②CD⊥BD;③HE=2HD;④BH2+BG2=AG2;⑤若点F是CD的中点,则CE=( 1)BE。
三、解答题(本大题共 10 个小题,共 90 分。请写出文字说明、证明过程或演算步骤。)
16.(本小题满分 7 分)因式分解:(1)3x2 12; (2)a2b3 4ab2+4b。
=3(x2﹣4) =b(a2b2﹣4ab+4)
=3(x+2)(x﹣2) =b(ab﹣2)2
17.(本小题满分 7 分)先化简,再求值:( )·,其中x=1。
解原式=·
=2x+12
将x=1代入得14
18.(本小题满分 7 分)如图,在□ABCD中,E,F是对角线BD上的两点,且BE=DF,求证:AE∥CF。
证明∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∴∠ABE=∠CDF
∵BE=DF
∴△ABE≌△CDF
∴∠AEB=∠CFD
∴180°﹣∠AEB=180°﹣∠CFD
∴∠AEF=∠CFE
∴AE∥CF
19.(本小题满分 8 分)
(1)解不等式组: (2)解分式方程:﹣3=
(1)解不等式①得x≥﹣1
解不等式②得x>3
不等式组的解集x>3
(2)1﹣3(x﹣2)=x﹣1
x=2
经检验x=2是原方程的增根,此方程无解。
20.(本小题满分 8 分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A( 3,2),B(0,4),C(0,2)。
(1)将△ABC绕点C旋转180 得到△A1B1C,画出△A1B1C;
(2)平移△ABC,使点A的对应点A2的坐标为(1, 4),画出平移后对应的△A2B2C2;
(3)观察发现△A1B1C与△A2B2C2关于某点成中心对称,则该点的坐标为______。
(1)(2)略
(3)(2,﹣1)
21.(本小题满分 9 分)请根据材料中的信息,解决相关问题:
背景知识 为了健全分时电价机制,引导电动汽车在用电低谷时段充电,某市实施峰谷分时电价制度。
相关素材 素材一:用电高峰时段(简称峰时)为 7:00 - 23:00,用电低谷时段(简称谷时)为 23:00 - 次日 7:00,峰时电价比谷时电价高 0.2 元 / 度; 素材二:小明家的电动汽车用家用充电桩充电,三月份的峰时电费为 50 元,谷时电费为 30 元,并且峰时用电量与谷时用电量相等; 素材三:李老师家的电动汽车用家用充电桩充电,三月份的充电量为 180 度,电费不超过 64 元。
问题解决 问题 1:求该市峰时电价与谷时电价; 问题 2:三月份李老师家的谷时用电量至少为多少度?
问题1
设谷时电价为 x 元/度,则峰时电价为( x +0.2)元/度。
根据题意,峰时用电量与谷时用电量相等:=
解得 x =0.3,故峰时电价为0.5元/度,谷时电价为0.3元/度。
答:峰时电价为0.5元/度,谷时电价为0.3元/度。
问题2
设谷时用电量为 y 度,则峰时用电量为(180- y )度。总电费不超过64元:
0.5(180- y )+0.3y≤64
解得 y ≥130。
答:三月份李老师家的谷时用电量至少为130度。
22.(本小题满分 10 分)在四边形ABCD中,AB∥CD,AD∥BC,E为边AD上一点,且AB=AE,连接BE。
(1)如图 1,求证:BE平分∠ABC;
(2)如图 2,过点A作AF⊥BE,垂足为F,延长AF,交DC的延长线于点G。若DE=2,求CG的长。
图1 图2
(1)证明:∵AB∥CD,AD∥BC
∴□ABCD是平行四边形。
∵AB=AE
∴∠ABE=∠AEB。又AD∥BC
∴∠AEB=∠EBC
∴∠ABE=∠EBC
即BE平分∠ABC。
(2)∵AB=AE,AF⊥BE
∴BF=EF
∵AB∥CD
∴∠ABF=∠CGF,∠BAF=∠G,△ABF≌△GCF(AAS)
∴AB=CG
∵DE=2
∴AD AE=2,又AB=AE
∴CG=2
23.(本小题满分 10 分)【阅读材料】
类比分数学分式
将分式拆分成一个整式与一个真分式的和(差)的形式,有助于我们解决分式中的整除问题。
通过阅读上述材料,解决下列问题:
【理解知识】
(1)假分式可以写成带分式的形式为______。
【掌握知识】
(2)已知x是正整数,当分式的值为整数时,求x的值;
【应用知识】
(3)已知M=是一个四位数,且为正数,由M的前两位数字所组成的两位数记为,由M的后两位数字组成的两位数记为,若比小 5,且的平方能被整除,求这个四位数。
(1)+2
(2)=x+3﹣
∴x 1=±1或±11
∴x=0或2或12或﹣10
∴x=2或12
(3)设=x,=x+5
∴==x﹣10+
∴x=1,5或25
∴=2025
24.(本小题满分 12 分)在平面直角坐标系中,点A,B的坐标分别为A( 2,5),B( 2,0),将线段AB向右平移t个单位长度(t>0),再向下平移 1 个单位长度,得到线段CD,其中点A与点C是对应点,点B与点D是对应点,连接AC,BD。
(1)判断四边形ABDC的形状,并说明理由;
(2)分别连接AD,BC,交点为M,
①如图,连接OM,当OM⊥AD时,求t的值;
②作与△ABM关于点O成中心对称的△A1B1M1,当点D位于△A1B1M1的内部或边上时,直接写出t的取值范围。
(1)四边形ABDC是平行四边形
∵AB平移得CD,
∴AB∥CD且AB=CD
∴四边形ABDC是平行四边形
(2)①A( 2,5),B( 2,0),平移后C( 2+t,4),D( 2+t, 1)
AD中点M( 2+t,2)
∵AD斜率 ,OM斜率
∵OM⊥AD
∴ ·=﹣1
解得t=6
②2≤t≤4
25.(本小题满分 12 分)
(一)类比探究已知△ABC是等腰直角三角形,AB=AC,∠BAC=90 ,点D为平面内一动点,连接AD,将线段AD绕点A逆时针旋转90 得到线段AE,连接CE。
(1)如图 1,当点D在斜边BC上时,线段BD与线段CE的数量关系是______,BD与CE的位置关系是______;
(2)如图 2,当点D为△ABC的边AB左侧一点时,延长CE,BD交于点M,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由;
(二)学以致用
(3)如图 3,已知△ABC是等腰直角三角形,AB=AC,∠BAC=90 ,点D为△ABC的边BC下方一点,连接AD,BD,CD,若∠BDC=90°,AD=4,求△BDC面积的最大值。
(1)BD=CE,BD⊥CE。
(2)成立
(3)8
考试时间 120 分钟 满分 150 分
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.春晚主标识通过视觉元素传达出春晚的主题和寓意。下列主标识中,是中心对称图形的是( )
D.
2.下列等式从左到右的变形中,属于因式分解的是( )
A. (x+2)(x 2)=x2 4 B. x2 x 2=(x+1)(x 2) C. x2 x+1=x(x 1)+1 D. x2 1=(x 1)2
3.在平面直角坐标系中,将点E( 2,0)先向左平移 2 个单位长度,再向上平移 4 个单位长度,得到点E′,则点E′的坐标是( )
A. (0,4) B. (0, 4) C. ( 4, 4) D. ( 4,4)
4.关于平行四边形的性质,下列说法错误的是( )
A. 对角线互相平分 B. 对边平行且相等 C. 对角线相等 D. 对角相等
5.若分式 是最简分式,则Δ表示的整式可能是( )
A. 2a+2b B. a2+b2 C. a2+2ab+b2 D. (a b)2
6.图 1 是装满了液体的高脚杯(数据如图所示),图 2 是用去部分液体后的高脚杯(数据如图所示),则图 2 中液面AB的宽度为( )
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
7.如图,△ABC是边长为 4 的等边三角形,点D在边BC的延长线上且CD=1,连接AD,将线段AD绕点D顺时针旋转60 得到线段DE,连接AE,则DE的长为( )
A. B. 3 C. D.2
8.我国明代《永乐大典》中记载了 “绫罗尺价” 问题:“今有绫、罗共三丈,各值钱八百九十六文,只云绫、罗各一尺共值钱一百二十文。问绫、罗尺价各几何?” 其大意为:“现在有绫布和罗布长共 3 丈(1 丈 = 10 尺),已知绫布和罗布分别出售均能收入 896 文,一尺绫布和一尺罗布一共需要 120 文。问绫布有多少尺,罗布有多少尺?” 设绫布有x尺,则可得方程为( )
A. 120= B. +120= C. +120= D. +=120
9.如图,把正方形铁片OABC置于平面直角坐标系中,顶点C的坐标为(0,3),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90 ,第一次旋转至图①位置,第二次旋转至图②位置,则正方形铁片连续旋转 6 次后,点P的坐标变为( )
A. (17,1) B. (17,2) C. (20,1) D. (20,2)
10.如图,在□ABCD中,AC,BD相交于点O,AC=2,BD=4。以点C为圆心,BC的长为半径作弧交AB于点E,再分别以点B,E为圆心,大于BE的长为半径向下作弧,两弧交于点M,作直线CM交AB于点F。记BF长为x,AB长为y。当x,y的值发生变化时,下列代数式的值不变的是( )
A. xy B. x y C. x2+y2 D. x+y
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11. 若分式的值为 0,则x= 。
12. 如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,要使四边形ABCD是行四边形,只需要添加一个条件是 。
13. 若x2 kx+9是一个完全平方式,则k= 。
14. 如图,将四边形ABCD沿射线AD的方向平移 10cm 得到四边形EFGH,其中∠C=90°,
CD=24cm,WG=8cm,则阴影部分的面积为 cm2。
15. 如图,BD为平行四边形ABCD的对角线,∠DBC=45 ,DE⊥BC于点E,BF⊥CD于点F,DE,BF相交于点H,直线BF交线段AD的延长线于点G,下列结论中正确的有 。
①∠A=∠BHE;②CD⊥BD;③HE=2HD;④BH2+BG2=AG2;⑤若点F是CD的中点,则CE=( 1)BE。
三、解答题(本大题共 10 个小题,共 90 分。请写出文字说明、证明过程或演算步骤。)
16.(本小题满分 7 分)因式分解:(1)3x2 12; (2)a2b3 4ab2+4b。
17.(本小题满分 7 分)先化简,再求值:( )·,其中x=1。
18.(本小题满分 7 分)如图,在□ABCD中,E,F是对角线BD上的两点,且BE=DF,求证:AE∥CF。
19.(本小题满分 8 分)
(1)解不等式组: (2)解分式方程:﹣3=
20.(本小题满分 8 分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A( 3,2),B(0,4),C(0,2)。
(1)将△ABC绕点C旋转180 得到△A1B1C,画出△A1B1C;
(2)平移△ABC,使点A的对应点A2的坐标为(1, 4),画出平移后对应的△A2B2C2;
(3)观察发现△A1B1C与△A2B2C2关于某点成中心对称,则该点的坐标为______。
21.(本小题满分 9 分)请根据材料中的信息,解决相关问题:
背景知识 为了健全分时电价机制,引导电动汽车在用电低谷时段充电,某市实施峰谷分时电价制度。
相关素材 素材一:用电高峰时段(简称峰时)为 7:00 - 23:00,用电低谷时段(简称谷时)为 23:00 - 次日 7:00,峰时电价比谷时电价高 0.2 元 / 度; 素材二:小明家的电动汽车用家用充电桩充电,三月份的峰时电费为 50 元,谷时电费为 30 元,并且峰时用电量与谷时用电量相等; 素材三:李老师家的电动汽车用家用充电桩充电,三月份的充电量为 180 度,电费不超过 64 元。
问题解决 问题 1:求该市峰时电价与谷时电价; 问题 2:三月份李老师家的谷时用电量至少为多少度?
22.(本小题满分 10 分)在四边形ABCD中,AB∥CD,AD∥BC,E为边AD上一点,且AB=AE,连接BE。
(1)如图 1,求证:BE平分∠ABC;
(2)如图 2,过点A作AF⊥BE,垂足为F,延长AF,交DC的延长线于点G。若DE=2,求CG的长。
图1 图2
23.(本小题满分 10 分)【阅读材料】
类比分数学分式
将分式拆分成一个整式与一个真分式的和(差)的形式,有助于我们解决分式中的整除问题。
通过阅读上述材料,解决下列问题:
【理解知识】
(1)假分式可以写成带分式的形式为______。
【掌握知识】
(2)已知x是正整数,当分式的值为整数时,求x的值;
【应用知识】
(3)已知M=是一个四位数,且为正数,由M的前两位数字所组成的两位数记为,由M的后两位数字组成的两位数记为,若比小 5,且的平方能被整除,求这个四位数。
24.(本小题满分 12 分)在平面直角坐标系中,点A,B的坐标分别为A( 2,5),B( 2,0),将线段AB向右平移t个单位长度(t>0),再向下平移 1 个单位长度,得到线段CD,其中点A与点C是对应点,点B与点D是对应点,连接AC,BD。
(1)判断四边形ABDC的形状,并说明理由;
(2)分别连接AD,BC,交点为M,
①如图,连接OM,当OM⊥AD时,求t的值;
②作与△ABM关于点O成中心对称的△A1B1M1,当点D位于△A1B1M1的内部或边上时,直接写出t的取值范围。
25.(本小题满分 12 分)
(一)类比探究已知△ABC是等腰直角三角形,AB=AC,∠BAC=90 ,点D为平面内一动点,连接AD,将线段AD绕点A逆时针旋转90 得到线段AE,连接CE。
(1)如图 1,当点D在斜边BC上时,线段BD与线段CE的数量关系是______,BD与CE的位置关系是______;
(2)如图 2,当点D为△ABC的边AB左侧一点时,延长CE,BD交于点M,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由;
(二)学以致用
(3)如图 3,已知△ABC是等腰直角三角形,AB=AC,∠BAC=90 ,点D为△ABC的边BC下方一点,连接AD,BD,CD,若∠BDC=90°,AD=4,求△BDC面积的最大值。
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.春晚主标识通过视觉元素传达出春晚的主题和寓意。下列主标识中,是中心对称图形的是( D )
D.
2.下列等式从左到右的变形中,属于因式分解的是( B )
A. (x+2)(x 2)=x2 4 B. x2 x 2=(x+1)(x 2) C. x2 x+1=x(x 1)+1 D. x2 1=(x 1)2
3.在平面直角坐标系中,将点E( 2,0)先向左平移 2 个单位长度,再向上平移 4 个单位长度,得到点E′,则点E′的坐标是( D )
A. (0,4) B. (0, 4) C. ( 4, 4) D. ( 4,4)
4.关于平行四边形的性质,下列说法错误的是( C )
A. 对角线互相平分 B. 对边平行且相等 C. 对角线相等 D. 对角相等
5.若分式 是最简分式,则Δ表示的整式可能是( B )
A. 2a+2b B. a2+b2 C. a2+2ab+b2 D. (a b)2
6.图 1 是装满了液体的高脚杯(数据如图所示),图 2 是用去部分液体后的高脚杯(数据如图所示),则图 2 中液面AB的宽度为( C )
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
7.如图,△ABC是边长为 4 的等边三角形,点D在边BC的延长线上且CD=1,连接AD,将线段AD绕点D顺时针旋转60 得到线段DE,连接AE,则DE的长为( A )
A. B. 3 C. D.2
8.我国明代《永乐大典》中记载了 “绫罗尺价” 问题:“今有绫、罗共三丈,各值钱八百九十六文,只云绫、罗各一尺共值钱一百二十文。问绫、罗尺价各几何?” 其大意为:“现在有绫布和罗布长共 3 丈(1 丈 = 10 尺),已知绫布和罗布分别出售均能收入 896 文,一尺绫布和一尺罗布一共需要 120 文。问绫布有多少尺,罗布有多少尺?” 设绫布有x尺,则可得方程为( D )
A. 120= B. +120= C. +120= D. +=120
9.如图,把正方形铁片OABC置于平面直角坐标系中,顶点C的坐标为(0,3),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90 ,第一次旋转至图①位置,第二次旋转至图②位置,则正方形铁片连续旋转 6 次后,点P的坐标变为( C )
A. (17,1) B. (17,2) C. (20,1) D. (20,2)
10.如图,在□ABCD中,AC,BD相交于点O,AC=2,BD=4。以点C为圆心,BC的长为半径作弧交AB于点E,再分别以点B,E为圆心,大于BE的长为半径向下作弧,两弧交于点M,作直线CM交AB于点F。记BF长为x,AB长为y。当x,y的值发生变化时,下列代数式的值不变的是( A )
A. xy B. x y C. x2+y2 D. x+y
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11. 若分式的值为 0,则x= 0 。
12. 如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,要使四边形ABCD是行四边形,只需要添加一个条件是 OB=OD 。
13. 若x2 kx+9是一个完全平方式,则k= ±6 。
14. 如图,将四边形ABCD沿射线AD的方向平移 10cm 得到四边形EFGH,其中∠C=90°,
CD=24cm,WG=8cm,则阴影部分的面积为 168 cm2。
15. 如图,BD为平行四边形ABCD的对角线,∠DBC=45 ,DE⊥BC于点E,BF⊥CD于点F,DE,BF相交于点H,直线BF交线段AD的延长线于点G,下列结论中正确的有 ①④⑤ 。
①∠A=∠BHE;②CD⊥BD;③HE=2HD;④BH2+BG2=AG2;⑤若点F是CD的中点,则CE=( 1)BE。
三、解答题(本大题共 10 个小题,共 90 分。请写出文字说明、证明过程或演算步骤。)
16.(本小题满分 7 分)因式分解:(1)3x2 12; (2)a2b3 4ab2+4b。
=3(x2﹣4) =b(a2b2﹣4ab+4)
=3(x+2)(x﹣2) =b(ab﹣2)2
17.(本小题满分 7 分)先化简,再求值:( )·,其中x=1。
解原式=·
=2x+12
将x=1代入得14
18.(本小题满分 7 分)如图,在□ABCD中,E,F是对角线BD上的两点,且BE=DF,求证:AE∥CF。
证明∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∴∠ABE=∠CDF
∵BE=DF
∴△ABE≌△CDF
∴∠AEB=∠CFD
∴180°﹣∠AEB=180°﹣∠CFD
∴∠AEF=∠CFE
∴AE∥CF
19.(本小题满分 8 分)
(1)解不等式组: (2)解分式方程:﹣3=
(1)解不等式①得x≥﹣1
解不等式②得x>3
不等式组的解集x>3
(2)1﹣3(x﹣2)=x﹣1
x=2
经检验x=2是原方程的增根,此方程无解。
20.(本小题满分 8 分)如图,在平面直角坐标系中,△ABC的三个顶点分别是A( 3,2),B(0,4),C(0,2)。
(1)将△ABC绕点C旋转180 得到△A1B1C,画出△A1B1C;
(2)平移△ABC,使点A的对应点A2的坐标为(1, 4),画出平移后对应的△A2B2C2;
(3)观察发现△A1B1C与△A2B2C2关于某点成中心对称,则该点的坐标为______。
(1)(2)略
(3)(2,﹣1)
21.(本小题满分 9 分)请根据材料中的信息,解决相关问题:
背景知识 为了健全分时电价机制,引导电动汽车在用电低谷时段充电,某市实施峰谷分时电价制度。
相关素材 素材一:用电高峰时段(简称峰时)为 7:00 - 23:00,用电低谷时段(简称谷时)为 23:00 - 次日 7:00,峰时电价比谷时电价高 0.2 元 / 度; 素材二:小明家的电动汽车用家用充电桩充电,三月份的峰时电费为 50 元,谷时电费为 30 元,并且峰时用电量与谷时用电量相等; 素材三:李老师家的电动汽车用家用充电桩充电,三月份的充电量为 180 度,电费不超过 64 元。
问题解决 问题 1:求该市峰时电价与谷时电价; 问题 2:三月份李老师家的谷时用电量至少为多少度?
问题1
设谷时电价为 x 元/度,则峰时电价为( x +0.2)元/度。
根据题意,峰时用电量与谷时用电量相等:=
解得 x =0.3,故峰时电价为0.5元/度,谷时电价为0.3元/度。
答:峰时电价为0.5元/度,谷时电价为0.3元/度。
问题2
设谷时用电量为 y 度,则峰时用电量为(180- y )度。总电费不超过64元:
0.5(180- y )+0.3y≤64
解得 y ≥130。
答:三月份李老师家的谷时用电量至少为130度。
22.(本小题满分 10 分)在四边形ABCD中,AB∥CD,AD∥BC,E为边AD上一点,且AB=AE,连接BE。
(1)如图 1,求证:BE平分∠ABC;
(2)如图 2,过点A作AF⊥BE,垂足为F,延长AF,交DC的延长线于点G。若DE=2,求CG的长。
图1 图2
(1)证明:∵AB∥CD,AD∥BC
∴□ABCD是平行四边形。
∵AB=AE
∴∠ABE=∠AEB。又AD∥BC
∴∠AEB=∠EBC
∴∠ABE=∠EBC
即BE平分∠ABC。
(2)∵AB=AE,AF⊥BE
∴BF=EF
∵AB∥CD
∴∠ABF=∠CGF,∠BAF=∠G,△ABF≌△GCF(AAS)
∴AB=CG
∵DE=2
∴AD AE=2,又AB=AE
∴CG=2
23.(本小题满分 10 分)【阅读材料】
类比分数学分式
将分式拆分成一个整式与一个真分式的和(差)的形式,有助于我们解决分式中的整除问题。
通过阅读上述材料,解决下列问题:
【理解知识】
(1)假分式可以写成带分式的形式为______。
【掌握知识】
(2)已知x是正整数,当分式的值为整数时,求x的值;
【应用知识】
(3)已知M=是一个四位数,且为正数,由M的前两位数字所组成的两位数记为,由M的后两位数字组成的两位数记为,若比小 5,且的平方能被整除,求这个四位数。
(1)+2
(2)=x+3﹣
∴x 1=±1或±11
∴x=0或2或12或﹣10
∴x=2或12
(3)设=x,=x+5
∴==x﹣10+
∴x=1,5或25
∴=2025
24.(本小题满分 12 分)在平面直角坐标系中,点A,B的坐标分别为A( 2,5),B( 2,0),将线段AB向右平移t个单位长度(t>0),再向下平移 1 个单位长度,得到线段CD,其中点A与点C是对应点,点B与点D是对应点,连接AC,BD。
(1)判断四边形ABDC的形状,并说明理由;
(2)分别连接AD,BC,交点为M,
①如图,连接OM,当OM⊥AD时,求t的值;
②作与△ABM关于点O成中心对称的△A1B1M1,当点D位于△A1B1M1的内部或边上时,直接写出t的取值范围。
(1)四边形ABDC是平行四边形
∵AB平移得CD,
∴AB∥CD且AB=CD
∴四边形ABDC是平行四边形
(2)①A( 2,5),B( 2,0),平移后C( 2+t,4),D( 2+t, 1)
AD中点M( 2+t,2)
∵AD斜率 ,OM斜率
∵OM⊥AD
∴ ·=﹣1
解得t=6
②2≤t≤4
25.(本小题满分 12 分)
(一)类比探究已知△ABC是等腰直角三角形,AB=AC,∠BAC=90 ,点D为平面内一动点,连接AD,将线段AD绕点A逆时针旋转90 得到线段AE,连接CE。
(1)如图 1,当点D在斜边BC上时,线段BD与线段CE的数量关系是______,BD与CE的位置关系是______;
(2)如图 2,当点D为△ABC的边AB左侧一点时,延长CE,BD交于点M,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由;
(二)学以致用
(3)如图 3,已知△ABC是等腰直角三角形,AB=AC,∠BAC=90 ,点D为△ABC的边BC下方一点,连接AD,BD,CD,若∠BDC=90°,AD=4,求△BDC面积的最大值。
(1)BD=CE,BD⊥CE。
(2)成立
(3)8
同课章节目录
