2024-2025学年山东省济南高新区七年级第二学期数学期中考试试题(含答案)
文档属性
| 名称 | 2024-2025学年山东省济南高新区七年级第二学期数学期中考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 249.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 20:37:10 | ||
图片预览



文档简介
2024 - 2025 学年第二学期期中学业水平测试初中数学七年级试题
注意事项
本试题分第 Ⅰ 卷(选择题)和第 Ⅱ 卷(非选择题)两部分。第 Ⅰ 卷共 2 页,满分为 48 分;第Ⅱ卷共 4 页,满分为 102 分。本试题共 6 页,满分为 150 分。考试时间为 120分钟。答卷前,考生务必用 0.5 毫米黑色墨水签字笔将自己的考点、姓名、准考证号、座号填写在答题卡上和试卷规定的位置上。考试结束后,将本试卷和答题卡一并交回。本考试不允许使用计算器。
一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.下列图形中,∠1与∠2一定相等的是( )
2.“春江潮水连海平,海上明月共潮生”,水是诗人钟爱的意象,经测算,一个水分子的直径约为 0.0000004mm,数据 0.0000004 用科学记数法表示为( )
A. 4×10 7 B. 4×10 8 C. 0.4×10 7 D. 0.4×10 8
3.下列运算错误的是( )
A. b2·b3=b5 B. (a b)(b+a)=a2 b2 C. a5+b5=a10 D. ( a2b)2=b2a4
4.如图,把三角尺的直角顶点放在直尺的一边上,若∠1=28 ,则∠2的度数为( )
A. 68 B.62 C. 52 D. 28
5.掷一枚质地均匀的硬币 200 次,下列说法正确的是( )
A. 不可能 200 次正面朝上 B. 不可能 100 次正面朝上
C. 必有 100 次正面朝上 D. 可能 100 次正面朝上
6.如果x2+(n 3)x+16是个完全平方式,那么n的值是( )
A. 11 B. -5 C. 11 或 -5 D. ±8
7.如图所示,△ABC≌△DBE。若∠E=70 ,∠A=20 ,则( )
A.10 B. 30 C. 70 D. 90
8.下列说法:①三角形的高、中线、角平分线都是线段;②垂直于同一条直线的两条直线互相平行;③两条平行直线被第三条直线所截,同位角相等;④因为∠1=∠2,∠2=∠3,所以∠1=∠3。其中正确的是( )
A. ①③④ B. ②③④ C. ①②④ D. ③④
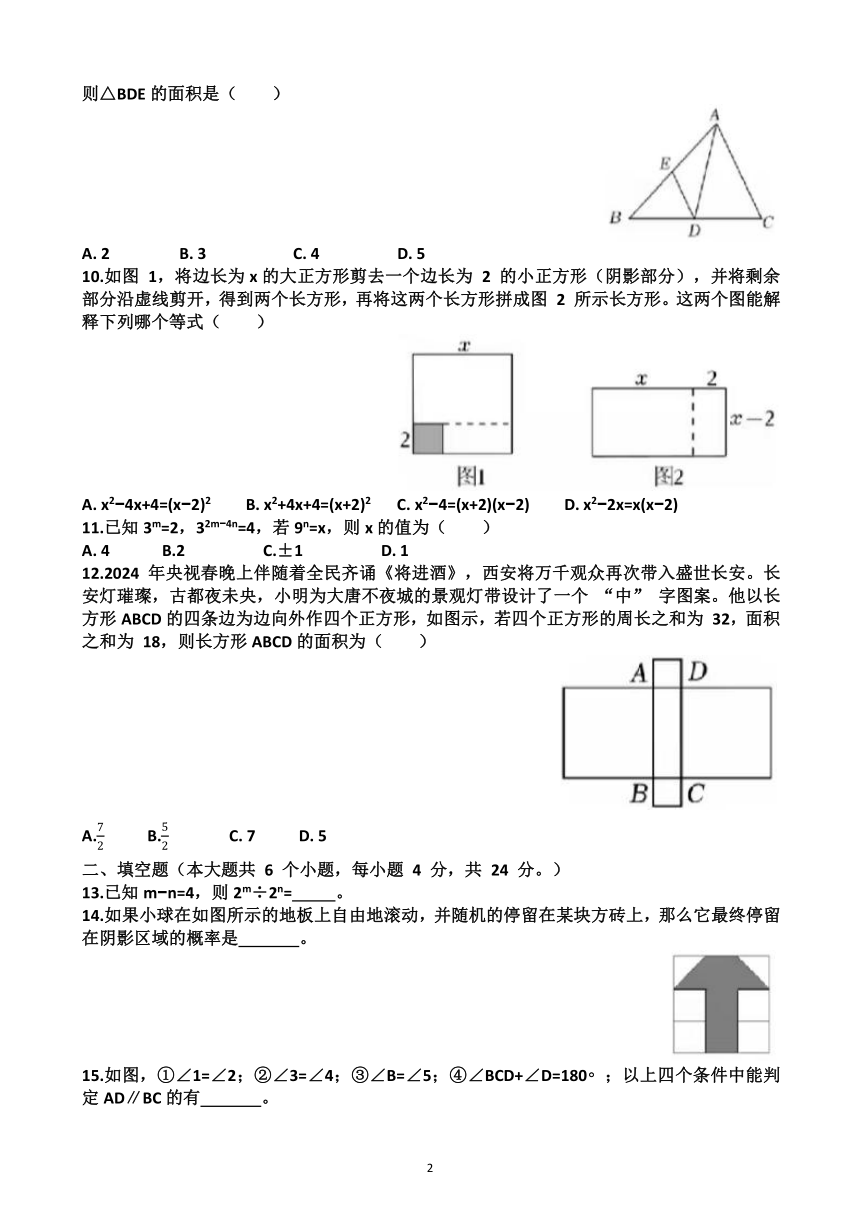
9.如图,在△ABC中,点D,E分别是边BC,AB的中点,连接AD,DE。若△ABC的面积是 8,则△BDE的面积是( )
A. 2 B. 3 C. 4 D. 5
10.如图 1,将边长为x的大正方形剪去一个边长为 2 的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图 2 所示长方形。这两个图能解释下列哪个等式( )
A. x2 4x+4=(x 2)2 B. x2+4x+4=(x+2)2 C. x2 4=(x+2)(x 2) D. x2 2x=x(x 2)
11.已知3m=2,32m 4n=4,若9n=x,则x的值为( )
A. 4 B.2 C.±1 D. 1
12.2024 年央视春晚上伴随着全民齐诵《将进酒》,西安将万千观众再次带入盛世长安。长安灯璀璨,古都夜未央,小明为大唐不夜城的景观灯带设计了一个 “中” 字图案。他以长方形ABCD的四条边为边向外作四个正方形,如图示,若四个正方形的周长之和为 32,面积之和为 18,则长方形ABCD的面积为( )
A. B. C. 7 D. 5
二、填空题(本大题共 6 个小题,每小题 4 分,共 24 分。)
13.已知m n=4,则2m÷2n= 。
14.如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是 。
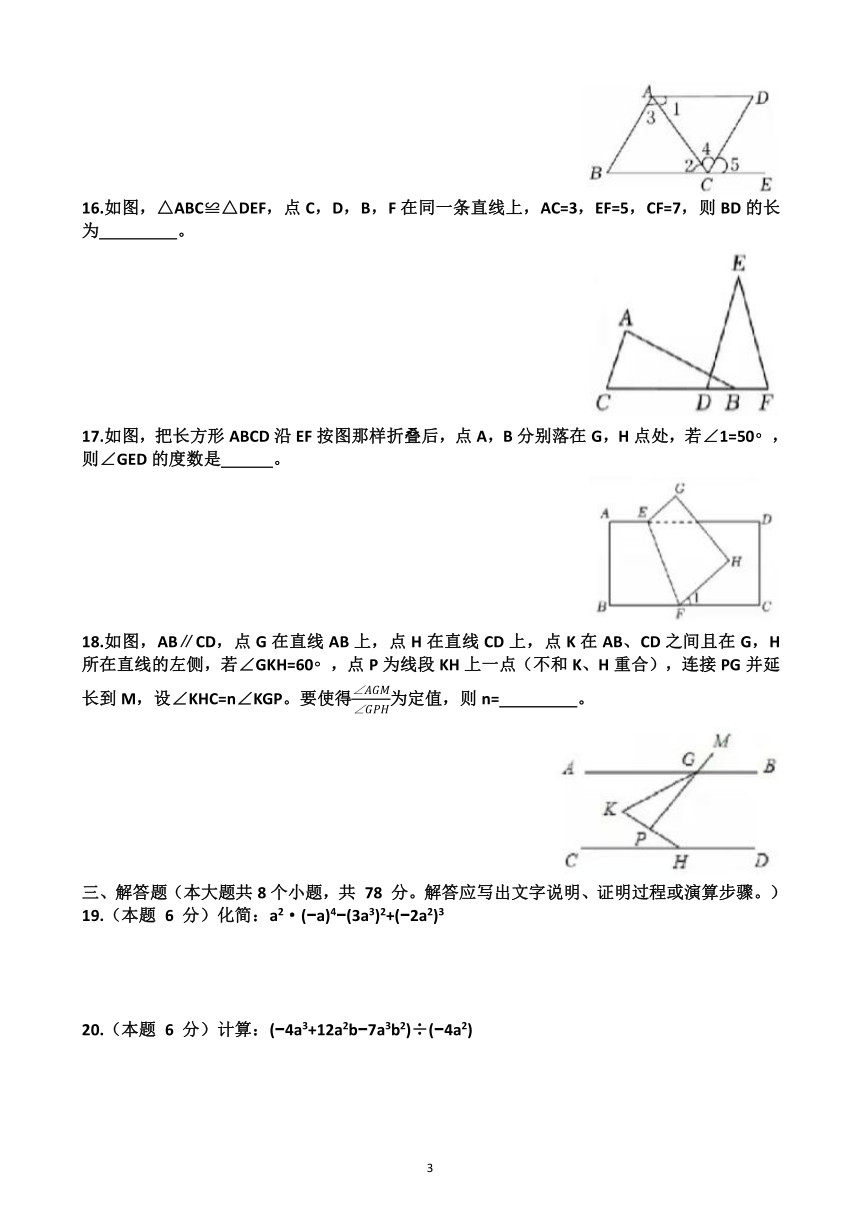
15.如图,①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠BCD+∠D=180 ;以上四个条件中能判定AD∥BC的有 。
16.如图,△ABC≌△DEF,点C,D,B,F在同一条直线上,AC=3,EF=5,CF=7,则BD的长为 。
17.如图,把长方形ABCD沿EF按图那样折叠后,点A,B分别落在G,H点处,若∠1=50 ,则∠GED的度数是 。
18.如图,AB∥CD,点G在直线AB上,点H在直线CD上,点K在AB、CD之间且在G,H所在直线的左侧,若∠GKH=60 ,点P为线段KH上一点(不和K、H重合),连接PG并延长到M,设∠KHC=n∠KGP。要使得为定值,则n= 。
三、解答题(本大题共8个小题,共 78 分。解答应写出文字说明、证明过程或演算步骤。)
19.(本题 6 分)化简:a2·( a)4 (3a3)2+( 2a2)3
20.(本题 6 分)计算:( 4a3+12a2b 7a3b2)÷( 4a2)
21.(本题 5 分)先化简,再求值:(x 2y)2 (x y)(x+y),其中x=2,y= 1
22.(本题 4 分)推理填空:
如图,AD∥BC,AE∥DC,点E在线段BC上,点F在射线BA上,若∠B=∠C,则AD平分∠FAE,请说明理由。
解:理由如下:
∵AD∥BC
∴∠DAE=∠AEB。(两直线平行,内错角相等)
又∵AE∥DC
∴∠AEB=∠ ,( )
∴∠DAE=∠C。(等量代换)
又∵∠B=∠C
∴∠DAE=∠B
∵AD∥BC
∴∠FAD=∠ ,(两直线平行,同位角相等)
∴∠FAD=∠ 。(等量代换)
∴AD平分∠FAE
23.(本题 5 分)如图在△ABC中,∠ABC=24 ,∠ACB=118 ,AD平分∠BAC,AE⊥BC于点E,求∠DAE的度数。
24.(本题 6 分)如图,在△ABC中,AB∥DG,∠1+∠2=180 。
(1)求证:AD∥EF;
(2)若DG是∠ADC的平分线,∠2=150 ,求∠B的度数。
25.(本题 6 分)口袋中有 5 张完全相同的卡片,分别写有 2cm,3cm,4cm,5cm 和 6cm,口袋外有 2 张卡片,分别写有 4cm 和 6cm,现随机从袋中取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度。回答下列问题。
(1)根据题目要求,写出组合成的三条线段的长度的所有可能的结果;
(2)求这三条线段能构成三角形的概率;
(3)求这三条线段能构成等腰三角形的概率。
26.(本题 8 分)如图,某小区有一块长为(2a+4b)米,宽为(2a b)米的长方形地块,角上有四个边长为(a b)米的小正方形空地,开发商计划将阴影部分进行绿化。
(1)用含有a、b的式子表示绿化的总面积(结果写成最简形式);
(2)物业找来阳光绿化团队完成此项绿化任务,已知该队每小时可绿化8b平方米,每小时收费 200 元,则该物业应该支付绿化队多少费用?(用含a、b的代数式表示)
27.(本题 10 分)(1)填空:(a b)(a+b)= ;
(a b)(a2+ab+b2)= ;
(a b)(a3+a2b+ab2+b3)= 。
(2)猜想:(a b)(an 1+an 2b+...+abn 2+bn 1)= 。(其中n为正整数,且n≥2)。
(3)利用(2)猜想的结论计算:
①27+26+25+24+23+22+2+1;
②29 28+27 ...+23 22+2。
28.(本题 10 分)
【阅读材料】若x满足(8 x)(x 3)=4,求(8 x)2+(x 3)2的值。
解:设8 x=a,x 3=b。则(8 x)(x 3)=ab=4,a+b=8 x+(x 3)=5。
∴(8 x)2+(x 3)2=a2+b2=(a+b)2 2ab=52 2×4=17。
【类比探究】解决下列问题:
(1)若x满足(4 x)(x 2)=1,则(4 x)2+(x 2)2的值为 。
(2)若(n 2022)2+(2025 n)2=4,求(n 2022)(2025 n)的值。
【拓展应用】
(3)已知正方形ABCD的边长为x,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是 24,分别以MF,DF为边长作正方形MFRN和正方形GFDH,求阴影部分的面积。
29.(本题 12 分)如图,直线MN∥PQ,将一副三角板中的两块直角三角板如图 1 放置,∠ACB=∠EDF=90 ,∠ABC=∠BAC=45 ,∠DFE=30 ,∠DEF=60 ,此时点A与点E重合。
(1)对于图 1,固定△ABC的位置不变,将△DEF绕点E按顺时针方向进行旋转,旋转至DE与BC首次平行,如图 2 所示,求此时∠FAC的度数。
(2)对于图 1,固定△ABC的位置不变,将△DEF沿AC方向平移至点F正好落在直线MN上,再将△DEF绕点F按顺时针方向进行旋转,如图 3 所示。
①若边EF与边BC交于点G,试判断∠BGF ∠EFN的值是否为定值,若是定值,则求出该定值,若不是定值,请说明理由;
②对于图 3,固定△ABC的位置不变,将△DEF绕点F顺时针方向以每秒5 的速度进行旋转,当EF与直线MN首次重合时停止运动,当经过t秒时,线段DE与△ABC的一条边平行,求满足条件的t的值。
答案
一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.下列图形中,∠1与∠2一定相等的是( B )
2.“春江潮水连海平,海上明月共潮生”,水是诗人钟爱的意象,经测算,一个水分子的直径约为 0.0000004mm,数据 0.0000004 用科学记数法表示为( A )
A. 4×10 7 B. 4×10 8 C. 0.4×10 7 D. 0.4×10 8
3.下列运算错误的是( C )
A. b2·b3=b5 B. (a b)(b+a)=a2 b2 C. a5+b5=a10 D. ( a2b)2=b2a4
4.如图,把三角尺的直角顶点放在直尺的一边上,若∠1=28 ,则∠2的度数为( B )
A. 68 B.62 C. 52 D. 28
5.掷一枚质地均匀的硬币 200 次,下列说法正确的是( D )
A. 不可能 200 次正面朝上 B. 不可能 100 次正面朝上
C. 必有 100 次正面朝上 D. 可能 100 次正面朝上
6.如果x2+(n 3)x+16是个完全平方式,那么n的值是( C )
A. 11 B. -5 C. 11 或 -5 D. ±8
7.如图所示,△ABC≌△DBE。若∠E=70 ,∠A=20 ,则( D )
A.10 B. 30 C. 70 D. 90
8.下列说法:①三角形的高、中线、角平分线都是线段;②垂直于同一条直线的两条直线互相平行;③两条平行直线被第三条直线所截,同位角相等;④因为∠1=∠2,∠2=∠3,所以∠1=∠3。其中正确的是( A )
A. ①③④ B. ②③④ C. ①②④ D. ③④
9.如图,在△ABC中,点D,E分别是边BC,AB的中点,连接AD,DE。若△ABC的面积是 8,则△BDE的面积是( A )
A. 2 B. 3 C. 4 D. 5
10.如图 1,将边长为x的大正方形剪去一个边长为 2 的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图 2 所示长方形。这两个图能解释下列哪个等式( C )
A. x2 4x+4=(x 2)2 B. x2+4x+4=(x+2)2 C. x2 4=(x+2)(x 2) D. x2 2x=x(x 2)
11.已知3m=2,32m 4n=4,若9n=x,则x的值为( D )
A. 4 B.2 C.±1 D. 1
12.2024 年央视春晚上伴随着全民齐诵《将进酒》,西安将万千观众再次带入盛世长安。长安灯璀璨,古都夜未央,小明为大唐不夜城的景观灯带设计了一个 “中” 字图案。他以长方形ABCD的四条边为边向外作四个正方形,如图示,若四个正方形的周长之和为 32,面积之和为 18,则长方形ABCD的面积为( A )
A. B. C. 7 D. 5
二、填空题(本大题共 6 个小题,每小题 4 分,共 24 分。)
13.已知m n=4,则2m÷2n= 16 。
14.如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是 。
15.如图,①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠BCD+∠D=180 ;以上四个条件中能判定AD∥BC的②④。
16.如图,△ABC≌△DEF,点C,D,B,F在同一条直线上,AC=3,EF=5,CF=7,则BD的长为 1 。
17.如图,把长方形ABCD沿EF按图那样折叠后,点A,B分别落在G,H点处,若∠1=50 ,则∠GED的度数是 80° 。
18.如图,AB∥CD,点G在直线AB上,点H在直线CD上,点K在AB、CD之间且在G,H所在直线的左侧,若∠GKH=60 ,点P为线段KH上一点(不和K、H重合),连接PG并延长到M,设∠KHC=n∠KGP。要使得为定值,则n= 3 。
三、解答题(本大题共8个小题,共 78 分。解答应写出文字说明、证明过程或演算步骤。)
19.(本题 6 分)化简:a2·( a)4 (3a3)2+( 2a2)3
=a6﹣9a6﹣8a6
=﹣16a6
20.(本题 6 分)计算:( 4a3+12a2b 7a3b2)÷( 4a2)
=a﹣3b+ab2
21.(本题 5 分)先化简,再求值:(x 2y)2 (x y)(x+y),其中x=2,y= 1
解原式=x2﹣4xy+4y2﹣x2+y2
=﹣4xy+5y2
将x=2,y= 1代入得8+5=13
22.(本题 4 分)推理填空:
如图,AD∥BC,AE∥DC,点E在线段BC上,点F在射线BA上,若∠B=∠C,则AD平分∠FAE,请说明理由。
解:理由如下:
∵AD∥BC
∴∠DAE=∠AEB。(两直线平行,内错角相等)
又∵AE∥DC
∴∠AEB=∠ C ,( 两直线平行,同位角相等 )
∴∠DAE=∠C。(等量代换)
又∵∠B=∠C
∴∠DAE=∠B
∵AD∥BC
∴∠FAD=∠ B ,(两直线平行,同位角相等)
∴∠FAD=∠ DAE 。(等量代换)
∴AD平分∠FAE
23.(本题 5 分)如图在△ABC中,∠ABC=24 ,∠ACB=118 ,AD平分∠BAC,AE⊥BC于点E,求∠DAE的度数。
∵在三角形 ABC 中知∠ABC =24°,∠ACB =118°
∴∠BAC =180°-∠ABC -∠ACB =180°-24°-118°=38°
又∵AD 平分 LBAC ,
∴∠DAC =∠BAC =19°.
又∵∠BCA 是三角形ACE 的一个外角,∠ACB =118°,∠AEB =90°
∴∠CAE +∠BEA =∠ACB,即∠CAE =28°.
由题意知∠DAE =∠DAC +∠CAE ,
∴∠DAE=19°+28°=47°.
24.(本题 6 分)如图,在△ABC中,AB∥DG,∠1+∠2=180 。
(1)求证:AD∥EF;
(2)若DG是∠ADC的平分线,∠2=150 ,求∠B的度数。
(1)证明:∵AB // DG
∴∠BAD =∠1
∵∠1+∠2=180°
∴∠2+∠BAD =180°
∴AD // EF ;
(2)∵∠1+∠2=180°,∠2=150°
∴∠1=30°
∵DG 是∠ADC 的平分线
∴∠GDC =∠1=30°
∵AB // DG
∴∠B =∠GDC =30°.
25.(本题 6 分)口袋中有 5 张完全相同的卡片,分别写有 2cm,3cm,4cm,5cm 和 6cm,口袋外有 2 张卡片,分别写有 4cm 和 6cm,现随机从袋中取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度。回答下列问题。
(1)根据题目要求,写出组合成的三条线段的长度的所有可能的结果;
(2)求这三条线段能构成三角形的概率;
(3)求这三条线段能构成等腰三角形的概率。
(1)共有5种可能的结果数,它们是:2、4、6;6、4、6;4、4、6;5、4、6;6、4、6;
(2)这三条线段能构成一个三角形的结果数为4,4所以这三条线段能构成一个三角形的概率=
(3)这三条线段能构成等腰三角形的结果数3,所以这三条线段能构成等腰三角形的概率是
26.(本题 8 分)如图,某小区有一块长为(2a+4b)米,宽为(2a b)米的长方形地块,角上有四个边长为(a b)米的小正方形空地,开发商计划将阴影部分进行绿化。
(1)用含有a、b的式子表示绿化的总面积(结果写成最简形式);
(2)物业找来阳光绿化团队完成此项绿化任务,已知该队每小时可绿化8b平方米,每小时收费 200 元,则该物业应该支付绿化队多少费用?(用含a、b的代数式表示)
(1)根据题意得:
(2a- b )(2a+4b)-4(a-b )2
=4a2+8ab-2ab-4b2-4(a2-2ab+b2)
=4a2+6ab-4b-4a2+8ab-4b2
=(14ab-8b2)平方米,
答:绿化的面积是(14ab-8b2)平方米;
(2)根据题意得:
(14ab-8b2)+8bx200
=(a - b)x200
=(350a-2006)元,
答:该物业应该支付绿化队需要(350a-200b)元费用.
27.(本题 10 分)(1)填空:(a b)(a+b)= ;
(a b)(a2+ab+b2)= ;
(a b)(a3+a2b+ab2+b3)= 。
(2)猜想:(a b)(an 1+an 2b+...+abn 2+bn 1)= 。(其中n为正整数,且n≥2)。
(3)利用(2)猜想的结论计算:
①27+26+25+24+23+22+2+1;
②29 28+27 ...+23 22+2。
(1)a2﹣b2 a3﹣b3 a4﹣b4
(2)an﹣bn
(3)①=(2﹣1)(27+26+25+24+23+22+2+1)
=28﹣1
=255
②=[2﹣(﹣1)](29 28+27 ...+23 22+2﹣1)
=210﹣1
∴29 28+27 ...+23 22+2=342
28.(本题 10 分)
【阅读材料】若x满足(8 x)(x 3)=4,求(8 x)2+(x 3)2的值。
解:设8 x=a,x 3=b。则(8 x)(x 3)=ab=4,a+b=8 x+(x 3)=5。
∴(8 x)2+(x 3)2=a2+b2=(a+b)2 2ab=52 2×4=17。
【类比探究】解决下列问题:
(1)若x满足(4 x)(x 2)=1,则(4 x)2+(x 2)2的值为 。
(2)若(n 2022)2+(2025 n)2=4,求(n 2022)(2025 n)的值。
【拓展应用】
(3)已知正方形ABCD的边长为x,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是 24,分别以MF,DF为边长作正方形MFRN和正方形GFDH,求阴影部分的面积。
(1)2
(2)2.5
(3)阴影部分面积=(x﹣1)2﹣(x﹣3)2=10×2=20
29.(本题 12 分)如图,直线MN∥PQ,将一副三角板中的两块直角三角板如图 1 放置,∠ACB=∠EDF=90 ,∠ABC=∠BAC=45 ,∠DFE=30 ,∠DEF=60 ,此时点A与点E重合。
(1)对于图 1,固定△ABC的位置不变,将△DEF绕点E按顺时针方向进行旋转,旋转至DE与BC首次平行,如图 2 所示,求此时∠FAC的度数。
(2)对于图 1,固定△ABC的位置不变,将△DEF沿AC方向平移至点F正好落在直线MN上,再将△DEF绕点F按顺时针方向进行旋转,如图 3 所示。
①若边EF与边BC交于点G,试判断∠BGF ∠EFN的值是否为定值,若是定值,则求出该定值,若不是定值,请说明理由;
②对于图 3,固定△ABC的位置不变,将△DEF绕点F顺时针方向以每秒5 的速度进行旋转,当EF与直线MN首次重合时停止运动,当经过t秒时,线段DE与△ABC的一条边平行,求满足条件的t的值。
启点:
(1)∵DE // BC ,
∴∠CED =∠BCA =90°
∴∠FAC =∠CED -∠F AD =90°-60°=30°
(2)①过点 G 作直线HL // MN ,则HL // PQ .
∴∠HGF =∠EFN ,∠BGH =∠ABC
∴∠BGF =∠HGF +∠BGH =∠EFN +∠ABC
∴∠BGF -∠EFN =∠ABC =45°
②共分三种情况:
情况1:DE// BC 时,5t=30,. t =6.
情况2:DE// AB 时,5t=75, t =15.
情况3:DE// AC 时,5t=120,t =24.
综上, t =6或15或24.
注意事项
本试题分第 Ⅰ 卷(选择题)和第 Ⅱ 卷(非选择题)两部分。第 Ⅰ 卷共 2 页,满分为 48 分;第Ⅱ卷共 4 页,满分为 102 分。本试题共 6 页,满分为 150 分。考试时间为 120分钟。答卷前,考生务必用 0.5 毫米黑色墨水签字笔将自己的考点、姓名、准考证号、座号填写在答题卡上和试卷规定的位置上。考试结束后,将本试卷和答题卡一并交回。本考试不允许使用计算器。
一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.下列图形中,∠1与∠2一定相等的是( )
2.“春江潮水连海平,海上明月共潮生”,水是诗人钟爱的意象,经测算,一个水分子的直径约为 0.0000004mm,数据 0.0000004 用科学记数法表示为( )
A. 4×10 7 B. 4×10 8 C. 0.4×10 7 D. 0.4×10 8
3.下列运算错误的是( )
A. b2·b3=b5 B. (a b)(b+a)=a2 b2 C. a5+b5=a10 D. ( a2b)2=b2a4
4.如图,把三角尺的直角顶点放在直尺的一边上,若∠1=28 ,则∠2的度数为( )
A. 68 B.62 C. 52 D. 28
5.掷一枚质地均匀的硬币 200 次,下列说法正确的是( )
A. 不可能 200 次正面朝上 B. 不可能 100 次正面朝上
C. 必有 100 次正面朝上 D. 可能 100 次正面朝上
6.如果x2+(n 3)x+16是个完全平方式,那么n的值是( )
A. 11 B. -5 C. 11 或 -5 D. ±8
7.如图所示,△ABC≌△DBE。若∠E=70 ,∠A=20 ,则( )
A.10 B. 30 C. 70 D. 90
8.下列说法:①三角形的高、中线、角平分线都是线段;②垂直于同一条直线的两条直线互相平行;③两条平行直线被第三条直线所截,同位角相等;④因为∠1=∠2,∠2=∠3,所以∠1=∠3。其中正确的是( )
A. ①③④ B. ②③④ C. ①②④ D. ③④
9.如图,在△ABC中,点D,E分别是边BC,AB的中点,连接AD,DE。若△ABC的面积是 8,则△BDE的面积是( )
A. 2 B. 3 C. 4 D. 5
10.如图 1,将边长为x的大正方形剪去一个边长为 2 的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图 2 所示长方形。这两个图能解释下列哪个等式( )
A. x2 4x+4=(x 2)2 B. x2+4x+4=(x+2)2 C. x2 4=(x+2)(x 2) D. x2 2x=x(x 2)
11.已知3m=2,32m 4n=4,若9n=x,则x的值为( )
A. 4 B.2 C.±1 D. 1
12.2024 年央视春晚上伴随着全民齐诵《将进酒》,西安将万千观众再次带入盛世长安。长安灯璀璨,古都夜未央,小明为大唐不夜城的景观灯带设计了一个 “中” 字图案。他以长方形ABCD的四条边为边向外作四个正方形,如图示,若四个正方形的周长之和为 32,面积之和为 18,则长方形ABCD的面积为( )
A. B. C. 7 D. 5
二、填空题(本大题共 6 个小题,每小题 4 分,共 24 分。)
13.已知m n=4,则2m÷2n= 。
14.如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是 。
15.如图,①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠BCD+∠D=180 ;以上四个条件中能判定AD∥BC的有 。
16.如图,△ABC≌△DEF,点C,D,B,F在同一条直线上,AC=3,EF=5,CF=7,则BD的长为 。
17.如图,把长方形ABCD沿EF按图那样折叠后,点A,B分别落在G,H点处,若∠1=50 ,则∠GED的度数是 。
18.如图,AB∥CD,点G在直线AB上,点H在直线CD上,点K在AB、CD之间且在G,H所在直线的左侧,若∠GKH=60 ,点P为线段KH上一点(不和K、H重合),连接PG并延长到M,设∠KHC=n∠KGP。要使得为定值,则n= 。
三、解答题(本大题共8个小题,共 78 分。解答应写出文字说明、证明过程或演算步骤。)
19.(本题 6 分)化简:a2·( a)4 (3a3)2+( 2a2)3
20.(本题 6 分)计算:( 4a3+12a2b 7a3b2)÷( 4a2)
21.(本题 5 分)先化简,再求值:(x 2y)2 (x y)(x+y),其中x=2,y= 1
22.(本题 4 分)推理填空:
如图,AD∥BC,AE∥DC,点E在线段BC上,点F在射线BA上,若∠B=∠C,则AD平分∠FAE,请说明理由。
解:理由如下:
∵AD∥BC
∴∠DAE=∠AEB。(两直线平行,内错角相等)
又∵AE∥DC
∴∠AEB=∠ ,( )
∴∠DAE=∠C。(等量代换)
又∵∠B=∠C
∴∠DAE=∠B
∵AD∥BC
∴∠FAD=∠ ,(两直线平行,同位角相等)
∴∠FAD=∠ 。(等量代换)
∴AD平分∠FAE
23.(本题 5 分)如图在△ABC中,∠ABC=24 ,∠ACB=118 ,AD平分∠BAC,AE⊥BC于点E,求∠DAE的度数。
24.(本题 6 分)如图,在△ABC中,AB∥DG,∠1+∠2=180 。
(1)求证:AD∥EF;
(2)若DG是∠ADC的平分线,∠2=150 ,求∠B的度数。
25.(本题 6 分)口袋中有 5 张完全相同的卡片,分别写有 2cm,3cm,4cm,5cm 和 6cm,口袋外有 2 张卡片,分别写有 4cm 和 6cm,现随机从袋中取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度。回答下列问题。
(1)根据题目要求,写出组合成的三条线段的长度的所有可能的结果;
(2)求这三条线段能构成三角形的概率;
(3)求这三条线段能构成等腰三角形的概率。
26.(本题 8 分)如图,某小区有一块长为(2a+4b)米,宽为(2a b)米的长方形地块,角上有四个边长为(a b)米的小正方形空地,开发商计划将阴影部分进行绿化。
(1)用含有a、b的式子表示绿化的总面积(结果写成最简形式);
(2)物业找来阳光绿化团队完成此项绿化任务,已知该队每小时可绿化8b平方米,每小时收费 200 元,则该物业应该支付绿化队多少费用?(用含a、b的代数式表示)
27.(本题 10 分)(1)填空:(a b)(a+b)= ;
(a b)(a2+ab+b2)= ;
(a b)(a3+a2b+ab2+b3)= 。
(2)猜想:(a b)(an 1+an 2b+...+abn 2+bn 1)= 。(其中n为正整数,且n≥2)。
(3)利用(2)猜想的结论计算:
①27+26+25+24+23+22+2+1;
②29 28+27 ...+23 22+2。
28.(本题 10 分)
【阅读材料】若x满足(8 x)(x 3)=4,求(8 x)2+(x 3)2的值。
解:设8 x=a,x 3=b。则(8 x)(x 3)=ab=4,a+b=8 x+(x 3)=5。
∴(8 x)2+(x 3)2=a2+b2=(a+b)2 2ab=52 2×4=17。
【类比探究】解决下列问题:
(1)若x满足(4 x)(x 2)=1,则(4 x)2+(x 2)2的值为 。
(2)若(n 2022)2+(2025 n)2=4,求(n 2022)(2025 n)的值。
【拓展应用】
(3)已知正方形ABCD的边长为x,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是 24,分别以MF,DF为边长作正方形MFRN和正方形GFDH,求阴影部分的面积。
29.(本题 12 分)如图,直线MN∥PQ,将一副三角板中的两块直角三角板如图 1 放置,∠ACB=∠EDF=90 ,∠ABC=∠BAC=45 ,∠DFE=30 ,∠DEF=60 ,此时点A与点E重合。
(1)对于图 1,固定△ABC的位置不变,将△DEF绕点E按顺时针方向进行旋转,旋转至DE与BC首次平行,如图 2 所示,求此时∠FAC的度数。
(2)对于图 1,固定△ABC的位置不变,将△DEF沿AC方向平移至点F正好落在直线MN上,再将△DEF绕点F按顺时针方向进行旋转,如图 3 所示。
①若边EF与边BC交于点G,试判断∠BGF ∠EFN的值是否为定值,若是定值,则求出该定值,若不是定值,请说明理由;
②对于图 3,固定△ABC的位置不变,将△DEF绕点F顺时针方向以每秒5 的速度进行旋转,当EF与直线MN首次重合时停止运动,当经过t秒时,线段DE与△ABC的一条边平行,求满足条件的t的值。
答案
一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.下列图形中,∠1与∠2一定相等的是( B )
2.“春江潮水连海平,海上明月共潮生”,水是诗人钟爱的意象,经测算,一个水分子的直径约为 0.0000004mm,数据 0.0000004 用科学记数法表示为( A )
A. 4×10 7 B. 4×10 8 C. 0.4×10 7 D. 0.4×10 8
3.下列运算错误的是( C )
A. b2·b3=b5 B. (a b)(b+a)=a2 b2 C. a5+b5=a10 D. ( a2b)2=b2a4
4.如图,把三角尺的直角顶点放在直尺的一边上,若∠1=28 ,则∠2的度数为( B )
A. 68 B.62 C. 52 D. 28
5.掷一枚质地均匀的硬币 200 次,下列说法正确的是( D )
A. 不可能 200 次正面朝上 B. 不可能 100 次正面朝上
C. 必有 100 次正面朝上 D. 可能 100 次正面朝上
6.如果x2+(n 3)x+16是个完全平方式,那么n的值是( C )
A. 11 B. -5 C. 11 或 -5 D. ±8
7.如图所示,△ABC≌△DBE。若∠E=70 ,∠A=20 ,则( D )
A.10 B. 30 C. 70 D. 90
8.下列说法:①三角形的高、中线、角平分线都是线段;②垂直于同一条直线的两条直线互相平行;③两条平行直线被第三条直线所截,同位角相等;④因为∠1=∠2,∠2=∠3,所以∠1=∠3。其中正确的是( A )
A. ①③④ B. ②③④ C. ①②④ D. ③④
9.如图,在△ABC中,点D,E分别是边BC,AB的中点,连接AD,DE。若△ABC的面积是 8,则△BDE的面积是( A )
A. 2 B. 3 C. 4 D. 5
10.如图 1,将边长为x的大正方形剪去一个边长为 2 的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图 2 所示长方形。这两个图能解释下列哪个等式( C )
A. x2 4x+4=(x 2)2 B. x2+4x+4=(x+2)2 C. x2 4=(x+2)(x 2) D. x2 2x=x(x 2)
11.已知3m=2,32m 4n=4,若9n=x,则x的值为( D )
A. 4 B.2 C.±1 D. 1
12.2024 年央视春晚上伴随着全民齐诵《将进酒》,西安将万千观众再次带入盛世长安。长安灯璀璨,古都夜未央,小明为大唐不夜城的景观灯带设计了一个 “中” 字图案。他以长方形ABCD的四条边为边向外作四个正方形,如图示,若四个正方形的周长之和为 32,面积之和为 18,则长方形ABCD的面积为( A )
A. B. C. 7 D. 5
二、填空题(本大题共 6 个小题,每小题 4 分,共 24 分。)
13.已知m n=4,则2m÷2n= 16 。
14.如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是 。
15.如图,①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠BCD+∠D=180 ;以上四个条件中能判定AD∥BC的②④。
16.如图,△ABC≌△DEF,点C,D,B,F在同一条直线上,AC=3,EF=5,CF=7,则BD的长为 1 。
17.如图,把长方形ABCD沿EF按图那样折叠后,点A,B分别落在G,H点处,若∠1=50 ,则∠GED的度数是 80° 。
18.如图,AB∥CD,点G在直线AB上,点H在直线CD上,点K在AB、CD之间且在G,H所在直线的左侧,若∠GKH=60 ,点P为线段KH上一点(不和K、H重合),连接PG并延长到M,设∠KHC=n∠KGP。要使得为定值,则n= 3 。
三、解答题(本大题共8个小题,共 78 分。解答应写出文字说明、证明过程或演算步骤。)
19.(本题 6 分)化简:a2·( a)4 (3a3)2+( 2a2)3
=a6﹣9a6﹣8a6
=﹣16a6
20.(本题 6 分)计算:( 4a3+12a2b 7a3b2)÷( 4a2)
=a﹣3b+ab2
21.(本题 5 分)先化简,再求值:(x 2y)2 (x y)(x+y),其中x=2,y= 1
解原式=x2﹣4xy+4y2﹣x2+y2
=﹣4xy+5y2
将x=2,y= 1代入得8+5=13
22.(本题 4 分)推理填空:
如图,AD∥BC,AE∥DC,点E在线段BC上,点F在射线BA上,若∠B=∠C,则AD平分∠FAE,请说明理由。
解:理由如下:
∵AD∥BC
∴∠DAE=∠AEB。(两直线平行,内错角相等)
又∵AE∥DC
∴∠AEB=∠ C ,( 两直线平行,同位角相等 )
∴∠DAE=∠C。(等量代换)
又∵∠B=∠C
∴∠DAE=∠B
∵AD∥BC
∴∠FAD=∠ B ,(两直线平行,同位角相等)
∴∠FAD=∠ DAE 。(等量代换)
∴AD平分∠FAE
23.(本题 5 分)如图在△ABC中,∠ABC=24 ,∠ACB=118 ,AD平分∠BAC,AE⊥BC于点E,求∠DAE的度数。
∵在三角形 ABC 中知∠ABC =24°,∠ACB =118°
∴∠BAC =180°-∠ABC -∠ACB =180°-24°-118°=38°
又∵AD 平分 LBAC ,
∴∠DAC =∠BAC =19°.
又∵∠BCA 是三角形ACE 的一个外角,∠ACB =118°,∠AEB =90°
∴∠CAE +∠BEA =∠ACB,即∠CAE =28°.
由题意知∠DAE =∠DAC +∠CAE ,
∴∠DAE=19°+28°=47°.
24.(本题 6 分)如图,在△ABC中,AB∥DG,∠1+∠2=180 。
(1)求证:AD∥EF;
(2)若DG是∠ADC的平分线,∠2=150 ,求∠B的度数。
(1)证明:∵AB // DG
∴∠BAD =∠1
∵∠1+∠2=180°
∴∠2+∠BAD =180°
∴AD // EF ;
(2)∵∠1+∠2=180°,∠2=150°
∴∠1=30°
∵DG 是∠ADC 的平分线
∴∠GDC =∠1=30°
∵AB // DG
∴∠B =∠GDC =30°.
25.(本题 6 分)口袋中有 5 张完全相同的卡片,分别写有 2cm,3cm,4cm,5cm 和 6cm,口袋外有 2 张卡片,分别写有 4cm 和 6cm,现随机从袋中取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度。回答下列问题。
(1)根据题目要求,写出组合成的三条线段的长度的所有可能的结果;
(2)求这三条线段能构成三角形的概率;
(3)求这三条线段能构成等腰三角形的概率。
(1)共有5种可能的结果数,它们是:2、4、6;6、4、6;4、4、6;5、4、6;6、4、6;
(2)这三条线段能构成一个三角形的结果数为4,4所以这三条线段能构成一个三角形的概率=
(3)这三条线段能构成等腰三角形的结果数3,所以这三条线段能构成等腰三角形的概率是
26.(本题 8 分)如图,某小区有一块长为(2a+4b)米,宽为(2a b)米的长方形地块,角上有四个边长为(a b)米的小正方形空地,开发商计划将阴影部分进行绿化。
(1)用含有a、b的式子表示绿化的总面积(结果写成最简形式);
(2)物业找来阳光绿化团队完成此项绿化任务,已知该队每小时可绿化8b平方米,每小时收费 200 元,则该物业应该支付绿化队多少费用?(用含a、b的代数式表示)
(1)根据题意得:
(2a- b )(2a+4b)-4(a-b )2
=4a2+8ab-2ab-4b2-4(a2-2ab+b2)
=4a2+6ab-4b-4a2+8ab-4b2
=(14ab-8b2)平方米,
答:绿化的面积是(14ab-8b2)平方米;
(2)根据题意得:
(14ab-8b2)+8bx200
=(a - b)x200
=(350a-2006)元,
答:该物业应该支付绿化队需要(350a-200b)元费用.
27.(本题 10 分)(1)填空:(a b)(a+b)= ;
(a b)(a2+ab+b2)= ;
(a b)(a3+a2b+ab2+b3)= 。
(2)猜想:(a b)(an 1+an 2b+...+abn 2+bn 1)= 。(其中n为正整数,且n≥2)。
(3)利用(2)猜想的结论计算:
①27+26+25+24+23+22+2+1;
②29 28+27 ...+23 22+2。
(1)a2﹣b2 a3﹣b3 a4﹣b4
(2)an﹣bn
(3)①=(2﹣1)(27+26+25+24+23+22+2+1)
=28﹣1
=255
②=[2﹣(﹣1)](29 28+27 ...+23 22+2﹣1)
=210﹣1
∴29 28+27 ...+23 22+2=342
28.(本题 10 分)
【阅读材料】若x满足(8 x)(x 3)=4,求(8 x)2+(x 3)2的值。
解:设8 x=a,x 3=b。则(8 x)(x 3)=ab=4,a+b=8 x+(x 3)=5。
∴(8 x)2+(x 3)2=a2+b2=(a+b)2 2ab=52 2×4=17。
【类比探究】解决下列问题:
(1)若x满足(4 x)(x 2)=1,则(4 x)2+(x 2)2的值为 。
(2)若(n 2022)2+(2025 n)2=4,求(n 2022)(2025 n)的值。
【拓展应用】
(3)已知正方形ABCD的边长为x,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是 24,分别以MF,DF为边长作正方形MFRN和正方形GFDH,求阴影部分的面积。
(1)2
(2)2.5
(3)阴影部分面积=(x﹣1)2﹣(x﹣3)2=10×2=20
29.(本题 12 分)如图,直线MN∥PQ,将一副三角板中的两块直角三角板如图 1 放置,∠ACB=∠EDF=90 ,∠ABC=∠BAC=45 ,∠DFE=30 ,∠DEF=60 ,此时点A与点E重合。
(1)对于图 1,固定△ABC的位置不变,将△DEF绕点E按顺时针方向进行旋转,旋转至DE与BC首次平行,如图 2 所示,求此时∠FAC的度数。
(2)对于图 1,固定△ABC的位置不变,将△DEF沿AC方向平移至点F正好落在直线MN上,再将△DEF绕点F按顺时针方向进行旋转,如图 3 所示。
①若边EF与边BC交于点G,试判断∠BGF ∠EFN的值是否为定值,若是定值,则求出该定值,若不是定值,请说明理由;
②对于图 3,固定△ABC的位置不变,将△DEF绕点F顺时针方向以每秒5 的速度进行旋转,当EF与直线MN首次重合时停止运动,当经过t秒时,线段DE与△ABC的一条边平行,求满足条件的t的值。
启点:
(1)∵DE // BC ,
∴∠CED =∠BCA =90°
∴∠FAC =∠CED -∠F AD =90°-60°=30°
(2)①过点 G 作直线HL // MN ,则HL // PQ .
∴∠HGF =∠EFN ,∠BGH =∠ABC
∴∠BGF =∠HGF +∠BGH =∠EFN +∠ABC
∴∠BGF -∠EFN =∠ABC =45°
②共分三种情况:
情况1:DE// BC 时,5t=30,. t =6.
情况2:DE// AB 时,5t=75, t =15.
情况3:DE// AC 时,5t=120,t =24.
综上, t =6或15或24.
同课章节目录
