2024-2025学年山东省济南历城区八年级第二学期数学期中考试试题(含答案)
文档属性
| 名称 | 2024-2025学年山东省济南历城区八年级第二学期数学期中考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 351.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 20:41:43 | ||
图片预览

文档简介
2024 - 2025 学年度第二学期期中质量检测八年级数学试题(2025.4)
(时间120分钟 满分150分)
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量。下面有关我国航天领域的图标,其图标是中心对称图形的是( )
2.下列等式从左到右的变形,属于因式分解的是( )
A. (a+4)(a 4)=a2 16 B.x2 4y2=(x+4y)(x 4y) C. x2 2x+1=x(x 1)+1 D. x2 8x+16=(x 4)2
3.不等式3x+1≤2x+2的解集在数轴上表示为( )
A. B.
C. D.
4.若a>b,则下列不等式变形正确的是( )
A. 1 3a<1 3b B. a 2
5.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,那么BC的长等于( )
A. 27 B. 50 C. 23 D. 13
6.若+a=1,则的值为( )
A. 3 B. 2 C. 1 D.
7.根据下列表格中的部分值信息,分式y可能是( )
A. B. C. D.
8.若关于x的分式方程=2+的解为正数,则满足条件的正整数m的值为( )
A. 1,2,3 B. 1,2 C. 1,3,4 D. 1,3
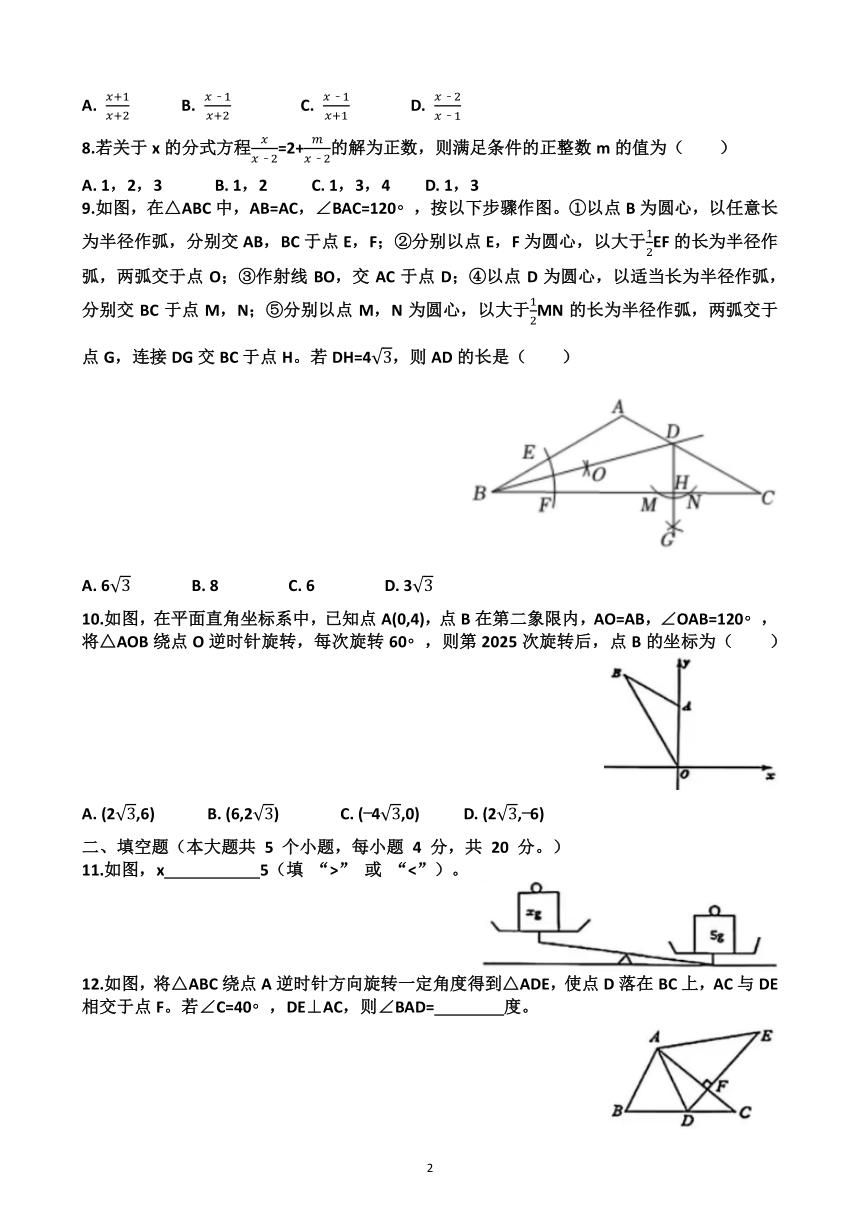
9.如图,在△ABC中,AB=AC,∠BAC=120 ,按以下步骤作图。①以点B为圆心,以任意长为半径作弧,分别交AB,BC于点E,F;②分别以点E,F为圆心,以大于EF的长为半径作弧,两弧交于点O;③作射线BO,交AC于点D;④以点D为圆心,以适当长为半径作弧,分别交BC于点M,N;⑤分别以点M,N为圆心,以大于MN的长为半径作弧,两弧交于点G,连接DG交BC于点H。若DH=4,则AD的长是( )
A. 6 B. 8 C. 6 D. 3
10.如图,在平面直角坐标系中,已知点A(0,4),点B在第二象限内,AO=AB,∠OAB=120 ,将△AOB绕点O逆时针旋转,每次旋转60 ,则第2025次旋转后,点B的坐标为( )
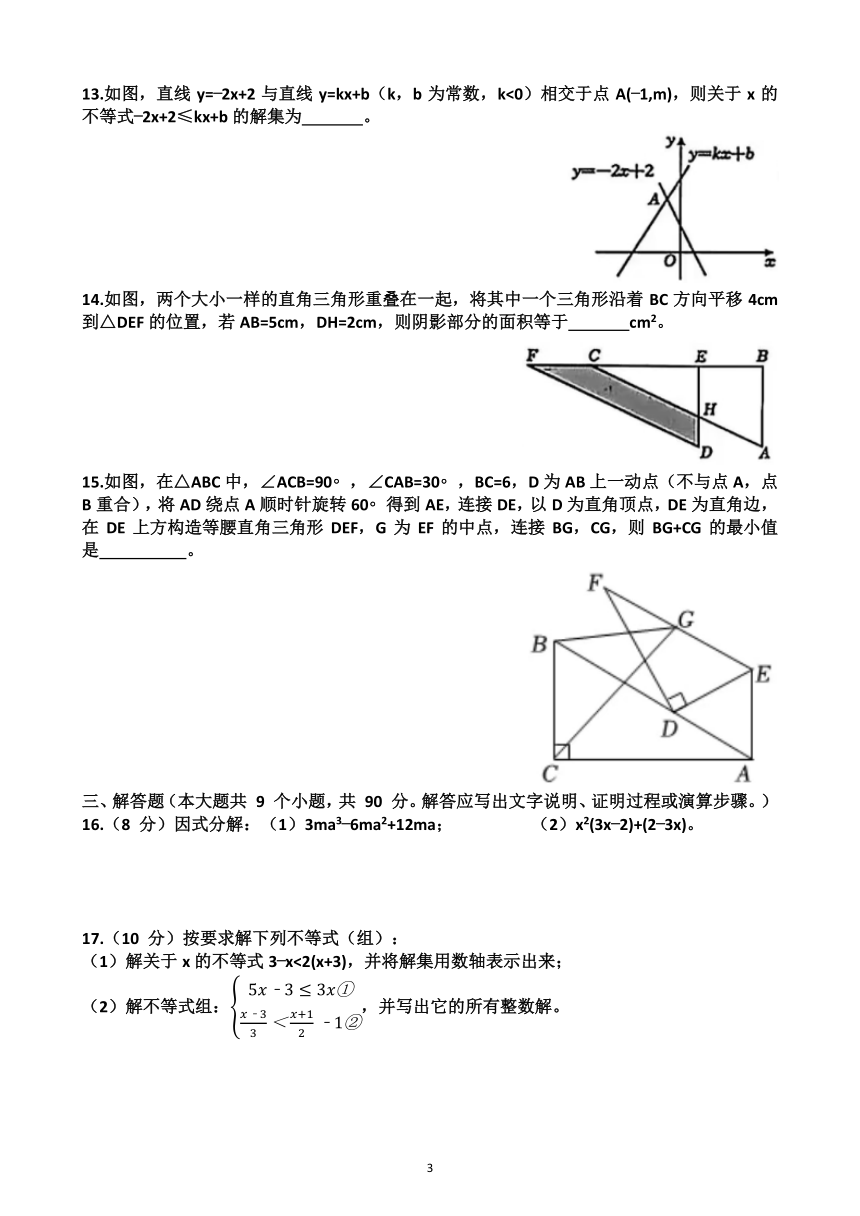
A. (2,6) B. (6,2) C. ( 4,0) D. (2, 6)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11.如图,x 5(填 “>” 或 “<”)。
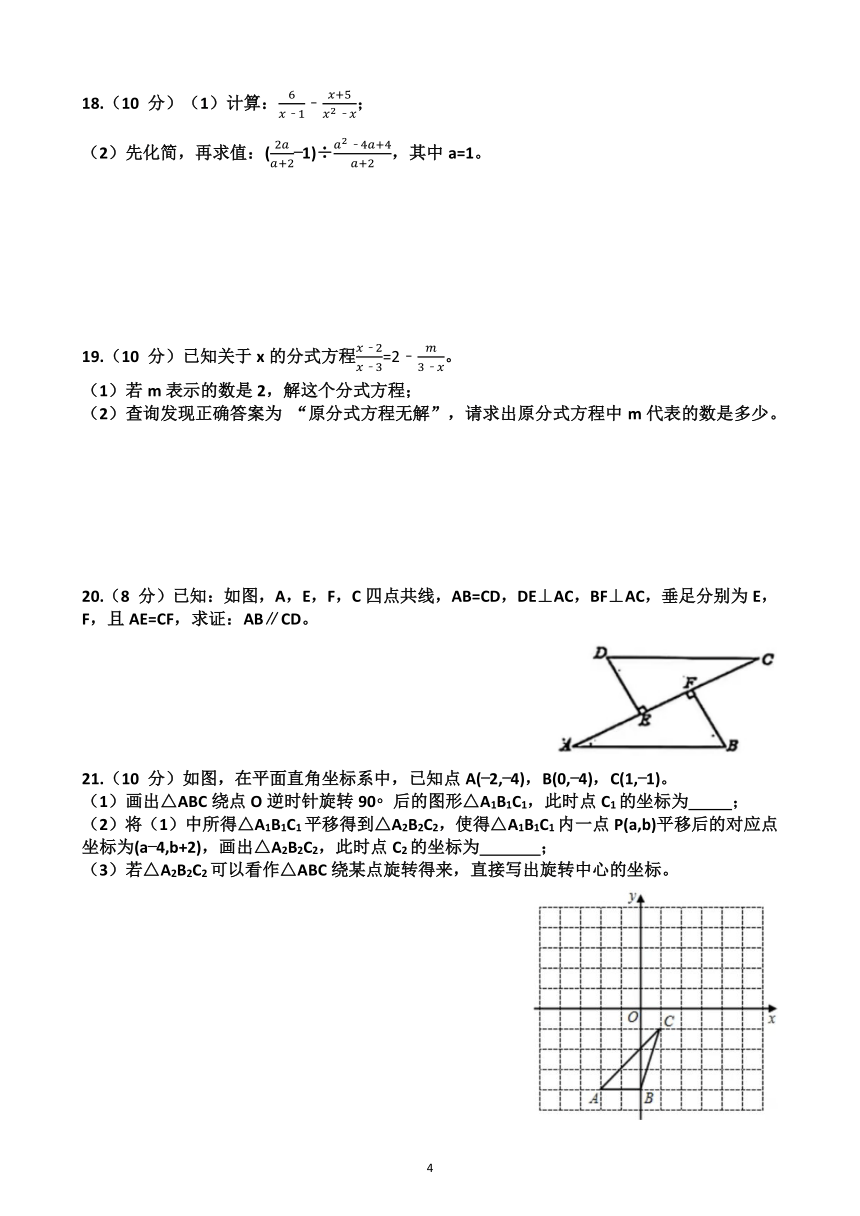
12.如图,将△ABC绕点A逆时针方向旋转一定角度得到△ADE,使点D落在BC上,AC与DE相交于点F。若∠C=40 ,DE⊥AC,则∠BAD= 度。
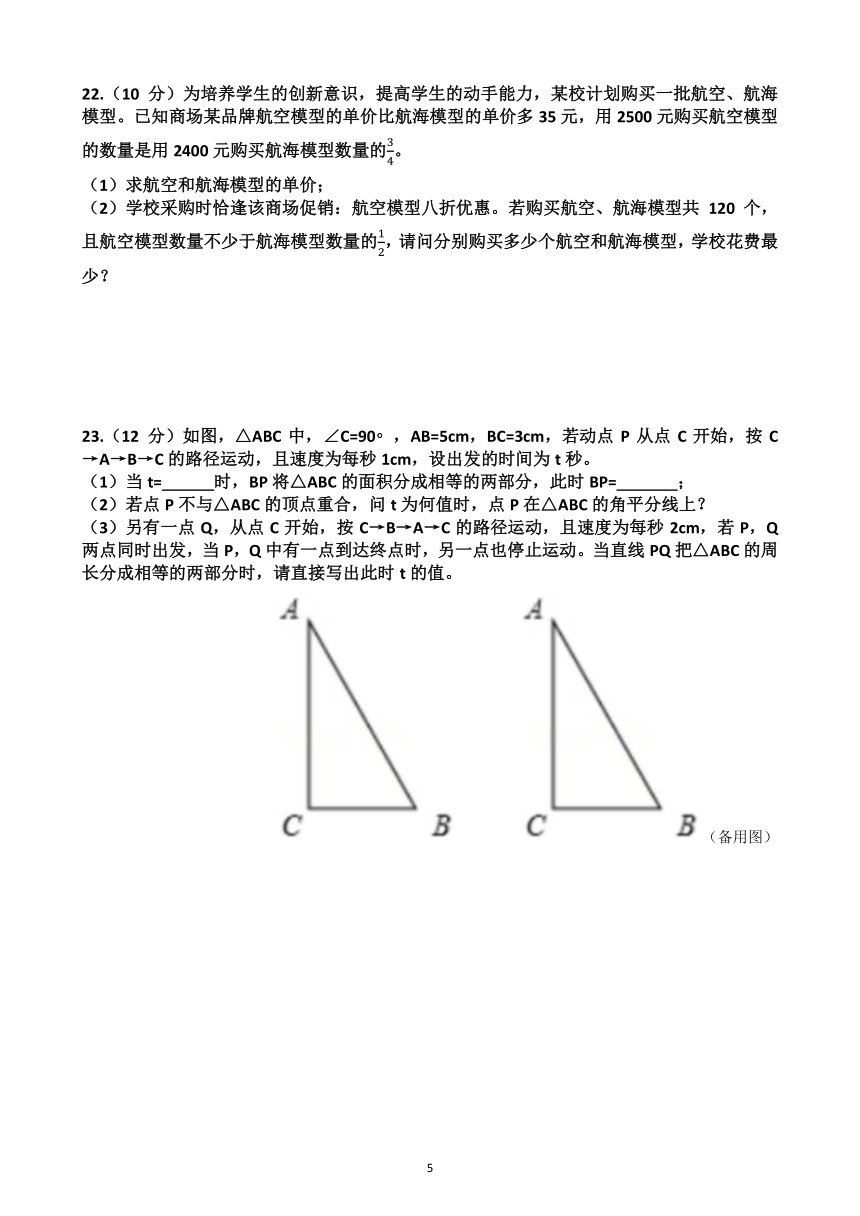
13.如图,直线y= 2x+2与直线y=kx+b(k,b为常数,k<0)相交于点A( 1,m),则关于x的不等式 2x+2≤kx+b的解集为 。
14.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着BC方向平移4cm到△DEF的位置,若AB=5cm,DH=2cm,则阴影部分的面积等于 cm2。
15.如图,在△ABC中,∠ACB=90 ,∠CAB=30 ,BC=6,D为AB上一动点(不与点A,点B重合),将AD绕点A顺时针旋转60 得到AE,连接DE,以D为直角顶点,DE为直角边,在DE上方构造等腰直角三角形DEF,G为EF的中点,连接BG,CG,则BG+CG的最小值是 。
三、解答题(本大题共 9 个小题,共 90 分。解答应写出文字说明、证明过程或演算步骤。)
16.(8 分)因式分解:(1)3ma3 6ma2+12ma; (2)x2(3x 2)+(2 3x)。
17.(10 分)按要求解下列不等式(组):
(1)解关于x的不等式3 x<2(x+3),并将解集用数轴表示出来;
(2)解不等式组:,并写出它的所有整数解。
18.(10 分)(1)计算:﹣;
(2)先化简,再求值:( 1)÷,其中a=1。
19.(10 分)已知关于x的分式方程=2﹣。
(1)若m表示的数是2,解这个分式方程;
(2)查询发现正确答案为 “原分式方程无解”,请求出原分式方程中m代表的数是多少。
20.(8 分)已知:如图,A,E,F,C四点共线,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且AE=CF,求证:AB∥CD。
21.(10 分)如图,在平面直角坐标系中,已知点A( 2, 4),B(0, 4),C(1, 1)。
(1)画出△ABC绕点O逆时针旋转90 后的图形△A1B1C1,此时点C1的坐标为 ;
(2)将(1)中所得△A1B1C1平移得到△A2B2C2,使得△A1B1C1内一点P(a,b)平移后的对应点坐标为(a 4,b+2),画出△A2B2C2,此时点C2的坐标为 ;
(3)若△A2B2C2可以看作△ABC绕某点旋转得来,直接写出旋转中心的坐标。
22.(10 分)为培养学生的创新意识,提高学生的动手能力,某校计划购买一批航空、航海模型。已知商场某品牌航空模型的单价比航海模型的单价多35元,用2500元购买航空模型的数量是用2400元购买航海模型数量的。
(1)求航空和航海模型的单价;
(2)学校采购时恰逢该商场促销:航空模型八折优惠。若购买航空、航海模型共120个,且航空模型数量不少于航海模型数量的,请问分别购买多少个航空和航海模型,学校花费最少?
23.(12 分)如图,△ABC中,∠C=90 ,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒。
(1)当t= 时,BP将△ABC的面积分成相等的两部分,此时BP= ;
(2)若点P不与△ABC的顶点重合,问t为何值时,点P在△ABC的角平分线上?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P,Q两点同时出发,当P,Q中有一点到达终点时,另一点也停止运动。当直线PQ把△ABC的周长分成相等的两部分时,请直接写出此时t的值。
(备用图)
24.(12 分)如图所示,△ABC为等腰三角形,AB=AC,点D是BC上一点,连接AD。
(1)当∠BAC=90 时,
①如图 1,若BD=2DC=4,把AD绕A顺时针旋转90 到AE,连接BE,DE,则DE= ;
②如图 2,将线段DC绕点D逆时针旋转90 到DE,点E落在AC上,连接BE,点O为线段BE的中点,连接AO,AD,此时AO与AD的数量关系为 ;
小明同学提出以下解决问题的思路,仅供大家参考:
延长AO到点F,使OF=OA,连接EF,DF,通过证明两组三角形全等,再进一步分析研究△ADF来解决问题;
(2)当∠BAC=120 时,
①如图 3,将线段DC绕点D逆时针旋转60 到DE,连接BE,点O为线段BE的中点,连接
AO,AD,此时AO与AD有怎样的数量关系,并说明理由;
②如图 4,点Q为△ABC内一点,若∠AQB=90 ,∠BQC=150 ,请直接写出的值。
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量。下面有关我国航天领域的图标,其图标是中心对称图形的是( C )
2.下列等式从左到右的变形,属于因式分解的是( D )
A. (a+4)(a 4)=a2 16 B.x2 4y2=(x+4y)(x 4y) C. x2 2x+1=x(x 1)+1 D. x2 8x+16=(x 4)2
3.不等式3x+1≤2x+2的解集在数轴上表示为( A )
A. B.
C. D.
4.若a>b,则下列不等式变形正确的是( A )
A. 1 3a<1 3b B. a 2
5.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,那么BC的长等于( C )
A. 27 B. 50 C. 23 D. 13
6.若+a=1,则的值为( B )
A. 3 B. 2 C. 1 D.
7.根据下列表格中的部分值信息,分式y可能是( B )
A. B. C. D.
8.若关于x的分式方程=2+的解为正数,则满足条件的正整数m的值为( D )
A. 1,2,3 B. 1,2 C. 1,3,4 D. 1,3
9.如图,在△ABC中,AB=AC,∠BAC=120 ,按以下步骤作图。①以点B为圆心,以任意长为半径作弧,分别交AB,BC于点E,F;②分别以点E,F为圆心,以大于EF的长为半径作弧,两弧交于点O;③作射线BO,交AC于点D;④以点D为圆心,以适当长为半径作弧,分别交BC于点M,N;⑤分别以点M,N为圆心,以大于MN的长为半径作弧,两弧交于点G,连接DG交BC于点H。若DH=4,则AD的长是( B )
A. 6 B. 8 C. 6 D. 3
10.如图,在平面直角坐标系中,已知点A(0,4),点B在第二象限内,AO=AB,∠OAB=120 ,将△AOB绕点O逆时针旋转,每次旋转60 ,则第2025次旋转后,点B的坐标为( D )
A. (2,6) B. (6,2) C. ( 4,0) D. (2, 6)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11.如图,x < 5(填 “>” 或 “<”)。
12.如图,将△ABC绕点A逆时针方向旋转一定角度得到△ADE,使点D落在BC上,AC与DE相交于点F。若∠C=40 ,DE⊥AC,则∠BAD= 50 度。
13.如图,直线y= 2x+2与直线y=kx+b(k,b为常数,k<0)相交于点A( 1,m),则关于x的不等式 2x+2≤kx+b的解集为 x≥﹣1 。
14.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着BC方向平移4cm到△DEF的位置,若AB=5cm,DH=2cm,则阴影部分的面积等于 16 cm2。
15.如图,在△ABC中,∠ACB=90 ,∠CAB=30 ,BC=6,D为AB上一动点(不与点A,点B重合),将AD绕点A顺时针旋转60 得到AE,连接DE,以D为直角顶点,DE为直角边,在DE上方构造等腰直角三角形DEF,G为EF的中点,连接BG,CG,则BG+CG的最小值是 6 。
三、解答题(本大题共 9 个小题,共 90 分。解答应写出文字说明、证明过程或演算步骤。)
16.(8 分)因式分解:(1)3ma3 6ma2+12ma; (2)x2(3x 2)+(2 3x)。
=3ma(a2﹣2a+4) =(3x﹣2)(x2﹣1)
=(3x﹣2)(x﹣1)(x+1)
17.(10 分)按要求解下列不等式(组):
(1)解关于x的不等式3 x<2(x+3),并将解集用数轴表示出来;
(2)解不等式组:,并写出它的所有整数解。
(1)3﹣x<2x+6
x>﹣1
(2)解不等式①得x≤1.5
解不等式①得x>﹣3
不等式组解集为﹣3<x<1.5
整数解为﹣2,﹣1,0,1
18.(10 分)(1)计算:﹣;
(2)先化简,再求值:( 1)÷,其中a=1。
(1)=﹣
=
=
(2)原式=×
=
将a=1代入得﹣1
19.(10 分)已知关于x的分式方程=2﹣。
(1)若m表示的数是2,解这个分式方程;
(2)查询发现正确答案为 “原分式方程无解”,请求出原分式方程中m代表的数是多少。
(1)=2﹣
x﹣2=2(x﹣3)+2
x=2
经检验x=2是原方程的根
(2)x﹣2=2(x﹣3)+m
当x=3时,此方程无解
将x=3代入得3﹣2=m
m=1
20.(8 分)已知:如图,A,E,F,C四点共线,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且AE=CF,求证:AB∥CD。
证明:∵AE=CF
∴AE+EF=CF+EF
∴AF=CE
又∵DE⊥AC , BF⊥AC
∴∠AFB =∠CED =90°
在Rt△CDE和Rt△ABF
∴Rt△CDE≌Rt△ABF
∴∠C=∠A
∴AB∥CD
21.(10 分)如图,在平面直角坐标系中,已知点A( 2, 4),B(0, 4),C(1, 1)。
(1)画出△ABC绕点O逆时针旋转90 后的图形△A1B1C1,此时点C1的坐标为 ;
(2)将(1)中所得△A1B1C1平移得到△A2B2C2,使得△A1B1C1内一点P(a,b)平移后的对应点坐标为(a 4,b+2),画出△A2B2C2,此时点C2的坐标为 ;
(3)若△A2B2C2可以看作△ABC绕某点旋转得来,直接写出旋转中心的坐标。
(1)(1,1)
(2)(﹣3,3)
(3)(﹣3,﹣1)
22.(10 分)为培养学生的创新意识,提高学生的动手能力,某校计划购买一批航空、航海模型。已知商场某品牌航空模型的单价比航海模型的单价多35元,用2500元购买航空模型的数量是用2400元购买航海模型数量的。
(1)求航空和航海模型的单价;
(2)学校采购时恰逢该商场促销:航空模型八折优惠。若购买航空、航海模型共120个,且航空模型数量不少于航海模型数量的,请问分别购买多少个航空和航海模型,学校花费最少?
解:(1)设航空模型的单价为x 元,则航海模型的单价为(x -35)元。
根据题意得:=×
解得 x =125
经检验,x =125是方程的解,也符合题意,
∴x -35=125-35=90,
答:航空模型的单价为125元,航海模型的单价为90元。
(2)设购买航空模型 m 个,学校花费元,则购买航海模型(120- m)个,
∵航空模型数量不少于航海模型数量的
∴m≥(120- m )
解得m ≥40
根据题意得:W =125x0.8m+90(120-m )=10m+10800
∵10>0,
∴当 m =40时,W 取最小值,最小值为10x40+10800=11200
此时120- m =120-40=80
∴购买航空模型40个,购买航海模型80个,学校花费最少。
23.(12 分)如图,△ABC中,∠C=90 ,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒。
(1)当t= 时,BP将△ABC的面积分成相等的两部分,此时BP= ;
(2)若点P不与△ABC的顶点重合,问t为何值时,点P在△ABC的角平分线上?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P,Q两点同时出发,当P,Q中有一点到达终点时,另一点也停止运动。当直线PQ把△ABC的周长分成相等的两部分时,请直接写出此时t的值。
(备用图)
23.(1)2
(2)分三种情况:(每种情况2分)
①点 P 恰好在 ZABC 的角平分线上时,
如图所示,过点P 作PG⊥AB 于点G
∴PG = PC
在Rt△BPC和Rt△BPG
∴Rt△BPC和≌Rt△BPG( HL ),
∴BG = BC =3cm,
∴AG =5-3=2cm.
设 PC= x cm ,则PA =(4- x )
在Rt△APG 中,PG2+AG2=PA2
即x2+22=(4- x)2
解得:x =1.5
当t=1.5时,点 P 恰好在∠ABC 的角平分线上;
另外t=或,点 P 恰好在∠ABC 的角平分线上;
(3)t=2或6时,直线PQ把△ABC的周长分成相等的两部分
24.(12 分)如图所示,△ABC为等腰三角形,AB=AC,点D是BC上一点,连接AD。
(1)当∠BAC=90 时,
①如图 1,若BD=2DC=4,把AD绕A顺时针旋转90 到AE,连接BE,DE,则DE= ;
②如图 2,将线段DC绕点D逆时针旋转90 到DE,点E落在AC上,连接BE,点O为线段BE的中点,连接AO,AD,此时AO与AD的数量关系为 ;
小明同学提出以下解决问题的思路,仅供大家参考:
延长AO到点F,使OF=OA,连接EF,DF,通过证明两组三角形全等,再进一步分析研究△ADF来解决问题;
(2)当∠BAC=120 时,
①如图 3,将线段DC绕点D逆时针旋转60 到DE,连接BE,点O为线段BE的中点,连接
AO,AD,此时AO与AD有怎样的数量关系,并说明理由;
②如图 4,点Q为△ABC内一点,若∠AQB=90 ,∠BQC=150 ,请直接写出的值。
(1)①DE=2 ②AD=AO
(2)启点:
(2)①证明:如图,延长 AO 到点 F ,使 OF = AO ,连接 EF , DF , EF 与 BC 交于点 M ,则AO=AF
∵点 O 是BE 的中点
∴BO = OE
∵∠AOB =∠FOE
∴△AOB≌△FOE ( SAS )
∴AB = EF=AC,∠ABO =∠FEO
∴AB // EF
∴∠EMD =∠ABC =30°
∵∠EDC =60°
∴∠DEM =30°=∠C
由旋转可知,CD = DE
∵AB =EF =AC
∴△DEF≌△DCA ( SAS )
∴∠ADC =∠EDF , AD = DF
∴∠ADF =∠CDE =60°
∴△ADF是等边三角形
∴AF=AD
∴AD=2AO
②2
(时间120分钟 满分150分)
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量。下面有关我国航天领域的图标,其图标是中心对称图形的是( )
2.下列等式从左到右的变形,属于因式分解的是( )
A. (a+4)(a 4)=a2 16 B.x2 4y2=(x+4y)(x 4y) C. x2 2x+1=x(x 1)+1 D. x2 8x+16=(x 4)2
3.不等式3x+1≤2x+2的解集在数轴上表示为( )
A. B.
C. D.
4.若a>b,则下列不等式变形正确的是( )
A. 1 3a<1 3b B. a 2
5.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,那么BC的长等于( )
A. 27 B. 50 C. 23 D. 13
6.若+a=1,则的值为( )
A. 3 B. 2 C. 1 D.
7.根据下列表格中的部分值信息,分式y可能是( )
A. B. C. D.
8.若关于x的分式方程=2+的解为正数,则满足条件的正整数m的值为( )
A. 1,2,3 B. 1,2 C. 1,3,4 D. 1,3
9.如图,在△ABC中,AB=AC,∠BAC=120 ,按以下步骤作图。①以点B为圆心,以任意长为半径作弧,分别交AB,BC于点E,F;②分别以点E,F为圆心,以大于EF的长为半径作弧,两弧交于点O;③作射线BO,交AC于点D;④以点D为圆心,以适当长为半径作弧,分别交BC于点M,N;⑤分别以点M,N为圆心,以大于MN的长为半径作弧,两弧交于点G,连接DG交BC于点H。若DH=4,则AD的长是( )
A. 6 B. 8 C. 6 D. 3
10.如图,在平面直角坐标系中,已知点A(0,4),点B在第二象限内,AO=AB,∠OAB=120 ,将△AOB绕点O逆时针旋转,每次旋转60 ,则第2025次旋转后,点B的坐标为( )
A. (2,6) B. (6,2) C. ( 4,0) D. (2, 6)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11.如图,x 5(填 “>” 或 “<”)。
12.如图,将△ABC绕点A逆时针方向旋转一定角度得到△ADE,使点D落在BC上,AC与DE相交于点F。若∠C=40 ,DE⊥AC,则∠BAD= 度。
13.如图,直线y= 2x+2与直线y=kx+b(k,b为常数,k<0)相交于点A( 1,m),则关于x的不等式 2x+2≤kx+b的解集为 。
14.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着BC方向平移4cm到△DEF的位置,若AB=5cm,DH=2cm,则阴影部分的面积等于 cm2。
15.如图,在△ABC中,∠ACB=90 ,∠CAB=30 ,BC=6,D为AB上一动点(不与点A,点B重合),将AD绕点A顺时针旋转60 得到AE,连接DE,以D为直角顶点,DE为直角边,在DE上方构造等腰直角三角形DEF,G为EF的中点,连接BG,CG,则BG+CG的最小值是 。
三、解答题(本大题共 9 个小题,共 90 分。解答应写出文字说明、证明过程或演算步骤。)
16.(8 分)因式分解:(1)3ma3 6ma2+12ma; (2)x2(3x 2)+(2 3x)。
17.(10 分)按要求解下列不等式(组):
(1)解关于x的不等式3 x<2(x+3),并将解集用数轴表示出来;
(2)解不等式组:,并写出它的所有整数解。
18.(10 分)(1)计算:﹣;
(2)先化简,再求值:( 1)÷,其中a=1。
19.(10 分)已知关于x的分式方程=2﹣。
(1)若m表示的数是2,解这个分式方程;
(2)查询发现正确答案为 “原分式方程无解”,请求出原分式方程中m代表的数是多少。
20.(8 分)已知:如图,A,E,F,C四点共线,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且AE=CF,求证:AB∥CD。
21.(10 分)如图,在平面直角坐标系中,已知点A( 2, 4),B(0, 4),C(1, 1)。
(1)画出△ABC绕点O逆时针旋转90 后的图形△A1B1C1,此时点C1的坐标为 ;
(2)将(1)中所得△A1B1C1平移得到△A2B2C2,使得△A1B1C1内一点P(a,b)平移后的对应点坐标为(a 4,b+2),画出△A2B2C2,此时点C2的坐标为 ;
(3)若△A2B2C2可以看作△ABC绕某点旋转得来,直接写出旋转中心的坐标。
22.(10 分)为培养学生的创新意识,提高学生的动手能力,某校计划购买一批航空、航海模型。已知商场某品牌航空模型的单价比航海模型的单价多35元,用2500元购买航空模型的数量是用2400元购买航海模型数量的。
(1)求航空和航海模型的单价;
(2)学校采购时恰逢该商场促销:航空模型八折优惠。若购买航空、航海模型共120个,且航空模型数量不少于航海模型数量的,请问分别购买多少个航空和航海模型,学校花费最少?
23.(12 分)如图,△ABC中,∠C=90 ,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒。
(1)当t= 时,BP将△ABC的面积分成相等的两部分,此时BP= ;
(2)若点P不与△ABC的顶点重合,问t为何值时,点P在△ABC的角平分线上?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P,Q两点同时出发,当P,Q中有一点到达终点时,另一点也停止运动。当直线PQ把△ABC的周长分成相等的两部分时,请直接写出此时t的值。
(备用图)
24.(12 分)如图所示,△ABC为等腰三角形,AB=AC,点D是BC上一点,连接AD。
(1)当∠BAC=90 时,
①如图 1,若BD=2DC=4,把AD绕A顺时针旋转90 到AE,连接BE,DE,则DE= ;
②如图 2,将线段DC绕点D逆时针旋转90 到DE,点E落在AC上,连接BE,点O为线段BE的中点,连接AO,AD,此时AO与AD的数量关系为 ;
小明同学提出以下解决问题的思路,仅供大家参考:
延长AO到点F,使OF=OA,连接EF,DF,通过证明两组三角形全等,再进一步分析研究△ADF来解决问题;
(2)当∠BAC=120 时,
①如图 3,将线段DC绕点D逆时针旋转60 到DE,连接BE,点O为线段BE的中点,连接
AO,AD,此时AO与AD有怎样的数量关系,并说明理由;
②如图 4,点Q为△ABC内一点,若∠AQB=90 ,∠BQC=150 ,请直接写出的值。
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量。下面有关我国航天领域的图标,其图标是中心对称图形的是( C )
2.下列等式从左到右的变形,属于因式分解的是( D )
A. (a+4)(a 4)=a2 16 B.x2 4y2=(x+4y)(x 4y) C. x2 2x+1=x(x 1)+1 D. x2 8x+16=(x 4)2
3.不等式3x+1≤2x+2的解集在数轴上表示为( A )
A. B.
C. D.
4.若a>b,则下列不等式变形正确的是( A )
A. 1 3a<1 3b B. a 2
5.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,那么BC的长等于( C )
A. 27 B. 50 C. 23 D. 13
6.若+a=1,则的值为( B )
A. 3 B. 2 C. 1 D.
7.根据下列表格中的部分值信息,分式y可能是( B )
A. B. C. D.
8.若关于x的分式方程=2+的解为正数,则满足条件的正整数m的值为( D )
A. 1,2,3 B. 1,2 C. 1,3,4 D. 1,3
9.如图,在△ABC中,AB=AC,∠BAC=120 ,按以下步骤作图。①以点B为圆心,以任意长为半径作弧,分别交AB,BC于点E,F;②分别以点E,F为圆心,以大于EF的长为半径作弧,两弧交于点O;③作射线BO,交AC于点D;④以点D为圆心,以适当长为半径作弧,分别交BC于点M,N;⑤分别以点M,N为圆心,以大于MN的长为半径作弧,两弧交于点G,连接DG交BC于点H。若DH=4,则AD的长是( B )
A. 6 B. 8 C. 6 D. 3
10.如图,在平面直角坐标系中,已知点A(0,4),点B在第二象限内,AO=AB,∠OAB=120 ,将△AOB绕点O逆时针旋转,每次旋转60 ,则第2025次旋转后,点B的坐标为( D )
A. (2,6) B. (6,2) C. ( 4,0) D. (2, 6)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11.如图,x < 5(填 “>” 或 “<”)。
12.如图,将△ABC绕点A逆时针方向旋转一定角度得到△ADE,使点D落在BC上,AC与DE相交于点F。若∠C=40 ,DE⊥AC,则∠BAD= 50 度。
13.如图,直线y= 2x+2与直线y=kx+b(k,b为常数,k<0)相交于点A( 1,m),则关于x的不等式 2x+2≤kx+b的解集为 x≥﹣1 。
14.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着BC方向平移4cm到△DEF的位置,若AB=5cm,DH=2cm,则阴影部分的面积等于 16 cm2。
15.如图,在△ABC中,∠ACB=90 ,∠CAB=30 ,BC=6,D为AB上一动点(不与点A,点B重合),将AD绕点A顺时针旋转60 得到AE,连接DE,以D为直角顶点,DE为直角边,在DE上方构造等腰直角三角形DEF,G为EF的中点,连接BG,CG,则BG+CG的最小值是 6 。
三、解答题(本大题共 9 个小题,共 90 分。解答应写出文字说明、证明过程或演算步骤。)
16.(8 分)因式分解:(1)3ma3 6ma2+12ma; (2)x2(3x 2)+(2 3x)。
=3ma(a2﹣2a+4) =(3x﹣2)(x2﹣1)
=(3x﹣2)(x﹣1)(x+1)
17.(10 分)按要求解下列不等式(组):
(1)解关于x的不等式3 x<2(x+3),并将解集用数轴表示出来;
(2)解不等式组:,并写出它的所有整数解。
(1)3﹣x<2x+6
x>﹣1
(2)解不等式①得x≤1.5
解不等式①得x>﹣3
不等式组解集为﹣3<x<1.5
整数解为﹣2,﹣1,0,1
18.(10 分)(1)计算:﹣;
(2)先化简,再求值:( 1)÷,其中a=1。
(1)=﹣
=
=
(2)原式=×
=
将a=1代入得﹣1
19.(10 分)已知关于x的分式方程=2﹣。
(1)若m表示的数是2,解这个分式方程;
(2)查询发现正确答案为 “原分式方程无解”,请求出原分式方程中m代表的数是多少。
(1)=2﹣
x﹣2=2(x﹣3)+2
x=2
经检验x=2是原方程的根
(2)x﹣2=2(x﹣3)+m
当x=3时,此方程无解
将x=3代入得3﹣2=m
m=1
20.(8 分)已知:如图,A,E,F,C四点共线,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且AE=CF,求证:AB∥CD。
证明:∵AE=CF
∴AE+EF=CF+EF
∴AF=CE
又∵DE⊥AC , BF⊥AC
∴∠AFB =∠CED =90°
在Rt△CDE和Rt△ABF
∴Rt△CDE≌Rt△ABF
∴∠C=∠A
∴AB∥CD
21.(10 分)如图,在平面直角坐标系中,已知点A( 2, 4),B(0, 4),C(1, 1)。
(1)画出△ABC绕点O逆时针旋转90 后的图形△A1B1C1,此时点C1的坐标为 ;
(2)将(1)中所得△A1B1C1平移得到△A2B2C2,使得△A1B1C1内一点P(a,b)平移后的对应点坐标为(a 4,b+2),画出△A2B2C2,此时点C2的坐标为 ;
(3)若△A2B2C2可以看作△ABC绕某点旋转得来,直接写出旋转中心的坐标。
(1)(1,1)
(2)(﹣3,3)
(3)(﹣3,﹣1)
22.(10 分)为培养学生的创新意识,提高学生的动手能力,某校计划购买一批航空、航海模型。已知商场某品牌航空模型的单价比航海模型的单价多35元,用2500元购买航空模型的数量是用2400元购买航海模型数量的。
(1)求航空和航海模型的单价;
(2)学校采购时恰逢该商场促销:航空模型八折优惠。若购买航空、航海模型共120个,且航空模型数量不少于航海模型数量的,请问分别购买多少个航空和航海模型,学校花费最少?
解:(1)设航空模型的单价为x 元,则航海模型的单价为(x -35)元。
根据题意得:=×
解得 x =125
经检验,x =125是方程的解,也符合题意,
∴x -35=125-35=90,
答:航空模型的单价为125元,航海模型的单价为90元。
(2)设购买航空模型 m 个,学校花费元,则购买航海模型(120- m)个,
∵航空模型数量不少于航海模型数量的
∴m≥(120- m )
解得m ≥40
根据题意得:W =125x0.8m+90(120-m )=10m+10800
∵10>0,
∴当 m =40时,W 取最小值,最小值为10x40+10800=11200
此时120- m =120-40=80
∴购买航空模型40个,购买航海模型80个,学校花费最少。
23.(12 分)如图,△ABC中,∠C=90 ,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒。
(1)当t= 时,BP将△ABC的面积分成相等的两部分,此时BP= ;
(2)若点P不与△ABC的顶点重合,问t为何值时,点P在△ABC的角平分线上?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P,Q两点同时出发,当P,Q中有一点到达终点时,另一点也停止运动。当直线PQ把△ABC的周长分成相等的两部分时,请直接写出此时t的值。
(备用图)
23.(1)2
(2)分三种情况:(每种情况2分)
①点 P 恰好在 ZABC 的角平分线上时,
如图所示,过点P 作PG⊥AB 于点G
∴PG = PC
在Rt△BPC和Rt△BPG
∴Rt△BPC和≌Rt△BPG( HL ),
∴BG = BC =3cm,
∴AG =5-3=2cm.
设 PC= x cm ,则PA =(4- x )
在Rt△APG 中,PG2+AG2=PA2
即x2+22=(4- x)2
解得:x =1.5
当t=1.5时,点 P 恰好在∠ABC 的角平分线上;
另外t=或,点 P 恰好在∠ABC 的角平分线上;
(3)t=2或6时,直线PQ把△ABC的周长分成相等的两部分
24.(12 分)如图所示,△ABC为等腰三角形,AB=AC,点D是BC上一点,连接AD。
(1)当∠BAC=90 时,
①如图 1,若BD=2DC=4,把AD绕A顺时针旋转90 到AE,连接BE,DE,则DE= ;
②如图 2,将线段DC绕点D逆时针旋转90 到DE,点E落在AC上,连接BE,点O为线段BE的中点,连接AO,AD,此时AO与AD的数量关系为 ;
小明同学提出以下解决问题的思路,仅供大家参考:
延长AO到点F,使OF=OA,连接EF,DF,通过证明两组三角形全等,再进一步分析研究△ADF来解决问题;
(2)当∠BAC=120 时,
①如图 3,将线段DC绕点D逆时针旋转60 到DE,连接BE,点O为线段BE的中点,连接
AO,AD,此时AO与AD有怎样的数量关系,并说明理由;
②如图 4,点Q为△ABC内一点,若∠AQB=90 ,∠BQC=150 ,请直接写出的值。
(1)①DE=2 ②AD=AO
(2)启点:
(2)①证明:如图,延长 AO 到点 F ,使 OF = AO ,连接 EF , DF , EF 与 BC 交于点 M ,则AO=AF
∵点 O 是BE 的中点
∴BO = OE
∵∠AOB =∠FOE
∴△AOB≌△FOE ( SAS )
∴AB = EF=AC,∠ABO =∠FEO
∴AB // EF
∴∠EMD =∠ABC =30°
∵∠EDC =60°
∴∠DEM =30°=∠C
由旋转可知,CD = DE
∵AB =EF =AC
∴△DEF≌△DCA ( SAS )
∴∠ADC =∠EDF , AD = DF
∴∠ADF =∠CDE =60°
∴△ADF是等边三角形
∴AF=AD
∴AD=2AO
②2
同课章节目录
