浙江中考复习——集训中考题(三)(含解析)
文档属性
| 名称 | 浙江中考复习——集训中考题(三)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 17:21:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江中考复习——集训中考题(三)
一、选择题
1.已知直线与抛物线对称轴左侧部分的图象有且只有一个交点,则m的取值范围是( )
A. B.或 C. D.或
2.已知点是二次函数函数图象上的两个点,若关于的一元二次方程有两根,则( )
A. B.
C. D.
3.如图是由四个全等的直角三角形(,,,)组成的新图形,若,,则正方形的边长为( )
A.5 B. C. D.6
4.如图,在由四个全等的直角三角形拼成的“赵爽弦图”中,四边形与四边形均为正方形,连结并延长,分别交边,于点,.若,,则的长为( )
A. B. C. D.
二、填空题
5.古希腊一位庄园主把一边长为米的正方形土地租给老农,第二年他对老农说:“我把这块地的一边增加米,相邻的一边减少米,变成长方形土地继续租给你,租金不变”后来老农发现收益减少,感觉吃亏了聪明的你帮老农算出土地面积其实减少了 平方米.
6.如图,在平面直角坐标系中,O为原点,已知点,把向上平移m个单位长度,对应得到,若反比例函数的图象经过的重心和点,则k的值为
7.如图,锐角三角形内接于于点D,连结并延长交线段于点E(点E不与点B,D重合),设(m,n为正数),则m关于n的函数表达式为
8.如图,点P是正方形的中心,过点P的线段和将正方形分割成4个相同的四边形,这4个四边形拼成正方形.连接,记和的面积分别为,设;
(1)若A,B,Q三点共线,则
(2)正方形和的面积之比为 .(用含k的代数式表示)
三、尺规作图
9.如图,在中,.
(1)实践与操作:用尺规作图法作的平分线交于点D;(保留作图痕迹,不要求写作法)
(2)应用与证明:在(1)的条件下,以点D为圆心,长为半径作.求证:与相切.
10.按下列要求完成作图:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.
(1)如图1是的正方形网格,点,均在格点上,作线段的中点;
(2)如图2,在,点为的中点,作边的中点.
四、几何图形
11.如图,在中,点D是的中点,点E在上,将沿翻折至,使点F落在上,延长与的延长线交于点G.
(1)求证:;
(2)若,,求的长.
12.如图,正方形的对角线相交于点.是线段上的点(不与、重合),过点作,交于点.
(1)求证:;
(2)若平分,求的长.
五、一次函数与反比例函数
13.已知反比例函数与一次函数(,,b是常数,,)的图象交于点,.
(1)求函数和的表达式.
(2)若点P是反比例函数图象上一点,将点P先向右平移4个单位,再向下平移3个单位得点M,点M恰好落在一次函数图象上,求点P的坐标.
14.如图,在平面直角坐标系中,一次函数与轴、轴分别交于点A、B,与反比例函数交于点,D两点,直线垂直于轴分别与一次函数和反比例函数交于、,连接.
(1)求的值;
(2)点在线段上(不与端点、重合),若,求的面积;
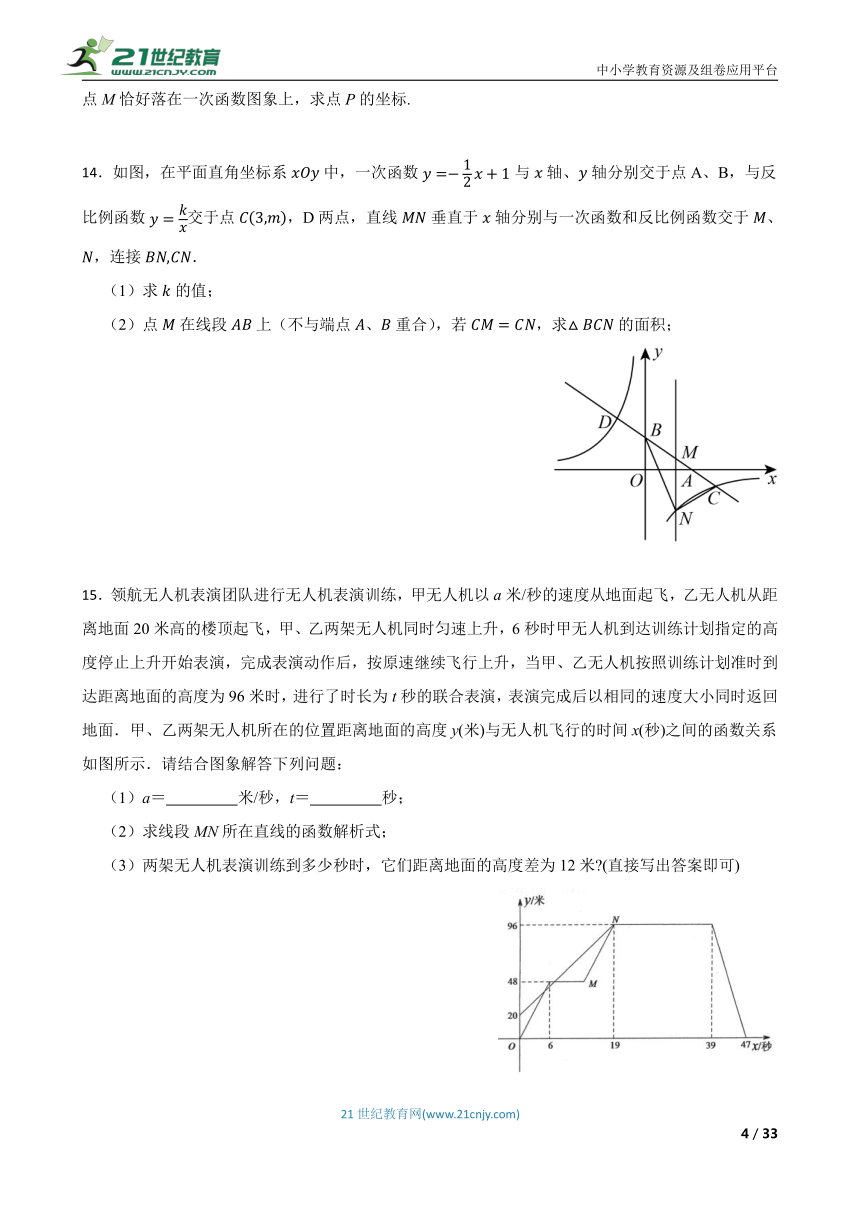
15.领航无人机表演团队进行无人机表演训练,甲无人机以a米/秒的速度从地面起飞,乙无人机从距离地面20米高的楼顶起飞,甲、乙两架无人机同时匀速上升,6秒时甲无人机到达训练计划指定的高度停止上升开始表演,完成表演动作后,按原速继续飞行上升,当甲、乙无人机按照训练计划准时到达距离地面的高度为96米时,进行了时长为t秒的联合表演,表演完成后以相同的速度大小同时返回地面.甲、乙两架无人机所在的位置距离地面的高度y(米)与无人机飞行的时间x(秒)之间的函数关系如图所示.请结合图象解答下列问题:
(1)a= 米/秒,t= 秒;
(2)求线段MN所在直线的函数解析式;
(3)两架无人机表演训练到多少秒时,它们距离地面的高度差为12米 (直接写出答案即可)
六、解直角三角形
16.用某型号拖把去拖沙发底部地面的截面示意图如图所示,拖把头为矩形,.该沙发与地面的空隙为矩形,,.拖把杆为线段,长为, O为的中点,与所成角的可变范围是当大小固定时,若经过点G,或点A与点E重合,则此时的长即为沙发底部可拖最大深度.
(1)如图1,当时,求沙发底部可拖最大深度的长.(结果保留根号)
(2)如图2,为了能将沙发底部地面拖干净,将α减小到,请通过计算,判断此时沙发底部可拖最大深度的长能否达到?(,)
17.某款便捷式手机支架如图1所示,通过调节两支架夹角的大小可改变手机屏幕的高度.图2是该款手机支架的平面示意图,已知,.
(1)当时,求点到水平桌面的距离.
(2)当由调整到时,则点到水平桌面的距离将抬高多少?(结果精确到.参考数据:,,.)
18.综合与实践
如图1是实验室中的一种机械装置,在地面上,所在等腰直角三角形是固定支架,机械臂可以绕点A旋转,同时机械臂可以绕点D旋转,已知,,.
(1)如图2,把机械臂顺时针旋转,点D旋转到点E处,连结,当,
①连接,探究与的数量关系和位置关系,并说明理由;
②当时,求的长
(2)如图3,机械臂A、D、M三点共线,,此时机械臂顺时针旋转,机械臂一端恰好落在边上,标记为点N,求支架的长.
七、二次函数
19.已知二次函数(k为常数).
(1)用含k的代数式表示该二次函数的顶点坐标;
(2)当时,y随x的增大而减小,求k的取值范围;
(3)当时,该函数有最小值,求k的值.
20.已知二次函数(a为常数).
(1)若该二次函数的图象经过点
①求a的值.
②自变量x在什么范围内时,y随x的增大而增大?
(2)若点均在该二次函数的图象上,求证:.
21.定义:对于y关于x的函数,函数在范围内的最大值,记作如函数,在范围内,该函数的最大值是6, 即,.
请根据以上信息,完成以下问题:
已知函数(a为常数)
(1)若.
①直接写出该函数的表达式,并求的值;
②已知求p的值.
(2)若该函数的图象经过点, 且, 求k的值.
八、圆的几何图形
22.如图,在中,,以为直径的交于点,,垂足为的延长线交于点.
(1)求的值;
(2)求证:;
(3)求证:与互相平分.
23.如图,在中,∠B是锐角,,,在射线上取一点P,过P作于点E,过P,E,C三点作.
(1)当时,
①如图1,若与相切于点P,连结,求的长;
②如图2,若经过点D,求的半径长.
(2)如图3,已知与射线交于另一点F,将沿所在的直线翻折,点B的对应点记为,且恰好同时落在和边上,求此时的长.
24.如图,内接于,,与直径交于点.
(1)如图1,若,.则的长为______.
(2)如图2,在上取点,使,连接并延长交于点.求证:平分.
(3)如图3,在(2)的条件下,已知,.求线段的长.
答案解析部分
1.【答案】D
【解析】【解答】解:由题意,当直线与抛物线相切时,图象只有一个交点,
∴,即.
∴.
∴.
令,则,
∴,
记直线与y轴交于点,
又当抛物线过,且对称轴在y轴右侧,
∴.
∴,此时刚好在对称轴左侧有一个交点,如图:
又继续向左平移符合题意,符合题意,如图:
∴.
综上,或.
故答案为:D.
【分析】当直线与抛物线相切时符合题意,函数联立,根据,求出m的值;当抛物线过,且对称轴在y轴右侧时符合题意,代入,求出此时的m的值,以及抛物线继续向左平移,仍符合题意,即可得到答案.
2.【答案】C
【解析】【解答】解:A、B在二次函数的图像上,故①,②
而m>0,故,由韦达定理知,即
②-①得得|n|>|m|,而m>0>n得-n>m故,由韦达定理得即
综上所述:
故答案为:C.
【分析】分别将A、B坐标代入函数得①,②,可得k>1,②-①得-n>m,得,由韦达定理即可得两根之和与积的范围.
3.【答案】C
【解析】【解答】解:由题意得:,
,
,,
设,则,
,
,
,
,
则正方形的边长为,
故答案为:C.
【分析】由全等三角形的对应边相等得AF=CH,AE=BF=CG,结合EF=AF-AE=2,CG+CH=GH=8求得AE=BF=3,AF=5,在Rt△ABF中,利用勾股定理即可算出AB的长,从而得到答案.
4.【答案】C
5.【答案】16
【解析】【解答】解:由题意可得土地减少的面积为:a2-(a+4)(a-4)=a2-a2+16=16(平方米).
故答案为:16.
【分析】根据土地减少的面积=原土地的面积-第二年长方形土地的面积并结合长方形及正方形面积计算方法列出式子,然后根据整式混合运算顺序计算可得答案.
6.【答案】
【解析】【解答】解:∵,
∴中点坐标为 ,中点坐标为,
设 解析式为 ,解析式为,
将代入得,则,即 解析式为;
∵ ,,
∴,解得,则解析式为;
解,得,
∴的重心坐标为,
∵把向上平移m个单位长度, 对应得到,
∴,的重心为,
∵点B'与的重心都在反比例函数的图象上,
∴,解得:;
∴,
故答案为:.
【分析】先根据A、B两点的坐标,分别求得OB,AB两线段的中点C、D两点的坐标,设 解析式为 ,解析式为,将D点的坐标代入,求出其解析式,将A,C两点的坐标代入,求出其解析式,求出OD与AC的交点即为的重心,再根据平移方式确定的重心和点坐标,再代入反比例函数解析式求出m,就可求出k.
7.【答案】
【解析】【解答】解:连接,
设,
,,
,
,
,
,
,
,
,
故答案为:.
【分析】设,可用表示出与,再三角形的内角和定理,可用表示出,根据平角的定义就可得出m关于n的函数表达式.
8.【答案】(1)
(2)
【解析】【解答】解:(1)如图,连接BQ,
设BF=x,
由题意可得,,
,,
,
,
,
,,
,
.
故答案为:.
(2)设AB=m,PF=n,
,,
,
,
,
,
,
.
故答案为:.
【分析】(1)设BF=x,当A,B,Q三点共线时,易证,利用相似三角形的性质求得,由勾股定理可得,进而证得,然后计算出四边形GPFB的面积,从而计算出k的值.
(2)设AB=m,PF=n,由题意可得PH=PF=FQ=n,故,,进而得到,再利用 求得,继而得到,而,故可得.
9.【答案】(1)解:如图1,即为所作;
(2)解:以点D为圆心,CD为半径作圆,作于,如图所示:
∵是的平分线,∠ACD=90°,,
∴,
∵CD是半径,
∴DC是半径,
∴与相切.
【解析】【分析】(1)利用尺规作角平分线的方法解答即可;
(2)以点D为圆心,CD为半径作圆,作于,由角平分线的性质定理可得,由是半径,即可证得结论.
(1)解:如图1,即为所作;
(2)证明:如图2,作于,
∵是的平分线,,,
∴,
∵是半径,,
∴与相切.
10.【答案】(1)解:如图所示,点G即为所求;
(2)解:如图所示,点F即为所求.
【解析】【分析】(1)将点A向左平移2个单位长度得到点E,将点B向右平移2个单位长度得到点F,连接EF交AB于点G,利用平行四边形的对角线互相平分可得点G就是AB的中点;
(2)连接AC,BD交于点O,由平行四边形的对角线互相平分得点O是AC的中点;连接EO并延长交AB于点T,根据平行四边形的中心对称性可得T为AB的中点;连接CT交BD于点K,根据三角形的三条中线交于一点可得点K是△ABC的重心,连接AK并延长交BC于点F,点F即为所求.
11.【答案】(1)证明:沿翻折至,点是的中点,
,,
,
,
,
(2)解:,
,
,
,,
,
,
,
,且点是BC的中点,
,
点是AB的中点,
,
【解析】【分析】(1)先利用翻折的性质证得,,再利用等边对等角证得,接着利用三角形外角的性质可得出,然后利用平行线的判断;
(2)利用平行线分线段成比例,列出比例式,可求出,再利用勾股定理可求出,然后利用正切求出,再利用平行线分线段成比例可求出,最后利用勾股定理求得AC.
12.【答案】(1)解:∵正方形,∴,
∵,
∴,,
∴,
∴,
∴,
∴,
∴
(2)解:过点E作,垂足为P,如下图所示,
∵平分,,,
∴,
∵,
∴,
∴
∵,
∴,
∴
【解析】【分析】(1)证明,即可得到;
(2)过点E作,垂足为P,根据角平分线定理得到,即可求得,在根据是等腰直角三角形即可求出的长.
13.【答案】(1)解:将点代入,得,则.
将点代入,得,
将点A,B代入,
得,解得,
(2)解:设,则,
,得,
【解析】【分析】(1)将A点代入反比例函数中,即可求出k1的值,从而知道反比例函数的解析式,再将B嗲代入反比例函数中可求出m的值,同时将A和B点坐标代入一次函数中即可知道一次函数的解析式.
(2)设,即可求出平移后M点的坐标,将M点的坐标代入一次函数解析式中即可求出x的值,从而求出P点坐标.
14.【答案】(1)解: 点在直线上,代入得,
,
点.
将代入得,,
解得
(2)解:由(1)可得直线解析式为,双曲线解析式为,,
设、的横坐标为,由于在直线上,在双曲线上,
,,
,,
过作于点,如图,
,
点为中点,
点纵坐标为,与点纵坐标相等,
,
解得,,
直线,与坐标轴交点为,,点在线段上(不与端点、重合)
.
∴,,,
【解析】【分析】(1)先求出C点的坐标,再代入反比例函数,求出解析式;
(2)先设出M、N两点的坐标,再说明点为中点,得到关于t的方程求解,从而可求得M,N两点的坐标,再求出MN,然后三角形面积公式求出的面积;
15.【答案】(1)8;20
(2)解:由图象可知,N(19,96),
∵甲无人机的速度为8米/秒,
∴甲无人机匀速上升从0米到96米所用时间为96÷8=12(秒),
∴甲无人机单独表演所用时间为19-12=7(秒),
∴6+7=13(秒),
∴M(13,48),
设线段MN所在直线的函数解析式为y=kx+b(k≠0),
将M(13,48),N(19,96)代入得:,
解得:,
∴线段MN所在直线的函数解析式为:y=8x-56;
(3)解:两架无人机表演训练到2秒或10秒或16秒时,它们距离地面的高度差为12米.
【解析】【解答】解:(1)根据题意,得甲无人机的飞行速度为a=48÷6=8(米/秒),
t=39-19=20(秒),
故答案为:8,20;
(3)设点A(0,20),B(6,48),
∴同理可得线段OB所在直线的函数解析式为yOB=8x,yAN=4x+20,yBM=48,
∵线段MN所在直线的函数解析式为y=8x-56,
∴当0≤t≤6时,|yOB-yAN|=|8x-4x-20|=12,解得x=2或x=8(舍去),
当6当13∴两架无人机表演训练到2秒或10秒或16秒时,它们距离地面的高度差为12米.
【分析】(1)观察函数图象进行计算即可求解;
(2)先求出甲无人机单独表演的时间,从而得点M的坐标,最后用待定系数法求线段MN所在直线的函数解析式即可;
(3)设点A(0,20),B(6,48),然后利用待定系数法先求线段OB、AN、BM所在直线的函数解析式,再通过观察函数图象可知要分三种情况讨论:当0≤t≤6时,有|yOB-yAN|=|8x-4x-20|=12,解方程求出x的值;当616.【答案】(1)解:如图,设与的延长线交于点,则,
∵四边形和四边都是矩形,且在上,
∴, ,
∴,
,
.
为的中点,
,
。
(2)解:如图,设经过点,与的延长线交于点,∵四边形和四边都是矩形,且在上,
∴, ,
∴,
,
.
.
所以此时最大可拖深度的长不能达到.
【解析】【分析】本题主要考查了矩形的性质以及解直角三角形.
(1)设与的延长线交于点,求出,解直角三角形,求出,再求出,即可求出.
(2)设经过点,与的延长线交于点,解直角三角形求出,即可求出,则可做出判断.
17.【答案】(1)解:如图1,当时,
,
.
过点作于点,
,,
.
点到水平桌面的距离为.
(2)解:如图2,当由调整到时,则,
过点C作,作于点,
,
,,
.
当由调整到时,点到水平桌面的距离将抬高.
【解析】【分析】(1)先证明CD//AB,再利用正弦求出AH即可;
(2)先求出,再利用余弦求出即可.
18.【答案】(1)解:①连接,
由旋转可知,,,
是等腰三角形,,
,
,
,
,
∵
②,,
,
,
,,
,
.
(2)解:过点N作 ,如图所示:
∵顺时针旋转
,
∵
∵
∵
∴,
∴
∴
∴,
∴.
【解析】【分析】(1)①连接CD,先利用“AAS”证出,利用全等三角形的性质可得,,再利用角的运算和等量代换可得,从而可证出;
②先利用角的运算求出,利用勾股定理求出CD的长,再利用全等三角形的性质可得;
(2)过点N作 ,先求出,利用含30°角的直角三角形的性质可得,最后利用线段的和差求出AB的长即可.
19.【答案】(1)解:
.
(2)解:,
当时,y随x的增大而减小 ,
.
(3)解:当k<0时,
当时,该函数有最小值,
当x=0时,y=k=-1;
当时,
当时,该函数有最小值,
当x=k时,,解得(舍去);
当k>3时,
当时,该函数有最小值,
当x=3时,,解得(舍去),
综上所述,k=或.
【解析】【分析】(1)利用配方法将二次函数解析式化为顶点式,即可求得顶点坐标.
(2)由二次函数的性质可得当时,y随x的增大而减小 ,故.
(3)利用二次函数的性质对k的取值范围进行分类讨论,当k<0时,当x=0时,y有最小值,解得k=-1;当时,当x=k时,y有最小值,解得(舍去);当k>3时,当x=3时,y有最小值,解得(舍去),综上所述,k=或.
20.【答案】(1)解:①将代入得:,解得.
②由①得二次函数的表达式为.
∴二次函数图象的对称轴为直线.
∵a=1>0,抛物线开口向上,
∴当自变量时,y随x的增大而增大.
(2)证明:由题意可得,
将点代入得,
.
【解析】【分析】(1)①将代入,计算可得a的值;
②由题意得,抛物线开口向上,对称轴为直线,进而可得当时,y随x的增大而增大;
(2)由题意设,将点代入得,进而可得.
21.【答案】(1)解:①,
.
该函数的图象对称轴为直线,且开口向上,
在范围内,当时,有最大值,
当时,,即.
②,该函数的图象对称轴为直线,且开口向上,
又当时,,
,解得,.
,
(2)解:函数图象经过点,
,即,
当,函数为正比例函数,随的增大而减小,
,
,即;
当时,函数为二次函数,函数图象开口向下,对称轴为直线.当时,随的增大而增大;当时,随的增大而减小.
,
若,则,解得,,
;
若,则,解得,
;
综上所述,的值是12,或2。
【解析】【分析】本题考查二次函数与正比例函数的图形与性质,二次函数的对称轴.
(1)①a=2,则,进而可得该函数的图象对称轴为直线,且开口向上,据此可得当时,有最大值,进而可求出的值;
先求出二次函数解析式,根据二次函数对称轴,开口方向即可找到范围内的最大值,进而得出结果;
②根据该函数的图象对称轴为直线,且开口向上, 可推出当时,,进而可列出方程,解方程可求出p值;
(2)根据函数图象经过点,可列出方程,解方程可求出,分两种情况:当;当时,根据,可列出方程或或,解方程可求出k的值,进而可求出答案.
22.【答案】(1)解:,且是的直径,
,
,
在中,.
,
在中,.
,
.
(2)证明:过点B作 BM∥AE,交EO延长线于点M,
∴∠BAE=∠ABM,∠AEO=∠BMO=90°.
∵AO=BO,
∴△AOE≌△BOM(AAS),
∴AE=BM,OE=OM,
,
∴BM=2OE=EM,
∴∠MEB=∠MBE=45°,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∴∠MBE=∠ABC,
∴∠ABM=∠CBE,
∵∠AEB=∠AEO+∠MEB=135°,∠BEC=180°-∠MEB=135°,
∴∠AEB=∠BEC,
∴△AEB∽△BEC.
(3)证明:连接DE,DF,
∵AB是⊙O的直径,
∴∠ADB=∠AFB=90°,AB=2AO,
∵AB=AC,∠BAC=90°,
∴BC=2BD,∠DAB=45°,
由(2)知,△AEB∽△BEC,
,∠EAO=∠EBD,
∴△AOE∽△BDE,
∴∠BED=∠AEO=90°,
∴∠DEF=90°,
∴∠AFB=∠DEF,
∴AF∥DE,
由(2)知,∠AEB=135°,
∴∠AEF=180°-∠AEB=45°.
∵∠DFB=∠DAB=45°,
∴∠DFB=∠AEF,
∴AE∥FD,
∴四边形AEDF是平行四边形,
∴AD与EF互相平分.
【解析】【分析】(1)先求得AC=2AO,再根据锐角三角函数得出,即可求解;
(2)过点B作 BM∥AE,交EO延长线于点M,根据两直线平行,内错角相等可得∠BAE=∠ABM,根据两角及其一角的对边对应相等的三角形全等,全等三角形的对应边相等可得AE=BM,OE=OM,推得BM=2OE=EM,根据等腰直角三角形的性质可推得∠MBE=∠ABC,即可得出∠ABM=∠CBE,∠AEB=∠BEC,根据有两个角对应相等的两个三角形是相似三角形即可证明;
(3)连接DE,DF,根据直角所对的圆周角是直角可得∠ADB=∠AFB=90°,根据等腰直角三角形的性质可推得∠DAB=45°,根据相似三角形的对应边之比相等,两边成比例且夹角相等的两个三角形相似可得△AOE∽△BDE,根据相似三角形的对应角相等可得∠BED=∠AEO=90°,推得∠AFB=∠DEF,根据内错角相等,两直线平行可得AF∥DE,结合(2)中结论可得∠DFB=∠AEF,根据内错角相等,两直线平行可得AE∥FD,根据两组对边分别平行的四边形是平行四边形,平行四边形的对角线互相平分即可证明.
23.【答案】(1)解:①,即,
是的直径,
与相切于点,
.
,,
,
根据勾股定理,得;
②如图,连接,,
,
∴是的直径,,
四边形是平行四边形,
∴,,,,
,,,,
,
根据勾股定理,得,
.
的半径长为。
(2)解:如图,过点作交的延长线于点,连接,,记于交于点,
,,
,
,
,
,
是直径,
,
,,
,
,
,
,即.
为平行四边形边上的高,
,
又,
.
设,则,,
,
,
根据勾股定理,得,即,
解得,
.
【解析】【分析】本题考查切线的性质,解直角三角形,圆周角定理,平行四边形的性质,等腰直角三角形的判定与性质、折叠的性质.(1)①利用切线的性质可得:,进而可推出CP是的直径,再根据AB与相切于点,利用切线的性质可得,利用余弦的定义可得:,代入数据可求出BP,再利用勾股定理可求出CP.
②连结,,根据,可推出是的直径,,利用平行四边形的性质可得:,,,,,,利用余弦的定义可得:,代入数据可求出AP,利用勾股定理可求出,进而可求出PC.
(2)过点作交的延长线于点,连结,,是直径,据此可推出,利用余弦的定义可求出和的长,再利用勾股定理求得.再根据NE为平行四边形边上的高,利用正弦的定义可求出NE,设,利用线段的运算可得:,,,利用勾股定理列出方程,解方程可求出x的值,进而可求出答案.
24.【答案】(1)4
(2)解:,
,
,
,
,
∴平分.
(3)解:,∴设,则,
如图,延长交的延长线于H,连接,
为直径,
,
∴,
平分,
∴,
∵,
∴,
,,
∵,
,
∵,
,
也是等腰三角形,即:,
,
∵,,,
∴FC:10=(10-8x):2CF,
解得:,
∵,
由,
解得:负值已舍去,
∴,,,
∵B是的中点,为等腰直角三角形,
∴,
如图,过点A作于点M,
∵,,
∴为等腰直角三角形,
∴,
∴,
∴,
,,
,
∴,
∴,
解得:,
,
答:线段的长为.
【解析】【解答】解:(1)如图,连接,
,
,即:B是的中点,
∴为等腰直角三角形,
∵,
,,
在中,
,
;
故答案为:4.
【分析】(1)先求得,再求得∠ABC,然后利用两角的差求出∠OBE;
(2)先证明,,根据,可证明,从而可得;
(3)先证,列出比例式,可用x表示出CF2,再证明,列出比例式,可求得BE,然后利用线段的差求出EG.
21世纪教育网(www.21cnjy.com)
1 / 1
浙江中考复习——集训中考题(三)
一、选择题
1.已知直线与抛物线对称轴左侧部分的图象有且只有一个交点,则m的取值范围是( )
A. B.或 C. D.或
2.已知点是二次函数函数图象上的两个点,若关于的一元二次方程有两根,则( )
A. B.
C. D.
3.如图是由四个全等的直角三角形(,,,)组成的新图形,若,,则正方形的边长为( )
A.5 B. C. D.6
4.如图,在由四个全等的直角三角形拼成的“赵爽弦图”中,四边形与四边形均为正方形,连结并延长,分别交边,于点,.若,,则的长为( )
A. B. C. D.
二、填空题
5.古希腊一位庄园主把一边长为米的正方形土地租给老农,第二年他对老农说:“我把这块地的一边增加米,相邻的一边减少米,变成长方形土地继续租给你,租金不变”后来老农发现收益减少,感觉吃亏了聪明的你帮老农算出土地面积其实减少了 平方米.
6.如图,在平面直角坐标系中,O为原点,已知点,把向上平移m个单位长度,对应得到,若反比例函数的图象经过的重心和点,则k的值为
7.如图,锐角三角形内接于于点D,连结并延长交线段于点E(点E不与点B,D重合),设(m,n为正数),则m关于n的函数表达式为
8.如图,点P是正方形的中心,过点P的线段和将正方形分割成4个相同的四边形,这4个四边形拼成正方形.连接,记和的面积分别为,设;
(1)若A,B,Q三点共线,则
(2)正方形和的面积之比为 .(用含k的代数式表示)
三、尺规作图
9.如图,在中,.
(1)实践与操作:用尺规作图法作的平分线交于点D;(保留作图痕迹,不要求写作法)
(2)应用与证明:在(1)的条件下,以点D为圆心,长为半径作.求证:与相切.
10.按下列要求完成作图:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.
(1)如图1是的正方形网格,点,均在格点上,作线段的中点;
(2)如图2,在,点为的中点,作边的中点.
四、几何图形
11.如图,在中,点D是的中点,点E在上,将沿翻折至,使点F落在上,延长与的延长线交于点G.
(1)求证:;
(2)若,,求的长.
12.如图,正方形的对角线相交于点.是线段上的点(不与、重合),过点作,交于点.
(1)求证:;
(2)若平分,求的长.
五、一次函数与反比例函数
13.已知反比例函数与一次函数(,,b是常数,,)的图象交于点,.
(1)求函数和的表达式.
(2)若点P是反比例函数图象上一点,将点P先向右平移4个单位,再向下平移3个单位得点M,点M恰好落在一次函数图象上,求点P的坐标.
14.如图,在平面直角坐标系中,一次函数与轴、轴分别交于点A、B,与反比例函数交于点,D两点,直线垂直于轴分别与一次函数和反比例函数交于、,连接.
(1)求的值;
(2)点在线段上(不与端点、重合),若,求的面积;
15.领航无人机表演团队进行无人机表演训练,甲无人机以a米/秒的速度从地面起飞,乙无人机从距离地面20米高的楼顶起飞,甲、乙两架无人机同时匀速上升,6秒时甲无人机到达训练计划指定的高度停止上升开始表演,完成表演动作后,按原速继续飞行上升,当甲、乙无人机按照训练计划准时到达距离地面的高度为96米时,进行了时长为t秒的联合表演,表演完成后以相同的速度大小同时返回地面.甲、乙两架无人机所在的位置距离地面的高度y(米)与无人机飞行的时间x(秒)之间的函数关系如图所示.请结合图象解答下列问题:
(1)a= 米/秒,t= 秒;
(2)求线段MN所在直线的函数解析式;
(3)两架无人机表演训练到多少秒时,它们距离地面的高度差为12米 (直接写出答案即可)
六、解直角三角形
16.用某型号拖把去拖沙发底部地面的截面示意图如图所示,拖把头为矩形,.该沙发与地面的空隙为矩形,,.拖把杆为线段,长为, O为的中点,与所成角的可变范围是当大小固定时,若经过点G,或点A与点E重合,则此时的长即为沙发底部可拖最大深度.
(1)如图1,当时,求沙发底部可拖最大深度的长.(结果保留根号)
(2)如图2,为了能将沙发底部地面拖干净,将α减小到,请通过计算,判断此时沙发底部可拖最大深度的长能否达到?(,)
17.某款便捷式手机支架如图1所示,通过调节两支架夹角的大小可改变手机屏幕的高度.图2是该款手机支架的平面示意图,已知,.
(1)当时,求点到水平桌面的距离.
(2)当由调整到时,则点到水平桌面的距离将抬高多少?(结果精确到.参考数据:,,.)
18.综合与实践
如图1是实验室中的一种机械装置,在地面上,所在等腰直角三角形是固定支架,机械臂可以绕点A旋转,同时机械臂可以绕点D旋转,已知,,.
(1)如图2,把机械臂顺时针旋转,点D旋转到点E处,连结,当,
①连接,探究与的数量关系和位置关系,并说明理由;
②当时,求的长
(2)如图3,机械臂A、D、M三点共线,,此时机械臂顺时针旋转,机械臂一端恰好落在边上,标记为点N,求支架的长.
七、二次函数
19.已知二次函数(k为常数).
(1)用含k的代数式表示该二次函数的顶点坐标;
(2)当时,y随x的增大而减小,求k的取值范围;
(3)当时,该函数有最小值,求k的值.
20.已知二次函数(a为常数).
(1)若该二次函数的图象经过点
①求a的值.
②自变量x在什么范围内时,y随x的增大而增大?
(2)若点均在该二次函数的图象上,求证:.
21.定义:对于y关于x的函数,函数在范围内的最大值,记作如函数,在范围内,该函数的最大值是6, 即,.
请根据以上信息,完成以下问题:
已知函数(a为常数)
(1)若.
①直接写出该函数的表达式,并求的值;
②已知求p的值.
(2)若该函数的图象经过点, 且, 求k的值.
八、圆的几何图形
22.如图,在中,,以为直径的交于点,,垂足为的延长线交于点.
(1)求的值;
(2)求证:;
(3)求证:与互相平分.
23.如图,在中,∠B是锐角,,,在射线上取一点P,过P作于点E,过P,E,C三点作.
(1)当时,
①如图1,若与相切于点P,连结,求的长;
②如图2,若经过点D,求的半径长.
(2)如图3,已知与射线交于另一点F,将沿所在的直线翻折,点B的对应点记为,且恰好同时落在和边上,求此时的长.
24.如图,内接于,,与直径交于点.
(1)如图1,若,.则的长为______.
(2)如图2,在上取点,使,连接并延长交于点.求证:平分.
(3)如图3,在(2)的条件下,已知,.求线段的长.
答案解析部分
1.【答案】D
【解析】【解答】解:由题意,当直线与抛物线相切时,图象只有一个交点,
∴,即.
∴.
∴.
令,则,
∴,
记直线与y轴交于点,
又当抛物线过,且对称轴在y轴右侧,
∴.
∴,此时刚好在对称轴左侧有一个交点,如图:
又继续向左平移符合题意,符合题意,如图:
∴.
综上,或.
故答案为:D.
【分析】当直线与抛物线相切时符合题意,函数联立,根据,求出m的值;当抛物线过,且对称轴在y轴右侧时符合题意,代入,求出此时的m的值,以及抛物线继续向左平移,仍符合题意,即可得到答案.
2.【答案】C
【解析】【解答】解:A、B在二次函数的图像上,故①,②
而m>0,故,由韦达定理知,即
②-①得得|n|>|m|,而m>0>n得-n>m故,由韦达定理得即
综上所述:
故答案为:C.
【分析】分别将A、B坐标代入函数得①,②,可得k>1,②-①得-n>m,得,由韦达定理即可得两根之和与积的范围.
3.【答案】C
【解析】【解答】解:由题意得:,
,
,,
设,则,
,
,
,
,
则正方形的边长为,
故答案为:C.
【分析】由全等三角形的对应边相等得AF=CH,AE=BF=CG,结合EF=AF-AE=2,CG+CH=GH=8求得AE=BF=3,AF=5,在Rt△ABF中,利用勾股定理即可算出AB的长,从而得到答案.
4.【答案】C
5.【答案】16
【解析】【解答】解:由题意可得土地减少的面积为:a2-(a+4)(a-4)=a2-a2+16=16(平方米).
故答案为:16.
【分析】根据土地减少的面积=原土地的面积-第二年长方形土地的面积并结合长方形及正方形面积计算方法列出式子,然后根据整式混合运算顺序计算可得答案.
6.【答案】
【解析】【解答】解:∵,
∴中点坐标为 ,中点坐标为,
设 解析式为 ,解析式为,
将代入得,则,即 解析式为;
∵ ,,
∴,解得,则解析式为;
解,得,
∴的重心坐标为,
∵把向上平移m个单位长度, 对应得到,
∴,的重心为,
∵点B'与的重心都在反比例函数的图象上,
∴,解得:;
∴,
故答案为:.
【分析】先根据A、B两点的坐标,分别求得OB,AB两线段的中点C、D两点的坐标,设 解析式为 ,解析式为,将D点的坐标代入,求出其解析式,将A,C两点的坐标代入,求出其解析式,求出OD与AC的交点即为的重心,再根据平移方式确定的重心和点坐标,再代入反比例函数解析式求出m,就可求出k.
7.【答案】
【解析】【解答】解:连接,
设,
,,
,
,
,
,
,
,
,
故答案为:.
【分析】设,可用表示出与,再三角形的内角和定理,可用表示出,根据平角的定义就可得出m关于n的函数表达式.
8.【答案】(1)
(2)
【解析】【解答】解:(1)如图,连接BQ,
设BF=x,
由题意可得,,
,,
,
,
,
,,
,
.
故答案为:.
(2)设AB=m,PF=n,
,,
,
,
,
,
,
.
故答案为:.
【分析】(1)设BF=x,当A,B,Q三点共线时,易证,利用相似三角形的性质求得,由勾股定理可得,进而证得,然后计算出四边形GPFB的面积,从而计算出k的值.
(2)设AB=m,PF=n,由题意可得PH=PF=FQ=n,故,,进而得到,再利用 求得,继而得到,而,故可得.
9.【答案】(1)解:如图1,即为所作;
(2)解:以点D为圆心,CD为半径作圆,作于,如图所示:
∵是的平分线,∠ACD=90°,,
∴,
∵CD是半径,
∴DC是半径,
∴与相切.
【解析】【分析】(1)利用尺规作角平分线的方法解答即可;
(2)以点D为圆心,CD为半径作圆,作于,由角平分线的性质定理可得,由是半径,即可证得结论.
(1)解:如图1,即为所作;
(2)证明:如图2,作于,
∵是的平分线,,,
∴,
∵是半径,,
∴与相切.
10.【答案】(1)解:如图所示,点G即为所求;
(2)解:如图所示,点F即为所求.
【解析】【分析】(1)将点A向左平移2个单位长度得到点E,将点B向右平移2个单位长度得到点F,连接EF交AB于点G,利用平行四边形的对角线互相平分可得点G就是AB的中点;
(2)连接AC,BD交于点O,由平行四边形的对角线互相平分得点O是AC的中点;连接EO并延长交AB于点T,根据平行四边形的中心对称性可得T为AB的中点;连接CT交BD于点K,根据三角形的三条中线交于一点可得点K是△ABC的重心,连接AK并延长交BC于点F,点F即为所求.
11.【答案】(1)证明:沿翻折至,点是的中点,
,,
,
,
,
(2)解:,
,
,
,,
,
,
,
,且点是BC的中点,
,
点是AB的中点,
,
【解析】【分析】(1)先利用翻折的性质证得,,再利用等边对等角证得,接着利用三角形外角的性质可得出,然后利用平行线的判断;
(2)利用平行线分线段成比例,列出比例式,可求出,再利用勾股定理可求出,然后利用正切求出,再利用平行线分线段成比例可求出,最后利用勾股定理求得AC.
12.【答案】(1)解:∵正方形,∴,
∵,
∴,,
∴,
∴,
∴,
∴,
∴
(2)解:过点E作,垂足为P,如下图所示,
∵平分,,,
∴,
∵,
∴,
∴
∵,
∴,
∴
【解析】【分析】(1)证明,即可得到;
(2)过点E作,垂足为P,根据角平分线定理得到,即可求得,在根据是等腰直角三角形即可求出的长.
13.【答案】(1)解:将点代入,得,则.
将点代入,得,
将点A,B代入,
得,解得,
(2)解:设,则,
,得,
【解析】【分析】(1)将A点代入反比例函数中,即可求出k1的值,从而知道反比例函数的解析式,再将B嗲代入反比例函数中可求出m的值,同时将A和B点坐标代入一次函数中即可知道一次函数的解析式.
(2)设,即可求出平移后M点的坐标,将M点的坐标代入一次函数解析式中即可求出x的值,从而求出P点坐标.
14.【答案】(1)解: 点在直线上,代入得,
,
点.
将代入得,,
解得
(2)解:由(1)可得直线解析式为,双曲线解析式为,,
设、的横坐标为,由于在直线上,在双曲线上,
,,
,,
过作于点,如图,
,
点为中点,
点纵坐标为,与点纵坐标相等,
,
解得,,
直线,与坐标轴交点为,,点在线段上(不与端点、重合)
.
∴,,,
【解析】【分析】(1)先求出C点的坐标,再代入反比例函数,求出解析式;
(2)先设出M、N两点的坐标,再说明点为中点,得到关于t的方程求解,从而可求得M,N两点的坐标,再求出MN,然后三角形面积公式求出的面积;
15.【答案】(1)8;20
(2)解:由图象可知,N(19,96),
∵甲无人机的速度为8米/秒,
∴甲无人机匀速上升从0米到96米所用时间为96÷8=12(秒),
∴甲无人机单独表演所用时间为19-12=7(秒),
∴6+7=13(秒),
∴M(13,48),
设线段MN所在直线的函数解析式为y=kx+b(k≠0),
将M(13,48),N(19,96)代入得:,
解得:,
∴线段MN所在直线的函数解析式为:y=8x-56;
(3)解:两架无人机表演训练到2秒或10秒或16秒时,它们距离地面的高度差为12米.
【解析】【解答】解:(1)根据题意,得甲无人机的飞行速度为a=48÷6=8(米/秒),
t=39-19=20(秒),
故答案为:8,20;
(3)设点A(0,20),B(6,48),
∴同理可得线段OB所在直线的函数解析式为yOB=8x,yAN=4x+20,yBM=48,
∵线段MN所在直线的函数解析式为y=8x-56,
∴当0≤t≤6时,|yOB-yAN|=|8x-4x-20|=12,解得x=2或x=8(舍去),
当6
【分析】(1)观察函数图象进行计算即可求解;
(2)先求出甲无人机单独表演的时间,从而得点M的坐标,最后用待定系数法求线段MN所在直线的函数解析式即可;
(3)设点A(0,20),B(6,48),然后利用待定系数法先求线段OB、AN、BM所在直线的函数解析式,再通过观察函数图象可知要分三种情况讨论:当0≤t≤6时,有|yOB-yAN|=|8x-4x-20|=12,解方程求出x的值;当6
∵四边形和四边都是矩形,且在上,
∴, ,
∴,
,
.
为的中点,
,
。
(2)解:如图,设经过点,与的延长线交于点,∵四边形和四边都是矩形,且在上,
∴, ,
∴,
,
.
.
所以此时最大可拖深度的长不能达到.
【解析】【分析】本题主要考查了矩形的性质以及解直角三角形.
(1)设与的延长线交于点,求出,解直角三角形,求出,再求出,即可求出.
(2)设经过点,与的延长线交于点,解直角三角形求出,即可求出,则可做出判断.
17.【答案】(1)解:如图1,当时,
,
.
过点作于点,
,,
.
点到水平桌面的距离为.
(2)解:如图2,当由调整到时,则,
过点C作,作于点,
,
,,
.
当由调整到时,点到水平桌面的距离将抬高.
【解析】【分析】(1)先证明CD//AB,再利用正弦求出AH即可;
(2)先求出,再利用余弦求出即可.
18.【答案】(1)解:①连接,
由旋转可知,,,
是等腰三角形,,
,
,
,
,
∵
②,,
,
,
,,
,
.
(2)解:过点N作 ,如图所示:
∵顺时针旋转
,
∵
∵
∵
∴,
∴
∴
∴,
∴.
【解析】【分析】(1)①连接CD,先利用“AAS”证出,利用全等三角形的性质可得,,再利用角的运算和等量代换可得,从而可证出;
②先利用角的运算求出,利用勾股定理求出CD的长,再利用全等三角形的性质可得;
(2)过点N作 ,先求出,利用含30°角的直角三角形的性质可得,最后利用线段的和差求出AB的长即可.
19.【答案】(1)解:
.
(2)解:,
当时,y随x的增大而减小 ,
.
(3)解:当k<0时,
当时,该函数有最小值,
当x=0时,y=k=-1;
当时,
当时,该函数有最小值,
当x=k时,,解得(舍去);
当k>3时,
当时,该函数有最小值,
当x=3时,,解得(舍去),
综上所述,k=或.
【解析】【分析】(1)利用配方法将二次函数解析式化为顶点式,即可求得顶点坐标.
(2)由二次函数的性质可得当时,y随x的增大而减小 ,故.
(3)利用二次函数的性质对k的取值范围进行分类讨论,当k<0时,当x=0时,y有最小值,解得k=-1;当时,当x=k时,y有最小值,解得(舍去);当k>3时,当x=3时,y有最小值,解得(舍去),综上所述,k=或.
20.【答案】(1)解:①将代入得:,解得.
②由①得二次函数的表达式为.
∴二次函数图象的对称轴为直线.
∵a=1>0,抛物线开口向上,
∴当自变量时,y随x的增大而增大.
(2)证明:由题意可得,
将点代入得,
.
【解析】【分析】(1)①将代入,计算可得a的值;
②由题意得,抛物线开口向上,对称轴为直线,进而可得当时,y随x的增大而增大;
(2)由题意设,将点代入得,进而可得.
21.【答案】(1)解:①,
.
该函数的图象对称轴为直线,且开口向上,
在范围内,当时,有最大值,
当时,,即.
②,该函数的图象对称轴为直线,且开口向上,
又当时,,
,解得,.
,
(2)解:函数图象经过点,
,即,
当,函数为正比例函数,随的增大而减小,
,
,即;
当时,函数为二次函数,函数图象开口向下,对称轴为直线.当时,随的增大而增大;当时,随的增大而减小.
,
若,则,解得,,
;
若,则,解得,
;
综上所述,的值是12,或2。
【解析】【分析】本题考查二次函数与正比例函数的图形与性质,二次函数的对称轴.
(1)①a=2,则,进而可得该函数的图象对称轴为直线,且开口向上,据此可得当时,有最大值,进而可求出的值;
先求出二次函数解析式,根据二次函数对称轴,开口方向即可找到范围内的最大值,进而得出结果;
②根据该函数的图象对称轴为直线,且开口向上, 可推出当时,,进而可列出方程,解方程可求出p值;
(2)根据函数图象经过点,可列出方程,解方程可求出,分两种情况:当;当时,根据,可列出方程或或,解方程可求出k的值,进而可求出答案.
22.【答案】(1)解:,且是的直径,
,
,
在中,.
,
在中,.
,
.
(2)证明:过点B作 BM∥AE,交EO延长线于点M,
∴∠BAE=∠ABM,∠AEO=∠BMO=90°.
∵AO=BO,
∴△AOE≌△BOM(AAS),
∴AE=BM,OE=OM,
,
∴BM=2OE=EM,
∴∠MEB=∠MBE=45°,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∴∠MBE=∠ABC,
∴∠ABM=∠CBE,
∵∠AEB=∠AEO+∠MEB=135°,∠BEC=180°-∠MEB=135°,
∴∠AEB=∠BEC,
∴△AEB∽△BEC.
(3)证明:连接DE,DF,
∵AB是⊙O的直径,
∴∠ADB=∠AFB=90°,AB=2AO,
∵AB=AC,∠BAC=90°,
∴BC=2BD,∠DAB=45°,
由(2)知,△AEB∽△BEC,
,∠EAO=∠EBD,
∴△AOE∽△BDE,
∴∠BED=∠AEO=90°,
∴∠DEF=90°,
∴∠AFB=∠DEF,
∴AF∥DE,
由(2)知,∠AEB=135°,
∴∠AEF=180°-∠AEB=45°.
∵∠DFB=∠DAB=45°,
∴∠DFB=∠AEF,
∴AE∥FD,
∴四边形AEDF是平行四边形,
∴AD与EF互相平分.
【解析】【分析】(1)先求得AC=2AO,再根据锐角三角函数得出,即可求解;
(2)过点B作 BM∥AE,交EO延长线于点M,根据两直线平行,内错角相等可得∠BAE=∠ABM,根据两角及其一角的对边对应相等的三角形全等,全等三角形的对应边相等可得AE=BM,OE=OM,推得BM=2OE=EM,根据等腰直角三角形的性质可推得∠MBE=∠ABC,即可得出∠ABM=∠CBE,∠AEB=∠BEC,根据有两个角对应相等的两个三角形是相似三角形即可证明;
(3)连接DE,DF,根据直角所对的圆周角是直角可得∠ADB=∠AFB=90°,根据等腰直角三角形的性质可推得∠DAB=45°,根据相似三角形的对应边之比相等,两边成比例且夹角相等的两个三角形相似可得△AOE∽△BDE,根据相似三角形的对应角相等可得∠BED=∠AEO=90°,推得∠AFB=∠DEF,根据内错角相等,两直线平行可得AF∥DE,结合(2)中结论可得∠DFB=∠AEF,根据内错角相等,两直线平行可得AE∥FD,根据两组对边分别平行的四边形是平行四边形,平行四边形的对角线互相平分即可证明.
23.【答案】(1)解:①,即,
是的直径,
与相切于点,
.
,,
,
根据勾股定理,得;
②如图,连接,,
,
∴是的直径,,
四边形是平行四边形,
∴,,,,
,,,,
,
根据勾股定理,得,
.
的半径长为。
(2)解:如图,过点作交的延长线于点,连接,,记于交于点,
,,
,
,
,
,
是直径,
,
,,
,
,
,
,即.
为平行四边形边上的高,
,
又,
.
设,则,,
,
,
根据勾股定理,得,即,
解得,
.
【解析】【分析】本题考查切线的性质,解直角三角形,圆周角定理,平行四边形的性质,等腰直角三角形的判定与性质、折叠的性质.(1)①利用切线的性质可得:,进而可推出CP是的直径,再根据AB与相切于点,利用切线的性质可得,利用余弦的定义可得:,代入数据可求出BP,再利用勾股定理可求出CP.
②连结,,根据,可推出是的直径,,利用平行四边形的性质可得:,,,,,,利用余弦的定义可得:,代入数据可求出AP,利用勾股定理可求出,进而可求出PC.
(2)过点作交的延长线于点,连结,,是直径,据此可推出,利用余弦的定义可求出和的长,再利用勾股定理求得.再根据NE为平行四边形边上的高,利用正弦的定义可求出NE,设,利用线段的运算可得:,,,利用勾股定理列出方程,解方程可求出x的值,进而可求出答案.
24.【答案】(1)4
(2)解:,
,
,
,
,
∴平分.
(3)解:,∴设,则,
如图,延长交的延长线于H,连接,
为直径,
,
∴,
平分,
∴,
∵,
∴,
,,
∵,
,
∵,
,
也是等腰三角形,即:,
,
∵,,,
∴FC:10=(10-8x):2CF,
解得:,
∵,
由,
解得:负值已舍去,
∴,,,
∵B是的中点,为等腰直角三角形,
∴,
如图,过点A作于点M,
∵,,
∴为等腰直角三角形,
∴,
∴,
∴,
,,
,
∴,
∴,
解得:,
,
答:线段的长为.
【解析】【解答】解:(1)如图,连接,
,
,即:B是的中点,
∴为等腰直角三角形,
∵,
,,
在中,
,
;
故答案为:4.
【分析】(1)先求得,再求得∠ABC,然后利用两角的差求出∠OBE;
(2)先证明,,根据,可证明,从而可得;
(3)先证,列出比例式,可用x表示出CF2,再证明,列出比例式,可求得BE,然后利用线段的差求出EG.
21世纪教育网(www.21cnjy.com)
1 / 1
同课章节目录
