山东省巨野县第一中学人教版高中数学必修四课件:1.5 函数y=Asin(ωx+φ)的图象(一) (共38张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教版高中数学必修四课件:1.5 函数y=Asin(ωx+φ)的图象(一) (共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 701.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-02 00:00:00 | ||
图片预览







文档简介
课件38张PPT。1. 通过对三角函数图象的动态演示进一步让学生了解三角函数图象各种变换的实质和内在规律. (重点)
2. 通过对函数y = Asin(ωx+φ)(A>0,ω>0)图象的探讨,让学生进一步掌握三角函数图象各种变换的内在联系.(重点、难点)1.5 函数 的图象(一)3.能用“五点法”作出函数y=Asin(ωx+ )(A>0,ω>0)的简图.(重点)
4.熟悉函数y=Asin(ωx+ )与y=sinx图象间的关系,知道y=Asin(ωx+ )的图象可由正弦曲线y=sinx怎样变化得到. (重点、难点)
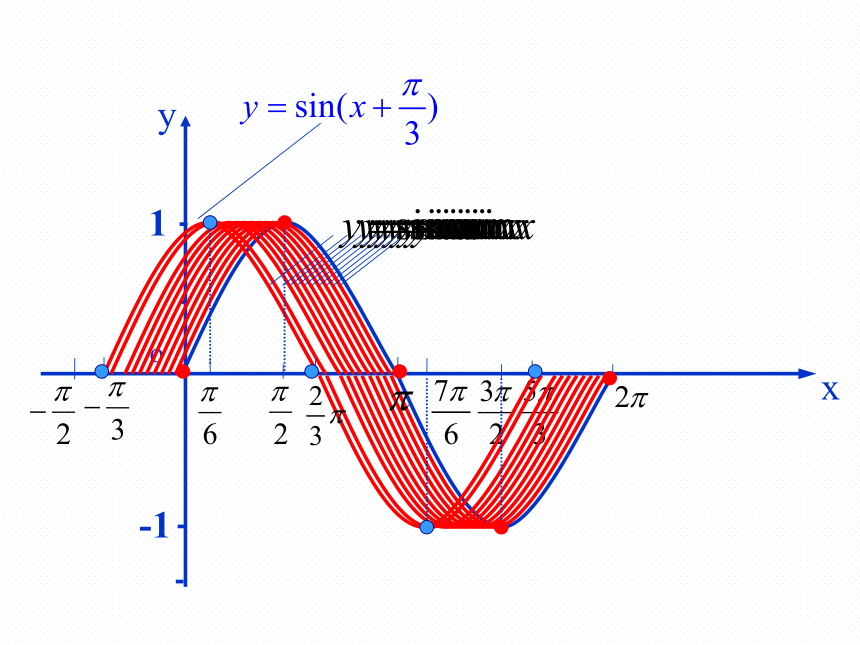
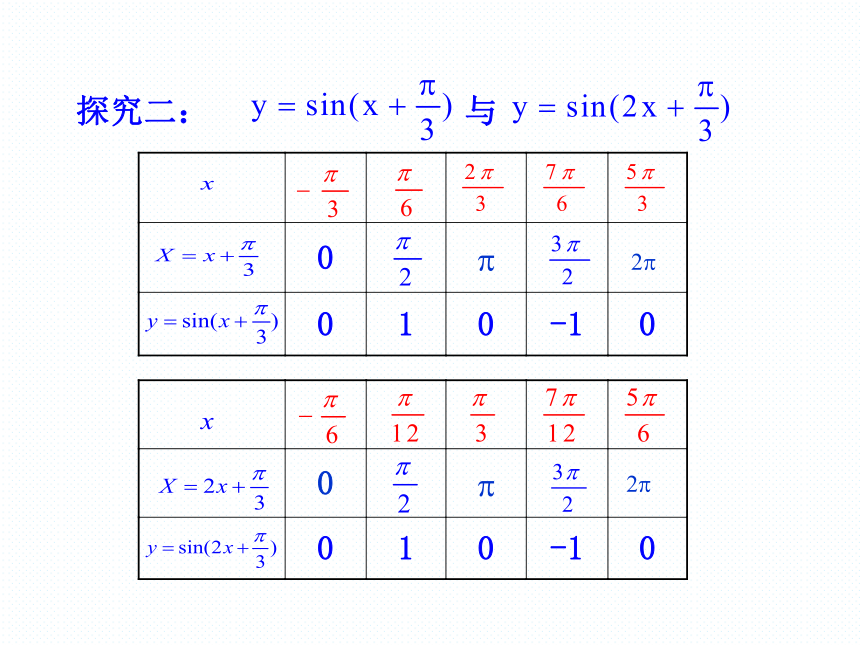
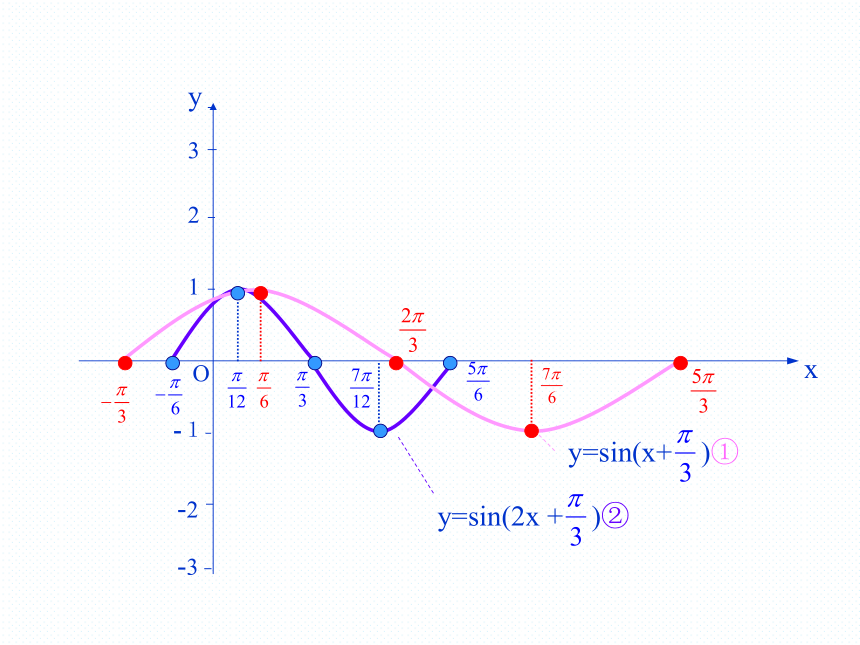
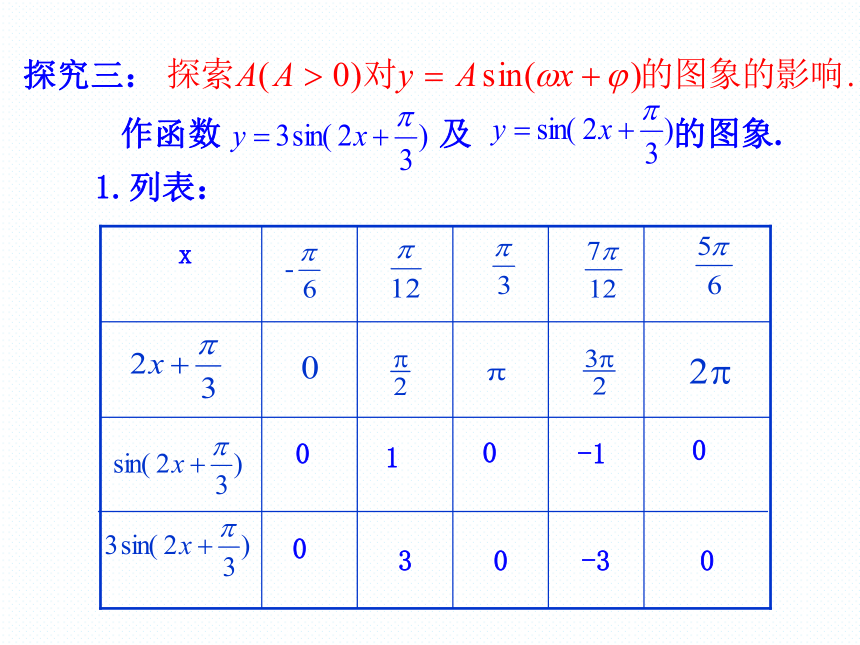
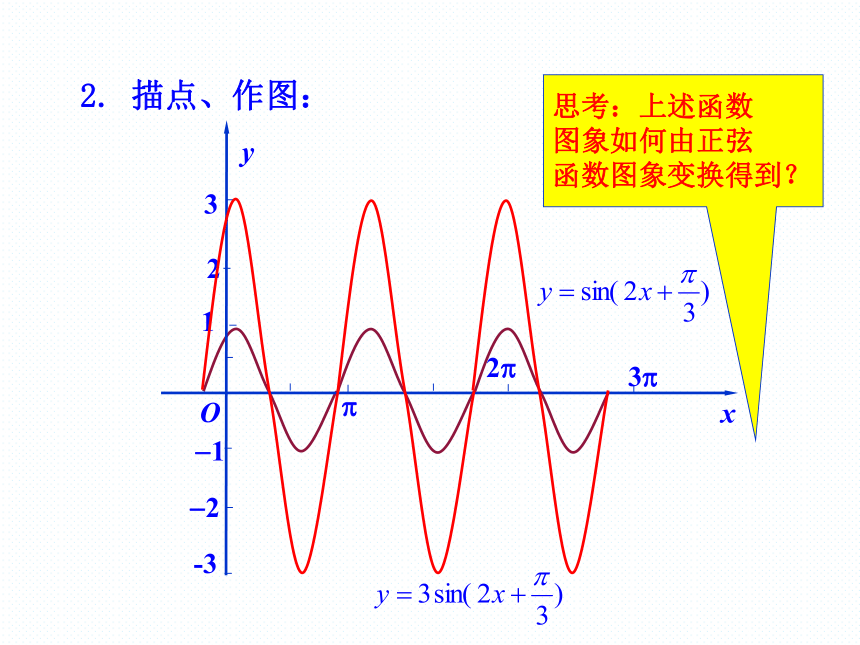
5.了解函数y=Asin(ωx+ )(A>0, >0)的振幅、周期、频率、相位、初相的概念.探究一: 与1-1规律一、φ对y=sin(x+φ)的图象的影响 一般地,函数y=sin(x+φ)(φ≠0)的图象,可以看作是把y=sinx的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位长度而得到.2? 探究二: 与xyO规律二、ω(ω>0)对y=sin(ωx+φ)的图象的影响 一般地,函数y=sin(ωx+φ)的图象,可以看作是把y=sin(x+φ)的图象上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的1/ω倍 (纵坐标不变)而得到的.1.列表:x010-10 作函数 及 的图象. 探究三: 2. 描点、作图:x?Oy2?12?2?13?-33思考:上述函数
图象如何由正弦
函数图象变换得到?规律三:可以看出 的图象可以看作是把
的图象上所有点的纵坐标伸长到原
来的3倍(横坐标不变)而得到的. φφφ参数φ, ω, A(ω>0, A>0)对图象的影响ω: 横坐标伸长或缩短为原来的1/ωA:纵坐标伸长或缩短为原来的A倍y=3sin(2x+ ) 根据周期性将作出的简图左右扩展。 总结函数 y =3sin(2 + )的简图得到的方式. 因为T=?,所以用“五点法”先作长度为一个周期的闭区间上的简图.函数 y=sinx y=sin(x+ ) 的图象(1)向左平移还可以通过平移伸缩变换得到.2??方法1:先平移后伸缩演示先平移后伸缩一般规律(2)向左平移
【思考交流】还有其他变换方式吗?2??y=sin2x① 方法2:先伸缩后平移演示先伸缩后平移一般规律y=Asin(ωx+φ)和y=sinx的图象两种变换关系图作y=sinx(长度为2?的某闭区间)y=sin(x+φ)y=sinωxy=sin(ωx+φ)作y=Asin(ωx+φ)的图象,先作一个周期闭区间上的图象再扩充到R上沿x轴平移 |φ|个单位纵坐标 变为A倍沿x轴平移 个单位1-12-2xoy3-32? 函数y=Asin(ωx+ ),A>0,ω>0,x∈[0,+∞)的物理意义. 物理中,描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关.课堂探究 2 单位时间内往复运动的次数f= ,
它叫做简谐运动的频率.ωx+ 叫做相位, 叫做初相(即当x=0时的相位). A表示做简谐运动的物体离开平衡位置的最大距离,通常把它叫做这个简谐运动的振幅. 往复运动一次所需要的时间 ,它叫做简谐运动的周期.例2.下图是某简谐运动的图象.试根据图象回答下列问题:
这个简谐运动的振幅、周期与频率各是多少?
(2)从O点算起, 到曲线上的哪一点, 表示完成了一次往复运动?如从A点算起呢?
(3)写出这个简谐运动的函数表达式.BOC2ADFy/cmEx/s0.40.81.2解:(1)从图象上可以看到,这个简谐运动的振幅为2cm;
周期0.8s;频率为(2)如果从O点算起,到曲线上的D点,表示完成了一次往复运动;如果从A点算起,则到曲线上的E点,表示完成了一次往复运动.(3)设这个简谐运动的函数表达式为于是所求函数表达式是例3.若简谐运动f(x)=2sin( x+ )(| |< )的图象过点(0,1),则该简谐运动的最小正周期T和初相 分别是 ( )AA.T=6, = B.T=6, =
C.T=6π, = D.T=6π, =ACD4.函数y=Asin(ωx+ )(A,ω, 为常数,A>0,ω>0)在闭区间[-π,0]上的图象如图
所示,则ω=________.35.已知函数 的图象为C,为了得到函数
的图象,只要把C上所有的点( )A.横坐标伸长到原来的3倍,纵坐标不变
B.横坐标缩短到原来的1/3,纵坐标不变
C.纵坐标伸长到原来的3倍,横坐标不变
D.纵坐标缩短到原来的1/3,横坐标不变ADC8.作出函数 和 在一个周期上的简图.1.作正弦函数y=Asin(?x+?) 的图象的方法:
(1)利用变换关系作图;
(2)用“五点法”作图.
2.“五点法”作图时,一般是令ωx+?取0, ,π, , 2π,算出相应的x的值,再列表,描点作图.
3.函数图象变换主要是平移与伸缩变换,要注意平移与伸缩的多少与方向.
2. 通过对函数y = Asin(ωx+φ)(A>0,ω>0)图象的探讨,让学生进一步掌握三角函数图象各种变换的内在联系.(重点、难点)1.5 函数 的图象(一)3.能用“五点法”作出函数y=Asin(ωx+ )(A>0,ω>0)的简图.(重点)
4.熟悉函数y=Asin(ωx+ )与y=sinx图象间的关系,知道y=Asin(ωx+ )的图象可由正弦曲线y=sinx怎样变化得到. (重点、难点)
5.了解函数y=Asin(ωx+ )(A>0, >0)的振幅、周期、频率、相位、初相的概念.探究一: 与1-1规律一、φ对y=sin(x+φ)的图象的影响 一般地,函数y=sin(x+φ)(φ≠0)的图象,可以看作是把y=sinx的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位长度而得到.2? 探究二: 与xyO规律二、ω(ω>0)对y=sin(ωx+φ)的图象的影响 一般地,函数y=sin(ωx+φ)的图象,可以看作是把y=sin(x+φ)的图象上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的1/ω倍 (纵坐标不变)而得到的.1.列表:x010-10 作函数 及 的图象. 探究三: 2. 描点、作图:x?Oy2?12?2?13?-33思考:上述函数
图象如何由正弦
函数图象变换得到?规律三:可以看出 的图象可以看作是把
的图象上所有点的纵坐标伸长到原
来的3倍(横坐标不变)而得到的. φφφ参数φ, ω, A(ω>0, A>0)对图象的影响ω: 横坐标伸长或缩短为原来的1/ωA:纵坐标伸长或缩短为原来的A倍y=3sin(2x+ ) 根据周期性将作出的简图左右扩展。 总结函数 y =3sin(2 + )的简图得到的方式. 因为T=?,所以用“五点法”先作长度为一个周期的闭区间上的简图.函数 y=sinx y=sin(x+ ) 的图象(1)向左平移还可以通过平移伸缩变换得到.2??方法1:先平移后伸缩演示先平移后伸缩一般规律(2)向左平移
【思考交流】还有其他变换方式吗?2??y=sin2x① 方法2:先伸缩后平移演示先伸缩后平移一般规律y=Asin(ωx+φ)和y=sinx的图象两种变换关系图作y=sinx(长度为2?的某闭区间)y=sin(x+φ)y=sinωxy=sin(ωx+φ)作y=Asin(ωx+φ)的图象,先作一个周期闭区间上的图象再扩充到R上沿x轴平移 |φ|个单位纵坐标 变为A倍沿x轴平移 个单位1-12-2xoy3-32? 函数y=Asin(ωx+ ),A>0,ω>0,x∈[0,+∞)的物理意义. 物理中,描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关.课堂探究 2 单位时间内往复运动的次数f= ,
它叫做简谐运动的频率.ωx+ 叫做相位, 叫做初相(即当x=0时的相位). A表示做简谐运动的物体离开平衡位置的最大距离,通常把它叫做这个简谐运动的振幅. 往复运动一次所需要的时间 ,它叫做简谐运动的周期.例2.下图是某简谐运动的图象.试根据图象回答下列问题:
这个简谐运动的振幅、周期与频率各是多少?
(2)从O点算起, 到曲线上的哪一点, 表示完成了一次往复运动?如从A点算起呢?
(3)写出这个简谐运动的函数表达式.BOC2ADFy/cmEx/s0.40.81.2解:(1)从图象上可以看到,这个简谐运动的振幅为2cm;
周期0.8s;频率为(2)如果从O点算起,到曲线上的D点,表示完成了一次往复运动;如果从A点算起,则到曲线上的E点,表示完成了一次往复运动.(3)设这个简谐运动的函数表达式为于是所求函数表达式是例3.若简谐运动f(x)=2sin( x+ )(| |< )的图象过点(0,1),则该简谐运动的最小正周期T和初相 分别是 ( )AA.T=6, = B.T=6, =
C.T=6π, = D.T=6π, =ACD4.函数y=Asin(ωx+ )(A,ω, 为常数,A>0,ω>0)在闭区间[-π,0]上的图象如图
所示,则ω=________.35.已知函数 的图象为C,为了得到函数
的图象,只要把C上所有的点( )A.横坐标伸长到原来的3倍,纵坐标不变
B.横坐标缩短到原来的1/3,纵坐标不变
C.纵坐标伸长到原来的3倍,横坐标不变
D.纵坐标缩短到原来的1/3,横坐标不变ADC8.作出函数 和 在一个周期上的简图.1.作正弦函数y=Asin(?x+?) 的图象的方法:
(1)利用变换关系作图;
(2)用“五点法”作图.
2.“五点法”作图时,一般是令ωx+?取0, ,π, , 2π,算出相应的x的值,再列表,描点作图.
3.函数图象变换主要是平移与伸缩变换,要注意平移与伸缩的多少与方向.
