山东省巨野县第一中学人教版高中数学选修2-3课件:1.3.2“杨辉三角”与二项式系数的性质 (共18张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教版高中数学选修2-3课件:1.3.2“杨辉三角”与二项式系数的性质 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 454.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-02 17:28:35 | ||
图片预览



文档简介
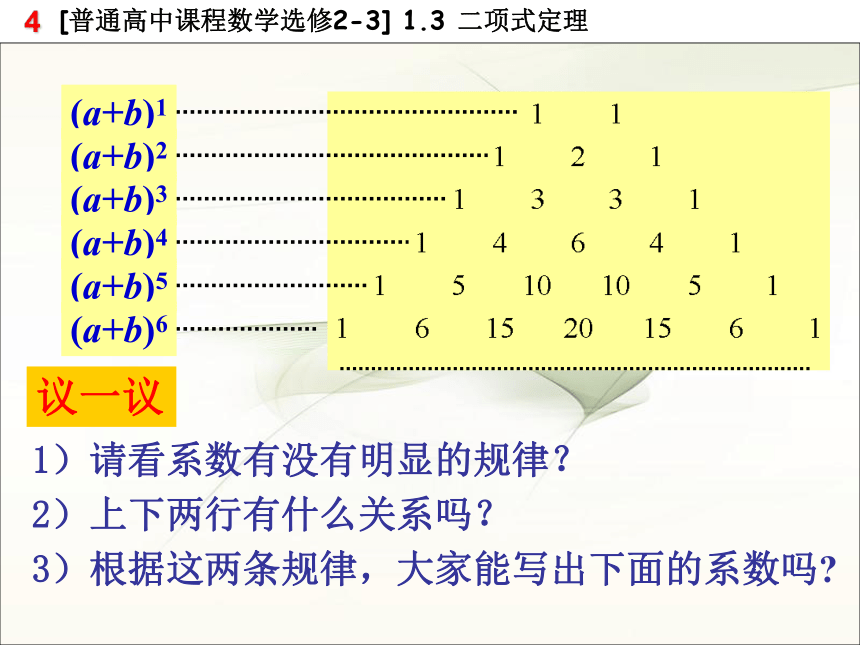
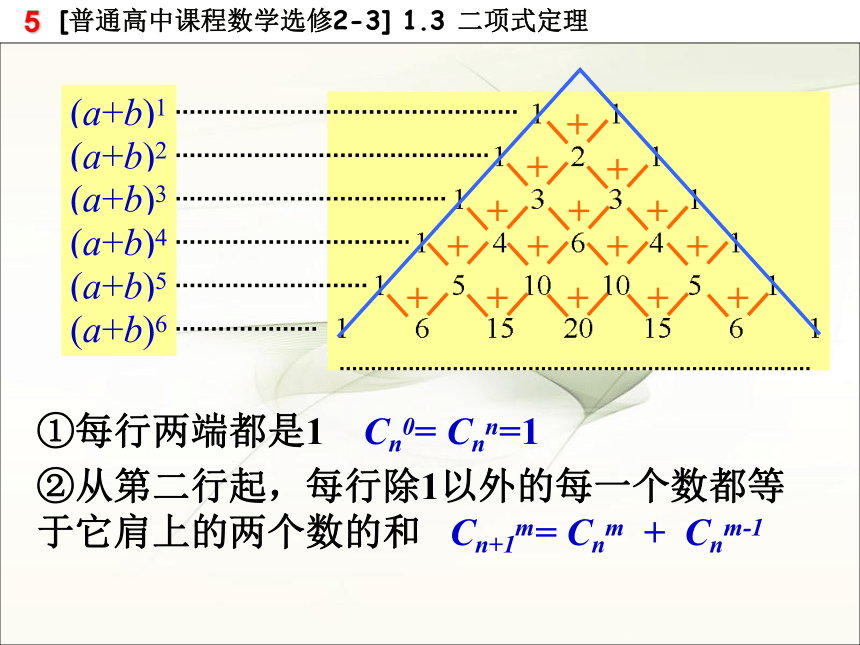
课件18张PPT。1.求(1 + x + x2)(1-x)10展开式中含 x 项的系数3.求(1+x)+(1+x)2+…+(1+x)10展开式中x3的系数6.若( x + 1 )n = x n +…+ ax3 + bx2 +…+1(n∈N*), 且 a : b=3 : 1 ,那么 n =_____ (95上海高考) 2.,则1.3.2 “杨辉三角”与二项式系数的性质新课引入二项展开式中的二项式系数指的是那些?共有多少个? 下面我们来研究二项式系数有些什么性质?我们先通过观察n为特殊值时,二项式系数有什么特点?议一议1)请看系数有没有明显的规律?2)上下两行有什么关系吗? 3)根据这两条规律,大家能写出下面的系数吗?①每行两端都是1 Cn0= Cnn=1
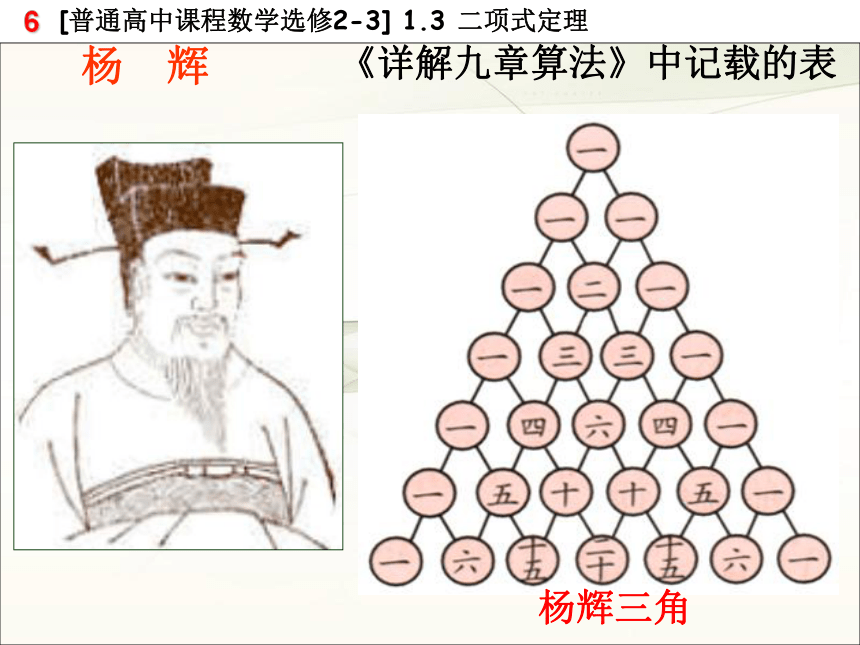
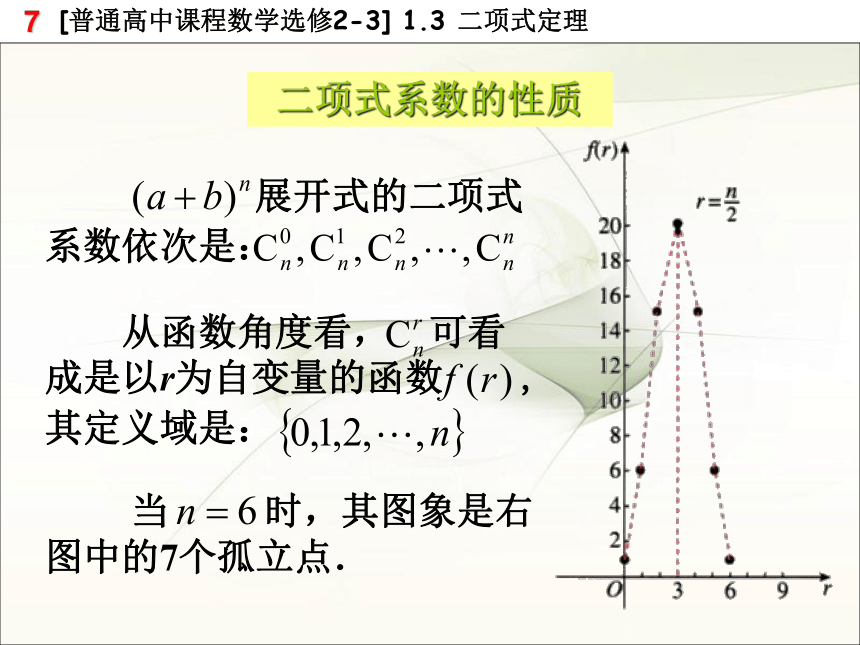
②从第二行起,每行除1以外的每一个数都等于它肩上的两个数的和 Cn+1m= Cnm + Cnm-1《详解九章算法》中记载的表杨 辉杨辉三角二项式系数的性质 展开式的二项式系数依次是: 从函数角度看, 可看成是以r为自变量的函数 ,其定义域是: 当 时,其图象是右图中的7个孤立点.①对称性 与首末两端“等距离”的两个二项式系数相等. 这一性质可直接由公式
得到.图象的对称轴:二项式系数的性质2、若(a+b)n的展开式中,第三项的二项式系数与第七项的二项式系数相等,知识对接测查11、在(a+b)6展开式中,与倒数第三项二项式系数相等是( )A 第2项 B 第3项 C 第4项 D 第5项则n=__________B8②增减性与最大值 由于:所以 相对于 的增减情况由 决定二项式系数的性质由: 即二项式系数前半部分是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。 可知,当 时,②增减性与最大值 二项式系数的性质1.在(1+x)10的展开式中,二项式系数最大为 ;
在(1-x)11的展开式中,二项式系数最大为 .3.在二项式(x-1)11的展开式中,求系数最小的项的系数。最大的系数呢?知识对接测查22.指出(a+2b)15的展开式中哪些项的二项式系数最大,并求出其最大的二项式系数变式:若将“只有第10项”改为“第10项”呢?解③各二项式系数的和 在二项式定理中,令 ,则: 这就是说, 的展开式的各二项式系数的和等于:同时由于 ,上式还可以写成:这是组合总数公式. 二项式系数的性质例 证明在(a+b)n展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。在二项式定理中,令 ,则: 赋值法证明:知识对接测查3 2.求证:证明:∵倒序相加法(1)二项式系数的三个性质 (2) 数学思想:函数思想 a 单调性; b 图象;c 最值。小结6、已知a,b∈N,m,n ∈Z ,且2m + n = 0,如果二项式( ax m + bx n )12 的展开式中系数最大的项恰好是常数项,求 a : b 的取值范围。 解:令m (12 – r )+ nr = 0,将 n =﹣2m 代入,解得 r = 4
故T5 为常数项,且系数最大。
②从第二行起,每行除1以外的每一个数都等于它肩上的两个数的和 Cn+1m= Cnm + Cnm-1《详解九章算法》中记载的表杨 辉杨辉三角二项式系数的性质 展开式的二项式系数依次是: 从函数角度看, 可看成是以r为自变量的函数 ,其定义域是: 当 时,其图象是右图中的7个孤立点.①对称性 与首末两端“等距离”的两个二项式系数相等. 这一性质可直接由公式
得到.图象的对称轴:二项式系数的性质2、若(a+b)n的展开式中,第三项的二项式系数与第七项的二项式系数相等,知识对接测查11、在(a+b)6展开式中,与倒数第三项二项式系数相等是( )A 第2项 B 第3项 C 第4项 D 第5项则n=__________B8②增减性与最大值 由于:所以 相对于 的增减情况由 决定二项式系数的性质由: 即二项式系数前半部分是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。 可知,当 时,②增减性与最大值 二项式系数的性质1.在(1+x)10的展开式中,二项式系数最大为 ;
在(1-x)11的展开式中,二项式系数最大为 .3.在二项式(x-1)11的展开式中,求系数最小的项的系数。最大的系数呢?知识对接测查22.指出(a+2b)15的展开式中哪些项的二项式系数最大,并求出其最大的二项式系数变式:若将“只有第10项”改为“第10项”呢?解③各二项式系数的和 在二项式定理中,令 ,则: 这就是说, 的展开式的各二项式系数的和等于:同时由于 ,上式还可以写成:这是组合总数公式. 二项式系数的性质例 证明在(a+b)n展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。在二项式定理中,令 ,则: 赋值法证明:知识对接测查3 2.求证:证明:∵倒序相加法(1)二项式系数的三个性质 (2) 数学思想:函数思想 a 单调性; b 图象;c 最值。小结6、已知a,b∈N,m,n ∈Z ,且2m + n = 0,如果二项式( ax m + bx n )12 的展开式中系数最大的项恰好是常数项,求 a : b 的取值范围。 解:令m (12 – r )+ nr = 0,将 n =﹣2m 代入,解得 r = 4
故T5 为常数项,且系数最大。
