专题十九二次函数等腰三角形存在性问题(含解析) 2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题十九二次函数等腰三角形存在性问题(含解析) 2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 243.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 12:30:58 | ||
图片预览




文档简介
二次函数等腰三角形存在性问题
模型原理
1.两圆一线法
前提: “两定一动”型等腰三角形可借助“两圆一线”法定性分析:
如图,使△ABC构成等腰三角形的点C必在“两圆一线”上,所谓两圆,即分别以点A、B为圆心,线段AB的长为半径作圆,对应以AB为腰的两种情形;
所谓一线,即线段AB的中垂线,对应以AB为底的一种情形;
此“两圆一线”上除不能构成三角形的点外,皆为所求点C.
“两圆一线”法的优势在于可以精准作图,清楚直观.
【知识复习】
1.对已知线段AB和直线l,要在直线l上找点P、使△ABP为等腰三角形,有以下方法:①几何法(两圆一线)
②代数法
设点P的坐标为(m,n),利用两点间的距离公式表示出AB、AP、BP的长度,然后关于底边的情况作分类讨论.
注意事项:
对于等腰三角形存在性问题,最右图中的直线 k是线段 AB 的中垂线、它与直线l的交点. 满足 即此时点. 是所求等腰三角形的顶点;这里用到了线段垂直平分线的性质和判定.
真题精炼
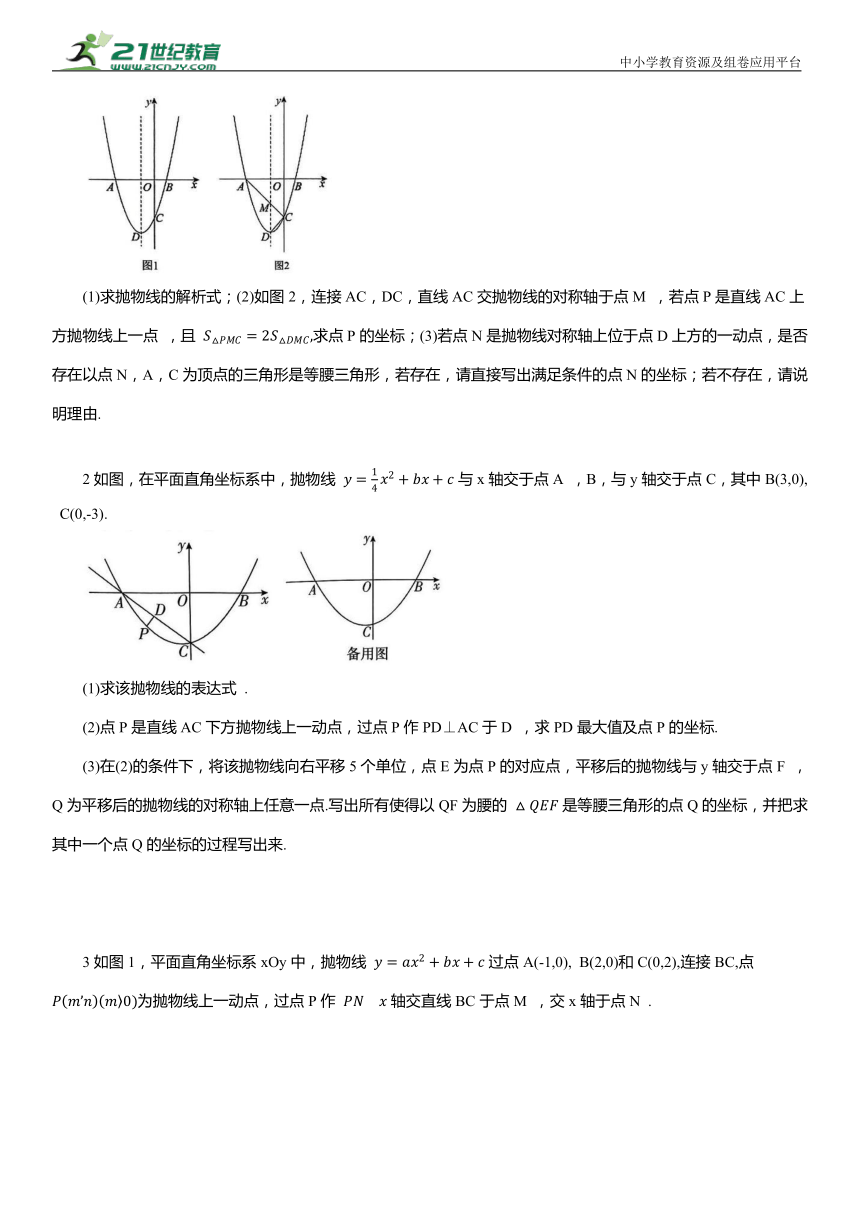
1如图1,抛物线 与x轴交于点A(-3,0)和点B(1,0), 与y轴交于点C.点D是抛物线的顶点 .
(1)求抛物线的解析式;(2)如图2,连接AC,DC,直线AC交抛物线的对称轴于点M ,若点P是直线AC上方抛物线上一点 ,且 求点P的坐标;(3)若点N是抛物线对称轴上位于点D上方的一动点,是否存在以点N,A,C为顶点的三角形是等腰三角形,若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
2如图,在平面直角坐标系中,抛物线 与x轴交于点A ,B,与y轴交于点C,其中B(3,0), C(0,-3).
(1)求该抛物线的表达式 .
(2)点P是直线AC下方抛物线上一动点,过点P作PD⊥AC于D ,求PD最大值及点P的坐标.
(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F ,Q为平移后的抛物线的对称轴上任意一点.写出所有使得以QF为腰的 是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.
3如图1,平面直角坐标系xOy中,抛物线 过点A(-1,0), B(2,0)和C(0,2),连接BC,点 为抛物线上一动点,过点P作 轴交直线BC于点M ,交x轴于点N .
(1)直接写出抛物线和直线BC的解析式;
(2)如图2, 连接OM,当 为等腰三角形时,求m的值;
4如图,抛物线 过点A(-1,0),B(3,0) , 与y轴交于点C .
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上一动点,当△PCB是以BC为底边的等腰三角形时,求点P的坐标;
5如图,抛物线 的对称轴是直线a ,与x轴交于点A , B(3,0), 与y轴交于点C,
连接AC.
(1)求此抛物线的解析式 ;
(2)已知点D是第一象限内抛物线上的一个动点,过点D作 轴,垂足为点M ,DM交直线BC于点N ,是否存在这样的点N ,使得以A,C,N为顶点的三角形是等腰三角形.若存在,请求出点N的坐标,若不存在,请说明理由 ;
6综合与探究
如图,二次函数 的图象与x轴交于A ,B两点(点A在点B的左侧),与y轴交于点C.点P是第一象限内二次函数图象上的一个动点,设点P的横坐标为m .过点P作直线 轴于点D ,作直线BC交PD于点E .
(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式.
(2)当△CEP是以PE为底边的等腰三角形时,求点P的坐标.
1如图1,抛物线 与z轴交于点A(-3,0)和点B(1,0),与y轴交于点C、点D是抛物线的顶点.
(1)求抛物线的解析式;
(2)如图2,连接AC,DC,直线AC交抛物线的对称轴于点M ,若点P是直线AC上方抛物线上一点,且S△PMO=2S△DMC,求点P的坐标;
(3)若点N是抛物线对称轴上位于点D上方的一动点,是否存在以点N,A,C为顶点的三角形是等腰三角形,若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
【答案】
(2)P(1,0)或P(-4,5);
或 或(-1, - 1)或(-1, -3)
【解析】
【分析】
(1)待定系数法求解析式,即可求解;
(2)先求得C,M,D的坐标,根据勾股定理的逆定理得出△MOD是等腰三角形,进而根据 得出 ,连接MB,设MD交z轴于点E,则ME=EB=2得出△MBE是等腹直角三角形,进而得出 则点P与点B重合时符合题意,P(1,0),过点B作BP∥AO交抛物线于点P,得出直线BP的解析式为y=-x+1,联立抛物线解析式,即可求解;
(3)勾股定理求得AC ,AN ,CN ,根据等腰三角形的性质,分类讨论解方程,即可求解.【详解】
(1)解:∵抛物线 与x轴交于点A(-3,0)和点B(1,0),
抛物线的解析式为
(2)由 当x=0时,y=-3,则C(0,-3)
则D(-1,-4),对称轴为直线x=-1
设直线AC的解析式为y=k x+b ,代入A(-3,0),C(0,-3)
解得:
∴直线AC的解析式为y=-z-3,
当x=-1时,y=-2,则M(-1,-2)
∴△MCD是等腰三角形,
连接MB,设MD交x轴于点E,则ME=EB=2
∴△MBE是等腰直角三角形,
∴BM⊥AC
∴点P与点B重合时符合题意,P(1,0)
如图所示,过点B作BP∥AC交抛物线于点P,
设直线BP的解析式为y=-x+m,将B(1,0)代入得,
0=-1+m
解得:m=1
∴直线BP的解析式为y=-z+1
联立
解得:
∴P(-4,5)
综上所述, P(1,0)或P(-4,5);
(3)解:∵A(-3,0),C(0,-3),
∵点N是抛物线对称轴上位于点D上方的一动点,设N(-1,n)其中n >-4
①当AN=AC时, 解得:n= 或n=-
②当NA=NC时, 解得:n=-1
③当CA=CN时, 解得: 3或 (舍去)
综上所述,N(-1, )或( 或(-1, - 1)或
2.如图,在平面直角坐标系中,抛物线 与z轴交于点A,B,与y轴交于点C,其中B(3,0),C(0,-3).
(1)求该抛物线的表达式.
(2)点P是直线AC下方抛物线上一动点,过点P作PD⊥AC于点D,求PD的最大值及此时点P的坐标.
(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F ,Q为平移后的抛物线的对称轴上任意一点.写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.
【答案】
(2) PD的最大值为 ,此时
(3)Q点的坐标为 或 或
【解析】(1)将点B(3,0),
解得:
∴抛物线的表达式为
与z轴交于点A,B,
当y=(0时
解得
∴A(-4,0),
∵C(0,-3),
设直线AC的解析式为y= kz-3,
∴-4k-3=0,
解得
∴直线AC的解析式为
如图所示,过点P作PE⊥z轴于点E,交AC于点Q,
8 则Q
∵∠AQE=∠PQD,∠AEQ=∠QDP=90°,
∴∠OAC=∠QPD,
·OA=4,OO=3,
∴AC=5,
·当t=-2时, PD取得最大值为
(3)·.抛物线
将该抛物线向右平移5个单位,得到 对称轴为直线:
点/ 向右平移5个单位得到E
∵平移后的抛物线与y轴交于点F,令x=0,则
∴F(0,2).
∵Q为平移后的抛物线的对称轴上任意一点.
则Q点的横坐标为
设(
中小学教育资源及组卷应用平台
当QF=EF时(
解得:m=-1或m=5,
当QE=QF时
解得
综上所述,Q点的坐标为( ,-1)四( ,5)m ( ,
3.如图1,平面直角坐标系xOy中,抛物线 c过点A(-1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥α轴交直线BC于点M ,交m轴于点N.
(1)直接写出抛物线和直线BC的解析式;
(2)如图2,连接OM,当△OCM为等腰三角形时,求m的值;
【答案】(1)抛物线: 直线BC:y=-z+2(2)m=1或m= 或m=2
【解析】(1)解:∵抛物线过点A(-1,0), B(2,0),
、·抛物线的表达式为y=a(x+1)(x-2),
将点C(0,2)代入上式,得2=-2a,
∴a=-1.
∴抛物线的表达式为y=-(x+1)(x-2),
即
设直线BC的表达式为y= kz+t,
将点B(2,0),C(0,2)代入直线表达式,
得
解得
∴直线BC的表达式为y=-x+2.
(2)解:∵点M在直线BC上,且P(m,n),
∴点M的坐标为(m,-m+2).
当△OCM为等腰三角形时,
①若OM=OM,则( 即
解得m=1.
②若CM=OC,则 即
解得 (舍去)
③若OM=OC,则 即
解得m=0(舍去)或m=2.
综上所述m=1或
4如图,抛物线 c过点A(-1,0),B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上一动点,当△PCB是以BC为底边的等腰三角形时,求点P的坐标;
【答案】 (2)点P坐标为(1,1);
【解析】【分析】
(1)把A(-1,0),B(3,0)代入 c即可的得出抛物线解析式;
(2)通过题意可得出即P点在∠COB的平分线上且在抛物线的对称轴上利用等腰三角形的性质,即可得出P点的坐标;
(2)利用铅垂线ME,即可表达出S△BCM,再由S 即可列出方程求解(1)通过题意,得 解得 ∴抛物线解析式为:
(2)由(1)得 ∴点C(0,3),且点B(3,0),∴OC=OB=3.∵当△PCB是以BC为底边的等腰三角形∴PC=PB,∵OP=OP, ∴△COF≌△BOF,
设抛物线的对称轴与z轴交于H点,则∠OPH =90°.
∴∠OPH=∠POH=45°,∴OH=PH, ∵抛物线对称轴
【点睛】此题考查了求抛物线的解析式、等腰三角形的存在性问题,三角形的面积,掌握待定系数法求抛物线的解析式,等腰三角形与函数的特征,三角形面积与函数的做法是解题的关键.
5如图,抛物线y c的对称轴是直线x=1,与x轴交于点A ,B(3,0),与y轴交于点C,
(1)求此抛物线的解析式;
(2)已知点D是第一象限内抛物线上的一个动点,过点D作DM⊥x轴,垂足为点M ,DM交直线BC于点N,是否存在这样的点N,使得以A,C,N为顶点的三角形是等腰三角形、若存在,请求出点N的坐标,若不存在,请说明理由:
【答案】 (2)存在这样的点N(2,1)或 或 使得以A,O,N为顶点的三角形是等腰三角形
【解析】【分析】
(1)根据抛物线的对称轴是直线x=1,可得a=-1,再把点B(3,0)代入,即可求解;
(2)先求出. 设点N(m,-m+3) ,可得 再分三种情况讨论:当AC=AN时,当AC=CN时,当AN=CN时,即可求解;
(1)解:∵抛物线 c的对称轴是直线 解得:a=-1,∵抛物线过点B(3,0),∴-9+6+c=0,解得:c=3, ∴抛物线解析式为
(2)解:存在这样的点N,使得以A,C,N为顶点的三角形是等腰三角形.理由如下:令y=0,则 解得: ∴点A的坐标为(-1,0),∴OA=1,当x=0时,y=3, ∴点C的坐标为(0,3),即 设直线BC的解析式为y= kx+b(k≠0),把点B(3,0),C(0,3)代入得: 解得: ∴直线BC的解析式为y=-x+3,设点N(m,-m+3) , ∴MN=-m+3
当AC=AN时,2m -4m+10=10, 解得:m=2或0(舍去) , ∴此时点N(2,1) ; 当AC=CN时, 解得:m= - (舍去) , ∴此时点N 当AN=CN时, 解
得 ∴此时点N 综上所述,存在这样的点N(2,1)或 或 使得以A,C,N为顶点的三角形是等腰三角形;
6综合与探究
如图,二次函数 4的图象与z轴交于A,B两点(点A在点B的左侧),与y轴交于点C.点P是第一象限内二次函数图象上的一个动点,设点P的横坐标为m ,过点P作直线PD⊥x轴于点D ,作直线BC交PD于点E.
(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式.
(2)当△CEP是以PE为底边的等腰三角形时,求点P的坐标.
【答案】(1) A(-2,0),B(8,0),C(0,4),
(2) P(4,6).
【解析】(1)在 中,
令z=0得y=4,令y=0得z=8或x=-2,
∴A(-2,0),B(8,0),C(0,4).
设直线BC的函数表达式为y= kz+4,将B(8,0)代入得:
8k+4=0,
解得
∴直线BC的函数表达式为
(2)过C作CG⊥PD于G,如图:
∴四边形CODG是矩形,
∴DG=00=4,CG=OD=m,
∵CP=CE,CG⊥PD,
∵∠GCE=∠OBC,∠CGE=90°=∠BOC,
∴△CGE∽△BOC,
1
解得m=0(舍去)或m=4,
∴P(4,6).
【标注】【知识点】二次函数与全等三角形结合
模型原理
1.两圆一线法
前提: “两定一动”型等腰三角形可借助“两圆一线”法定性分析:
如图,使△ABC构成等腰三角形的点C必在“两圆一线”上,所谓两圆,即分别以点A、B为圆心,线段AB的长为半径作圆,对应以AB为腰的两种情形;
所谓一线,即线段AB的中垂线,对应以AB为底的一种情形;
此“两圆一线”上除不能构成三角形的点外,皆为所求点C.
“两圆一线”法的优势在于可以精准作图,清楚直观.
【知识复习】
1.对已知线段AB和直线l,要在直线l上找点P、使△ABP为等腰三角形,有以下方法:①几何法(两圆一线)
②代数法
设点P的坐标为(m,n),利用两点间的距离公式表示出AB、AP、BP的长度,然后关于底边的情况作分类讨论.
注意事项:
对于等腰三角形存在性问题,最右图中的直线 k是线段 AB 的中垂线、它与直线l的交点. 满足 即此时点. 是所求等腰三角形的顶点;这里用到了线段垂直平分线的性质和判定.
真题精炼
1如图1,抛物线 与x轴交于点A(-3,0)和点B(1,0), 与y轴交于点C.点D是抛物线的顶点 .
(1)求抛物线的解析式;(2)如图2,连接AC,DC,直线AC交抛物线的对称轴于点M ,若点P是直线AC上方抛物线上一点 ,且 求点P的坐标;(3)若点N是抛物线对称轴上位于点D上方的一动点,是否存在以点N,A,C为顶点的三角形是等腰三角形,若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
2如图,在平面直角坐标系中,抛物线 与x轴交于点A ,B,与y轴交于点C,其中B(3,0), C(0,-3).
(1)求该抛物线的表达式 .
(2)点P是直线AC下方抛物线上一动点,过点P作PD⊥AC于D ,求PD最大值及点P的坐标.
(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F ,Q为平移后的抛物线的对称轴上任意一点.写出所有使得以QF为腰的 是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.
3如图1,平面直角坐标系xOy中,抛物线 过点A(-1,0), B(2,0)和C(0,2),连接BC,点 为抛物线上一动点,过点P作 轴交直线BC于点M ,交x轴于点N .
(1)直接写出抛物线和直线BC的解析式;
(2)如图2, 连接OM,当 为等腰三角形时,求m的值;
4如图,抛物线 过点A(-1,0),B(3,0) , 与y轴交于点C .
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上一动点,当△PCB是以BC为底边的等腰三角形时,求点P的坐标;
5如图,抛物线 的对称轴是直线a ,与x轴交于点A , B(3,0), 与y轴交于点C,
连接AC.
(1)求此抛物线的解析式 ;
(2)已知点D是第一象限内抛物线上的一个动点,过点D作 轴,垂足为点M ,DM交直线BC于点N ,是否存在这样的点N ,使得以A,C,N为顶点的三角形是等腰三角形.若存在,请求出点N的坐标,若不存在,请说明理由 ;
6综合与探究
如图,二次函数 的图象与x轴交于A ,B两点(点A在点B的左侧),与y轴交于点C.点P是第一象限内二次函数图象上的一个动点,设点P的横坐标为m .过点P作直线 轴于点D ,作直线BC交PD于点E .
(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式.
(2)当△CEP是以PE为底边的等腰三角形时,求点P的坐标.
1如图1,抛物线 与z轴交于点A(-3,0)和点B(1,0),与y轴交于点C、点D是抛物线的顶点.
(1)求抛物线的解析式;
(2)如图2,连接AC,DC,直线AC交抛物线的对称轴于点M ,若点P是直线AC上方抛物线上一点,且S△PMO=2S△DMC,求点P的坐标;
(3)若点N是抛物线对称轴上位于点D上方的一动点,是否存在以点N,A,C为顶点的三角形是等腰三角形,若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
【答案】
(2)P(1,0)或P(-4,5);
或 或(-1, - 1)或(-1, -3)
【解析】
【分析】
(1)待定系数法求解析式,即可求解;
(2)先求得C,M,D的坐标,根据勾股定理的逆定理得出△MOD是等腰三角形,进而根据 得出 ,连接MB,设MD交z轴于点E,则ME=EB=2得出△MBE是等腹直角三角形,进而得出 则点P与点B重合时符合题意,P(1,0),过点B作BP∥AO交抛物线于点P,得出直线BP的解析式为y=-x+1,联立抛物线解析式,即可求解;
(3)勾股定理求得AC ,AN ,CN ,根据等腰三角形的性质,分类讨论解方程,即可求解.【详解】
(1)解:∵抛物线 与x轴交于点A(-3,0)和点B(1,0),
抛物线的解析式为
(2)由 当x=0时,y=-3,则C(0,-3)
则D(-1,-4),对称轴为直线x=-1
设直线AC的解析式为y=k x+b ,代入A(-3,0),C(0,-3)
解得:
∴直线AC的解析式为y=-z-3,
当x=-1时,y=-2,则M(-1,-2)
∴△MCD是等腰三角形,
连接MB,设MD交x轴于点E,则ME=EB=2
∴△MBE是等腰直角三角形,
∴BM⊥AC
∴点P与点B重合时符合题意,P(1,0)
如图所示,过点B作BP∥AC交抛物线于点P,
设直线BP的解析式为y=-x+m,将B(1,0)代入得,
0=-1+m
解得:m=1
∴直线BP的解析式为y=-z+1
联立
解得:
∴P(-4,5)
综上所述, P(1,0)或P(-4,5);
(3)解:∵A(-3,0),C(0,-3),
∵点N是抛物线对称轴上位于点D上方的一动点,设N(-1,n)其中n >-4
①当AN=AC时, 解得:n= 或n=-
②当NA=NC时, 解得:n=-1
③当CA=CN时, 解得: 3或 (舍去)
综上所述,N(-1, )或( 或(-1, - 1)或
2.如图,在平面直角坐标系中,抛物线 与z轴交于点A,B,与y轴交于点C,其中B(3,0),C(0,-3).
(1)求该抛物线的表达式.
(2)点P是直线AC下方抛物线上一动点,过点P作PD⊥AC于点D,求PD的最大值及此时点P的坐标.
(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F ,Q为平移后的抛物线的对称轴上任意一点.写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.
【答案】
(2) PD的最大值为 ,此时
(3)Q点的坐标为 或 或
【解析】(1)将点B(3,0),
解得:
∴抛物线的表达式为
与z轴交于点A,B,
当y=(0时
解得
∴A(-4,0),
∵C(0,-3),
设直线AC的解析式为y= kz-3,
∴-4k-3=0,
解得
∴直线AC的解析式为
如图所示,过点P作PE⊥z轴于点E,交AC于点Q,
8 则Q
∵∠AQE=∠PQD,∠AEQ=∠QDP=90°,
∴∠OAC=∠QPD,
·OA=4,OO=3,
∴AC=5,
·当t=-2时, PD取得最大值为
(3)·.抛物线
将该抛物线向右平移5个单位,得到 对称轴为直线:
点/ 向右平移5个单位得到E
∵平移后的抛物线与y轴交于点F,令x=0,则
∴F(0,2).
∵Q为平移后的抛物线的对称轴上任意一点.
则Q点的横坐标为
设(
中小学教育资源及组卷应用平台
当QF=EF时(
解得:m=-1或m=5,
当QE=QF时
解得
综上所述,Q点的坐标为( ,-1)四( ,5)m ( ,
3.如图1,平面直角坐标系xOy中,抛物线 c过点A(-1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥α轴交直线BC于点M ,交m轴于点N.
(1)直接写出抛物线和直线BC的解析式;
(2)如图2,连接OM,当△OCM为等腰三角形时,求m的值;
【答案】(1)抛物线: 直线BC:y=-z+2(2)m=1或m= 或m=2
【解析】(1)解:∵抛物线过点A(-1,0), B(2,0),
、·抛物线的表达式为y=a(x+1)(x-2),
将点C(0,2)代入上式,得2=-2a,
∴a=-1.
∴抛物线的表达式为y=-(x+1)(x-2),
即
设直线BC的表达式为y= kz+t,
将点B(2,0),C(0,2)代入直线表达式,
得
解得
∴直线BC的表达式为y=-x+2.
(2)解:∵点M在直线BC上,且P(m,n),
∴点M的坐标为(m,-m+2).
当△OCM为等腰三角形时,
①若OM=OM,则( 即
解得m=1.
②若CM=OC,则 即
解得 (舍去)
③若OM=OC,则 即
解得m=0(舍去)或m=2.
综上所述m=1或
4如图,抛物线 c过点A(-1,0),B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上一动点,当△PCB是以BC为底边的等腰三角形时,求点P的坐标;
【答案】 (2)点P坐标为(1,1);
【解析】【分析】
(1)把A(-1,0),B(3,0)代入 c即可的得出抛物线解析式;
(2)通过题意可得出即P点在∠COB的平分线上且在抛物线的对称轴上利用等腰三角形的性质,即可得出P点的坐标;
(2)利用铅垂线ME,即可表达出S△BCM,再由S 即可列出方程求解(1)通过题意,得 解得 ∴抛物线解析式为:
(2)由(1)得 ∴点C(0,3),且点B(3,0),∴OC=OB=3.∵当△PCB是以BC为底边的等腰三角形∴PC=PB,∵OP=OP, ∴△COF≌△BOF,
设抛物线的对称轴与z轴交于H点,则∠OPH =90°.
∴∠OPH=∠POH=45°,∴OH=PH, ∵抛物线对称轴
【点睛】此题考查了求抛物线的解析式、等腰三角形的存在性问题,三角形的面积,掌握待定系数法求抛物线的解析式,等腰三角形与函数的特征,三角形面积与函数的做法是解题的关键.
5如图,抛物线y c的对称轴是直线x=1,与x轴交于点A ,B(3,0),与y轴交于点C,
(1)求此抛物线的解析式;
(2)已知点D是第一象限内抛物线上的一个动点,过点D作DM⊥x轴,垂足为点M ,DM交直线BC于点N,是否存在这样的点N,使得以A,C,N为顶点的三角形是等腰三角形、若存在,请求出点N的坐标,若不存在,请说明理由:
【答案】 (2)存在这样的点N(2,1)或 或 使得以A,O,N为顶点的三角形是等腰三角形
【解析】【分析】
(1)根据抛物线的对称轴是直线x=1,可得a=-1,再把点B(3,0)代入,即可求解;
(2)先求出. 设点N(m,-m+3) ,可得 再分三种情况讨论:当AC=AN时,当AC=CN时,当AN=CN时,即可求解;
(1)解:∵抛物线 c的对称轴是直线 解得:a=-1,∵抛物线过点B(3,0),∴-9+6+c=0,解得:c=3, ∴抛物线解析式为
(2)解:存在这样的点N,使得以A,C,N为顶点的三角形是等腰三角形.理由如下:令y=0,则 解得: ∴点A的坐标为(-1,0),∴OA=1,当x=0时,y=3, ∴点C的坐标为(0,3),即 设直线BC的解析式为y= kx+b(k≠0),把点B(3,0),C(0,3)代入得: 解得: ∴直线BC的解析式为y=-x+3,设点N(m,-m+3) , ∴MN=-m+3
当AC=AN时,2m -4m+10=10, 解得:m=2或0(舍去) , ∴此时点N(2,1) ; 当AC=CN时, 解得:m= - (舍去) , ∴此时点N 当AN=CN时, 解
得 ∴此时点N 综上所述,存在这样的点N(2,1)或 或 使得以A,C,N为顶点的三角形是等腰三角形;
6综合与探究
如图,二次函数 4的图象与z轴交于A,B两点(点A在点B的左侧),与y轴交于点C.点P是第一象限内二次函数图象上的一个动点,设点P的横坐标为m ,过点P作直线PD⊥x轴于点D ,作直线BC交PD于点E.
(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式.
(2)当△CEP是以PE为底边的等腰三角形时,求点P的坐标.
【答案】(1) A(-2,0),B(8,0),C(0,4),
(2) P(4,6).
【解析】(1)在 中,
令z=0得y=4,令y=0得z=8或x=-2,
∴A(-2,0),B(8,0),C(0,4).
设直线BC的函数表达式为y= kz+4,将B(8,0)代入得:
8k+4=0,
解得
∴直线BC的函数表达式为
(2)过C作CG⊥PD于G,如图:
∴四边形CODG是矩形,
∴DG=00=4,CG=OD=m,
∵CP=CE,CG⊥PD,
∵∠GCE=∠OBC,∠CGE=90°=∠BOC,
∴△CGE∽△BOC,
1
解得m=0(舍去)或m=4,
∴P(4,6).
【标注】【知识点】二次函数与全等三角形结合
同课章节目录
