专题十一 中点模型(含解析) 2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题十一 中点模型(含解析) 2025年中考数学几何模型专题讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 727.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 00:00:00 | ||
图片预览

文档简介
中点模型
模型原理
三角形是是历年中考命题的热点 .其中,三角形各边中点、中线及中位线的应用,是中考的必考内容.与中点有关的辅助线,我们总结下列四种类型:
1.类型一见中线,可倍长
1.倍长中线或类中线(与中点有关的线段)构造全等三角形或平行四边形.如图.
2.有些几何题在利用“倍长中线”证完一次全等后,还需再证一次全等,即“二次全等”
在证明第二次全等时,难点通常会体现在倒角上,常见的倒角方法有:①“8”字型(如图1-8);
②平行线;③180°(平角 ;三角形内角和);
④360°(周角; 四边形内角和) ; ⑤小旗子(三角形外角); ⑥90°(互余角) .
2.类型二 见等腰三角形,想“三线合一”
已知等腰三角形底边的中点,可以考虑与顶点连接,用“三线合一”
3.类型三 见斜边,想中线
已知直角三角形斜边的中点,可以考虑构造斜边中线,目的是得到三条等线段和两对等角.
4.类型四 见多个中点,想中位线
已知三角形的两边有中点,可以连接这两个中点构造中位线;
已知一边中点,可以在另一边上取中点,连接构造中位线;
已知一边中点,过中点作平行线可构造相似三角形.
真题精炼
1.在Rt△ABC中,∠ACB=90°, AC= BC,过点B作BD//AC.
(1) 如图1,若点D在点B的左侧,连接CD, 过点A作AE⊥CD交BC于点E .若点E是BC的中点,求证:AC=2BD.
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF.过点F作FM⊥BG交AB于点M ,CN平分∠ACB交BG于点N,求证:
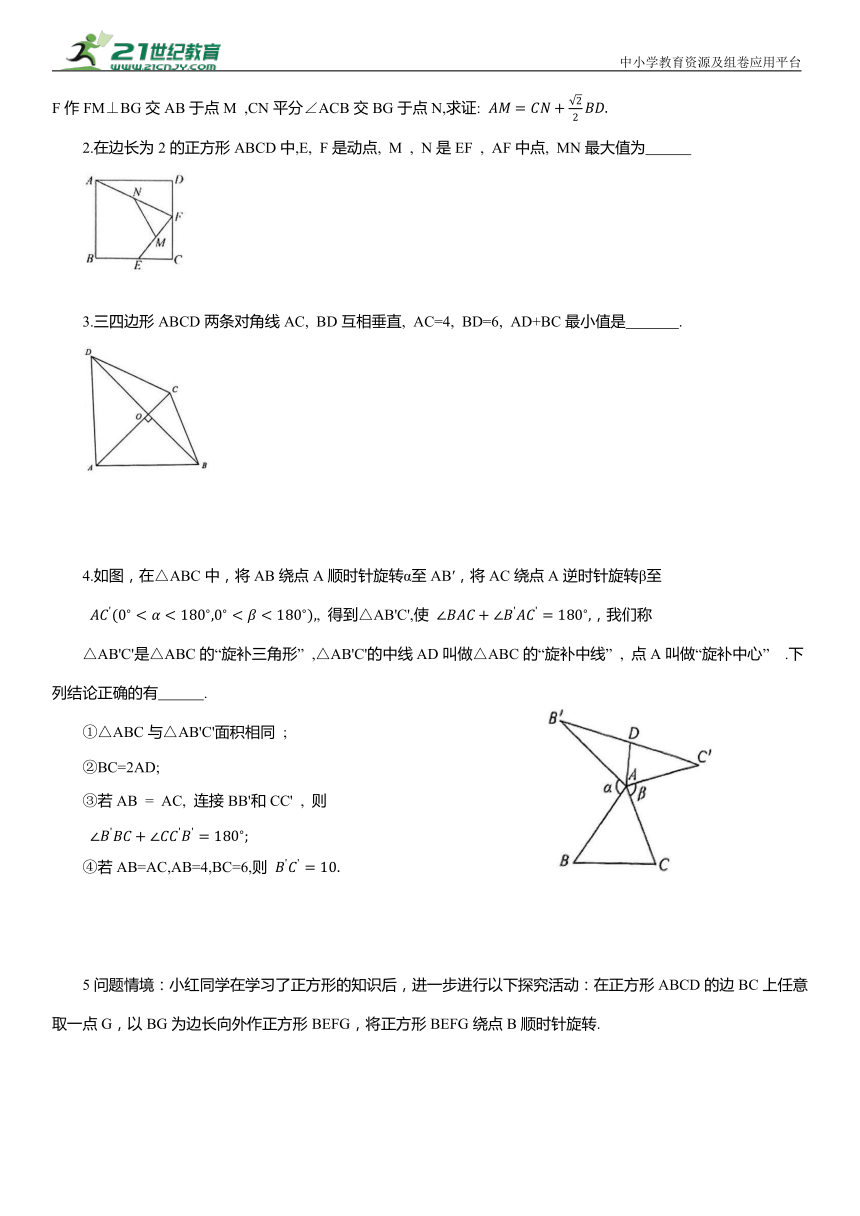
2.在边长为2的正方形ABCD中,E, F是动点, M , N是EF , AF中点, MN最大值为
3.三四边形ABCD两条对角线AC, BD互相垂直, AC=4, BD=6, AD+BC最小值是 .
4.如图,在△ABC中,将AB绕点A顺时针旋转α至AB′,将AC绕点A逆时针旋转β至
, 得到△AB'C',使 ,我们称
△AB'C'是△ABC的“旋补三角形” ,△AB'C'的中线AD叫做△ABC的“旋补中线” , 点A叫做“旋补中心” .下列结论正确的有 .
①△ABC与△AB'C'面积相同 ;
②BC=2AD;
③若AB = AC, 连接BB'和CC' , 则
④若AB=AC,AB=4,BC=6,则
5问题情境:小红同学在学习了正方形的知识后,进一步进行以下探究活动:在正方形ABCD的边BC上任意取一点G,以BG为边长向外作正方形BEFG,将正方形BEFG绕点B顺时针旋转.
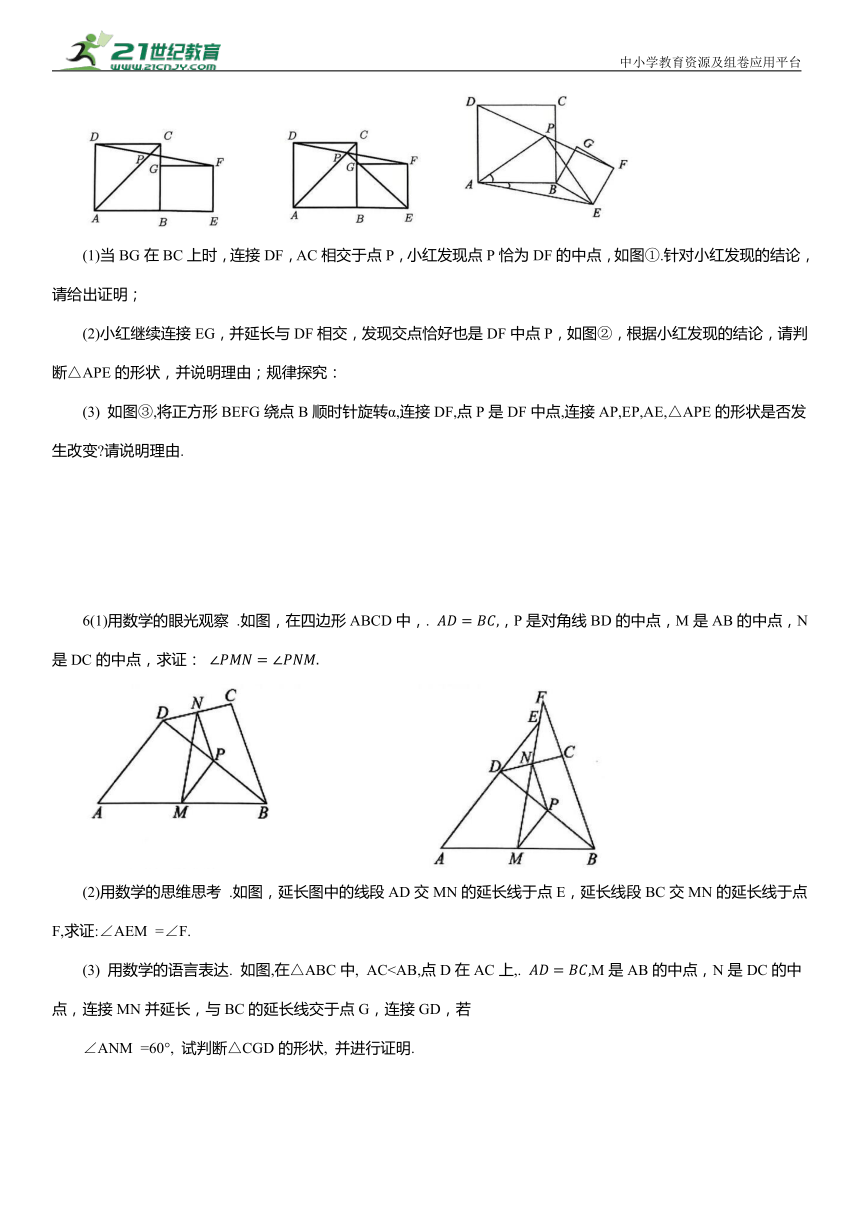
(1)当BG在BC上时,连接DF,AC相交于点P,小红发现点P恰为DF的中点,如图①.针对小红发现的结论,请给出证明;
(2)小红继续连接EG,并延长与DF相交,发现交点恰好也是DF中点P,如图②,根据小红发现的结论,请判断△APE的形状,并说明理由;规律探究:
(3) 如图③,将正方形BEFG绕点B顺时针旋转α,连接DF,点P是DF中点,连接AP,EP,AE,△APE的形状是否发生改变 请说明理由.
6(1)用数学的眼光观察 .如图,在四边形ABCD中,. ,P是对角线BD的中点,M是AB的中点,N是DC的中点,求证:
(2)用数学的思维思考 .如图,延长图中的线段AD交MN的延长线于点E,延长线段BC交MN的延长线于点F,求证:∠AEM =∠F.
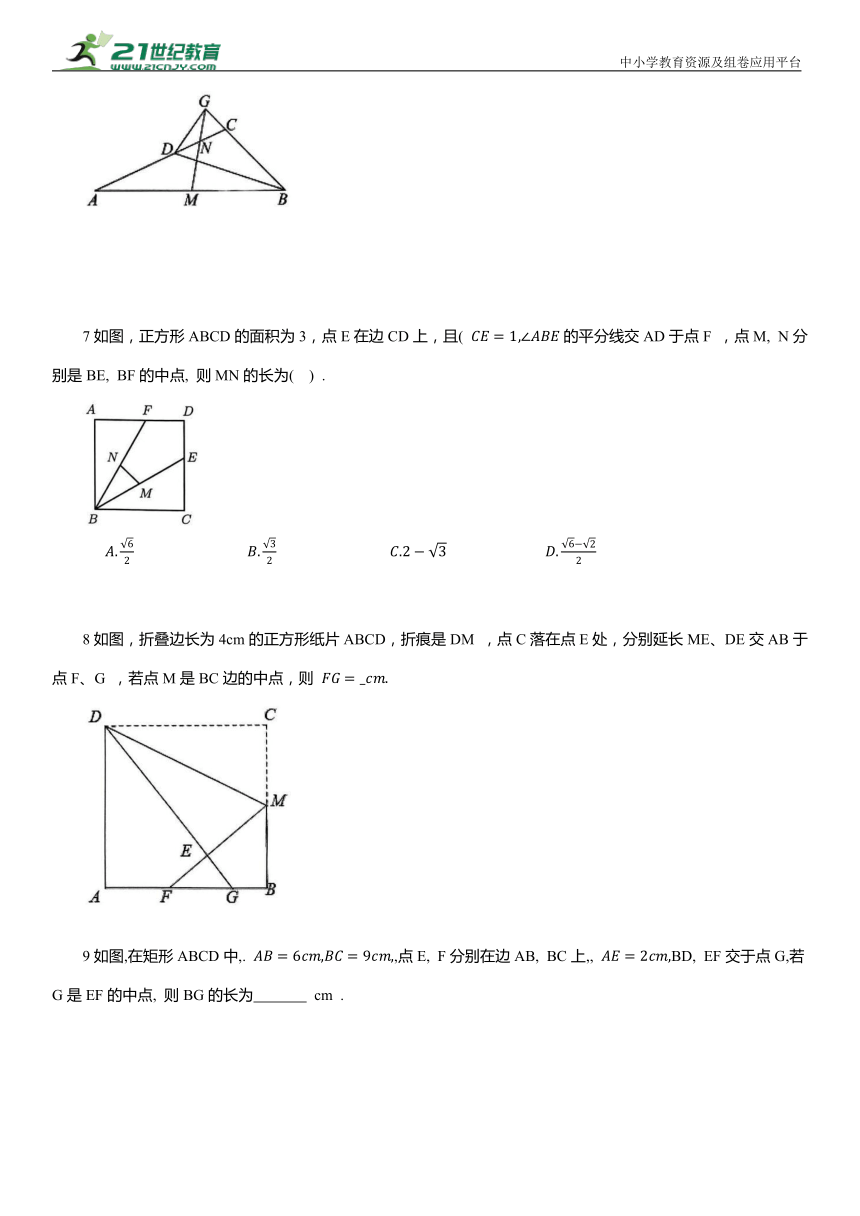
(3) 用数学的语言表达. 如图,在△ABC中, AC∠ANM =60°, 试判断△CGD的形状, 并进行证明.
7如图,正方形ABCD的面积为3,点E在边CD上,且( 的平分线交AD于点F ,点M, N分别是BE, BF的中点, 则MN的长为( ) .
8如图,折叠边长为4cm的正方形纸片ABCD,折痕是DM ,点C落在点E处,分别延长ME、DE交AB于点F、G ,若点M是BC边的中点,则
9如图,在矩形ABCD中,. ,点E, F分别在边AB, BC上,, BD, EF交于点G,若G是EF的中点, 则BG的长为 cm .
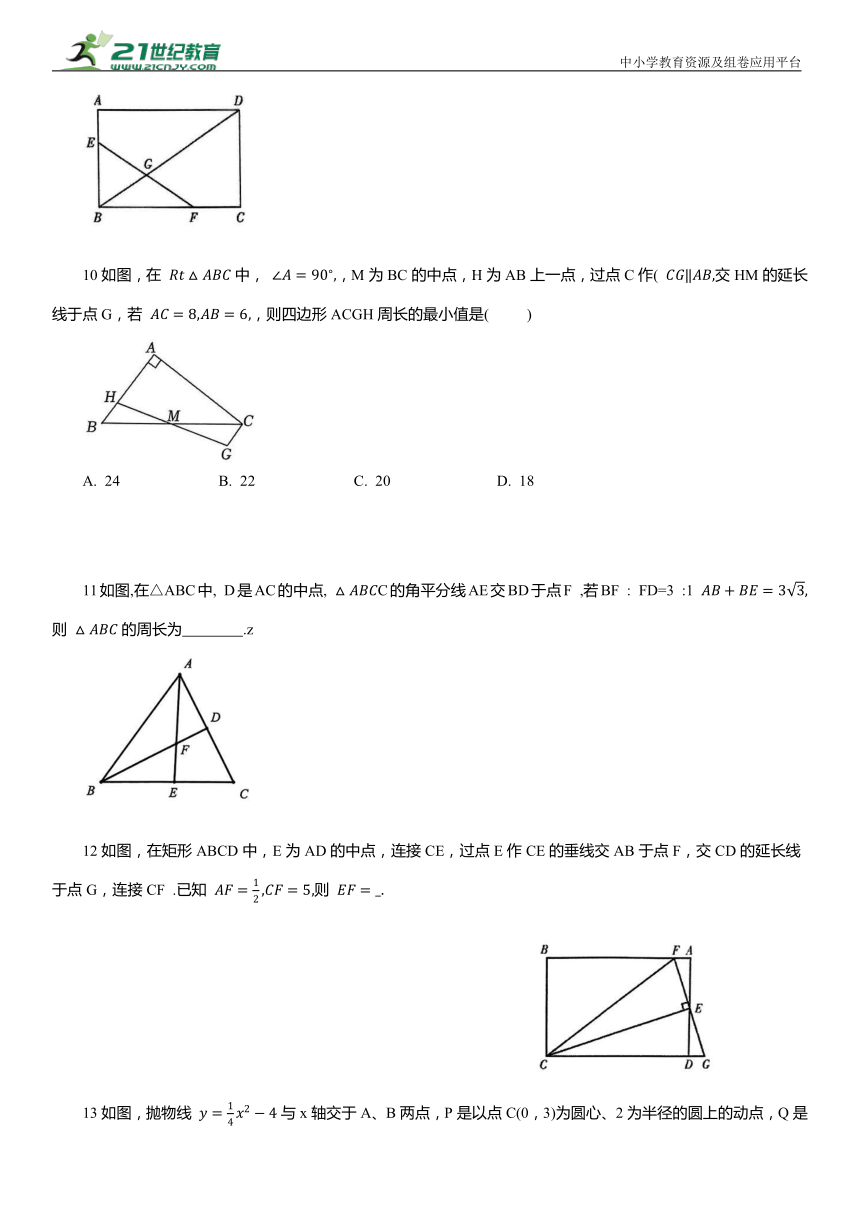
10如图,在 中, ,M为BC的中点,H为AB上一点,过点C作( 交HM的延长线于点G,若 ,则四边形ACGH周长的最小值是( )
A. 24 B. 22 C. 20 D. 18
11如图,在△ABC中, D是AC的中点, C的角平分线AE交BD于点F ,若BF : FD=3 :1 则 的周长为 .z
12如图,在矩形ABCD中,E为AD的中点,连接CE,过点E作CE的垂线交AB于点F,交CD的延长线于点G,连接CF .已知 则
13如图,抛物线 与x轴交于A、B两点,P是以点C(0,3)为圆心、2为半径的圆上的动点,Q是线段PA的中点,连接OQ .则线段OQ的最大值是( ).
A. 3 C. D.4
14如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,. 且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B. 4 C. 6 D.8
15如图,在平行四边形ABCD中, AB=5,BC=8. E是边BC的中点, F是平行四边形ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )
A C. 3 D.2
16如图,在边长为2 的正方形ABCD中, 点E, F分别是边AB, BC的中点, 连接EC, FD,点G, H分别是EC, FD的中点, 连接GH ,则GH的长度为
17如图,在矩形ABCD中, E, F分别为边AB、AD的中点, BF与EC、ED分别交于点M , N.已知AB=4,BC=6,则MN的长为 .
18如图,在 中, AD,BE分别是BC, AC边上的中线,且 垂足为点F,设BC=a,AC=b,AB=c,则下列关系式中成立的是( )
19如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF , M、N分别是DC、DF的中点, 连接MN .若 则
20若 和 均为等腰三角形,且
(1)如图1,点B是DE的中点,判定四边形BEAC的形状,并说明理由.
(2)如图2,若点G是EC的中点,连接GB并延长至点F,使( CD.求证:
① EB=DC .
②∠EBG=∠BFC.
21如图,在△ABC中,∠ACB=120°,BC=4, D为AB的中点,DC⊥BC,则△ABC的面积是 .
22如图,在平行四边形ABCD中, E为CD的中点, BF⊥AE, 垂足为F, AD=AE =1,∠DAE=30°,EF= .
23问题背景:数学小组在一次课外学习交流时,组内一同学提出如下问题:△ABC中,∠ACB=90°,D为BC边上一点, 但不与点B,点C重合,过点D作DE⊥AB于点E .连接AD,M为AD的中点, 连接EM , CM .
(1)观察发现:如图1,EM与CM之间的数量关系是 .
(2)思考分享:如图2,将△BDE绕点B顺时针旋转,其他条件不变,则(1)中的结论还成立,请证明.小明是这样思考的:延长DE至点D',使得ED'=DE,连接AD'运用三角形中位线定理,……按照他的思路或采用其他方法证明.
(3) 探究计算:若∠ABC=30°,AC=4, DE=2,在△BDE绕点B旋转一周的过程中,当直线DE经过点A时,线段AD的长为 .
24在 中, ,D是AB的中点. E为直线AC上一动点,连接DE,过点D作 交直线BC于点F ,连接EF.
(1)如图1,当E是线段AC的中点时,设. ,求EF的长(用含a,b的式子表示)
(2)当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE ,EF ,BF之间的数量关系,并证明.
25在 中, 以AB为边作 ,AC交BD于点E.
(1) 如图1,若 求CE的长度.
(2) 如图2,若 ,延长DA至点F ,连接CF交BD于点H ,若点H为CF的中点,证明:
(3) 如图3,若 将 绕点A逆时针旋转得到 连接CN,取CN的中点G ,连接BG.在 旋转过程中,当 时,直接写出 的面积.
26(1)问题提出
如图①, AD是 C的中线,则. . (填“>” “<”或“=” )
(2)问题探究
如图②, 在矩形ABCD中,( ,点E为BC的中点,点F为CD上任意一点,当 的周长最小时,求CF的长.
(3)问题解决
如图③, 在矩形ABCD中, ,点O为对角线AC的中点,点P为AB上任意一点,点Q为AC上任意一点,连接PO、PQ、BQ,是否存在这样的点Q ,使折线OPQB的长度最小 若存在,请确定点Q的位置,并求出折线OPQB的最小长度;若不存在,请说明理由.
1在Rt△ABC中,∠ACB=90°,AC=BC,过点B作BD∥AC.
(1) 如图1,若点D在点B的左侧,连接CD,过点A作AE⊥CD交BC于点E .若点E是BC的中点,求证:AC=2BD.
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF .过点F作FM⊥BG交AB于点M,CN平分∠ACB交BG于点N,求证:
【答案】(1)见解析
(2)见解析
【解析】(1)∵∠ACB=90°,BD∥AC,
∵AE⊥CD,
∴∠CAE=∠BCD,
又∵AC=CB,∠CBD=∠ACE=90°,
∴△ACE≌△CBD(ASA),
∵BD=CE,
∵点E是BC的中点,
.△HFM≌△CFN(AAS).
∴HM=CN,
∵AM=AH+HM,
【标注】【知识点】等腰直角三角形与全等
2如图,在边长为2的正方形ABCD中,E,F分别是BC , CD上的动点,M, N分别是EF , AF的中点,则MN的最大值为 .
【答案】
【解析】
【分析】
首先证明出MN是△AEF的中位线,得到 然后由正方形的性质和勾股定理得到 证明出当BE最大时,AE最大,此时MN最大,进而得到当点E和点C重合时,BE最大,即BC的长度,最后代入求解即可.
【详解】
如图所示,连接AE,
∵M,N分别是EF , AF的中点,
∴MN是△AEF的中位线,
∵四边形ABCD是正方形,
∴∠B=90°,
∴当BB最大时,AE最大,此时MN最大,
∵点E是BC上的动点,
∴当点B和点C重合时,BB最大,即BC的长度,
∴此时.
∴MN的最大值为
故答案为:
【点睛】
此题考查了正方形的性质,三角形中位线的性质,勾股定理等知识,解赜的关键是熟练掌握以上知识点.
【标注】【知识点】正方形的性质
【知识点】勾股定理
【知识点】三角形的中位线
3如图,四边形ABCD的两条对角线AC,BD互相垂直,AC=4,BD=6,则AD+BC的最小值是 .
【答案】2
【解析】设AC,BD的交点为O,AB,BC,OD,DA的中点分别是P,Q ,R,S,连接PQ,QR,RS,SP,OQ,OS,QS,如图:
∵AC,BD互相垂直,
∴△AOD和△BOC为直角三角形,且AD,BC分别为斜边,
∴AD=2OS,BC=2OQ,
∴AD+BC=2(OS+OQ),
∴当OS+OQ为最小时, AD+BO为最小,
根据“两点之间线段最短”得:OQ+OS≥QS,
∴当点O在线段QS上时,OQ+OS为最小,最小值为线段QS的长,
∵点P,Q分别为AB, BC的中点,
∴PQ为△ABC的中位线,
同理:
SP//BD,
∴PQ//AC//RS. QR//BD//SP,
∴四边形PQRS为平行四边形,
∵AC⊥BD,PQ∥AC,SP∥BD,
∴PQ⊥SP,
∴四边形PQRS为矩形,
在Rt△PQS中, PO-2 SD-2
由勾股定理得:
∴OQ+OS的最小值为
∴AD+BC的最小值为2
故答案为:2
【标注】【知识点】线段和的最小值
【思想】数形结合思想
4如图,在△ABC中,将AB绕点A顺时针旋转α至AB',将AC绕点A逆时针旋转β至
AC'(0°<α<180°,0°<β<180°),得到△AB'C',使 ,我们称
△AB'C'是△ABC的“旋补三角形”,△AB'C'的中线AD叫做△ABC的 “旋补中线”,点A叫做“旋补中心”.下列结论正确的有 .
①△ABC与△AB'C'面积相同:
②BC=2AD;
③若AB=AC,连接BB'和OC',则
∠B'BC+∠OC'B'=180°;
④若AB=AC,AB=4,BC=6,则B'C'=10.
【答案】①②③
【解析】解:延长B'A,并截取AE=AB,连接C'E,如图所示:
∵∠BAC+∠B'AO'=180°,
∴α+β=360°-180°=180°,
∵a+∠BAE=180°,
∴∠BAE=β,
∴∠BAO+∠OAE=∠CAE+∠EAO',
∴∠BAC=∠EAC',
根据旋转可知,AC=AC',AB=AB',
∵AB=AB,
∴△ABCα△AEC',
∵AB=AB',AB=AE,
∴AE=AB',
,即△ABC与△AB'C'面积相同,故①正确;
∵AE=AB',B'D=C'D,
.. AD是△B'C'E的中位线,
∵BC=C'E,
∴BC=2AD,故②正确;
当AB=AC时,AB=AB'=AC'=AC,
∴∠AB'B=∠ABB',∠AB'C'=∠AC'B',∠AC'C'=∠ACC',∠ABC=∠ACB,
∵∠AB'B+∠ABB'+∠AB'C'+∠AC'B'+∠AC'C+∠ACO'+∠ABC+∠ACB=360°
∴∠ABB'+∠ABC+∠AC'B'+∠AC'C=∠AB'B+∠ACB+∠AB'C'+∠ACC'=180°
即∠B'BC+∠CC'B'=180°,故③正确;
∵BC=6,
∴根据②可知,
∵当AB=AC时,AB=AB'=AC'=AC=4,AD为中线,
∴AD⊥B'C'.
∴∠ADB'=90°.
故④错误;
综上分析可知,正确的是①②③、
【标注】【知识点】旋转
5问题情境:小红同学在学习了正方形的知识后,进一步进行以下探究活动:在正方形ABCD的边BC上任意取一点G,以BG为边长向外作正方形BEFG,将正方形BEFG绕点B顺时针旋转.
(1)当BG在BC上时,连接DF,AC相交于点P,小红发现点P恰为DF的中点,如图①.针对小红发现的结论,请给出证明;
(2)小红继续连接EG,并延长与DP相交,发现交点恰好也是DF中点P,如图②,根据小红发现的结论,请判断△APE的形状,并说明理由;规律探究:
(3) 如图③,将正方形BEFG绕点B顺时针旋转α,连接DF,点P是DF中点,连接AP,EP,AE,△APE的形状是否发生改变 请说明理由.
【答案】(1)见解析
(2)见解析
(3)见解析
【解析】(1)解:证明:连接BD,BF,BP,
∵四边形ABOD,BEFG都是正方形.
∴∠CBD=∠FB'=∠5G,
∴∠DBF=90°,
∵四边形ABOD是正方形.
∴∠DAC=∠BAC=45°
又∵AP= AP
∴△APD≌△APB(SAS)
∴BP=DP,
∴∠PDB=∠PBD
∴∠PBF=∠PFB
∴PB=PF
∴PD=PF,
即点P恰为DF的中点;
(2)△APE是等腰直角三角形,理由如下:
∵四边形ABCD,BEFG都是正方形,
∴∠CAE=∠PEA=45°
∴AP=EP,∠APE=90°,
∴△APE是等腰直角三角形;
(3)△APE的形状不改变,
延长EP至点M,使PM=EP,连接MA,MD,
∵四边形ABCD、四边形BEFG都是正方形,
∴AB=AD,∠BAD=∠ABC=∠EBG=90°,BE=EF,BG∥,
∵点P为DF的中点,
∴PD=PF
∵∠DPM=∠EPF,
∴△MPD≌△EPF(SAS)
∴DM=∠DMP=∠PF,∠PEF
∴BE=DM//EF,
∴BG∥DM
设DF交BO于点H,交BG于点N,
∴∠MDN=∠DNB
∵AD∥BC
∴∠ADN=∠BHN
∵∠BHN+∠BNH+∠HBN=180°,
∴∠ADM=∠ADN+∠MDN =∠BHN+∠BNH=180°-∠HBN
∴∠ABE=360°-∠ABC-∠EBG-∠HBN=180°-∠HBN
∴∠ADM =∠ABE
又∵AD=AB
∴△ADM≌△ABE(SAS)
∴AM=∠DAM =∠BAE
∵PM=EP
∴AP⊥ME,即∠
∴∠BAE+∠MAB=90°,即∠MAE=90°,
∴∠PEA=∠PAE
∴AP=EP
∴△APE是等腰直角三角形.
6(1)用数学的眼光观察.
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点, M是AB的中点, N是DC的中点,求证:∠PMN=∠PNM.
(2)用数学的思维思考.
如图,延长图中的线段AD交MN的延长线于点E,延长线段BC交MN的延长线于点F,求证:∠AEM=∠F.
(3)用数学的语言表达.
如图,在△ABC中,AC【答案】(1)见解析;(2)见解析;(3)△OGD是直角三角形,证明见解析.
【解析】
【分析】
(1)根据中位线定理即可求出PM=PN,利用等腰三角形的性质即可证明
∠PMN=∠PNM;
(2)根据中位线定理即可求出∠PNM =∠F和∠PMN=∠AEM ,通过第(1)问的结果进行等量代换即可证明∠AEM=∠F;
(3)根据中位线定理推出PM∥AD和PN∥BC从而求出∠PNM=∠PMN=∠ANM=∠OGN=∠GNC=60°,证明△CGN是等边三角形,利用中点求出∠NGD=30°,从而求出∠DGC度数,即可求证△CGD的形状.
【详解】
证明: (1)∵P的中点, M是AB的中点,
同理,
∵AD=BC,
∴PM=PN.
∴∠PMN=∠PNM.
(2)∵P的中点,M是AB的中点,
∴PN∥BC,
∴∠PNM =∠F.
同理,∠PMN=∠AEM.
由(1)可知∠PMN=∠PNM,
∴∠AEM=∠F.
(3)△CGD是直角三角形,证明如下:
如图,取BD的中点P,连接PM, PN,
M是AB的中点,
∴PM∥AD,PM= AD.
同理,PN∥.BC,PN= BC.
∵AD=BC,
∴PM=PN.
∴∠PMN=∠PNM.
∵PM∥AD,
∴∠PMN=∠ANM=60°,
∴∠PNM =∠PMN=60°.
∵PN∥BC,
又∵∠CNG=∠ANM=60°,
∴△OGN是等边三角形,
∴CN=GN.
又∵CN=DN,
∴DN=GN.
∴∠CGD=∠CGN+∠NGD=60°+30°=90°.
∴△CGD是直角三角形.
故答案为:△CGD是直角三角形.
【点睛】
本题考查了三角形的中位线定理,等腰三角形的性质,等边三角形的性质以及直角三角形的判定,解题的关键在于灵活运用中位线定理.
【标注】【业务题型】证明题
【知识点】等边三角形的性质与判定综合问题
【知识点】三角形的中位线
8如图,正方形ABCD的面积为3,点E在边CD上,且CE=1,∠ABE的平分线交AD于点F,点M ,N分别是BE,BF的中点,则MN的长为( )
中小学教育资源及组卷应用平台
【答案】D
【解析】连接EF,如图:
∵正方形ABCD的面积为3,
∴AB=BC=CD=AD=
∵CE=1,
∴∠EBC=30°,
∴∠ABE=∠ABC-∠EBC=60°,
∵AF平分∠ABE,
在Rt△ABF中,
∴DE=DF,△DEF是等腰直角三角形,
∵M,N分别是BE,BF的中点,
∴MN是△BEF的中位线,
故选 D.
9如图,折叠边长为4cm的正方形纸片ABCD,折痕是DM,点C落在点E处,分别延长ME、DE交AB于点F、G,若点M是BC边的中点,则FG= cm.
【答案】53
【解析】解:连接DF,如下图所示,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA=4,∠A=∠B=∠C=∠CDA=90°.
∵点M为BC的中点,
由折叠得,
设FE=x,则有
又在Rt△FMB中,FM=2+x,BM=2,
在Rt△DAF中,
解得 舍去)(
..∠FEG=90°
∴∠FEG=∠B,
又∠GFE=∠MFB.
∴△FEG~△FBM
即
因此正确答案为:
【标注】【知识点】轴对称
10如图,在矩形ABCD中,AB=6cm,BC=9cm,点E,P分别在边AB,BC上,AE=2cm,BD,EF交于点G,若G是EF的中点,则BG的长为 cm.
【答案】
【解析】解:∵四边形ABCD是矩形,
∴AB=CD=6cm,∠ABC=∠C=90°,AB∥CD,
∴∠ABD=∠BDC,
∵AE=2cm,
∴BE=AB-AE=6-2=4(cm),
∵G是EF的中点,
∴∠BEG=∠ABD,
∴∠BEG=∠BDC,
△EBF∽△DCB,
∴BF=6,
因此正确答案为:
【标注】【知识点】特殊平行四边形
11如图,在Rt△ABC中,∠A=90°,M为BC的中点, H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是( )
A. 24 B. 22 C. 20 D.18
【答案】B
【解析】
∵CG∥AB,
..∠B=∠MCG,
∴M是BC的中点,
∴BM=CM,
在△BMH和△CMG中,
.△BMH≌△CMG(ASA),
. HM=GM,BH=CG,
·AB=6,AC=8,
∴四边形ACGH的周长=AC+CG+AH+GH=AB+AC+GH=14+GH,
当GH最小时,即MH⊥AB时四边形ACGH的周长有最小值,
∵∠A=90°, MH⊥AB,
∴GH∥AC,
∴四边形ACGH为矩形,
∴GH=8,
∴四边形ACGH的周长最小值为14+8=22,
因此正确答案为:B.
【标注】【知识点】最短路径问题
12如图,在△ABC中, D是AC的中点,△ABC的角平分线AE交BD于点F ,若BF : FD=3 :1,AB+BE=3 ,则△ABC的周长为 .
【答案】5
【解析】
解:如下图所示,过点F作FM⊥AB于点M , FN⊥AC于点N,过点D作DT//AE交BC于点T
∵AE平分∠BAC,FM⊥AB,FN⊥AC,
∴FM=FN,
∴AB=3AD,
设AD=DC=a,则AB=3a,
∵AD=DC,DT//AE,
∴ET=CT.
设ET=CT=b,则BE=3b,
∵AB+BE=3
∴△ABC的周长=AB+AC+BC=5a+5b=5
因此正确答案为:5
【标注】【知识点】三角形及多边形
13如图,在矩形ABOD中,E为AD的中点,连接CE,过点E作CE的垂线交AB于点F,交CD的延长线于点G,连接CF.已知 则EF= .
【答案】
【解析】解:通过题意,在矩形ABCD中,则
∵E为AD的中点,
∵CE⊥FG,
在直角△BCP中,由勾股定理则
∴AD=3,
在直角△AEP中,由勾股定理则
因此正确答案为:
【标注】【知识点】特殊平行四边形
14如图,抛物线 与x轴交于A、B两点,P是以点C(0,3)为圆心、2为半径的圆上的动点,Q是线段PA的中点,连接OQ.则线段OQ的最大值是( ).
A.3 D.4
【答案】C
【解析】如图,连接BP,
当 时, 解得 则A(-4,0),B(4,0),
∵Q是线段PA的中点,
∴OQ为 的中位线,
当BP的值最大时,OQ的值最大,
而BP过圆心C时,BP的值最大,如图,点P运动到P'位置时,BP的值最大,最大值为BP'的长度,
∴线段OQ的最大值是
故选C.
【标注】【知识点】二次函数与圆的综合问题
15如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,. 且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
【答案】C
【解析】:
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点 当点P位于 位置时, 取得最小值,
又
故选C.
16如图,在平行四边形ABCD中, E是边BC的中点,F是平行四边形ABCD内一点,且 连接AF并延长,交CD于点G.若 则DG的长为( )
C. 3 D.2
【答案】D
【解析】∵点E为BC中点,
∴EF为四边形ABCG中位线,
∴EF=4,
又
即
故选D.
17如图,在边长为 的正方形ABCD中,点E,F分别是边AB, BC的中点,连接BC,FD,点G,H分别是BC,FD的中点,连接GH,则GH的长度为
【答案】1
【解析】方法一:解:设DF,CE交于O,
、四边形ABCD是正方形,
∴∠B=∠DCF=90°,BC=OD=AB,
∵点E, F分别是边AB, BC的中点,
∴BE=OF.
∴△CBE≌△DCF(SAS),
∴CE=DF.∠BCE=∠CDF.
∴DF⊥CE.
∵点G ,H分别是EC , FD的中点,
∵∠DCF=90°,CO⊥DF.
故答案为:1.
方法二:以点B为圆心,BC所在直线为x轴,BA所在直线为y轴,建立平面直角坐标系,
∵正方形ABCD的边长为2 ,E、F、G、H分别为AB、BC、CE、FD的中点,
18如图,在矩形ABCD中,E,F分别为边AB、AD的中点,BF与EC、ED分别交于点M ,N.已知AB=4,BC=6,则MN的长为 .
【答案】
【解析】过点E作EH//AD,交BF于点G,交CD于点H,
由题意可知:EH//BC,
∴△BEG∽△BAF,
∴AB=4,BC=6,点E为AB中点,F为AB中点,
∴BE=2,AF=3,
:EH//BC,
∴△EGN∽△DFN,△EGM∽△OBM,
∴2NG=NF,4MG=MB,
∵E为AB中点,EH∥BC,
∴G为BF中点,
故答案为
19如图,在△ABC中,AD,BE分别是BO,AC边上的中线,且AD⊥BE,垂足为点F,设BC=a,AC=b,AB=c,则下列关系式中成立的是( ) .
B. a +b =4c C. a +b =3c D. a +b =2c
【答案】A
【解析】设EF=x,DF=y,
∵AD,BE分别是BC,AO边上的中线,
∴点F为△ABC的重心,
∴AF=2DF=2y,BF=2EF=2x,
∵AD⊥BE,
∴∠AFB=∠AFE=∠BFD=90°,
在Rt△AFB中,
在Rt△AEF中,
在Rt△BFD中.
即
故选A.
20如图,已知点B在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN= .
【答案】
【解析】∵正方形ABCD和正方形BEFG中,AB=7,BE=5,
∴GF=GB=5,BC=7,
∴GC=GB+BC=5+7=12,
∵M、N分别是DC、DF的中点,
故答案为:2.
21若△ABC和△AED均为等腰三角形,且∠BAC=∠EAD =90°,
(1)如图1,点B是DE的中点,判定四边形BEAC的形状,并说明理由.
(2)如图2,若点G是EC的中点,连接GB并延长至点F,使CF=CD.求证:
① EB=DC.
②∠EBG=∠BFC.
【答案】(1)四边形BEAC是平行四边形,证明见解析.
(2)①证明见解析.
② 证明见解析.
【解析】(1)四边形BEAC是平行四边形.理由如下:
∵△EAD为等腰三角形且
∵B是DE的中点,
∴AB⊥DE,
∵△ABC是等腰三角形,∠BAC=90°,
∴∠CBA =45°,
∴∠BAE=∠CBA,
∴BC//EA,
又∵AB⊥DE,
∴∠EBA=∠BAC=90°,
.. BE//AC,
..四边形BEAC是平行四边形.
(2)① ∵△AED和△ABO为等腰三角形,
∴AE=AD,AB=AC,
∵∠EAD=∠BAC=90°,
∴∠EAD+∠DAB=∠BAC+∠DAB,
即∠EAB=∠DAC,
∴△AEB≌△ADC.
∴EB=DC.
② 延长FG至点H,使GH=FG.
∵G是EC的中点,
∴EG=CG,
又∠EGH=∠FGC,
∴△EHG≌△CFG,
∴∠BFC=∠H,CF=EH,
∵CF=CD,BE=CD,
∴BE=CF,
∴BE=EH,
..∠EBG=∠H,
∴∠EBG=∠BFC.
22如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点, DC⊥BC,则△ABC的面积是 .
【答案】8
【解析】∵DC⊥BC,
延长CD到H使DH=CD,
∵D为AB的中点,
∴AD=BD,
在△ADH与△BDO中,
∴△ADH≌△BDC(SAS),
∴AH=BC=4,∠H=∠BCD=90°,
∴CD=2
∴△ABC的面积
故答案为:8
23如图,在平行四边形ABCD中,E为CD的中点,BF⊥AE,垂足为F,AD=AE=1,∠DAE=30°,EF= .
【答案】
【解析】延长AE,BC交于M.
在平行四边形ABCD中,AD//BC,
..∠DAE=∠M=30°,∠D=∠ECM,
∵E为CD的中点,
∴CE=DE,
∴△ADE≌△MCE,
.. ME=AE=CM=1,
∴BM=2,
∵BF⊥AE,
24问题背景:数学小组在一次课外学习交流时,组内一同学提出如下问题:△ABC中,
D为BC边上一点,但不与点B ,点C重合,过点D作DE⊥AB于点E.连接AD,M为AD的中点,连接EM,CM.
(1)观察发现:如图1,EM与CM之间的数量关系是
(2)思考分享:如图2,将△BDE绕点B顺时针旋转,其他条件不变,则(1)中的结论还成立,请证明.小明是这样思考的:延长DE至点D',使得ED'=DE,连接AD'运用三角形中位线定理,…按照他的思路或采用其他方法证明.
(3) 探究计算:若∠ABC=30°,AC=4,DE=2,在△BDE绕点B旋转一周的过程中,当直线DE经过点A时,线段AD的长为
【答案】(1) EM=CM
(2)证明见解析.
【解析】(1)∵∠ACB=90°,M为AD中点,
(直角三角形斜边中线等于斜边一半),
∵DE⊥AB,M为AD中点,
∴EM=CM.
(2)延长DE至D'使D'E=DE,连接AD',
则EM为△ADD'的中位线,
延长AC至A'点使CA'=AC ,连接A'D , A'B,
则CM为△AA'D的中位线,
∴BE⊥DD',
又∵DE=D'E,
∴BD=BD',∠D'BE=∠DBE=∠ABC,
∵∠ACB=∠A'CB=90°, AC=A'C,
∴AB=A'B,∠ABA'=2∠ABC,
∴∠D'BD+∠DBA=∠ABA'+∠DBA,
∴∠D'BA=∠DBA',
在△ABD'和△A'BD中,
∴△ABD'≌△A'BD(SAS),
∴AD'=A'D,
∴EM=CM.
(3)如图(2) ,当直线DE过点A时,
∵∠DBE=∠ABC=30°,AC=4,DE=2,
∴AB=2AC=8,BD=2DE=4,
∴在Rt△ABE中,
如图(3) ,直线DB过点A时,
∵∠DBE=∠ABC=30°,
,
综上AD的长为2
【标注】【知识点】倍长(类)中线
25在△ABC中,∠C=90°,AC>BC,D是AB的中点. E为直线AC上一动点,连接DE,过点D作DF⊥DE,交直线BO于点F,连接EF.
(1) 如图1,当E是线段AC的中点时,设AE=a,BF=b,求EF的长(用含a,b的式子表示) .
(2)当点B在线段CA的延长线上时,依题意补全图2,用等式表示线段AE,EF ,BF之间的数量关系,并证明.
【答案】
证明见解析.
【解析】(1)∵D是AB的中点,E是线段AC的中点,
∴DE为△ABC的中位线,
.. DE//BC.
∵∠C=90°,
∵∠DEC=90°,
∵DF⊥DE,
∴∠EDF=90°.
∴四边形DEOF为矩形
∴BF=CF,
(2)过点B作AC的平行线交ED延长线于点G ,连接FG,
∵BG∥AC,
∴∠EAD=∠GBD,∠DEA=∠DGB,
∵D是AB的中点,
∴AD=BD,
∴△EAD≌△GBD.
∴ED=GD,AE=BG.
∵DF⊥DE,
∴DF是线段EG的垂直平分线,
∴EF=FG,
∵∠C=90°,BG∥AC,
∴∠GBF=90°,
在Rt△BGF中,
26在Rt△ABC中,∠ABC=90°,以AB为边作Rt△ABD,∠ADB=90°,∠ABD=30°,AC交BD于点E.
(1)如图1,若∠CAB=30°,AD=2 ,求CE的长度.
(2)如图2,若∠CAB=45°,延长DA至点F,连接CF交BD于点H,若点H为CF的中点,证明:
(3)如图3,若∠CAB=60°,AB=2,将△ADB绕点A逆时针旋转得到△AMN,连接CN,取CN的中点G,连接BG.在△AMN旋转过程中,当 直接写出△ANC的面积.
【答案】(1)4.
(2)证明见解析.
(3)2
【解析】(1)如图1,过点E作EF⊥AB,垂足为F,
∵∠EBA=∠EAB=30°, AD=2
∴EA=EB,AF=FB, AB=4
设BC=x,则AC=2x,根据勾股定理,得
解得x=4,即BC=4,
∵∠EBA=∠EAB=30°,
∴∠EBC=∠ECB=60°,
∴△CBE是等边三角形,
∴EC=BO=4.
(2)过点O作CQ//FD,交BD于点Q,
∵BD⊥AD,
∴CQ⊥BD,
∴∠FDH=∠OQH,
在△FDH和△OQH中,
∴△FDH≌△CQH(AAS),
∴DH=HQ,FD=OQ,
∴∠DAB=∠QBC=60°,∠QOB=30°,
∴∠ABD=∠BCQ,
∴BA=OB,
在ARAD和△CBO中.
∴△BAD≌△CBQ(AAS),
∴AD=BQ,BD=CQ,
∴BD=FD,
∴BD-BQ=FD-AD,
∴DQ=FA.
∴DH+HQ=FA,
∴2DH=FA,
(3) 根据题意,得当B,A,N三点共线时,BG是Rt△BNC斜边CN上的中线,
∴AN=AB=2,
∵∠BCA=30°,
∴AC=4,
根据勾股定理,得.
∴△ANC的面积为
27(1)问题提出
如图①,AD是△ABC的中线,则AB+AC 2AD.(填“>” “<”或“=”)
(2)问题探究
如图②.在矩形ABCD中,CD=3,BC=4,点E为BC的中点,点F为CD上任意一点,当△AEF的周长最小时,求CF的长.
(3)问题解决
如图③,在矩形ABCD中,AC=4,BC=2,点O为对角线AC的中点,点P为AB上任意一点,点Q为AC上任意一点,连接PO、PQ、BQ,是否存在这样的点Q ,使折线OPQB的长度最小 若存在,请确定点Q的位置,并求出折线OPQB的最小长度;若不存在,请说明理由.
【答案】(1)>
(2)1.
(3)存在,点Q与AC的中点O重合时,折线OPQB的长度最小,最小长度为4.
【解析】(1)如图,
延长AD到E,使DE=AD,
∵AD是BC中线,
∴BD=DC.
在△ADC和△EDB中,
∴△ADC≌△EDB(SAS),
∴AC=BE.
∵AB+BE>AB,
∴AB+AC>AD+DE.
即AB+AC>2AD.
(2)如解图①,作点E关于CD的对称点G ,连接AG交CD于点F,
则EF=FG,此时△AEF的周长最小.
∵CD=3,BC=4,点E为BC的中点,
∴BG=4+2=6.
∵在矩形ABCD中,CF//AB,
∴△FCG∽△ABG,
∴CF=1.
(3) 如解图②,作点B关于AC的对称点B',作点O关于AB的对称点O',连接AB'、QB'、AO'、PO'、B'O',
则QB=QB',OP=O'P,
∴折线OPQB的长度=OP+PQ+QB=O'P+PQ+QB'.
由“两点之间,线段最短”可知O'P+PQ+QB'≥B'O',当且仅当B'、Q、P、O'四点共线时,折线OPQB的最小长度为B'O'的长度.
∵在矩形ABCD中,AC=4,BC=2,∠ABC=90°,
∴∠BAO=30°,
∴AB=2
∵AC=4,点O为AO的中点,
∴AO=2.
∵点B与点B'关于AC'对称,点O与点O'关于AB对称,
∴∠B'AC=∠BAC=30°,AB'=AB=2
∠O'AB=∠BAC=30°,AO'=AO=2,
∴∠B'AO'=∠B'AC+∠BAC+∠O'AB =90°,
∴设B'O'交AC于点Q'.
在Rt△AB'O'中,AO'=2,B'O'=4,
∴∠AB'O'=30°,
∴∠AO'B'=60°.
又∵∠O'AQ'=∠BAC+∠O'AB=60°,
∴△AO'Q'是等边三角形,
∴AQ'=AO'=2.
∵AO=2,
∴AQ'=AO,
∴点Q'与AC的中点O重合,
故当点Q与AC的中点O重合时,折线OPQB的长度最小,最小长度为4.
模型原理
三角形是是历年中考命题的热点 .其中,三角形各边中点、中线及中位线的应用,是中考的必考内容.与中点有关的辅助线,我们总结下列四种类型:
1.类型一见中线,可倍长
1.倍长中线或类中线(与中点有关的线段)构造全等三角形或平行四边形.如图.
2.有些几何题在利用“倍长中线”证完一次全等后,还需再证一次全等,即“二次全等”
在证明第二次全等时,难点通常会体现在倒角上,常见的倒角方法有:①“8”字型(如图1-8);
②平行线;③180°(平角 ;三角形内角和);
④360°(周角; 四边形内角和) ; ⑤小旗子(三角形外角); ⑥90°(互余角) .
2.类型二 见等腰三角形,想“三线合一”
已知等腰三角形底边的中点,可以考虑与顶点连接,用“三线合一”
3.类型三 见斜边,想中线
已知直角三角形斜边的中点,可以考虑构造斜边中线,目的是得到三条等线段和两对等角.
4.类型四 见多个中点,想中位线
已知三角形的两边有中点,可以连接这两个中点构造中位线;
已知一边中点,可以在另一边上取中点,连接构造中位线;
已知一边中点,过中点作平行线可构造相似三角形.
真题精炼
1.在Rt△ABC中,∠ACB=90°, AC= BC,过点B作BD//AC.
(1) 如图1,若点D在点B的左侧,连接CD, 过点A作AE⊥CD交BC于点E .若点E是BC的中点,求证:AC=2BD.
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF.过点F作FM⊥BG交AB于点M ,CN平分∠ACB交BG于点N,求证:
2.在边长为2的正方形ABCD中,E, F是动点, M , N是EF , AF中点, MN最大值为
3.三四边形ABCD两条对角线AC, BD互相垂直, AC=4, BD=6, AD+BC最小值是 .
4.如图,在△ABC中,将AB绕点A顺时针旋转α至AB′,将AC绕点A逆时针旋转β至
, 得到△AB'C',使 ,我们称
△AB'C'是△ABC的“旋补三角形” ,△AB'C'的中线AD叫做△ABC的“旋补中线” , 点A叫做“旋补中心” .下列结论正确的有 .
①△ABC与△AB'C'面积相同 ;
②BC=2AD;
③若AB = AC, 连接BB'和CC' , 则
④若AB=AC,AB=4,BC=6,则
5问题情境:小红同学在学习了正方形的知识后,进一步进行以下探究活动:在正方形ABCD的边BC上任意取一点G,以BG为边长向外作正方形BEFG,将正方形BEFG绕点B顺时针旋转.
(1)当BG在BC上时,连接DF,AC相交于点P,小红发现点P恰为DF的中点,如图①.针对小红发现的结论,请给出证明;
(2)小红继续连接EG,并延长与DF相交,发现交点恰好也是DF中点P,如图②,根据小红发现的结论,请判断△APE的形状,并说明理由;规律探究:
(3) 如图③,将正方形BEFG绕点B顺时针旋转α,连接DF,点P是DF中点,连接AP,EP,AE,△APE的形状是否发生改变 请说明理由.
6(1)用数学的眼光观察 .如图,在四边形ABCD中,. ,P是对角线BD的中点,M是AB的中点,N是DC的中点,求证:
(2)用数学的思维思考 .如图,延长图中的线段AD交MN的延长线于点E,延长线段BC交MN的延长线于点F,求证:∠AEM =∠F.
(3) 用数学的语言表达. 如图,在△ABC中, AC
7如图,正方形ABCD的面积为3,点E在边CD上,且( 的平分线交AD于点F ,点M, N分别是BE, BF的中点, 则MN的长为( ) .
8如图,折叠边长为4cm的正方形纸片ABCD,折痕是DM ,点C落在点E处,分别延长ME、DE交AB于点F、G ,若点M是BC边的中点,则
9如图,在矩形ABCD中,. ,点E, F分别在边AB, BC上,, BD, EF交于点G,若G是EF的中点, 则BG的长为 cm .
10如图,在 中, ,M为BC的中点,H为AB上一点,过点C作( 交HM的延长线于点G,若 ,则四边形ACGH周长的最小值是( )
A. 24 B. 22 C. 20 D. 18
11如图,在△ABC中, D是AC的中点, C的角平分线AE交BD于点F ,若BF : FD=3 :1 则 的周长为 .z
12如图,在矩形ABCD中,E为AD的中点,连接CE,过点E作CE的垂线交AB于点F,交CD的延长线于点G,连接CF .已知 则
13如图,抛物线 与x轴交于A、B两点,P是以点C(0,3)为圆心、2为半径的圆上的动点,Q是线段PA的中点,连接OQ .则线段OQ的最大值是( ).
A. 3 C. D.4
14如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,. 且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B. 4 C. 6 D.8
15如图,在平行四边形ABCD中, AB=5,BC=8. E是边BC的中点, F是平行四边形ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )
A C. 3 D.2
16如图,在边长为2 的正方形ABCD中, 点E, F分别是边AB, BC的中点, 连接EC, FD,点G, H分别是EC, FD的中点, 连接GH ,则GH的长度为
17如图,在矩形ABCD中, E, F分别为边AB、AD的中点, BF与EC、ED分别交于点M , N.已知AB=4,BC=6,则MN的长为 .
18如图,在 中, AD,BE分别是BC, AC边上的中线,且 垂足为点F,设BC=a,AC=b,AB=c,则下列关系式中成立的是( )
19如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF , M、N分别是DC、DF的中点, 连接MN .若 则
20若 和 均为等腰三角形,且
(1)如图1,点B是DE的中点,判定四边形BEAC的形状,并说明理由.
(2)如图2,若点G是EC的中点,连接GB并延长至点F,使( CD.求证:
① EB=DC .
②∠EBG=∠BFC.
21如图,在△ABC中,∠ACB=120°,BC=4, D为AB的中点,DC⊥BC,则△ABC的面积是 .
22如图,在平行四边形ABCD中, E为CD的中点, BF⊥AE, 垂足为F, AD=AE =1,∠DAE=30°,EF= .
23问题背景:数学小组在一次课外学习交流时,组内一同学提出如下问题:△ABC中,∠ACB=90°,D为BC边上一点, 但不与点B,点C重合,过点D作DE⊥AB于点E .连接AD,M为AD的中点, 连接EM , CM .
(1)观察发现:如图1,EM与CM之间的数量关系是 .
(2)思考分享:如图2,将△BDE绕点B顺时针旋转,其他条件不变,则(1)中的结论还成立,请证明.小明是这样思考的:延长DE至点D',使得ED'=DE,连接AD'运用三角形中位线定理,……按照他的思路或采用其他方法证明.
(3) 探究计算:若∠ABC=30°,AC=4, DE=2,在△BDE绕点B旋转一周的过程中,当直线DE经过点A时,线段AD的长为 .
24在 中, ,D是AB的中点. E为直线AC上一动点,连接DE,过点D作 交直线BC于点F ,连接EF.
(1)如图1,当E是线段AC的中点时,设. ,求EF的长(用含a,b的式子表示)
(2)当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE ,EF ,BF之间的数量关系,并证明.
25在 中, 以AB为边作 ,AC交BD于点E.
(1) 如图1,若 求CE的长度.
(2) 如图2,若 ,延长DA至点F ,连接CF交BD于点H ,若点H为CF的中点,证明:
(3) 如图3,若 将 绕点A逆时针旋转得到 连接CN,取CN的中点G ,连接BG.在 旋转过程中,当 时,直接写出 的面积.
26(1)问题提出
如图①, AD是 C的中线,则. . (填“>” “<”或“=” )
(2)问题探究
如图②, 在矩形ABCD中,( ,点E为BC的中点,点F为CD上任意一点,当 的周长最小时,求CF的长.
(3)问题解决
如图③, 在矩形ABCD中, ,点O为对角线AC的中点,点P为AB上任意一点,点Q为AC上任意一点,连接PO、PQ、BQ,是否存在这样的点Q ,使折线OPQB的长度最小 若存在,请确定点Q的位置,并求出折线OPQB的最小长度;若不存在,请说明理由.
1在Rt△ABC中,∠ACB=90°,AC=BC,过点B作BD∥AC.
(1) 如图1,若点D在点B的左侧,连接CD,过点A作AE⊥CD交BC于点E .若点E是BC的中点,求证:AC=2BD.
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF .过点F作FM⊥BG交AB于点M,CN平分∠ACB交BG于点N,求证:
【答案】(1)见解析
(2)见解析
【解析】(1)∵∠ACB=90°,BD∥AC,
∵AE⊥CD,
∴∠CAE=∠BCD,
又∵AC=CB,∠CBD=∠ACE=90°,
∴△ACE≌△CBD(ASA),
∵BD=CE,
∵点E是BC的中点,
.△HFM≌△CFN(AAS).
∴HM=CN,
∵AM=AH+HM,
【标注】【知识点】等腰直角三角形与全等
2如图,在边长为2的正方形ABCD中,E,F分别是BC , CD上的动点,M, N分别是EF , AF的中点,则MN的最大值为 .
【答案】
【解析】
【分析】
首先证明出MN是△AEF的中位线,得到 然后由正方形的性质和勾股定理得到 证明出当BE最大时,AE最大,此时MN最大,进而得到当点E和点C重合时,BE最大,即BC的长度,最后代入求解即可.
【详解】
如图所示,连接AE,
∵M,N分别是EF , AF的中点,
∴MN是△AEF的中位线,
∵四边形ABCD是正方形,
∴∠B=90°,
∴当BB最大时,AE最大,此时MN最大,
∵点E是BC上的动点,
∴当点B和点C重合时,BB最大,即BC的长度,
∴此时.
∴MN的最大值为
故答案为:
【点睛】
此题考查了正方形的性质,三角形中位线的性质,勾股定理等知识,解赜的关键是熟练掌握以上知识点.
【标注】【知识点】正方形的性质
【知识点】勾股定理
【知识点】三角形的中位线
3如图,四边形ABCD的两条对角线AC,BD互相垂直,AC=4,BD=6,则AD+BC的最小值是 .
【答案】2
【解析】设AC,BD的交点为O,AB,BC,OD,DA的中点分别是P,Q ,R,S,连接PQ,QR,RS,SP,OQ,OS,QS,如图:
∵AC,BD互相垂直,
∴△AOD和△BOC为直角三角形,且AD,BC分别为斜边,
∴AD=2OS,BC=2OQ,
∴AD+BC=2(OS+OQ),
∴当OS+OQ为最小时, AD+BO为最小,
根据“两点之间线段最短”得:OQ+OS≥QS,
∴当点O在线段QS上时,OQ+OS为最小,最小值为线段QS的长,
∵点P,Q分别为AB, BC的中点,
∴PQ为△ABC的中位线,
同理:
SP//BD,
∴PQ//AC//RS. QR//BD//SP,
∴四边形PQRS为平行四边形,
∵AC⊥BD,PQ∥AC,SP∥BD,
∴PQ⊥SP,
∴四边形PQRS为矩形,
在Rt△PQS中, PO-2 SD-2
由勾股定理得:
∴OQ+OS的最小值为
∴AD+BC的最小值为2
故答案为:2
【标注】【知识点】线段和的最小值
【思想】数形结合思想
4如图,在△ABC中,将AB绕点A顺时针旋转α至AB',将AC绕点A逆时针旋转β至
AC'(0°<α<180°,0°<β<180°),得到△AB'C',使 ,我们称
△AB'C'是△ABC的“旋补三角形”,△AB'C'的中线AD叫做△ABC的 “旋补中线”,点A叫做“旋补中心”.下列结论正确的有 .
①△ABC与△AB'C'面积相同:
②BC=2AD;
③若AB=AC,连接BB'和OC',则
∠B'BC+∠OC'B'=180°;
④若AB=AC,AB=4,BC=6,则B'C'=10.
【答案】①②③
【解析】解:延长B'A,并截取AE=AB,连接C'E,如图所示:
∵∠BAC+∠B'AO'=180°,
∴α+β=360°-180°=180°,
∵a+∠BAE=180°,
∴∠BAE=β,
∴∠BAO+∠OAE=∠CAE+∠EAO',
∴∠BAC=∠EAC',
根据旋转可知,AC=AC',AB=AB',
∵AB=AB,
∴△ABCα△AEC',
∵AB=AB',AB=AE,
∴AE=AB',
,即△ABC与△AB'C'面积相同,故①正确;
∵AE=AB',B'D=C'D,
.. AD是△B'C'E的中位线,
∵BC=C'E,
∴BC=2AD,故②正确;
当AB=AC时,AB=AB'=AC'=AC,
∴∠AB'B=∠ABB',∠AB'C'=∠AC'B',∠AC'C'=∠ACC',∠ABC=∠ACB,
∵∠AB'B+∠ABB'+∠AB'C'+∠AC'B'+∠AC'C+∠ACO'+∠ABC+∠ACB=360°
∴∠ABB'+∠ABC+∠AC'B'+∠AC'C=∠AB'B+∠ACB+∠AB'C'+∠ACC'=180°
即∠B'BC+∠CC'B'=180°,故③正确;
∵BC=6,
∴根据②可知,
∵当AB=AC时,AB=AB'=AC'=AC=4,AD为中线,
∴AD⊥B'C'.
∴∠ADB'=90°.
故④错误;
综上分析可知,正确的是①②③、
【标注】【知识点】旋转
5问题情境:小红同学在学习了正方形的知识后,进一步进行以下探究活动:在正方形ABCD的边BC上任意取一点G,以BG为边长向外作正方形BEFG,将正方形BEFG绕点B顺时针旋转.
(1)当BG在BC上时,连接DF,AC相交于点P,小红发现点P恰为DF的中点,如图①.针对小红发现的结论,请给出证明;
(2)小红继续连接EG,并延长与DP相交,发现交点恰好也是DF中点P,如图②,根据小红发现的结论,请判断△APE的形状,并说明理由;规律探究:
(3) 如图③,将正方形BEFG绕点B顺时针旋转α,连接DF,点P是DF中点,连接AP,EP,AE,△APE的形状是否发生改变 请说明理由.
【答案】(1)见解析
(2)见解析
(3)见解析
【解析】(1)解:证明:连接BD,BF,BP,
∵四边形ABOD,BEFG都是正方形.
∴∠CBD=∠FB'=∠5G,
∴∠DBF=90°,
∵四边形ABOD是正方形.
∴∠DAC=∠BAC=45°
又∵AP= AP
∴△APD≌△APB(SAS)
∴BP=DP,
∴∠PDB=∠PBD
∴∠PBF=∠PFB
∴PB=PF
∴PD=PF,
即点P恰为DF的中点;
(2)△APE是等腰直角三角形,理由如下:
∵四边形ABCD,BEFG都是正方形,
∴∠CAE=∠PEA=45°
∴AP=EP,∠APE=90°,
∴△APE是等腰直角三角形;
(3)△APE的形状不改变,
延长EP至点M,使PM=EP,连接MA,MD,
∵四边形ABCD、四边形BEFG都是正方形,
∴AB=AD,∠BAD=∠ABC=∠EBG=90°,BE=EF,BG∥,
∵点P为DF的中点,
∴PD=PF
∵∠DPM=∠EPF,
∴△MPD≌△EPF(SAS)
∴DM=∠DMP=∠PF,∠PEF
∴BE=DM//EF,
∴BG∥DM
设DF交BO于点H,交BG于点N,
∴∠MDN=∠DNB
∵AD∥BC
∴∠ADN=∠BHN
∵∠BHN+∠BNH+∠HBN=180°,
∴∠ADM=∠ADN+∠MDN =∠BHN+∠BNH=180°-∠HBN
∴∠ABE=360°-∠ABC-∠EBG-∠HBN=180°-∠HBN
∴∠ADM =∠ABE
又∵AD=AB
∴△ADM≌△ABE(SAS)
∴AM=∠DAM =∠BAE
∵PM=EP
∴AP⊥ME,即∠
∴∠BAE+∠MAB=90°,即∠MAE=90°,
∴∠PEA=∠PAE
∴AP=EP
∴△APE是等腰直角三角形.
6(1)用数学的眼光观察.
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点, M是AB的中点, N是DC的中点,求证:∠PMN=∠PNM.
(2)用数学的思维思考.
如图,延长图中的线段AD交MN的延长线于点E,延长线段BC交MN的延长线于点F,求证:∠AEM=∠F.
(3)用数学的语言表达.
如图,在△ABC中,AC
【解析】
【分析】
(1)根据中位线定理即可求出PM=PN,利用等腰三角形的性质即可证明
∠PMN=∠PNM;
(2)根据中位线定理即可求出∠PNM =∠F和∠PMN=∠AEM ,通过第(1)问的结果进行等量代换即可证明∠AEM=∠F;
(3)根据中位线定理推出PM∥AD和PN∥BC从而求出∠PNM=∠PMN=∠ANM=∠OGN=∠GNC=60°,证明△CGN是等边三角形,利用中点求出∠NGD=30°,从而求出∠DGC度数,即可求证△CGD的形状.
【详解】
证明: (1)∵P的中点, M是AB的中点,
同理,
∵AD=BC,
∴PM=PN.
∴∠PMN=∠PNM.
(2)∵P的中点,M是AB的中点,
∴PN∥BC,
∴∠PNM =∠F.
同理,∠PMN=∠AEM.
由(1)可知∠PMN=∠PNM,
∴∠AEM=∠F.
(3)△CGD是直角三角形,证明如下:
如图,取BD的中点P,连接PM, PN,
M是AB的中点,
∴PM∥AD,PM= AD.
同理,PN∥.BC,PN= BC.
∵AD=BC,
∴PM=PN.
∴∠PMN=∠PNM.
∵PM∥AD,
∴∠PMN=∠ANM=60°,
∴∠PNM =∠PMN=60°.
∵PN∥BC,
又∵∠CNG=∠ANM=60°,
∴△OGN是等边三角形,
∴CN=GN.
又∵CN=DN,
∴DN=GN.
∴∠CGD=∠CGN+∠NGD=60°+30°=90°.
∴△CGD是直角三角形.
故答案为:△CGD是直角三角形.
【点睛】
本题考查了三角形的中位线定理,等腰三角形的性质,等边三角形的性质以及直角三角形的判定,解题的关键在于灵活运用中位线定理.
【标注】【业务题型】证明题
【知识点】等边三角形的性质与判定综合问题
【知识点】三角形的中位线
8如图,正方形ABCD的面积为3,点E在边CD上,且CE=1,∠ABE的平分线交AD于点F,点M ,N分别是BE,BF的中点,则MN的长为( )
中小学教育资源及组卷应用平台
【答案】D
【解析】连接EF,如图:
∵正方形ABCD的面积为3,
∴AB=BC=CD=AD=
∵CE=1,
∴∠EBC=30°,
∴∠ABE=∠ABC-∠EBC=60°,
∵AF平分∠ABE,
在Rt△ABF中,
∴DE=DF,△DEF是等腰直角三角形,
∵M,N分别是BE,BF的中点,
∴MN是△BEF的中位线,
故选 D.
9如图,折叠边长为4cm的正方形纸片ABCD,折痕是DM,点C落在点E处,分别延长ME、DE交AB于点F、G,若点M是BC边的中点,则FG= cm.
【答案】53
【解析】解:连接DF,如下图所示,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA=4,∠A=∠B=∠C=∠CDA=90°.
∵点M为BC的中点,
由折叠得,
设FE=x,则有
又在Rt△FMB中,FM=2+x,BM=2,
在Rt△DAF中,
解得 舍去)(
..∠FEG=90°
∴∠FEG=∠B,
又∠GFE=∠MFB.
∴△FEG~△FBM
即
因此正确答案为:
【标注】【知识点】轴对称
10如图,在矩形ABCD中,AB=6cm,BC=9cm,点E,P分别在边AB,BC上,AE=2cm,BD,EF交于点G,若G是EF的中点,则BG的长为 cm.
【答案】
【解析】解:∵四边形ABCD是矩形,
∴AB=CD=6cm,∠ABC=∠C=90°,AB∥CD,
∴∠ABD=∠BDC,
∵AE=2cm,
∴BE=AB-AE=6-2=4(cm),
∵G是EF的中点,
∴∠BEG=∠ABD,
∴∠BEG=∠BDC,
△EBF∽△DCB,
∴BF=6,
因此正确答案为:
【标注】【知识点】特殊平行四边形
11如图,在Rt△ABC中,∠A=90°,M为BC的中点, H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是( )
A. 24 B. 22 C. 20 D.18
【答案】B
【解析】
∵CG∥AB,
..∠B=∠MCG,
∴M是BC的中点,
∴BM=CM,
在△BMH和△CMG中,
.△BMH≌△CMG(ASA),
. HM=GM,BH=CG,
·AB=6,AC=8,
∴四边形ACGH的周长=AC+CG+AH+GH=AB+AC+GH=14+GH,
当GH最小时,即MH⊥AB时四边形ACGH的周长有最小值,
∵∠A=90°, MH⊥AB,
∴GH∥AC,
∴四边形ACGH为矩形,
∴GH=8,
∴四边形ACGH的周长最小值为14+8=22,
因此正确答案为:B.
【标注】【知识点】最短路径问题
12如图,在△ABC中, D是AC的中点,△ABC的角平分线AE交BD于点F ,若BF : FD=3 :1,AB+BE=3 ,则△ABC的周长为 .
【答案】5
【解析】
解:如下图所示,过点F作FM⊥AB于点M , FN⊥AC于点N,过点D作DT//AE交BC于点T
∵AE平分∠BAC,FM⊥AB,FN⊥AC,
∴FM=FN,
∴AB=3AD,
设AD=DC=a,则AB=3a,
∵AD=DC,DT//AE,
∴ET=CT.
设ET=CT=b,则BE=3b,
∵AB+BE=3
∴△ABC的周长=AB+AC+BC=5a+5b=5
因此正确答案为:5
【标注】【知识点】三角形及多边形
13如图,在矩形ABOD中,E为AD的中点,连接CE,过点E作CE的垂线交AB于点F,交CD的延长线于点G,连接CF.已知 则EF= .
【答案】
【解析】解:通过题意,在矩形ABCD中,则
∵E为AD的中点,
∵CE⊥FG,
在直角△BCP中,由勾股定理则
∴AD=3,
在直角△AEP中,由勾股定理则
因此正确答案为:
【标注】【知识点】特殊平行四边形
14如图,抛物线 与x轴交于A、B两点,P是以点C(0,3)为圆心、2为半径的圆上的动点,Q是线段PA的中点,连接OQ.则线段OQ的最大值是( ).
A.3 D.4
【答案】C
【解析】如图,连接BP,
当 时, 解得 则A(-4,0),B(4,0),
∵Q是线段PA的中点,
∴OQ为 的中位线,
当BP的值最大时,OQ的值最大,
而BP过圆心C时,BP的值最大,如图,点P运动到P'位置时,BP的值最大,最大值为BP'的长度,
∴线段OQ的最大值是
故选C.
【标注】【知识点】二次函数与圆的综合问题
15如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,. 且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
【答案】C
【解析】:
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点 当点P位于 位置时, 取得最小值,
又
故选C.
16如图,在平行四边形ABCD中, E是边BC的中点,F是平行四边形ABCD内一点,且 连接AF并延长,交CD于点G.若 则DG的长为( )
C. 3 D.2
【答案】D
【解析】∵点E为BC中点,
∴EF为四边形ABCG中位线,
∴EF=4,
又
即
故选D.
17如图,在边长为 的正方形ABCD中,点E,F分别是边AB, BC的中点,连接BC,FD,点G,H分别是BC,FD的中点,连接GH,则GH的长度为
【答案】1
【解析】方法一:解:设DF,CE交于O,
、四边形ABCD是正方形,
∴∠B=∠DCF=90°,BC=OD=AB,
∵点E, F分别是边AB, BC的中点,
∴BE=OF.
∴△CBE≌△DCF(SAS),
∴CE=DF.∠BCE=∠CDF.
∴DF⊥CE.
∵点G ,H分别是EC , FD的中点,
∵∠DCF=90°,CO⊥DF.
故答案为:1.
方法二:以点B为圆心,BC所在直线为x轴,BA所在直线为y轴,建立平面直角坐标系,
∵正方形ABCD的边长为2 ,E、F、G、H分别为AB、BC、CE、FD的中点,
18如图,在矩形ABCD中,E,F分别为边AB、AD的中点,BF与EC、ED分别交于点M ,N.已知AB=4,BC=6,则MN的长为 .
【答案】
【解析】过点E作EH//AD,交BF于点G,交CD于点H,
由题意可知:EH//BC,
∴△BEG∽△BAF,
∴AB=4,BC=6,点E为AB中点,F为AB中点,
∴BE=2,AF=3,
:EH//BC,
∴△EGN∽△DFN,△EGM∽△OBM,
∴2NG=NF,4MG=MB,
∵E为AB中点,EH∥BC,
∴G为BF中点,
故答案为
19如图,在△ABC中,AD,BE分别是BO,AC边上的中线,且AD⊥BE,垂足为点F,设BC=a,AC=b,AB=c,则下列关系式中成立的是( ) .
B. a +b =4c C. a +b =3c D. a +b =2c
【答案】A
【解析】设EF=x,DF=y,
∵AD,BE分别是BC,AO边上的中线,
∴点F为△ABC的重心,
∴AF=2DF=2y,BF=2EF=2x,
∵AD⊥BE,
∴∠AFB=∠AFE=∠BFD=90°,
在Rt△AFB中,
在Rt△AEF中,
在Rt△BFD中.
即
故选A.
20如图,已知点B在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN= .
【答案】
【解析】∵正方形ABCD和正方形BEFG中,AB=7,BE=5,
∴GF=GB=5,BC=7,
∴GC=GB+BC=5+7=12,
∵M、N分别是DC、DF的中点,
故答案为:2.
21若△ABC和△AED均为等腰三角形,且∠BAC=∠EAD =90°,
(1)如图1,点B是DE的中点,判定四边形BEAC的形状,并说明理由.
(2)如图2,若点G是EC的中点,连接GB并延长至点F,使CF=CD.求证:
① EB=DC.
②∠EBG=∠BFC.
【答案】(1)四边形BEAC是平行四边形,证明见解析.
(2)①证明见解析.
② 证明见解析.
【解析】(1)四边形BEAC是平行四边形.理由如下:
∵△EAD为等腰三角形且
∵B是DE的中点,
∴AB⊥DE,
∵△ABC是等腰三角形,∠BAC=90°,
∴∠CBA =45°,
∴∠BAE=∠CBA,
∴BC//EA,
又∵AB⊥DE,
∴∠EBA=∠BAC=90°,
.. BE//AC,
..四边形BEAC是平行四边形.
(2)① ∵△AED和△ABO为等腰三角形,
∴AE=AD,AB=AC,
∵∠EAD=∠BAC=90°,
∴∠EAD+∠DAB=∠BAC+∠DAB,
即∠EAB=∠DAC,
∴△AEB≌△ADC.
∴EB=DC.
② 延长FG至点H,使GH=FG.
∵G是EC的中点,
∴EG=CG,
又∠EGH=∠FGC,
∴△EHG≌△CFG,
∴∠BFC=∠H,CF=EH,
∵CF=CD,BE=CD,
∴BE=CF,
∴BE=EH,
..∠EBG=∠H,
∴∠EBG=∠BFC.
22如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点, DC⊥BC,则△ABC的面积是 .
【答案】8
【解析】∵DC⊥BC,
延长CD到H使DH=CD,
∵D为AB的中点,
∴AD=BD,
在△ADH与△BDO中,
∴△ADH≌△BDC(SAS),
∴AH=BC=4,∠H=∠BCD=90°,
∴CD=2
∴△ABC的面积
故答案为:8
23如图,在平行四边形ABCD中,E为CD的中点,BF⊥AE,垂足为F,AD=AE=1,∠DAE=30°,EF= .
【答案】
【解析】延长AE,BC交于M.
在平行四边形ABCD中,AD//BC,
..∠DAE=∠M=30°,∠D=∠ECM,
∵E为CD的中点,
∴CE=DE,
∴△ADE≌△MCE,
.. ME=AE=CM=1,
∴BM=2,
∵BF⊥AE,
24问题背景:数学小组在一次课外学习交流时,组内一同学提出如下问题:△ABC中,
D为BC边上一点,但不与点B ,点C重合,过点D作DE⊥AB于点E.连接AD,M为AD的中点,连接EM,CM.
(1)观察发现:如图1,EM与CM之间的数量关系是
(2)思考分享:如图2,将△BDE绕点B顺时针旋转,其他条件不变,则(1)中的结论还成立,请证明.小明是这样思考的:延长DE至点D',使得ED'=DE,连接AD'运用三角形中位线定理,…按照他的思路或采用其他方法证明.
(3) 探究计算:若∠ABC=30°,AC=4,DE=2,在△BDE绕点B旋转一周的过程中,当直线DE经过点A时,线段AD的长为
【答案】(1) EM=CM
(2)证明见解析.
【解析】(1)∵∠ACB=90°,M为AD中点,
(直角三角形斜边中线等于斜边一半),
∵DE⊥AB,M为AD中点,
∴EM=CM.
(2)延长DE至D'使D'E=DE,连接AD',
则EM为△ADD'的中位线,
延长AC至A'点使CA'=AC ,连接A'D , A'B,
则CM为△AA'D的中位线,
∴BE⊥DD',
又∵DE=D'E,
∴BD=BD',∠D'BE=∠DBE=∠ABC,
∵∠ACB=∠A'CB=90°, AC=A'C,
∴AB=A'B,∠ABA'=2∠ABC,
∴∠D'BD+∠DBA=∠ABA'+∠DBA,
∴∠D'BA=∠DBA',
在△ABD'和△A'BD中,
∴△ABD'≌△A'BD(SAS),
∴AD'=A'D,
∴EM=CM.
(3)如图(2) ,当直线DE过点A时,
∵∠DBE=∠ABC=30°,AC=4,DE=2,
∴AB=2AC=8,BD=2DE=4,
∴在Rt△ABE中,
如图(3) ,直线DB过点A时,
∵∠DBE=∠ABC=30°,
,
综上AD的长为2
【标注】【知识点】倍长(类)中线
25在△ABC中,∠C=90°,AC>BC,D是AB的中点. E为直线AC上一动点,连接DE,过点D作DF⊥DE,交直线BO于点F,连接EF.
(1) 如图1,当E是线段AC的中点时,设AE=a,BF=b,求EF的长(用含a,b的式子表示) .
(2)当点B在线段CA的延长线上时,依题意补全图2,用等式表示线段AE,EF ,BF之间的数量关系,并证明.
【答案】
证明见解析.
【解析】(1)∵D是AB的中点,E是线段AC的中点,
∴DE为△ABC的中位线,
.. DE//BC.
∵∠C=90°,
∵∠DEC=90°,
∵DF⊥DE,
∴∠EDF=90°.
∴四边形DEOF为矩形
∴BF=CF,
(2)过点B作AC的平行线交ED延长线于点G ,连接FG,
∵BG∥AC,
∴∠EAD=∠GBD,∠DEA=∠DGB,
∵D是AB的中点,
∴AD=BD,
∴△EAD≌△GBD.
∴ED=GD,AE=BG.
∵DF⊥DE,
∴DF是线段EG的垂直平分线,
∴EF=FG,
∵∠C=90°,BG∥AC,
∴∠GBF=90°,
在Rt△BGF中,
26在Rt△ABC中,∠ABC=90°,以AB为边作Rt△ABD,∠ADB=90°,∠ABD=30°,AC交BD于点E.
(1)如图1,若∠CAB=30°,AD=2 ,求CE的长度.
(2)如图2,若∠CAB=45°,延长DA至点F,连接CF交BD于点H,若点H为CF的中点,证明:
(3)如图3,若∠CAB=60°,AB=2,将△ADB绕点A逆时针旋转得到△AMN,连接CN,取CN的中点G,连接BG.在△AMN旋转过程中,当 直接写出△ANC的面积.
【答案】(1)4.
(2)证明见解析.
(3)2
【解析】(1)如图1,过点E作EF⊥AB,垂足为F,
∵∠EBA=∠EAB=30°, AD=2
∴EA=EB,AF=FB, AB=4
设BC=x,则AC=2x,根据勾股定理,得
解得x=4,即BC=4,
∵∠EBA=∠EAB=30°,
∴∠EBC=∠ECB=60°,
∴△CBE是等边三角形,
∴EC=BO=4.
(2)过点O作CQ//FD,交BD于点Q,
∵BD⊥AD,
∴CQ⊥BD,
∴∠FDH=∠OQH,
在△FDH和△OQH中,
∴△FDH≌△CQH(AAS),
∴DH=HQ,FD=OQ,
∴∠DAB=∠QBC=60°,∠QOB=30°,
∴∠ABD=∠BCQ,
∴BA=OB,
在ARAD和△CBO中.
∴△BAD≌△CBQ(AAS),
∴AD=BQ,BD=CQ,
∴BD=FD,
∴BD-BQ=FD-AD,
∴DQ=FA.
∴DH+HQ=FA,
∴2DH=FA,
(3) 根据题意,得当B,A,N三点共线时,BG是Rt△BNC斜边CN上的中线,
∴AN=AB=2,
∵∠BCA=30°,
∴AC=4,
根据勾股定理,得.
∴△ANC的面积为
27(1)问题提出
如图①,AD是△ABC的中线,则AB+AC 2AD.(填“>” “<”或“=”)
(2)问题探究
如图②.在矩形ABCD中,CD=3,BC=4,点E为BC的中点,点F为CD上任意一点,当△AEF的周长最小时,求CF的长.
(3)问题解决
如图③,在矩形ABCD中,AC=4,BC=2,点O为对角线AC的中点,点P为AB上任意一点,点Q为AC上任意一点,连接PO、PQ、BQ,是否存在这样的点Q ,使折线OPQB的长度最小 若存在,请确定点Q的位置,并求出折线OPQB的最小长度;若不存在,请说明理由.
【答案】(1)>
(2)1.
(3)存在,点Q与AC的中点O重合时,折线OPQB的长度最小,最小长度为4.
【解析】(1)如图,
延长AD到E,使DE=AD,
∵AD是BC中线,
∴BD=DC.
在△ADC和△EDB中,
∴△ADC≌△EDB(SAS),
∴AC=BE.
∵AB+BE>AB,
∴AB+AC>AD+DE.
即AB+AC>2AD.
(2)如解图①,作点E关于CD的对称点G ,连接AG交CD于点F,
则EF=FG,此时△AEF的周长最小.
∵CD=3,BC=4,点E为BC的中点,
∴BG=4+2=6.
∵在矩形ABCD中,CF//AB,
∴△FCG∽△ABG,
∴CF=1.
(3) 如解图②,作点B关于AC的对称点B',作点O关于AB的对称点O',连接AB'、QB'、AO'、PO'、B'O',
则QB=QB',OP=O'P,
∴折线OPQB的长度=OP+PQ+QB=O'P+PQ+QB'.
由“两点之间,线段最短”可知O'P+PQ+QB'≥B'O',当且仅当B'、Q、P、O'四点共线时,折线OPQB的最小长度为B'O'的长度.
∵在矩形ABCD中,AC=4,BC=2,∠ABC=90°,
∴∠BAO=30°,
∴AB=2
∵AC=4,点O为AO的中点,
∴AO=2.
∵点B与点B'关于AC'对称,点O与点O'关于AB对称,
∴∠B'AC=∠BAC=30°,AB'=AB=2
∠O'AB=∠BAC=30°,AO'=AO=2,
∴∠B'AO'=∠B'AC+∠BAC+∠O'AB =90°,
∴设B'O'交AC于点Q'.
在Rt△AB'O'中,AO'=2,B'O'=4,
∴∠AB'O'=30°,
∴∠AO'B'=60°.
又∵∠O'AQ'=∠BAC+∠O'AB=60°,
∴△AO'Q'是等边三角形,
∴AQ'=AO'=2.
∵AO=2,
∴AQ'=AO,
∴点Q'与AC的中点O重合,
故当点Q与AC的中点O重合时,折线OPQB的长度最小,最小长度为4.
同课章节目录
