专题二十八 与圆相关的几何综合(含解析)2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题二十八 与圆相关的几何综合(含解析)2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 434.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 12:38:30 | ||
图片预览



文档简介
与圆相关的几何综合
模型原理
【总结】
圆与相似结合的几何压轴题,一般利用圆的相关定理(添加辅助线)倒边或倒角,并结合相似基本图形来求解,已知相似图形直接求;构造相似图形间接求(往往作平行线或作垂线来构造).
有时也要利用锐角三角函数、勾股定理求边长,要注意的是它们必须在直角三角形中才可应用,若没有直角三角形,则需作垂直构造直角 .
圆相关定理用途:
在圆中找到相等线段: ①连半径出等腰三角形 ②垂径定理出等线段 ③切线长定理出等线段 ④等弧对等弦
在圆中找到相等角 : ①同弧或等弧所对圆周角相等 ②直径配垂直,构造直角三角形 ③结合三角形外角内角等知识
真题精炼
1如图,在△ABC中, ,以AB为直径的⊙O交BC于点D,. 垂足为E ,BE的延长线交 于点F.
(1)求 的值.
(2) 求证:△AEB∽△BEC .
(3) 求证: AD与EF互相平分.
2如图, 内接于⊙O,直径交于点G ,过点D作射线DF ,使得 ,延长DC交过点B的切线于点E ,连接BC.
(1) 求证: DF是⊙O的切线.
(2) 若
① 求DE的长.
②求⊙O的半径.
3如图, AB是⊙O的直径,△ABC内接于⊙O , 点I为△ABC的内心, 连接CI并延长交⊙O于点D,E是 上任意一点,连接AD,BD, BE,CE.
(1) 若∠ABC=25°, 求∠CEB的度数 .
(2)找出图中所有与DI相等的线段,并证明.
(3)若 求△ABC的周长.
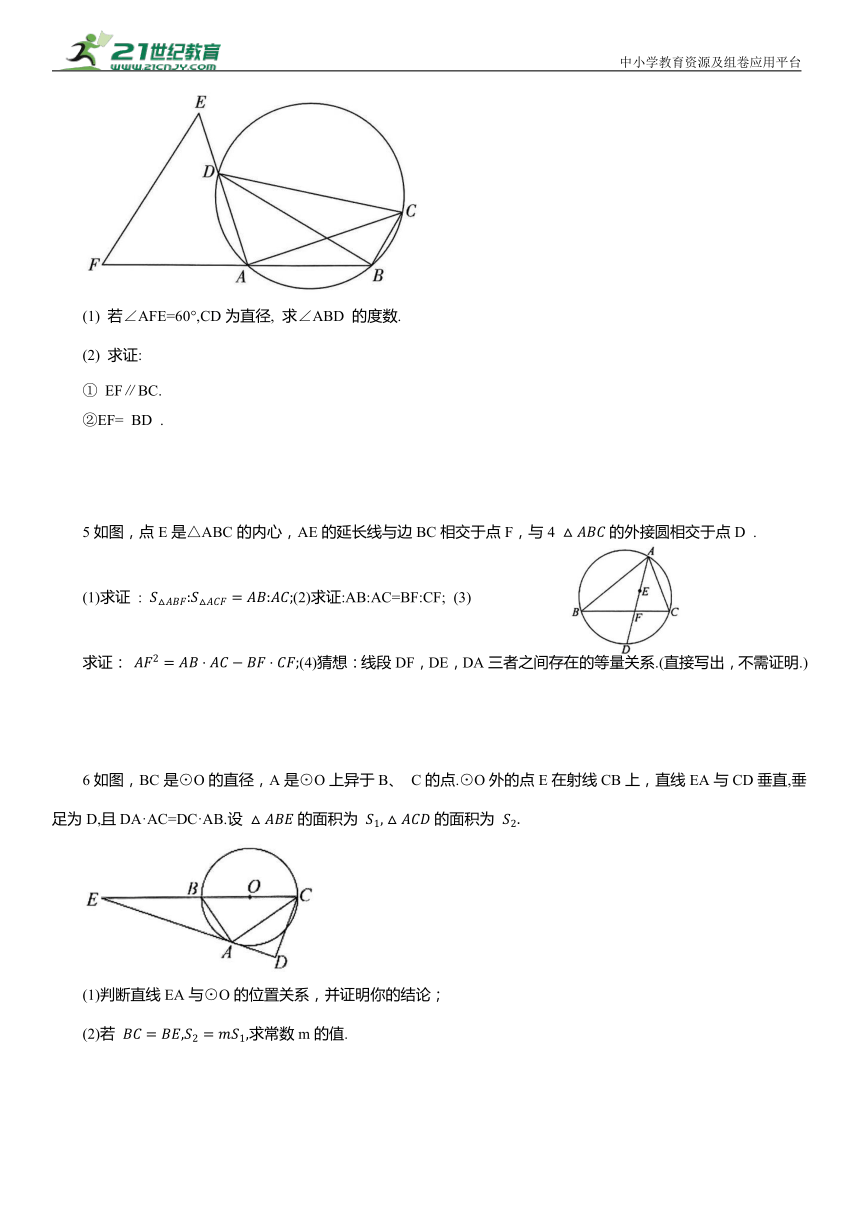
4如图,在圆内接四边形ABCD中, AD(1) 若∠AFE=60°,CD为直径, 求∠ABD 的度数.
(2) 求证:
① EF∥BC.
②EF= BD .
5如图,点E是△ABC的内心,AE的延长线与边BC相交于点F,与4 的外接圆相交于点D .
(1)求证 : (2)求证:AB:AC=BF:CF; (3)
求证: (4)猜想:线段DF,DE,DA三者之间存在的等量关系.(直接写出,不需证明.)
6如图,BC是⊙O的直径,A是⊙O上异于B、 C的点.⊙O外的点E在射线CB上,直线EA与CD垂直,垂足为D,且DA·AC=DC·AB.设 的面积为 的面积为
(1)判断直线EA与⊙O的位置关系,并证明你的结论;
(2)若 求常数m的值.
-
7已知:射线OP平分 , A为OP上一点, ⊙A交射线OM于点 B,C, 交射线ON于点D,E, 连接AB,AC,AD.
(1) 如图1, 若 ,试判断四边形OBAD的形状,并说明理由.
(2) 如图2, 过点C作( ,交OP于点F ;过点D作 ,OP于点G. 求证:
8如图,在平面直角坐标系xOy中,直线l: 分别与x轴,y轴相交于A ,B两点,点P(x,y)为直线l在第二象限的点 .
(1) 求A, B两点的坐标.
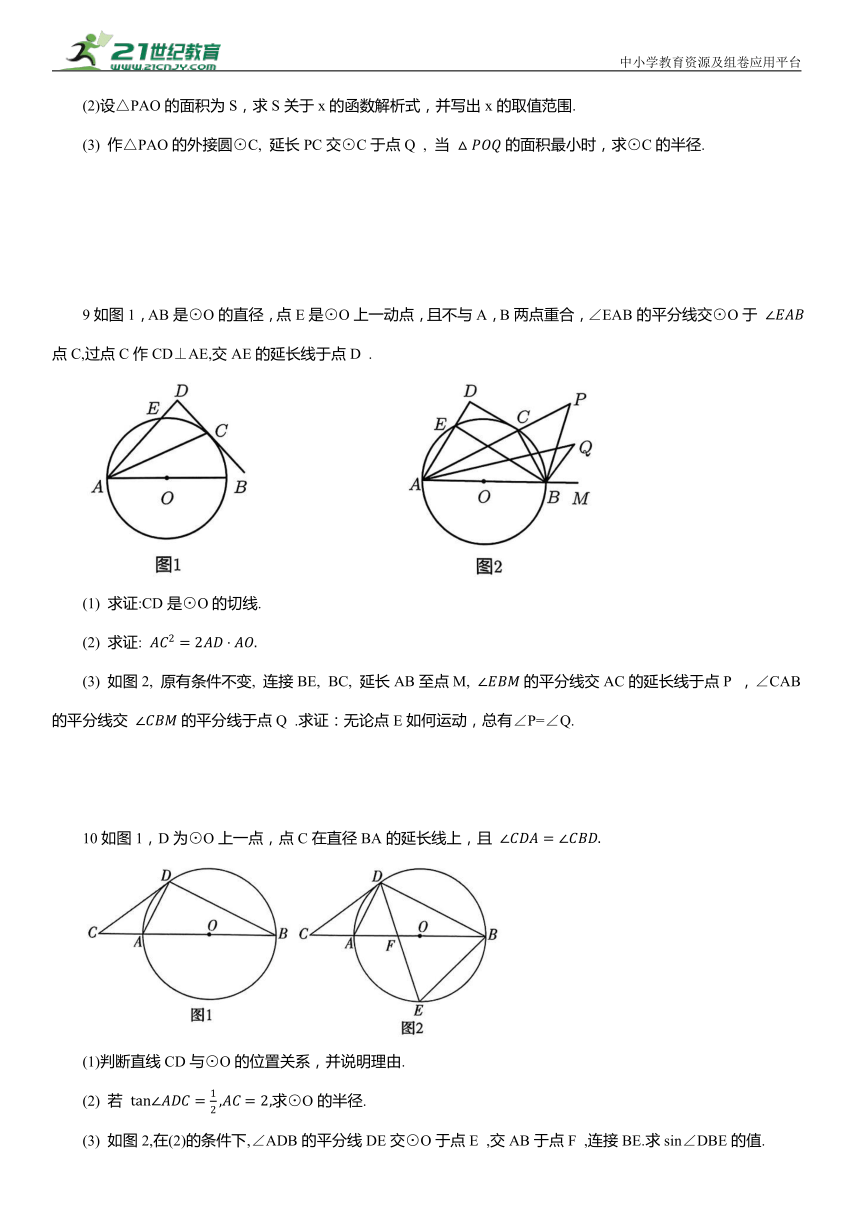
(2)设△PAO的面积为S,求S关于x的函数解析式,并写出x的取值范围.
(3) 作△PAO的外接圆⊙C, 延长PC交⊙C于点Q , 当 的面积最小时,求⊙C的半径.
9如图1,AB是⊙O的直径,点E是⊙O上一动点,且不与A,B两点重合,∠EAB的平分线交⊙O于 点C,过点C作CD⊥AE,交AE的延长线于点D .
(1) 求证:CD是⊙O的切线.
(2) 求证:
(3) 如图2, 原有条件不变, 连接BE, BC, 延长AB至点M, 的平分线交AC的延长线于点P ,∠CAB的平分线交 的平分线于点Q .求证:无论点E如何运动,总有∠P=∠Q.
10如图1,D为⊙O上一点,点C在直径BA的延长线上,且
(1)判断直线CD与⊙O的位置关系,并说明理由.
(2) 若 求⊙O的半径.
(3) 如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E ,交AB于点F ,连接BE.求sin∠DBE的值.
11如图所示,AB是⊙O的直径,点C、D是⊙O上不同的两点,直线BD交线段OC于点E、交过点C的直线CF于点F , 若OC=3CE,且
(1) 求证:直线CF是⊙O的切线.
(2) 连接OD、AD、AC、DC .若
① 求证:
② 过点E作 交线段AC于点G,点M为线段AC的中点,若 求线段MG的长度.
12.我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是⊙O的直径,直线l是⊙O的切线,B为切点. P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D .
(1)如图1, 当 的长为π时,求BC的长.
(2)如图2,当 时,求 的值.
(3)如图3,当 时,连接BP ,PQ ,直接写出 的值.
1.如图,在△ABO中. ,以AB为直径的⊙O交BC于点D,AE⊥OC,垂足为E,BE的延长线交AD于点F
(1)求 的值
(2)求证:△AEB∽△BEC.
(3)求证:AD与EF互相平分.
【答案】
(2)证明见解析
(3)证明见解析
【解析】(1)∵AB=AC,且AB是⊙O的直径
∴AC=2AO,
.∠BAC=90°
·在Rt△AOO中.
∵AE⊥OC
.在Rt△AOE中
(2) 过点B作BM//AE,交EO延长线于点M,
由(2)知:△AEB∽△BEC.
△AOE∽△BDE,
∠BED=∠AEO=90°.
∠DEF=90°.
∠AFB=∠DEF,
.. AF//DE.
由(2)知,
.∠DFB=∠AEF,
AE//FD.
·.四边形AEDF是平行四边形,
AD与EF互相平分.
2如图 △ACD内接于⊙O,直径交于点G,过点D作射线DF,使得∠ADF=∠ACD,延长DC交过点B的切线于点E ,连接BC、
(1) 求证:DF是⊙O的切线.
(2)若
①求DE的长.
②求⊙O的半径.
【答案】(1)证明见解析
(2)①9
【解析】(1)连接ODBD,则∠ACD=∠ABD,
∵∠ADF=∠ACD,
∴∠ABD=∠ADF.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABF+∠BAD=90°,
∵OA=OD,
∴∠OAD=∠ODA.
∴∠ABF+∠ODA=90°.
即∠ODF=90°,
∴OD⊥DF,
又∵OD为⊙O的半径,
∴DF是⊙O的切线;
(2)① ∵BE是⊙O的切线,
∵AB⊥BE,
∴∠ABC+∠CBE=90°,
∵AB是⊙O的直径,
.∠ABO+∠BAC=90°,
∴∠CBE=∠BAC,
∵∠BAC=∠BDC.
∴∠CBE=∠BDC.
即∠CBE=∠BDE.
又∵∠E=∠E,
∴△CBE∽△BDE,
·BE=3CE=3,
∴CE=1,
.. DE=9.
②∵DE=9,CE=1,
∴CD=DE-CE=9-1=8..
∴DG=CD-CG=8-3=5,GE=CG+CE=3+1=4,
∵∠GBE=90°,
∵∠BAC=∠BDC,∠AGC=∠DGB,
∴△AGC∽△DGB.
即
∴⊙O的半径为
3如图,AB是⊙O的直径,△ABC内接于⊙O,点I为△ABC的内心,连接CI并延长交⊙O于点D,E是BC上任意一点,连接AD,BD,BE,CE.
中小学教育资源及组卷应用平台
(1) 若∠ABC=25°,求∠CEB的度数.
(2)找出图中所有与DI相等的线段,并证明.
(3)若 求△ABC的周长.
【答案】(1)115°
(2) DI=AD=BD,证明见解析
(3)30
【解析】(1)∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
又∠ABO=25°,
∵四边形ABEC是⊙O内接四边形,
(2)连接AI,
∵点I为△ABC的内心,
∴∠DAB=∠DOB=∠AOI,AD=BD.
∵∠DAI=∠DAB+∠BAI,∠DIA=∠ACI+∠CAI,
∴∠DAI=∠DIA,
∴DI=AD=BD.
(3)过I分别作IQ⊥AB,IF⊥AC,IP⊥BC,垂足分别为Q、F、P,
∵点I为△ABC的内心,即为△ABC的内切圆的圆心,
∴Q、F、P分别为该内切圆与△ABC三边的切点,
∴AQ=AF,CF=CP,BQ=BP,
∵CI=2 ,∠IFC=90°,∠ACI=45°,
∴CF=CI·cos45°=2=CP,
∴△ABC的周长为
AB+AO+BO
=AB+AF+CF+CP+BP
=AB+AQ+BQ+2OF
=2AB+2CF
=2×13+2×2
=30.
4如图,在圆内接四边形ABOD中,AD(1)若∠AFE=60°,CD为直径,求∠ABD的度数.
(2)求证:
①EF∥BC.
②EF=BD.
【答案】(1)30°.
(2)①证明见解析.
② 证明见解析、
【解析】(1)∵CD为直径,
.∠CAD=90°.
(2)① 证明:如图, 延长AB,
∵四边形ABCD是圆内接四边形,
∴∠CBM=∠ADC.
又∵∠AFE=∠ADC,
∴∠AFE=∠CBM,
∴EF//BC.
② 证明:过点D作DG//BC交⊙O于点G,连接AG,CG,
∵DG∥BC,
∴BD=CG,
∴BD=CG.
∵四边形ACGD 是圆内接四边形,
∴∠GDE=∠ACG,
∵EF//DG
∴∠DEF=∠GDE,
∴∠DEF=∠ACG,
∵∠AFE=∠ADC,∠ADC=∠AGC,
∴∠AFE=∠AGC,
∵AE=AC,
∴△AEF≌△ACG(AAS).
∴EF=CG,
.. EF=BD.
【标注】【知识点】圆内接四边形的性质定理
5如图,点E是△ABC的内心,AE的延长线与边BC相交于点F,与△ABC的外接圆相交于点D.
(1)求证:
(2)求证:AB:AC=BF:CF;
(3)求证:.
(4)猜想:线段DF,DE,DA三者之间存在的等量关系.(直接写出,不需证明.)
【答案】(1)见解析
(2)见解析
(3)见解析
【解析】(1)证明:过点D作DH⊥AC,DG⊥AB垂足分别为H,G,具体如下图所示:
∵点E是△ABC的内心,
∴AD是∠BAC的角平分线,
∵DH⊥AC,DG⊥AB,
∴DG=DH,
(2)证明:过点A作AM⊥BO于点M,具体如下图所示
由(1)可得S△ABP:S△AOP=AB:AC,
∴AB:AC=BF:CF;
(3)证明:连接DB,DO,如下图所示:
:AB=AB,DC=DC
.∠ACF=∠BDF,∠FAC=∠FBD
△BFD∽△AFC
. BF·CF=AF·DF
:AC=AC,
∴∠FBA=∠ADC,
又∠BAD=∠DAC,
△ABF∽△ADC,
. AB·AC=AD·AF;
(4):解:连接BE,具体如下图所示:
∵点E是△ABC的内心,
∴BE是∠BAC的角平分线,
∴∠ABE=∠FBE,
∵∠CBD=∠OAD=∠BAD,∠ADB=∠BDF
∴△ABD∽△BFD,
∴DR=DA. DF.
∴∠BED=∠DBE.
∴DB=DE,
【标注】【知识点】与圆有关的计算
6如图,BC是⊙O的直径,A是⊙O上异于B、C的点.⊙O外的点E在射线CB上,直线EA与CD垂直,垂足为D,且DA·AC=DC·AB.设△ABE的面积为S ,△ACD的面积为S .
(1)判断直线EA与⊙O的位置关系,并证明你的结论;
(2)若BC=BE,S =mS ,求常数m的值.
【答案】(1)EA与⊙O相切,理由见解析
(2)【解析】(1)解:EA与⊙O相切,理由如下:
∵BC是⊙O的直径,直线EA与CD垂直,
∴∠BAC=∠ADC=90°,
∵DA·AC=DC·AB,
∴△BAC∽△ADC
..∠ABO=∠DAC.
∵OA=OB,
∴∠ABO=∠BAO=∠DAC,
∵∠BAC=∠BAO+∠OAC=90°,
∴∠OAD=∠OAC+∠DAC=90°.
∴OA⊥DE.
∴EA与⊙O相切;
(2)解:∵BC=BE.
∵OA⊥DE,
∴∠OAB+∠BAE=∠OAE=90°,
∵∠BAC=90°,∠OBA=∠OBA,
∴∠OBA+∠BCA=90°,
∴∠EAB=∠ECA.
∵∠E=∠E,
∴△EAB∽△ECA,
【标注】【知识点】与圆有关的位置关系
7已知:射线OP平分∠MON,A为OP上一点,⊙A交射线OM于点 B,C,交射线ON于点D,E,连接AB,AC,AD.
(1)如图1,若AD∥OM ,试判断四边形OBAD的形状,并说明理由.
(2) 如图2,过点O作CF⊥OM,交OP于点F;过点D作DG⊥ON,,OP于点G .求证:AG=AF.
【答案】(1)见解析
(2)见解析
【解析】(1)解:四边形OBAD是菱形,
理由如下:过点A作AF⊥ON于F,AG⊥OM于G,如图1,
∵OP平分∠MON,AF⊥ON ,AG⊥OM,
∴AF=AG
∵AD=AB
∴RT△AFD≌RT△AGB(HL)
∴FD=GB
∵OA=OA,AF=AG
∴RT△AFO≌ RT△ACO(HL)
∴OP=OC
∴OF-FD=OG-GB,
即OD=OB
∵OP平分∠MON,
∴∠AOD=∠AOB
∵AD∥OM
∴∠AOB=∠OAD
∴∠AOD=∠OAD
∴OD=AD
∴OD=AB=AD=OB
∴四边形OBAD是菱形.
(2)解:
证明连接EF,过点A作AH⊥ON于H,作AG⊥OM于G,如图2,
∵OP平分∠MON,AH⊥ON,AG⊥OM,
∴AH=AG,
∵AD=AB
∴RT△AHD≌RT△AGO(HL)$$
∴DH=BG,
∵AH⊥ON,AG⊥OM
∴EH =DH=OG,
∵OA=OA,AH=AG,
∴RT△AHO≌RT△AGO(HL)
∴OH=OG,
∴EH=CO
∴OH+EH=OG+CO,即OO=OE,
∵∠EOF=∠COF,OF=OF,
∴△OBF≌△OCF(SAS)
∴∠OEF=∠OCF=90°
∴EF⊥ON
∵DG⊥ON,AH⊥ON,
∴DG∥AH∥EF,
∵DH=EH
∴AG=AF
8如图,在平面直角坐标系xOy中,直线l 分别与x轴,y轴相交于A,B两点,点P(z,y)为直线l在第二象限的点.
(1)求A, B两点的坐标.
(2)设△PAO的面积为S,求S关于x的函数解析式,并写出x的取值范围.
(3)作△PAO的外接圆⊙C,延长PC交⊙C于点Q ,当△POQ的面积最小时,求⊙C的半径.
【答案】(1)A(-8,0),B(0,4).
(2)S=2x+16(-8(3)半径为4.
【解析】 得:z=-8,
∴A(-8,0).
∴B(0,4).
(2)∵点P(z,y)为直线l在第二象限的点,
=2z÷16(-8(3)⊙C中,∠PAO=∠PQO,∠POQ=90°,
设OP=m,OQ=OP÷tan∠PQO=2m.
当m最小时,△POQ面积最小.
此时OP⊥AB,AO为⊙C直径.
∴半径为4.
9如图1,AB是⊙O的直径,点B是⊙O上一动点,且不与A,B两点重合,∠EAB的平分线交⊙O于点C,过点C作CD⊥AE,交AB的延长线于点D.
(1)求证:CD是⊙O的切线.
(2)求证:
(3)如图2,原有条件不变,连接BE,BC,延长AB至点M,∠EBM的平分线交AC的延长线于点P,∠CAB的平分线交∠CBM的平分线于点Q .求证:无论点E如何运动,总有∠P=∠Q.
【答案】(1)证明见解析.
(2)证明见解析.
(3)证明见解析.
【解析】(1)连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BOC=2∠OAC,
∵AO平分∠BAE,
∴∠BAE=2∠OAC,
∴∠BAE=∠BOC,
∴CO//AD.
∵∠D=90°,
∴OC⊥CD,
∴CD是⊙O的切线.
(2)∵AO平分∠BAE,
∴∠BAC=∠CAD,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠D=∠BCA,
∴△BAC∽△CAD,
(3)∵∠CAB、∠CBM的平分线交于点Q,
∵∠QBM是△QAB的一个外角,∠CBM是△ABC的一个外角,
同理可证:∠P=45°,
∴∠P=∠Q.
【标注】【知识点】圆与相似
10如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD与⊙O的位置关系,并说明理由.
(2)若 求⊙O的半径.
(3)如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连接BE.求sin∠DBE的值.
【答案】(1)相切,证明见解析.
(2)3.
【解析】(1)CD与⊙O相切,理由:如图1,连接OD,
∵OB=OD,
∴∠ODB=∠CBD,
:∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB为⊙O的直径,
∴∠ADB=∠ADO+∠ODB=90°,
∴∠CDO=90°,
∴OD⊥CD,
∴CD与⊙O相切.
(2)由(1)知,∠CBD=∠ADC,
在Rt△ADB中,
∵∠C=∠C,∠ADC=∠CBD,
∴△CAD∽△CDB
∴CD=2CA=4,
∴CB=2CD=8,
∴AB=CB-CA=8-2=6,
(3) 如图2,连接OE,过点E作EG⊥BD于G,
∵DE平分∠ADB,
在Rt△ABD中,
:EG⊥BD,∠BDE=45°,
∴∠DEG=∠BDE=45°,
∴DG=EG,
设DG=EG=z,
则
在Rt△BEG中,
或x= (舍),
11如图所示,AB是⊙O的直径,点O、D是⊙O上不同的两点,直线BD交线段OC于点E、交过点C的直线CF于点F,若OC=3CE,且9
(1) 求证:直线CF是⊙O的切线.
(2)连接OD、AD、AC、DC.若∠COD=2∠BOC.
①求证:△ACD∽△OBE.
②过点E作EG∥AB,交线段AC于点G,点M为线段AC的中点,若AD=4,求线段MG的长度.
【答案】(1)证明见解析.
(2)①证明见解析.
②1.
【解析】(1)已知:OC=3CE,
已知:!
在△EOF中,
∴△ECF是直角△, EF为斜边,
∴∠ECF=90°,EC⊥CF,即OC⊥CF,
∴直线CF是⊙O的切线.
(2)① 已知:∠COD=2∠BOC.
∠COD=2∠DAC(同弧圆心角是圆周角的2倍) ,
∴∠BOC=∠DAC.
在△ADC和△OBE中,
∠DAC=∠EOB.
∠EBO=∠DCA(同弧圆周角相等) ,
∴△ACD∽△OBE(AA).
② ①中已证明:△ACD∽△OBE,
已知:AD=4.
∵OC=3CE,OC=OE+CE=OB+ OC.
∵OC=OB,
在△CAO中,GE∥AB,且OC=3CE,
∵M为AC的中点,
∴MG=MC-GC
=3-2
=1.
12.我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是⊙O的直径,直线l是⊙O的切线,B为切点. P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D.
(1)如图1,当AB=6,BP的长为π时,求BC的长.
(2)如图2,当 时,求 的值.
(3)如图3,当 si 时,连接BP,PQ,直接写出 的值.
【答案】(1)2
【解析】(1)解:如图1,连接OP,设∠BOP的度数为n.
∵AB=6,BP的长为π,
∴n=60,即∠BOP=60°.
··直线l是⊙O的切线,
(2)解:如图2,连接BQ,过点C作CF⊥AD于点F,
∵AB为直径,
∴∠BAC=∠DAC.
∵CF⊥AD,AB⊥BC,
∴CF=CB.
∵∠BAQ+∠ADB=90°,∠FCD+∠ADB=90°,
∴∠FCD=∠BAQ.
(3)解: 的值为 理由如下:
如图3,连接BQ,
∵AB⊥BC,BQ⊥AD,
∵.∠ABQ+∠BAD=90°,∠ADB+∠BAD=90°.
∴∠ABQ=∠ADC.
·∠ABQ=∠APQ,
:∠APQ=∠ADC.
∵∠PAQ=∠CAD,
∴△APQ∽△ADC.
①∵∠BAP=∠BAC,∠ABC=∠APB=90°,
∴△APB∽△ABC,
②∵BC=CD,①÷②得,
∵sin
模型原理
【总结】
圆与相似结合的几何压轴题,一般利用圆的相关定理(添加辅助线)倒边或倒角,并结合相似基本图形来求解,已知相似图形直接求;构造相似图形间接求(往往作平行线或作垂线来构造).
有时也要利用锐角三角函数、勾股定理求边长,要注意的是它们必须在直角三角形中才可应用,若没有直角三角形,则需作垂直构造直角 .
圆相关定理用途:
在圆中找到相等线段: ①连半径出等腰三角形 ②垂径定理出等线段 ③切线长定理出等线段 ④等弧对等弦
在圆中找到相等角 : ①同弧或等弧所对圆周角相等 ②直径配垂直,构造直角三角形 ③结合三角形外角内角等知识
真题精炼
1如图,在△ABC中, ,以AB为直径的⊙O交BC于点D,. 垂足为E ,BE的延长线交 于点F.
(1)求 的值.
(2) 求证:△AEB∽△BEC .
(3) 求证: AD与EF互相平分.
2如图, 内接于⊙O,直径交于点G ,过点D作射线DF ,使得 ,延长DC交过点B的切线于点E ,连接BC.
(1) 求证: DF是⊙O的切线.
(2) 若
① 求DE的长.
②求⊙O的半径.
3如图, AB是⊙O的直径,△ABC内接于⊙O , 点I为△ABC的内心, 连接CI并延长交⊙O于点D,E是 上任意一点,连接AD,BD, BE,CE.
(1) 若∠ABC=25°, 求∠CEB的度数 .
(2)找出图中所有与DI相等的线段,并证明.
(3)若 求△ABC的周长.
4如图,在圆内接四边形ABCD中, AD
(2) 求证:
① EF∥BC.
②EF= BD .
5如图,点E是△ABC的内心,AE的延长线与边BC相交于点F,与4 的外接圆相交于点D .
(1)求证 : (2)求证:AB:AC=BF:CF; (3)
求证: (4)猜想:线段DF,DE,DA三者之间存在的等量关系.(直接写出,不需证明.)
6如图,BC是⊙O的直径,A是⊙O上异于B、 C的点.⊙O外的点E在射线CB上,直线EA与CD垂直,垂足为D,且DA·AC=DC·AB.设 的面积为 的面积为
(1)判断直线EA与⊙O的位置关系,并证明你的结论;
(2)若 求常数m的值.
-
7已知:射线OP平分 , A为OP上一点, ⊙A交射线OM于点 B,C, 交射线ON于点D,E, 连接AB,AC,AD.
(1) 如图1, 若 ,试判断四边形OBAD的形状,并说明理由.
(2) 如图2, 过点C作( ,交OP于点F ;过点D作 ,OP于点G. 求证:
8如图,在平面直角坐标系xOy中,直线l: 分别与x轴,y轴相交于A ,B两点,点P(x,y)为直线l在第二象限的点 .
(1) 求A, B两点的坐标.
(2)设△PAO的面积为S,求S关于x的函数解析式,并写出x的取值范围.
(3) 作△PAO的外接圆⊙C, 延长PC交⊙C于点Q , 当 的面积最小时,求⊙C的半径.
9如图1,AB是⊙O的直径,点E是⊙O上一动点,且不与A,B两点重合,∠EAB的平分线交⊙O于 点C,过点C作CD⊥AE,交AE的延长线于点D .
(1) 求证:CD是⊙O的切线.
(2) 求证:
(3) 如图2, 原有条件不变, 连接BE, BC, 延长AB至点M, 的平分线交AC的延长线于点P ,∠CAB的平分线交 的平分线于点Q .求证:无论点E如何运动,总有∠P=∠Q.
10如图1,D为⊙O上一点,点C在直径BA的延长线上,且
(1)判断直线CD与⊙O的位置关系,并说明理由.
(2) 若 求⊙O的半径.
(3) 如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E ,交AB于点F ,连接BE.求sin∠DBE的值.
11如图所示,AB是⊙O的直径,点C、D是⊙O上不同的两点,直线BD交线段OC于点E、交过点C的直线CF于点F , 若OC=3CE,且
(1) 求证:直线CF是⊙O的切线.
(2) 连接OD、AD、AC、DC .若
① 求证:
② 过点E作 交线段AC于点G,点M为线段AC的中点,若 求线段MG的长度.
12.我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是⊙O的直径,直线l是⊙O的切线,B为切点. P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D .
(1)如图1, 当 的长为π时,求BC的长.
(2)如图2,当 时,求 的值.
(3)如图3,当 时,连接BP ,PQ ,直接写出 的值.
1.如图,在△ABO中. ,以AB为直径的⊙O交BC于点D,AE⊥OC,垂足为E,BE的延长线交AD于点F
(1)求 的值
(2)求证:△AEB∽△BEC.
(3)求证:AD与EF互相平分.
【答案】
(2)证明见解析
(3)证明见解析
【解析】(1)∵AB=AC,且AB是⊙O的直径
∴AC=2AO,
.∠BAC=90°
·在Rt△AOO中.
∵AE⊥OC
.在Rt△AOE中
(2) 过点B作BM//AE,交EO延长线于点M,
由(2)知:△AEB∽△BEC.
△AOE∽△BDE,
∠BED=∠AEO=90°.
∠DEF=90°.
∠AFB=∠DEF,
.. AF//DE.
由(2)知,
.∠DFB=∠AEF,
AE//FD.
·.四边形AEDF是平行四边形,
AD与EF互相平分.
2如图 △ACD内接于⊙O,直径交于点G,过点D作射线DF,使得∠ADF=∠ACD,延长DC交过点B的切线于点E ,连接BC、
(1) 求证:DF是⊙O的切线.
(2)若
①求DE的长.
②求⊙O的半径.
【答案】(1)证明见解析
(2)①9
【解析】(1)连接ODBD,则∠ACD=∠ABD,
∵∠ADF=∠ACD,
∴∠ABD=∠ADF.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABF+∠BAD=90°,
∵OA=OD,
∴∠OAD=∠ODA.
∴∠ABF+∠ODA=90°.
即∠ODF=90°,
∴OD⊥DF,
又∵OD为⊙O的半径,
∴DF是⊙O的切线;
(2)① ∵BE是⊙O的切线,
∵AB⊥BE,
∴∠ABC+∠CBE=90°,
∵AB是⊙O的直径,
.∠ABO+∠BAC=90°,
∴∠CBE=∠BAC,
∵∠BAC=∠BDC.
∴∠CBE=∠BDC.
即∠CBE=∠BDE.
又∵∠E=∠E,
∴△CBE∽△BDE,
·BE=3CE=3,
∴CE=1,
.. DE=9.
②∵DE=9,CE=1,
∴CD=DE-CE=9-1=8..
∴DG=CD-CG=8-3=5,GE=CG+CE=3+1=4,
∵∠GBE=90°,
∵∠BAC=∠BDC,∠AGC=∠DGB,
∴△AGC∽△DGB.
即
∴⊙O的半径为
3如图,AB是⊙O的直径,△ABC内接于⊙O,点I为△ABC的内心,连接CI并延长交⊙O于点D,E是BC上任意一点,连接AD,BD,BE,CE.
中小学教育资源及组卷应用平台
(1) 若∠ABC=25°,求∠CEB的度数.
(2)找出图中所有与DI相等的线段,并证明.
(3)若 求△ABC的周长.
【答案】(1)115°
(2) DI=AD=BD,证明见解析
(3)30
【解析】(1)∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
又∠ABO=25°,
∵四边形ABEC是⊙O内接四边形,
(2)连接AI,
∵点I为△ABC的内心,
∴∠DAB=∠DOB=∠AOI,AD=BD.
∵∠DAI=∠DAB+∠BAI,∠DIA=∠ACI+∠CAI,
∴∠DAI=∠DIA,
∴DI=AD=BD.
(3)过I分别作IQ⊥AB,IF⊥AC,IP⊥BC,垂足分别为Q、F、P,
∵点I为△ABC的内心,即为△ABC的内切圆的圆心,
∴Q、F、P分别为该内切圆与△ABC三边的切点,
∴AQ=AF,CF=CP,BQ=BP,
∵CI=2 ,∠IFC=90°,∠ACI=45°,
∴CF=CI·cos45°=2=CP,
∴△ABC的周长为
AB+AO+BO
=AB+AF+CF+CP+BP
=AB+AQ+BQ+2OF
=2AB+2CF
=2×13+2×2
=30.
4如图,在圆内接四边形ABOD中,AD
(2)求证:
①EF∥BC.
②EF=BD.
【答案】(1)30°.
(2)①证明见解析.
② 证明见解析、
【解析】(1)∵CD为直径,
.∠CAD=90°.
(2)① 证明:如图, 延长AB,
∵四边形ABCD是圆内接四边形,
∴∠CBM=∠ADC.
又∵∠AFE=∠ADC,
∴∠AFE=∠CBM,
∴EF//BC.
② 证明:过点D作DG//BC交⊙O于点G,连接AG,CG,
∵DG∥BC,
∴BD=CG,
∴BD=CG.
∵四边形ACGD 是圆内接四边形,
∴∠GDE=∠ACG,
∵EF//DG
∴∠DEF=∠GDE,
∴∠DEF=∠ACG,
∵∠AFE=∠ADC,∠ADC=∠AGC,
∴∠AFE=∠AGC,
∵AE=AC,
∴△AEF≌△ACG(AAS).
∴EF=CG,
.. EF=BD.
【标注】【知识点】圆内接四边形的性质定理
5如图,点E是△ABC的内心,AE的延长线与边BC相交于点F,与△ABC的外接圆相交于点D.
(1)求证:
(2)求证:AB:AC=BF:CF;
(3)求证:.
(4)猜想:线段DF,DE,DA三者之间存在的等量关系.(直接写出,不需证明.)
【答案】(1)见解析
(2)见解析
(3)见解析
【解析】(1)证明:过点D作DH⊥AC,DG⊥AB垂足分别为H,G,具体如下图所示:
∵点E是△ABC的内心,
∴AD是∠BAC的角平分线,
∵DH⊥AC,DG⊥AB,
∴DG=DH,
(2)证明:过点A作AM⊥BO于点M,具体如下图所示
由(1)可得S△ABP:S△AOP=AB:AC,
∴AB:AC=BF:CF;
(3)证明:连接DB,DO,如下图所示:
:AB=AB,DC=DC
.∠ACF=∠BDF,∠FAC=∠FBD
△BFD∽△AFC
. BF·CF=AF·DF
:AC=AC,
∴∠FBA=∠ADC,
又∠BAD=∠DAC,
△ABF∽△ADC,
. AB·AC=AD·AF;
(4):解:连接BE,具体如下图所示:
∵点E是△ABC的内心,
∴BE是∠BAC的角平分线,
∴∠ABE=∠FBE,
∵∠CBD=∠OAD=∠BAD,∠ADB=∠BDF
∴△ABD∽△BFD,
∴DR=DA. DF.
∴∠BED=∠DBE.
∴DB=DE,
【标注】【知识点】与圆有关的计算
6如图,BC是⊙O的直径,A是⊙O上异于B、C的点.⊙O外的点E在射线CB上,直线EA与CD垂直,垂足为D,且DA·AC=DC·AB.设△ABE的面积为S ,△ACD的面积为S .
(1)判断直线EA与⊙O的位置关系,并证明你的结论;
(2)若BC=BE,S =mS ,求常数m的值.
【答案】(1)EA与⊙O相切,理由见解析
(2)【解析】(1)解:EA与⊙O相切,理由如下:
∵BC是⊙O的直径,直线EA与CD垂直,
∴∠BAC=∠ADC=90°,
∵DA·AC=DC·AB,
∴△BAC∽△ADC
..∠ABO=∠DAC.
∵OA=OB,
∴∠ABO=∠BAO=∠DAC,
∵∠BAC=∠BAO+∠OAC=90°,
∴∠OAD=∠OAC+∠DAC=90°.
∴OA⊥DE.
∴EA与⊙O相切;
(2)解:∵BC=BE.
∵OA⊥DE,
∴∠OAB+∠BAE=∠OAE=90°,
∵∠BAC=90°,∠OBA=∠OBA,
∴∠OBA+∠BCA=90°,
∴∠EAB=∠ECA.
∵∠E=∠E,
∴△EAB∽△ECA,
【标注】【知识点】与圆有关的位置关系
7已知:射线OP平分∠MON,A为OP上一点,⊙A交射线OM于点 B,C,交射线ON于点D,E,连接AB,AC,AD.
(1)如图1,若AD∥OM ,试判断四边形OBAD的形状,并说明理由.
(2) 如图2,过点O作CF⊥OM,交OP于点F;过点D作DG⊥ON,,OP于点G .求证:AG=AF.
【答案】(1)见解析
(2)见解析
【解析】(1)解:四边形OBAD是菱形,
理由如下:过点A作AF⊥ON于F,AG⊥OM于G,如图1,
∵OP平分∠MON,AF⊥ON ,AG⊥OM,
∴AF=AG
∵AD=AB
∴RT△AFD≌RT△AGB(HL)
∴FD=GB
∵OA=OA,AF=AG
∴RT△AFO≌ RT△ACO(HL)
∴OP=OC
∴OF-FD=OG-GB,
即OD=OB
∵OP平分∠MON,
∴∠AOD=∠AOB
∵AD∥OM
∴∠AOB=∠OAD
∴∠AOD=∠OAD
∴OD=AD
∴OD=AB=AD=OB
∴四边形OBAD是菱形.
(2)解:
证明连接EF,过点A作AH⊥ON于H,作AG⊥OM于G,如图2,
∵OP平分∠MON,AH⊥ON,AG⊥OM,
∴AH=AG,
∵AD=AB
∴RT△AHD≌RT△AGO(HL)$$
∴DH=BG,
∵AH⊥ON,AG⊥OM
∴EH =DH=OG,
∵OA=OA,AH=AG,
∴RT△AHO≌RT△AGO(HL)
∴OH=OG,
∴EH=CO
∴OH+EH=OG+CO,即OO=OE,
∵∠EOF=∠COF,OF=OF,
∴△OBF≌△OCF(SAS)
∴∠OEF=∠OCF=90°
∴EF⊥ON
∵DG⊥ON,AH⊥ON,
∴DG∥AH∥EF,
∵DH=EH
∴AG=AF
8如图,在平面直角坐标系xOy中,直线l 分别与x轴,y轴相交于A,B两点,点P(z,y)为直线l在第二象限的点.
(1)求A, B两点的坐标.
(2)设△PAO的面积为S,求S关于x的函数解析式,并写出x的取值范围.
(3)作△PAO的外接圆⊙C,延长PC交⊙C于点Q ,当△POQ的面积最小时,求⊙C的半径.
【答案】(1)A(-8,0),B(0,4).
(2)S=2x+16(-8
【解析】 得:z=-8,
∴A(-8,0).
∴B(0,4).
(2)∵点P(z,y)为直线l在第二象限的点,
=2z÷16(-8
设OP=m,OQ=OP÷tan∠PQO=2m.
当m最小时,△POQ面积最小.
此时OP⊥AB,AO为⊙C直径.
∴半径为4.
9如图1,AB是⊙O的直径,点B是⊙O上一动点,且不与A,B两点重合,∠EAB的平分线交⊙O于点C,过点C作CD⊥AE,交AB的延长线于点D.
(1)求证:CD是⊙O的切线.
(2)求证:
(3)如图2,原有条件不变,连接BE,BC,延长AB至点M,∠EBM的平分线交AC的延长线于点P,∠CAB的平分线交∠CBM的平分线于点Q .求证:无论点E如何运动,总有∠P=∠Q.
【答案】(1)证明见解析.
(2)证明见解析.
(3)证明见解析.
【解析】(1)连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BOC=2∠OAC,
∵AO平分∠BAE,
∴∠BAE=2∠OAC,
∴∠BAE=∠BOC,
∴CO//AD.
∵∠D=90°,
∴OC⊥CD,
∴CD是⊙O的切线.
(2)∵AO平分∠BAE,
∴∠BAC=∠CAD,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠D=∠BCA,
∴△BAC∽△CAD,
(3)∵∠CAB、∠CBM的平分线交于点Q,
∵∠QBM是△QAB的一个外角,∠CBM是△ABC的一个外角,
同理可证:∠P=45°,
∴∠P=∠Q.
【标注】【知识点】圆与相似
10如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD与⊙O的位置关系,并说明理由.
(2)若 求⊙O的半径.
(3)如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连接BE.求sin∠DBE的值.
【答案】(1)相切,证明见解析.
(2)3.
【解析】(1)CD与⊙O相切,理由:如图1,连接OD,
∵OB=OD,
∴∠ODB=∠CBD,
:∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB为⊙O的直径,
∴∠ADB=∠ADO+∠ODB=90°,
∴∠CDO=90°,
∴OD⊥CD,
∴CD与⊙O相切.
(2)由(1)知,∠CBD=∠ADC,
在Rt△ADB中,
∵∠C=∠C,∠ADC=∠CBD,
∴△CAD∽△CDB
∴CD=2CA=4,
∴CB=2CD=8,
∴AB=CB-CA=8-2=6,
(3) 如图2,连接OE,过点E作EG⊥BD于G,
∵DE平分∠ADB,
在Rt△ABD中,
:EG⊥BD,∠BDE=45°,
∴∠DEG=∠BDE=45°,
∴DG=EG,
设DG=EG=z,
则
在Rt△BEG中,
或x= (舍),
11如图所示,AB是⊙O的直径,点O、D是⊙O上不同的两点,直线BD交线段OC于点E、交过点C的直线CF于点F,若OC=3CE,且9
(1) 求证:直线CF是⊙O的切线.
(2)连接OD、AD、AC、DC.若∠COD=2∠BOC.
①求证:△ACD∽△OBE.
②过点E作EG∥AB,交线段AC于点G,点M为线段AC的中点,若AD=4,求线段MG的长度.
【答案】(1)证明见解析.
(2)①证明见解析.
②1.
【解析】(1)已知:OC=3CE,
已知:!
在△EOF中,
∴△ECF是直角△, EF为斜边,
∴∠ECF=90°,EC⊥CF,即OC⊥CF,
∴直线CF是⊙O的切线.
(2)① 已知:∠COD=2∠BOC.
∠COD=2∠DAC(同弧圆心角是圆周角的2倍) ,
∴∠BOC=∠DAC.
在△ADC和△OBE中,
∠DAC=∠EOB.
∠EBO=∠DCA(同弧圆周角相等) ,
∴△ACD∽△OBE(AA).
② ①中已证明:△ACD∽△OBE,
已知:AD=4.
∵OC=3CE,OC=OE+CE=OB+ OC.
∵OC=OB,
在△CAO中,GE∥AB,且OC=3CE,
∵M为AC的中点,
∴MG=MC-GC
=3-2
=1.
12.我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是⊙O的直径,直线l是⊙O的切线,B为切点. P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D.
(1)如图1,当AB=6,BP的长为π时,求BC的长.
(2)如图2,当 时,求 的值.
(3)如图3,当 si 时,连接BP,PQ,直接写出 的值.
【答案】(1)2
【解析】(1)解:如图1,连接OP,设∠BOP的度数为n.
∵AB=6,BP的长为π,
∴n=60,即∠BOP=60°.
··直线l是⊙O的切线,
(2)解:如图2,连接BQ,过点C作CF⊥AD于点F,
∵AB为直径,
∴∠BAC=∠DAC.
∵CF⊥AD,AB⊥BC,
∴CF=CB.
∵∠BAQ+∠ADB=90°,∠FCD+∠ADB=90°,
∴∠FCD=∠BAQ.
(3)解: 的值为 理由如下:
如图3,连接BQ,
∵AB⊥BC,BQ⊥AD,
∵.∠ABQ+∠BAD=90°,∠ADB+∠BAD=90°.
∴∠ABQ=∠ADC.
·∠ABQ=∠APQ,
:∠APQ=∠ADC.
∵∠PAQ=∠CAD,
∴△APQ∽△ADC.
①∵∠BAP=∠BAC,∠ABC=∠APB=90°,
∴△APB∽△ABC,
②∵BC=CD,①÷②得,
∵sin
同课章节目录
