专题三十 平移变换引起的几何压轴(含解析) 2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题三十 平移变换引起的几何压轴(含解析) 2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 468.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 12:41:09 | ||
图片预览



文档简介
平移变换引起的几何压轴
模型原理
1.平行四边形与平移
由于在平移变换下,如图3-1--1,□ABCD中,△ABE沿着AD方向平移后,成为 即AB//DCAE//DF ,BE//CF,因此,对于已知条件中有平行四边形的几何题,考虑用平移变换.
2.共线相等线段与平移
如图△ABC沿着BC方向平移至△DEF ,与平移方向平行的线段例如BC,变为共线且相等的线段,即BC=EF ,BC与EF共线,因此,对于有共线且相等的线段的几何问题,考虑用平移变换处理.
3.不共线线段与平移
两条线段既不平行也不共线,但是我们可以通过平移变换移动其中一条线段,使两条线段有一个公共端点,并且可以形成等腰三角形或其他特殊三角形. 总结:线段相等不等腰,平移共点变等腰.
1.如图,若 ,并相交 ,平移CD与AB共顶点 ,出现平行四边形( 和等腰
2.如图,若AB=CD无交点,平移CD与AB共顶点,同样产生平行四边形和等腰
真题精炼
1.如图,△ABC是边长为2的等边三角形,将 沿直线AC翻折,得到 再将 在直线AC上平移,得到 连接 则△A'I 3的周长的最小值是
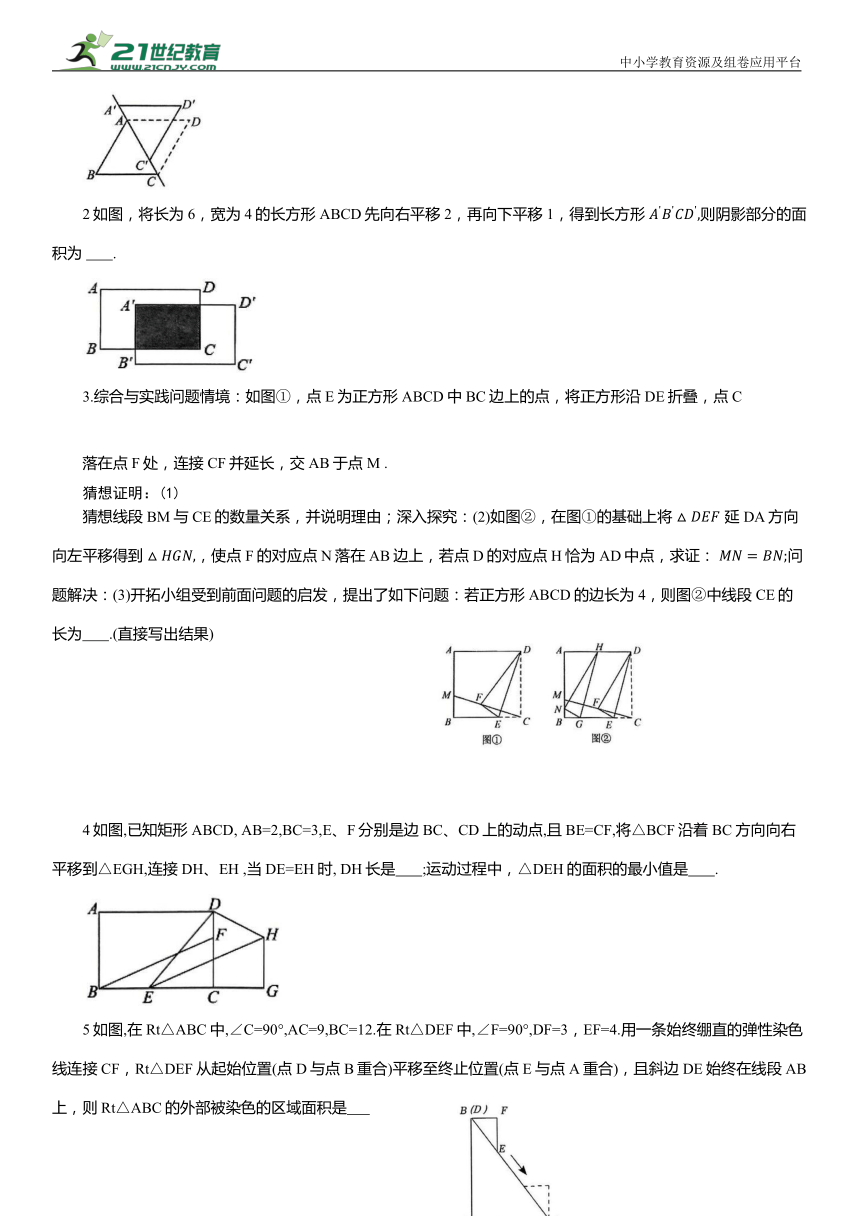
2如图,将长为6,宽为4的长方形ABCD先向右平移2,再向下平移1,得到长方形 则阴影部分的面积为 .
3.综合与实践问题情境:如图①,点E为正方形ABCD中BC边上的点,将正方形沿DE折叠,点C
落在点F处,连接CF并延长,交AB于点M .
猜想证明:(1)
猜想线段BM与CE的数量关系,并说明理由;深入探究:(2)如图②,在图①的基础上将 延DA方向向左平移得到 ,使点F的对应点N落在AB边上,若点D的对应点H恰为AD中点,求证: 问题解决:(3)开拓小组受到前面问题的启发,提出了如下问题:若正方形ABCD的边长为4,则图②中线段CE的长为 .(直接写出结果)
4如图,已知矩形ABCD, AB=2,BC=3,E、F分别是边BC、CD上的动点,且BE=CF,将△BCF沿着BC方向向右平移到△EGH,连接DH、EH ,当DE=EH时, DH长是 ;运动过程中,△DEH的面积的最小值是 .
5如图,在Rt△ABC中,∠C=90°,AC=9,BC=12.在Rt△DEF中,∠F=90°,DF=3,EF=4.用一条始终绷直的弹性染色线连接CF,Rt△DEF从起始位置(点D与点B重合)平移至终止位置(点E与点A重合),且斜边DE始终在线段AB上,则Rt△ABC的外部被染色的区域面积是
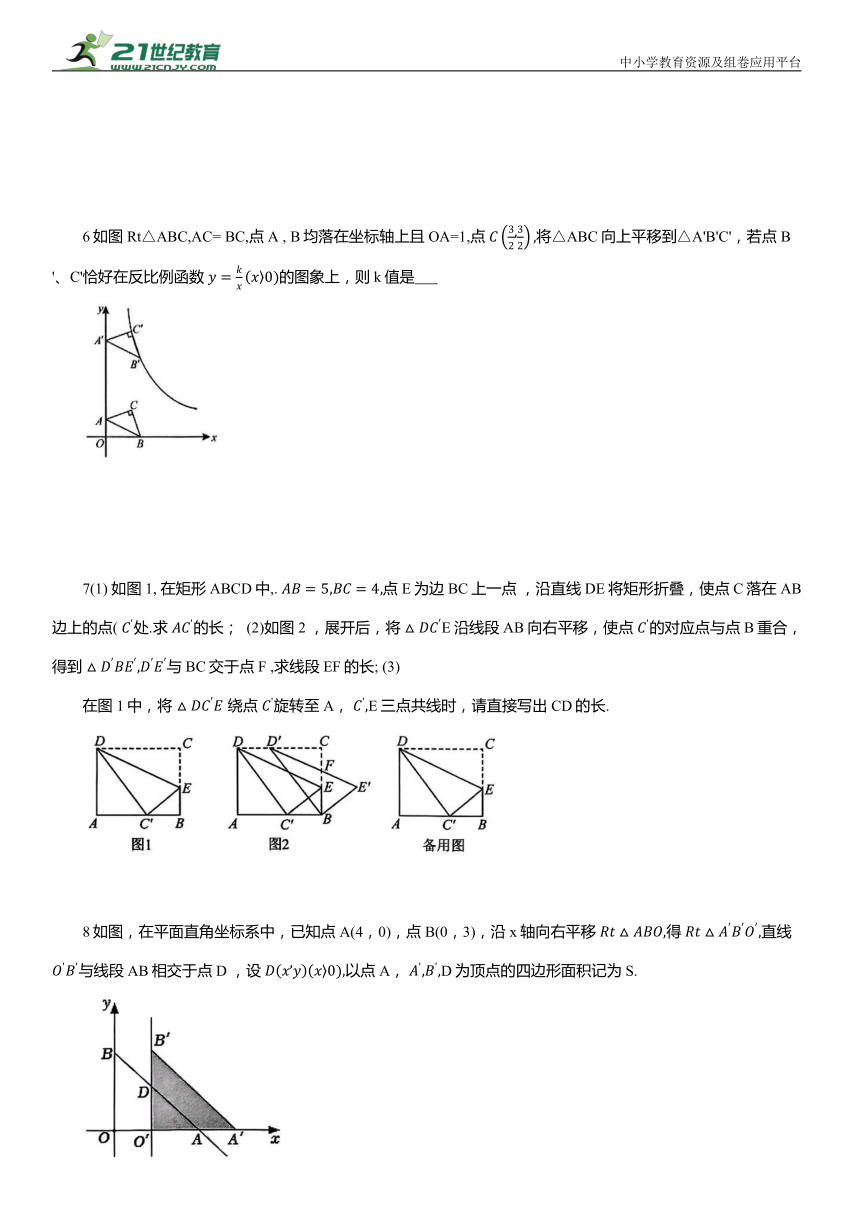
6如图Rt△ABC,AC= BC,点A , B均落在坐标轴上且OA=1,点 将△ABC向上平移到△A'B'C',若点B'、C'恰好在反比例函数 的图象上,则k值是
7(1) 如图1, 在矩形ABCD中,. 点E为边BC上一点 ,沿直线DE将矩形折叠,使点C落在AB边上的点( 处.求 的长; (2)如图2 ,展开后,将 E沿线段AB向右平移,使点 的对应点与点B重合,得到 与BC交于点F ,求线段EF的长; (3)
在图1中,将 绕点 旋转至A, E三点共线时,请直接写出CD的长.
8如图,在平面直角坐标系中,已知点A(4,0),点B(0,3),沿x轴向右平移 得 直线 与线段AB相交于点D ,设 以点A, D为顶点的四边形面积记为S.
(1)求AB的长和y与x的函数关系式;(用相似)
(2)用含 的式子表示S;
(3)当 求点D的坐标(直接写出结果).
9如图1,在平面直角坐标系中,直线 与x轴、y轴相交于A、B两点 ,点C在线段OA上,将线段CB绕着点C顺时针旋转9 得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x 轴于点E
(1) 求证:
(2)如图2,将 沿x轴正方向平移得 当 经过点D时,求点D的坐标及△BCD平移的距离;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形 若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
10阅读下面材料:
小伟遇到这样一个问题:如图1,在梯形ABCD中,. ,对角线AC、BD相交于点O .若梯形ABCD的面积为1, 求AC、BD、. 的长度为三边长的三角形的面积 .
小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可,他先后尝试了翻折、旋转、平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E ,得到的 即是以AC、BD、 的长度为三边长的三角形(如图2) .
(1)请你回答 :图2中. C的面积等于
(2) 如图3, 的三条中线分别为AD、BE、CF .在图3中利用图形变换画出并指明以ADBE、CF的长度为三边长的一个三角形(保留画图痕迹).
若 的面积为1 ,则以AD、BE、CF的长度为三边长的三角形的面积等于 .
1如图,△ABC是边长为2的等边三角形,将△ABC沿直线AC翻折,得到△ACD,再将△ACD在直线AC上平移,得到△A'C'D'.连接A'B,D'B,则△A'D'B的周长的最小值是 .
【答案】 2+2
【解析】
【分析】
本题主要考查了翻折,平移的性质,等边三角形的性质以及菱形的判定与性质,熟练掌握性质定理是解题的关键.作D关于点B的对称点B',BD交AC于点O,连接B'C,利用勾股定理求出B'C即可得到答案.
【详解】
解:作D关于点B的对称点B', BD交AC于点O,连接B'C,
由题意可知,将△ABC沿直线AC翻折,得到△AOD,再将△ACD在直线AC上平移,得到△A'C'D',
∴△A'D'B的周长的最小值转化为△BDC周长的最小值,
当B'、B、C三点共线时,BD+BC最小为CB'的长,
∵△ABC、△ACD均为等边三角形,
∴AB=BC=CD=AB,
∴四边形ABCD是菱形,
在Rt△CEO中,
∴△BDC周长的最小值为
故△A'D'B的周长的最小值为
故答案为:
【标注】【知识点】平移的性质
【知识点】折纸问题与剪拼
2如图,将长为6,宽为4的长方形ABCD先向右平移2,再向下平移1,得到长方形A'B'CD',则阴影部分的面积为 .
【答案】12
【解析】
【分析】
本题主要考查图形的平移,掌握图形平移求线段长度的方法是解题的关键.
根据图形移动可求出A'B',B'C的长,根据几何图形面积的计算方法即可求解.
【详解】
解:由题意可得,阴影部分是矩形,长B'C=6-2=4,宽A'C=4-1=3,
∴阴影部分的面积=4×3=12,
故答案为:12.
3综合与实践
问题情境:
如图①,点E为正方形ABCD中BC边上的点,将正方形沿DE折叠,点C落在点/处,连接CF并延长,交AB于点M.
猜想证明:
(1)猜想线段BM与CE的数量关系,并说明理由;
深入探究:
(2)如图②,在图①的基础上将△DEF延DA方向向左平移得到△HGN ,使点/的对应点N落在AB边上,若点D的对应点H恰为AD中点,求证:MN=BN;
问题解决:
(3)开拓小组受到前面问题的启发,提出了如下问题:若正方形ABCD的边长为4,则图②中线段CE的长为 .(直接写出结果)
【答案】(1)BM=CE,理由见解析
(2)见解析
(3)8-4
【解析】
(1)BM=CE,理由如下:
证明:∵四边形ABCD是正方形,
∴BC=CD,∠B=∠BCD=90°
∴∠DCM+∠MCB=90°.
由折叠得:DE⊥CF,
∴∠DCM+∠EDC=90°.
∴∠MCB=∠EDO.
中小学教育资源及组卷应用平台
∴△CBM≌△DCE.
∴BM=CE;
(2)解法一:∵点H是AD的中点,
∵四边形ABCD是正方形,
∴AD=CD,∠A=∠B=∠BCD=90°.
由折叠得:DF=CD,CE=EF,∠DFE=∠BCD=90°.
由平移得:HN=DF,EF=NG,∠HNG=∠DFE=90°.
:在Rt△ANH中,:
∴∠ANH=30°
∴∠BNG=180°-∠ANH--∠HNG=60°
∴∠BGN=30°.
∵在Rt△BNG中,
由(1)得:CE=BM,
∴MN=BN.
解法二:如下图所示,连接NF.
由平移得:NF∥DH,NF=DH.
∵点H是AD的中点,
:在正方形ABCD中,AD∥BC,AD=BO;
∴FN∥BC,
∴∠MNF=∠B,∠MFN=∠MCB.
∴△MNF∽△MBC.
BM=2MN,即MN=BN.
(3)根据翻折可知:EC=EF,
根据平移可知:NG=EF,GE=HD,
根据(1)有CE=BM.
根据(2)有
∵AD=4,
BG=BC-GE-CE=2-CE,
在Rt△BNG中,
解得:
∵CE因此正确答案为:
【标注】【知识点】相似三角形的性质与判定综合
【知识点】正方形的性质
【知识点】矩形的性质
【知识点】平移的性质
【业务题型】其他
4如图,已知矩形ABCD,AB=2,BC=3,E、F分别是边BC、CD上的动点,且BE=CF,将△BCF沿着BC方向向右平移到△EGH,连接DH、EH,当DE=EH时,DH长是 ;运动过程中,△DEH的面积的最小值是 .
【答案】
【解析】
【分析】
结合图形,由已知先证明CGHF为正方形,设BE=x,则CF=FH=HG=x,求出z的长,进而求出DH;由 得到S 利用二次函数的性质即可求得△DEH的面积的最小值.
【详解】
解:连接FH ,如图所示:
∵△EGH≌△BCF,
∴∠DCB=∠G=90°,FC=GH,BC=EG=3,
∴FC∥GH,BE=CG,
∴四边形FCGH是平行四边形,
∵∠FOG=90°.
∴四边形FCGH是矩形,
∵BE=CF,
∴CG=CF.
∴四边形CGHF为正方形,
∴EH=CF.
设BE=x,则CF=FH=HG=x,
∴EC=3-x,
∵DE=EH,
解得
∴△DEH的面积的最小值是
故答案为:
5.如图,在Rt△ABC中,∠C=90°,AC=9,BC=12.在Rt△DEF中;∠F=90°,DF=3,EF=4.用一条始终绷直的弹性染色线连接CF,Rt△DEF从起始位置(点D与点β重合)平移至终止位置(点E与点A重合),且斜边DE始终在线段AB上,则Rt△ABC的外部被染色的区域面积是 .
B(D) F
【答案】21
【解析】解:如下图所示,连接CF交AB于点M,连接CF'交AB于点N,过点/作FG⊥AB于点H,过点F'作F'H⊥AB于点H,连接FF',则四边形FGHF'是矩形,Rt△ABC的外部被染色的区域是梯形MFF'N.
在Rt△DEF中,DF=3,EF=4,
在Rt△ABO中,AC=9,BC=12,
∴FF'=GH=AB-BG-AH=15-5=10,
∵BF∥AC,
同法可证
∴Rt△ABC的外部被染色的区域的面积 因此正确答案为:21.
答案9
:∠N=∠M=∠NOB=90°,
∴四边形NOBM为矩形,
∴B(2,0),
设△ABC向上平移m个单位,
则 则B'(2,m).
又点C'和B'在该比例函数图象上,
解得
∴k=9,
故答案为:9.
7(1)如图1,在矩形ABCD中,AB=5,BC=4,点E为边BC上一点,沿直线DE将矩形折叠,使点C落在AB边上的点C'处.求AC'的长;
(2)如图2,展开后,将△DC'E沿线段AB向右平移,使点C'的对应点与点B重合,得到△D'BE',D'E'与BC交于点F,求线段EF的长;
(3)在图1中,将△DC'E绕点O'旋转至A,C',E三点共线时,请直接写出CD的长.
【答案】 (1)3; (2)1; (3) 或
【解析】
【分析】
(1)本题利用折叠和矩形的性质得出CD=C'D=AB=6,AD=BC=4,再利用勾股定理即可解题;
(2)本题利用平移的性质证得△CDE∽△CD'F,设EB长为x,利用勾股定理算出x,推出CE,再利用相似三角形的性质得到 算出CF,从而求得EF的长;
(3)本题根据A,C',E三点共线,分以下两种情况讨论,①当E旋转到C'左侧时,②当E旋转到C'右侧时,根据以上两种情况作辅助线构造直角三角形,利用旋转的性质、矩形的性质和判定、以及勾股定理进行分析求解,即可解题
【详解】
(1)解:∵ABCD为矩形,AB=5,BC=4,
∴CD=C'D=AB=5,AD=BC=4,
(2)解:∵△D'BE'为△DC'E平移后的图形,AC'=3,AB=5,
∴△CDE∽△CD'F,
设EB长为x,
解得
∴EF=CE-CF=1;
(3)解:将△DO'E绕点C'旋转至A,C',E三点共线,分以下两种情况:
①当E旋转到C'左侧时,如图所示:
作DM⊥CB,交CB的延长线于点M,
由(2)可知/
由旋转性质可知,.
.四边形BMDC'为矩形,
②当E旋转到C'右侧时,如图所示:
作DN⊥BC,交BO的延长线于点N,
由(2)可知BC'=2,
由旋转性质可知,
∴四边形BNDC'为矩形,
∴CN=BN-BC=5-4=1,
8如图,在平面直角坐标系中,已知点A(4,0),点B(0,3) ,沿z轴向右平移Rt△ABO,得四边形面积记为S.
(1)求AB的长和y与x的函数关系式;(用相似)
(2)用含x(x≠4)的式子表示S;
(3)当 求点D的坐标(直接写出结果).
【答案】
【解析】
(1)解:∵A(4,0)、B(0,3)
∴OA=4,OB=3,
当点O'与点A不重合时,
∵B'O'∥OB,
如图(1) ,点D在AB上,
图(1)
有AO'=AO-O'O=4-z
即
如图(2),点D在BA延长线上,
有AO'=00-AO=x-4
即
当点O'与点A重合时,D与A重合,此时:z=4, y=0.
∴y与x的关系是:
(2)解:①如图(1) ,当0则四边形AA'B'D的面积=△A'O'B的面积-△AO'D的面积
把 入可得
②如图(2) ,当x>4时,点D在BA延长线上.
∵平移△AOB得到△A'O'B'.
代入可得:
综上所述
(3)解: 把 可得 (舍弃) .
把 代入 得y=2.
把 代. 可得 (舍弃)或 (舍弃)
综上所述点D的坐标为
9如图1,在平面直角坐标系中,直线 与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)如图2,将△BCD沿x轴正方向平移得△BC' D' ,当BC' 经过点D时,求点D的坐标及△BCD平移的距离;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形 若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】(1)见解析; (2)点D的坐标为(4,1) ,。BCD平移的距离为 ;(3)存在,点P的坐标为(0, ) 或(0, ).
【解析】
【分析】
(1)利用同角的余角相等可得出∠OBC=∠ECD,由旋转的性质可得出BC=CD,结合∠BOC=∠CED=90°即可证出△BOC≌△CED(AAS) ;
(2)利用一次函数图象上点的坐标特征可求出点B的坐标,设OC=m,则点D的坐标为(m+3,m),利用一次函数图象上点的坐标特征可求出m值,进而可得出点C,D的坐标,由点B,C的坐标,利用待定系数法可求出直线BC的解析式,结合BC∥BC及点D在直线BC上可求出直线BC的解析式,再利用一次函数图象上点的坐标特征可求出点C的坐标,结合点C的坐标即可得出△BCD平移的距离;
(3)设点P的坐标为(0,m),点Q的坐标为 分CD为边及CD为对角线两种情
【详解】
(1)证明:∵∠BOC=∠BCD=∠CED=90°,
∴∠OCB+∠OBC=90°,∠OCB+∠ECD=90°,
∴∠OBC=∠ECD.
∵将线段CB绕着点C顺时针旋转90°得到CD,
∴BC=CD.
在△BOC和△CED中,C H OH+3O 点燃2CO +3H O,
∴△BOC≌△CED(AAS) .
(2)解:∵直线 与x轴、y轴相交于A、B两点,
∴点B的坐标为(0,3) ,点A的坐标为(6,0).
设OC=m,
∵△BOCB△CED,
∴OC=ED=m,BO=CE=3,
∴点D的坐标为(m+3, m).
∵点D在直线
解得: m=1,
∴点D的坐标为(4,1) ,点C的坐标为(1,0) .
∵点B的坐标为(0,3) ,点C的坐标为(1,0),
∴直线BC的解析式为y=-3x+3.
设直线B'C的解析式为y=-3x+b,
将D(4,1)代入y=·3x+b,得:1--3x4+b,解得:b=13,
∴直线BC的解析式为y=-3x+13,
∴点C的坐标为
∴BCD平移的距离为 3.
(3)解:设点P的坐标为(0,m),点Q的坐标为
分两种情况考虑,如图3所示:
①若CD为边,当四边形CDQP为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n
解得
∴点P 的坐标为(0.2);
当四边形CDPQ为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,- n+3) ,
解得:
∴点P 的坐标为
②若CD为对角线,∵C(1,0),D(4,1),P(0,m),Q(n,- n+3),
解得:
∴点P的坐标为
综上所述:存在,点P的坐标为(0, )或((0,
【点睛】
本题考查了全等三角形的判定与性质、旋转的性质、一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及平行四边形的性质,解题的关键是掌握利用全等三角形的判定定理AAS;利用一次函数图象上点的坐标特征;利用平行四边形的对角线互相平分的性质.
10阅读下面材料:
小伟遇到这样一个问题:如图1,在梯形ABCD中,AD//BC,对角线AC、BD相交于点O.若梯形ABCD的面积为1,求AC、BD、AD+BC的长度为三边长的三角形的面积.
小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可,他先后尝试了翻折、旋转、平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC、BD、AD+BC的长度为三边长的三角形(如图2).
(1)请你回答:图2中△BDE的面积等于 .
(2)如图3,△ABC的三条中线分别为AD、BE、CF .在图3中利用图形变换画出并指明以AD
BE、CF的长度为三边长的一个三角形(保留画图痕迹).
(3)若△ABC的面积为1,则以AD、BE、CF的长度为三边长的三角形的面积等于 .
【答案】(1)1
(2)画图见解析.
(3)
(2)以AD、BE、CF的长度为三边长的一个三角形是△CFP
(3)以AD、BE、CF的长度为三边长的三角形的面积等于
模型原理
1.平行四边形与平移
由于在平移变换下,如图3-1--1,□ABCD中,△ABE沿着AD方向平移后,成为 即AB//DCAE//DF ,BE//CF,因此,对于已知条件中有平行四边形的几何题,考虑用平移变换.
2.共线相等线段与平移
如图△ABC沿着BC方向平移至△DEF ,与平移方向平行的线段例如BC,变为共线且相等的线段,即BC=EF ,BC与EF共线,因此,对于有共线且相等的线段的几何问题,考虑用平移变换处理.
3.不共线线段与平移
两条线段既不平行也不共线,但是我们可以通过平移变换移动其中一条线段,使两条线段有一个公共端点,并且可以形成等腰三角形或其他特殊三角形. 总结:线段相等不等腰,平移共点变等腰.
1.如图,若 ,并相交 ,平移CD与AB共顶点 ,出现平行四边形( 和等腰
2.如图,若AB=CD无交点,平移CD与AB共顶点,同样产生平行四边形和等腰
真题精炼
1.如图,△ABC是边长为2的等边三角形,将 沿直线AC翻折,得到 再将 在直线AC上平移,得到 连接 则△A'I 3的周长的最小值是
2如图,将长为6,宽为4的长方形ABCD先向右平移2,再向下平移1,得到长方形 则阴影部分的面积为 .
3.综合与实践问题情境:如图①,点E为正方形ABCD中BC边上的点,将正方形沿DE折叠,点C
落在点F处,连接CF并延长,交AB于点M .
猜想证明:(1)
猜想线段BM与CE的数量关系,并说明理由;深入探究:(2)如图②,在图①的基础上将 延DA方向向左平移得到 ,使点F的对应点N落在AB边上,若点D的对应点H恰为AD中点,求证: 问题解决:(3)开拓小组受到前面问题的启发,提出了如下问题:若正方形ABCD的边长为4,则图②中线段CE的长为 .(直接写出结果)
4如图,已知矩形ABCD, AB=2,BC=3,E、F分别是边BC、CD上的动点,且BE=CF,将△BCF沿着BC方向向右平移到△EGH,连接DH、EH ,当DE=EH时, DH长是 ;运动过程中,△DEH的面积的最小值是 .
5如图,在Rt△ABC中,∠C=90°,AC=9,BC=12.在Rt△DEF中,∠F=90°,DF=3,EF=4.用一条始终绷直的弹性染色线连接CF,Rt△DEF从起始位置(点D与点B重合)平移至终止位置(点E与点A重合),且斜边DE始终在线段AB上,则Rt△ABC的外部被染色的区域面积是
6如图Rt△ABC,AC= BC,点A , B均落在坐标轴上且OA=1,点 将△ABC向上平移到△A'B'C',若点B'、C'恰好在反比例函数 的图象上,则k值是
7(1) 如图1, 在矩形ABCD中,. 点E为边BC上一点 ,沿直线DE将矩形折叠,使点C落在AB边上的点( 处.求 的长; (2)如图2 ,展开后,将 E沿线段AB向右平移,使点 的对应点与点B重合,得到 与BC交于点F ,求线段EF的长; (3)
在图1中,将 绕点 旋转至A, E三点共线时,请直接写出CD的长.
8如图,在平面直角坐标系中,已知点A(4,0),点B(0,3),沿x轴向右平移 得 直线 与线段AB相交于点D ,设 以点A, D为顶点的四边形面积记为S.
(1)求AB的长和y与x的函数关系式;(用相似)
(2)用含 的式子表示S;
(3)当 求点D的坐标(直接写出结果).
9如图1,在平面直角坐标系中,直线 与x轴、y轴相交于A、B两点 ,点C在线段OA上,将线段CB绕着点C顺时针旋转9 得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x 轴于点E
(1) 求证:
(2)如图2,将 沿x轴正方向平移得 当 经过点D时,求点D的坐标及△BCD平移的距离;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形 若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
10阅读下面材料:
小伟遇到这样一个问题:如图1,在梯形ABCD中,. ,对角线AC、BD相交于点O .若梯形ABCD的面积为1, 求AC、BD、. 的长度为三边长的三角形的面积 .
小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可,他先后尝试了翻折、旋转、平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E ,得到的 即是以AC、BD、 的长度为三边长的三角形(如图2) .
(1)请你回答 :图2中. C的面积等于
(2) 如图3, 的三条中线分别为AD、BE、CF .在图3中利用图形变换画出并指明以ADBE、CF的长度为三边长的一个三角形(保留画图痕迹).
若 的面积为1 ,则以AD、BE、CF的长度为三边长的三角形的面积等于 .
1如图,△ABC是边长为2的等边三角形,将△ABC沿直线AC翻折,得到△ACD,再将△ACD在直线AC上平移,得到△A'C'D'.连接A'B,D'B,则△A'D'B的周长的最小值是 .
【答案】 2+2
【解析】
【分析】
本题主要考查了翻折,平移的性质,等边三角形的性质以及菱形的判定与性质,熟练掌握性质定理是解题的关键.作D关于点B的对称点B',BD交AC于点O,连接B'C,利用勾股定理求出B'C即可得到答案.
【详解】
解:作D关于点B的对称点B', BD交AC于点O,连接B'C,
由题意可知,将△ABC沿直线AC翻折,得到△AOD,再将△ACD在直线AC上平移,得到△A'C'D',
∴△A'D'B的周长的最小值转化为△BDC周长的最小值,
当B'、B、C三点共线时,BD+BC最小为CB'的长,
∵△ABC、△ACD均为等边三角形,
∴AB=BC=CD=AB,
∴四边形ABCD是菱形,
在Rt△CEO中,
∴△BDC周长的最小值为
故△A'D'B的周长的最小值为
故答案为:
【标注】【知识点】平移的性质
【知识点】折纸问题与剪拼
2如图,将长为6,宽为4的长方形ABCD先向右平移2,再向下平移1,得到长方形A'B'CD',则阴影部分的面积为 .
【答案】12
【解析】
【分析】
本题主要考查图形的平移,掌握图形平移求线段长度的方法是解题的关键.
根据图形移动可求出A'B',B'C的长,根据几何图形面积的计算方法即可求解.
【详解】
解:由题意可得,阴影部分是矩形,长B'C=6-2=4,宽A'C=4-1=3,
∴阴影部分的面积=4×3=12,
故答案为:12.
3综合与实践
问题情境:
如图①,点E为正方形ABCD中BC边上的点,将正方形沿DE折叠,点C落在点/处,连接CF并延长,交AB于点M.
猜想证明:
(1)猜想线段BM与CE的数量关系,并说明理由;
深入探究:
(2)如图②,在图①的基础上将△DEF延DA方向向左平移得到△HGN ,使点/的对应点N落在AB边上,若点D的对应点H恰为AD中点,求证:MN=BN;
问题解决:
(3)开拓小组受到前面问题的启发,提出了如下问题:若正方形ABCD的边长为4,则图②中线段CE的长为 .(直接写出结果)
【答案】(1)BM=CE,理由见解析
(2)见解析
(3)8-4
【解析】
(1)BM=CE,理由如下:
证明:∵四边形ABCD是正方形,
∴BC=CD,∠B=∠BCD=90°
∴∠DCM+∠MCB=90°.
由折叠得:DE⊥CF,
∴∠DCM+∠EDC=90°.
∴∠MCB=∠EDO.
中小学教育资源及组卷应用平台
∴△CBM≌△DCE.
∴BM=CE;
(2)解法一:∵点H是AD的中点,
∵四边形ABCD是正方形,
∴AD=CD,∠A=∠B=∠BCD=90°.
由折叠得:DF=CD,CE=EF,∠DFE=∠BCD=90°.
由平移得:HN=DF,EF=NG,∠HNG=∠DFE=90°.
:在Rt△ANH中,:
∴∠ANH=30°
∴∠BNG=180°-∠ANH--∠HNG=60°
∴∠BGN=30°.
∵在Rt△BNG中,
由(1)得:CE=BM,
∴MN=BN.
解法二:如下图所示,连接NF.
由平移得:NF∥DH,NF=DH.
∵点H是AD的中点,
:在正方形ABCD中,AD∥BC,AD=BO;
∴FN∥BC,
∴∠MNF=∠B,∠MFN=∠MCB.
∴△MNF∽△MBC.
BM=2MN,即MN=BN.
(3)根据翻折可知:EC=EF,
根据平移可知:NG=EF,GE=HD,
根据(1)有CE=BM.
根据(2)有
∵AD=4,
BG=BC-GE-CE=2-CE,
在Rt△BNG中,
解得:
∵CE
【标注】【知识点】相似三角形的性质与判定综合
【知识点】正方形的性质
【知识点】矩形的性质
【知识点】平移的性质
【业务题型】其他
4如图,已知矩形ABCD,AB=2,BC=3,E、F分别是边BC、CD上的动点,且BE=CF,将△BCF沿着BC方向向右平移到△EGH,连接DH、EH,当DE=EH时,DH长是 ;运动过程中,△DEH的面积的最小值是 .
【答案】
【解析】
【分析】
结合图形,由已知先证明CGHF为正方形,设BE=x,则CF=FH=HG=x,求出z的长,进而求出DH;由 得到S 利用二次函数的性质即可求得△DEH的面积的最小值.
【详解】
解:连接FH ,如图所示:
∵△EGH≌△BCF,
∴∠DCB=∠G=90°,FC=GH,BC=EG=3,
∴FC∥GH,BE=CG,
∴四边形FCGH是平行四边形,
∵∠FOG=90°.
∴四边形FCGH是矩形,
∵BE=CF,
∴CG=CF.
∴四边形CGHF为正方形,
∴EH=CF.
设BE=x,则CF=FH=HG=x,
∴EC=3-x,
∵DE=EH,
解得
∴△DEH的面积的最小值是
故答案为:
5.如图,在Rt△ABC中,∠C=90°,AC=9,BC=12.在Rt△DEF中;∠F=90°,DF=3,EF=4.用一条始终绷直的弹性染色线连接CF,Rt△DEF从起始位置(点D与点β重合)平移至终止位置(点E与点A重合),且斜边DE始终在线段AB上,则Rt△ABC的外部被染色的区域面积是 .
B(D) F
【答案】21
【解析】解:如下图所示,连接CF交AB于点M,连接CF'交AB于点N,过点/作FG⊥AB于点H,过点F'作F'H⊥AB于点H,连接FF',则四边形FGHF'是矩形,Rt△ABC的外部被染色的区域是梯形MFF'N.
在Rt△DEF中,DF=3,EF=4,
在Rt△ABO中,AC=9,BC=12,
∴FF'=GH=AB-BG-AH=15-5=10,
∵BF∥AC,
同法可证
∴Rt△ABC的外部被染色的区域的面积 因此正确答案为:21.
答案9
:∠N=∠M=∠NOB=90°,
∴四边形NOBM为矩形,
∴B(2,0),
设△ABC向上平移m个单位,
则 则B'(2,m).
又点C'和B'在该比例函数图象上,
解得
∴k=9,
故答案为:9.
7(1)如图1,在矩形ABCD中,AB=5,BC=4,点E为边BC上一点,沿直线DE将矩形折叠,使点C落在AB边上的点C'处.求AC'的长;
(2)如图2,展开后,将△DC'E沿线段AB向右平移,使点C'的对应点与点B重合,得到△D'BE',D'E'与BC交于点F,求线段EF的长;
(3)在图1中,将△DC'E绕点O'旋转至A,C',E三点共线时,请直接写出CD的长.
【答案】 (1)3; (2)1; (3) 或
【解析】
【分析】
(1)本题利用折叠和矩形的性质得出CD=C'D=AB=6,AD=BC=4,再利用勾股定理即可解题;
(2)本题利用平移的性质证得△CDE∽△CD'F,设EB长为x,利用勾股定理算出x,推出CE,再利用相似三角形的性质得到 算出CF,从而求得EF的长;
(3)本题根据A,C',E三点共线,分以下两种情况讨论,①当E旋转到C'左侧时,②当E旋转到C'右侧时,根据以上两种情况作辅助线构造直角三角形,利用旋转的性质、矩形的性质和判定、以及勾股定理进行分析求解,即可解题
【详解】
(1)解:∵ABCD为矩形,AB=5,BC=4,
∴CD=C'D=AB=5,AD=BC=4,
(2)解:∵△D'BE'为△DC'E平移后的图形,AC'=3,AB=5,
∴△CDE∽△CD'F,
设EB长为x,
解得
∴EF=CE-CF=1;
(3)解:将△DO'E绕点C'旋转至A,C',E三点共线,分以下两种情况:
①当E旋转到C'左侧时,如图所示:
作DM⊥CB,交CB的延长线于点M,
由(2)可知/
由旋转性质可知,.
.四边形BMDC'为矩形,
②当E旋转到C'右侧时,如图所示:
作DN⊥BC,交BO的延长线于点N,
由(2)可知BC'=2,
由旋转性质可知,
∴四边形BNDC'为矩形,
∴CN=BN-BC=5-4=1,
8如图,在平面直角坐标系中,已知点A(4,0),点B(0,3) ,沿z轴向右平移Rt△ABO,得四边形面积记为S.
(1)求AB的长和y与x的函数关系式;(用相似)
(2)用含x(x≠4)的式子表示S;
(3)当 求点D的坐标(直接写出结果).
【答案】
【解析】
(1)解:∵A(4,0)、B(0,3)
∴OA=4,OB=3,
当点O'与点A不重合时,
∵B'O'∥OB,
如图(1) ,点D在AB上,
图(1)
有AO'=AO-O'O=4-z
即
如图(2),点D在BA延长线上,
有AO'=00-AO=x-4
即
当点O'与点A重合时,D与A重合,此时:z=4, y=0.
∴y与x的关系是:
(2)解:①如图(1) ,当0
把 入可得
②如图(2) ,当x>4时,点D在BA延长线上.
∵平移△AOB得到△A'O'B'.
代入可得:
综上所述
(3)解: 把 可得 (舍弃) .
把 代入 得y=2.
把 代. 可得 (舍弃)或 (舍弃)
综上所述点D的坐标为
9如图1,在平面直角坐标系中,直线 与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)如图2,将△BCD沿x轴正方向平移得△BC' D' ,当BC' 经过点D时,求点D的坐标及△BCD平移的距离;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形 若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】(1)见解析; (2)点D的坐标为(4,1) ,。BCD平移的距离为 ;(3)存在,点P的坐标为(0, ) 或(0, ).
【解析】
【分析】
(1)利用同角的余角相等可得出∠OBC=∠ECD,由旋转的性质可得出BC=CD,结合∠BOC=∠CED=90°即可证出△BOC≌△CED(AAS) ;
(2)利用一次函数图象上点的坐标特征可求出点B的坐标,设OC=m,则点D的坐标为(m+3,m),利用一次函数图象上点的坐标特征可求出m值,进而可得出点C,D的坐标,由点B,C的坐标,利用待定系数法可求出直线BC的解析式,结合BC∥BC及点D在直线BC上可求出直线BC的解析式,再利用一次函数图象上点的坐标特征可求出点C的坐标,结合点C的坐标即可得出△BCD平移的距离;
(3)设点P的坐标为(0,m),点Q的坐标为 分CD为边及CD为对角线两种情
【详解】
(1)证明:∵∠BOC=∠BCD=∠CED=90°,
∴∠OCB+∠OBC=90°,∠OCB+∠ECD=90°,
∴∠OBC=∠ECD.
∵将线段CB绕着点C顺时针旋转90°得到CD,
∴BC=CD.
在△BOC和△CED中,C H OH+3O 点燃2CO +3H O,
∴△BOC≌△CED(AAS) .
(2)解:∵直线 与x轴、y轴相交于A、B两点,
∴点B的坐标为(0,3) ,点A的坐标为(6,0).
设OC=m,
∵△BOCB△CED,
∴OC=ED=m,BO=CE=3,
∴点D的坐标为(m+3, m).
∵点D在直线
解得: m=1,
∴点D的坐标为(4,1) ,点C的坐标为(1,0) .
∵点B的坐标为(0,3) ,点C的坐标为(1,0),
∴直线BC的解析式为y=-3x+3.
设直线B'C的解析式为y=-3x+b,
将D(4,1)代入y=·3x+b,得:1--3x4+b,解得:b=13,
∴直线BC的解析式为y=-3x+13,
∴点C的坐标为
∴BCD平移的距离为 3.
(3)解:设点P的坐标为(0,m),点Q的坐标为
分两种情况考虑,如图3所示:
①若CD为边,当四边形CDQP为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n
解得
∴点P 的坐标为(0.2);
当四边形CDPQ为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,- n+3) ,
解得:
∴点P 的坐标为
②若CD为对角线,∵C(1,0),D(4,1),P(0,m),Q(n,- n+3),
解得:
∴点P的坐标为
综上所述:存在,点P的坐标为(0, )或((0,
【点睛】
本题考查了全等三角形的判定与性质、旋转的性质、一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及平行四边形的性质,解题的关键是掌握利用全等三角形的判定定理AAS;利用一次函数图象上点的坐标特征;利用平行四边形的对角线互相平分的性质.
10阅读下面材料:
小伟遇到这样一个问题:如图1,在梯形ABCD中,AD//BC,对角线AC、BD相交于点O.若梯形ABCD的面积为1,求AC、BD、AD+BC的长度为三边长的三角形的面积.
小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可,他先后尝试了翻折、旋转、平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC、BD、AD+BC的长度为三边长的三角形(如图2).
(1)请你回答:图2中△BDE的面积等于 .
(2)如图3,△ABC的三条中线分别为AD、BE、CF .在图3中利用图形变换画出并指明以AD
BE、CF的长度为三边长的一个三角形(保留画图痕迹).
(3)若△ABC的面积为1,则以AD、BE、CF的长度为三边长的三角形的面积等于 .
【答案】(1)1
(2)画图见解析.
(3)
(2)以AD、BE、CF的长度为三边长的一个三角形是△CFP
(3)以AD、BE、CF的长度为三边长的三角形的面积等于
同课章节目录
