专题二十一 二次函数平行四边形存在性问题(含解析) 2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题二十一 二次函数平行四边形存在性问题(含解析) 2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 397.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 12:44:58 | ||
图片预览



文档简介
二次函数平行四边形存在性问题
模型原理
1.平行四边形存在性问题的通解通法
所有的平行四边形存在性问题,基本都可以利用上述模型求解,更重要的是实现盲解盲算,具体步骤如下:
第一步:写出或设出三个顶点的坐标;
第二步:以“哪两个顶点相对”(即对角线)为分类标准,分三类讨论,利用上述模型,求出第四个顶点的坐标;
第三步:将第四个顶点坐标代入相应的函数关系式即可.
举例:问以A、B、C、D为顶点的四边形为平行四边形,求点D的坐标.
先写出或设出三个顶点的坐标,如A(x ,y )、B(x ,y )及C(x ,y );
再分三种情况讨论如下:
①当AB为对角线时,有 则 代入点D所在图象的函数关系式;
②当AC为对角线时,有 则 代入点D所在图象的函数关系式;
③当AD为对角线时,有 则 代入点D所在图象的函数关系式.
真题精炼
1如图1,抛物线 与x轴交于A(-1,0), B(3,0)两点, 与y轴交于点C.
(1)求抛物线的解析式;
(2)点P在抛物线上,点Q在x轴上,以B ,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;
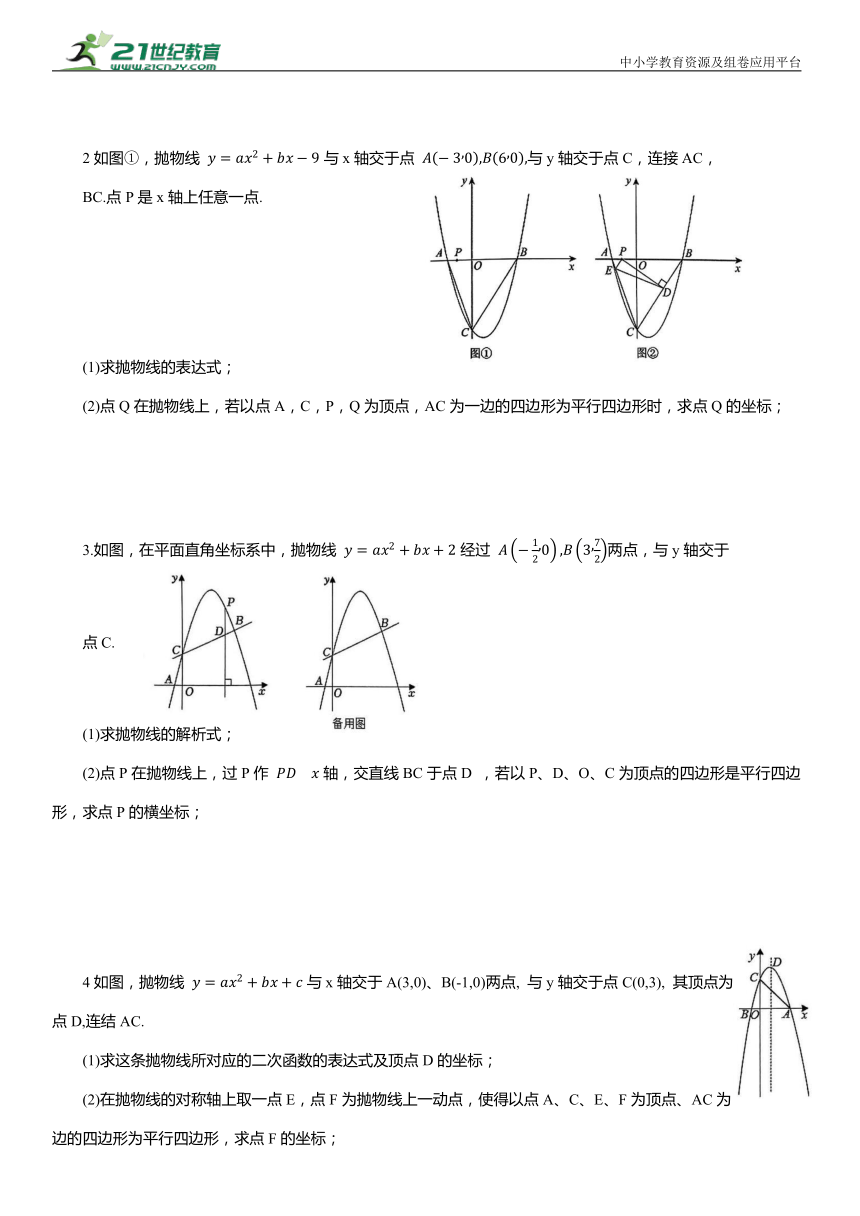
2如图①,抛物线 与x轴交于点 与y轴交于点C,连接AC,
BC.点P是x轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;
3.如图,在平面直角坐标系中,抛物线 经过 两点,与y轴交于
点C.
(1)求抛物线的解析式;
(2)点P在抛物线上,过P作 轴,交直线BC于点D ,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;
4如图,抛物线 与x轴交于A(3,0)、B(-1,0)两点, 与y轴交于点C(0,3), 其顶点为点D,连结AC.
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标;
5如图,二次函数 的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为-1, 点M(1,m)是其对称轴上一点, y轴上一点B(0,1).
求二次函数的表达式;
二次函数在第四象限的图象上有一点P ,连结PA,PB,设点P的横坐标为t,△PAB的面积为S,求S与t的函数关系式;
(3)在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形 若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.
在平面直角坐标系中,抛物线 c与x轴交于点A ,B (点A在点B的左侧),与y轴交于点C,且点A的坐标为(-5,0).
求点C的坐标;
如图1,若点P是第二象限内抛物线上一动点,求点P到直线AC距离的最大值;
(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形 若存在,请直接写出点M的坐标;若不存在,请说明理由.
7已知二次函数 的图象过点 且对任意实数x,都有
(1)求该二次函数的解析式 .
(2)若(1)中二次函数图象与x轴的正半轴交点为A,与y轴交点为C;点M是(1)中二次函数图象上的动点.问在x轴上是否存在点N ,使得以A、C、M、N为顶点的四边形是平行四边形.若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.
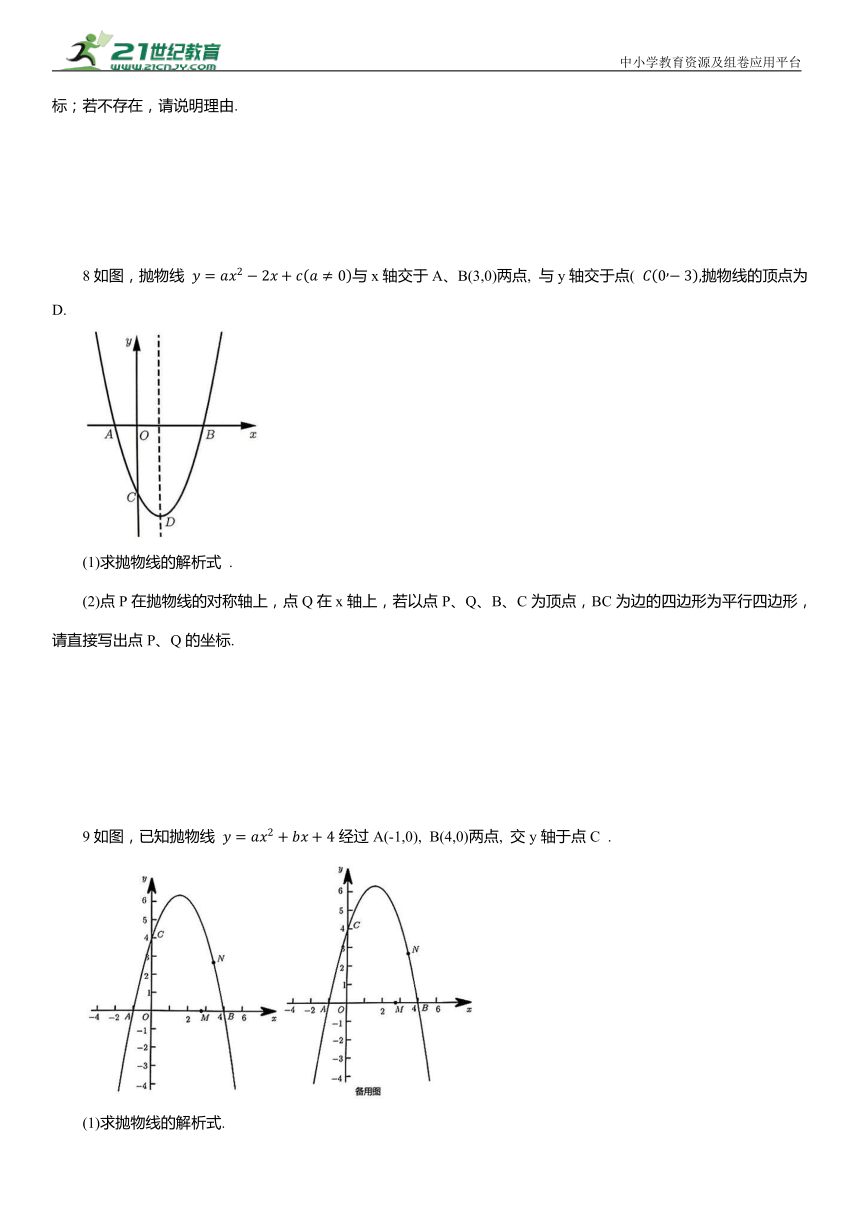
8如图,抛物线 与x轴交于A、B(3,0)两点, 与y轴交于点( 抛物线的顶点为D.
(1)求抛物线的解析式 .
(2)点P在抛物线的对称轴上,点Q在x轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标.
9如图,已知抛物线 经过A(-1,0), B(4,0)两点, 交y轴于点C .
(1)求抛物线的解析式.
(2)连接BC,求直线BC的解析式.
(3)请在抛物线的对称轴上找一点P ,使 的值最小,求点P的坐标,并求出此时 的最小值 .
(4)点M为x轴上一动点,在抛物线上是否存在一点N ,使得以A、C、M、N四点为顶点的四边形是平行四边形 若存在,求出点N的坐标;若不存在,请说明理由.
10在平面直角坐标系中,抛物线 与x轴交于A ,B两点.与y轴交于点C .且点A的坐标为(-1, 0) , 点C的坐标为(0, 5)
(1)求该抛物线的解析式;
(2)如图(甲).若点P是第一象限内抛物线上的一动点.当点P到直线BC的距离最大时,求点P的坐标;
(3)图(乙)中,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使得以B,C,M,N为顶点的四边形是平行四边形 若存在,请求出点M的坐标;若不存在,请说明理由.
1.如图1,抛物线 与x轴交于A(-1,0), B(3,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P在抛物线上,点Q在z轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;
【答案】 )或(1- ,-3)或(1+ ,-3)
【解析】【分析】
(1)将A(-1,0),B(3,0)两点代入抛物线的解析式即可求解;
(2)根据P,Q的不确定性,进行分类讨论:①过C作CP∥z轴,交抛物线于P ,过P 作P Q ‖BC,交x轴于Q ,可得vp =3,由 可求解;②在z轴的负半轴上取点Q ,过Q 作Q P Ⅱ.BC,交抛物线于P ,同时使( 连接CQ 、BP ,过P 作P D⊥z轴,交z轴于D,yB =-3,即可求解;③当BC为平行四边形的对角线时,在①中,只要点Q在点B的左边,且满足BQ=BQ ,也满足条件,只是点P的坐标仍是①中的坐标;
【详解】
(1)解:∵抛物线 )与z轴交于A(-1,0),B(3,0)两点, 解得 故抛物线的解析式为
(2)解:①如图,过C作CP∥z轴,交抛物线于P ,过P 作P Q ∥BC,交z轴于Q ,
∴四边形BCP Q 是平行四边形,∴yA=3,
解得:z =2,z =0,P (2,3);
②如图,在a轴的负半轴上取点Q ,过Q 作Q P ∥BC,交抛物线于P ,同时使 连接CQ 、BP ,过P 作P D⊥x轴,交x轴于D,
∴四边形BCQ P 是平行四边形,
,在△CBQ 和△P Q B中.
△CBQ =△P Q B(SAS),∴P D=CO=3,∴yA =-3,∴-x +2x+3=-3,解
得 z =1- ,z =1+ ,∴P (1- ,-3);
如上图,根据对称性:P (1+ ,-3),
中小学教育资源及组卷应用平台
③当BC为平行四边形的对角线时,由①知,点Q在点B的左边,且BQ=BQ =2时,也满足条件,此时点P的坐标仍为(2,3); 综上所述: P的坐标为(2,3)或(1- ,-3)或(1+ ,-3).
2.如图①,抛物线y 9与z轴交于点A(-3,0), B(6,0),与y轴交于点C,连接AC,
BC.点P是z轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;
【答案】 (2)点Q坐标(3,-9),或
【解析】【分析】
(1)将A(-3,0), B(6,0)f 待定系数法确定函数解析式;
(2)由二次函数 求得点C(0,-9),设点P(m,0),点 ,分类讨论:当AC为边,AQ为对角线时,当AC为边,AP为对角线时,运用平行四边形对角线互相平分性质,构建方程求解;
【详解】
(1)将A(-3,0), B(6,0)代入y=az +b∞-9,得 解得 抛物线解析式为
(2)二次函数 当x=0时,y=-9∴点C(0,-9)设点P(m,0),点 当AC为边,AQ为对角线时,∵四边形ACQP为平行四边形,∴AQ,OP互相平分 解得,n=0(舍去)或n=3点Q坐标(3,-9);
同理得 解得
点Q坐标 或 综上,点Q坐标(3,-9)
1 g
3.如图,在平面直角坐标系中,抛物线 经过A((- ,0),B(3, 两点,与y轴交于
点C.
(1)求抛物线的解析式;
(2)点P在抛物线上,过P作PD⊥x轴,交直线BC于点D ,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;
【答案】 (2)点P的横坐标为1或2或
【解析】(1)解:将点A(- ,0),B(3, )代入y=ax + bx+2得 解得则抛物线的解析式为
(2)解:设点 对于二次函数 当x=0时,
y=2,即C(0,2),CO=2, 设直线BC的解析式为y= kz+c,将点B(3, ),C(0,2)代入
得 解得 则直线BC的解析式为
∵PD⊥x轴,(OC⊥x轴,
∴PD∥CO,∴当PD=CO时,以P、D、O、C为顶点的四边形是平行四边形,
解得m=1或m=2或 可 则点P的横坐标为1或2或 或
【标注】【知识点】二次函数与几何综合
4.如图,抛物线 c与x轴交于A(3,0)、B(-1,0)两点,与y轴交于点C(0,3),其顶点为
点D,连结AC.
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E ,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标;
【答案】 顶点D的坐标为(1,4)(2)F(-2,-5)或F(4,-5)
【解析】(1)解:∵抛物线; c经过点A(3,0), B(-1,0),C(0,3),
解得: ∴抛物线的解析式为 ·顶点D的坐标为(1,4);
(2)解:设直线AC的解析式为:y= kz+b,把点A(3,0),C(0,3)代入得:k=-1,b=3
∴直线AC解析式为:y=-x+3, 过点F作FG⊥DE于点G,
以A、C、E、F四点为顶点的四边形是以AC为边的平行四边形,∴AC∥EF,AC=EP,又:OA∥FG,∴∠OAC=∠GFE∴△OAC±△GFE,∴OA=GF=3, 设F点的坐标为 则G点的坐标为((1,-m +2m+3),.. FG=|m-1|=3.
m=-2或m=4,当m=-2时,-m +2m+3=-5,∴F (-2,-5),当m=4时,-m +2m+3=-5∴F (4,-5), ∴F(-2,-5)或F(4,-5);
5.如图,二次函数 c的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为-1,点M(1,m)是其对称轴上一点, y轴上一点B(0,1).
(1)求二次函数的表达式;
(2)二次函数在第四象限的图象上有一点P,连结PA,PB,设点P的横坐标为t,△PAB的面积为S,求S与t的函数关系式;
(3)在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形 若存在,直接写出所有符合条件的点M的坐标,若不存在,请说明理由.
【答案】
(3)存在,N(1,-1)或(3,3)或(-1,3)
【解析】
(1)解:∵二次函数的最小值为-1,点M(1,m)是其对称轴上一点,
∴二次函数顶点为(1,-1),
设二次函数解析式为
将点O(0,0)代入得,a-1=0,
∴a=1,
(2)如下图所示,连接OP,
当y=0时,x -2x=0,
∴∞=0或2,∴A(2,0).
∵点P在抛物线y
∴点P的纵坐标为
(3)设N
当AB为对角线时,由中点坐标公式得,2+0=1+n,∴n=1,∴N(1,-1),当AM为对角线时,由中点坐标公式得,2+1=n+0,∴n=3,∴N(3,3),当AN为对角线时,由中点坐标公式得,2+n=0+1,∴n=-1,∴N(-1,3).
综上: N(1,-1)或(3,3)或(-1,3).
【标注】【知识点】二次函数与几何综合
6.在平面直角坐标系中,抛物线y c与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,且点A的坐标为(-5,0).
(1)求点C的坐标;
(2)如图1,若点P是第二象限内抛物线上一动点,求点P到直线AC距离的最大值;
(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形 若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)(0,5)
(2)PE最大为
(3)存在, M的坐标为(-3,8)或(3,-16)或(-7,-16)
【解析】
(1) (1)∵点A(-5,0)在抛物线 d的图象上,
. c=5.
∴点C的坐标为(0,5);
(2)过P作PE⊥AC于点B,过点P作PF⊥x轴交AC于点H,如图:
∵A(-5,0),C(0,5)
∴OA=OC,
∴△AOC是等腰直角三角形,
∴∠CAO=45°,
∵PF⊥x轴,
∴∠AHF=45°=∠PHE,
∴△PHE是等腰直角三角形,
∴当PH最大时,PE最大,
设直线AC解析式为y= kz+5,
将A(-5,0)代入得0=5k+5,
∴k=1.
∴直线AC解析式为y=x+5,
设) 则H(m,m+5),
∵a=-1<0,
∴当 时,PH最大为
∴此时PE最大为 即点P到直线AC的距离值最大;
(3)存在.
∴抛物线的对称轴为直线x=-2,
设点N的坐标为(-2,m),点M的坐标为
分三种情况:①当AC为平行四边形ANMC的边时,如下图所示,
·A(-5,0),C(0,5),
∴zo-xA=xM-zN,即x-(-2)=0-(-5)
解得,x=3.
∴点M的坐标为(3,-16)
②当AC为平行四边形AMNC的边长时,如下图所示,
方法同①可得,x=-7,
∴点M的坐标为(-7,-16) ;
③当AC为对角线时,如下图所示,
∵A(-5,0),C(0,5),
∴线段AC的中点H的坐标为( 即
解得,z=-3.
∴点M的坐标为(-3,8)
综上所述点M的坐标为:(-3,8)或(3,-16)或(-7,-16).
【标注】【知识点】二次函数与几何综合
7已知二次函数 c的图象过点(-1,0).且对任意实数x,都有
(1)求该二次函数的解析式.
(2)若(1)中二次函数图象与z轴的正半轴交点为A,与g轴交点为C;点M是(1)中二次函数图象上的动点.问在z轴上是否存在点N,使得以A、C、M、N为顶点的四边形是平行四边形.若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.
【答案】
(2)存在, N点坐标为(1,0)或(5,0)或( 或
【解析】(1)不妨令 解得x =x =3,
当x=3时,(
又
∴y=ax -2ax-3a,
s
∴a>0且△=0,
∴a=1,
∴b=-2,c=-3,
(2)令 3中y=0,得x=3,则A点坐标为(3,0);
令x=0,得y=-3,则点C坐标为(0,-3).
设
根据平行四边形对角线性质以及中点坐标公式可得:
①当AC为对角线时,
解得m =0(舍),m =2,
∴n=1,即N (1,0).
②当AM为对角线时,
解得m =0(舍),m =2,
∴n=5,即N (5,0)
③当AN为对角线时,
解得
综上所述: N点坐标为(1,0)或(5,0)或( )或
【标注】【知识点】二次函数与平行四边形
8.如图,抛物线 0)与x轴交于A、B(3,0)两点,与y轴交于点C(0,-3), 抛物线的顶点为D.
(1)求抛物线的解析式.
(2)点P在抛物线的对称轴上,点Q在z轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标.
【答案】(
(2)点P(1,-3)、点Q(4,0)或点P(1,3),Q(-2,0).
【解析】(1)将点B(3,0), C(0,-3)分别代入 c中,得:
解得
∴抛物线的函数解析式为:
∴对称轴为直线z=1,
∵以点P、Q、B、C为顶点的四边形是以BC为边的平行四边形,当PC|/BQ,(图1).
∵C(0,-3).
. P(1,-3),
:CP=1,
. BQ=1.
B(3,0),
··Q(4,0).
当CP为对角线时,(图2).
设P(1,y),Q(x,0),
B(3,0),C(0,-3).
解得z=-2,y=3,
∴P(1,3),Q(-2,0),
综上P(1,-3),Q(4,0)或P(1,3),Q(-2,0).
9.如图,已知抛物线 4经过A(-1,0), B(4,0)两点,交y轴于点C.
(1)求抛物线的解析式.
(2)连接BC,求直线BC的解析式.
(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值.
(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形 若存在,求出点N的坐标;若不存在,请说明理由.
【答案】
(2)yBC=-x+4.
(3)P( ,),AP+PC的最小值4
(4) N(3,4)或
【解析】 -4经过A(-1,0), B(4,0),
解得
(2)∵抛物线 4交y轴于C,
∴C(0,4),
设y= mx+n过B(4,0),C(0,4),
解得
∵VBC=-x+4.
(3)对称轴
设
∵A, B关于 对称,
∴AP=BP,
当B,C,P共线时AP+PC最小,
最小值为
在y=-x+4上,
(4) 由题设M(m,0), ①当AC为对角线时,
解得
∴N(3,4);
②当AM为对角线时,
③当AN为对角线时,
解得n=3,
∴N(3,4).
∴N(3,4)或
【标注】【知识点】二次函数与平行四边形
10在平面直角坐标系中,抛物线 与x轴交于A,B两点.与y轴交于点C.且点A的坐标为(-1,0) ,点C的坐标为(0,5) .
(1)求该抛物线的解析式;
(2)如图(甲).若点P是第一象限内抛物线上的一动点.当点P到直线BC的距离最大时,求点P的坐标;
(3)图(乙)中,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使得以B,C. M. N为顶点的四边形是平行四边形 若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】
(3)存在,M的坐标为: (3,8)或(-3,-16)或(7,-16) .
【解析】解:(1)将A的坐标(-1,0) ,点C的坐(0,5)代入 c得:
解得
∴抛物线的解析式为
(2)过P作PD⊥x轴于D,交BC于Q,过P作PH⊥BC于H,如图:
在y=-x +4x+5中,
解得x=5或x=-1.
∴B(5,0),
∴OB=OC,△BOC是等腰直角三角形,
∴∠CBO=45°,
∵PD⊥x轴,
∵∠BQD=45°=∠PQH,
∴△PHQ是等腰直角三角形,
∴当PQ最大时, PH最大,
设直线BC解析式为y= kx+5,将B(5,0)代入得0=5k+5,
:k=-1,
.直线BC解析式为y=-x+5,
设P ,则Q(m,-m+5),
∵a=-1<0,
∴当 时,PQ最大为
时,PH最大,即点P到直线BC的距离最大,此时F
(3)存在,理由如下:
抛物线 5对称轴为直线x=2,
设M(s,-s +4s+5),N(2,t),而B(5,0),C(0,5),
①以MN、BC为对角线,则MN、BC的中点重合,如图:
解得
∴M(3,8),
②以MB、NC为对角线,则MB、NC的中点重合,如图:
解得
∴M(-3,-16) ,
③以MC、NB为对角线,则MC、NB中点重合,如图:
解得
∴M(7,-16);
综上所述, M的坐标为:(3,8)或(-3,-16)或(7,-16).
模型原理
1.平行四边形存在性问题的通解通法
所有的平行四边形存在性问题,基本都可以利用上述模型求解,更重要的是实现盲解盲算,具体步骤如下:
第一步:写出或设出三个顶点的坐标;
第二步:以“哪两个顶点相对”(即对角线)为分类标准,分三类讨论,利用上述模型,求出第四个顶点的坐标;
第三步:将第四个顶点坐标代入相应的函数关系式即可.
举例:问以A、B、C、D为顶点的四边形为平行四边形,求点D的坐标.
先写出或设出三个顶点的坐标,如A(x ,y )、B(x ,y )及C(x ,y );
再分三种情况讨论如下:
①当AB为对角线时,有 则 代入点D所在图象的函数关系式;
②当AC为对角线时,有 则 代入点D所在图象的函数关系式;
③当AD为对角线时,有 则 代入点D所在图象的函数关系式.
真题精炼
1如图1,抛物线 与x轴交于A(-1,0), B(3,0)两点, 与y轴交于点C.
(1)求抛物线的解析式;
(2)点P在抛物线上,点Q在x轴上,以B ,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;
2如图①,抛物线 与x轴交于点 与y轴交于点C,连接AC,
BC.点P是x轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;
3.如图,在平面直角坐标系中,抛物线 经过 两点,与y轴交于
点C.
(1)求抛物线的解析式;
(2)点P在抛物线上,过P作 轴,交直线BC于点D ,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;
4如图,抛物线 与x轴交于A(3,0)、B(-1,0)两点, 与y轴交于点C(0,3), 其顶点为点D,连结AC.
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标;
5如图,二次函数 的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为-1, 点M(1,m)是其对称轴上一点, y轴上一点B(0,1).
求二次函数的表达式;
二次函数在第四象限的图象上有一点P ,连结PA,PB,设点P的横坐标为t,△PAB的面积为S,求S与t的函数关系式;
(3)在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形 若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.
在平面直角坐标系中,抛物线 c与x轴交于点A ,B (点A在点B的左侧),与y轴交于点C,且点A的坐标为(-5,0).
求点C的坐标;
如图1,若点P是第二象限内抛物线上一动点,求点P到直线AC距离的最大值;
(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形 若存在,请直接写出点M的坐标;若不存在,请说明理由.
7已知二次函数 的图象过点 且对任意实数x,都有
(1)求该二次函数的解析式 .
(2)若(1)中二次函数图象与x轴的正半轴交点为A,与y轴交点为C;点M是(1)中二次函数图象上的动点.问在x轴上是否存在点N ,使得以A、C、M、N为顶点的四边形是平行四边形.若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.
8如图,抛物线 与x轴交于A、B(3,0)两点, 与y轴交于点( 抛物线的顶点为D.
(1)求抛物线的解析式 .
(2)点P在抛物线的对称轴上,点Q在x轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标.
9如图,已知抛物线 经过A(-1,0), B(4,0)两点, 交y轴于点C .
(1)求抛物线的解析式.
(2)连接BC,求直线BC的解析式.
(3)请在抛物线的对称轴上找一点P ,使 的值最小,求点P的坐标,并求出此时 的最小值 .
(4)点M为x轴上一动点,在抛物线上是否存在一点N ,使得以A、C、M、N四点为顶点的四边形是平行四边形 若存在,求出点N的坐标;若不存在,请说明理由.
10在平面直角坐标系中,抛物线 与x轴交于A ,B两点.与y轴交于点C .且点A的坐标为(-1, 0) , 点C的坐标为(0, 5)
(1)求该抛物线的解析式;
(2)如图(甲).若点P是第一象限内抛物线上的一动点.当点P到直线BC的距离最大时,求点P的坐标;
(3)图(乙)中,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使得以B,C,M,N为顶点的四边形是平行四边形 若存在,请求出点M的坐标;若不存在,请说明理由.
1.如图1,抛物线 与x轴交于A(-1,0), B(3,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P在抛物线上,点Q在z轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;
【答案】 )或(1- ,-3)或(1+ ,-3)
【解析】【分析】
(1)将A(-1,0),B(3,0)两点代入抛物线的解析式即可求解;
(2)根据P,Q的不确定性,进行分类讨论:①过C作CP∥z轴,交抛物线于P ,过P 作P Q ‖BC,交x轴于Q ,可得vp =3,由 可求解;②在z轴的负半轴上取点Q ,过Q 作Q P Ⅱ.BC,交抛物线于P ,同时使( 连接CQ 、BP ,过P 作P D⊥z轴,交z轴于D,yB =-3,即可求解;③当BC为平行四边形的对角线时,在①中,只要点Q在点B的左边,且满足BQ=BQ ,也满足条件,只是点P的坐标仍是①中的坐标;
【详解】
(1)解:∵抛物线 )与z轴交于A(-1,0),B(3,0)两点, 解得 故抛物线的解析式为
(2)解:①如图,过C作CP∥z轴,交抛物线于P ,过P 作P Q ∥BC,交z轴于Q ,
∴四边形BCP Q 是平行四边形,∴yA=3,
解得:z =2,z =0,P (2,3);
②如图,在a轴的负半轴上取点Q ,过Q 作Q P ∥BC,交抛物线于P ,同时使 连接CQ 、BP ,过P 作P D⊥x轴,交x轴于D,
∴四边形BCQ P 是平行四边形,
,在△CBQ 和△P Q B中.
△CBQ =△P Q B(SAS),∴P D=CO=3,∴yA =-3,∴-x +2x+3=-3,解
得 z =1- ,z =1+ ,∴P (1- ,-3);
如上图,根据对称性:P (1+ ,-3),
中小学教育资源及组卷应用平台
③当BC为平行四边形的对角线时,由①知,点Q在点B的左边,且BQ=BQ =2时,也满足条件,此时点P的坐标仍为(2,3); 综上所述: P的坐标为(2,3)或(1- ,-3)或(1+ ,-3).
2.如图①,抛物线y 9与z轴交于点A(-3,0), B(6,0),与y轴交于点C,连接AC,
BC.点P是z轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;
【答案】 (2)点Q坐标(3,-9),或
【解析】【分析】
(1)将A(-3,0), B(6,0)f 待定系数法确定函数解析式;
(2)由二次函数 求得点C(0,-9),设点P(m,0),点 ,分类讨论:当AC为边,AQ为对角线时,当AC为边,AP为对角线时,运用平行四边形对角线互相平分性质,构建方程求解;
【详解】
(1)将A(-3,0), B(6,0)代入y=az +b∞-9,得 解得 抛物线解析式为
(2)二次函数 当x=0时,y=-9∴点C(0,-9)设点P(m,0),点 当AC为边,AQ为对角线时,∵四边形ACQP为平行四边形,∴AQ,OP互相平分 解得,n=0(舍去)或n=3点Q坐标(3,-9);
同理得 解得
点Q坐标 或 综上,点Q坐标(3,-9)
1 g
3.如图,在平面直角坐标系中,抛物线 经过A((- ,0),B(3, 两点,与y轴交于
点C.
(1)求抛物线的解析式;
(2)点P在抛物线上,过P作PD⊥x轴,交直线BC于点D ,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;
【答案】 (2)点P的横坐标为1或2或
【解析】(1)解:将点A(- ,0),B(3, )代入y=ax + bx+2得 解得则抛物线的解析式为
(2)解:设点 对于二次函数 当x=0时,
y=2,即C(0,2),CO=2, 设直线BC的解析式为y= kz+c,将点B(3, ),C(0,2)代入
得 解得 则直线BC的解析式为
∵PD⊥x轴,(OC⊥x轴,
∴PD∥CO,∴当PD=CO时,以P、D、O、C为顶点的四边形是平行四边形,
解得m=1或m=2或 可 则点P的横坐标为1或2或 或
【标注】【知识点】二次函数与几何综合
4.如图,抛物线 c与x轴交于A(3,0)、B(-1,0)两点,与y轴交于点C(0,3),其顶点为
点D,连结AC.
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E ,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标;
【答案】 顶点D的坐标为(1,4)(2)F(-2,-5)或F(4,-5)
【解析】(1)解:∵抛物线; c经过点A(3,0), B(-1,0),C(0,3),
解得: ∴抛物线的解析式为 ·顶点D的坐标为(1,4);
(2)解:设直线AC的解析式为:y= kz+b,把点A(3,0),C(0,3)代入得:k=-1,b=3
∴直线AC解析式为:y=-x+3, 过点F作FG⊥DE于点G,
以A、C、E、F四点为顶点的四边形是以AC为边的平行四边形,∴AC∥EF,AC=EP,又:OA∥FG,∴∠OAC=∠GFE∴△OAC±△GFE,∴OA=GF=3, 设F点的坐标为 则G点的坐标为((1,-m +2m+3),.. FG=|m-1|=3.
m=-2或m=4,当m=-2时,-m +2m+3=-5,∴F (-2,-5),当m=4时,-m +2m+3=-5∴F (4,-5), ∴F(-2,-5)或F(4,-5);
5.如图,二次函数 c的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为-1,点M(1,m)是其对称轴上一点, y轴上一点B(0,1).
(1)求二次函数的表达式;
(2)二次函数在第四象限的图象上有一点P,连结PA,PB,设点P的横坐标为t,△PAB的面积为S,求S与t的函数关系式;
(3)在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形 若存在,直接写出所有符合条件的点M的坐标,若不存在,请说明理由.
【答案】
(3)存在,N(1,-1)或(3,3)或(-1,3)
【解析】
(1)解:∵二次函数的最小值为-1,点M(1,m)是其对称轴上一点,
∴二次函数顶点为(1,-1),
设二次函数解析式为
将点O(0,0)代入得,a-1=0,
∴a=1,
(2)如下图所示,连接OP,
当y=0时,x -2x=0,
∴∞=0或2,∴A(2,0).
∵点P在抛物线y
∴点P的纵坐标为
(3)设N
当AB为对角线时,由中点坐标公式得,2+0=1+n,∴n=1,∴N(1,-1),当AM为对角线时,由中点坐标公式得,2+1=n+0,∴n=3,∴N(3,3),当AN为对角线时,由中点坐标公式得,2+n=0+1,∴n=-1,∴N(-1,3).
综上: N(1,-1)或(3,3)或(-1,3).
【标注】【知识点】二次函数与几何综合
6.在平面直角坐标系中,抛物线y c与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,且点A的坐标为(-5,0).
(1)求点C的坐标;
(2)如图1,若点P是第二象限内抛物线上一动点,求点P到直线AC距离的最大值;
(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形 若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)(0,5)
(2)PE最大为
(3)存在, M的坐标为(-3,8)或(3,-16)或(-7,-16)
【解析】
(1) (1)∵点A(-5,0)在抛物线 d的图象上,
. c=5.
∴点C的坐标为(0,5);
(2)过P作PE⊥AC于点B,过点P作PF⊥x轴交AC于点H,如图:
∵A(-5,0),C(0,5)
∴OA=OC,
∴△AOC是等腰直角三角形,
∴∠CAO=45°,
∵PF⊥x轴,
∴∠AHF=45°=∠PHE,
∴△PHE是等腰直角三角形,
∴当PH最大时,PE最大,
设直线AC解析式为y= kz+5,
将A(-5,0)代入得0=5k+5,
∴k=1.
∴直线AC解析式为y=x+5,
设) 则H(m,m+5),
∵a=-1<0,
∴当 时,PH最大为
∴此时PE最大为 即点P到直线AC的距离值最大;
(3)存在.
∴抛物线的对称轴为直线x=-2,
设点N的坐标为(-2,m),点M的坐标为
分三种情况:①当AC为平行四边形ANMC的边时,如下图所示,
·A(-5,0),C(0,5),
∴zo-xA=xM-zN,即x-(-2)=0-(-5)
解得,x=3.
∴点M的坐标为(3,-16)
②当AC为平行四边形AMNC的边长时,如下图所示,
方法同①可得,x=-7,
∴点M的坐标为(-7,-16) ;
③当AC为对角线时,如下图所示,
∵A(-5,0),C(0,5),
∴线段AC的中点H的坐标为( 即
解得,z=-3.
∴点M的坐标为(-3,8)
综上所述点M的坐标为:(-3,8)或(3,-16)或(-7,-16).
【标注】【知识点】二次函数与几何综合
7已知二次函数 c的图象过点(-1,0).且对任意实数x,都有
(1)求该二次函数的解析式.
(2)若(1)中二次函数图象与z轴的正半轴交点为A,与g轴交点为C;点M是(1)中二次函数图象上的动点.问在z轴上是否存在点N,使得以A、C、M、N为顶点的四边形是平行四边形.若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.
【答案】
(2)存在, N点坐标为(1,0)或(5,0)或( 或
【解析】(1)不妨令 解得x =x =3,
当x=3时,(
又
∴y=ax -2ax-3a,
s
∴a>0且△=0,
∴a=1,
∴b=-2,c=-3,
(2)令 3中y=0,得x=3,则A点坐标为(3,0);
令x=0,得y=-3,则点C坐标为(0,-3).
设
根据平行四边形对角线性质以及中点坐标公式可得:
①当AC为对角线时,
解得m =0(舍),m =2,
∴n=1,即N (1,0).
②当AM为对角线时,
解得m =0(舍),m =2,
∴n=5,即N (5,0)
③当AN为对角线时,
解得
综上所述: N点坐标为(1,0)或(5,0)或( )或
【标注】【知识点】二次函数与平行四边形
8.如图,抛物线 0)与x轴交于A、B(3,0)两点,与y轴交于点C(0,-3), 抛物线的顶点为D.
(1)求抛物线的解析式.
(2)点P在抛物线的对称轴上,点Q在z轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标.
【答案】(
(2)点P(1,-3)、点Q(4,0)或点P(1,3),Q(-2,0).
【解析】(1)将点B(3,0), C(0,-3)分别代入 c中,得:
解得
∴抛物线的函数解析式为:
∴对称轴为直线z=1,
∵以点P、Q、B、C为顶点的四边形是以BC为边的平行四边形,当PC|/BQ,(图1).
∵C(0,-3).
. P(1,-3),
:CP=1,
. BQ=1.
B(3,0),
··Q(4,0).
当CP为对角线时,(图2).
设P(1,y),Q(x,0),
B(3,0),C(0,-3).
解得z=-2,y=3,
∴P(1,3),Q(-2,0),
综上P(1,-3),Q(4,0)或P(1,3),Q(-2,0).
9.如图,已知抛物线 4经过A(-1,0), B(4,0)两点,交y轴于点C.
(1)求抛物线的解析式.
(2)连接BC,求直线BC的解析式.
(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值.
(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形 若存在,求出点N的坐标;若不存在,请说明理由.
【答案】
(2)yBC=-x+4.
(3)P( ,),AP+PC的最小值4
(4) N(3,4)或
【解析】 -4经过A(-1,0), B(4,0),
解得
(2)∵抛物线 4交y轴于C,
∴C(0,4),
设y= mx+n过B(4,0),C(0,4),
解得
∵VBC=-x+4.
(3)对称轴
设
∵A, B关于 对称,
∴AP=BP,
当B,C,P共线时AP+PC最小,
最小值为
在y=-x+4上,
(4) 由题设M(m,0), ①当AC为对角线时,
解得
∴N(3,4);
②当AM为对角线时,
③当AN为对角线时,
解得n=3,
∴N(3,4).
∴N(3,4)或
【标注】【知识点】二次函数与平行四边形
10在平面直角坐标系中,抛物线 与x轴交于A,B两点.与y轴交于点C.且点A的坐标为(-1,0) ,点C的坐标为(0,5) .
(1)求该抛物线的解析式;
(2)如图(甲).若点P是第一象限内抛物线上的一动点.当点P到直线BC的距离最大时,求点P的坐标;
(3)图(乙)中,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使得以B,C. M. N为顶点的四边形是平行四边形 若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】
(3)存在,M的坐标为: (3,8)或(-3,-16)或(7,-16) .
【解析】解:(1)将A的坐标(-1,0) ,点C的坐(0,5)代入 c得:
解得
∴抛物线的解析式为
(2)过P作PD⊥x轴于D,交BC于Q,过P作PH⊥BC于H,如图:
在y=-x +4x+5中,
解得x=5或x=-1.
∴B(5,0),
∴OB=OC,△BOC是等腰直角三角形,
∴∠CBO=45°,
∵PD⊥x轴,
∵∠BQD=45°=∠PQH,
∴△PHQ是等腰直角三角形,
∴当PQ最大时, PH最大,
设直线BC解析式为y= kx+5,将B(5,0)代入得0=5k+5,
:k=-1,
.直线BC解析式为y=-x+5,
设P ,则Q(m,-m+5),
∵a=-1<0,
∴当 时,PQ最大为
时,PH最大,即点P到直线BC的距离最大,此时F
(3)存在,理由如下:
抛物线 5对称轴为直线x=2,
设M(s,-s +4s+5),N(2,t),而B(5,0),C(0,5),
①以MN、BC为对角线,则MN、BC的中点重合,如图:
解得
∴M(3,8),
②以MB、NC为对角线,则MB、NC的中点重合,如图:
解得
∴M(-3,-16) ,
③以MC、NB为对角线,则MC、NB中点重合,如图:
解得
∴M(7,-16);
综上所述, M的坐标为:(3,8)或(-3,-16)或(7,-16).
同课章节目录
