专题二十二 二次函数特殊四边形存在性问题(含解析)2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题二十二 二次函数特殊四边形存在性问题(含解析)2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 478.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 12:43:04 | ||
图片预览


文档简介
二次函数特殊四边形存在性问题
模型原理
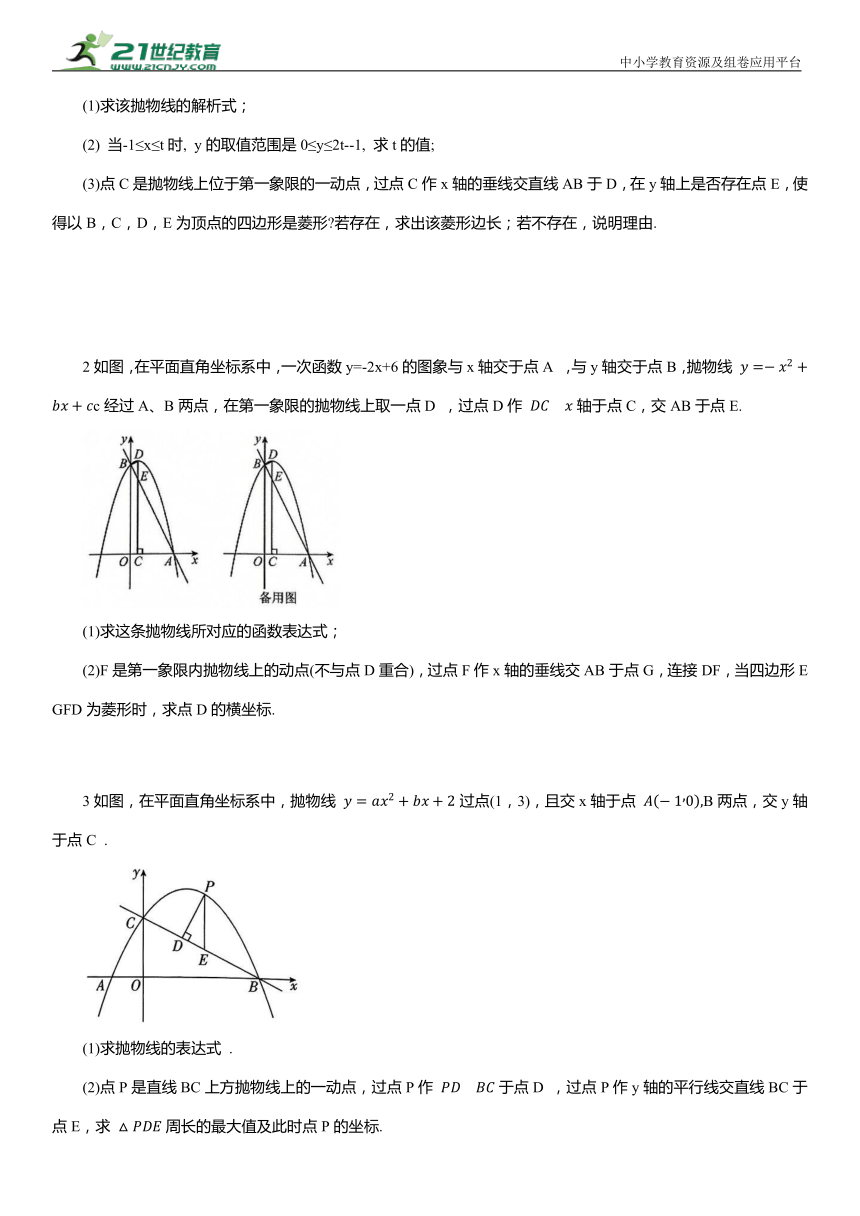
1.菱形的存在性
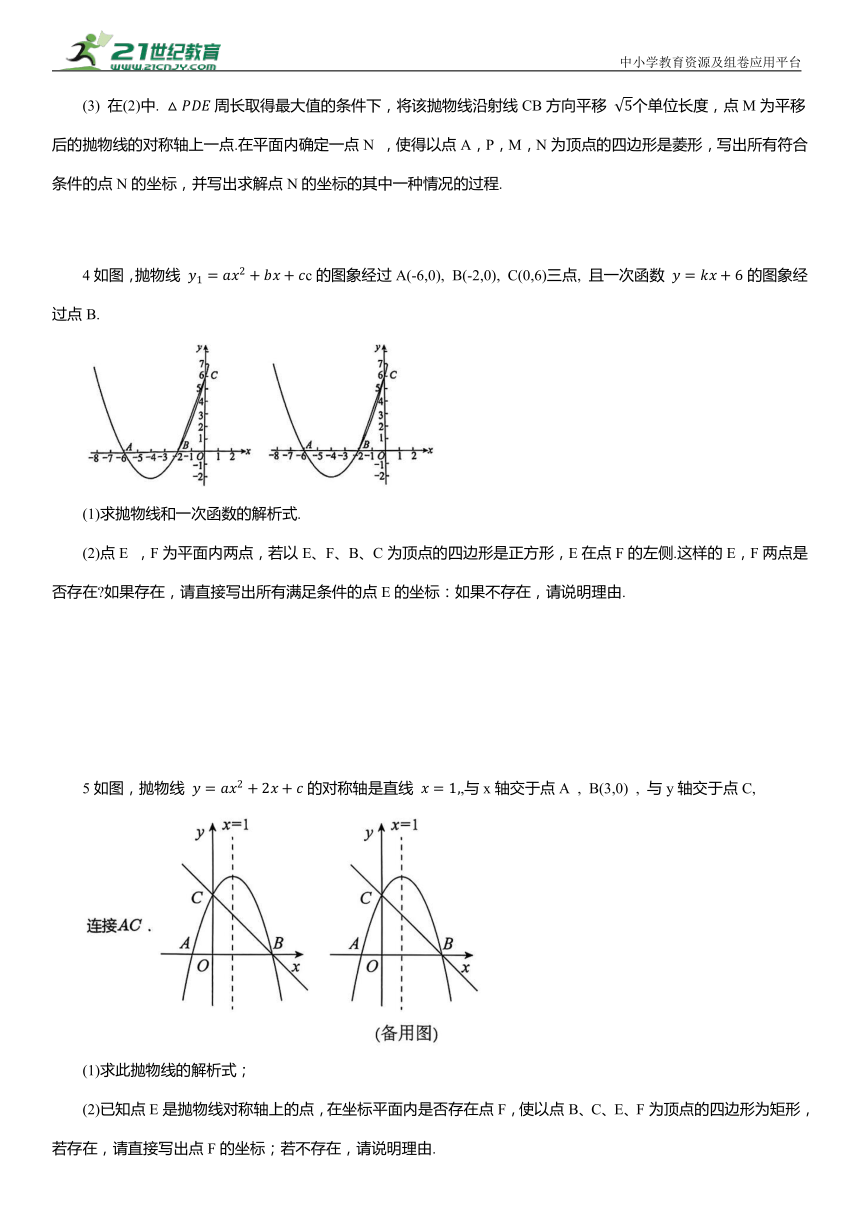
2.矩形的存在性
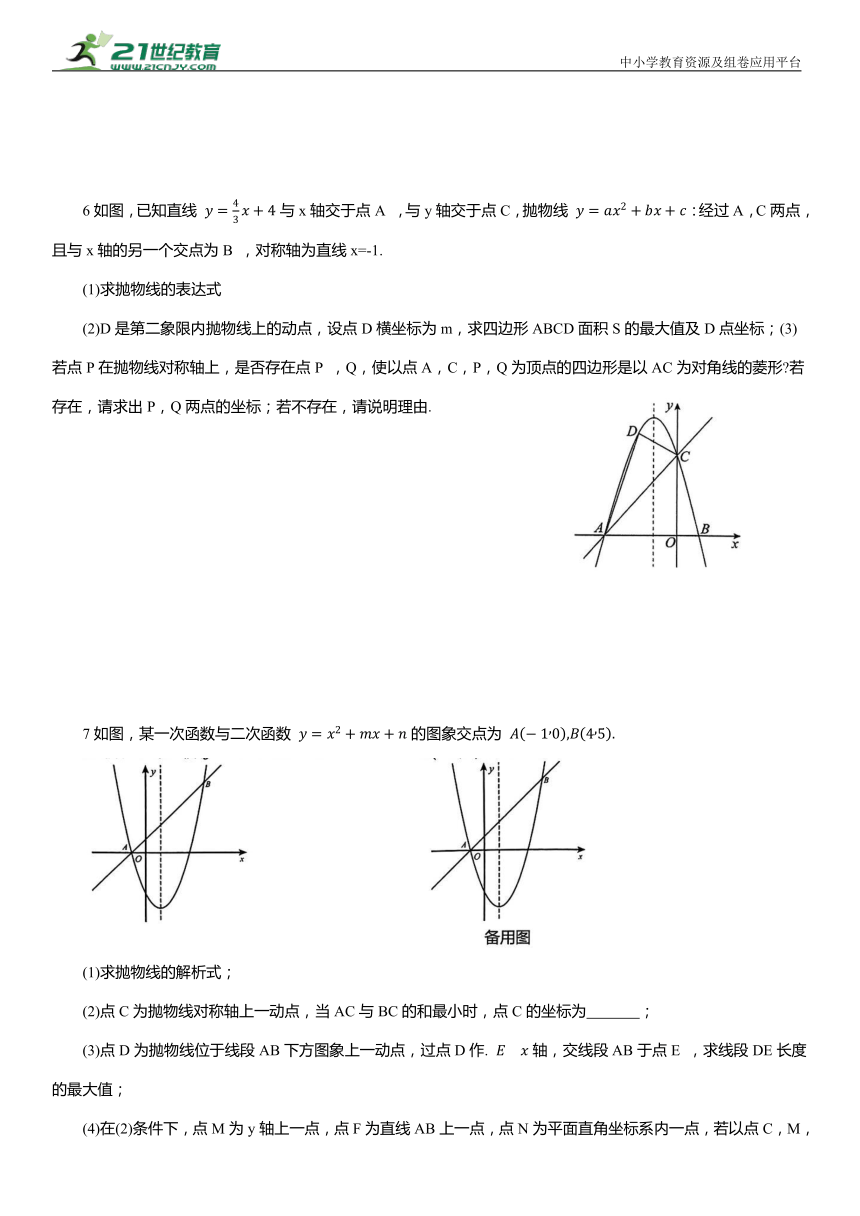
3.正方形的存在性
真题精炼
1如图,在平面直角坐标系xOy中,已知抛物线 经过点A(3,0), 与y轴交于点B, 且关于直线x =1对称.
(1)求该抛物线的解析式;
(2) 当-1≤x≤t时, y的取值范围是0≤y≤2t--1, 求t的值;
(3)点C是抛物线上位于第一象限的一动点,过点C作x轴的垂线交直线AB于D,在y轴上是否存在点E,使得以B,C,D,E为顶点的四边形是菱形 若存在,求出该菱形边长;若不存在,说明理由.
2如图,在平面直角坐标系中,一次函数y=-2x+6的图象与x轴交于点A ,与y轴交于点B,抛物线 c经过A、B两点,在第一象限的抛物线上取一点D ,过点D作 轴于点C,交AB于点E.
(1)求这条抛物线所对应的函数表达式;
(2)F是第一象限内抛物线上的动点(不与点D重合),过点F作x轴的垂线交AB于点G,连接DF,当四边形EGFD为菱形时,求点D的横坐标.
3如图,在平面直角坐标系中,抛物线 过点(1,3),且交x轴于点 B两点,交y轴于点C .
(1)求抛物线的表达式 .
(2)点P是直线BC上方抛物线上的一动点,过点P作 于点D ,过点P作y轴的平行线交直线BC于点E,求 周长的最大值及此时点P的坐标.
(3) 在(2)中. 周长取得最大值的条件下,将该抛物线沿射线CB方向平移 个单位长度,点M为平移后的抛物线的对称轴上一点.在平面内确定一点N ,使得以点A,P,M,N为顶点的四边形是菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
4如图,抛物线 c的图象经过A(-6,0), B(-2,0), C(0,6)三点, 且一次函数 的图象经过点B.
(1)求抛物线和一次函数的解析式.
(2)点E ,F为平面内两点,若以E、F、B、C为顶点的四边形是正方形,E在点F的左侧.这样的E,F两点是否存在 如果存在,请直接写出所有满足条件的点E的坐标:如果不存在,请说明理由.
5如图,抛物线 的对称轴是直线 ,与x轴交于点A , B(3,0) , 与y轴交于点C,
(1)求此抛物线的解析式;
(2)已知点E是抛物线对称轴上的点,在坐标平面内是否存在点F,使以点B、C、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
6如图,已知直线 与x轴交于点A ,与y轴交于点C,抛物线 :经过A,C两点,且与x轴的另一个交点为B ,对称轴为直线x=-1.
(1)求抛物线的表达式
(2)D是第二象限内抛物线上的动点,设点D横坐标为m,求四边形ABCD面积S的最大值及D点坐标;(3)若点P在抛物线对称轴上,是否存在点P ,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形 若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
7如图,某一次函数与二次函数 的图象交点为
(1)求抛物线的解析式;
(2)点C为抛物线对称轴上一动点,当AC与BC的和最小时,点C的坐标为 ;
(3)点D为抛物线位于线段AB下方图象上一动点,过点D作. 轴,交线段AB于点E ,求线段DE长度的最大值;
(4)在(2)条件下,点M为y轴上一点,点F为直线AB上一点,点N为平面直角坐标系内一点,若以点C,M,F,N为顶点的四边形是正方形,请直接写出点N的坐标.
8如图,在平面直角坐标系中,抛物线 交x轴于点A和C(1,0) , 交y轴于点B(0,3),抛物线的对称轴交x轴于点E,交抛物线于点F.
(1)求抛物线的解析式 .
(2)M为平面直角坐标系中一点,在抛物线上是否存在一点N ,使得以A,B,M,N为顶点的四边形为矩形 若存在,请直接写出点N的横坐标;若不存在,请说明理由.
9在平面直角坐标系中 ,抛物线 交x轴于A(-3,0), B(4,0)两点, 交y轴于点C .
(1)求抛物线的表达式.
(2)如图,直线 与抛物线交于A ,D两点,与直线BC交于点E .若M(m,0)是线段
AB上的动点,过点M作x轴垂线,交抛物线于F,交直线AD于点G,交直线BC于点H .
①当点F在直线AD上方的抛物线上,且 时,求m的值;
②在平面内是否在点P,使四边形EFHP为正方形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
10如图,在平面直角坐标系中,抛物线 与x轴交于点A、B ,与y轴交于点C,连接BC,,对称轴为: 点D为此抛物线的顶点 .
(1)求抛物线的解析式.
(2)抛物线上C、D两点之间的距离是 .
(3)点E是第一象限内抛物线上的动点,连接BE和CE.求 面积的最大值.
(4)点P在抛物线对称轴上,平面内存在点Q ,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
1.如图,在平面直角坐标系xOy中,已知抛物线 经过点A(3,0),与y轴交于点B,且关于直线x=1对称.
(2) 当-1≤x≤t时, y的取值范围是0≤y≤2t-1,求t的值;
(3)点C是抛物线上位于第一象限的一个动点,过点C作x轴的垂线交直线AB于点D,在y轴上是否存在点E,使得以B,C,D,E为顶点的四边形是菱形 若存在,求出该菱形的边长;若不存在,说明理由.
【答案】
(3)存在点以B,C,D,E为顶点的四边形是菱形,边长为3 -2或2
【解析】(1)【分析】本题考查二次函数的综合应用,菱形的性质,正确的求出函数解析式,利用数形结合和分类讨论的思想进行求解,是解题的关键.
待定系数法求出函数解析式即可;
【详解】解:∵抛物线y 3经过点A(3,0),与y轴交于点B,且关于直线x=1对称,解得
(2)【分析】分t≤1和t>1,两种情况,结合二次函数的增减性进行求解即可.
【详解】∵抛物线的开口向下,对称轴为直线x=1,∴抛物线上点到对称轴上的距离越远,函数值越小,∵-1≤x≤t时,0≤y≤2t-1,①当t≤1时,则:当x=t时,函数有最大值,即:26-1=-t +2t+3,解得:t=-2或t=2,均不符合题意,舍去;②当t>1时,则:当x=1时,函数有最大值,即: 解得 故
(3)【分析】分BD为菱形的边和菱形的对角线两种情况进行讨论求解即可.
【详解】存在;当 0时,解得:: ,当x=0时,y=3,∴A(3,0),B(0,3), 设直线AB的解析式为y= kx+3,把A(3,0)代入,得:k=-1,∴y=-∞+3,设 则:D(m,-m+3)
当B,C,D,E为顶点的四边形是菱形时,分两种情况:①当BD为边时,则:BD=CD,即 解得:m=0(舍去)或m=3- ,此时菱形的边长为 ②当BD为对角线时,则:BC=CD,即:
解得:m=2或m=0(舍去)此时菱形的边长为 综上:存在以B,C,D,E为顶点的四边形是菱形,边长为
2如图,在平面直角坐标系中,一次函数y=-2x+6的图象与z轴交于点A,与y轴交于点B,抛物线 B两点,在第一象限的抛物线上取一点D,过点D作DC⊥z轴于点C,交AB于点E
(1)求这条抛物线所对应的函数表达式;
(2)F是第一象限内抛物线上的动点(不与点D重合),过点F作z轴的垂线交AB于点G,连接DF,当四边形EGFD为菱形时,求点D的横坐标.
【答案】
【解析】【分析】
(1)先求出A、B的坐标,然后代入 求出b、c的值即可;
(2)由对顶角的性质性质知∠AEC=∠DEB,若存在△BDE和△ACE相似,则有△ACE∽△BDE和△ACE∽△DBE两种情况,然后分情况讨论,利用相似三角形的性质求解即可;
(3)设点L ,E(m,-2m+6),F(n,-n +n+6),G(n,-2n+6),则 ,根据菱形的性质得出 可求出n=3-m,过点G作GK⊥DB于K,可得∠EGK =∠BAC,利用等角的余弦值相等得出 求出 根据菱形的性质得出 解方程求出m的值即可.
【详解】
(1)解:令y=0,则-2x+6=0,!则x=3;令x=0,则y=6∴A(3,0),B(0,6)把A(3,0), B(0,6)代入 得: 解得 这条抛物线所对应的函数表达式为
(2)如图3,∵四边形EGFD为菱形
∴DE∥FG,DE=FG,ED=EG设点 E(m,-2m+6),
,即(m-n)(m+n-3)=0∵m-n≠0∴m+n-3=0,即m+n=3或n=3-m∵A(3,0),B(0,6)∴AO=3,BO=6∴
过点G作GK⊥DE于K∴KG∥AC∴∠EGK=∠BAC∴
即
解得 (不合题意,舍去)或
故 答:点D的横坐标为 【点睛】本题是常见的中考数学压轴题型,综合性比较强,涉及到知识点较多;主要考查了待定系数法求二次函数的解析式,相似三角形的性质,菱形的性质;解题时要能够灵活运用所学的数学知识,要会分类讨论
3.如图,在平面直角坐标系中,抛物线y 2过点(1,3),且交x轴于点A(-1,0), B两点,交y轴于点C.
(1)求抛物线的表达式.
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标.
(3)在(2)中△PDE周长取得最大值的条件下,将该抛物线沿射线CB方向平移 个单位长度,点M为平移后的抛物线的对称轴上一点.在平面内确定一点N,使得以点A,P,M,N为顶点的四边形是菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
【答案】
(2)△PDE周长的最大值为 此时点P(2,3).
(3)点N的坐标为((-5,2,2))=(1,3, )=(
【解析】(1)把(1,3)、A(-1,0)代入 2得
解得
∴抛物线的表达式为
(2)如图,延长PE交z轴于F,
:PD⊥BC于点D ,PE//y轴,
∴∠DEP=∠BCO,∠PDE=∠COB=90°,
∴△DPE∽△OBC.
∴△DPE的周长=BC·△OBC周长,
∴当PE最大时△PDE的周长最大,
··抛物线的表达式为1
.. B(4,0),C(0,2),
∴直线BC的解析式为:
设 则B
∴当m=2时PE最大,最大值为2,此时P(2,3),
∵△BOC的周长为OC+OB+BC=6+2
∴△PDE周长的最大值为 此时P(2,3),
即△PDE周长的最大值为 此时点P(2,3).
(3)∵将该抛物线沿射线CB方向平移 个单位长度,可以看成是向右平移2个单位长度再向下平移一个单位长度4
如图,抛物线 c的图象经过A(-6,0),B(-2,0). C(0,6)三点,且一次函数y= kx+6的图象经过点B.
(1)求抛物线和一次函数的解析式.
(2)点E,F为平面内两点,若以E、F、B、C为顶点的四边形是正方形,且点E在点F的左侧.这样的B,F两点是否存在 如果存在,请直接写出所有满足条件的点E的坐标:如果不存在,请说明理由.
【答案】
(2)满足条件的E、F两点存在, E (-8,2),E (4,-2),E (-4,4)
【解析】(1)解:把A(-6,0),B(-2,0),σ(0,6)代入v =ax + bx+c得
解得
把B(-2,0)代入v= kx+6得k=3
∵v=3x+6
(2)满足条件的E、F两点存在, B (-8,2),E (4,-2), E (-4,4)
解:①当BC为正方形的边长时,分别过B点C点作E E ⊥BC,F F ⊥BC,使 连接E F 、B F .
∴平移后的解析式为 此抛物
线对称轴为直线
∴设M( ,m). N ,t)
∵P(2.3),A(-1.0)
当PA为对角线时,此时以点A,P,M,N为顶点的四边形是菱形,
∴PA与MN互相平分,且PM=AM,
解得
∵PA中点坐标为 MN中点坐标为
解得
此时
当PA为边长且AM和PN是对角线时,此时以点A,P,M,N为顶点的四边形是菱形,∴AM与PN互相平分,且PM=PA,
解得
∵ PN中点坐标为 AM中点坐标为
解得
此时 或N
同理可得,当PA为边长且AN和PM是对角线时,此时以点A,P,M,N为顶点的四边形是菱形,
∴AN和PM互相平分,且AM=PA,
此方程无解.
综上所述,点N的坐标为 )=(1,∵2)=(3,-2,
【标注】【知识点】二次函数与动点问题
过点E 作E H ⊥x轴于H .
∴B (-8,2)同理可得, E (4,-2)
②以BO为正方形的对角线时,过BO的中点G作B F ⊥BC,使E F 与BC互相平分且相等,则四边形E BF C为正方形,过点E 作E N⊥y轴于点N ,过点B作BM⊥E N于点M
∴E B=2 在Rt△E NC中,
解得CN=2或4当CN=4时,E (2,2),此时点E在点F右侧故舍去;
当CN=2时,E (-4,4).
综上所述:E (-8,2),E (4,-2), E (-4,4)
5如图,抛物线 c的对称轴是直线x=1,与x轴交于点A,B(3,0),与y轴交于点C,
连接AC.
(1)求此抛物线的解析式;
(2)已知点E是抛物线对称轴上的点,在坐标平面内是否存在点F,使以点B、C、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
【答案】
(2)存在点F的坐标为(4,1)或(-2,1)或
【解析】【分析】
(1)根据抛物线的对称轴是直线x=1,可得a=-1,再把点B(3,0)代入,即可求解;
(2)设点E(1,n) ,点F(s,t) ,然后分两种情况讨论:当BC为边时,当BC为对角线时,即可求解.
(1)解:∵抛物线 c的对称轴是直线 解得:a=-1, ∵抛物线过点B(3,0), ..-9+6+c=0,解得:c=3,∴抛物线解析式为: (2)解:存在,理由如下:∵点B(3,0) ,C(0,3) ,∴OB=OC,∴BC=3 ,设点E(1,n),点F(s,t),当BC为边时,点C向右平移3个单位向下平移3个单位得到点B,同样E(F)向右平移3个单位向下平移3个单位得到点F(E) ,且BE=CF(CE=BF) ,如下图所示,
解得: ∴此时点F的坐标为(4,1)或(-2,1) ;当BO为对角线时,BC=EF,且EF与BC的中点重合,如下图所示, 解得∴此时点F的坐标为 综上所述,存在点F的坐标为(4,1)或(-2,1)]e ヨ 【点睛】本题主要考查了二次函数的综合题,熟练掌握二次函数的图象和性质,等腰三角形的性质,矩形的性质,并利用分类讨论思想解答是解题的关键是解题的关键.
6如图,已知直线 与x轴交于点A,与y轴交于点C,抛物线 c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=-1.
中小学教育资源及组卷应用平台
(1)求抛物线的表达式;
(2)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;
(3)若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形 若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
【答案】
(3)存在
【解析】
【分析】
(1)先求得A,C,B三点的坐标,将抛物线设为交点式,进一步求得结果;
(2)作DF⊥AB于F,交AC于E,根据点D和点E坐标可表示出DE的长,进而表示出三角形ADC的面积,进而表示出S的函数关系式,进一步求得结果;
(3)根据菱形性质可得PA=PC,进而求得点P的坐标,根据菱形性质,进一步求得点Q坐标.(1)
解:当x=0时,y=4,
∴C(0,4),
当y=0时
∴x=-3,
∴A (-3,0),
∵对称轴为直线x=-1,
∴B(1,0) ,
∴设抛物线的表达式:y=a(x-1)·(x+3) ,
:4=·3a,
∴抛物线的表达式为
(2)
如下图1所示,,
作DF⊥AB于F,交AC于E,
∴当 时
当 时
(3)
设P(-1,n).
∵以A,C,P,Q为顶点的四边形是以AC为对角线的菱形,
∴PA=PC,
即:PA =PC ,
∵xp+xQ=xA+ xc,yP+yQ=yA+ yc
【点睛】
本题考查了二次函数及其图象性质,勾股定理,菱形性质等知识,解决问题的关键是熟练掌握相关二次函数和菱形性质
7如图,某一次函数与二次函数 n的图象交点为A(-1,0), B(4,5).
(1)求抛物线的解析式;
(2)点C为抛物线对称轴上一动点,当AC与BC的和最小时,点C的坐标为 ;
(3)点D为抛物线位于线段AB下方图象上一动点,过点D作E⊥z轴,交线段AB于点E ,求线段DE长度的最大值;
(4)在(2)条件下,点M为y轴上一点,点F为直线AB上一点,点N为平面直角坐标系内一点,若以点C,M,F,N为顶点的四边形是正方形,请直接写出点N的坐标.
【答案】
(2)(1,2):
【解析】【分析】(1)将A(-1,0),B(4,5)代入 得到关于m,n的二元一次方程组求解即可:
(2)两点之间线段最短,求出直线AB与对称轴的交点即可求解;
(3)设D(d,d -2d-3),则E(d,d+1),则
根据二次函数的性质求解即可;
(4)根据题意画出图形,分情况求解即可.
【解析】(1)将A(-1,0),B(4,5)代入 得 解这个方程组得 ·抛物线的解析式为:
(2)设直线AB的解析式为:y= kx+b,把点A(-1,0),B(4,5)代入y= kz+b,得 解得 .直线AB的解析式为:y=x+1 ,由(1)知抛物线 3的对称轴为x ∴点C为抛物线对称轴上一动点,
AC+BC≥AB,∴当点C在AB上时,AC+BC最小,把x=1代入y=z+1,得y=2,∴点C的坐标为(1,2);
(3)如图,由(2)知直线AB的解析式为y=x+1设D(d,d -2d-3).则E(d,d+1),则 当 时,DE有最大值为254.
(4)由(2)知C(1,2).
如图,∵直线AB的解析式为:y=x+1,
∴直线与y轴的交点为D(0,1),OD=1.
∵A(-1,0),OA=1,∴OA=OD,∠DAO=∠ADO=45°.
若以点C,M,F,N为顶点的四边形是正方形,
从△DMC为等腰直角三角形分情况讨论:
①∠MCF=45°,因为CF在直线AB上,显然F不在点C上方,否则此时M不存在,故点F在C下方,过C作z轴平行线交y轴于M ,则M(0,2).
(i)M (0,2),CM 为等腰△DM C直角边,过M 作竖直线,即y轴,交AB于F ,则F (0,1),因为CM F N 是正方形,易得点N 的坐标为(1,1);
(ii)M (0,2),CM 为等腰△DM C斜边,取F C的中点F ,则F 因为CM F N 是正方形,,易得N 的坐标为
②∠MCF=90°,因为CF在直线AB上,过C作CM⊥AB交y轴于M ,则M(0,3).
(i)M (0,3),F 在点C下方,过M 作竖直线交AB于F ,则F (0,1),四边形OM N F 是正方形,则点N 的坐标为(-1,2);
(ii)M (0,3), F 在点C上方,过M 作横直线交AB于F ,则P (2,3),四边形CM N F 是正方形,则N,的坐标为(1,4);
综上所述,点N的坐标为:
【点睛】本题考查了用待定系数法求一次函数和二次函数的解析式,二次函数的性质,正方形的判定,根据题意正确圆图是解本题的关键.
8如图,在平面直角坐标系中,抛物线 c交z轴于点A和C(1,0),交;轴于点B(0,3),抛物线的对称轴交x轴于点E,交抛物线于点F.
(1)求抛物线的解析式.
(2)M为平面直角坐标系中一点,在抛物线上是否存在一点N,使得以A,B,M,N为顶点的四边形为矩形 若存在,请直接写出点N的横坐标;若不存在,请说明理由.
【答案】
(2)存在,N点的横坐标分别为:2, 或
【解析】(1)∵y=-x + bx+c过O(1,0),B(0,3),
.. b=-2,c=3,
∴抛物线的解析式为
(2)∵A(-3,0), B(0,3),
∵四边形ABMN是矩形,
..△ABN是直角三角形,
若AB是斜边,则
即1
解得:
∴N的横坐标为 或
若AN是斜边,则
即(
解得n =-1,
..N的横坐标为-1.
若BN是斜边,则
E
解得n=2,
. N的横坐标为2.
综上所述,N的横坐标为 或 或-1或2.
【标注】【知识点】二次函数与相似三角形结合
9在平面直角坐标系中,抛物线 c交x轴于A(-3,0), B(4,0)两点, 交y轴于点C.
(1)求抛物线的表达式.
(2)如图,直线 与抛物线交于A,D两点,与直线BC交于点E .若M(m,0)是线段AB上的动点,过点M作x轴的垂线,交抛物线于点F,交直线AD于点G,交直线BC于点H
①当点F在直线AD上方的抛物线上,且 时,求m的值;
②在平面内是否在点P,使四边形EFHP为正方形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】
(2)见解析
【解析】(1)∵抛物线 c交z轴于A(-3,0), B(4,0)两点,
(2) ①如图1,∵B(4,0),C(0,4),
∴设直线BC的解析式为y= kx+b,
则 解得
·直线BC的解析式为y=-z+4,
由
解得:x=1,
E(1,3),
·M(m,0),且MH⊥z轴.
解得:
②存在,由①知:E(1,3),
∵四边形EFHP是正方形,
∴FH=EF,∠EFH=∠FHP=∠HPE=90°,
∵M(m,0),且MH⊥z轴,
分两种情况:
i)当-3≤m<1时,如图2,点F在EP的左侧,
∵EF=FH,
解得: (舍)
ii)当1同理得
解得
同理得
综上,点P的坐标为: )m(, =3=0)
【标注】 【知识点】二次函数应用;二次函数与几何综合
10.如图,在平面直角坐标系中,抛物线y 与x轴交于点A、B,与y轴交于点O,连接BC,OA=1,对称轴为x=2,点D为此抛物线的顶点.
(1)求抛物线的解析式.
(2)抛物线上C、D两点之间的距离是 .
(3)点E是第一象限内抛物线上的动点,连接BE和CE.求△BCE面积的最大值.
(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
【答案】
(2) 2
(4)(3,4)或 或(7,4)或
【解析】(1)∵OA=1,
.. A(-1,0),
又∵对称轴为直线x=2,
∴B(5,0),
将A,B两点代入解析式得:
解得
(2)由(1)得:
故答案为:2
(3)∵B(5,0),c(0, ).
∴直线BC的解析式为:
设E
作EF//y轴交BC于点F,
则F
由二次函数的性质得:在0即S△BCE有最大值为
(4)设P(2,y),Q(m,n),
由(1)知B(5,0),
若BC为矩形的对角线,
则
解得:
又
即:
解得
或n=4,
∴Q(3,4)或Q
若BP为矩形的对角线,
则
解得
又∵∠BCP=90°,
即:
解得
∴Q(7,4),
若BQ为矩形的对角线,
则
解得:
又∵∠BCQ=90°,
即
解得
综上,点Q的坐标为(3,4)或 或(7,4)或|
【标注】【知识点】二次函数与特殊平行四边形
模型原理
1.菱形的存在性
2.矩形的存在性
3.正方形的存在性
真题精炼
1如图,在平面直角坐标系xOy中,已知抛物线 经过点A(3,0), 与y轴交于点B, 且关于直线x =1对称.
(1)求该抛物线的解析式;
(2) 当-1≤x≤t时, y的取值范围是0≤y≤2t--1, 求t的值;
(3)点C是抛物线上位于第一象限的一动点,过点C作x轴的垂线交直线AB于D,在y轴上是否存在点E,使得以B,C,D,E为顶点的四边形是菱形 若存在,求出该菱形边长;若不存在,说明理由.
2如图,在平面直角坐标系中,一次函数y=-2x+6的图象与x轴交于点A ,与y轴交于点B,抛物线 c经过A、B两点,在第一象限的抛物线上取一点D ,过点D作 轴于点C,交AB于点E.
(1)求这条抛物线所对应的函数表达式;
(2)F是第一象限内抛物线上的动点(不与点D重合),过点F作x轴的垂线交AB于点G,连接DF,当四边形EGFD为菱形时,求点D的横坐标.
3如图,在平面直角坐标系中,抛物线 过点(1,3),且交x轴于点 B两点,交y轴于点C .
(1)求抛物线的表达式 .
(2)点P是直线BC上方抛物线上的一动点,过点P作 于点D ,过点P作y轴的平行线交直线BC于点E,求 周长的最大值及此时点P的坐标.
(3) 在(2)中. 周长取得最大值的条件下,将该抛物线沿射线CB方向平移 个单位长度,点M为平移后的抛物线的对称轴上一点.在平面内确定一点N ,使得以点A,P,M,N为顶点的四边形是菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
4如图,抛物线 c的图象经过A(-6,0), B(-2,0), C(0,6)三点, 且一次函数 的图象经过点B.
(1)求抛物线和一次函数的解析式.
(2)点E ,F为平面内两点,若以E、F、B、C为顶点的四边形是正方形,E在点F的左侧.这样的E,F两点是否存在 如果存在,请直接写出所有满足条件的点E的坐标:如果不存在,请说明理由.
5如图,抛物线 的对称轴是直线 ,与x轴交于点A , B(3,0) , 与y轴交于点C,
(1)求此抛物线的解析式;
(2)已知点E是抛物线对称轴上的点,在坐标平面内是否存在点F,使以点B、C、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
6如图,已知直线 与x轴交于点A ,与y轴交于点C,抛物线 :经过A,C两点,且与x轴的另一个交点为B ,对称轴为直线x=-1.
(1)求抛物线的表达式
(2)D是第二象限内抛物线上的动点,设点D横坐标为m,求四边形ABCD面积S的最大值及D点坐标;(3)若点P在抛物线对称轴上,是否存在点P ,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形 若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
7如图,某一次函数与二次函数 的图象交点为
(1)求抛物线的解析式;
(2)点C为抛物线对称轴上一动点,当AC与BC的和最小时,点C的坐标为 ;
(3)点D为抛物线位于线段AB下方图象上一动点,过点D作. 轴,交线段AB于点E ,求线段DE长度的最大值;
(4)在(2)条件下,点M为y轴上一点,点F为直线AB上一点,点N为平面直角坐标系内一点,若以点C,M,F,N为顶点的四边形是正方形,请直接写出点N的坐标.
8如图,在平面直角坐标系中,抛物线 交x轴于点A和C(1,0) , 交y轴于点B(0,3),抛物线的对称轴交x轴于点E,交抛物线于点F.
(1)求抛物线的解析式 .
(2)M为平面直角坐标系中一点,在抛物线上是否存在一点N ,使得以A,B,M,N为顶点的四边形为矩形 若存在,请直接写出点N的横坐标;若不存在,请说明理由.
9在平面直角坐标系中 ,抛物线 交x轴于A(-3,0), B(4,0)两点, 交y轴于点C .
(1)求抛物线的表达式.
(2)如图,直线 与抛物线交于A ,D两点,与直线BC交于点E .若M(m,0)是线段
AB上的动点,过点M作x轴垂线,交抛物线于F,交直线AD于点G,交直线BC于点H .
①当点F在直线AD上方的抛物线上,且 时,求m的值;
②在平面内是否在点P,使四边形EFHP为正方形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
10如图,在平面直角坐标系中,抛物线 与x轴交于点A、B ,与y轴交于点C,连接BC,,对称轴为: 点D为此抛物线的顶点 .
(1)求抛物线的解析式.
(2)抛物线上C、D两点之间的距离是 .
(3)点E是第一象限内抛物线上的动点,连接BE和CE.求 面积的最大值.
(4)点P在抛物线对称轴上,平面内存在点Q ,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
1.如图,在平面直角坐标系xOy中,已知抛物线 经过点A(3,0),与y轴交于点B,且关于直线x=1对称.
(2) 当-1≤x≤t时, y的取值范围是0≤y≤2t-1,求t的值;
(3)点C是抛物线上位于第一象限的一个动点,过点C作x轴的垂线交直线AB于点D,在y轴上是否存在点E,使得以B,C,D,E为顶点的四边形是菱形 若存在,求出该菱形的边长;若不存在,说明理由.
【答案】
(3)存在点以B,C,D,E为顶点的四边形是菱形,边长为3 -2或2
【解析】(1)【分析】本题考查二次函数的综合应用,菱形的性质,正确的求出函数解析式,利用数形结合和分类讨论的思想进行求解,是解题的关键.
待定系数法求出函数解析式即可;
【详解】解:∵抛物线y 3经过点A(3,0),与y轴交于点B,且关于直线x=1对称,解得
(2)【分析】分t≤1和t>1,两种情况,结合二次函数的增减性进行求解即可.
【详解】∵抛物线的开口向下,对称轴为直线x=1,∴抛物线上点到对称轴上的距离越远,函数值越小,∵-1≤x≤t时,0≤y≤2t-1,①当t≤1时,则:当x=t时,函数有最大值,即:26-1=-t +2t+3,解得:t=-2或t=2,均不符合题意,舍去;②当t>1时,则:当x=1时,函数有最大值,即: 解得 故
(3)【分析】分BD为菱形的边和菱形的对角线两种情况进行讨论求解即可.
【详解】存在;当 0时,解得:: ,当x=0时,y=3,∴A(3,0),B(0,3), 设直线AB的解析式为y= kx+3,把A(3,0)代入,得:k=-1,∴y=-∞+3,设 则:D(m,-m+3)
当B,C,D,E为顶点的四边形是菱形时,分两种情况:①当BD为边时,则:BD=CD,即 解得:m=0(舍去)或m=3- ,此时菱形的边长为 ②当BD为对角线时,则:BC=CD,即:
解得:m=2或m=0(舍去)此时菱形的边长为 综上:存在以B,C,D,E为顶点的四边形是菱形,边长为
2如图,在平面直角坐标系中,一次函数y=-2x+6的图象与z轴交于点A,与y轴交于点B,抛物线 B两点,在第一象限的抛物线上取一点D,过点D作DC⊥z轴于点C,交AB于点E
(1)求这条抛物线所对应的函数表达式;
(2)F是第一象限内抛物线上的动点(不与点D重合),过点F作z轴的垂线交AB于点G,连接DF,当四边形EGFD为菱形时,求点D的横坐标.
【答案】
【解析】【分析】
(1)先求出A、B的坐标,然后代入 求出b、c的值即可;
(2)由对顶角的性质性质知∠AEC=∠DEB,若存在△BDE和△ACE相似,则有△ACE∽△BDE和△ACE∽△DBE两种情况,然后分情况讨论,利用相似三角形的性质求解即可;
(3)设点L ,E(m,-2m+6),F(n,-n +n+6),G(n,-2n+6),则 ,根据菱形的性质得出 可求出n=3-m,过点G作GK⊥DB于K,可得∠EGK =∠BAC,利用等角的余弦值相等得出 求出 根据菱形的性质得出 解方程求出m的值即可.
【详解】
(1)解:令y=0,则-2x+6=0,!则x=3;令x=0,则y=6∴A(3,0),B(0,6)把A(3,0), B(0,6)代入 得: 解得 这条抛物线所对应的函数表达式为
(2)如图3,∵四边形EGFD为菱形
∴DE∥FG,DE=FG,ED=EG设点 E(m,-2m+6),
,即(m-n)(m+n-3)=0∵m-n≠0∴m+n-3=0,即m+n=3或n=3-m∵A(3,0),B(0,6)∴AO=3,BO=6∴
过点G作GK⊥DE于K∴KG∥AC∴∠EGK=∠BAC∴
即
解得 (不合题意,舍去)或
故 答:点D的横坐标为 【点睛】本题是常见的中考数学压轴题型,综合性比较强,涉及到知识点较多;主要考查了待定系数法求二次函数的解析式,相似三角形的性质,菱形的性质;解题时要能够灵活运用所学的数学知识,要会分类讨论
3.如图,在平面直角坐标系中,抛物线y 2过点(1,3),且交x轴于点A(-1,0), B两点,交y轴于点C.
(1)求抛物线的表达式.
(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标.
(3)在(2)中△PDE周长取得最大值的条件下,将该抛物线沿射线CB方向平移 个单位长度,点M为平移后的抛物线的对称轴上一点.在平面内确定一点N,使得以点A,P,M,N为顶点的四边形是菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
【答案】
(2)△PDE周长的最大值为 此时点P(2,3).
(3)点N的坐标为((-5,2,2))=(1,3, )=(
【解析】(1)把(1,3)、A(-1,0)代入 2得
解得
∴抛物线的表达式为
(2)如图,延长PE交z轴于F,
:PD⊥BC于点D ,PE//y轴,
∴∠DEP=∠BCO,∠PDE=∠COB=90°,
∴△DPE∽△OBC.
∴△DPE的周长=BC·△OBC周长,
∴当PE最大时△PDE的周长最大,
··抛物线的表达式为1
.. B(4,0),C(0,2),
∴直线BC的解析式为:
设 则B
∴当m=2时PE最大,最大值为2,此时P(2,3),
∵△BOC的周长为OC+OB+BC=6+2
∴△PDE周长的最大值为 此时P(2,3),
即△PDE周长的最大值为 此时点P(2,3).
(3)∵将该抛物线沿射线CB方向平移 个单位长度,可以看成是向右平移2个单位长度再向下平移一个单位长度4
如图,抛物线 c的图象经过A(-6,0),B(-2,0). C(0,6)三点,且一次函数y= kx+6的图象经过点B.
(1)求抛物线和一次函数的解析式.
(2)点E,F为平面内两点,若以E、F、B、C为顶点的四边形是正方形,且点E在点F的左侧.这样的B,F两点是否存在 如果存在,请直接写出所有满足条件的点E的坐标:如果不存在,请说明理由.
【答案】
(2)满足条件的E、F两点存在, E (-8,2),E (4,-2),E (-4,4)
【解析】(1)解:把A(-6,0),B(-2,0),σ(0,6)代入v =ax + bx+c得
解得
把B(-2,0)代入v= kx+6得k=3
∵v=3x+6
(2)满足条件的E、F两点存在, B (-8,2),E (4,-2), E (-4,4)
解:①当BC为正方形的边长时,分别过B点C点作E E ⊥BC,F F ⊥BC,使 连接E F 、B F .
∴平移后的解析式为 此抛物
线对称轴为直线
∴设M( ,m). N ,t)
∵P(2.3),A(-1.0)
当PA为对角线时,此时以点A,P,M,N为顶点的四边形是菱形,
∴PA与MN互相平分,且PM=AM,
解得
∵PA中点坐标为 MN中点坐标为
解得
此时
当PA为边长且AM和PN是对角线时,此时以点A,P,M,N为顶点的四边形是菱形,∴AM与PN互相平分,且PM=PA,
解得
∵ PN中点坐标为 AM中点坐标为
解得
此时 或N
同理可得,当PA为边长且AN和PM是对角线时,此时以点A,P,M,N为顶点的四边形是菱形,
∴AN和PM互相平分,且AM=PA,
此方程无解.
综上所述,点N的坐标为 )=(1,∵2)=(3,-2,
【标注】【知识点】二次函数与动点问题
过点E 作E H ⊥x轴于H .
∴B (-8,2)同理可得, E (4,-2)
②以BO为正方形的对角线时,过BO的中点G作B F ⊥BC,使E F 与BC互相平分且相等,则四边形E BF C为正方形,过点E 作E N⊥y轴于点N ,过点B作BM⊥E N于点M
∴E B=2 在Rt△E NC中,
解得CN=2或4当CN=4时,E (2,2),此时点E在点F右侧故舍去;
当CN=2时,E (-4,4).
综上所述:E (-8,2),E (4,-2), E (-4,4)
5如图,抛物线 c的对称轴是直线x=1,与x轴交于点A,B(3,0),与y轴交于点C,
连接AC.
(1)求此抛物线的解析式;
(2)已知点E是抛物线对称轴上的点,在坐标平面内是否存在点F,使以点B、C、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
【答案】
(2)存在点F的坐标为(4,1)或(-2,1)或
【解析】【分析】
(1)根据抛物线的对称轴是直线x=1,可得a=-1,再把点B(3,0)代入,即可求解;
(2)设点E(1,n) ,点F(s,t) ,然后分两种情况讨论:当BC为边时,当BC为对角线时,即可求解.
(1)解:∵抛物线 c的对称轴是直线 解得:a=-1, ∵抛物线过点B(3,0), ..-9+6+c=0,解得:c=3,∴抛物线解析式为: (2)解:存在,理由如下:∵点B(3,0) ,C(0,3) ,∴OB=OC,∴BC=3 ,设点E(1,n),点F(s,t),当BC为边时,点C向右平移3个单位向下平移3个单位得到点B,同样E(F)向右平移3个单位向下平移3个单位得到点F(E) ,且BE=CF(CE=BF) ,如下图所示,
解得: ∴此时点F的坐标为(4,1)或(-2,1) ;当BO为对角线时,BC=EF,且EF与BC的中点重合,如下图所示, 解得∴此时点F的坐标为 综上所述,存在点F的坐标为(4,1)或(-2,1)]e ヨ 【点睛】本题主要考查了二次函数的综合题,熟练掌握二次函数的图象和性质,等腰三角形的性质,矩形的性质,并利用分类讨论思想解答是解题的关键是解题的关键.
6如图,已知直线 与x轴交于点A,与y轴交于点C,抛物线 c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=-1.
中小学教育资源及组卷应用平台
(1)求抛物线的表达式;
(2)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;
(3)若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形 若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
【答案】
(3)存在
【解析】
【分析】
(1)先求得A,C,B三点的坐标,将抛物线设为交点式,进一步求得结果;
(2)作DF⊥AB于F,交AC于E,根据点D和点E坐标可表示出DE的长,进而表示出三角形ADC的面积,进而表示出S的函数关系式,进一步求得结果;
(3)根据菱形性质可得PA=PC,进而求得点P的坐标,根据菱形性质,进一步求得点Q坐标.(1)
解:当x=0时,y=4,
∴C(0,4),
当y=0时
∴x=-3,
∴A (-3,0),
∵对称轴为直线x=-1,
∴B(1,0) ,
∴设抛物线的表达式:y=a(x-1)·(x+3) ,
:4=·3a,
∴抛物线的表达式为
(2)
如下图1所示,,
作DF⊥AB于F,交AC于E,
∴当 时
当 时
(3)
设P(-1,n).
∵以A,C,P,Q为顶点的四边形是以AC为对角线的菱形,
∴PA=PC,
即:PA =PC ,
∵xp+xQ=xA+ xc,yP+yQ=yA+ yc
【点睛】
本题考查了二次函数及其图象性质,勾股定理,菱形性质等知识,解决问题的关键是熟练掌握相关二次函数和菱形性质
7如图,某一次函数与二次函数 n的图象交点为A(-1,0), B(4,5).
(1)求抛物线的解析式;
(2)点C为抛物线对称轴上一动点,当AC与BC的和最小时,点C的坐标为 ;
(3)点D为抛物线位于线段AB下方图象上一动点,过点D作E⊥z轴,交线段AB于点E ,求线段DE长度的最大值;
(4)在(2)条件下,点M为y轴上一点,点F为直线AB上一点,点N为平面直角坐标系内一点,若以点C,M,F,N为顶点的四边形是正方形,请直接写出点N的坐标.
【答案】
(2)(1,2):
【解析】【分析】(1)将A(-1,0),B(4,5)代入 得到关于m,n的二元一次方程组求解即可:
(2)两点之间线段最短,求出直线AB与对称轴的交点即可求解;
(3)设D(d,d -2d-3),则E(d,d+1),则
根据二次函数的性质求解即可;
(4)根据题意画出图形,分情况求解即可.
【解析】(1)将A(-1,0),B(4,5)代入 得 解这个方程组得 ·抛物线的解析式为:
(2)设直线AB的解析式为:y= kx+b,把点A(-1,0),B(4,5)代入y= kz+b,得 解得 .直线AB的解析式为:y=x+1 ,由(1)知抛物线 3的对称轴为x ∴点C为抛物线对称轴上一动点,
AC+BC≥AB,∴当点C在AB上时,AC+BC最小,把x=1代入y=z+1,得y=2,∴点C的坐标为(1,2);
(3)如图,由(2)知直线AB的解析式为y=x+1设D(d,d -2d-3).则E(d,d+1),则 当 时,DE有最大值为254.
(4)由(2)知C(1,2).
如图,∵直线AB的解析式为:y=x+1,
∴直线与y轴的交点为D(0,1),OD=1.
∵A(-1,0),OA=1,∴OA=OD,∠DAO=∠ADO=45°.
若以点C,M,F,N为顶点的四边形是正方形,
从△DMC为等腰直角三角形分情况讨论:
①∠MCF=45°,因为CF在直线AB上,显然F不在点C上方,否则此时M不存在,故点F在C下方,过C作z轴平行线交y轴于M ,则M(0,2).
(i)M (0,2),CM 为等腰△DM C直角边,过M 作竖直线,即y轴,交AB于F ,则F (0,1),因为CM F N 是正方形,易得点N 的坐标为(1,1);
(ii)M (0,2),CM 为等腰△DM C斜边,取F C的中点F ,则F 因为CM F N 是正方形,,易得N 的坐标为
②∠MCF=90°,因为CF在直线AB上,过C作CM⊥AB交y轴于M ,则M(0,3).
(i)M (0,3),F 在点C下方,过M 作竖直线交AB于F ,则F (0,1),四边形OM N F 是正方形,则点N 的坐标为(-1,2);
(ii)M (0,3), F 在点C上方,过M 作横直线交AB于F ,则P (2,3),四边形CM N F 是正方形,则N,的坐标为(1,4);
综上所述,点N的坐标为:
【点睛】本题考查了用待定系数法求一次函数和二次函数的解析式,二次函数的性质,正方形的判定,根据题意正确圆图是解本题的关键.
8如图,在平面直角坐标系中,抛物线 c交z轴于点A和C(1,0),交;轴于点B(0,3),抛物线的对称轴交x轴于点E,交抛物线于点F.
(1)求抛物线的解析式.
(2)M为平面直角坐标系中一点,在抛物线上是否存在一点N,使得以A,B,M,N为顶点的四边形为矩形 若存在,请直接写出点N的横坐标;若不存在,请说明理由.
【答案】
(2)存在,N点的横坐标分别为:2, 或
【解析】(1)∵y=-x + bx+c过O(1,0),B(0,3),
.. b=-2,c=3,
∴抛物线的解析式为
(2)∵A(-3,0), B(0,3),
∵四边形ABMN是矩形,
..△ABN是直角三角形,
若AB是斜边,则
即1
解得:
∴N的横坐标为 或
若AN是斜边,则
即(
解得n =-1,
..N的横坐标为-1.
若BN是斜边,则
E
解得n=2,
. N的横坐标为2.
综上所述,N的横坐标为 或 或-1或2.
【标注】【知识点】二次函数与相似三角形结合
9在平面直角坐标系中,抛物线 c交x轴于A(-3,0), B(4,0)两点, 交y轴于点C.
(1)求抛物线的表达式.
(2)如图,直线 与抛物线交于A,D两点,与直线BC交于点E .若M(m,0)是线段AB上的动点,过点M作x轴的垂线,交抛物线于点F,交直线AD于点G,交直线BC于点H
①当点F在直线AD上方的抛物线上,且 时,求m的值;
②在平面内是否在点P,使四边形EFHP为正方形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】
(2)见解析
【解析】(1)∵抛物线 c交z轴于A(-3,0), B(4,0)两点,
(2) ①如图1,∵B(4,0),C(0,4),
∴设直线BC的解析式为y= kx+b,
则 解得
·直线BC的解析式为y=-z+4,
由
解得:x=1,
E(1,3),
·M(m,0),且MH⊥z轴.
解得:
②存在,由①知:E(1,3),
∵四边形EFHP是正方形,
∴FH=EF,∠EFH=∠FHP=∠HPE=90°,
∵M(m,0),且MH⊥z轴,
分两种情况:
i)当-3≤m<1时,如图2,点F在EP的左侧,
∵EF=FH,
解得: (舍)
ii)当1
解得
同理得
综上,点P的坐标为: )m(, =3=0)
【标注】 【知识点】二次函数应用;二次函数与几何综合
10.如图,在平面直角坐标系中,抛物线y 与x轴交于点A、B,与y轴交于点O,连接BC,OA=1,对称轴为x=2,点D为此抛物线的顶点.
(1)求抛物线的解析式.
(2)抛物线上C、D两点之间的距离是 .
(3)点E是第一象限内抛物线上的动点,连接BE和CE.求△BCE面积的最大值.
(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
【答案】
(2) 2
(4)(3,4)或 或(7,4)或
【解析】(1)∵OA=1,
.. A(-1,0),
又∵对称轴为直线x=2,
∴B(5,0),
将A,B两点代入解析式得:
解得
(2)由(1)得:
故答案为:2
(3)∵B(5,0),c(0, ).
∴直线BC的解析式为:
设E
作EF//y轴交BC于点F,
则F
由二次函数的性质得:在0
(4)设P(2,y),Q(m,n),
由(1)知B(5,0),
若BC为矩形的对角线,
则
解得:
又
即:
解得
或n=4,
∴Q(3,4)或Q
若BP为矩形的对角线,
则
解得
又∵∠BCP=90°,
即:
解得
∴Q(7,4),
若BQ为矩形的对角线,
则
解得:
又∵∠BCQ=90°,
即
解得
综上,点Q的坐标为(3,4)或 或(7,4)或|
【标注】【知识点】二次函数与特殊平行四边形
同课章节目录
