专题十七 平面坐标系动点找规律(含解析)2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题十七 平面坐标系动点找规律(含解析)2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 260.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 12:51:58 | ||
图片预览



文档简介
平面坐标系动点找规律
模型原理
这类问题往往将变换、函数、相似等知识结合在一起,常涉及到转化、整体和数形结合等方法,具有很强的综合性,解决这类问题的关键是要注意观察和分析图形.
1.函数与平移
(1)一次函数y= kx+b(k≠0)的平移
左加右减,上加下减,一次函数解析式为y=k(x±m)+b±n
(2)反比例函数 的平移
左加右减,上加下减,反比例函数解析式为
(3)二次函数 的平移
左加右减,上加下减,二次函数解析式为
2.函数与对称
(1)一次函数y = kx+b(k≠0)的对称
①关于x轴对称后的解析式为y=-kx-b②关于y轴对称后的解析式为y=-kx+b
③关于原点中心对称后的解析式为y = kx-b
(2)反比例函数 的对称
①关于x轴对称后的解析式为 ②关于y轴对称后的解析式为
③关于原点对称后的解析式为
(3)二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达
①关于x轴对称
关于x轴对称后,得到的解析式是
②关于y轴对称
关于y轴对称后,得到的解析式是
③关于原点对称
:关于原点中心对称后,得到的解析式是
真题精炼
1如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,( 连接AB,过点O作 于点 过点 作 轴于点. 过点 作 于点 过点 作 轴于点 过点 作 于点 过点 作 轴于点 按照如此规律操作下去,则点 的坐标为 .
2如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1), 是以点B为圆心,BA为半径的圆弧; 是以点O为圆心, 为半径的圆弧, 是以点C为圆心, 为半径的圆弧, 是以点A为圆心 , 为半径的圆弧,继续以点B,O,C,A为圆心按上述作法得到的曲线. ·称为正方形的“渐开线” ,则点 的坐标是
3在平面直角坐标系中,点. ·在x轴的正半轴上,点 ·在直线 上,若点 的坐标为(2,0) , 且4 ·均为等边三角形.则点. 的纵坐标为 .
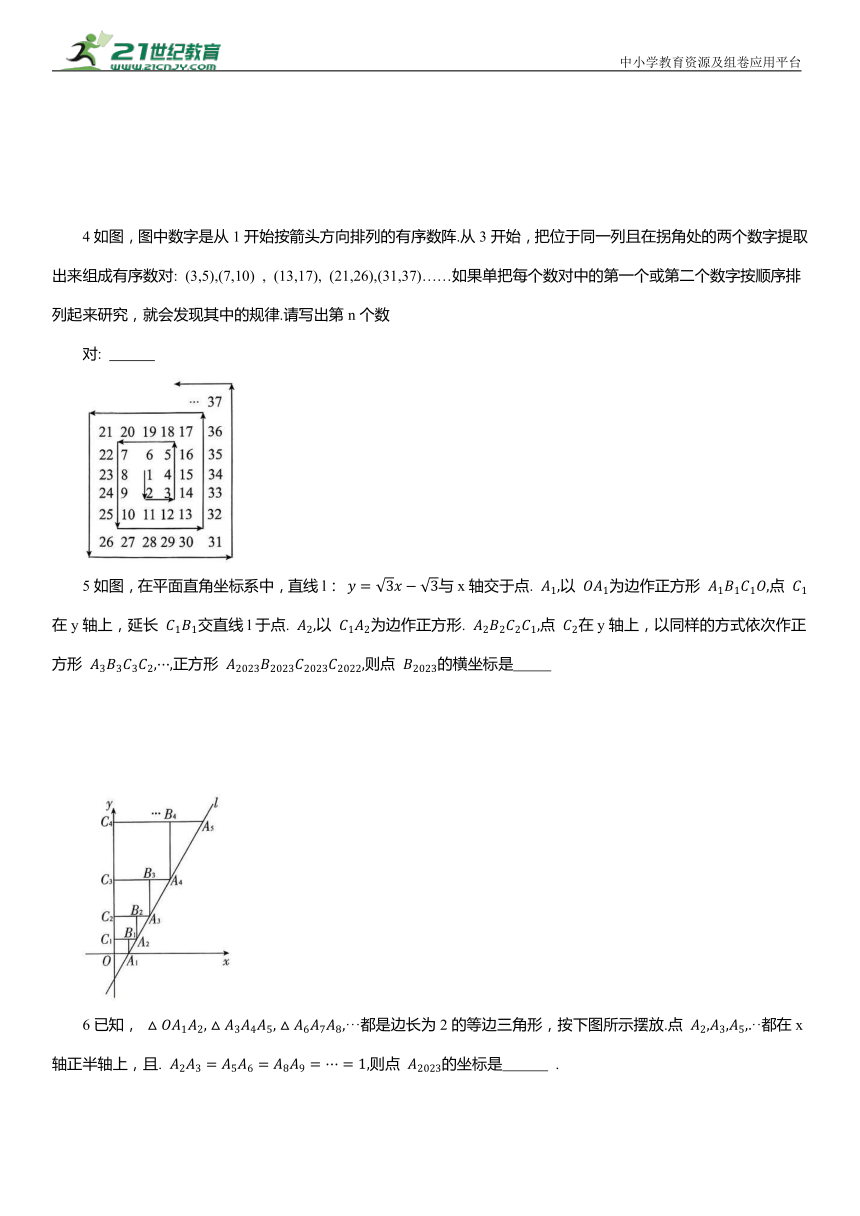
4如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对: (3,5),(7,10) , (13,17), (21,26),(31,37)……如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数
对:
5如图,在平面直角坐标系中,直线l: 与x轴交于点. 以 为边作正方形 点 在y轴上,延长 交直线l于点. 以 为边作正方形. 点 在y轴上,以同样的方式依次作正方形 正方形 则点 的横坐标是
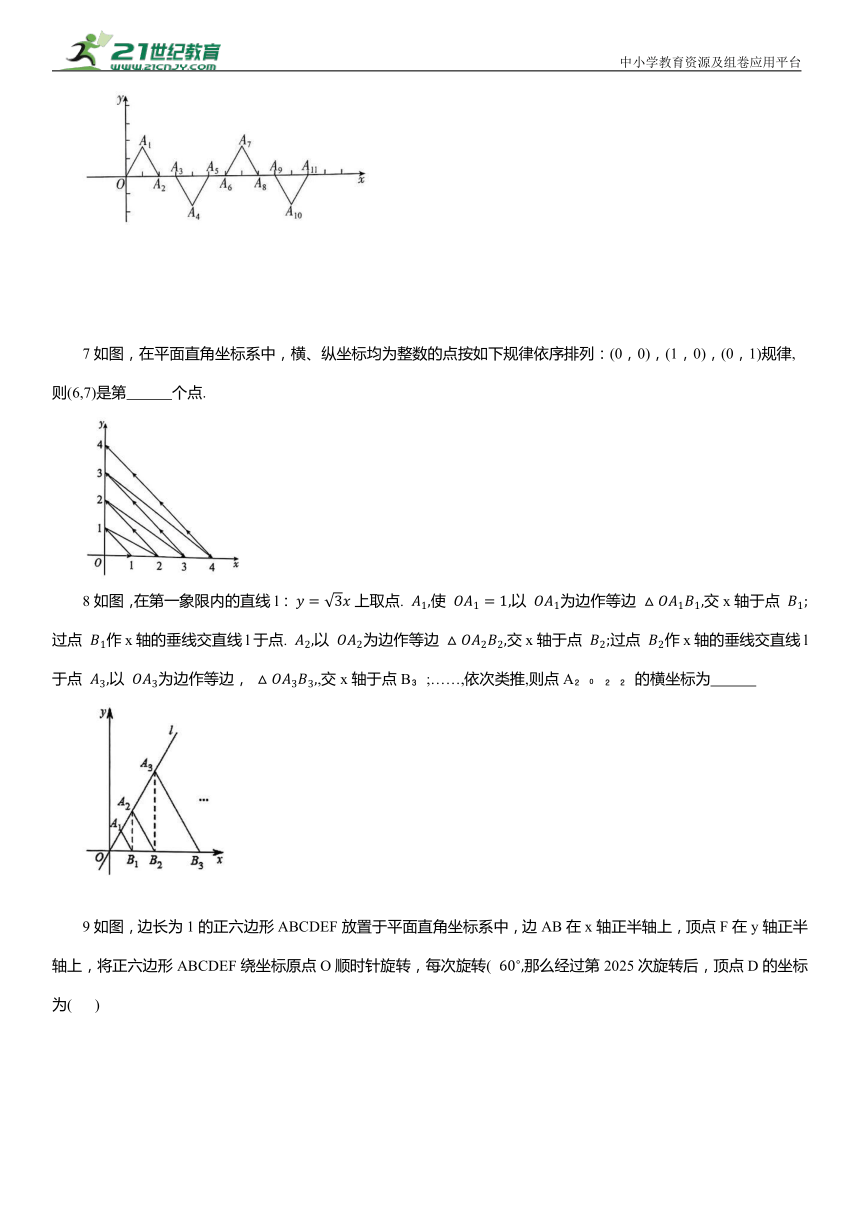
6已知, ···都是边长为2的等边三角形,按下图所示摆放.点 ··都在x轴正半轴上,且. 则点 的坐标是 .
7如图,在平面直角坐标系中,横、纵坐标均为整数的点按如下规律依序排列:(0,0),(1,0),(0,1)规律,则(6,7)是第 个点.
8如图,在第一象限内的直线l: 上取点. 使 以 为边作等边 交x轴于点 过点 作x轴的垂线交直线l于点. 以 为边作等边 交x轴于点 过点 作x轴的垂线交直线l于点 以 为边作等边, ,交x轴于点B ;……,依次类推,则点A 的横坐标为
9如图,边长为1的正六边形ABCDEF放置于平面直角坐标系中,边AB在x轴正半轴上,顶点F在y轴正半轴上,将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转( 那么经过第2025次旋转后,顶点D的坐标为( )
10如图,在平面直角坐标系中A(-1,1), B(-1,-2),C(3,-2), D(3,1) , 一只瓢虫从点A出发以2个单位长度/秒的速度沿 ·循环爬行,问第2021秒瓢虫在( )处.
A. (3,1)
11在平面直角坐标系中,等边 3如图放置,点A的坐标为(1,0),每一次将 3绕着点O逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到 ,第二次旋转后得到 依次类推,则A 的坐标为( ) .
12在直角坐标系中,点 从原点出发,沿如图所示的方向运动,到达位置的坐标依次为: ·.若到达终点, 则n的值为 .
1如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,OA=OB=4,连接AB,过点O作OA ⊥AB于点A ,过点A 作A B ⊥x轴于点B ;过点B 作B A ⊥AB于点A ,过点A 作A B ⊥z轴于点B ;过点B 作B A ⊥A B于点A ,过点A 作A B ⊥x轴于点B ;……;按照如此规律操作下去,则点A 的坐标为 .
【答案】
【解析】解:在平面直角坐标系中,点A在y轴上,点B在z轴上,OA=OB=4,
∴△OAB是等腰直角三角形,.
∵OA ⊥AB,
∴△OA B是等腰直角三角形,
同理可得:△OA B ,△A B B均为等腰直角三角形,
∴A (2,2),
根据图中所有的三角形均为等腰直角三角形.
依次可得:
由此可推出:点A 的坐标为
故答案为:
【标注】【知识点】规律探究
2如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),AA 是以点B为圆心,BA为半径的圆弧; 是以点O为圆心,OA 为半径的圆弧,A A 是以点C为圆心,CA 为半径的圆弧,ASA 是以点A为圆心,AA 为半径的圆弧,继续以点B,O,C,A为圆心按上述作法得到的曲线 ·称为正方形的“渐开线”,则点A2023的坐标是
【答案】(-2023,1)
【解析】∵A点坐标为(1,1),且A 为A点绕B点顺时针旋转90°所得,
∴A 点坐标为(2,0).
又∵A 为A 点绕O点顺时针旋转90°所得,
∴A 点坐标为(0.-2),
又∵A 为A 点绕C点顺时针旋转90°所得,
∴A 点坐标为(-3,1),
又∵A 为A 点绕A点顺时针旋转90°所得,
∴A 点坐标为(1,5),
由此可得出规律:A 为绕B、O、C、A四点作为圆心依次循环顺时针旋转90°,且半径为1、2、3、…、n,每次增加1.
∵2023÷5=505…3,
故A 为以点C为圆心,半径为2022的A 顺时针旋转90°所得
故A 点坐标为(-2023,1).
因此正确答案为:(-2023,1).
【标注】【知识点】规律探究
3在平面直角坐标系中,点A 、A 、A 、A ···在x轴的正半轴上,点B 、B 、B ···在直线 上,若点A 的坐标为(2,0),且△A B A 、△A B A 、△A B A ···均为等边三角形.则点B 的纵坐标为 .
【答案】2
【解析】
【分析】
过点A 作A M⊥x轴,交直线 于点M,过点B 作B C⊥x轴于点C,先求出∠A OM=30°,再根据等边三角形的性质、等腰三角形的判定可得. 然后解直角三角形可得B C的长,即可得点B 的纵坐标,同样的方法分别求出点B ,B ,B 的纵坐标,最后归纳类推出一般规律,由此即可得.
【详解】
解:如图,过点A 作A M⊥x轴,交直线 于点M ,过点B 作B C⊥x轴于点C
∵A (2,0),
∴OA =2,
当x=2时. 即λ
∵△A B A 是等边三角形.
即点B 的纵坐标为
同理可得:点B 的纵坐标为
点B 的纵坐标为
点B 的纵坐标为
归纳类推得:点B 的纵坐标为2° n为正整数),
则点B 的纵坐标为
故答案为:
【点睛】
本题考查了点坐标的规律探索、等边三角形的性质、正比例函数的应用、解直角三角形等知识点,正确归纳类推出一般规律是解题关键.
4如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5),(7,10),(13,17),(21,26),(31,37)……如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对: .
中小学教育资源及组卷应用平台
【答案】
【解析】每个数对的第一个数分别为3,7,13,21,31,…
即:1×2+1,2×3+1,3×4+1,4×5+1,5×6+1,….
则第n个数对的第一个数为:π
每个数对的第二个数分别为5,10,17,26,37,…,
即:
则第n个数对的第二个数为:
∴第n个数对为:
故答案为:
【标注】【知识点】数列找规律-其他数列规律
5如图,在平面直角坐标系中,直线l 与x轴交于点A ,以OA 为边作正方形A B C O,点C 在y轴上,延长C B 交直线l于点A ,以O A 为边作正方形A B O O ,点C 在y轴上,以同样的方式依次作正方形A B C C ,…,正方形A 023B 023C 023C 022,则点B 023的横坐标是 .
【答案】
【解析】当y=0时, 解得x=1,
∴点A (1,0),
∵四边形A B C O是正方形,
·点B (1,1).
∴点B 的横坐标是1,
当y=1时, 解得
∴点
∵四边形A B C C 是正方形,
后 即点B 的横坐标是
当 时 解得
.点
∵四边形A B C C 是正方形,
∴点B 的横坐标是 ……以此类推,
则点B 023的横坐标是
故答案为:
【标注】【知识点】一次函数与找规律
【知识点】坐标系基础
【知识点】正方形的性质
6.A ,A ,A ,…都在z轴正半轴上,且 则点A 的坐标是 .
【答案】(2023,
【解析】如图,过点A ,A ,A ,A ,A ,…A O 分别作x轴的垂线,
∵△A A O是边长为2的正三角形,
∴点A 的横坐标为1.
由题意可得,点A 的横坐标为2,点A 的横坐标为3,点A 的横坐标为4,…,因此点A 的横坐标为2023,
∵2023÷3=674……1,而674是偶数,
∴点A 在第一象限,
∴点A 的纵坐标为
即点A (2023, ),
故答案为:(2023, ).
【标注】【知识点】规律探究
7如图,在平面直角坐标系中,横、纵坐标均为整数的点按如下规律依序排列:(0,0),(1,0),(0,1)
规律,则(6,7)是第 个点.
【答案】99
【解析】横纵坐标和是0的有1个点,横纵坐标和是1的有2个点,横纵坐标和是2的有3个点,
横纵坐标和是3的有4个点,……,横纵坐标和是n的有(n+1)个点,
6+7=13,
∴横纵坐标和是13的有14点,分别为:(13,0)、(12,1)、(11,2)、(10,3)、(9,4)、(8,5)、(7,6)、(6,7)、(5,8)、(4,9)、(3,10)、(2,11)、(1,12)、(0,13).
∴(6,7)是第91+8=99个点.
故答案为:99.
8.如图,在第一象限内的直线l: 上取点A ,使OA =1,以OA 为边作等边△OA B ,交x轴于点B ;过点B 作z轴的垂线交直线l于点A ,以OA 为边作等边△OA B ,交z轴于点B ;过点B 作x轴的垂线交直线l于点A ,以OA 为边作等边△OA B ,交z轴于点B ;……,依次类推,
则点A 的横坐标为 .
【答案】22020
【解析】解:过点A 作A C⊥z轴于点C,点B 作B A ⊥x轴交直线l于点A ,
∵△OA B 是等边三角形,OA =1,
∴点A 的横坐标为 ,即2 ,
∵△OA B 是等边三角形, A B ⊥z轴,OB =1,
∴点A 的横坐标为1,即
是等边三角形, A B ⊥x轴,
∴点A 的横坐标为2,R
∵△OA B 是等边三角形,A B ⊥z轴,
∴点A 的横坐标为4,即2 ,
以此类推,点A 的横坐标为2 ,
.当n =2022时, 点A 的横坐标为22020
9.如图,边长为1的正六边形ABCDEF放置于平面直角坐标系中,边AB在x轴正半轴上,顶点F在y轴正半轴上,将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,那么经过第2025次旋转后,顶点D的坐标为( ).
C.(- ,
【答案】A
【解析】如图,连接AD,BD,
在正六边形ABCDEF中,AB=1,AD=2,∠ABD=90°,
在Rt△AOF中,AF=1,∠OAF=60°,
∴将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,
∴6次一个循环,
∵2025÷6=337…3,
∴经过第2025次旋转后,顶点D的坐标与第三次旋转得到的D 的坐标相同,
∵D与D 关于原点对称,
∴经过第2025次旋转后,顶点D的坐标
故选:A.
10.如图,在平面直角坐标系中A(-1,1),B(-1,-2),C(3,-2),D(3,1),一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A→ 循环爬行,问第2021秒瓢虫在( )处.
A.(3,1) B. (-1,-2) C.(1,-2) D.(3,-2)
【答案】A
【解析】∵A(-1,1),B(-1,-2),C(3,-2),D(3,1),
∴AB=CD=3,AD=BC=4,
∴C BABOD=2(AB+AD)=14.
∵2021=288×(14÷2)+1.5+2÷1.5,
∴第2021秒瓢虫在点D处,
∴此时点瓢虫的坐标为(3,1).
故选: A.
11.在平面直角坐标系中,等边△AOB如图放置,点A的坐标为(1,0),每一次将△AOB绕着点O逆时针方向旋转60°,同时每边扩大为原来的2倍,第一次旋转后得到△A OB ,第二次旋转后得到△A OB ,…,依次类推,则A 的坐标为( )
【答案】C
【解析】∵点A的坐标为(1,0),
∴OA=1.
∴每6次一个循环,OAc 一定落在x轴正半轴上.
∵2021÷6=336……5,
∴OA 落在第四象限,与x轴正半轴的夹角为60°.
过A 作A H⊥z轴于点H,
∴∠A OH=60°,∠OHA =90°.
∴点A 的坐标为(
故选C.
12.在直角坐标系中,点A 从原点出发,沿如图所示的方向运动,到达位置的坐标依次为:A (1,0),A (1,1),A (-1,1), As(-1,-1), Ac(2,-1), Ar(2,2),….若到达终点, A (606,-505),则n的值为 .
【答案】2022
【解析】∵到达终点A (506,-505),且此点在第四象限,
根据题意和图的坐标可知:A (2,-1),
A (3,-2),A (4,-3),…,
∵6=2+4×(2-1),
10=2+4×(3-1),
14=2+4×(4-1),
…
n=2+4×(506-1)=2022.
故答案为:2022.
模型原理
这类问题往往将变换、函数、相似等知识结合在一起,常涉及到转化、整体和数形结合等方法,具有很强的综合性,解决这类问题的关键是要注意观察和分析图形.
1.函数与平移
(1)一次函数y= kx+b(k≠0)的平移
左加右减,上加下减,一次函数解析式为y=k(x±m)+b±n
(2)反比例函数 的平移
左加右减,上加下减,反比例函数解析式为
(3)二次函数 的平移
左加右减,上加下减,二次函数解析式为
2.函数与对称
(1)一次函数y = kx+b(k≠0)的对称
①关于x轴对称后的解析式为y=-kx-b②关于y轴对称后的解析式为y=-kx+b
③关于原点中心对称后的解析式为y = kx-b
(2)反比例函数 的对称
①关于x轴对称后的解析式为 ②关于y轴对称后的解析式为
③关于原点对称后的解析式为
(3)二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达
①关于x轴对称
关于x轴对称后,得到的解析式是
②关于y轴对称
关于y轴对称后,得到的解析式是
③关于原点对称
:关于原点中心对称后,得到的解析式是
真题精炼
1如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,( 连接AB,过点O作 于点 过点 作 轴于点. 过点 作 于点 过点 作 轴于点 过点 作 于点 过点 作 轴于点 按照如此规律操作下去,则点 的坐标为 .
2如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1), 是以点B为圆心,BA为半径的圆弧; 是以点O为圆心, 为半径的圆弧, 是以点C为圆心, 为半径的圆弧, 是以点A为圆心 , 为半径的圆弧,继续以点B,O,C,A为圆心按上述作法得到的曲线. ·称为正方形的“渐开线” ,则点 的坐标是
3在平面直角坐标系中,点. ·在x轴的正半轴上,点 ·在直线 上,若点 的坐标为(2,0) , 且4 ·均为等边三角形.则点. 的纵坐标为 .
4如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对: (3,5),(7,10) , (13,17), (21,26),(31,37)……如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数
对:
5如图,在平面直角坐标系中,直线l: 与x轴交于点. 以 为边作正方形 点 在y轴上,延长 交直线l于点. 以 为边作正方形. 点 在y轴上,以同样的方式依次作正方形 正方形 则点 的横坐标是
6已知, ···都是边长为2的等边三角形,按下图所示摆放.点 ··都在x轴正半轴上,且. 则点 的坐标是 .
7如图,在平面直角坐标系中,横、纵坐标均为整数的点按如下规律依序排列:(0,0),(1,0),(0,1)规律,则(6,7)是第 个点.
8如图,在第一象限内的直线l: 上取点. 使 以 为边作等边 交x轴于点 过点 作x轴的垂线交直线l于点. 以 为边作等边 交x轴于点 过点 作x轴的垂线交直线l于点 以 为边作等边, ,交x轴于点B ;……,依次类推,则点A 的横坐标为
9如图,边长为1的正六边形ABCDEF放置于平面直角坐标系中,边AB在x轴正半轴上,顶点F在y轴正半轴上,将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转( 那么经过第2025次旋转后,顶点D的坐标为( )
10如图,在平面直角坐标系中A(-1,1), B(-1,-2),C(3,-2), D(3,1) , 一只瓢虫从点A出发以2个单位长度/秒的速度沿 ·循环爬行,问第2021秒瓢虫在( )处.
A. (3,1)
11在平面直角坐标系中,等边 3如图放置,点A的坐标为(1,0),每一次将 3绕着点O逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到 ,第二次旋转后得到 依次类推,则A 的坐标为( ) .
12在直角坐标系中,点 从原点出发,沿如图所示的方向运动,到达位置的坐标依次为: ·.若到达终点, 则n的值为 .
1如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,OA=OB=4,连接AB,过点O作OA ⊥AB于点A ,过点A 作A B ⊥x轴于点B ;过点B 作B A ⊥AB于点A ,过点A 作A B ⊥z轴于点B ;过点B 作B A ⊥A B于点A ,过点A 作A B ⊥x轴于点B ;……;按照如此规律操作下去,则点A 的坐标为 .
【答案】
【解析】解:在平面直角坐标系中,点A在y轴上,点B在z轴上,OA=OB=4,
∴△OAB是等腰直角三角形,.
∵OA ⊥AB,
∴△OA B是等腰直角三角形,
同理可得:△OA B ,△A B B均为等腰直角三角形,
∴A (2,2),
根据图中所有的三角形均为等腰直角三角形.
依次可得:
由此可推出:点A 的坐标为
故答案为:
【标注】【知识点】规律探究
2如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),AA 是以点B为圆心,BA为半径的圆弧; 是以点O为圆心,OA 为半径的圆弧,A A 是以点C为圆心,CA 为半径的圆弧,ASA 是以点A为圆心,AA 为半径的圆弧,继续以点B,O,C,A为圆心按上述作法得到的曲线 ·称为正方形的“渐开线”,则点A2023的坐标是
【答案】(-2023,1)
【解析】∵A点坐标为(1,1),且A 为A点绕B点顺时针旋转90°所得,
∴A 点坐标为(2,0).
又∵A 为A 点绕O点顺时针旋转90°所得,
∴A 点坐标为(0.-2),
又∵A 为A 点绕C点顺时针旋转90°所得,
∴A 点坐标为(-3,1),
又∵A 为A 点绕A点顺时针旋转90°所得,
∴A 点坐标为(1,5),
由此可得出规律:A 为绕B、O、C、A四点作为圆心依次循环顺时针旋转90°,且半径为1、2、3、…、n,每次增加1.
∵2023÷5=505…3,
故A 为以点C为圆心,半径为2022的A 顺时针旋转90°所得
故A 点坐标为(-2023,1).
因此正确答案为:(-2023,1).
【标注】【知识点】规律探究
3在平面直角坐标系中,点A 、A 、A 、A ···在x轴的正半轴上,点B 、B 、B ···在直线 上,若点A 的坐标为(2,0),且△A B A 、△A B A 、△A B A ···均为等边三角形.则点B 的纵坐标为 .
【答案】2
【解析】
【分析】
过点A 作A M⊥x轴,交直线 于点M,过点B 作B C⊥x轴于点C,先求出∠A OM=30°,再根据等边三角形的性质、等腰三角形的判定可得. 然后解直角三角形可得B C的长,即可得点B 的纵坐标,同样的方法分别求出点B ,B ,B 的纵坐标,最后归纳类推出一般规律,由此即可得.
【详解】
解:如图,过点A 作A M⊥x轴,交直线 于点M ,过点B 作B C⊥x轴于点C
∵A (2,0),
∴OA =2,
当x=2时. 即λ
∵△A B A 是等边三角形.
即点B 的纵坐标为
同理可得:点B 的纵坐标为
点B 的纵坐标为
点B 的纵坐标为
归纳类推得:点B 的纵坐标为2° n为正整数),
则点B 的纵坐标为
故答案为:
【点睛】
本题考查了点坐标的规律探索、等边三角形的性质、正比例函数的应用、解直角三角形等知识点,正确归纳类推出一般规律是解题关键.
4如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5),(7,10),(13,17),(21,26),(31,37)……如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对: .
中小学教育资源及组卷应用平台
【答案】
【解析】每个数对的第一个数分别为3,7,13,21,31,…
即:1×2+1,2×3+1,3×4+1,4×5+1,5×6+1,….
则第n个数对的第一个数为:π
每个数对的第二个数分别为5,10,17,26,37,…,
即:
则第n个数对的第二个数为:
∴第n个数对为:
故答案为:
【标注】【知识点】数列找规律-其他数列规律
5如图,在平面直角坐标系中,直线l 与x轴交于点A ,以OA 为边作正方形A B C O,点C 在y轴上,延长C B 交直线l于点A ,以O A 为边作正方形A B O O ,点C 在y轴上,以同样的方式依次作正方形A B C C ,…,正方形A 023B 023C 023C 022,则点B 023的横坐标是 .
【答案】
【解析】当y=0时, 解得x=1,
∴点A (1,0),
∵四边形A B C O是正方形,
·点B (1,1).
∴点B 的横坐标是1,
当y=1时, 解得
∴点
∵四边形A B C C 是正方形,
后 即点B 的横坐标是
当 时 解得
.点
∵四边形A B C C 是正方形,
∴点B 的横坐标是 ……以此类推,
则点B 023的横坐标是
故答案为:
【标注】【知识点】一次函数与找规律
【知识点】坐标系基础
【知识点】正方形的性质
6.A ,A ,A ,…都在z轴正半轴上,且 则点A 的坐标是 .
【答案】(2023,
【解析】如图,过点A ,A ,A ,A ,A ,…A O 分别作x轴的垂线,
∵△A A O是边长为2的正三角形,
∴点A 的横坐标为1.
由题意可得,点A 的横坐标为2,点A 的横坐标为3,点A 的横坐标为4,…,因此点A 的横坐标为2023,
∵2023÷3=674……1,而674是偶数,
∴点A 在第一象限,
∴点A 的纵坐标为
即点A (2023, ),
故答案为:(2023, ).
【标注】【知识点】规律探究
7如图,在平面直角坐标系中,横、纵坐标均为整数的点按如下规律依序排列:(0,0),(1,0),(0,1)
规律,则(6,7)是第 个点.
【答案】99
【解析】横纵坐标和是0的有1个点,横纵坐标和是1的有2个点,横纵坐标和是2的有3个点,
横纵坐标和是3的有4个点,……,横纵坐标和是n的有(n+1)个点,
6+7=13,
∴横纵坐标和是13的有14点,分别为:(13,0)、(12,1)、(11,2)、(10,3)、(9,4)、(8,5)、(7,6)、(6,7)、(5,8)、(4,9)、(3,10)、(2,11)、(1,12)、(0,13).
∴(6,7)是第91+8=99个点.
故答案为:99.
8.如图,在第一象限内的直线l: 上取点A ,使OA =1,以OA 为边作等边△OA B ,交x轴于点B ;过点B 作z轴的垂线交直线l于点A ,以OA 为边作等边△OA B ,交z轴于点B ;过点B 作x轴的垂线交直线l于点A ,以OA 为边作等边△OA B ,交z轴于点B ;……,依次类推,
则点A 的横坐标为 .
【答案】22020
【解析】解:过点A 作A C⊥z轴于点C,点B 作B A ⊥x轴交直线l于点A ,
∵△OA B 是等边三角形,OA =1,
∴点A 的横坐标为 ,即2 ,
∵△OA B 是等边三角形, A B ⊥z轴,OB =1,
∴点A 的横坐标为1,即
是等边三角形, A B ⊥x轴,
∴点A 的横坐标为2,R
∵△OA B 是等边三角形,A B ⊥z轴,
∴点A 的横坐标为4,即2 ,
以此类推,点A 的横坐标为2 ,
.当n =2022时, 点A 的横坐标为22020
9.如图,边长为1的正六边形ABCDEF放置于平面直角坐标系中,边AB在x轴正半轴上,顶点F在y轴正半轴上,将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,那么经过第2025次旋转后,顶点D的坐标为( ).
C.(- ,
【答案】A
【解析】如图,连接AD,BD,
在正六边形ABCDEF中,AB=1,AD=2,∠ABD=90°,
在Rt△AOF中,AF=1,∠OAF=60°,
∴将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,
∴6次一个循环,
∵2025÷6=337…3,
∴经过第2025次旋转后,顶点D的坐标与第三次旋转得到的D 的坐标相同,
∵D与D 关于原点对称,
∴经过第2025次旋转后,顶点D的坐标
故选:A.
10.如图,在平面直角坐标系中A(-1,1),B(-1,-2),C(3,-2),D(3,1),一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A→ 循环爬行,问第2021秒瓢虫在( )处.
A.(3,1) B. (-1,-2) C.(1,-2) D.(3,-2)
【答案】A
【解析】∵A(-1,1),B(-1,-2),C(3,-2),D(3,1),
∴AB=CD=3,AD=BC=4,
∴C BABOD=2(AB+AD)=14.
∵2021=288×(14÷2)+1.5+2÷1.5,
∴第2021秒瓢虫在点D处,
∴此时点瓢虫的坐标为(3,1).
故选: A.
11.在平面直角坐标系中,等边△AOB如图放置,点A的坐标为(1,0),每一次将△AOB绕着点O逆时针方向旋转60°,同时每边扩大为原来的2倍,第一次旋转后得到△A OB ,第二次旋转后得到△A OB ,…,依次类推,则A 的坐标为( )
【答案】C
【解析】∵点A的坐标为(1,0),
∴OA=1.
∴每6次一个循环,OAc 一定落在x轴正半轴上.
∵2021÷6=336……5,
∴OA 落在第四象限,与x轴正半轴的夹角为60°.
过A 作A H⊥z轴于点H,
∴∠A OH=60°,∠OHA =90°.
∴点A 的坐标为(
故选C.
12.在直角坐标系中,点A 从原点出发,沿如图所示的方向运动,到达位置的坐标依次为:A (1,0),A (1,1),A (-1,1), As(-1,-1), Ac(2,-1), Ar(2,2),….若到达终点, A (606,-505),则n的值为 .
【答案】2022
【解析】∵到达终点A (506,-505),且此点在第四象限,
根据题意和图的坐标可知:A (2,-1),
A (3,-2),A (4,-3),…,
∵6=2+4×(2-1),
10=2+4×(3-1),
14=2+4×(4-1),
…
n=2+4×(506-1)=2022.
故答案为:2022.
同课章节目录
