2025年中考二轮复习数学对标考点:概率(含解析)
文档属性
| 名称 | 2025年中考二轮复习数学对标考点:概率(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 193.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 22:41:01 | ||
图片预览




文档简介
2025年中考数学对标考点:概率
一、选择题
1.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数相差的概率是( )
A. B. C. D.
2.如果一个三位数中任意两个相邻数字之差的绝对值不超过,则称该三位数为“平稳数”用,,这三个数字随机组成一个无重复数字的三位数,恰好是“平稳数”的概率为( )
A. B. C. D.
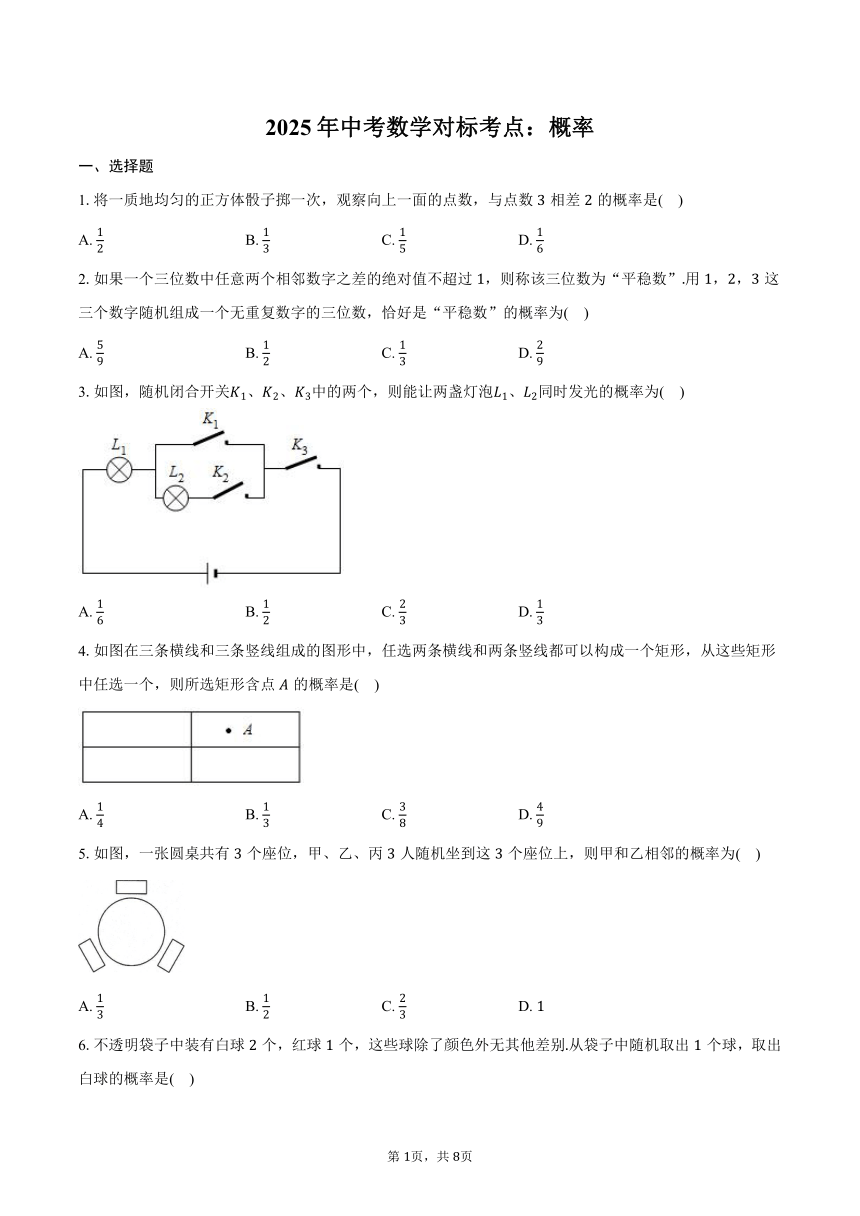
3.如图,随机闭合开关、、中的两个,则能让两盏灯泡、同时发光的概率为( )
A. B. C. D.
4.如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以构成一个矩形,从这些矩形中任选一个,则所选矩形含点的概率是( )
A. B. C. D.
5.如图,一张圆桌共有个座位,甲、乙、丙人随机坐到这个座位上,则甲和乙相邻的概率为( )
A. B. C. D.
6.不透明袋子中装有白球个,红球个,这些球除了颜色外无其他差别从袋子中随机取出个球,取出白球的概率是( )
A. B. C. D.
7.有一则笑话:妈妈正在给一对双胞胎洗澡,先洗哥哥,再洗弟弟,刚把两人洗完,就听到两个小家伙在床上笑,“你们笑什么?”妈妈问“妈妈”老大回答,“您给弟弟洗了两回,可是还没给我洗呢”此事件发生的概率为( )
A. B. C. D.
8.下列说法中,正确的是( )
A. 随机事件发生的概率为
B. 概率很小的事件不可能发生
C. 投掷一枚质地均匀的硬币次,正面朝上的次数一定为次
D. 不可能事件发生的概率为
9.下列事件中是必然事件的是( )
A. 抛掷一枚质地均匀的硬币,正面朝上
B. 随意翻到一本书的某页,这一页的页码是偶数
C. 打开电视机,正在播放广告
D. 从两个班级中任选三名学生,至少有两名学生来自同一个班级
二、填空题
10.不透明袋子中装有个球,其中有个红球、个绿球和个黑球,这些球除颜色外无其他差别,从袋子中随机取出个球,则它是绿球的概率是
11.汉代数学家赵爽在注解周髀算经时给出的“赵爽弦图”是我国古代数学的瑰宝如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为 .
12.不透明的袋中装有大小质地完全相同的个球,其中个黄球、个白球和个红球.从袋中任取个球,恰为个红球的概率是 .
13.不透明袋子中装有个球,其中有个红球、个绿球,这些球除颜色外无其他差别从袋子中随机取出个球,则它是红球的概率是______.
14.如图,转盘中个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,指针指向奇数的概率是______.
15.一个不透明的口袋中有三个小球,上面分别标有字母,,,除所标字母不同外,其它完全相同,从中随机摸出一个小球,记下字母后放回并搅匀,再随机摸出一个小球,用画树状图或列表的方法,求该同学两次摸出的小球所标字母相同的概率______.
答案和解析
1.【答案】
【解析】【分析】
题考查了概率公的应用.注用到的知识为概率所况数与总情况之比.一枚质地均匀的正方体骰的六面上分刻有到的数,掷一次这枚子向上的一面点数与点数相的种情况,直接利概率式求解即求得答案.
【解答】
解:一枚地均匀正方体子的六个面上别刻的点,掷次枚骰子,向上的一面的点数数相差的有种情况,
掷一次这骰子向上的一面的点数点相差概率:.故选B.
2.【答案】
【解析】此题考查用列举法求概率,弄清题中的数据是解本题的关键.选.
3.【答案】
【解析】【分析】
此题考查用列举法求概率,弄清题中的数据是解本题的关键.
找出随机闭合开关、、中的所有情况数以及能让两盏灯泡、同时发光的情况数,即可求出所求概率.
【解答】
解:画树状图,如图所示:
随机闭合开关、、中的两个有六种情况,
其中能让两盏灯泡、同时发光的有两种情况:闭合,闭合,
则能让两盏灯泡、同时发光的概率为.
故选:.
4.【答案】
【解析】将从左到右的三条竖线分别记作、、,将从上到下的三条横线分别记作、、,利用表格列出任选两条横线和两条竖线所围成的矩形的所有等可能情况,再从中找到所选矩形含点的的情况,继而利用概率公式可得答案.
本题主要考查列表法与树状图法,解题的关键是利用表格列出任选两条横线和两条竖线所围成的矩形的所有等可能情况,并从所有结果中找到符合条件的结果数.
【解答】
解:将从左到右的三条竖线分别记作、、,将从上到下的三条横线分别记作、、,列表如下,
、 、 、
、 、 、
、 、 、
由表可知共有种等可能结果,其中所选矩形含点的有、;、;、;、这种结果,
所选矩形含点的概率为,
故选:.
5.【答案】
【解析】此题考查用列举法求概率,弄清题中的数据是解本题的关键.选.
6.【答案】
【解析】解:袋子中装有个球,其中有个红球、个白球,
从袋子中随机摸出一个球,摸到白球的概率为:.
故选:.
据概率的求法,找准两点:全部情况的总数;符合条件的情况数目;二者的比值就是其发生的概率.
本题主要考查了概率的求法与运用,一般方法:如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种可能,那么事件的概率.
7.【答案】
【解析】【分析】本题考查了概率的意义,正确理解概率的含义是解决本题的关键.
根据概率是指某件事发生的可能性为多少解答即可.
【解答】
解:此事件发生的概率,
故选:.
8.【答案】
【解析】解:、随机事件发生的概率为随机,故A不符合题意;
B、概率很小的事件有可能发生,故B不符合题意;
C、投掷一枚质地均匀的硬币次,正面朝上的次数不一定为次,故C不符合题意;
D、不可能事件发生的概率为,故D符合题意;
故选:.
概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,机会大也不一定发生,机会小也有可能发生.
本题考查了概率的意义,概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,机会大也不一定发生,机会小也有可能发生.
9.【答案】
【解析】此题考查用列举法求概率,弄清题中的数据是解本题的关键.选.
10.【答案】
【解析】【分析】此题主要考查了概率的求法,如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率.
根据概率的求法,找准两点:全部情况的总数;符合条件的情况数目;二者的比值就是其发生的概率.
【解答】解:取到绿球.
11.【答案】
【解析】【分析】此题主要考查了几何概率问题,用到的知识点为:概率相应的面积与总面积之比针尖落在阴影区域的概率就是四个直角三角形的面积之和与大正方形面积的比.
【解答】解:设直角三角形的两直角边长分别是,,
则题图中大正方形边长是,小正方形边长为,
,,则,
针尖落在阴影区域.
12.【答案】
【解析】解:
由图可知,共有种可能的结果,其中个红球的结果出现次,
,
故答案为:.
先画出树状图,再根据树状图求概率.
本题考查了概率的求解,画出正确的树状图是解题的关键.
13.【答案】
【解析】解:袋子中共有个球,其中红球有个,
从袋子中随机取出个球,它是红球的概率是,
故答案为:.
根据概率的求法,找准两点:全部情况的总数;符合条件的情况数目;二者的比值就是其发生的概率.
本题考查概率的求法:如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率.
14.【答案】
【解析】【分析】
此题主要考查了概率公式,熟练掌握概率的定义及公式是解题的关键,让奇数的个数除以数的总个数即可得到答案.
【解答】指针指向转盘中个扇形的可能性相同,其中有个扇形里的数字是奇数,所以指针指向奇数.
15.【答案】解:列表得:
由列表可知可能出现的结果共种,其中两次摸出的小球所标字母相同的情况数有种,
所以该同学两次摸出的小球所标字母相同的概率.
【解析】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率所求情况数与总情况数之比.
列表得出所有等可能的情况数,再找出两次摸出的小球所标字母相同的情况数,即可求出其概率.
第2页,共8页
一、选择题
1.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数相差的概率是( )
A. B. C. D.
2.如果一个三位数中任意两个相邻数字之差的绝对值不超过,则称该三位数为“平稳数”用,,这三个数字随机组成一个无重复数字的三位数,恰好是“平稳数”的概率为( )
A. B. C. D.
3.如图,随机闭合开关、、中的两个,则能让两盏灯泡、同时发光的概率为( )
A. B. C. D.
4.如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以构成一个矩形,从这些矩形中任选一个,则所选矩形含点的概率是( )
A. B. C. D.
5.如图,一张圆桌共有个座位,甲、乙、丙人随机坐到这个座位上,则甲和乙相邻的概率为( )
A. B. C. D.
6.不透明袋子中装有白球个,红球个,这些球除了颜色外无其他差别从袋子中随机取出个球,取出白球的概率是( )
A. B. C. D.
7.有一则笑话:妈妈正在给一对双胞胎洗澡,先洗哥哥,再洗弟弟,刚把两人洗完,就听到两个小家伙在床上笑,“你们笑什么?”妈妈问“妈妈”老大回答,“您给弟弟洗了两回,可是还没给我洗呢”此事件发生的概率为( )
A. B. C. D.
8.下列说法中,正确的是( )
A. 随机事件发生的概率为
B. 概率很小的事件不可能发生
C. 投掷一枚质地均匀的硬币次,正面朝上的次数一定为次
D. 不可能事件发生的概率为
9.下列事件中是必然事件的是( )
A. 抛掷一枚质地均匀的硬币,正面朝上
B. 随意翻到一本书的某页,这一页的页码是偶数
C. 打开电视机,正在播放广告
D. 从两个班级中任选三名学生,至少有两名学生来自同一个班级
二、填空题
10.不透明袋子中装有个球,其中有个红球、个绿球和个黑球,这些球除颜色外无其他差别,从袋子中随机取出个球,则它是绿球的概率是
11.汉代数学家赵爽在注解周髀算经时给出的“赵爽弦图”是我国古代数学的瑰宝如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为 .
12.不透明的袋中装有大小质地完全相同的个球,其中个黄球、个白球和个红球.从袋中任取个球,恰为个红球的概率是 .
13.不透明袋子中装有个球,其中有个红球、个绿球,这些球除颜色外无其他差别从袋子中随机取出个球,则它是红球的概率是______.
14.如图,转盘中个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,指针指向奇数的概率是______.
15.一个不透明的口袋中有三个小球,上面分别标有字母,,,除所标字母不同外,其它完全相同,从中随机摸出一个小球,记下字母后放回并搅匀,再随机摸出一个小球,用画树状图或列表的方法,求该同学两次摸出的小球所标字母相同的概率______.
答案和解析
1.【答案】
【解析】【分析】
题考查了概率公的应用.注用到的知识为概率所况数与总情况之比.一枚质地均匀的正方体骰的六面上分刻有到的数,掷一次这枚子向上的一面点数与点数相的种情况,直接利概率式求解即求得答案.
【解答】
解:一枚地均匀正方体子的六个面上别刻的点,掷次枚骰子,向上的一面的点数数相差的有种情况,
掷一次这骰子向上的一面的点数点相差概率:.故选B.
2.【答案】
【解析】此题考查用列举法求概率,弄清题中的数据是解本题的关键.选.
3.【答案】
【解析】【分析】
此题考查用列举法求概率,弄清题中的数据是解本题的关键.
找出随机闭合开关、、中的所有情况数以及能让两盏灯泡、同时发光的情况数,即可求出所求概率.
【解答】
解:画树状图,如图所示:
随机闭合开关、、中的两个有六种情况,
其中能让两盏灯泡、同时发光的有两种情况:闭合,闭合,
则能让两盏灯泡、同时发光的概率为.
故选:.
4.【答案】
【解析】将从左到右的三条竖线分别记作、、,将从上到下的三条横线分别记作、、,利用表格列出任选两条横线和两条竖线所围成的矩形的所有等可能情况,再从中找到所选矩形含点的的情况,继而利用概率公式可得答案.
本题主要考查列表法与树状图法,解题的关键是利用表格列出任选两条横线和两条竖线所围成的矩形的所有等可能情况,并从所有结果中找到符合条件的结果数.
【解答】
解:将从左到右的三条竖线分别记作、、,将从上到下的三条横线分别记作、、,列表如下,
、 、 、
、 、 、
、 、 、
由表可知共有种等可能结果,其中所选矩形含点的有、;、;、;、这种结果,
所选矩形含点的概率为,
故选:.
5.【答案】
【解析】此题考查用列举法求概率,弄清题中的数据是解本题的关键.选.
6.【答案】
【解析】解:袋子中装有个球,其中有个红球、个白球,
从袋子中随机摸出一个球,摸到白球的概率为:.
故选:.
据概率的求法,找准两点:全部情况的总数;符合条件的情况数目;二者的比值就是其发生的概率.
本题主要考查了概率的求法与运用,一般方法:如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种可能,那么事件的概率.
7.【答案】
【解析】【分析】本题考查了概率的意义,正确理解概率的含义是解决本题的关键.
根据概率是指某件事发生的可能性为多少解答即可.
【解答】
解:此事件发生的概率,
故选:.
8.【答案】
【解析】解:、随机事件发生的概率为随机,故A不符合题意;
B、概率很小的事件有可能发生,故B不符合题意;
C、投掷一枚质地均匀的硬币次,正面朝上的次数不一定为次,故C不符合题意;
D、不可能事件发生的概率为,故D符合题意;
故选:.
概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,机会大也不一定发生,机会小也有可能发生.
本题考查了概率的意义,概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,机会大也不一定发生,机会小也有可能发生.
9.【答案】
【解析】此题考查用列举法求概率,弄清题中的数据是解本题的关键.选.
10.【答案】
【解析】【分析】此题主要考查了概率的求法,如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率.
根据概率的求法,找准两点:全部情况的总数;符合条件的情况数目;二者的比值就是其发生的概率.
【解答】解:取到绿球.
11.【答案】
【解析】【分析】此题主要考查了几何概率问题,用到的知识点为:概率相应的面积与总面积之比针尖落在阴影区域的概率就是四个直角三角形的面积之和与大正方形面积的比.
【解答】解:设直角三角形的两直角边长分别是,,
则题图中大正方形边长是,小正方形边长为,
,,则,
针尖落在阴影区域.
12.【答案】
【解析】解:
由图可知,共有种可能的结果,其中个红球的结果出现次,
,
故答案为:.
先画出树状图,再根据树状图求概率.
本题考查了概率的求解,画出正确的树状图是解题的关键.
13.【答案】
【解析】解:袋子中共有个球,其中红球有个,
从袋子中随机取出个球,它是红球的概率是,
故答案为:.
根据概率的求法,找准两点:全部情况的总数;符合条件的情况数目;二者的比值就是其发生的概率.
本题考查概率的求法:如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率.
14.【答案】
【解析】【分析】
此题主要考查了概率公式,熟练掌握概率的定义及公式是解题的关键,让奇数的个数除以数的总个数即可得到答案.
【解答】指针指向转盘中个扇形的可能性相同,其中有个扇形里的数字是奇数,所以指针指向奇数.
15.【答案】解:列表得:
由列表可知可能出现的结果共种,其中两次摸出的小球所标字母相同的情况数有种,
所以该同学两次摸出的小球所标字母相同的概率.
【解析】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率所求情况数与总情况数之比.
列表得出所有等可能的情况数,再找出两次摸出的小球所标字母相同的情况数,即可求出其概率.
第2页,共8页
同课章节目录
