2025年中考二轮复习数学对标考点:解直角三角形的应用(含解析)
文档属性
| 名称 | 2025年中考二轮复习数学对标考点:解直角三角形的应用(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 902.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 22:41:46 | ||
图片预览




文档简介
2025年中考数学对标考点:解直角三角形的应用
1.如图,山顶上有一个信号塔,已知信号塔高米,在山脚下点处测得塔底的仰角,塔顶的仰角,求山高点,,在同一条竖直线上.
参考数据:,,
2.如图,长沙九龙仓国际金融中心主楼高达,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼高,为了测量高楼上发射塔的高度,在楼底端点测得的仰角为,,在顶端点测得的仰角为,求发射塔的高度.
3.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树的高度,他在点处测得大树顶端的仰角为,再从点出发沿斜坡走米到达斜坡上点,在点处测得树顶端的仰角为,若斜坡的坡比为:点、、在同一水平线上.
求王刚同学从点到点的过程中上升的高度;
求大树的高度结果保留根号.
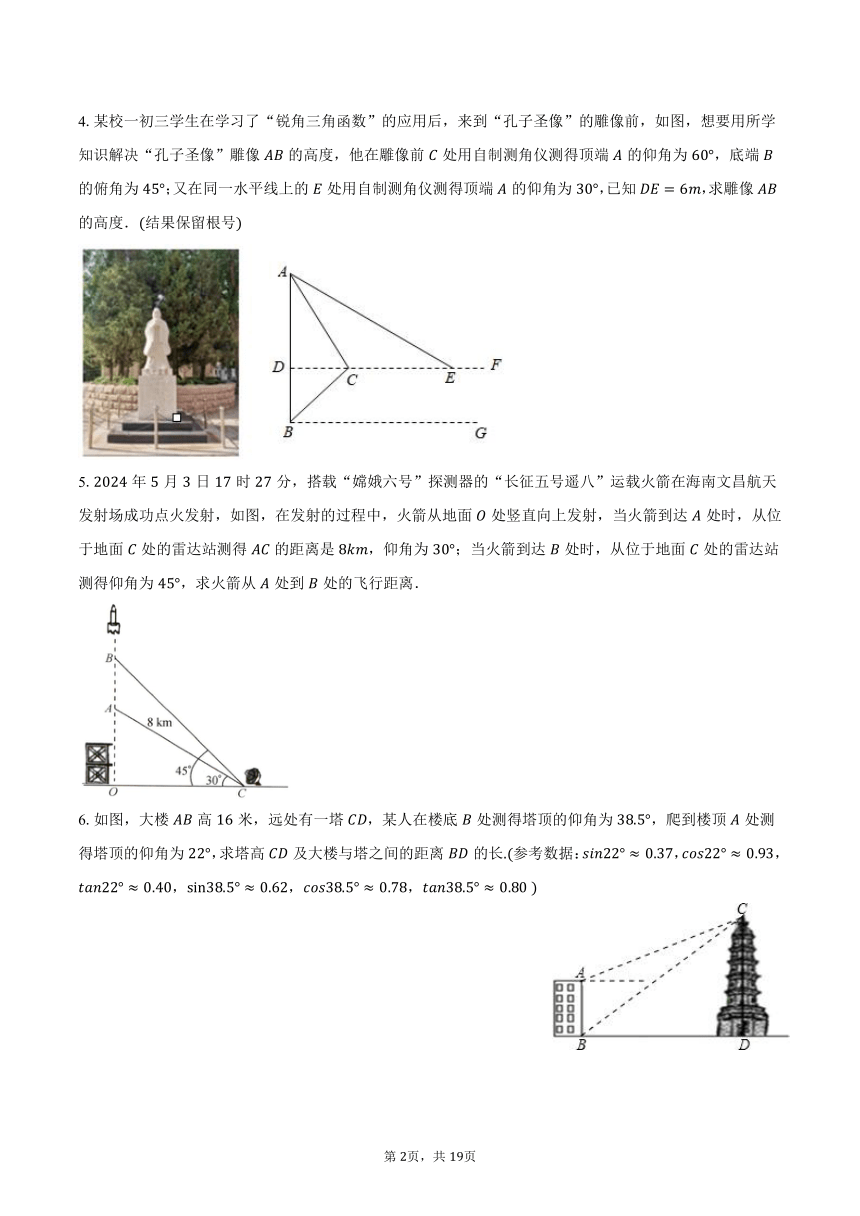
4.某校一初三学生在学习了“锐角三角函数”的应用后,来到“孔子圣像”的雕像前,如图,想要用所学知识解决“孔子圣像”雕像的高度,他在雕像前处用自制测角仪测得顶端的仰角为,底端的俯角为;又在同一水平线上的处用自制测角仪测得顶端的仰角为,已知,求雕像的高度.结果保留根号
5.年月日时分,搭载“嫦娥六号”探测器的“长征五号遥八”运载火箭在海南文昌航天发射场成功点火发射,如图,在发射的过程中,火箭从地面处竖直向上发射,当火箭到达处时,从位于地面处的雷达站测得的距离是,仰角为;当火箭到达处时,从位于地面处的雷达站测得仰角为,求火箭从处到处的飞行距离.
6.如图,大楼高米,远处有一塔,某人在楼底处测得塔顶的仰角为,爬到楼顶处测得塔顶的仰角为,求塔高及大楼与塔之间的距离的长参考数据:,,,,,
7.某游乐场一转角滑梯如图所示,滑梯立柱、均垂直于地面,点在线段上,在点测得点的仰角为,点的俯角也为,测得、间距离为米,立柱高米.求立柱的高结果保留根号
8.如图,,两点被池塘隔开,在外选一点,连接,测得,,根据测得的数据,求的长结果取整数.参考数据:,,.
9.科技社团选择学校游泳池进行一次光的折射实验,如图,光线自点处发出,经水面点折射到池底点处.已知与水平线的夹角,点到水面的距离,点处水深为,到池壁的水平距离点,,在同一条竖直线上,所有点都在同一竖直平面内。记入射角为,折射角为,求的值精确到.参考数据:,,.
10.如图,一艘海轮位于灯塔的北偏东方向,距离灯塔海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,求和的长结果取整数.
参考数据:,,,取.
11为了测量竖直旗杆的高度,某综合实践小组在地面处竖直放置标杆,并在地面上水平放置一个平面镜,使得,,在同一水平线上,如图所示该小组在标杆的处通过平面镜恰好观测到旗杆顶此时在处测得旗杆顶的仰角为,平面镜的俯角为,米,问旗杆的高度约为多少米结果保留整数参考数据:,
12.某校初三课外活动小组,在测量树高的一次活动中.如图所示,测得树底部中心到斜坡底的水平距离为,在阳光下某一时刻测得米的标杆影长为,树影落在斜坡上的部分,已知斜坡的坡比:,求树高结果保留整数,参考数据:.
13. “高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上,两点间的距离为低杠上点到直线的距离的长为,高杠上点到直线的距离的长为,已知低杠的支架与直线的夹角为.,高杠的支架与直线的夹角为.求高、低杠间的水平距离的长结果精确到参考数据:.,.,.,.,.,.
14.本小题分
如图,,是同一水平线上的两点,无人机从点竖直上升到点时,测得到点的距离为,点的俯角为,无人机继续竖直上升到点,测得点的俯角为求无人机从点到点的上升高度精确到.
参考数据:,,,,,.
15.筒车是我国古代发明的一种水利灌溉工具.如图,明朝科学家徐光启在农政全书中用图画描绘了筒车的工作原理.如图,筒车盛水桶的运行轨迹是以轴心为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦长为米,,若点为运行轨道的最高点的连线垂直于,求点到弦所在直线的距离.参考数据:,,
16.学生到工厂劳动实践,学习制作机械零件零件的截面如图阴影部分所示,已知四边形为矩形,点、分别在、上,,,,求零件的截面面积参考数据:,.
17.由我国完全自主设计、自主建造的首艘国产航母于年月成功完成第一次海上试验任务如图,航母由西向东航行,到达处时,测得小岛位于它的北偏东方向,且与航母相距海里,再航行一段时间后到达处,测得小岛位于它的北偏东方向如果航母继续航行至小岛的正南方向的处,求还需航行的距离的长参考数据:,,,,,
18.某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离于是,有一天,他们俩带着测倾器和皮尺来测量这个距离测量方案如下:如图,首先,小军站在“聚贤亭”的处,用测倾器测得“乡思柳”顶端点的仰角为,此时测得小军的眼睛距地面的高度为米然后,小军在处蹲下,用测倾器测得“乡思柳”顶端点的仰角为,这时测得小军的眼睛距地面的高度为米请你利用以上所测得的数据,计算“聚贤亭”与“乡思柳”之间的距离的长结果精确到米参考数据:,,,,,
19.如图,平台高为米,在处测得楼房顶部点的仰角为,底部点的俯角为,求楼房的高度
20.如图,在同一平面内,两条平行高速公路和间有一条“”型道路连通,其中段与高速公路成角,长为段与、段都垂直,长为段长为,求两高速公路间的距离结果保留根号.
答案和解析
1.【答案】解:由题意,在中,,
,
,
在中,,
,
,
,
,
米,
米,
答:山高约为米.
【解析】本题考查了解直角三角形的应用仰角俯角问题,注意方程思想与数形结合思想的应用.
根据锐角三角函数的定义得出,,利用,求出的长,即可求出的长.
2.【答案】解:作于,
则四边形为矩形,
,
设,
在中,,
,
由勾股定理得,,
,
在中,,
,
由题意得,,
解得,,
则,
,
答:发射塔的高度为.
【解析】作于,设,根据正弦的定义求出,根据勾股定理求出,根据题意列出方程求出,结合图形计算即可.
本题考查的是解直角三角形的应用仰角俯角问题,掌握锐角三角函数的定义、仰角俯角的概念是解题的关键.
3.【答案】解:如图,过点作交于点,
由题意知米,
斜坡的坡比为:,
,
设米,米,
在中,,
,
,舍
米,米,
答:王刚同学从点到点的过程中上升的高度为米;
如图,过点作交于点,设米,
,
四边形为矩形,
米,米,
,
米,
米,
,
在中,,
,
,
米,
答:大树的高度是米.
【解析】过点作交于点,解,即可求出;
过点作交于点,设米,用表示出、,根据列出方程,解方程得到答案.
本题考查的是解直角三角形的应用仰角俯角问题,掌握坡比的含义,锐角三角函数的定义、仰角俯角的概念是解题的关键.
4.【答案】解:设,
,,
,,
,,
,
,
解得,
.
答:雕像的高度为.
【解析】设,解与,用含的代数式表示出、,然后根据是含度角的直角三角形列出方程,解方程即可求的值,进而可得.
本题考查的是解直角三角形的应用仰角俯角问题,理解仰角俯角的概念、熟记锐角三角函数的概念是解题的关键.
5.【答案】
【解析】略
6.【答案】解:过点作于点,由题意可知:,,米
设大楼与塔之间的距离的长为米,则不设未知数也可以
在中,
在中,
即米
米
答:塔高是米,大楼与塔之间的距离的长为米.
【解析】过点作于点,由题意可知:,,米,设大楼与塔之间的距离的长为米,则,分别在中和中,用表示出和,利用得到有关的方程求得的值即可.
本题考查的是解直角三角形的应用仰角俯角问题,解答此题的关键是作出辅助线,构造出直角三角形,利用直角三角形的性质进行解答.
7.【答案】解:作于,
则四边形为矩形,
,
由题意得,,,
设米,则米,
在中,,
则,
,
在中,,即,
解得,,
答:立柱的高为米.
【解析】作于,得到,设米,根据正切的定义分别用表示出、,根据正切的定义列出方程,解方程即可.
本题考查的是解直角三角形的应用仰角俯角问题,掌握锐角三角函数的概念、仰角俯角的定义是解题的关键.
8.【答案】解:如图,过点作,垂足为,
,
,
设,
在中,,,
又,即,
,
解得,,
答:的长约为.
【解析】通过作高,构造直角三角形,利用直角三角形的边角关系,列方程求解即可.
本题考查直角三角形的边角关系,掌握直角三角形的边角关系,即锐角三角函数,是正确解答的前提,通过作辅助线构造直角三角形是常用的方法.
9.【答案】解:过点作于点,
由题意可知,.,,
,,
,
,
,
.
【解析】本题考查了解直角三角形的应用,理解题意得出线段长度是解题的关键.
过点作于点,根据题意得出,.,,从而求出,,的长,分别求出和的值,得出结果.
10.【答案】解:如图作于.
由题意,,海里,
在中,,,
海里,
海里,
在中,,
,
海里.
海里.
答:的长约为海里和的长约为海里.
【解析】本题考查了解直角三角形的应用--方位角问题,结合航海中的实际问题,解直角三角形即可,体现了数学应用于实际生活的思想.作于,分别在,中求解即可解决问题.
11.【答案】解:由题意知,,
.
在中,,
在和中,,,
,
,
米.
答:旗杆的高度约为米.
【解析】本题考查的是解直角三角形的应用仰角俯角问题,平行线的性质,掌握锐角三角函数的定义、仰角俯角的概念是解题的关键.
由题意可确定,从而可推出,最后由相似三角形中对应边的比相等求解,在由锐角三角函数求出.
12.【答案】解:过点作,,垂足分别为,,如图,
斜坡的坡比:,即,
,
而,
,,
,
,
在阳光下某一时刻测得米的标杆影长为,
,
,
.
答:树高为.
【解析】过点作,,垂足分别为,,根据坡比的定义得到,则,根据含度的直角三角形三边的关系得到,,所以,再根据三角形相似的性质得到,求出,即可得到.
本题考查了解直角三角形有关坡度的应用:斜坡的坡度等于铅直高度与它对应的水平距离的比值.也考查了相似三角形的性质.
13.【答案】解:在中,.
在中,.
.
四边形为矩形,.
即高、低杠间的水平距离的长约是.
【解析】【分析】
思路分析根据和中的边和角的数值,用正切
函数分别求得,的长度,得,由矩形的性质可
知,可以求出问题的答案.
方法总结解直角三角形的应用问题,一般根据题意抽象出几何
图形,结合所给的线段或角,借助边角关系、三角函数的定义解题,
若几何图形中无直角三角形,则需要根据条件构造直角三角形,再
解直角三角形,求出实际问题的答案.
14.【答案】解:依题意,.,,,
在中,.,
.,.,
在中,.,
..
米,
答:无人机从点到点的上升高度约为米.
【解析】在中,求得,,在中,求得,根据,即可求解.
本题考查了解直角三角形的应用,熟练掌握三角函数的定义是解题的关键.
15.【答案】解:连接并延长,与交于点,
,
米,
在中,,
,
即米,
,
即米,
则米.
点到弦所在直线的距离为米.
16.【答案】解:四边形为矩形,,
,,
,
在中,,,,
,,
,,
,
,
,
在中,,,
,,
,,
,
,
,
,
截面的面积.
17.【答案】解:由题可知,,.
在中,,,,
在中,,,.
答:还需要航行的距离的长为海里.
18.【答案】解:作,垂足为,作,垂足为.
设米,则米.
在中,米
在中,米
,
.
,
.
“聚贤亭”到“乡思柳”之间的距离约为米.
【解析】【分析】本题考查的是解直角三角形的应用仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.作,,垂足分别为点、,设米,则米,再由锐角三角函数的定义即可得出结论.
19.【答案】解:作于点,则.
在中,.
在中,.
.
楼房的高度约为米.
【解析】【分析】本题考查解直角三角形的应用,掌握解直角三角形的计算方法和步骤是解题关键.
过点作于,在中,求的长;在中,求的长;根据可求得的长
20.【答案】解:如图,过点作的垂线交的延长线于点,过点
作的垂线与、分别交于点、,则.
由题意知,,又,
四边形为矩形,
,.
.
又与成角,
,.
在中,,
在中,,
所以.
答:两条高速公路间的距离为.
第2页,共18页
1.如图,山顶上有一个信号塔,已知信号塔高米,在山脚下点处测得塔底的仰角,塔顶的仰角,求山高点,,在同一条竖直线上.
参考数据:,,
2.如图,长沙九龙仓国际金融中心主楼高达,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼高,为了测量高楼上发射塔的高度,在楼底端点测得的仰角为,,在顶端点测得的仰角为,求发射塔的高度.
3.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树的高度,他在点处测得大树顶端的仰角为,再从点出发沿斜坡走米到达斜坡上点,在点处测得树顶端的仰角为,若斜坡的坡比为:点、、在同一水平线上.
求王刚同学从点到点的过程中上升的高度;
求大树的高度结果保留根号.
4.某校一初三学生在学习了“锐角三角函数”的应用后,来到“孔子圣像”的雕像前,如图,想要用所学知识解决“孔子圣像”雕像的高度,他在雕像前处用自制测角仪测得顶端的仰角为,底端的俯角为;又在同一水平线上的处用自制测角仪测得顶端的仰角为,已知,求雕像的高度.结果保留根号
5.年月日时分,搭载“嫦娥六号”探测器的“长征五号遥八”运载火箭在海南文昌航天发射场成功点火发射,如图,在发射的过程中,火箭从地面处竖直向上发射,当火箭到达处时,从位于地面处的雷达站测得的距离是,仰角为;当火箭到达处时,从位于地面处的雷达站测得仰角为,求火箭从处到处的飞行距离.
6.如图,大楼高米,远处有一塔,某人在楼底处测得塔顶的仰角为,爬到楼顶处测得塔顶的仰角为,求塔高及大楼与塔之间的距离的长参考数据:,,,,,
7.某游乐场一转角滑梯如图所示,滑梯立柱、均垂直于地面,点在线段上,在点测得点的仰角为,点的俯角也为,测得、间距离为米,立柱高米.求立柱的高结果保留根号
8.如图,,两点被池塘隔开,在外选一点,连接,测得,,根据测得的数据,求的长结果取整数.参考数据:,,.
9.科技社团选择学校游泳池进行一次光的折射实验,如图,光线自点处发出,经水面点折射到池底点处.已知与水平线的夹角,点到水面的距离,点处水深为,到池壁的水平距离点,,在同一条竖直线上,所有点都在同一竖直平面内。记入射角为,折射角为,求的值精确到.参考数据:,,.
10.如图,一艘海轮位于灯塔的北偏东方向,距离灯塔海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,求和的长结果取整数.
参考数据:,,,取.
11为了测量竖直旗杆的高度,某综合实践小组在地面处竖直放置标杆,并在地面上水平放置一个平面镜,使得,,在同一水平线上,如图所示该小组在标杆的处通过平面镜恰好观测到旗杆顶此时在处测得旗杆顶的仰角为,平面镜的俯角为,米,问旗杆的高度约为多少米结果保留整数参考数据:,
12.某校初三课外活动小组,在测量树高的一次活动中.如图所示,测得树底部中心到斜坡底的水平距离为,在阳光下某一时刻测得米的标杆影长为,树影落在斜坡上的部分,已知斜坡的坡比:,求树高结果保留整数,参考数据:.
13. “高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上,两点间的距离为低杠上点到直线的距离的长为,高杠上点到直线的距离的长为,已知低杠的支架与直线的夹角为.,高杠的支架与直线的夹角为.求高、低杠间的水平距离的长结果精确到参考数据:.,.,.,.,.,.
14.本小题分
如图,,是同一水平线上的两点,无人机从点竖直上升到点时,测得到点的距离为,点的俯角为,无人机继续竖直上升到点,测得点的俯角为求无人机从点到点的上升高度精确到.
参考数据:,,,,,.
15.筒车是我国古代发明的一种水利灌溉工具.如图,明朝科学家徐光启在农政全书中用图画描绘了筒车的工作原理.如图,筒车盛水桶的运行轨迹是以轴心为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦长为米,,若点为运行轨道的最高点的连线垂直于,求点到弦所在直线的距离.参考数据:,,
16.学生到工厂劳动实践,学习制作机械零件零件的截面如图阴影部分所示,已知四边形为矩形,点、分别在、上,,,,求零件的截面面积参考数据:,.
17.由我国完全自主设计、自主建造的首艘国产航母于年月成功完成第一次海上试验任务如图,航母由西向东航行,到达处时,测得小岛位于它的北偏东方向,且与航母相距海里,再航行一段时间后到达处,测得小岛位于它的北偏东方向如果航母继续航行至小岛的正南方向的处,求还需航行的距离的长参考数据:,,,,,
18.某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离于是,有一天,他们俩带着测倾器和皮尺来测量这个距离测量方案如下:如图,首先,小军站在“聚贤亭”的处,用测倾器测得“乡思柳”顶端点的仰角为,此时测得小军的眼睛距地面的高度为米然后,小军在处蹲下,用测倾器测得“乡思柳”顶端点的仰角为,这时测得小军的眼睛距地面的高度为米请你利用以上所测得的数据,计算“聚贤亭”与“乡思柳”之间的距离的长结果精确到米参考数据:,,,,,
19.如图,平台高为米,在处测得楼房顶部点的仰角为,底部点的俯角为,求楼房的高度
20.如图,在同一平面内,两条平行高速公路和间有一条“”型道路连通,其中段与高速公路成角,长为段与、段都垂直,长为段长为,求两高速公路间的距离结果保留根号.
答案和解析
1.【答案】解:由题意,在中,,
,
,
在中,,
,
,
,
,
米,
米,
答:山高约为米.
【解析】本题考查了解直角三角形的应用仰角俯角问题,注意方程思想与数形结合思想的应用.
根据锐角三角函数的定义得出,,利用,求出的长,即可求出的长.
2.【答案】解:作于,
则四边形为矩形,
,
设,
在中,,
,
由勾股定理得,,
,
在中,,
,
由题意得,,
解得,,
则,
,
答:发射塔的高度为.
【解析】作于,设,根据正弦的定义求出,根据勾股定理求出,根据题意列出方程求出,结合图形计算即可.
本题考查的是解直角三角形的应用仰角俯角问题,掌握锐角三角函数的定义、仰角俯角的概念是解题的关键.
3.【答案】解:如图,过点作交于点,
由题意知米,
斜坡的坡比为:,
,
设米,米,
在中,,
,
,舍
米,米,
答:王刚同学从点到点的过程中上升的高度为米;
如图,过点作交于点,设米,
,
四边形为矩形,
米,米,
,
米,
米,
,
在中,,
,
,
米,
答:大树的高度是米.
【解析】过点作交于点,解,即可求出;
过点作交于点,设米,用表示出、,根据列出方程,解方程得到答案.
本题考查的是解直角三角形的应用仰角俯角问题,掌握坡比的含义,锐角三角函数的定义、仰角俯角的概念是解题的关键.
4.【答案】解:设,
,,
,,
,,
,
,
解得,
.
答:雕像的高度为.
【解析】设,解与,用含的代数式表示出、,然后根据是含度角的直角三角形列出方程,解方程即可求的值,进而可得.
本题考查的是解直角三角形的应用仰角俯角问题,理解仰角俯角的概念、熟记锐角三角函数的概念是解题的关键.
5.【答案】
【解析】略
6.【答案】解:过点作于点,由题意可知:,,米
设大楼与塔之间的距离的长为米,则不设未知数也可以
在中,
在中,
即米
米
答:塔高是米,大楼与塔之间的距离的长为米.
【解析】过点作于点,由题意可知:,,米,设大楼与塔之间的距离的长为米,则,分别在中和中,用表示出和,利用得到有关的方程求得的值即可.
本题考查的是解直角三角形的应用仰角俯角问题,解答此题的关键是作出辅助线,构造出直角三角形,利用直角三角形的性质进行解答.
7.【答案】解:作于,
则四边形为矩形,
,
由题意得,,,
设米,则米,
在中,,
则,
,
在中,,即,
解得,,
答:立柱的高为米.
【解析】作于,得到,设米,根据正切的定义分别用表示出、,根据正切的定义列出方程,解方程即可.
本题考查的是解直角三角形的应用仰角俯角问题,掌握锐角三角函数的概念、仰角俯角的定义是解题的关键.
8.【答案】解:如图,过点作,垂足为,
,
,
设,
在中,,,
又,即,
,
解得,,
答:的长约为.
【解析】通过作高,构造直角三角形,利用直角三角形的边角关系,列方程求解即可.
本题考查直角三角形的边角关系,掌握直角三角形的边角关系,即锐角三角函数,是正确解答的前提,通过作辅助线构造直角三角形是常用的方法.
9.【答案】解:过点作于点,
由题意可知,.,,
,,
,
,
,
.
【解析】本题考查了解直角三角形的应用,理解题意得出线段长度是解题的关键.
过点作于点,根据题意得出,.,,从而求出,,的长,分别求出和的值,得出结果.
10.【答案】解:如图作于.
由题意,,海里,
在中,,,
海里,
海里,
在中,,
,
海里.
海里.
答:的长约为海里和的长约为海里.
【解析】本题考查了解直角三角形的应用--方位角问题,结合航海中的实际问题,解直角三角形即可,体现了数学应用于实际生活的思想.作于,分别在,中求解即可解决问题.
11.【答案】解:由题意知,,
.
在中,,
在和中,,,
,
,
米.
答:旗杆的高度约为米.
【解析】本题考查的是解直角三角形的应用仰角俯角问题,平行线的性质,掌握锐角三角函数的定义、仰角俯角的概念是解题的关键.
由题意可确定,从而可推出,最后由相似三角形中对应边的比相等求解,在由锐角三角函数求出.
12.【答案】解:过点作,,垂足分别为,,如图,
斜坡的坡比:,即,
,
而,
,,
,
,
在阳光下某一时刻测得米的标杆影长为,
,
,
.
答:树高为.
【解析】过点作,,垂足分别为,,根据坡比的定义得到,则,根据含度的直角三角形三边的关系得到,,所以,再根据三角形相似的性质得到,求出,即可得到.
本题考查了解直角三角形有关坡度的应用:斜坡的坡度等于铅直高度与它对应的水平距离的比值.也考查了相似三角形的性质.
13.【答案】解:在中,.
在中,.
.
四边形为矩形,.
即高、低杠间的水平距离的长约是.
【解析】【分析】
思路分析根据和中的边和角的数值,用正切
函数分别求得,的长度,得,由矩形的性质可
知,可以求出问题的答案.
方法总结解直角三角形的应用问题,一般根据题意抽象出几何
图形,结合所给的线段或角,借助边角关系、三角函数的定义解题,
若几何图形中无直角三角形,则需要根据条件构造直角三角形,再
解直角三角形,求出实际问题的答案.
14.【答案】解:依题意,.,,,
在中,.,
.,.,
在中,.,
..
米,
答:无人机从点到点的上升高度约为米.
【解析】在中,求得,,在中,求得,根据,即可求解.
本题考查了解直角三角形的应用,熟练掌握三角函数的定义是解题的关键.
15.【答案】解:连接并延长,与交于点,
,
米,
在中,,
,
即米,
,
即米,
则米.
点到弦所在直线的距离为米.
16.【答案】解:四边形为矩形,,
,,
,
在中,,,,
,,
,,
,
,
,
在中,,,
,,
,,
,
,
,
,
截面的面积.
17.【答案】解:由题可知,,.
在中,,,,
在中,,,.
答:还需要航行的距离的长为海里.
18.【答案】解:作,垂足为,作,垂足为.
设米,则米.
在中,米
在中,米
,
.
,
.
“聚贤亭”到“乡思柳”之间的距离约为米.
【解析】【分析】本题考查的是解直角三角形的应用仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.作,,垂足分别为点、,设米,则米,再由锐角三角函数的定义即可得出结论.
19.【答案】解:作于点,则.
在中,.
在中,.
.
楼房的高度约为米.
【解析】【分析】本题考查解直角三角形的应用,掌握解直角三角形的计算方法和步骤是解题关键.
过点作于,在中,求的长;在中,求的长;根据可求得的长
20.【答案】解:如图,过点作的垂线交的延长线于点,过点
作的垂线与、分别交于点、,则.
由题意知,,又,
四边形为矩形,
,.
.
又与成角,
,.
在中,,
在中,,
所以.
答:两条高速公路间的距离为.
第2页,共18页
同课章节目录
