2.3 导数的计算 课件(21张PPT )
文档属性
| 名称 | 2.3 导数的计算 课件(21张PPT ) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 18:16:48 | ||
图片预览








文档简介
2.3 导数的计算
第二章 导数及其应用
1.进一步理解导数的概念,会用导数的定义求简单函数在某点处的导数;
2.理解导函数的概念,会根据导数公式表求简单函数的导数.
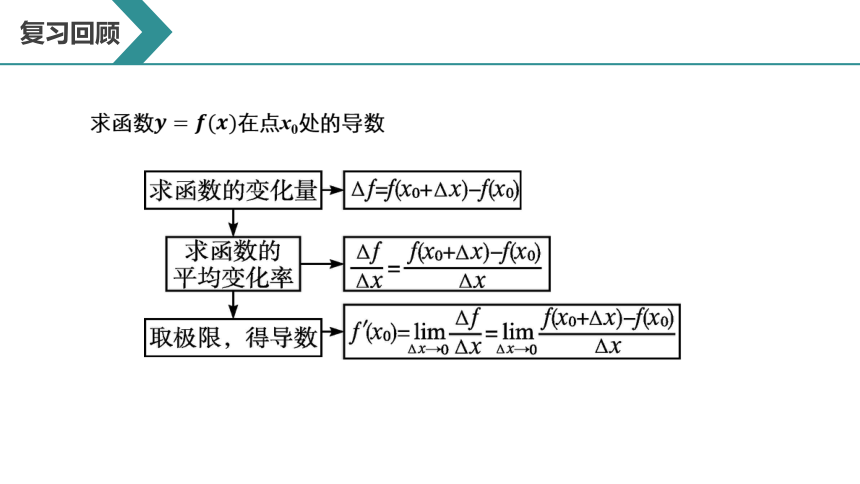
求函数????=????(????)在点x0处的导数
?
当Δx趋于0时,得到导数
对于定义域中的每一个自变量的取值x0,
(2)当x0在定义域内任意取值时,f′(x0)的值如何?
一般地,如果一个函数y=f(x)在区间(a,b)的每一点x处都有导数f′(x)
= ,那么f′(x)是关于x的函数,称f′(x)为y=f(x)的导函数,也简称为导数,有时也将导数记作y′.
概念讲解
思考:会区分“函数f(x)在点x0处的导数”与“导函数”吗?
“函数f(x)在点x0处的导数”是一个数值,
“导函数”是一个函数,
二者有本质的区别,但又有密切关系,f'(x0)是其导函数y=f'(x)在x=x0处的一个函数值.
【例2】分别求出下列函数的导数,并说说导数的意义.
(1)????????=????,其中????是常数;
?
x
????????
?
O
???????? = C
?
解:(1)根据定义可知
????′????=lim?????→0????????+??????????(????)?????=lim?????→0??????????????=lim?????→00=0.
?
若 ???????? = C 表示路程关于时间的函数,则 ????′????= 0 可以解释为某物体的瞬时速度始终为 0,即一直处于静止状态.
?
(2)????????=????;
?
(2)根据定义可知
????′????=lim?????→0????????+??????????(????)?????=lim?????→0????+???????????????=lim?????→01=1.
?
若 ????(????) = x 表示路程关于时间的函数,则 ????′????= 1 可以解释为某物体做瞬时速度为 1 的匀速直线运动.
?
x
????????
?
O
???????? = x
?
(3)????????=????3;
?
(3)根据定义可知
????′?????=lim?????→0????????+??????????(????)?????=lim?????→0????+?????3?????3?????
?????????????=lim?????→0[?3????2+3??????????+(?????)2]=3????2
?
由导数????′???? =3????2是偶函数可知,在曲线????=????3上,自变量互为相反数的两点,它们的切线斜率相等;????>0时,自变量越大,切线的斜率越大,????也越大,函数????????=????3增加得越来越快.
?
(4)????????=1????;
?
(4)根据定义可知
????′???? =lim?????→0????????+??????????(????)?????=lim?????→01????+??????1?????????=lim?????→0?1????(????+?????)=?1????2.
?
由导数????′????=?1????2是偶函数可知,在曲线????=1????上,自变量互为相反数的两点,它们的切线斜率相等;????>0时,自变量越大,切线的斜率越大,????越小,函数????(????)=1???? 减少得越来越慢.
?
(5)????????=????(????>0).
?
(5)根据定义可知
????′???? =lim?????→0????????+??????????(????)?????=lim?????→0????+???????????????
=lim?????→0??????????(????+?????+????)=lim?????→01????+?????+????=12????
?
在曲线????=????上,当 x > 0 时,自变量越大,切线的斜率越小, ????越小,函数????(????)?= ???? 增加得越来越慢.
?
x
y
O
y = ????
?
因为1???? =?????1,1????2=?????2,????=????12,1????=?????12,
?
思考:观察上述导函数,归纳出幂函数????????=????????(????≠0)的导函数具有的形式?
?
(????2)′ =2?????2?1=2????
?
(????3)′ =3?????3?1=3????2
?
(1????)′=(?????1)′=?1??????1?1=?1????2
?
(????)′=(????12)′=12?????12?1=12????
?
归纳:
原幂指数作为求导后的系数
原幂指数减1作为现幂指数
(????????)′ =?????????????1.
?
【例2】已知函数????????=????????,????????=????????????,求????′???? , ????′????.
?
解:在(????????)′ =????????????????????,中令????=????,可得(????????)′ =????????????????e=????????,
因此????′????=????????.
在(????????????????????)′ =1???????????????? ,中令????=????,可得(????????????????????)′ =1????????????????,
即(ln????)′=1????,
因此????′????=1????.
?
基本初等函数的导数公式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 原函数
导函数
f (x)=C(C为常数)
f ′(x)=_____________
f (x)=xα(α∈Q,且α≠0)
f ′(x)=_____________
f (x)=sin x
f ′(x)=_____________
f (x)=cos x
f ′(x)=_____________
f (x)=ax(a>0,且a≠1)
f ′(x)=_____________(a>0,且a≠1)
f (x)=ex
f ′(x)=_____________
f (x)=logax(a>0,且a≠1)
f ′(x)=_____________(a>0,且a≠1)
f (x)=ln x
f ′(x)=_____________
0
?????????????1
?
cos????
?
?sin????
?
????????ln????
?
????????
?
1????ln????
?
1????
?
归纳总结
【例3】求下列函数的导数:
{74C1A8A3-306A-4EB7-A6B1-4F7E0EB9C5D6}常用函数的求导公式
????
?
?????????????????
?
????????????????????
?
????????????????????
?
????????????????
?
?????????????????
?
????????
?
????????
?
B
2.下列函数求导运算正确的个数为( )
A.1 B.2 C.3 D.4
C
3.若f (x)=x2, g (x)=x3 ,则满足f ′(x)+1=g′(x)的x值为__________.
?
1或?13
?
4.设函数f (x)=log????????, f ′(1)=?1,则a=__________.
?
1????
第二章 导数及其应用
1.进一步理解导数的概念,会用导数的定义求简单函数在某点处的导数;
2.理解导函数的概念,会根据导数公式表求简单函数的导数.
求函数????=????(????)在点x0处的导数
?
当Δx趋于0时,得到导数
对于定义域中的每一个自变量的取值x0,
(2)当x0在定义域内任意取值时,f′(x0)的值如何?
一般地,如果一个函数y=f(x)在区间(a,b)的每一点x处都有导数f′(x)
= ,那么f′(x)是关于x的函数,称f′(x)为y=f(x)的导函数,也简称为导数,有时也将导数记作y′.
概念讲解
思考:会区分“函数f(x)在点x0处的导数”与“导函数”吗?
“函数f(x)在点x0处的导数”是一个数值,
“导函数”是一个函数,
二者有本质的区别,但又有密切关系,f'(x0)是其导函数y=f'(x)在x=x0处的一个函数值.
【例2】分别求出下列函数的导数,并说说导数的意义.
(1)????????=????,其中????是常数;
?
x
????????
?
O
???????? = C
?
解:(1)根据定义可知
????′????=lim?????→0????????+??????????(????)?????=lim?????→0??????????????=lim?????→00=0.
?
若 ???????? = C 表示路程关于时间的函数,则 ????′????= 0 可以解释为某物体的瞬时速度始终为 0,即一直处于静止状态.
?
(2)????????=????;
?
(2)根据定义可知
????′????=lim?????→0????????+??????????(????)?????=lim?????→0????+???????????????=lim?????→01=1.
?
若 ????(????) = x 表示路程关于时间的函数,则 ????′????= 1 可以解释为某物体做瞬时速度为 1 的匀速直线运动.
?
x
????????
?
O
???????? = x
?
(3)????????=????3;
?
(3)根据定义可知
????′?????=lim?????→0????????+??????????(????)?????=lim?????→0????+?????3?????3?????
?????????????=lim?????→0[?3????2+3??????????+(?????)2]=3????2
?
由导数????′???? =3????2是偶函数可知,在曲线????=????3上,自变量互为相反数的两点,它们的切线斜率相等;????>0时,自变量越大,切线的斜率越大,????也越大,函数????????=????3增加得越来越快.
?
(4)????????=1????;
?
(4)根据定义可知
????′???? =lim?????→0????????+??????????(????)?????=lim?????→01????+??????1?????????=lim?????→0?1????(????+?????)=?1????2.
?
由导数????′????=?1????2是偶函数可知,在曲线????=1????上,自变量互为相反数的两点,它们的切线斜率相等;????>0时,自变量越大,切线的斜率越大,????越小,函数????(????)=1???? 减少得越来越慢.
?
(5)????????=????(????>0).
?
(5)根据定义可知
????′???? =lim?????→0????????+??????????(????)?????=lim?????→0????+???????????????
=lim?????→0??????????(????+?????+????)=lim?????→01????+?????+????=12????
?
在曲线????=????上,当 x > 0 时,自变量越大,切线的斜率越小, ????越小,函数????(????)?= ???? 增加得越来越慢.
?
x
y
O
y = ????
?
因为1???? =?????1,1????2=?????2,????=????12,1????=?????12,
?
思考:观察上述导函数,归纳出幂函数????????=????????(????≠0)的导函数具有的形式?
?
(????2)′ =2?????2?1=2????
?
(????3)′ =3?????3?1=3????2
?
(1????)′=(?????1)′=?1??????1?1=?1????2
?
(????)′=(????12)′=12?????12?1=12????
?
归纳:
原幂指数作为求导后的系数
原幂指数减1作为现幂指数
(????????)′ =?????????????1.
?
【例2】已知函数????????=????????,????????=????????????,求????′???? , ????′????.
?
解:在(????????)′ =????????????????????,中令????=????,可得(????????)′ =????????????????e=????????,
因此????′????=????????.
在(????????????????????)′ =1???????????????? ,中令????=????,可得(????????????????????)′ =1????????????????,
即(ln????)′=1????,
因此????′????=1????.
?
基本初等函数的导数公式
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 原函数
导函数
f (x)=C(C为常数)
f ′(x)=_____________
f (x)=xα(α∈Q,且α≠0)
f ′(x)=_____________
f (x)=sin x
f ′(x)=_____________
f (x)=cos x
f ′(x)=_____________
f (x)=ax(a>0,且a≠1)
f ′(x)=_____________(a>0,且a≠1)
f (x)=ex
f ′(x)=_____________
f (x)=logax(a>0,且a≠1)
f ′(x)=_____________(a>0,且a≠1)
f (x)=ln x
f ′(x)=_____________
0
?????????????1
?
cos????
?
?sin????
?
????????ln????
?
????????
?
1????ln????
?
1????
?
归纳总结
【例3】求下列函数的导数:
{74C1A8A3-306A-4EB7-A6B1-4F7E0EB9C5D6}常用函数的求导公式
????
?
?????????????????
?
????????????????????
?
????????????????????
?
????????????????
?
?????????????????
?
????????
?
????????
?
B
2.下列函数求导运算正确的个数为( )
A.1 B.2 C.3 D.4
C
3.若f (x)=x2, g (x)=x3 ,则满足f ′(x)+1=g′(x)的x值为__________.
?
1或?13
?
4.设函数f (x)=log????????, f ′(1)=?1,则a=__________.
?
1????
同课章节目录
