2.6.2 函数的极值 课件课件(21张PPT)
文档属性
| 名称 | 2.6.2 函数的极值 课件课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 08:55:59 | ||
图片预览





文档简介
— 第二章 导数及其应用 —
2.6.2 函数的极值
1.理解极值、极值点的概念,了解函数在某点处取得极值的条件.
2.能利用导数求某些函数的极大值、极小值.
a
b
x1
x5
x4
x3
x2
O
y
x
问题:函数y=f(x)在x1,x2等点处的函数值与其左右附近的函数值什么关系?
f(x1),f(x3),f(x5)为极大值,x1,x3,x5为极大值点,
f(x2),f(x4)为极小值,x2,x4为极小值点.
设函数y=f(x)的定义域为D,设x0属于D,如果对x0附近的任意不同于x0的x,都有f(x)设函数y=f(x)的定义域为D,设x0属于D,如果对x0附近的任意不同于x0的x,都有f(x)>f(x0),则称x0为函数f(x)的一个极小值点,且f(x)在x0处取极小值.
x0
x0
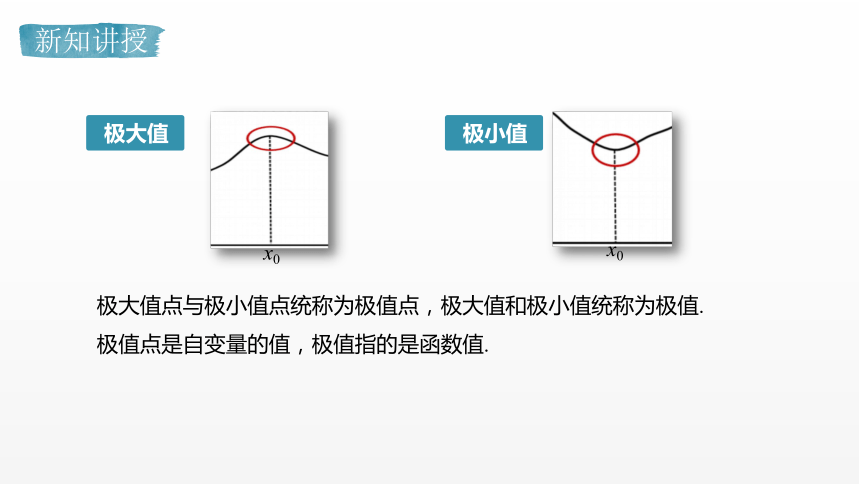
极大值
极小值
极大值点与极小值点统称为极值点,极大值和极小值统称为极值.
极值点是自变量的值,极值指的是函数值.
x0
x0
极大值
极小值
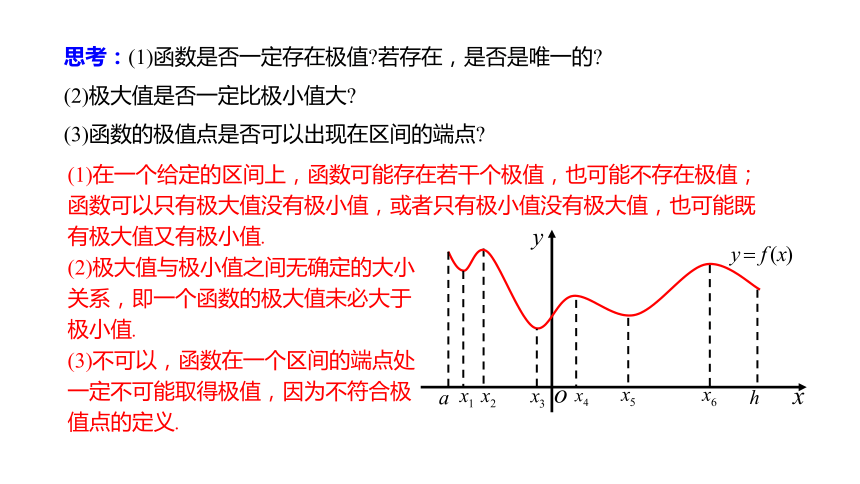
思考:(1)函数是否一定存在极值?若存在,是否是唯一的?
(2)极大值是否一定比极小值大?
(3)函数的极值点是否可以出现在区间的端点?
(1)在一个给定的区间上,函数可能存在若干个极值,也可能不存在极值;函数可以只有极大值没有极小值,或者只有极小值没有极大值,也可能既有极大值又有极小值.
(2)极大值与极小值之间无确定的大小
关系,即一个函数的极大值未必大于
极小值.
(3)不可以,函数在一个区间的端点处
一定不可能取得极值,因为不符合极
值点的定义.
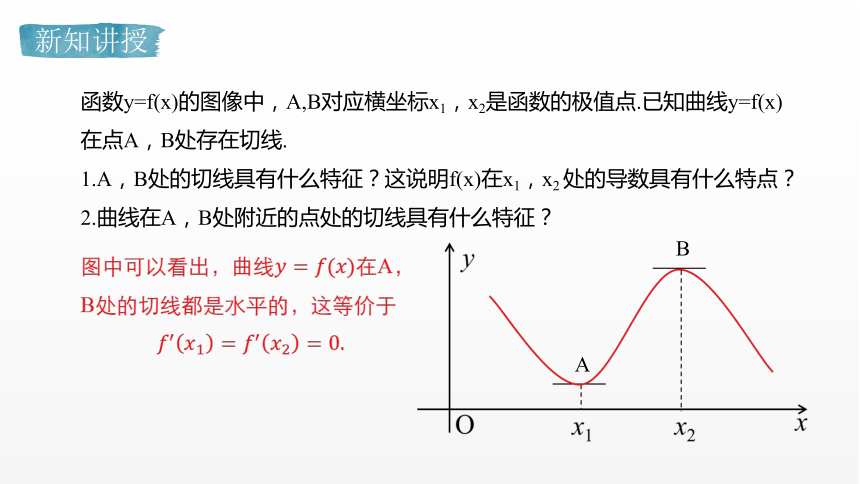
函数y=f(x)的图像中,A,B对应横坐标x1,x2是函数的极值点.已知曲线y=f(x)在点A,B处存在切线.
1.A,B处的切线具有什么特征?这说明f(x)在x1,x2 处的导数具有什么特点?
2.曲线在A,B处附近的点处的切线具有什么特征?
A
B
图中可以看出,曲线????=????(????)在A,B处的切线都是水平的,这等价于
????′????1=????′????2=0.
?
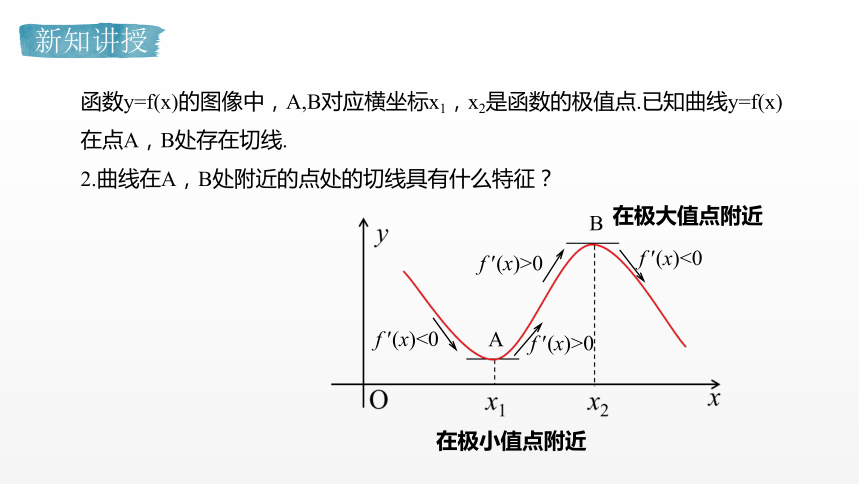
函数y=f(x)的图像中,A,B对应横坐标x1,x2是函数的极值点.已知曲线y=f(x)在点A,B处存在切线.
2.曲线在A,B处附近的点处的切线具有什么特征?
A
B
在极大值点附近
在极小值点附近
f ?(x)<0
f ?(x)>0
f ?(x)>0
f ?(x)<0
归纳总结
一般地,如果????0是????=????(????)的极值点,且????(????)在????0处可导,则必有
????′????0=0.
?
讨论:(1)若有????′????0=0,则????0一定是函数的极值点吗?
(2)函数的极值点与函数的单调性有什么关系?
?
(1)不一定,例如对于函数f(x)=x3,虽有f'(0)=0,但由于无论????>0,还是????<0,恒有f'(x)>0,即函数f(x)=x3是增函数,所以0不是函数f(x)=x3的极值点.
?
即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
(2)极大值点可以看成函数单调递增区间到单调递减区间的转折点,极小值点可以看成函数单调递减区间到单调递增区间的转折点.
结合导数与函数单调性的关系,我们可以得到如下表格:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(a,x0)
x0
(x0,b)
f ′(x)
+
-
y=f (x)
增加↗
极大值
减少↘
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(a,x0)
x0
(x0,b)
f ′(x)
-
+
y=f (x)
减少↘
极小值
增加↗
y
a
b
x0
O
x
y
a
b
x0
O
x
例1 函数y=f(x)的导函数的图象如图所示,给出下列判断:
①函数y=f(x)在区间(3,5)内单调递增;
②函数y=f(x)在区间?12,3内单调递减;
③函数y=f(x)在区间(-2,2)内单调递增;
④当x=-12时,函数y=f(x)有极大值;
⑤当x=2时,函数y=f(x)有极大值.
则上述判断中正确的序号是 .?
?
f'(x)的图象
x∈(3,4),f'(x)<0
x∈(4,5),f'(x)>0
f(x)单调递减←
f(x)单调递增←
(3,4)单调递减,(4,5)单调递增
x∈(?12,2),f'(x)>0
x∈(2,3),f'(x)<0
?
f(x)单调递增←
f(x)单调递减←
(?12,2)单调递增,(2,3)单调递减
?
例1 函数y=f(x)的导函数的图象如图所示,给出下列判断:
①函数y=f(x)在区间(3,5)内单调递增;
②函数y=f(x)在区间?12,3内单调递减;
③函数y=f(x)在区间(-2,2)内单调递增;
④当x=-12时,函数y=f(x)有极大值;
⑤当x=2时,函数y=f(x)有极大值.
则上述判断中正确的序号是 .?
?
③⑤
f'(x)的图象
x∈(-2,2),f'(x)>0
f(x)单调递增←
√
(3,4)单调递减,(4,5)单调递增
(?12,2)单调递增,(2,3)单调递减
?
×
√
方法归纳
对于这类问题要先搞清楚所给的图象是原函数还是导函数的,对于导函数的图象,重点考查在哪个区间上为正,哪个区间上为负,在哪个点处与x轴相交,在该点附近的导数值是如何变化的,
(1)如果“左正右负”,那么函数f(x)在这个根处取得极大值;
(2)如果“左负右正”,那么函数f(x)在这个根处取得极小值;
(3)如果左右符号不改变,那么函数f(x)在这个根处不取极值.
例2 求下列函数的极值:
(1)f?(x)=sin x-cos x+x+1(0 解:(1)f′(x)=cos x+sin x+1=1+2sin(x+????4),
令f′(x)=0,从而sin(x+????4)=﹣22,又0<x<2π,所以x=π或x=3????2.
?
求可导函数f(x)的极值的步骤:
①求导数f'(x).
②求方程f'(x)=0的根.
③观察f'(x)在方程f'(x)=0的根左右两边的符号,
如果左正右负,那么f(x)在这个方程根处取得极大值;
如果左负右正,那么f(x)在这个方程根处取得极小值.
方法归纳
例3 已知函数f(x)=13x3-x2+ax-2.
(1)若函数的极大值点是﹣1,求a的值;
(2)若函数f(x)有两个极值点,求a的取值范围.
?
解:(1)f′(x)=x2-2x+a,
由题意有f′(﹣1)=1+2+a=0,解得a=﹣3,
则f′(x)=x2-2x-3,
经验证可知,f(x)在x=﹣1处取得极大值,故a=﹣3.
(2)由题意有方程x2-2x+a=0有两个不等实根,
∴△=(﹣2)2-4a>0,解得a<1,
故a的取值范围是(﹣∞,1).
因为某点处的导数值等于0不是此点为极值点的充要条件,所以求解后必须检验.
1.下列函数中存在极值的是( )
A.y=1???? B.y=x-ex
C.y=2 D.y=x3
2.已知a是函数f(x)=x3-12x的极小值点,则a等于( )
A.-4 B.-2 C.4 D.2
3.函数f(x)=ln x-x在区间(0,e)上的极大值为( )
A.-e B.-1 C.1-e D.0
?
B
D
B
4.设函数f(x)在R上可导,其导函数为f'(x),且函数y=f'(x)的图象如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
D
回顾:结合本课内容,回答下列问题?
1. 什么是极值?极值点是一个点吗?
2. 函数在某点取得极值的充要条件是什么?
3. 如何求函数的极值?
2.6.2 函数的极值
1.理解极值、极值点的概念,了解函数在某点处取得极值的条件.
2.能利用导数求某些函数的极大值、极小值.
a
b
x1
x5
x4
x3
x2
O
y
x
问题:函数y=f(x)在x1,x2等点处的函数值与其左右附近的函数值什么关系?
f(x1),f(x3),f(x5)为极大值,x1,x3,x5为极大值点,
f(x2),f(x4)为极小值,x2,x4为极小值点.
设函数y=f(x)的定义域为D,设x0属于D,如果对x0附近的任意不同于x0的x,都有f(x)
x0
x0
极大值
极小值
极大值点与极小值点统称为极值点,极大值和极小值统称为极值.
极值点是自变量的值,极值指的是函数值.
x0
x0
极大值
极小值
思考:(1)函数是否一定存在极值?若存在,是否是唯一的?
(2)极大值是否一定比极小值大?
(3)函数的极值点是否可以出现在区间的端点?
(1)在一个给定的区间上,函数可能存在若干个极值,也可能不存在极值;函数可以只有极大值没有极小值,或者只有极小值没有极大值,也可能既有极大值又有极小值.
(2)极大值与极小值之间无确定的大小
关系,即一个函数的极大值未必大于
极小值.
(3)不可以,函数在一个区间的端点处
一定不可能取得极值,因为不符合极
值点的定义.
函数y=f(x)的图像中,A,B对应横坐标x1,x2是函数的极值点.已知曲线y=f(x)在点A,B处存在切线.
1.A,B处的切线具有什么特征?这说明f(x)在x1,x2 处的导数具有什么特点?
2.曲线在A,B处附近的点处的切线具有什么特征?
A
B
图中可以看出,曲线????=????(????)在A,B处的切线都是水平的,这等价于
????′????1=????′????2=0.
?
函数y=f(x)的图像中,A,B对应横坐标x1,x2是函数的极值点.已知曲线y=f(x)在点A,B处存在切线.
2.曲线在A,B处附近的点处的切线具有什么特征?
A
B
在极大值点附近
在极小值点附近
f ?(x)<0
f ?(x)>0
f ?(x)>0
f ?(x)<0
归纳总结
一般地,如果????0是????=????(????)的极值点,且????(????)在????0处可导,则必有
????′????0=0.
?
讨论:(1)若有????′????0=0,则????0一定是函数的极值点吗?
(2)函数的极值点与函数的单调性有什么关系?
?
(1)不一定,例如对于函数f(x)=x3,虽有f'(0)=0,但由于无论????>0,还是????<0,恒有f'(x)>0,即函数f(x)=x3是增函数,所以0不是函数f(x)=x3的极值点.
?
即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
(2)极大值点可以看成函数单调递增区间到单调递减区间的转折点,极小值点可以看成函数单调递减区间到单调递增区间的转折点.
结合导数与函数单调性的关系,我们可以得到如下表格:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(a,x0)
x0
(x0,b)
f ′(x)
+
-
y=f (x)
增加↗
极大值
减少↘
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(a,x0)
x0
(x0,b)
f ′(x)
-
+
y=f (x)
减少↘
极小值
增加↗
y
a
b
x0
O
x
y
a
b
x0
O
x
例1 函数y=f(x)的导函数的图象如图所示,给出下列判断:
①函数y=f(x)在区间(3,5)内单调递增;
②函数y=f(x)在区间?12,3内单调递减;
③函数y=f(x)在区间(-2,2)内单调递增;
④当x=-12时,函数y=f(x)有极大值;
⑤当x=2时,函数y=f(x)有极大值.
则上述判断中正确的序号是 .?
?
f'(x)的图象
x∈(3,4),f'(x)<0
x∈(4,5),f'(x)>0
f(x)单调递减←
f(x)单调递增←
(3,4)单调递减,(4,5)单调递增
x∈(?12,2),f'(x)>0
x∈(2,3),f'(x)<0
?
f(x)单调递增←
f(x)单调递减←
(?12,2)单调递增,(2,3)单调递减
?
例1 函数y=f(x)的导函数的图象如图所示,给出下列判断:
①函数y=f(x)在区间(3,5)内单调递增;
②函数y=f(x)在区间?12,3内单调递减;
③函数y=f(x)在区间(-2,2)内单调递增;
④当x=-12时,函数y=f(x)有极大值;
⑤当x=2时,函数y=f(x)有极大值.
则上述判断中正确的序号是 .?
?
③⑤
f'(x)的图象
x∈(-2,2),f'(x)>0
f(x)单调递增←
√
(3,4)单调递减,(4,5)单调递增
(?12,2)单调递增,(2,3)单调递减
?
×
√
方法归纳
对于这类问题要先搞清楚所给的图象是原函数还是导函数的,对于导函数的图象,重点考查在哪个区间上为正,哪个区间上为负,在哪个点处与x轴相交,在该点附近的导数值是如何变化的,
(1)如果“左正右负”,那么函数f(x)在这个根处取得极大值;
(2)如果“左负右正”,那么函数f(x)在这个根处取得极小值;
(3)如果左右符号不改变,那么函数f(x)在这个根处不取极值.
例2 求下列函数的极值:
(1)f?(x)=sin x-cos x+x+1(0
令f′(x)=0,从而sin(x+????4)=﹣22,又0<x<2π,所以x=π或x=3????2.
?
求可导函数f(x)的极值的步骤:
①求导数f'(x).
②求方程f'(x)=0的根.
③观察f'(x)在方程f'(x)=0的根左右两边的符号,
如果左正右负,那么f(x)在这个方程根处取得极大值;
如果左负右正,那么f(x)在这个方程根处取得极小值.
方法归纳
例3 已知函数f(x)=13x3-x2+ax-2.
(1)若函数的极大值点是﹣1,求a的值;
(2)若函数f(x)有两个极值点,求a的取值范围.
?
解:(1)f′(x)=x2-2x+a,
由题意有f′(﹣1)=1+2+a=0,解得a=﹣3,
则f′(x)=x2-2x-3,
经验证可知,f(x)在x=﹣1处取得极大值,故a=﹣3.
(2)由题意有方程x2-2x+a=0有两个不等实根,
∴△=(﹣2)2-4a>0,解得a<1,
故a的取值范围是(﹣∞,1).
因为某点处的导数值等于0不是此点为极值点的充要条件,所以求解后必须检验.
1.下列函数中存在极值的是( )
A.y=1???? B.y=x-ex
C.y=2 D.y=x3
2.已知a是函数f(x)=x3-12x的极小值点,则a等于( )
A.-4 B.-2 C.4 D.2
3.函数f(x)=ln x-x在区间(0,e)上的极大值为( )
A.-e B.-1 C.1-e D.0
?
B
D
B
4.设函数f(x)在R上可导,其导函数为f'(x),且函数y=f'(x)的图象如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
D
回顾:结合本课内容,回答下列问题?
1. 什么是极值?极值点是一个点吗?
2. 函数在某点取得极值的充要条件是什么?
3. 如何求函数的极值?
同课章节目录
