2.6.2 函数的极值 课件(22张PPT)
文档属性
| 名称 | 2.6.2 函数的极值 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 796.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 08:55:27 | ||
图片预览




文档简介
2.6.2 函数的极值
第二章 导数及其应用
1. 了解极值的概念.
2. 了解函数在某点取得极值的必要条件和充分条件.
3. 会用导数求函数的极值.
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的增减.如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
?
观察下图,我们发现,当 t = a 时,高台跳水运动员距水面的高度最大.
问题1 函数h(t)在此点的导数是多少呢? 此点附近的图象有什么特点? 相应地, 导数的符号有什么变化规律?
x
y
O
a
b
x
y
O
a
b
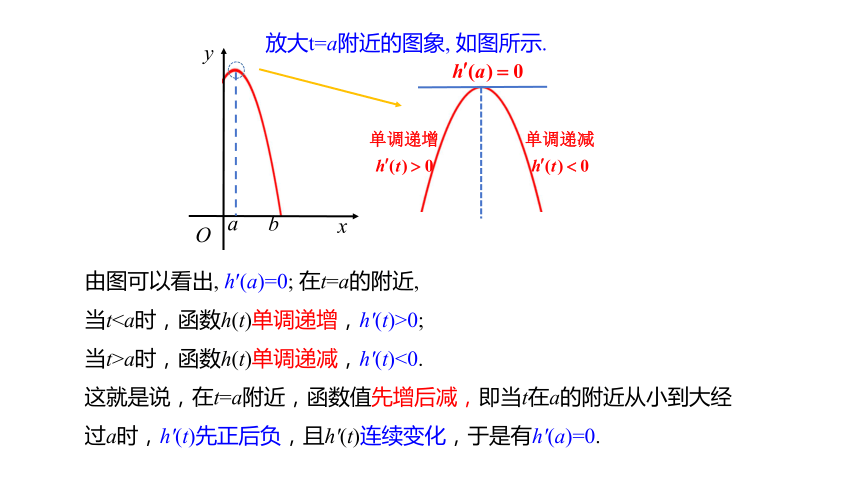
放大t=a附近的图象, 如图所示.
由图可以看出, h′(a)=0; 在t=a的附近,
当t0;
当t>a时,函数h(t)单调递减,h'(t)<0.
这就是说,在t=a附近,函数值先增后减,即当t在a的附近从小到大经过a时,h'(t)先正后负,且h'(t)连续变化,于是有h'(a)=0.
问题2 对于一般的函数y=f(x),是否也有同样的性质呢?
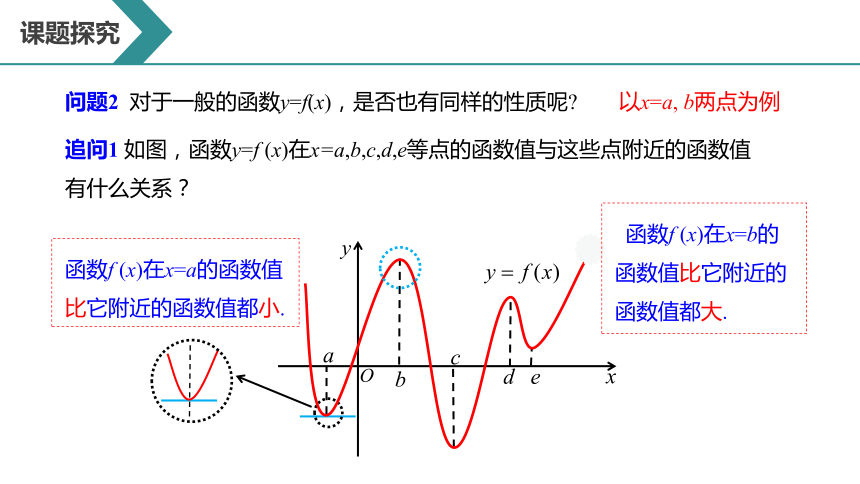
追问1 如图,函数y=f (x)在x=a,b,c,d,e等点的函数值与这些点附近的函数值有什么关系?
函数f (x)在x=a的函数值比它附近的函数值都小.
函数f (x)在x=b的函数值比它附近的函数值都大.
以x=a, b两点为例
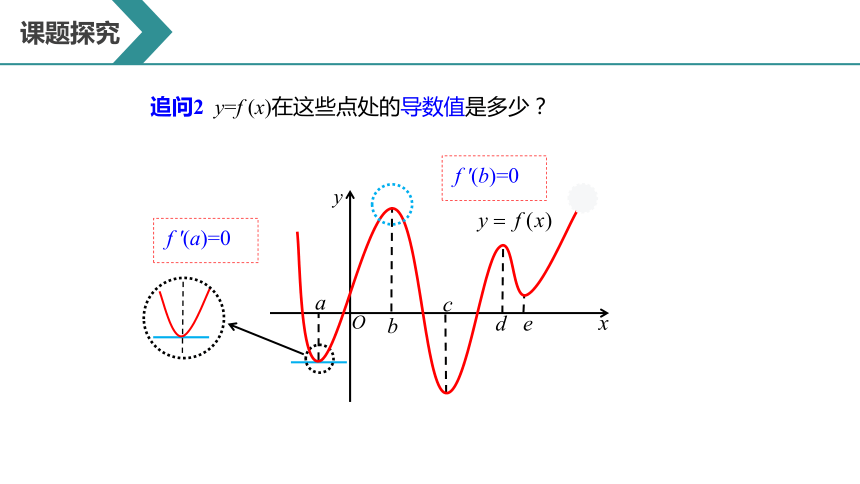
追问2 y=f (x)在这些点处的导数值是多少?
f ′(a)=0
f ′(b)=0
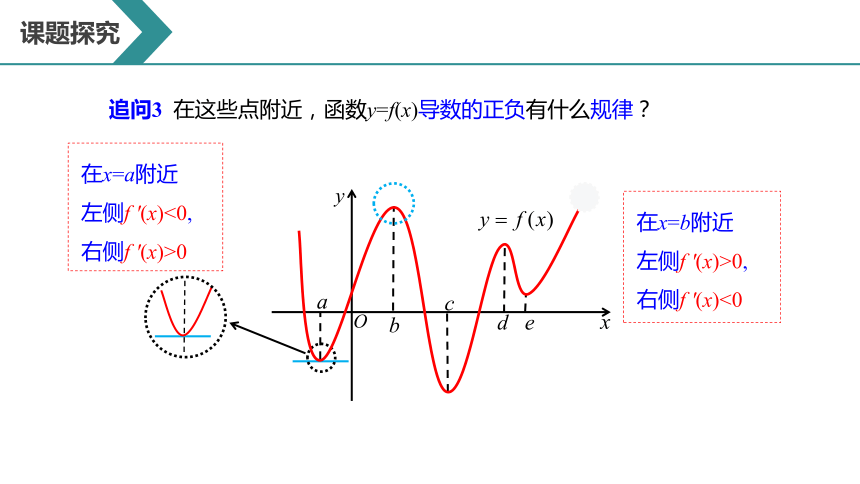
追问3 在这些点附近,函数y=f(x)导数的正负有什么规律?
在x=a附近
左侧f ′(x)<0,
右侧f ′(x)>0
在x=b附近
左侧f ′(x)>0,
右侧f ′(x)<0
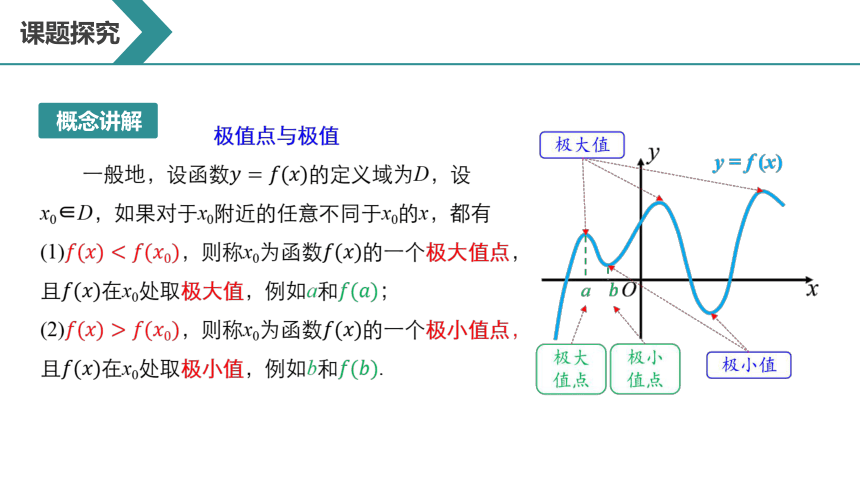
极值点与极值
一般地,设函数????=????(????)的定义域为D,设x0∈D,如果对于x0附近的任意不同于x0的x,都有
(1)????(????) (2)????(????)>????(????0),则称x0为函数????(????)的一个极小值点,且????(????)在x0处取极小值,例如b和????(????).
?
概念讲解
追问1 f ′(x0)=0是函数在x=x0处取得极值的什么条件?
x0是函数 f(x) 的极值点
f ′(x0)=0
x0是函数 f(x) 的极值点
x0左右两侧导数异号
f ′(x0)=0
结论:f ′(x0)=0 是可导函数在x0处取得极值的必要而不充分条件.
追问2 函数 y=f (x)在x=x0处取得极值的充分条件是什么?
x0左右侧导数异号
f ′(x0)=0
x0为极值点
问题3 函数的极大值一定大于极小值吗?函数的极大值与极小值是否有大小关系?
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
极大值与极小值没有必然的大小关系.一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值可能大于另一点的极大值.
极小值
极大值
(3) 极大值与极小值没有必然关系,极大值可能比极小值还小.
(1) 极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2) 函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
(4) 对于可导函数,若x0是极值点,则 f '(x0)=0;反之,若f '(x0)=0,则x0不一定是极值点.
归纳总结
【例1】已知函数f(x)=ax3+bx2+cx(a≠0),f′(-1)=f′(1)=0,且f(1)=-1.
(1)试求常数a,b,c的值;
(2)试判断x=±1是函数的极大值点还是极小值点?
解:(1)f′(x)=3ax2+2bx+c.
由f′(-1)=f′(1)=0,
得3a+2b+c=0,3a-2b+c=0.
又f(1)=-1,∴a+b+c=-1,
(2)试判断x=±1是函数的极大值点还是极小值点?
当x<-1或x>1时,f′(x)>0;
当-1<x<1时,f′(x)<0,
∴函数f(x)在(-∞,-1)和(1,+∞)上单调递增,在(-1,1)上单调递减.
∴x=1是函数的极小值点,x=-1是函数的极大值点.
【例2】求函数f(x)=x2e-x的极值点和极值.
解:函数f(x)的定义域为R.
f'(x)=2xe-x-x2e-x=x(2-x)e-x.
令f'(x)=0,得x=0或x=2.
当x变化时,f'(x),f(x)的变化情况如下表:
x
(-∞,0)
0
(0,2)
2
(2,+∞)
f'(x)
-
0
+
0
-
f(x)
↘
极小值
↗
极大值
↘
由上表可以看出,0为函数f(x)的极小值点,极小值为f(0)=0.
2为函数f(x)的极大值点,极大值为f(2)=4e-2.
【例3】已知函数????????=13????3?4????2+4,求函数的极值,并作出函数图象的示意图.
?
解:由题意可得????′????=????2?4 =(????+2)(?????2).
令????′????=0,解得????1=?2,????2=2.
当????变化时,????′????, ????????的变化情况如下表:
因此,当????=?2时,????????有极大值,极大值为?????2= 283;
当????=2时,????????有极小值,极小值为????2=- 43.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
-2
2
+
0
0
+
↗
↘
↗
函数????????=13????3?4????2+4的图像如图所示.
?
【例3】已知函数????????=13????3?4????2+4,求函数的极值,并作出函数图象的示意图.
?
方法归纳
一般地,求函数y=f(x)的极值的步骤
(1)求出函数的定义域及导数f ′(x);
(2)解方程f ′(x)=0,得方程的根x0(可能不止一个);
(3)用方程f ′(x)=0的根,顺次将函数的定义域分成若干个开区间,可将x,f ′(x),f(x)在每个区间内的变化情况列在同一个表格中;
(4)由f ′(x)在各个开区间内的符号,判断f (x)在f ′(x)=0的各个根处的极值情况:
如果左正右负,那么函数f(x)在这个根处取得极大值;
如果左负右正,那么函数f(x)在这个根处取得极小值;
如果导数值在这个根左右两侧同号,那么这个根不是极值点.
回顾:结合本课内容,回答下列问题?
1. 什么是极值?极值点是一个点吗?
2. 函数在某点取得极值的充要条件是什么?
3. 如何求函数的极值?
1.(多选)函数f(x)的定义域为R,它的导函数y=f′(x)的部分图象如图所示,则下面结论正确的是( )
A.在(1,2)上函数f(x)是增函数
B.在(3,4)上函数f(x)是减函数
C.在(1,3)上函数f(x)有极大值
D.x=3是函数f(x)在区间[1,5]上的极小值点
2.函数f(x)=ax-1-ln x(a≤0)在定义域内的极值点的个数为 .
ABC
0
3.函数f(x)=ln x-x在区间(0,e)上的极大值为( )
A.-e B.-1 C.1-e D.0
4.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
A.(-1,2)
B.(-3,6)
C.(-∞,-1)∪(2,+∞)
D.(-∞,-3)∪(6,+∞)
B
D
第二章 导数及其应用
1. 了解极值的概念.
2. 了解函数在某点取得极值的必要条件和充分条件.
3. 会用导数求函数的极值.
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的增减.如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
?
观察下图,我们发现,当 t = a 时,高台跳水运动员距水面的高度最大.
问题1 函数h(t)在此点的导数是多少呢? 此点附近的图象有什么特点? 相应地, 导数的符号有什么变化规律?
x
y
O
a
b
x
y
O
a
b
放大t=a附近的图象, 如图所示.
由图可以看出, h′(a)=0; 在t=a的附近,
当t
当t>a时,函数h(t)单调递减,h'(t)<0.
这就是说,在t=a附近,函数值先增后减,即当t在a的附近从小到大经过a时,h'(t)先正后负,且h'(t)连续变化,于是有h'(a)=0.
问题2 对于一般的函数y=f(x),是否也有同样的性质呢?
追问1 如图,函数y=f (x)在x=a,b,c,d,e等点的函数值与这些点附近的函数值有什么关系?
函数f (x)在x=a的函数值比它附近的函数值都小.
函数f (x)在x=b的函数值比它附近的函数值都大.
以x=a, b两点为例
追问2 y=f (x)在这些点处的导数值是多少?
f ′(a)=0
f ′(b)=0
追问3 在这些点附近,函数y=f(x)导数的正负有什么规律?
在x=a附近
左侧f ′(x)<0,
右侧f ′(x)>0
在x=b附近
左侧f ′(x)>0,
右侧f ′(x)<0
极值点与极值
一般地,设函数????=????(????)的定义域为D,设x0∈D,如果对于x0附近的任意不同于x0的x,都有
(1)????(????) (2)????(????)>????(????0),则称x0为函数????(????)的一个极小值点,且????(????)在x0处取极小值,例如b和????(????).
?
概念讲解
追问1 f ′(x0)=0是函数在x=x0处取得极值的什么条件?
x0是函数 f(x) 的极值点
f ′(x0)=0
x0是函数 f(x) 的极值点
x0左右两侧导数异号
f ′(x0)=0
结论:f ′(x0)=0 是可导函数在x0处取得极值的必要而不充分条件.
追问2 函数 y=f (x)在x=x0处取得极值的充分条件是什么?
x0左右侧导数异号
f ′(x0)=0
x0为极值点
问题3 函数的极大值一定大于极小值吗?函数的极大值与极小值是否有大小关系?
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
极大值与极小值没有必然的大小关系.一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值可能大于另一点的极大值.
极小值
极大值
(3) 极大值与极小值没有必然关系,极大值可能比极小值还小.
(1) 极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2) 函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
(4) 对于可导函数,若x0是极值点,则 f '(x0)=0;反之,若f '(x0)=0,则x0不一定是极值点.
归纳总结
【例1】已知函数f(x)=ax3+bx2+cx(a≠0),f′(-1)=f′(1)=0,且f(1)=-1.
(1)试求常数a,b,c的值;
(2)试判断x=±1是函数的极大值点还是极小值点?
解:(1)f′(x)=3ax2+2bx+c.
由f′(-1)=f′(1)=0,
得3a+2b+c=0,3a-2b+c=0.
又f(1)=-1,∴a+b+c=-1,
(2)试判断x=±1是函数的极大值点还是极小值点?
当x<-1或x>1时,f′(x)>0;
当-1<x<1时,f′(x)<0,
∴函数f(x)在(-∞,-1)和(1,+∞)上单调递增,在(-1,1)上单调递减.
∴x=1是函数的极小值点,x=-1是函数的极大值点.
【例2】求函数f(x)=x2e-x的极值点和极值.
解:函数f(x)的定义域为R.
f'(x)=2xe-x-x2e-x=x(2-x)e-x.
令f'(x)=0,得x=0或x=2.
当x变化时,f'(x),f(x)的变化情况如下表:
x
(-∞,0)
0
(0,2)
2
(2,+∞)
f'(x)
-
0
+
0
-
f(x)
↘
极小值
↗
极大值
↘
由上表可以看出,0为函数f(x)的极小值点,极小值为f(0)=0.
2为函数f(x)的极大值点,极大值为f(2)=4e-2.
【例3】已知函数????????=13????3?4????2+4,求函数的极值,并作出函数图象的示意图.
?
解:由题意可得????′????=????2?4 =(????+2)(?????2).
令????′????=0,解得????1=?2,????2=2.
当????变化时,????′????, ????????的变化情况如下表:
因此,当????=?2时,????????有极大值,极大值为?????2= 283;
当????=2时,????????有极小值,极小值为????2=- 43.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
-2
2
+
0
0
+
↗
↘
↗
函数????????=13????3?4????2+4的图像如图所示.
?
【例3】已知函数????????=13????3?4????2+4,求函数的极值,并作出函数图象的示意图.
?
方法归纳
一般地,求函数y=f(x)的极值的步骤
(1)求出函数的定义域及导数f ′(x);
(2)解方程f ′(x)=0,得方程的根x0(可能不止一个);
(3)用方程f ′(x)=0的根,顺次将函数的定义域分成若干个开区间,可将x,f ′(x),f(x)在每个区间内的变化情况列在同一个表格中;
(4)由f ′(x)在各个开区间内的符号,判断f (x)在f ′(x)=0的各个根处的极值情况:
如果左正右负,那么函数f(x)在这个根处取得极大值;
如果左负右正,那么函数f(x)在这个根处取得极小值;
如果导数值在这个根左右两侧同号,那么这个根不是极值点.
回顾:结合本课内容,回答下列问题?
1. 什么是极值?极值点是一个点吗?
2. 函数在某点取得极值的充要条件是什么?
3. 如何求函数的极值?
1.(多选)函数f(x)的定义域为R,它的导函数y=f′(x)的部分图象如图所示,则下面结论正确的是( )
A.在(1,2)上函数f(x)是增函数
B.在(3,4)上函数f(x)是减函数
C.在(1,3)上函数f(x)有极大值
D.x=3是函数f(x)在区间[1,5]上的极小值点
2.函数f(x)=ax-1-ln x(a≤0)在定义域内的极值点的个数为 .
ABC
0
3.函数f(x)=ln x-x在区间(0,e)上的极大值为( )
A.-e B.-1 C.1-e D.0
4.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
A.(-1,2)
B.(-3,6)
C.(-∞,-1)∪(2,+∞)
D.(-∞,-3)∪(6,+∞)
B
D
同课章节目录
