2.6.3 函数的最值 课件(20张PPT)
文档属性
| 名称 | 2.6.3 函数的最值 课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 742.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 08:52:27 | ||
图片预览






文档简介
2.6.3 函数的最值
第二章 导数及其应用
我们知道,极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域内的性质. 也就是说,如果x0是函数y=f(x)的极大(小)值点,那么在x= x0附近找不到比f(x0)更大(小)的值. 但是,在解决实际问题或研究函数的性质时,我们往往更关心函数在某个区间上,哪个值最大,哪个值最小. 如果x0是某个区间上函数y=f(x)的最大(小)值点,那么f(x0)不小(大)于函数y=f(x)在此区间上的所有函数值.
函数在什么条件下一定有最大、最小值?它们与函数极值关系如何?
理解极值与最值的区别和联系;
掌握求函数最值的方法.
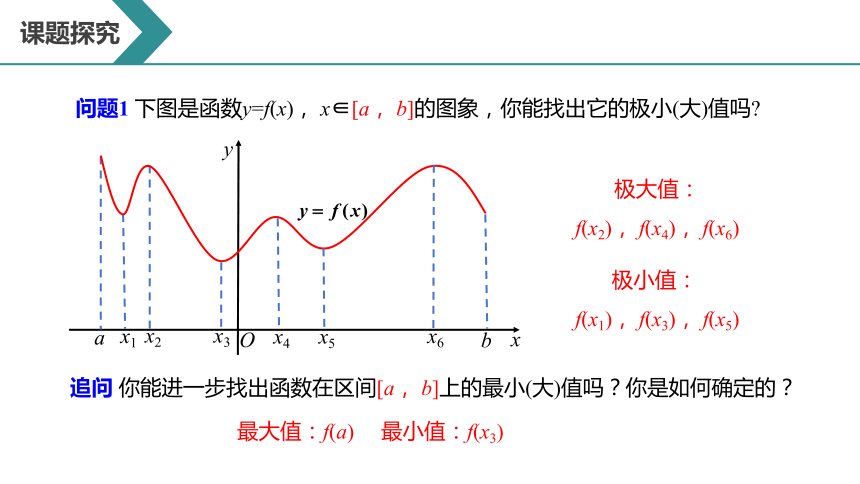
问题1 下图是函数y=f(x), x∈[a, b]的图象,你能找出它的极小(大)值吗?
追问 你能进一步找出函数在区间[a, b]上的最小(大)值吗?你是如何确定的?
x
y
O
a
b
x1
x2
x3
x4
x5
x6
极大值:
f(x2), f(x4), f(x6)
极小值:
f(x1), f(x3), f(x5)
最大值:f(a) 最小值:f(x3)
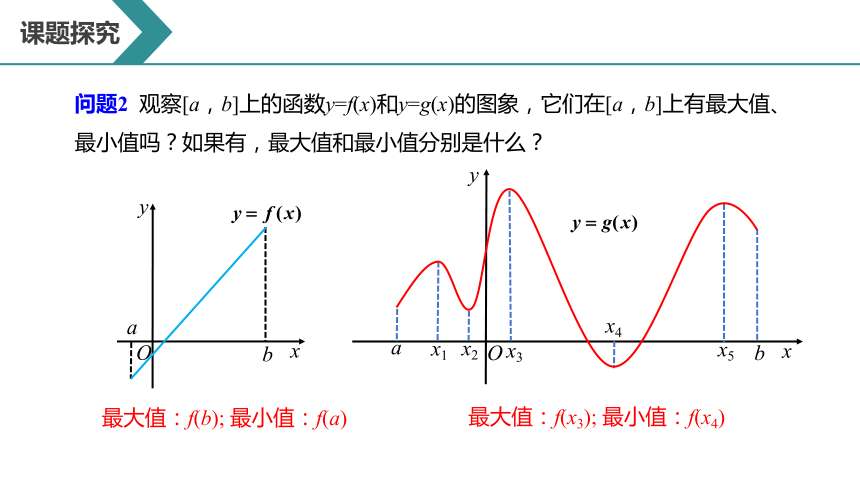
问题2 观察[a,b]上的函数y=f(x)和y=g(x)的图象,它们在[a,b]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
x
y
O
a
b
x
y
O
a
b
x1
x2
x3
x4
x5
最大值:f(b); 最小值:f(a)
最大值:f(x3); 最小值:f(x4)
问题3 以上函数既有最大值,又有最小值,是不是所有的函数都有最大(小)值?
不是
x
y
O
a
b
x
y
O
a
b
x1
x2
x3
x4
x5
最大值:f(b); 最小值:f(a)
最大值:f(x3); 最小值:f(x4)
O
x
y
a
b
y=f(x)
y=f(x)
O
x
y
a
b
O
x
y
a
b
y=f(x)
O
x
y
a
b
y=f(x)
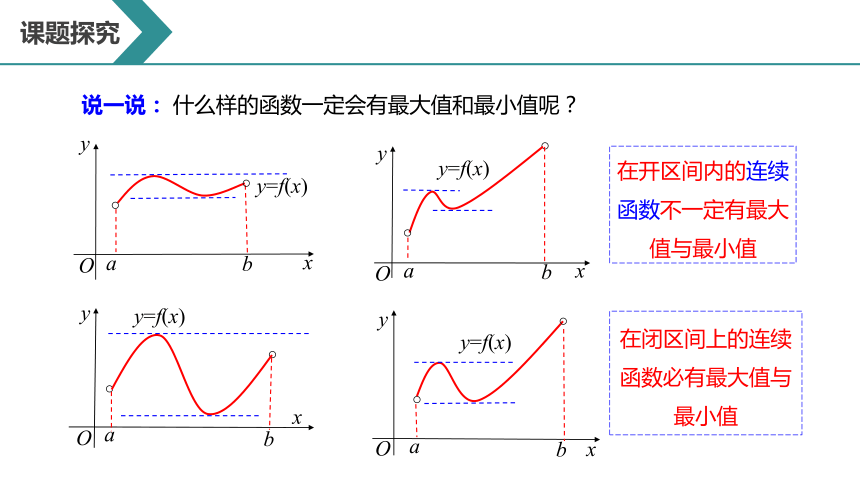
在开区间内的连续函数不一定有最大值与最小值
在闭区间上的连续函数必有最大值与最小值
说一说: 什么样的函数一定会有最大值和最小值呢?
归纳总结
对函数最值的理解:
(1)一般地,如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
(2)如果在函数定义域I内存在x0,使得对任意x∈I,总有f(x)≤f(x0),那么f(x0)为函数在定义域上的最大值;如果在函数定义域I内存在x0,使得对任意x∈I,总有f(x)≥f(x0),那么f(x0)为函数在定义域内的最小值.
【注意】(1)开区间不一定有最值,闭区间上的连续函数一定有最值;
(2)函数f(x)在闭区间[a,b]上连续是f(x)在闭区间[a,b]上有最大值和最小值的充分不必要条件.
【例1】求下列函数在相应区间上的最值:
(1)f(x)=x3-3x2-10,x∈[-1,1];
(2)f(x)=2sin x-x,x∈[-π2,π2].
?
解:(1)f'(x)=3x2-6x=3x(x-2),令f'(x)=0,得x=0(x=2舍去).
当x变化时,f'(x),f(x)的变化情况如下表:
x
-1
(-1,0)
0
(0,1)
1
f'(x)
?
+
0
-
?
f(x)
-14
↗
极大值-10
↘
-12
所以当x=-1时,函数取最小值f(-1)=-14,当x=0时,函数取最大值f(0)=-10.
(2)f(x)=2sin x-x,x∈[-π2,π2].
?
(2)f'(x)=2cos x-1,令f'(x)=0,得x1=π3,x2=-π3.
当x变化时,f'(x),f(x)的变化情况如下表:
?
由上表知,x=π3为极大值点,x=-π3为极小值点,
f(π3)=3?π3,f(-π3)=?3+π3,f(π2)=?2+π2,f(-π2)=2?π2,
通过比较,f(x)max=3?π3,f(x)min=?3+π3.
?
求函数f(x)在闭区间[a,b]上的最值的方法
1.求函数f(x)的导函数f'(x);
2.解方程f'(x)=0,求出使得f'(x)=0的所有点;
3.计算函数f(x)在区间[a,b]内使得f'(x)=0的所有点以及端点的函数值;
4.比较以上各个函数值,其中最大的是函数的最大值,最小的是函数的最小值.
方法归纳
【例2】求下列函数的最值:
(1)f(x)=?????1????2+3;(2)f(x)=(x2-3)ex.
?
解:(1)f'(x)=?(?????1)(?????3)(????2+3)2,令f'(x)=0,得x=-1或x=3,
容易验证函数在x=-1处取得极小值,在x=3处取得极大值,
又因为当x=1时y=0,当x<1时y<0,当x>1时y>0.
据此可以画出函数的大致图象,如图所示.
由图象知,f(x)max=f(3)=3?132+3=16,f(x)min=f(-1)=?1?1(?1)2+3=-12.
?
(2)f(x)=(x2-3)ex.
(2)函数的定义域是R,且f'(x)=2x·ex+(x2-3)ex=ex(x2+2x-3),
令f'(x)>0,得x>1或x<-3;令f'(x)<0,得-3 所以函数f(x)在(-∞,-3)和(1,+∞)内单调递增,在(-3,1)内单调递减,
因此函数f(x)在x=-3处取得极大值,极大值等于f(-3)=6e-3;
在x=1处取得极小值,极小值等于f(1)=-2e.
又由f(x)>0得x>3或x<-3;
由f(x)<0得-3<x<3,
所以函数的大致图象如图所示.
从函数图象可得f(x)min=f(1)=-2e,而函数无最大值.
?
求函数在开区间或无穷区间上最值的方法
求函数在无穷区间(或开区间)上的最值,不仅要研究其极值情况,还要研究其单调性,并通过单调性和极值情况,画出函数的大致图象,然后借助图象观察得到函数的最值.
方法归纳
【例3】已知函数f(x)=ax3-6ax2+b,x∈[-1,2]的最大值为3,最小值为-29,求a,b的值.
解:由题设知a≠0,否则f(x)=b为常函数,与题设矛盾.
求导得f'(x)=3ax2-12ax=3ax(x-4),
令f'(x)=0,得x1=0,x2=4(舍去).
①当a>0,且当x变化时,f'(x),f(x)的变化情况如下表:
x
-1
(-1,0)
0
(0,2)
2
f'(x)
?
+
0
-
?
f(x)
-7a+b
↗
b
↘
-16a+b
由表可知,当x=0时,f(x)取得极大值b,也就是函数在[-1,2]上的最大值,
∴f(0)=b=3.
又f(-1)=-7a+3,f(2)=-16a+3 ∴f(2)=-16a+3=-29,解得a=2.
②当a<0时,同理可得当x=0时,f(x)取得函数在[-1,2]上的最小值,
∴f(0)=b=-29.
又f(-1)=-7a-29,f(2)=-16a-29>f(-1),
∴f(2)=-16a-29=3,解得a=-2.
综上可得a=2,b=3或a=-2,b=-29.
(1)求出函数在给定区间上的极值及函数在区间端点处的函数值;
(2)通过比较它们的大小,判断出哪个是最大值,哪个是最小值;
(3)结合已知求出参数,进而使问题得以解决.
已知函数最值求参数的步骤:
方法归纳
回顾:结合本课内容,回答下列问题?
1. 函数的极值与最值有什么关系?
2. 如何求一个函数的最值?
1.如图所示,函数f(x)导函数的图象是一条直线,则( )
A.函数f(x)没有最大值也没有最小值
B.函数f(x)有最大值,没有最小值
C.函数f(x)没有最大值,有最小值
D.函数f(x)有最大值,也有最小值
C
2.函数f (x)=2x3-3x2-12x+5在[0,3]上的最大值和最小值分别是( )
A.5,-15 B.5,-4 C.-4,-15 D.5,-16
3.设函数f (x)=x3-????22-2x+5,若对任意x∈[-1,2],都有f (x)>m,则实数
m的取值范围是____________.
?
A
?∞,72
第二章 导数及其应用
我们知道,极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域内的性质. 也就是说,如果x0是函数y=f(x)的极大(小)值点,那么在x= x0附近找不到比f(x0)更大(小)的值. 但是,在解决实际问题或研究函数的性质时,我们往往更关心函数在某个区间上,哪个值最大,哪个值最小. 如果x0是某个区间上函数y=f(x)的最大(小)值点,那么f(x0)不小(大)于函数y=f(x)在此区间上的所有函数值.
函数在什么条件下一定有最大、最小值?它们与函数极值关系如何?
理解极值与最值的区别和联系;
掌握求函数最值的方法.
问题1 下图是函数y=f(x), x∈[a, b]的图象,你能找出它的极小(大)值吗?
追问 你能进一步找出函数在区间[a, b]上的最小(大)值吗?你是如何确定的?
x
y
O
a
b
x1
x2
x3
x4
x5
x6
极大值:
f(x2), f(x4), f(x6)
极小值:
f(x1), f(x3), f(x5)
最大值:f(a) 最小值:f(x3)
问题2 观察[a,b]上的函数y=f(x)和y=g(x)的图象,它们在[a,b]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
x
y
O
a
b
x
y
O
a
b
x1
x2
x3
x4
x5
最大值:f(b); 最小值:f(a)
最大值:f(x3); 最小值:f(x4)
问题3 以上函数既有最大值,又有最小值,是不是所有的函数都有最大(小)值?
不是
x
y
O
a
b
x
y
O
a
b
x1
x2
x3
x4
x5
最大值:f(b); 最小值:f(a)
最大值:f(x3); 最小值:f(x4)
O
x
y
a
b
y=f(x)
y=f(x)
O
x
y
a
b
O
x
y
a
b
y=f(x)
O
x
y
a
b
y=f(x)
在开区间内的连续函数不一定有最大值与最小值
在闭区间上的连续函数必有最大值与最小值
说一说: 什么样的函数一定会有最大值和最小值呢?
归纳总结
对函数最值的理解:
(1)一般地,如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
(2)如果在函数定义域I内存在x0,使得对任意x∈I,总有f(x)≤f(x0),那么f(x0)为函数在定义域上的最大值;如果在函数定义域I内存在x0,使得对任意x∈I,总有f(x)≥f(x0),那么f(x0)为函数在定义域内的最小值.
【注意】(1)开区间不一定有最值,闭区间上的连续函数一定有最值;
(2)函数f(x)在闭区间[a,b]上连续是f(x)在闭区间[a,b]上有最大值和最小值的充分不必要条件.
【例1】求下列函数在相应区间上的最值:
(1)f(x)=x3-3x2-10,x∈[-1,1];
(2)f(x)=2sin x-x,x∈[-π2,π2].
?
解:(1)f'(x)=3x2-6x=3x(x-2),令f'(x)=0,得x=0(x=2舍去).
当x变化时,f'(x),f(x)的变化情况如下表:
x
-1
(-1,0)
0
(0,1)
1
f'(x)
?
+
0
-
?
f(x)
-14
↗
极大值-10
↘
-12
所以当x=-1时,函数取最小值f(-1)=-14,当x=0时,函数取最大值f(0)=-10.
(2)f(x)=2sin x-x,x∈[-π2,π2].
?
(2)f'(x)=2cos x-1,令f'(x)=0,得x1=π3,x2=-π3.
当x变化时,f'(x),f(x)的变化情况如下表:
?
由上表知,x=π3为极大值点,x=-π3为极小值点,
f(π3)=3?π3,f(-π3)=?3+π3,f(π2)=?2+π2,f(-π2)=2?π2,
通过比较,f(x)max=3?π3,f(x)min=?3+π3.
?
求函数f(x)在闭区间[a,b]上的最值的方法
1.求函数f(x)的导函数f'(x);
2.解方程f'(x)=0,求出使得f'(x)=0的所有点;
3.计算函数f(x)在区间[a,b]内使得f'(x)=0的所有点以及端点的函数值;
4.比较以上各个函数值,其中最大的是函数的最大值,最小的是函数的最小值.
方法归纳
【例2】求下列函数的最值:
(1)f(x)=?????1????2+3;(2)f(x)=(x2-3)ex.
?
解:(1)f'(x)=?(?????1)(?????3)(????2+3)2,令f'(x)=0,得x=-1或x=3,
容易验证函数在x=-1处取得极小值,在x=3处取得极大值,
又因为当x=1时y=0,当x<1时y<0,当x>1时y>0.
据此可以画出函数的大致图象,如图所示.
由图象知,f(x)max=f(3)=3?132+3=16,f(x)min=f(-1)=?1?1(?1)2+3=-12.
?
(2)f(x)=(x2-3)ex.
(2)函数的定义域是R,且f'(x)=2x·ex+(x2-3)ex=ex(x2+2x-3),
令f'(x)>0,得x>1或x<-3;令f'(x)<0,得-3
因此函数f(x)在x=-3处取得极大值,极大值等于f(-3)=6e-3;
在x=1处取得极小值,极小值等于f(1)=-2e.
又由f(x)>0得x>3或x<-3;
由f(x)<0得-3<x<3,
所以函数的大致图象如图所示.
从函数图象可得f(x)min=f(1)=-2e,而函数无最大值.
?
求函数在开区间或无穷区间上最值的方法
求函数在无穷区间(或开区间)上的最值,不仅要研究其极值情况,还要研究其单调性,并通过单调性和极值情况,画出函数的大致图象,然后借助图象观察得到函数的最值.
方法归纳
【例3】已知函数f(x)=ax3-6ax2+b,x∈[-1,2]的最大值为3,最小值为-29,求a,b的值.
解:由题设知a≠0,否则f(x)=b为常函数,与题设矛盾.
求导得f'(x)=3ax2-12ax=3ax(x-4),
令f'(x)=0,得x1=0,x2=4(舍去).
①当a>0,且当x变化时,f'(x),f(x)的变化情况如下表:
x
-1
(-1,0)
0
(0,2)
2
f'(x)
?
+
0
-
?
f(x)
-7a+b
↗
b
↘
-16a+b
由表可知,当x=0时,f(x)取得极大值b,也就是函数在[-1,2]上的最大值,
∴f(0)=b=3.
又f(-1)=-7a+3,f(2)=-16a+3
②当a<0时,同理可得当x=0时,f(x)取得函数在[-1,2]上的最小值,
∴f(0)=b=-29.
又f(-1)=-7a-29,f(2)=-16a-29>f(-1),
∴f(2)=-16a-29=3,解得a=-2.
综上可得a=2,b=3或a=-2,b=-29.
(1)求出函数在给定区间上的极值及函数在区间端点处的函数值;
(2)通过比较它们的大小,判断出哪个是最大值,哪个是最小值;
(3)结合已知求出参数,进而使问题得以解决.
已知函数最值求参数的步骤:
方法归纳
回顾:结合本课内容,回答下列问题?
1. 函数的极值与最值有什么关系?
2. 如何求一个函数的最值?
1.如图所示,函数f(x)导函数的图象是一条直线,则( )
A.函数f(x)没有最大值也没有最小值
B.函数f(x)有最大值,没有最小值
C.函数f(x)没有最大值,有最小值
D.函数f(x)有最大值,也有最小值
C
2.函数f (x)=2x3-3x2-12x+5在[0,3]上的最大值和最小值分别是( )
A.5,-15 B.5,-4 C.-4,-15 D.5,-16
3.设函数f (x)=x3-????22-2x+5,若对任意x∈[-1,2],都有f (x)>m,则实数
m的取值范围是____________.
?
A
?∞,72
同课章节目录
