6.6.1 柱、锥、台的侧面展开与面积 课件(共14张PPT)
文档属性
| 名称 | 6.6.1 柱、锥、台的侧面展开与面积 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 415.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 18:29:58 | ||
图片预览




文档简介
(共14张PPT)
第六章 立体几何初步
6.6.1 柱、锥、台的侧面展开与面积
1.掌握柱体、锥体、台体的侧面积公式.
2.能应用公式求柱体、锥体、台体的侧面积,熟悉柱体与锥体、台体之间的转换关系.
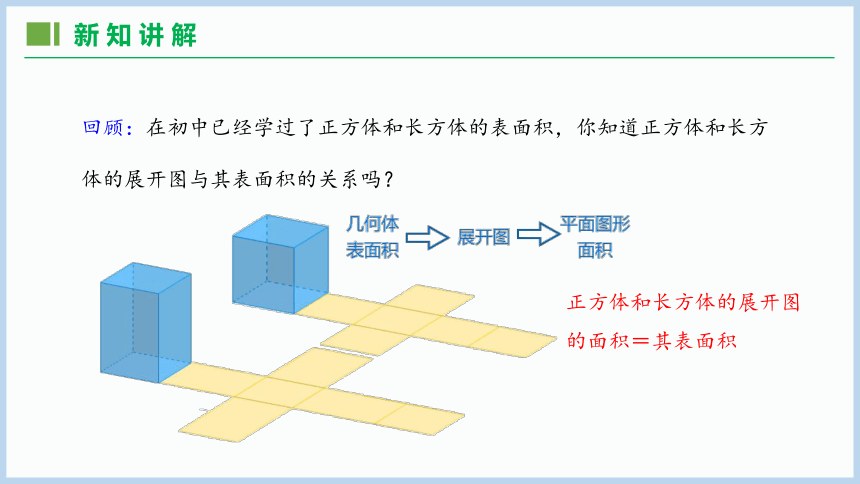
回顾:在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
正方体和长方体的展开图的面积=其表面积
知识点 1:圆柱、圆锥、圆台的的侧面积
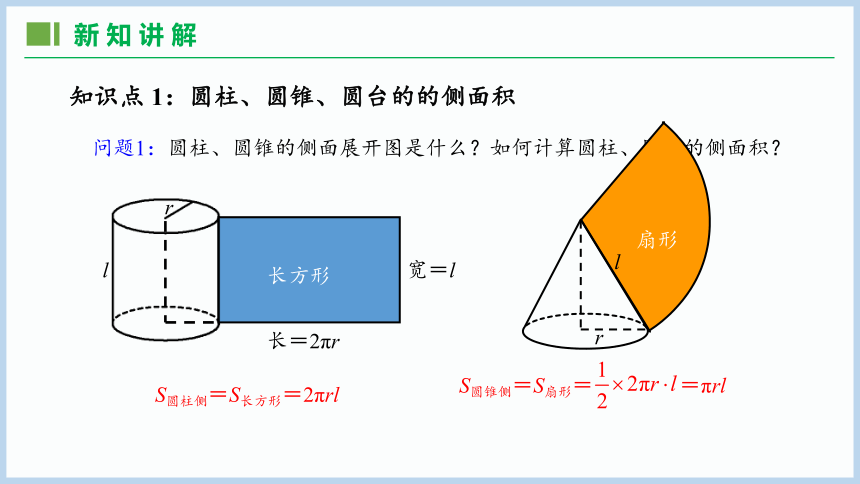
问题1:圆柱、圆锥的侧面展开图是什么?如何计算圆柱、圆锥的侧面积?
S圆柱侧=S长方形=2πrl
长方形
长=2πr
r
宽=l
l
r
l
S圆锥侧=S扇形= =πrl
扇形
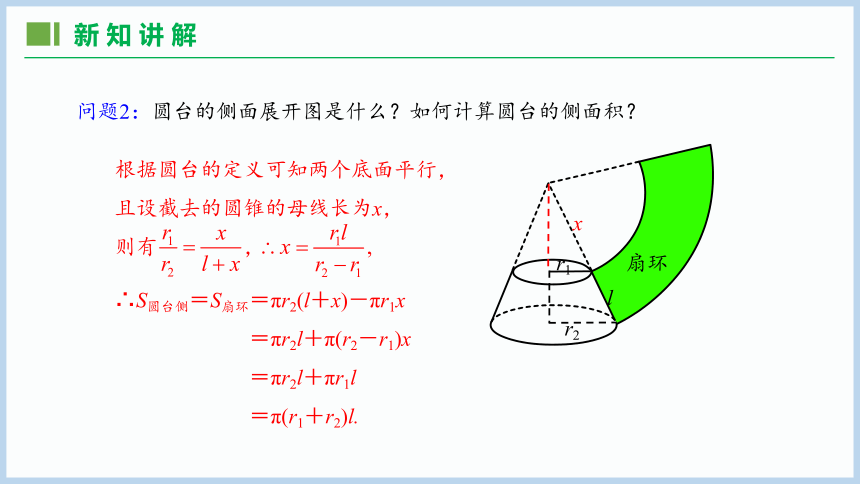
问题2:圆台的侧面展开图是什么?如何计算圆台的侧面积?
r2
l
r1
扇环
∴S圆台侧=S扇环=πr2(l+x)-πr1x
=πr2l+π(r2-r1)x
=πr2l+πr1l
=π(r1+r2)l.
x
根据圆台的定义可知两个底面平行,且设截去的圆锥的母线长为x,
则有 ,
练一练
1.底面半径为3,母线为5的圆锥的侧面积为( )
A.12π B.15π
C.24π D.36π
B
例1 一个圆柱形的锅炉,底面直径d=1m,高h=2.3m.求锅炉的表面积(精确到0.1m2).
因此锅炉的表面积约为8.8m2.
解:S=S侧面积+2S底面积=πdh+2π
=π×1×2.3+2π×0.25=2.8π≈8.8(m2),
圆柱、圆柱、圆台的表面积公式
归纳总结
圆柱的表面积公式:S圆柱表=2πr2+2πrl;
圆锥的表面积公式:S圆锥表=πr2+πrl=πr(r+l);
圆柱的表面积公式:S圆台表=πr12+πr22+π(r1+r2)l
=π(r12+r22+r1l+r2l).
例2 圆台的上、下底面半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的侧面积是多少?(结果中保留π)
解:如图,设圆台上底面周长为c cm.
∵圆环的圆心角是180°,∴c=π·SA.
又∵c=2π×10=20π(cm),∴SA=20cm.
同理SB=40cm,
∴AB=SB-SA=20(cm),
S圆台侧=π·(r1+r2)·AB=π(10+20)×20=600π(cm2),
因此,圆台的侧面积为600π cm2.
知识点 2:直棱柱、正棱锥、正棱台的侧面积
讨论:直棱柱、正棱锥、正棱台的侧面沿着一条侧棱展开,得到什么图形?如何计算其侧面积?
S直棱柱侧=ch
S正棱锥侧= ch'
S正棱台侧= (c1+c2)h'
c为棱柱、棱锥的底面周长,c1,c2为棱台的上下底面周长
例3 一个正三棱台的上、下底面边长分别为3cm和6cm,高是 cm.求这个正三棱台的侧面积.
连接A1O1并延长交B1C1于点D1,连接AO并延长交BC于点D,
过点D1作AD的垂线,垂直为点E,连接D1D.
解:如图,点O1,O分别是上、下底面的中心,则O1O= cm.
D1
D
E
在Rt△D1ED中,D1E=O1O= cm,
例3 一个正三棱台的上、下底面边长分别为3cm和6cm,高是 cm.求这个正三棱台的侧面积.
D1
D
E
∴S正三棱台侧=
因此,三棱台的侧面积为 cm2.
练一练
2.侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的侧面积是( )
B
根据今天所学,回顾下列知识点:
柱体、锥体、台体的侧面积公式.
第六章 立体几何初步
6.6.1 柱、锥、台的侧面展开与面积
1.掌握柱体、锥体、台体的侧面积公式.
2.能应用公式求柱体、锥体、台体的侧面积,熟悉柱体与锥体、台体之间的转换关系.
回顾:在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
正方体和长方体的展开图的面积=其表面积
知识点 1:圆柱、圆锥、圆台的的侧面积
问题1:圆柱、圆锥的侧面展开图是什么?如何计算圆柱、圆锥的侧面积?
S圆柱侧=S长方形=2πrl
长方形
长=2πr
r
宽=l
l
r
l
S圆锥侧=S扇形= =πrl
扇形
问题2:圆台的侧面展开图是什么?如何计算圆台的侧面积?
r2
l
r1
扇环
∴S圆台侧=S扇环=πr2(l+x)-πr1x
=πr2l+π(r2-r1)x
=πr2l+πr1l
=π(r1+r2)l.
x
根据圆台的定义可知两个底面平行,且设截去的圆锥的母线长为x,
则有 ,
练一练
1.底面半径为3,母线为5的圆锥的侧面积为( )
A.12π B.15π
C.24π D.36π
B
例1 一个圆柱形的锅炉,底面直径d=1m,高h=2.3m.求锅炉的表面积(精确到0.1m2).
因此锅炉的表面积约为8.8m2.
解:S=S侧面积+2S底面积=πdh+2π
=π×1×2.3+2π×0.25=2.8π≈8.8(m2),
圆柱、圆柱、圆台的表面积公式
归纳总结
圆柱的表面积公式:S圆柱表=2πr2+2πrl;
圆锥的表面积公式:S圆锥表=πr2+πrl=πr(r+l);
圆柱的表面积公式:S圆台表=πr12+πr22+π(r1+r2)l
=π(r12+r22+r1l+r2l).
例2 圆台的上、下底面半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的侧面积是多少?(结果中保留π)
解:如图,设圆台上底面周长为c cm.
∵圆环的圆心角是180°,∴c=π·SA.
又∵c=2π×10=20π(cm),∴SA=20cm.
同理SB=40cm,
∴AB=SB-SA=20(cm),
S圆台侧=π·(r1+r2)·AB=π(10+20)×20=600π(cm2),
因此,圆台的侧面积为600π cm2.
知识点 2:直棱柱、正棱锥、正棱台的侧面积
讨论:直棱柱、正棱锥、正棱台的侧面沿着一条侧棱展开,得到什么图形?如何计算其侧面积?
S直棱柱侧=ch
S正棱锥侧= ch'
S正棱台侧= (c1+c2)h'
c为棱柱、棱锥的底面周长,c1,c2为棱台的上下底面周长
例3 一个正三棱台的上、下底面边长分别为3cm和6cm,高是 cm.求这个正三棱台的侧面积.
连接A1O1并延长交B1C1于点D1,连接AO并延长交BC于点D,
过点D1作AD的垂线,垂直为点E,连接D1D.
解:如图,点O1,O分别是上、下底面的中心,则O1O= cm.
D1
D
E
在Rt△D1ED中,D1E=O1O= cm,
例3 一个正三棱台的上、下底面边长分别为3cm和6cm,高是 cm.求这个正三棱台的侧面积.
D1
D
E
∴S正三棱台侧=
因此,三棱台的侧面积为 cm2.
练一练
2.侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的侧面积是( )
B
根据今天所学,回顾下列知识点:
柱体、锥体、台体的侧面积公式.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
