6.6.2 柱、锥、台的体积 课件(共12张PPT)
文档属性
| 名称 | 6.6.2 柱、锥、台的体积 课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 445.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 18:27:21 | ||
图片预览




文档简介
(共12张PPT)
第六章 立体几何初步
6.6.2 柱、锥、台的体积
1.掌握柱体、锥体、台体的体积公式.
2.会利用柱、锥、台的体积公式求有关几何体的体积.
知识点 1:柱体、锥体的体积
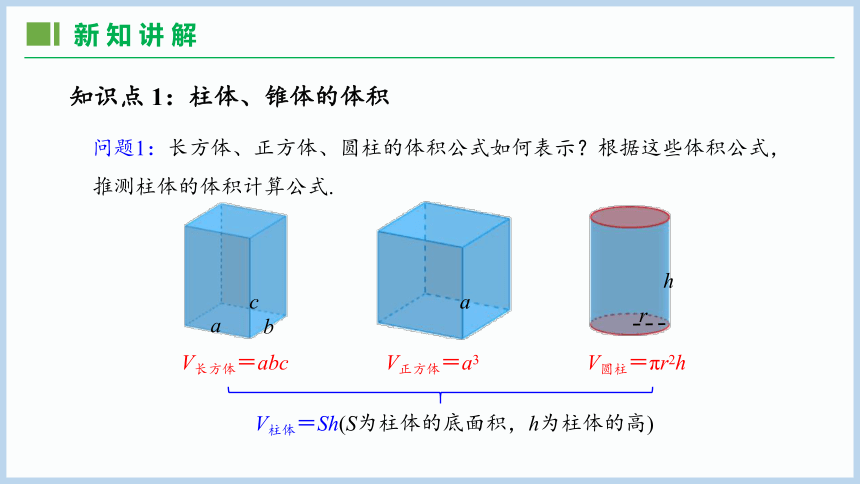
问题1:长方体、正方体、圆柱的体积公式如何表示?根据这些体积公式,推测柱体的体积计算公式.
V正方体=a3
a
V长方体=abc
a
b
c
V圆柱=πr2h
h
r
V柱体=Sh(S为柱体的底面积,h为柱体的高)
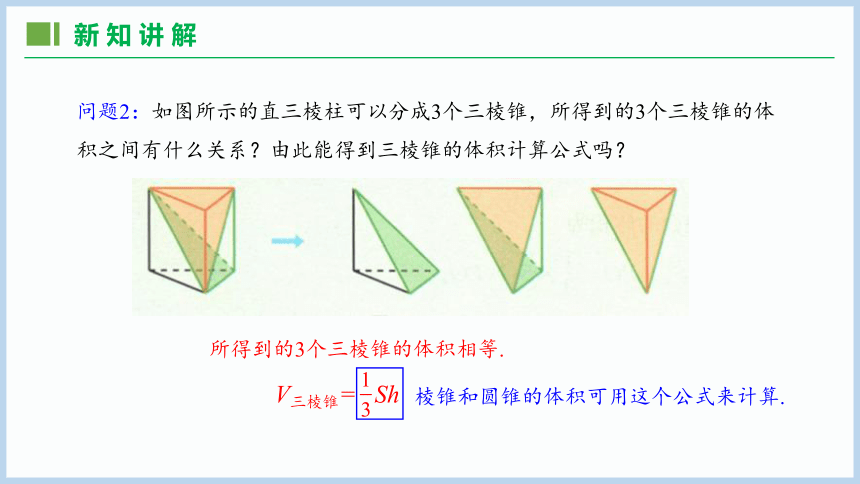
问题2:如图所示的直三棱柱可以分成3个三棱锥,所得到的3个三棱锥的体积之间有什么关系?由此能得到三棱锥的体积计算公式吗?
V三棱锥= Sh
所得到的3个三棱锥的体积相等.
棱锥和圆锥的体积可用这个公式来计算.
练一练
1.已知一个圆柱底面直径和母线长均为4,则该圆柱的体积为( )
A.2π B.4π C.8π D.16π
D
例1 埃及胡夫金字塔大约建于公元前2580年,其形状为正四棱锥.塔高约146.6m,底面边长约230.4m.求这座金字塔的侧面积和体积.(精确到0.1)
解:如图,AC为高,BC为底面的边心距,
则AC=146.6m,BC=115.2m,底面周长c=(4×230.4)m.
S侧面积=
=
V= S底·AC=
因此,金字塔的侧面积约为85914.9m2,体积约为2594046.0m3.
知识点 2:台体的体积
思考:根据台体的特征,如何求台体的体积?
由于棱台(圆台)是由棱锥(圆锥)截成的,因此可以利用两个锥体的体积差得到棱台(圆台)的体积公式.
如图,四棱台ABCD-A'B'C'D'的高为h,
四边形ABCD面积为S下,四边形A'B'C'D'面积为S上,
设四棱锥P-A'B'C'D'的高为h',
S上
S下
S上
S下
∴V台=VP-ABCD-VP-A'B'C'D'
= S下(h+h')- S上h'
= S下h+ (S下-S上)h'
= S下h+ (S下-S上)·
S下-
S上
S上
S上S下
= (S上+S下+ S上 · S下 )h.
台体的体积公式
由P-A'B'C'D'与P-ABCD相似得
S上
S下
S上
S下
S上
S下-
S上
S上
S上S下
交流讨论:柱体、锥体、台体的体积之间有什么关系?
上底扩大
S上=S
S下=S
上底缩小
S上=0
S下=S
例2 已知一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm.求其体积.
因此正四棱台的体积为112cm3.
解:V= (S上+S下+ S上 · S下 )h
=
=112(cm3),
练一练
2.已知高为3的直棱柱ABC-A1B1C1的底面是边长为1的正三角形(如图),则三棱锥B1-ABC的体积为( )
D
根据今天所学,回顾下列知识点:
柱体、锥体、台体的体积公式.
柱
锥
台
第六章 立体几何初步
6.6.2 柱、锥、台的体积
1.掌握柱体、锥体、台体的体积公式.
2.会利用柱、锥、台的体积公式求有关几何体的体积.
知识点 1:柱体、锥体的体积
问题1:长方体、正方体、圆柱的体积公式如何表示?根据这些体积公式,推测柱体的体积计算公式.
V正方体=a3
a
V长方体=abc
a
b
c
V圆柱=πr2h
h
r
V柱体=Sh(S为柱体的底面积,h为柱体的高)
问题2:如图所示的直三棱柱可以分成3个三棱锥,所得到的3个三棱锥的体积之间有什么关系?由此能得到三棱锥的体积计算公式吗?
V三棱锥= Sh
所得到的3个三棱锥的体积相等.
棱锥和圆锥的体积可用这个公式来计算.
练一练
1.已知一个圆柱底面直径和母线长均为4,则该圆柱的体积为( )
A.2π B.4π C.8π D.16π
D
例1 埃及胡夫金字塔大约建于公元前2580年,其形状为正四棱锥.塔高约146.6m,底面边长约230.4m.求这座金字塔的侧面积和体积.(精确到0.1)
解:如图,AC为高,BC为底面的边心距,
则AC=146.6m,BC=115.2m,底面周长c=(4×230.4)m.
S侧面积=
=
V= S底·AC=
因此,金字塔的侧面积约为85914.9m2,体积约为2594046.0m3.
知识点 2:台体的体积
思考:根据台体的特征,如何求台体的体积?
由于棱台(圆台)是由棱锥(圆锥)截成的,因此可以利用两个锥体的体积差得到棱台(圆台)的体积公式.
如图,四棱台ABCD-A'B'C'D'的高为h,
四边形ABCD面积为S下,四边形A'B'C'D'面积为S上,
设四棱锥P-A'B'C'D'的高为h',
S上
S下
S上
S下
∴V台=VP-ABCD-VP-A'B'C'D'
= S下(h+h')- S上h'
= S下h+ (S下-S上)h'
= S下h+ (S下-S上)·
S下-
S上
S上
S上S下
= (S上+S下+ S上 · S下 )h.
台体的体积公式
由P-A'B'C'D'与P-ABCD相似得
S上
S下
S上
S下
S上
S下-
S上
S上
S上S下
交流讨论:柱体、锥体、台体的体积之间有什么关系?
上底扩大
S上=S
S下=S
上底缩小
S上=0
S下=S
例2 已知一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm.求其体积.
因此正四棱台的体积为112cm3.
解:V= (S上+S下+ S上 · S下 )h
=
=112(cm3),
练一练
2.已知高为3的直棱柱ABC-A1B1C1的底面是边长为1的正三角形(如图),则三棱锥B1-ABC的体积为( )
D
根据今天所学,回顾下列知识点:
柱体、锥体、台体的体积公式.
柱
锥
台
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
