期末巩固复习卷(含解析)-2024-2025学年数学九年级下册人教版
文档属性
| 名称 | 期末巩固复习卷(含解析)-2024-2025学年数学九年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 16:50:15 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
期末巩固复习卷-2024-2025学年数学九年级下册人教版
一、单选题
1.如图所示的几何体的俯视图是( )
A. B.
C. D.
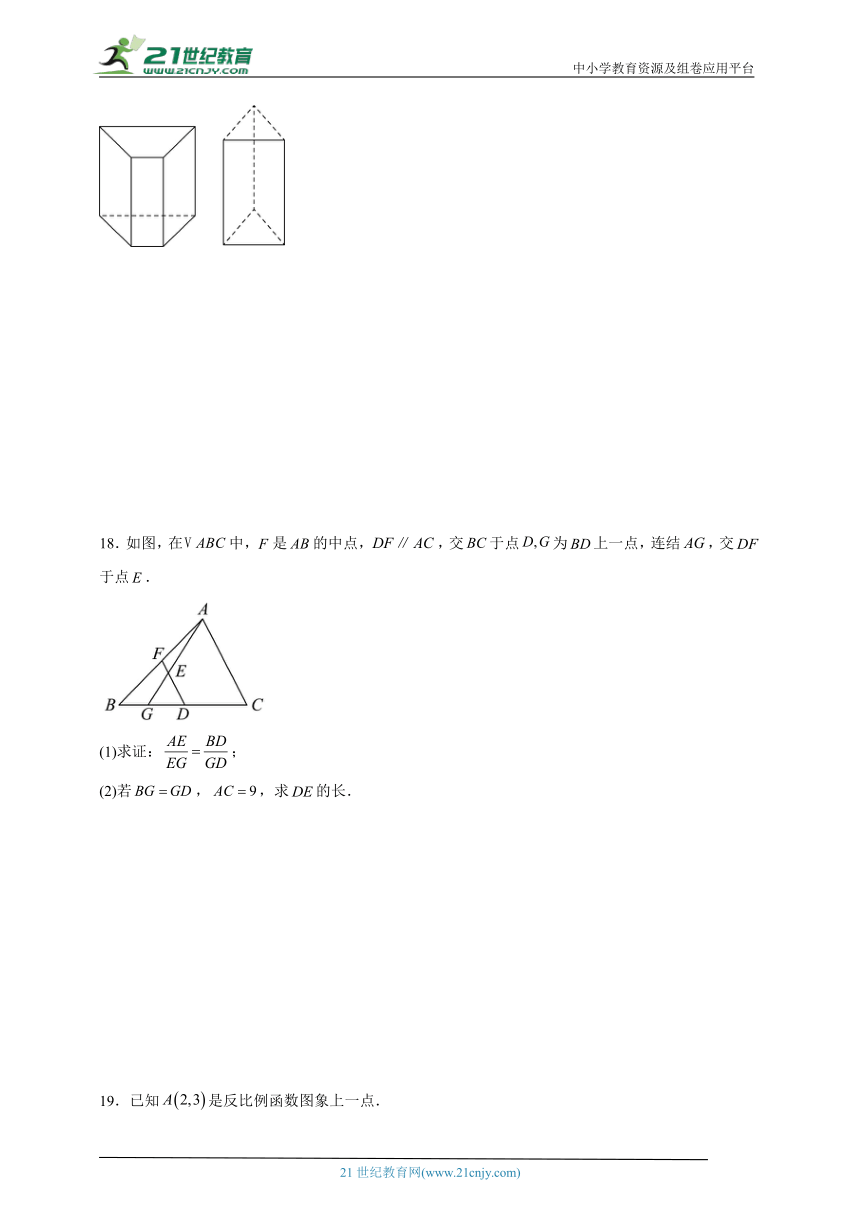
2.如图,四边形中,,,,,点M在折线段上运动,令,点D到的距离为y,则y的最小值为( )
A. B.3 C. D.4
3.在中,,交延长线于点,,垂足为若,,则的值为( )
A. B. C. D.
4.以下函数,符合当时,的是( )
A. B. C. D.
5.如图,和是以点O为位似中心的位似图形,若,则和的面积比是( )
A. B. C. D.
6.如图,矩形的顶点,,分别落在反比例函数,图象上,轴,矩形的面积为,则为( )
A.1 B. C. D.2
7.某数学研究性学习小组制作了如下的三角函数计算图尺,在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺的O刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出的值是( )
A. B. C. D.
二、填空题
8.已知反比例函数的图象在第二、四象限,请写出一个符合题意的值是 .
9.中,均为锐角,且满足,则 度.
10.如图,在中,,是上一点,且.若,则的长为 .
11.顶角为的等腰三角形,其底边长与腰长的比为,通常称它为“黄金三角形”,利用“黄金三角形”可以计算 .
12.如图,在矩形中,,,点O是矩形的中心,将直角的直角顶点与O重合,一条直角边与重合,使三角板沿逆时针方向绕点O旋转;两条直角边始终与直线,相交,交点分别为M,N.当, ,设时,,则y与x之间的函数关系式是 .
13.如图,在平面直角坐标系中,矩形的顶点B在反比例函数的图象上,反比例函数的图象与边交于点D,连接,则四边形的面积为 .
14.如图,正方形的边长为10,点P为的中点,连接、,点M、N分别为、上的动点,连接、,则的最小值为 .
15.如图,沿过点的直线翻折,使点的对应点刚好落在边的延长线上,折痕交线段于点,连接交边于点,连接,若,且,则的值为 .
三、解答题
16.计算:
(1).
(2)已知,求代数式的值.
17.(1)画出小颖在路灯下影长的线段.
(2)画出下列几何体的主视图.
18.如图,在中,是的中点,,交于点为上一点,连结,交于点.
(1)求证:;
(2)若,,求的长.
19.已知是反比例函数图象上一点.
(1)求这个反比例函数的解析式;
(2)若点是这个反比例函数图象上的点,连接(为坐标原点),过点作轴,求的面积.
20.近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了如图1所示的护眼灯,其侧面示意图如图2所示(台灯底座高度忽略不计),其中灯柱,灯臂,灯罩,,,分别可以绕点上下调节一定的角度.经使用发现:当,且时,台灯光线最佳.
(1)求台灯光线最佳时的度数;
(2)求台灯光线最佳时点到桌面的距离.(精确到,参考数值:,,)
21.如图,在矩形中,,,点P在射线上运动,以为直角边向右作,使得,,连接.
(1)若与相似,则______;
(2)当时,求的值;
(3)求的最小值.
22.李明在“鱼菜共生系统对水质的影响”实验研究中,针对水质中的氨氮含量进行了实时监测,如图是水质中氨氮含量与时间x(天)的变化图象,其中为一条线段,段满足反比例函数关系,
(1)段的函数解析式为________;
(2)李明以普通养殖塘为对照组,发现对照组的氨氮含量与时间满足直线的函数解析式,则在第40天时,鱼菜共生系统水中的氨氮含量比普通养殖塘低多少?
23.如图,在平面直角坐标系中,的顶点C在x轴正半轴上,顶点B在第一象限内,顶点A的坐标为,,且,P为线段上一点(不与端点重合).
(1)如图1,当时,过点B作垂直于x轴,垂足为D,连接.
①求证:;
②求的度数;
(2)如图2,若平分,M为线段(不含端点)上一动点,N为线段(不含端点)上一动点,连接.请在图3中作出点M、N使得的周长值最小,试猜想周长的最小值与线段的大小关系,并说明理由.
24.如图,在平面直角坐标系中,反比例函数图象上有A,B两点,其中点B在点A右侧,连接.
(1)如图1,设A点坐标为,若,,且.
①求k的值;
②若的面积为,求点B的坐标;
(2)如图2,延长交反比例函数的图象于点C,连接,点为上一点,连接并延长交于点E.若的面积与的面积相等,是否存在直线,使得点E始终在该直线下方,若存在,请求出a的最小值;若不存在,请说明理由.
《期末巩固复习卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7
答案 D B A C D C D
1.D
【分析】本题考查了简单组合体的三视图,俯视图是从上往下看得到的视图,由此可得出答案.
【详解】解:该几何体的俯视图是:
故选:D.
2.B
【分析】本题考查了勾股定理,点到直线的距离,反比例函数的图象与性质,巧用分类讨论的数学思想是解题关键.根据题意,对点M在和上的情况进行分类讨论即可解决问题.
【详解】解:当点M在上时,
,且,
点D到的距离为定值5,即;
当点M在上时,
过点M作于点,过点作于点,
,
,
,
,
,
,
即,
,
连接,
则,
点M在上,
,
则当时,y的值最小为
综上所述,y的最小值为
故选:B.
3.A
【分析】本题主要考查了解直角三角形和锐角三角比等知识点,熟练掌握锐角三角比是解题的关键.
利用等角的三角比相等和解直角三角形表示出相关的边,即可解此题.
【详解】解:由题可知,
,
,
又,,
,
,
,
,
,
在中,
,
令,,
又,
,
则,
在中,
,
,
.
故选:A.
4.C
【分析】本题考查了一次函数、反比例函数和二次函数的性质.根据一次函数、反比例函数和二次函数的性质即可求解.
【详解】解:∵当时,,
∴在时,函数随的增大而增大,
A、在和时,函数随的增大而增大,本选项不符合题意;
B、在和时,函数随的增大而减少,本选项不符合题意;
C、,对称轴为直线,在时,函数随的增大而增大,本选项符合题意;
D、,在时,函数随的增大而减少,本选项不符合题意;
故选:C.
5.D
【分析】本题考查的是位似变换、相似三角形的性质,熟记相似三角形的面积比等于相似比的平方是解题的关键.根据位似图形的概念得到,,证明,根据相似三角形的性质求出,再根据相似三角形的面积比等于相似比的平方计算,得到答案.
【详解】解:,
,
和是以点为位似中心的位似图形,
,,
,
,
与的面积比为:,
故选:D.
6.C
【分析】本题考查了反比例函数与矩形的性质,解一元二次方程,根据题意设,则,,根据矩形的面积为,列出方程,解方程,即可求解.
【详解】解:设,则,
∴
∵矩形的面积为,
∴,即
解得:或(舍去)
故选:C.
7.D
【分析】本题考查圆周角定理、直径的性质、锐角三角函数等知识,解题的关键是学会用转化的思想思考问题,连接,证明,最后利用锐角三角函数值求出的值.
【详解】解:如图,连接.
是直径,
,
,,
,
,,
,
故选:D.
8.(答案不唯一)
【分析】本题考查了反比例函数的图象性质.对于反比例函数,(1)当时,反比例函数图象在一、三象限;(2)当时,反比例函数图象在第二、四象限内.
根据反比例函数的图象在第二、四象限,列出不等式,求得m的取值范围,然后在m的取值范围内任取一个m值.
【详解】解:∵反比例函数的图象在第二、四象限,
∴,
∴,
∴m可以取,
故答案为:(答案不唯一).
9.75
【分析】本题考查特殊角的三角函数值,绝对值的非负性以及三角形的内角和.熟记特殊角的三角函数值是解题的关键.根据非负性,求出,进而求出,根据三角形内角和求出即可.
【详解】解:∵ ,
∴ ,
∴ ,
∴,
∴;
故答案为:75.
10.
【分析】本题主要考查了相似三角形的判定与性质,等腰三角形的性质,熟知相似三角形的判定与性质是解题的关键.根据题意,得出,再结合相似三角形的性质即可解决问题.
【详解】解:由题知,,
,
,
,
∴,
则,
,
,
又,
,
故答案为:2.
11.
【分析】本题考查了黄金分割,等腰三角形的性质,解直角三角形,熟练掌握等腰三角形的性质是解题的关键.
过点A作,垂足为D,先利用等腰三角形的三线合一性质可得,,然后在中,利用锐角三角函数的定义进行计算即可解答.
【详解】解:如图:过点A作,垂足为D,
∵,,
∴,,
在中,,
,
故答案为:.
12. /
【分析】过点作于点,的延长线交于点,过点作于点,如图,易得四边形和四边形都是矩形,则,再利用点是矩形的中心得到,设时,,则,接着证明,利用相似心得到,从而得到,由于当点在点时,;当点在点时,,则的取值范围为,然后计算对应的函数值.
【详解】解:过点作于点,的延长线交于点,过点作于点,如图,
,
∴四边形和四边形都是矩形,
∴,
∵点是矩形的中心,
,
设时,,则,
∵,
∴,
∵,
∴,
∵,
∴,
∴,即,
,
当点在点时,;当点在点时,,
∴的取值范围为,
当时,.
故答案为:.
【点睛】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角,公共边等隐含条件,以充分发挥基本图形的作用;灵活运用相似三角形的性质计算相应线段的长或表示线段之间的关系是解决问题的关键.也考查了矩形的性质和判定、旋转的性质和函数关系式.
13.
【分析】本题考查了反比例函数的比例系数k的几何意义,正确反比例函数的比例系数k的几何意义,是解题的关键.根据反比例函数的比例系数k的几何意义,可知,,再计算,即得答案.
【详解】矩形的顶点B在反比例函数的图象上,
,
反比例函数的图象与边交于点D,
,
四边形的面积为.
故答案为:.
14.
【分析】取的中点E,连接,过点B作于H,交于点M,过点M作于点N,求出,证明,则,得到,此时是最小值,证明,则,即可求出.
【详解】解:取的中点E,连接,过点B作于H,交于点M,过点M作于点N,
∵四边形是正方形,
∴,
∵点P为的中点,的中点E,
∴,
∴
∵,
∴,
∴,
∴,
∴此时是最小值,
∵,
∴,
∵,
∴
∴,
∴,
∴,
即的最小值为,
故答案为: .
【点睛】此题考查了相似三角形的判定和性质、正方形的性质、全等三角形的判定和性质、勾股定理、角平分线的性质定理等知识,添加辅助线找到是最小值是解题的关键.
15.
【分析】设,则,可得,由轴对称的性质可得:,,求解,利用,可得,利用,可得,再进一步求解即可.
【详解】解:∵,
∴设,则,
∴,
由轴对称的性质可得:,,
∵四边形是平行四边形,
∴,,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
而,
∴,
∴,
∴,
∴;
故答案为:
【点睛】本题考查的是轴对称的性质,平行四边形的性质,勾股定理的应用,锐角三角函数的应用,熟练的利用三角函数解决问题是关键.
16.(1)
(2)
【分析】本题考查了特殊角的三角函数值的计算,比例的性质,熟记三角函数值,掌握消元变形代入计算的技能是解题的关键.
(1)根据特殊角的三角函数值代入计算即可.
(2)变形得,代入化简计算即可.
【详解】(1)解:
.
(2)解:根据题意,即,
则.
17.见解析
【分析】本题考查视图和中心投影的特点与应用
(1)从路灯顶部向小颖的头部画一条直线,然后从这条直线向下延伸到地面,即可得小颖的影子.
(2)主视图是从物体的正面看得到的视图.
【详解】解:(1)如图,为所求;
(2)如图,
18.(1)见解析
(2)
【分析】本题主要考查相似三角形的判定与性质.
(1)由,易证,,由相似三角形的性质得,,得出,从而可得结论;
(2)由(1)知,推出,求出 ,再根据,即可求解.
【详解】(1)证明:∵,
∴,,
∴ ,,
∵是的中点,即,
∴,即,
∴即;
(2)解:由(1)知,
∵,
∴,
∴ ,
∵,
∴,
∵,
∴.
19.(1)
(2)
【分析】本题考查待定系数法求反比例函数的解析式,反比例函数图象上的点的坐标特征,解题的关键是掌握反比例函数的性质.
(1)设反比例函数的解析式为.利用待定系数法求解;
(2)求出点P的坐标,利用三角形面积公式求解.
【详解】(1)解:设反比例函数的解析式为.
∵是反比例函数图象上一点,
∴,
∴反比例函数的解析式为;
(2)解:∵点是这个反比例函数图象上的点,
∴,
∴,
∵轴,
∴的面积.
20.(1)
(2)点到桌面的距离约为
【分析】本题考查解直角三角形的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
(1)过点C作,由题意得,再结合,,利用平行线的性质即可解答;
(2)过点作,垂足为,过点作,垂足为,然后根据锐角三角函数,即可得到的长,再根据,即可求得的长,从而可以解答本题.
【详解】(1)解:过点C作,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
∴;
(2)解:过点作,垂足为,过点作,垂足为,如图所示,
∵,,,
∴,
∴四边形为矩形,
∴,,
又∵,,,
∴,
∴(cm),
答:点到桌面的距离约为.
21.(1)3或12
(2)
(3)
【分析】本题是相似形的综合题,考查了相似三角形的判定和性质,勾股定理,矩形的性质,熟练掌握相似三角形的判定和性质定理是解题的关键.
(1)根据矩形的性质得到,求得,根据相似三角形的性质即可得到结论;
(2)过点作于点,与BC交于点,则,,根据相似三角形的性质得到设,则,求得,根据勾股定理得到;
(3)由(2)得,,根据相似三角形的性质得到,设,则,求得,得到,根据勾股定理和二次函数的性质即可得到结论.
【详解】(1)∵四边形ABCD是矩形,
∴,
∴,
∵与相似,
,
,
,
故答案为:3或12;
(2)过点作于点,与BC交于点,:
则,
,
,
,
,
,
设
,
,
,
,
,
,
(3)由(2)得,,
,
设,则,
,
,
,
,
,
当时,的最小值为,
∴CQ长的最小值为.
22.(1)
(2)
【分析】本题主要考查了一次函数的应用、反比例函数的应用,解题时要熟练掌握并能灵活运用是关键.
(1)依据题意,设段的函数解析式为,故,从而可以得解;
(2)依据题意,设直线为,又,,从而,进而求出解析式,再令,求出y,又对于函数,当时,求出y,最后比较即可得解.
【详解】(1)解:由题意,设段的函数解析式为,
,
段的函数解析式为,
故答案为:;
(2)解:由题意,设直线为,
又∵,,
,
,,
直线为,
当时,,
又对于函数,
当时,
,
,
鱼菜共生系统水中的氨氮含量比普通养殖塘低.
23.(1)①见解析;②
(2)相等,见解析
【分析】本题属于几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,勾股定理,解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题.
(1)①利用全等三角形的性质证明,再证明可得结论;
②证明,都是等腰直角三角形即可;
(2)作点关于直线的对称点,点关于直线的对称点,连接交于点,交于点,连接,,此时的周长最小.求出,的长可得结论.
【详解】(1)①证明:如图1中,轴于点.
,
,
,,
,
,
,
,
,,
,
;
②解:,
,,
,
,即,
,
,
;
(2)解:如图,作点关于直线的对称点,点关于直线的对称点,连接交于点,交于点,连接,,此时的周长最小.
结论:的周长的最小值.
理由:过点作于.
在中,,,
,,,
平分,
,
,
,
,,
,关于对称,,关于对称,
,,,
,
,,
,
的周长的最小值的长,
的周长的最小值.
24.(1)①4;②
(2)存在,3
【分析】(1)①依题意,得,再解n的值,即可作答;
②过点A作轴于点M,过点B作轴于点N,易得,进而用坐标可以表示出的长度,建立方程求解即可;
(2)连接,易证E是中点,进而可表示出点A坐标,求出反比例函数表达式,设出B点坐标,再表示出E点坐标即可得解.
本题考查了反比例函数与几何综合,求反比例函数的解析式,因式分解法解方程,正确掌握相关性质内容是解题的关键.
【详解】(1)解:(1)①∵,,
∴,
∴,
∵,且,
∴,
∴A点坐标为,
∴;
②过点A作轴于点M,交于一点K,过点B作轴于点N,
设点B的坐标为,
∵反比例函数图象上有A,B两点,
∴,
∵,
∴,
∵的面积为,
∴,
即,
整理可得:,
解得(负值舍去),
∴点B的坐标为.
(2)解:连接,
∵的面积与的面积相等,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵O为中点,
∴
∴E为中点,
∴为的中位线
∴,
∵D点坐标为,
∴A点坐标为,
则,
∴反比例函数表达式为,
设点B的坐标为,
∴点C的坐标为,
∵A点坐标为,E为中点,
∴,
∴点E的坐标为,
∵点B在点A右侧,
∴,
∴,
∴点E始终在直线的下方,
∴a的最小值为3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末巩固复习卷-2024-2025学年数学九年级下册人教版
一、单选题
1.如图所示的几何体的俯视图是( )
A. B.
C. D.
2.如图,四边形中,,,,,点M在折线段上运动,令,点D到的距离为y,则y的最小值为( )
A. B.3 C. D.4
3.在中,,交延长线于点,,垂足为若,,则的值为( )
A. B. C. D.
4.以下函数,符合当时,的是( )
A. B. C. D.
5.如图,和是以点O为位似中心的位似图形,若,则和的面积比是( )
A. B. C. D.
6.如图,矩形的顶点,,分别落在反比例函数,图象上,轴,矩形的面积为,则为( )
A.1 B. C. D.2
7.某数学研究性学习小组制作了如下的三角函数计算图尺,在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺的O刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出的值是( )
A. B. C. D.
二、填空题
8.已知反比例函数的图象在第二、四象限,请写出一个符合题意的值是 .
9.中,均为锐角,且满足,则 度.
10.如图,在中,,是上一点,且.若,则的长为 .
11.顶角为的等腰三角形,其底边长与腰长的比为,通常称它为“黄金三角形”,利用“黄金三角形”可以计算 .
12.如图,在矩形中,,,点O是矩形的中心,将直角的直角顶点与O重合,一条直角边与重合,使三角板沿逆时针方向绕点O旋转;两条直角边始终与直线,相交,交点分别为M,N.当, ,设时,,则y与x之间的函数关系式是 .
13.如图,在平面直角坐标系中,矩形的顶点B在反比例函数的图象上,反比例函数的图象与边交于点D,连接,则四边形的面积为 .
14.如图,正方形的边长为10,点P为的中点,连接、,点M、N分别为、上的动点,连接、,则的最小值为 .
15.如图,沿过点的直线翻折,使点的对应点刚好落在边的延长线上,折痕交线段于点,连接交边于点,连接,若,且,则的值为 .
三、解答题
16.计算:
(1).
(2)已知,求代数式的值.
17.(1)画出小颖在路灯下影长的线段.
(2)画出下列几何体的主视图.
18.如图,在中,是的中点,,交于点为上一点,连结,交于点.
(1)求证:;
(2)若,,求的长.
19.已知是反比例函数图象上一点.
(1)求这个反比例函数的解析式;
(2)若点是这个反比例函数图象上的点,连接(为坐标原点),过点作轴,求的面积.
20.近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了如图1所示的护眼灯,其侧面示意图如图2所示(台灯底座高度忽略不计),其中灯柱,灯臂,灯罩,,,分别可以绕点上下调节一定的角度.经使用发现:当,且时,台灯光线最佳.
(1)求台灯光线最佳时的度数;
(2)求台灯光线最佳时点到桌面的距离.(精确到,参考数值:,,)
21.如图,在矩形中,,,点P在射线上运动,以为直角边向右作,使得,,连接.
(1)若与相似,则______;
(2)当时,求的值;
(3)求的最小值.
22.李明在“鱼菜共生系统对水质的影响”实验研究中,针对水质中的氨氮含量进行了实时监测,如图是水质中氨氮含量与时间x(天)的变化图象,其中为一条线段,段满足反比例函数关系,
(1)段的函数解析式为________;
(2)李明以普通养殖塘为对照组,发现对照组的氨氮含量与时间满足直线的函数解析式,则在第40天时,鱼菜共生系统水中的氨氮含量比普通养殖塘低多少?
23.如图,在平面直角坐标系中,的顶点C在x轴正半轴上,顶点B在第一象限内,顶点A的坐标为,,且,P为线段上一点(不与端点重合).
(1)如图1,当时,过点B作垂直于x轴,垂足为D,连接.
①求证:;
②求的度数;
(2)如图2,若平分,M为线段(不含端点)上一动点,N为线段(不含端点)上一动点,连接.请在图3中作出点M、N使得的周长值最小,试猜想周长的最小值与线段的大小关系,并说明理由.
24.如图,在平面直角坐标系中,反比例函数图象上有A,B两点,其中点B在点A右侧,连接.
(1)如图1,设A点坐标为,若,,且.
①求k的值;
②若的面积为,求点B的坐标;
(2)如图2,延长交反比例函数的图象于点C,连接,点为上一点,连接并延长交于点E.若的面积与的面积相等,是否存在直线,使得点E始终在该直线下方,若存在,请求出a的最小值;若不存在,请说明理由.
《期末巩固复习卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7
答案 D B A C D C D
1.D
【分析】本题考查了简单组合体的三视图,俯视图是从上往下看得到的视图,由此可得出答案.
【详解】解:该几何体的俯视图是:
故选:D.
2.B
【分析】本题考查了勾股定理,点到直线的距离,反比例函数的图象与性质,巧用分类讨论的数学思想是解题关键.根据题意,对点M在和上的情况进行分类讨论即可解决问题.
【详解】解:当点M在上时,
,且,
点D到的距离为定值5,即;
当点M在上时,
过点M作于点,过点作于点,
,
,
,
,
,
,
即,
,
连接,
则,
点M在上,
,
则当时,y的值最小为
综上所述,y的最小值为
故选:B.
3.A
【分析】本题主要考查了解直角三角形和锐角三角比等知识点,熟练掌握锐角三角比是解题的关键.
利用等角的三角比相等和解直角三角形表示出相关的边,即可解此题.
【详解】解:由题可知,
,
,
又,,
,
,
,
,
,
在中,
,
令,,
又,
,
则,
在中,
,
,
.
故选:A.
4.C
【分析】本题考查了一次函数、反比例函数和二次函数的性质.根据一次函数、反比例函数和二次函数的性质即可求解.
【详解】解:∵当时,,
∴在时,函数随的增大而增大,
A、在和时,函数随的增大而增大,本选项不符合题意;
B、在和时,函数随的增大而减少,本选项不符合题意;
C、,对称轴为直线,在时,函数随的增大而增大,本选项符合题意;
D、,在时,函数随的增大而减少,本选项不符合题意;
故选:C.
5.D
【分析】本题考查的是位似变换、相似三角形的性质,熟记相似三角形的面积比等于相似比的平方是解题的关键.根据位似图形的概念得到,,证明,根据相似三角形的性质求出,再根据相似三角形的面积比等于相似比的平方计算,得到答案.
【详解】解:,
,
和是以点为位似中心的位似图形,
,,
,
,
与的面积比为:,
故选:D.
6.C
【分析】本题考查了反比例函数与矩形的性质,解一元二次方程,根据题意设,则,,根据矩形的面积为,列出方程,解方程,即可求解.
【详解】解:设,则,
∴
∵矩形的面积为,
∴,即
解得:或(舍去)
故选:C.
7.D
【分析】本题考查圆周角定理、直径的性质、锐角三角函数等知识,解题的关键是学会用转化的思想思考问题,连接,证明,最后利用锐角三角函数值求出的值.
【详解】解:如图,连接.
是直径,
,
,,
,
,,
,
故选:D.
8.(答案不唯一)
【分析】本题考查了反比例函数的图象性质.对于反比例函数,(1)当时,反比例函数图象在一、三象限;(2)当时,反比例函数图象在第二、四象限内.
根据反比例函数的图象在第二、四象限,列出不等式,求得m的取值范围,然后在m的取值范围内任取一个m值.
【详解】解:∵反比例函数的图象在第二、四象限,
∴,
∴,
∴m可以取,
故答案为:(答案不唯一).
9.75
【分析】本题考查特殊角的三角函数值,绝对值的非负性以及三角形的内角和.熟记特殊角的三角函数值是解题的关键.根据非负性,求出,进而求出,根据三角形内角和求出即可.
【详解】解:∵ ,
∴ ,
∴ ,
∴,
∴;
故答案为:75.
10.
【分析】本题主要考查了相似三角形的判定与性质,等腰三角形的性质,熟知相似三角形的判定与性质是解题的关键.根据题意,得出,再结合相似三角形的性质即可解决问题.
【详解】解:由题知,,
,
,
,
∴,
则,
,
,
又,
,
故答案为:2.
11.
【分析】本题考查了黄金分割,等腰三角形的性质,解直角三角形,熟练掌握等腰三角形的性质是解题的关键.
过点A作,垂足为D,先利用等腰三角形的三线合一性质可得,,然后在中,利用锐角三角函数的定义进行计算即可解答.
【详解】解:如图:过点A作,垂足为D,
∵,,
∴,,
在中,,
,
故答案为:.
12. /
【分析】过点作于点,的延长线交于点,过点作于点,如图,易得四边形和四边形都是矩形,则,再利用点是矩形的中心得到,设时,,则,接着证明,利用相似心得到,从而得到,由于当点在点时,;当点在点时,,则的取值范围为,然后计算对应的函数值.
【详解】解:过点作于点,的延长线交于点,过点作于点,如图,
,
∴四边形和四边形都是矩形,
∴,
∵点是矩形的中心,
,
设时,,则,
∵,
∴,
∵,
∴,
∵,
∴,
∴,即,
,
当点在点时,;当点在点时,,
∴的取值范围为,
当时,.
故答案为:.
【点睛】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角,公共边等隐含条件,以充分发挥基本图形的作用;灵活运用相似三角形的性质计算相应线段的长或表示线段之间的关系是解决问题的关键.也考查了矩形的性质和判定、旋转的性质和函数关系式.
13.
【分析】本题考查了反比例函数的比例系数k的几何意义,正确反比例函数的比例系数k的几何意义,是解题的关键.根据反比例函数的比例系数k的几何意义,可知,,再计算,即得答案.
【详解】矩形的顶点B在反比例函数的图象上,
,
反比例函数的图象与边交于点D,
,
四边形的面积为.
故答案为:.
14.
【分析】取的中点E,连接,过点B作于H,交于点M,过点M作于点N,求出,证明,则,得到,此时是最小值,证明,则,即可求出.
【详解】解:取的中点E,连接,过点B作于H,交于点M,过点M作于点N,
∵四边形是正方形,
∴,
∵点P为的中点,的中点E,
∴,
∴
∵,
∴,
∴,
∴,
∴此时是最小值,
∵,
∴,
∵,
∴
∴,
∴,
∴,
即的最小值为,
故答案为: .
【点睛】此题考查了相似三角形的判定和性质、正方形的性质、全等三角形的判定和性质、勾股定理、角平分线的性质定理等知识,添加辅助线找到是最小值是解题的关键.
15.
【分析】设,则,可得,由轴对称的性质可得:,,求解,利用,可得,利用,可得,再进一步求解即可.
【详解】解:∵,
∴设,则,
∴,
由轴对称的性质可得:,,
∵四边形是平行四边形,
∴,,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
而,
∴,
∴,
∴,
∴;
故答案为:
【点睛】本题考查的是轴对称的性质,平行四边形的性质,勾股定理的应用,锐角三角函数的应用,熟练的利用三角函数解决问题是关键.
16.(1)
(2)
【分析】本题考查了特殊角的三角函数值的计算,比例的性质,熟记三角函数值,掌握消元变形代入计算的技能是解题的关键.
(1)根据特殊角的三角函数值代入计算即可.
(2)变形得,代入化简计算即可.
【详解】(1)解:
.
(2)解:根据题意,即,
则.
17.见解析
【分析】本题考查视图和中心投影的特点与应用
(1)从路灯顶部向小颖的头部画一条直线,然后从这条直线向下延伸到地面,即可得小颖的影子.
(2)主视图是从物体的正面看得到的视图.
【详解】解:(1)如图,为所求;
(2)如图,
18.(1)见解析
(2)
【分析】本题主要考查相似三角形的判定与性质.
(1)由,易证,,由相似三角形的性质得,,得出,从而可得结论;
(2)由(1)知,推出,求出 ,再根据,即可求解.
【详解】(1)证明:∵,
∴,,
∴ ,,
∵是的中点,即,
∴,即,
∴即;
(2)解:由(1)知,
∵,
∴,
∴ ,
∵,
∴,
∵,
∴.
19.(1)
(2)
【分析】本题考查待定系数法求反比例函数的解析式,反比例函数图象上的点的坐标特征,解题的关键是掌握反比例函数的性质.
(1)设反比例函数的解析式为.利用待定系数法求解;
(2)求出点P的坐标,利用三角形面积公式求解.
【详解】(1)解:设反比例函数的解析式为.
∵是反比例函数图象上一点,
∴,
∴反比例函数的解析式为;
(2)解:∵点是这个反比例函数图象上的点,
∴,
∴,
∵轴,
∴的面积.
20.(1)
(2)点到桌面的距离约为
【分析】本题考查解直角三角形的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
(1)过点C作,由题意得,再结合,,利用平行线的性质即可解答;
(2)过点作,垂足为,过点作,垂足为,然后根据锐角三角函数,即可得到的长,再根据,即可求得的长,从而可以解答本题.
【详解】(1)解:过点C作,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
∴;
(2)解:过点作,垂足为,过点作,垂足为,如图所示,
∵,,,
∴,
∴四边形为矩形,
∴,,
又∵,,,
∴,
∴(cm),
答:点到桌面的距离约为.
21.(1)3或12
(2)
(3)
【分析】本题是相似形的综合题,考查了相似三角形的判定和性质,勾股定理,矩形的性质,熟练掌握相似三角形的判定和性质定理是解题的关键.
(1)根据矩形的性质得到,求得,根据相似三角形的性质即可得到结论;
(2)过点作于点,与BC交于点,则,,根据相似三角形的性质得到设,则,求得,根据勾股定理得到;
(3)由(2)得,,根据相似三角形的性质得到,设,则,求得,得到,根据勾股定理和二次函数的性质即可得到结论.
【详解】(1)∵四边形ABCD是矩形,
∴,
∴,
∵与相似,
,
,
,
故答案为:3或12;
(2)过点作于点,与BC交于点,:
则,
,
,
,
,
,
设
,
,
,
,
,
,
(3)由(2)得,,
,
设,则,
,
,
,
,
,
当时,的最小值为,
∴CQ长的最小值为.
22.(1)
(2)
【分析】本题主要考查了一次函数的应用、反比例函数的应用,解题时要熟练掌握并能灵活运用是关键.
(1)依据题意,设段的函数解析式为,故,从而可以得解;
(2)依据题意,设直线为,又,,从而,进而求出解析式,再令,求出y,又对于函数,当时,求出y,最后比较即可得解.
【详解】(1)解:由题意,设段的函数解析式为,
,
段的函数解析式为,
故答案为:;
(2)解:由题意,设直线为,
又∵,,
,
,,
直线为,
当时,,
又对于函数,
当时,
,
,
鱼菜共生系统水中的氨氮含量比普通养殖塘低.
23.(1)①见解析;②
(2)相等,见解析
【分析】本题属于几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,勾股定理,解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题.
(1)①利用全等三角形的性质证明,再证明可得结论;
②证明,都是等腰直角三角形即可;
(2)作点关于直线的对称点,点关于直线的对称点,连接交于点,交于点,连接,,此时的周长最小.求出,的长可得结论.
【详解】(1)①证明:如图1中,轴于点.
,
,
,,
,
,
,
,
,,
,
;
②解:,
,,
,
,即,
,
,
;
(2)解:如图,作点关于直线的对称点,点关于直线的对称点,连接交于点,交于点,连接,,此时的周长最小.
结论:的周长的最小值.
理由:过点作于.
在中,,,
,,,
平分,
,
,
,
,,
,关于对称,,关于对称,
,,,
,
,,
,
的周长的最小值的长,
的周长的最小值.
24.(1)①4;②
(2)存在,3
【分析】(1)①依题意,得,再解n的值,即可作答;
②过点A作轴于点M,过点B作轴于点N,易得,进而用坐标可以表示出的长度,建立方程求解即可;
(2)连接,易证E是中点,进而可表示出点A坐标,求出反比例函数表达式,设出B点坐标,再表示出E点坐标即可得解.
本题考查了反比例函数与几何综合,求反比例函数的解析式,因式分解法解方程,正确掌握相关性质内容是解题的关键.
【详解】(1)解:(1)①∵,,
∴,
∴,
∵,且,
∴,
∴A点坐标为,
∴;
②过点A作轴于点M,交于一点K,过点B作轴于点N,
设点B的坐标为,
∵反比例函数图象上有A,B两点,
∴,
∵,
∴,
∵的面积为,
∴,
即,
整理可得:,
解得(负值舍去),
∴点B的坐标为.
(2)解:连接,
∵的面积与的面积相等,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵O为中点,
∴
∴E为中点,
∴为的中位线
∴,
∵D点坐标为,
∴A点坐标为,
则,
∴反比例函数表达式为,
设点B的坐标为,
∴点C的坐标为,
∵A点坐标为,E为中点,
∴,
∴点E的坐标为,
∵点B在点A右侧,
∴,
∴,
∴点E始终在直线的下方,
∴a的最小值为3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
