27.1.3 圆内接四边形 第2课时 课件(共17张PPT) 华东师大版九年级数学下册
文档属性
| 名称 | 27.1.3 圆内接四边形 第2课时 课件(共17张PPT) 华东师大版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 496.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
第2课时 圆内接四边形
27.1 圆的认识
3.圆周角
1.复习并巩固圆周角和圆心角的相关知识;
2. 理解并掌握圆内接四边形的概念及性质并学会运用. (重点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
回顾:什么是圆周角?什么是圆周角定理?
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
圆上一条弧所对的圆周角等于它所对的圆心角的一半.
O
A
B
C
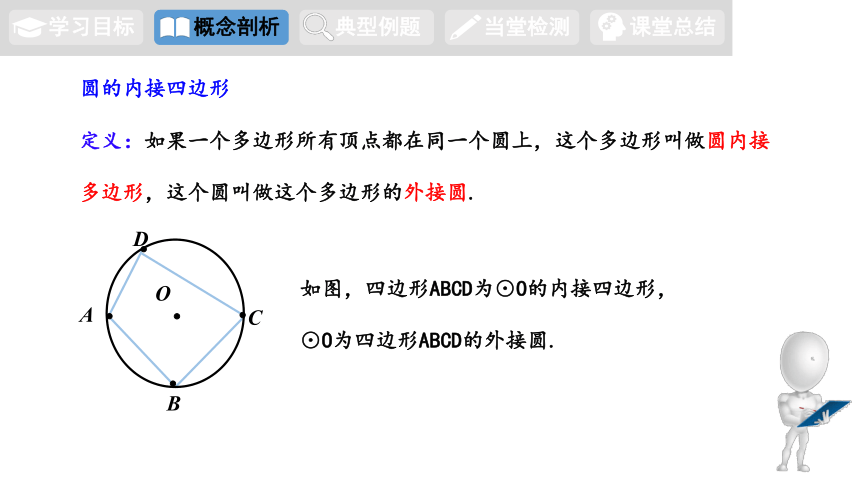
圆的内接四边形
定义:如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接
多边形,这个圆叫做这个多边形的外接圆.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
A
B
C
D
O
典型例题
当堂检测
学习目标
课堂总结
概念剖析
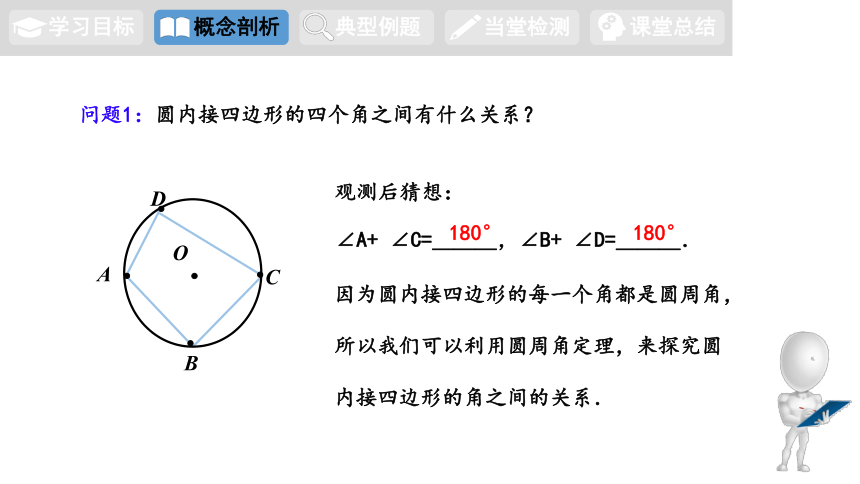
问题1:圆内接四边形的四个角之间有什么关系?
A
B
C
D
O
观测后猜想:
∠A+ ∠C=___,∠B+ ∠D=___.
180°
180°
因为圆内接四边形的每一个角都是圆周角,
所以我们可以利用圆周角定理,来探究圆
内接四边形的角之间的关系.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
A
B
C
D
O
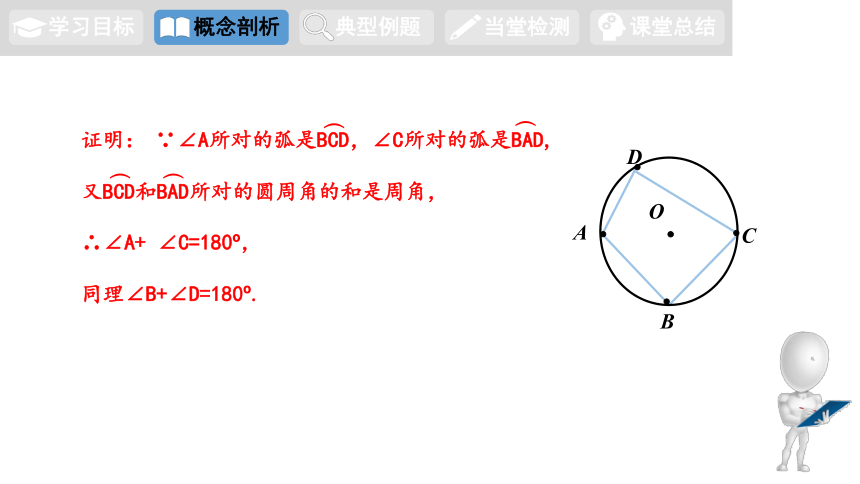
同理∠B+∠D=180 .
∴∠A+ ∠C=180 ,
又BCD和BAD所对的圆周角的和是周角,
(
(
证明:
∵∠A所对的弧是BCD,∠C所对的弧是BAD,
(
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
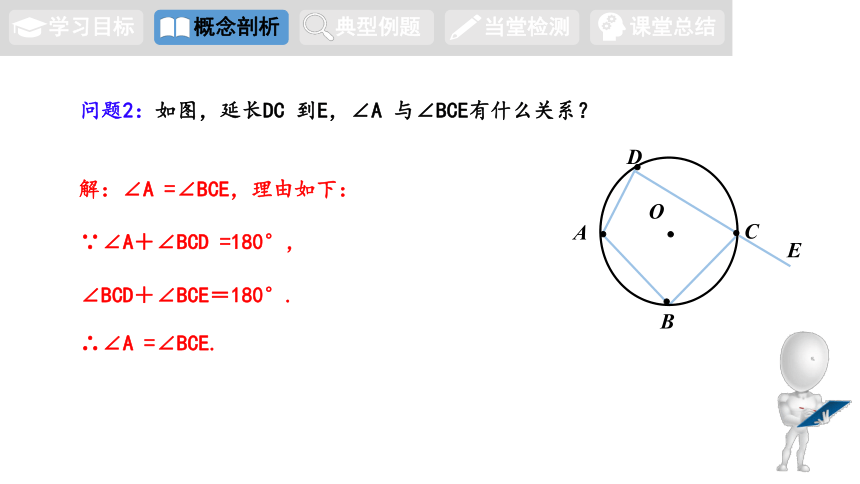
问题2:如图,延长DC 到E,∠A 与∠BCE有什么关系?
A
B
C
D
O
E
解:∠A =∠BCE,理由如下:
∵∠A+∠BCD =180°,
∠BCD+∠BCE=180°.
∴∠A =∠BCE.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
圆内接四边形的性质:
圆内接四边形的对角互补,且任何一个外角都等于它的内对角.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
填一填:
如图,四边形ABCD是⊙O的内接四边形,∠A =110°,∠B = 80°,
则∠DCB= ,∠D = ,∠DCE = .
A
E
C
D
B
O
70°
100°
110°
例1.在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰6.
求这个四边形各角的度数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:设∠A,∠B,∠C的度数分别等于2x,3x,6x.
∵ 四边形ABCD内接于圆,
∴ ∠A+ ∠C=∠B+∠D=180°,
∵ 2x+6x=180°,
∴ x = 22.5°.
∴∠A=45°,∠B=67.5°,∠C =135°,∠D=180°-67.5°=112.5°.
例2.如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形 OABC 为平行
四边形,求∠OAD 和∠OCD的角度之和.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:∵四边形ABCD是圆内接四边形,
∴∠OAD+∠OCD=∠ODA+∠ODC=∠ADC=60°.
∴∠OAD=∠ODA,∠OCD=∠ODC.
∵ AO=OD,CO=OD.
又由题意可知∠AOC=2∠ADC.
∵四边形OABC为平行四边形,
∴∠B+∠ADC=180°.
∴∠AOC=∠B.
∴∠ADC=180°÷3=60°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
圆内接四边形的角的“三种关系”:
(3)圆内接四边形的外角等于它的内对角.
(2)四个角的和是360°.若四边形ABCD为⊙O的内接四边形,
则∠A+∠B+∠C+∠D=360°;
(1)对角互补.若四边形ABCD为⊙O的内接四边形,则∠A+∠C=180°,
∠B+∠D=180°;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=90°,则∠BCD的度数是
( )
A.45° B.90°
C.135° D.150°
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.若ABCD为圆内接四边形,则下列哪个选项可能成立( )
B
A. ∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4
B. ∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4
C. ∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4
D. ∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,在⊙O中,∠CBD =30°,∠BDC =20°,求∠A.
解:∵∠CBD=30°,∠BDC=20°,
∴∠A=180°-∠C=50°.
∴∠C=180°-∠CBD-∠BDC=130°,
O
A
B
D
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,已知 A,B,C,D 是 ⊙O 上的四点,延长 DC,AB 相交于点E.
若BC=BE. 求证:△ADE是等腰三角形.
证明:∵BC=BE,
∴△ADE是等腰三角形.
∴∠A=∠BCE,∴∠A=∠E,
∵∠BCE+∠DCB=180°,
∴∠A+∠DCB=180°.
∵四边形ABCD是圆内接四边形,
∴∠BCE=∠E.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.圆内接多边形的定义
一个多边形的____________都在____________,这个多边形叫做圆的内接
多边形,这个圆叫做这个多边形的________.
2.圆内接四边形的性质
所有顶点
同一个圆上
外接圆
圆内接四边形的对角________,且任何一个外角都等于它的________.
互补
内对角
补充:若圆内接四边形的对角相等,则此时的四边形为矩形.
第2课时 圆内接四边形
27.1 圆的认识
3.圆周角
1.复习并巩固圆周角和圆心角的相关知识;
2. 理解并掌握圆内接四边形的概念及性质并学会运用. (重点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
回顾:什么是圆周角?什么是圆周角定理?
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
圆上一条弧所对的圆周角等于它所对的圆心角的一半.
O
A
B
C
圆的内接四边形
定义:如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接
多边形,这个圆叫做这个多边形的外接圆.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
A
B
C
D
O
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题1:圆内接四边形的四个角之间有什么关系?
A
B
C
D
O
观测后猜想:
∠A+ ∠C=___,∠B+ ∠D=___.
180°
180°
因为圆内接四边形的每一个角都是圆周角,
所以我们可以利用圆周角定理,来探究圆
内接四边形的角之间的关系.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
A
B
C
D
O
同理∠B+∠D=180 .
∴∠A+ ∠C=180 ,
又BCD和BAD所对的圆周角的和是周角,
(
(
证明:
∵∠A所对的弧是BCD,∠C所对的弧是BAD,
(
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题2:如图,延长DC 到E,∠A 与∠BCE有什么关系?
A
B
C
D
O
E
解:∠A =∠BCE,理由如下:
∵∠A+∠BCD =180°,
∠BCD+∠BCE=180°.
∴∠A =∠BCE.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
圆内接四边形的性质:
圆内接四边形的对角互补,且任何一个外角都等于它的内对角.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
填一填:
如图,四边形ABCD是⊙O的内接四边形,∠A =110°,∠B = 80°,
则∠DCB= ,∠D = ,∠DCE = .
A
E
C
D
B
O
70°
100°
110°
例1.在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰6.
求这个四边形各角的度数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:设∠A,∠B,∠C的度数分别等于2x,3x,6x.
∵ 四边形ABCD内接于圆,
∴ ∠A+ ∠C=∠B+∠D=180°,
∵ 2x+6x=180°,
∴ x = 22.5°.
∴∠A=45°,∠B=67.5°,∠C =135°,∠D=180°-67.5°=112.5°.
例2.如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形 OABC 为平行
四边形,求∠OAD 和∠OCD的角度之和.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:∵四边形ABCD是圆内接四边形,
∴∠OAD+∠OCD=∠ODA+∠ODC=∠ADC=60°.
∴∠OAD=∠ODA,∠OCD=∠ODC.
∵ AO=OD,CO=OD.
又由题意可知∠AOC=2∠ADC.
∵四边形OABC为平行四边形,
∴∠B+∠ADC=180°.
∴∠AOC=∠B.
∴∠ADC=180°÷3=60°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
圆内接四边形的角的“三种关系”:
(3)圆内接四边形的外角等于它的内对角.
(2)四个角的和是360°.若四边形ABCD为⊙O的内接四边形,
则∠A+∠B+∠C+∠D=360°;
(1)对角互补.若四边形ABCD为⊙O的内接四边形,则∠A+∠C=180°,
∠B+∠D=180°;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=90°,则∠BCD的度数是
( )
A.45° B.90°
C.135° D.150°
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.若ABCD为圆内接四边形,则下列哪个选项可能成立( )
B
A. ∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4
B. ∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4
C. ∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4
D. ∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,在⊙O中,∠CBD =30°,∠BDC =20°,求∠A.
解:∵∠CBD=30°,∠BDC=20°,
∴∠A=180°-∠C=50°.
∴∠C=180°-∠CBD-∠BDC=130°,
O
A
B
D
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,已知 A,B,C,D 是 ⊙O 上的四点,延长 DC,AB 相交于点E.
若BC=BE. 求证:△ADE是等腰三角形.
证明:∵BC=BE,
∴△ADE是等腰三角形.
∴∠A=∠BCE,∴∠A=∠E,
∵∠BCE+∠DCB=180°,
∴∠A+∠DCB=180°.
∵四边形ABCD是圆内接四边形,
∴∠BCE=∠E.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.圆内接多边形的定义
一个多边形的____________都在____________,这个多边形叫做圆的内接
多边形,这个圆叫做这个多边形的________.
2.圆内接四边形的性质
所有顶点
同一个圆上
外接圆
圆内接四边形的对角________,且任何一个外角都等于它的________.
互补
内对角
补充:若圆内接四边形的对角相等,则此时的四边形为矩形.
