27.1.2 圆的对称性 第2课时 课件(共21张PPT) 华东师大版九年级下册数学
文档属性
| 名称 | 27.1.2 圆的对称性 第2课时 课件(共21张PPT) 华东师大版九年级下册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 15:38:20 | ||
图片预览




文档简介
(共21张PPT)
第27章 圆
27.1.2 圆的对称性
第2课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.进一步认识圆,了解圆是轴对称图形
2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题
3.灵活运用垂径定理解决有关圆的问题
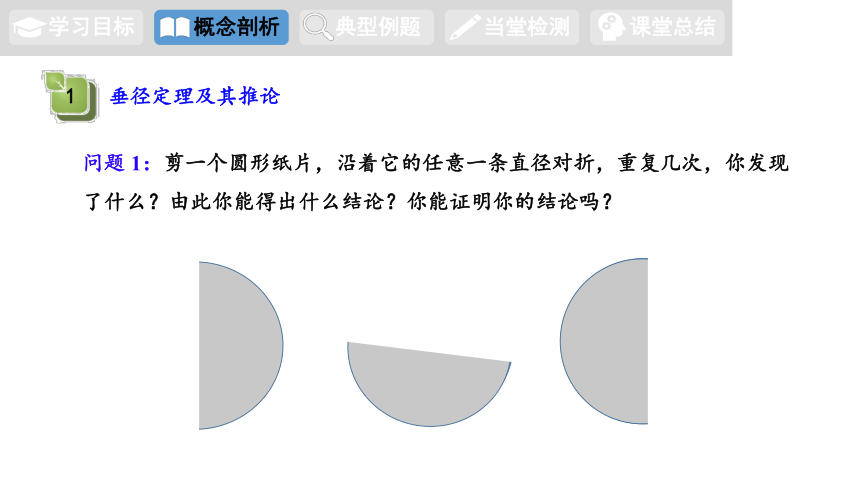
问题 1:剪一个圆形纸片,沿着它的任意一条直径对折,重复几次,你发现
了什么?由此你能得出什么结论?你能证明你的结论吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
垂径定理及其推论
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
O
O
归纳:圆的任何一条直径所在的直线都是圆的对称轴.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题 2:已知:如图,在⊙O中,CD是直径,AA'是弦,且CD⊥AA',
垂足为M.求证:CD是AA'的垂直平分线.
·
O
A
A'
D
M
C
证明:连接OA,OA'.
在△OAA'中,
∵OA=OA',
∴△OAA'是等腰三角形.
又∵AA'垂直CD,
∴MA=MA'.
即CD是AA'的垂直平分线.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
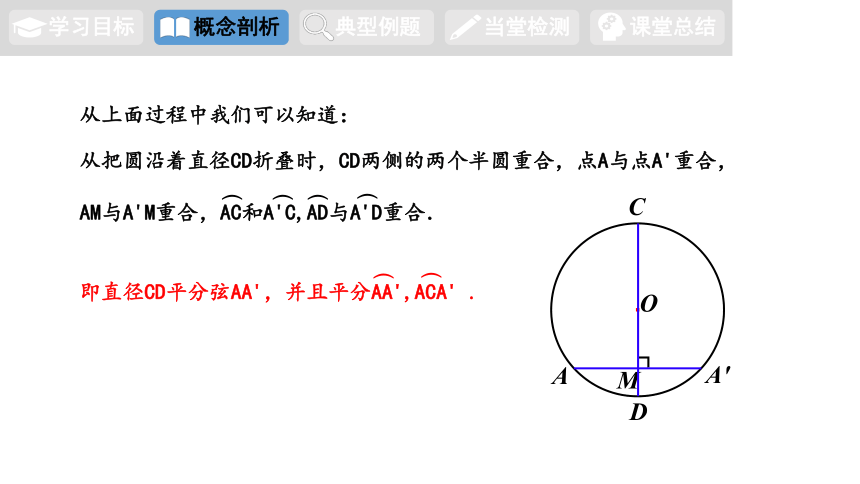
从上面过程中我们可以知道:
从把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点A'重合,
AM与A'M重合,AC和A'C,AD与A'D重合.
(
(
(
(
即直径CD平分弦AA',并且平分AA',ACA' .
(
(
·
O
A
A'
D
M
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
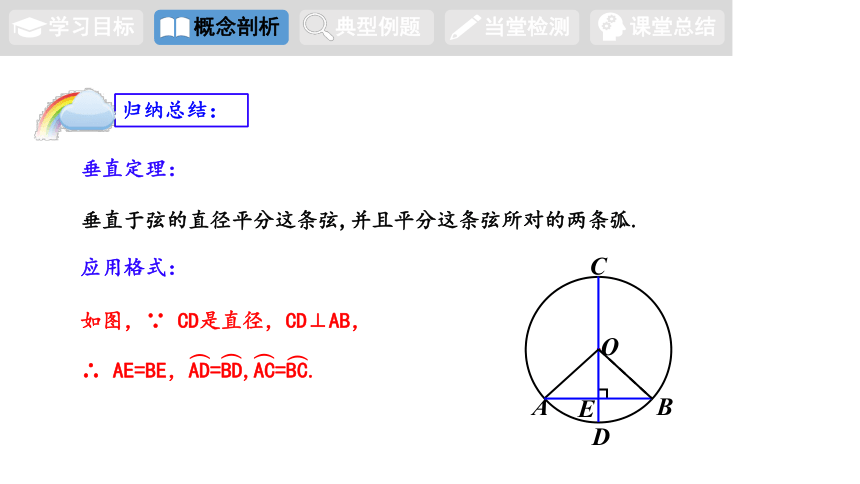
垂直定理:
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
·
O
A
B
C
D
E
应用格式:
如图,∵ CD是直径,CD⊥AB,
∴ AE=BE,AD=BD,AC=BC.
(
(
(
(
归纳总结:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
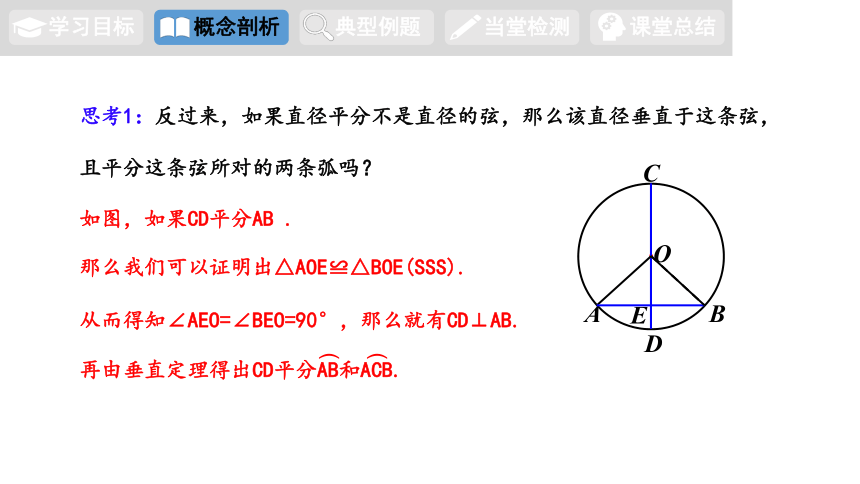
思考1:反过来,如果直径平分不是直径的弦,那么该直径垂直于这条弦,
且平分这条弦所对的两条弧吗?
·
O
A
B
C
D
E
如图,如果CD平分AB .
那么我们可以证明出△AOE≌△BOE(SSS).
从而得知∠AEO=∠BEO=90°,那么就有CD⊥AB.
再由垂直定理得出CD平分AB和ACB.
(
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
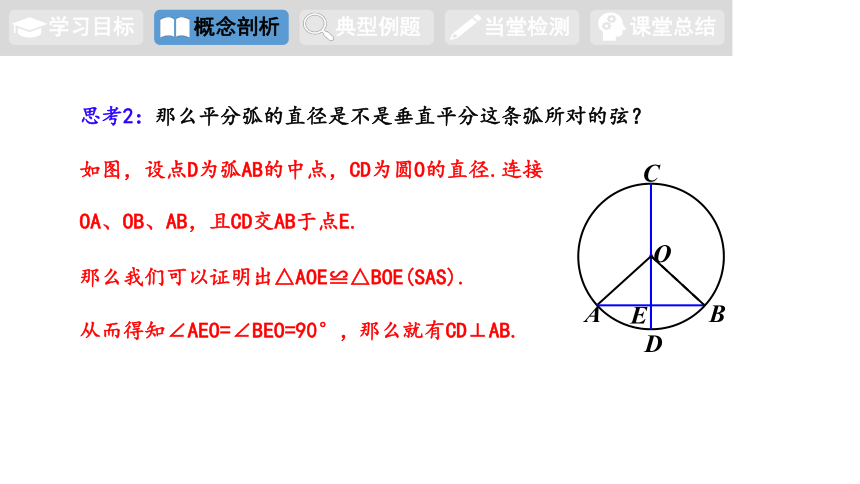
思考2:那么平分弧的直径是不是垂直平分这条弧所对的弦?
·
O
A
B
C
D
E
那么我们可以证明出△AOE≌△BOE(SAS).
从而得知∠AEO=∠BEO=90°,
那么就有CD⊥AB.
如图,设点D为弧AB的中点,CD为圆O的直径.连接OA、OB、AB,且CD交AB于点E.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
垂直定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分这条弦所对的两条弧.
注意:因为圆的两条直径是互相平分的,所以不是直径这个条件不能去掉.
归纳总结:
平分弧的直径垂直平分这条弧所对的弦.
例1.如图,⊙O的半径为5cm,弦AB为6cm,求圆心到弦AB的距离.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:连接OA,过圆心O作 OE⊥AB,垂足为E,则
·
O
A
B
E
又∵OA=5cm,∴在Rt△OEA中,有
答:圆心到弦AB的距离是4cm.
圆心到弦的距离
叫做弦心距.
例2.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC= 2cm,
求半径OC的长.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
·
O
A
B
E
C
D
解:连接OA,∵ CE⊥AB于D,
设 OC = x cm,则OD = (x - 2)cm,根据勾股定理,得
x2 = 42 + ( x-2)2 ,
解得 x=5.
即半径OC的长为5cm.
∴ .
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例3. 已知:⊙O中弦AB∥CD,求证:AC=BD.
(
(
.
C
D
A
B
O
M
N
解:证明:作直径 MN⊥AB,如图.
∵AB∥CD,∴MN⊥CD.
则AM=BM,CM=DM,(垂直平分弦的直径平分弦所对的弧)
(
(
(
(
∴AM-CM=BM-DM,
(
(
(
(
∴AC=BD.
(
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5 cm,CD=8 cm,
则AE=( )
A.8 cm B.9 cm
C.7 cm D.6 cm
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,⊙O的弦AB=8,半径ON交AB于点M,M是AB的中点,且OM=3,
则MN的长为( )
A.2 B.3
C.4 D.5
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,OE⊥AB于E,若⊙O的半径为10cm, OE=6cm,则AB = cm.
16
·
O
A
B
E
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,直径AB垂直于弦CD于点E,CD=4,AE=8,⊙O的半径长为________.
4
17
例4. 赵州桥的主桥是圆弧形,它的跨度(弧所对的弦长)为37.4m,拱高
(弧的中点到弦的距离)为7.2m,求赵州桥主桥拱的半径.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:如图,过桥拱所在圆的圆心O作AB的垂线,
交弧AB于点C,交AB于点D,则CD=7.2m.
A
B
O
C
D
∴r2 = (r-7.2)2 +18.72.
解得 r ≈ 27.9.
即赵州桥主桥拱的半径约为27.9m.
由勾股定理,得
OD=r-7.2,AD=18.7.
设⊙O的半径为r,在Rt△AOD中,AO=r,
由垂径定理,得AD = AB = 18.7 m,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.如图,有一个拱桥是圆弧形,它的跨度为60 m,拱高为18 m,求拱桥的半径.
解:连接OA,设圆弧的圆心为点O,过点O作OD⊥AB,交AB于点D,交圆弧于点E,
O
E
D
设拱桥的半径为x m,
解得x=34.
则(x-18)2+302=x2,
即拱桥的半径为34m.
则AD=BD= AB=30 m,DE=18m.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
垂直于弦的直径
垂弦定理
的推论
垂弦定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
平分弧的直径垂直平分这条弧所对的弦.
第27章 圆
27.1.2 圆的对称性
第2课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.进一步认识圆,了解圆是轴对称图形
2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题
3.灵活运用垂径定理解决有关圆的问题
问题 1:剪一个圆形纸片,沿着它的任意一条直径对折,重复几次,你发现
了什么?由此你能得出什么结论?你能证明你的结论吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
垂径定理及其推论
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
O
O
归纳:圆的任何一条直径所在的直线都是圆的对称轴.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题 2:已知:如图,在⊙O中,CD是直径,AA'是弦,且CD⊥AA',
垂足为M.求证:CD是AA'的垂直平分线.
·
O
A
A'
D
M
C
证明:连接OA,OA'.
在△OAA'中,
∵OA=OA',
∴△OAA'是等腰三角形.
又∵AA'垂直CD,
∴MA=MA'.
即CD是AA'的垂直平分线.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
从上面过程中我们可以知道:
从把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点A'重合,
AM与A'M重合,AC和A'C,AD与A'D重合.
(
(
(
(
即直径CD平分弦AA',并且平分AA',ACA' .
(
(
·
O
A
A'
D
M
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
垂直定理:
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
·
O
A
B
C
D
E
应用格式:
如图,∵ CD是直径,CD⊥AB,
∴ AE=BE,AD=BD,AC=BC.
(
(
(
(
归纳总结:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考1:反过来,如果直径平分不是直径的弦,那么该直径垂直于这条弦,
且平分这条弦所对的两条弧吗?
·
O
A
B
C
D
E
如图,如果CD平分AB .
那么我们可以证明出△AOE≌△BOE(SSS).
从而得知∠AEO=∠BEO=90°,那么就有CD⊥AB.
再由垂直定理得出CD平分AB和ACB.
(
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考2:那么平分弧的直径是不是垂直平分这条弧所对的弦?
·
O
A
B
C
D
E
那么我们可以证明出△AOE≌△BOE(SAS).
从而得知∠AEO=∠BEO=90°,
那么就有CD⊥AB.
如图,设点D为弧AB的中点,CD为圆O的直径.连接OA、OB、AB,且CD交AB于点E.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
垂直定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分这条弦所对的两条弧.
注意:因为圆的两条直径是互相平分的,所以不是直径这个条件不能去掉.
归纳总结:
平分弧的直径垂直平分这条弧所对的弦.
例1.如图,⊙O的半径为5cm,弦AB为6cm,求圆心到弦AB的距离.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:连接OA,过圆心O作 OE⊥AB,垂足为E,则
·
O
A
B
E
又∵OA=5cm,∴在Rt△OEA中,有
答:圆心到弦AB的距离是4cm.
圆心到弦的距离
叫做弦心距.
例2.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC= 2cm,
求半径OC的长.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
·
O
A
B
E
C
D
解:连接OA,∵ CE⊥AB于D,
设 OC = x cm,则OD = (x - 2)cm,根据勾股定理,得
x2 = 42 + ( x-2)2 ,
解得 x=5.
即半径OC的长为5cm.
∴ .
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例3. 已知:⊙O中弦AB∥CD,求证:AC=BD.
(
(
.
C
D
A
B
O
M
N
解:证明:作直径 MN⊥AB,如图.
∵AB∥CD,∴MN⊥CD.
则AM=BM,CM=DM,(垂直平分弦的直径平分弦所对的弧)
(
(
(
(
∴AM-CM=BM-DM,
(
(
(
(
∴AC=BD.
(
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5 cm,CD=8 cm,
则AE=( )
A.8 cm B.9 cm
C.7 cm D.6 cm
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,⊙O的弦AB=8,半径ON交AB于点M,M是AB的中点,且OM=3,
则MN的长为( )
A.2 B.3
C.4 D.5
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,OE⊥AB于E,若⊙O的半径为10cm, OE=6cm,则AB = cm.
16
·
O
A
B
E
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,直径AB垂直于弦CD于点E,CD=4,AE=8,⊙O的半径长为________.
4
17
例4. 赵州桥的主桥是圆弧形,它的跨度(弧所对的弦长)为37.4m,拱高
(弧的中点到弦的距离)为7.2m,求赵州桥主桥拱的半径.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:如图,过桥拱所在圆的圆心O作AB的垂线,
交弧AB于点C,交AB于点D,则CD=7.2m.
A
B
O
C
D
∴r2 = (r-7.2)2 +18.72.
解得 r ≈ 27.9.
即赵州桥主桥拱的半径约为27.9m.
由勾股定理,得
OD=r-7.2,AD=18.7.
设⊙O的半径为r,在Rt△AOD中,AO=r,
由垂径定理,得AD = AB = 18.7 m,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.如图,有一个拱桥是圆弧形,它的跨度为60 m,拱高为18 m,求拱桥的半径.
解:连接OA,设圆弧的圆心为点O,过点O作OD⊥AB,交AB于点D,交圆弧于点E,
O
E
D
设拱桥的半径为x m,
解得x=34.
则(x-18)2+302=x2,
即拱桥的半径为34m.
则AD=BD= AB=30 m,DE=18m.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
垂直于弦的直径
垂弦定理
的推论
垂弦定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
平分弧的直径垂直平分这条弧所对的弦.
