27.1.3 圆周角定理 第1课时 课件(共22张PPT) 华东师大版九年级数学下册
文档属性
| 名称 | 27.1.3 圆周角定理 第1课时 课件(共22张PPT) 华东师大版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 565.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 15:38:50 | ||
图片预览



文档简介
(共22张PPT)
第1课时 圆周角定理
27.1 圆的认识
3.圆周角
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系,并能运用圆周角定理解决简单
的几何问题.(重点)
3.理解并掌握圆周角定理的推论及其证明过程和运用.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
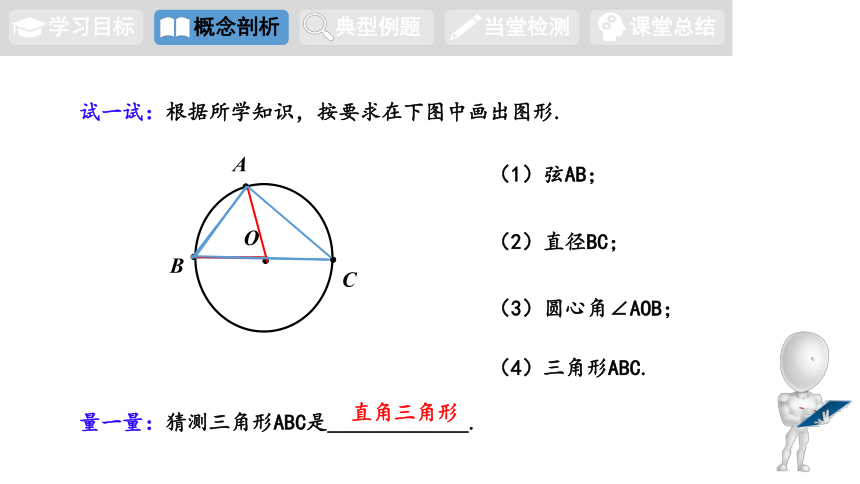
试一试:根据所学知识,按要求在下图中画出图形.
O
B
A
C
(4)三角形ABC.
(1)弦AB;
(2)直径BC;
(3)圆心角∠AOB;
量一量:猜测三角形ABC是_____________.
直角三角形
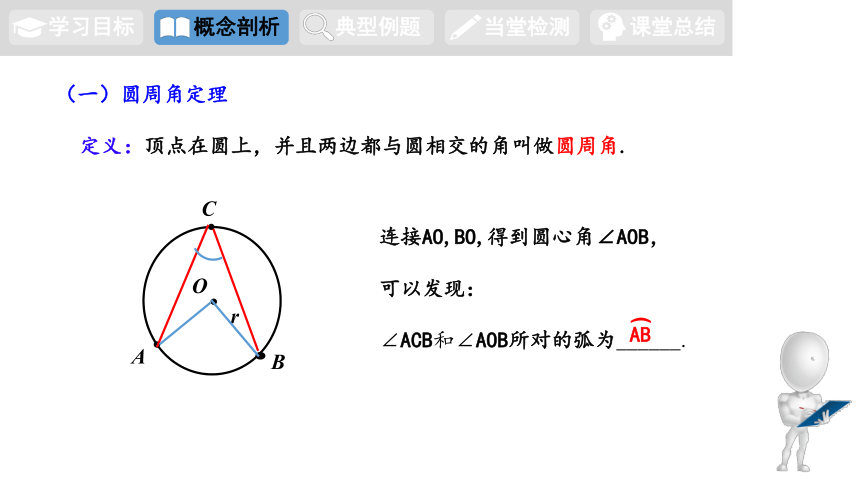
(一)圆周角定理
定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
r
B
A
C
连接AO,BO,得到圆心角∠AOB,
可以发现:
∠ACB和∠AOB所对的弧为______.
AB
(
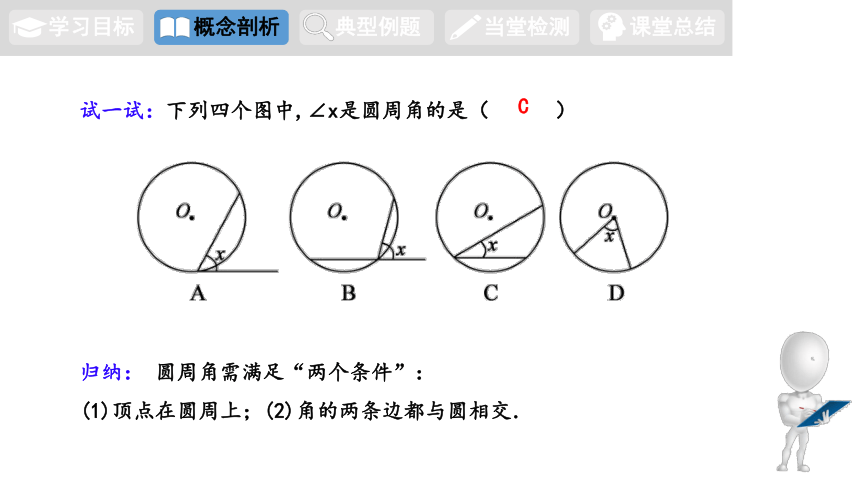
试一试:下列四个图中,∠x是圆周角的是( )
典型例题
当堂检测
学习目标
课堂总结
概念剖析
C
归纳: 圆周角需满足“两个条件”:
(1)顶点在圆周上;(2)角的两条边都与圆相交.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
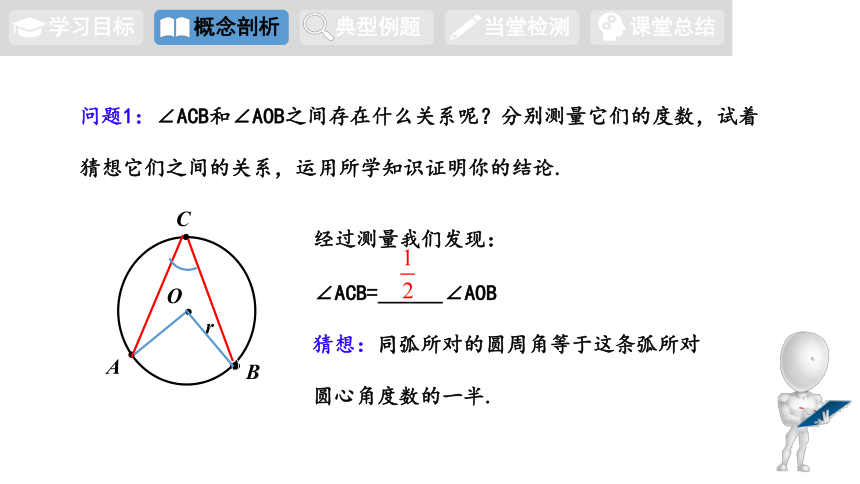
问题1:∠ACB和∠AOB之间存在什么关系呢?分别测量它们的度数,试着
猜想它们之间的关系,运用所学知识证明你的结论.
O
r
0
B
A
C
经过测量我们发现:
∠ACB=______∠AOB
猜想:同弧所对的圆周角等于这条弧所对
圆心角度数的一半.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
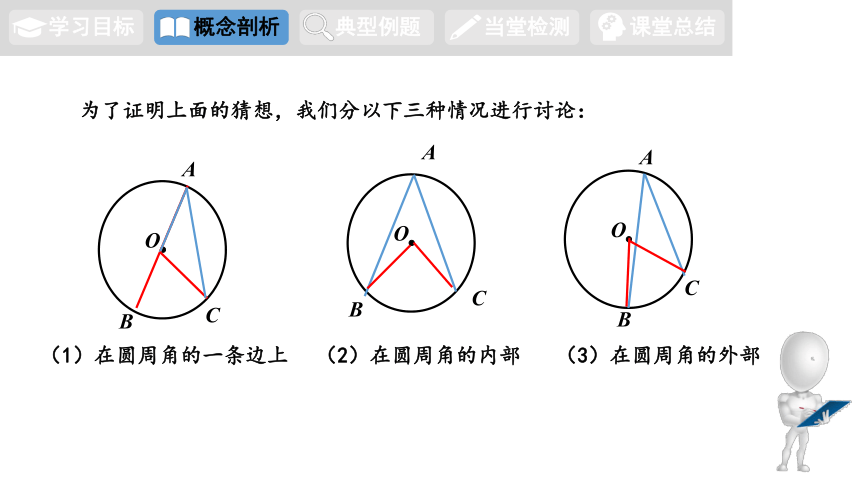
为了证明上面的猜想,我们分以下三种情况进行讨论:
(1)在圆周角的一条边上
(2)在圆周角的内部
(3)在圆周角的外部
O
B
A
C
O
B
A
C
O
B
A
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
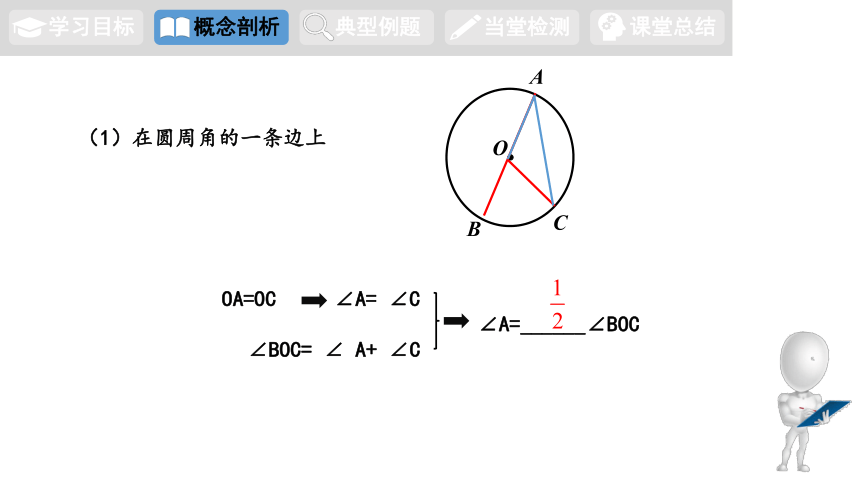
(1)在圆周角的一条边上
O
B
A
C
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
∠A=______∠BOC
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)在圆周角的内部
O
B
A
C
OA=OB=OC
2∠BAD= ∠BOD,
2∠CAD= ∠COD,
∠BOC= ∠ BOD+ ∠COD
∠A=______∠BOC
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(3)在圆周角的外部
O
B
A
C
OA=OB=OC
∠DOB=2∠OAB
∠DOC=2∠OAC
∠BOC= ∠ DOC- ∠DOB
∠A=______∠BOC
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
O
B
A
C
O
B
A
C
O
B
A
C
例1.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,求∠D的度数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:∵∠AOC=130°,∠AOB=180°,
∴∠BOC=∠AOB-∠AOC=50°,
∴∠D= ∠BOC=25°.(圆周角定理)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,点A、B、C在☉O上,∠BAC=35 .
那么∠BOC= ,理由是 .
一条弧所对的圆周角等于它所对的圆心角的一半
70°
O
0
C
B
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(二)圆周角定理的推论
问题1:根据圆周角定理,结合已经学习过的有关圆的知识,我们还能得到
哪些推论?
O
r
0
B
A
C
同弧或等弧所对的圆周角关系如何?
90°的圆周角所对的弦有什么特殊之处呢?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
推论一:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角
所对的弧也相等.
D
A
B
O
C
E
F
如图:
CD=EF
∠A=∠B
(
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
推论二:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
O
A
B
C1
C3
C2
例2.如图,AB为⊙O的直径,弦CD交AB于点P,∠ACD = 60°,∠ADC=70°. 求∠APC的度数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:连接BC,如图,则∠ACB=90°,
∴∠APC =∠BAD +∠ADC =30°+70°=100°.
∴∠BAD=∠DCB=30°,
∠DCB =∠ACB-∠ACD =90°-60°=30°.
. O
A
D
C
P
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
求圆周角度数的思路:
在圆内求圆周角要看圆周角所对的弧,找同弧或等弧所对的圆周角或圆心角
进行转化.如果有直径,一般利用直径所对的圆周角是直角求解.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
B
.
A
D
C
O
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,AB为⊙O的直径,已知∠DCB=20°,则∠DBA的度数为( )
A.50° B.20°
C.60° D.70°
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,OA,OB,OC 都是 ⊙O 的半径,∠AOB =2∠BOC.
求证:∠ACB = 2∠BAC.
A
O
B
C
∴∠ACB=2∠BAC.
证明:
∠AOB=2∠BOC,
∵
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.圆周角的定义
顶点在圆上,并且两边都与圆相交角叫做圆周角.
2.圆周角定理及推论
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角
所对的弧也相等.
推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
第1课时 圆周角定理
27.1 圆的认识
3.圆周角
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系,并能运用圆周角定理解决简单
的几何问题.(重点)
3.理解并掌握圆周角定理的推论及其证明过程和运用.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
试一试:根据所学知识,按要求在下图中画出图形.
O
B
A
C
(4)三角形ABC.
(1)弦AB;
(2)直径BC;
(3)圆心角∠AOB;
量一量:猜测三角形ABC是_____________.
直角三角形
(一)圆周角定理
定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
r
B
A
C
连接AO,BO,得到圆心角∠AOB,
可以发现:
∠ACB和∠AOB所对的弧为______.
AB
(
试一试:下列四个图中,∠x是圆周角的是( )
典型例题
当堂检测
学习目标
课堂总结
概念剖析
C
归纳: 圆周角需满足“两个条件”:
(1)顶点在圆周上;(2)角的两条边都与圆相交.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题1:∠ACB和∠AOB之间存在什么关系呢?分别测量它们的度数,试着
猜想它们之间的关系,运用所学知识证明你的结论.
O
r
0
B
A
C
经过测量我们发现:
∠ACB=______∠AOB
猜想:同弧所对的圆周角等于这条弧所对
圆心角度数的一半.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
为了证明上面的猜想,我们分以下三种情况进行讨论:
(1)在圆周角的一条边上
(2)在圆周角的内部
(3)在圆周角的外部
O
B
A
C
O
B
A
C
O
B
A
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(1)在圆周角的一条边上
O
B
A
C
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
∠A=______∠BOC
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)在圆周角的内部
O
B
A
C
OA=OB=OC
2∠BAD= ∠BOD,
2∠CAD= ∠COD,
∠BOC= ∠ BOD+ ∠COD
∠A=______∠BOC
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(3)在圆周角的外部
O
B
A
C
OA=OB=OC
∠DOB=2∠OAB
∠DOC=2∠OAC
∠BOC= ∠ DOC- ∠DOB
∠A=______∠BOC
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
O
B
A
C
O
B
A
C
O
B
A
C
例1.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,求∠D的度数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:∵∠AOC=130°,∠AOB=180°,
∴∠BOC=∠AOB-∠AOC=50°,
∴∠D= ∠BOC=25°.(圆周角定理)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,点A、B、C在☉O上,∠BAC=35 .
那么∠BOC= ,理由是 .
一条弧所对的圆周角等于它所对的圆心角的一半
70°
O
0
C
B
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(二)圆周角定理的推论
问题1:根据圆周角定理,结合已经学习过的有关圆的知识,我们还能得到
哪些推论?
O
r
0
B
A
C
同弧或等弧所对的圆周角关系如何?
90°的圆周角所对的弦有什么特殊之处呢?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
推论一:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角
所对的弧也相等.
D
A
B
O
C
E
F
如图:
CD=EF
∠A=∠B
(
(
典型例题
当堂检测
学习目标
课堂总结
概念剖析
推论二:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
O
A
B
C1
C3
C2
例2.如图,AB为⊙O的直径,弦CD交AB于点P,∠ACD = 60°,∠ADC=70°. 求∠APC的度数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:连接BC,如图,则∠ACB=90°,
∴∠APC =∠BAD +∠ADC =30°+70°=100°.
∴∠BAD=∠DCB=30°,
∠DCB =∠ACB-∠ACD =90°-60°=30°.
. O
A
D
C
P
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
求圆周角度数的思路:
在圆内求圆周角要看圆周角所对的弧,找同弧或等弧所对的圆周角或圆心角
进行转化.如果有直径,一般利用直径所对的圆周角是直角求解.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
B
.
A
D
C
O
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,AB为⊙O的直径,已知∠DCB=20°,则∠DBA的度数为( )
A.50° B.20°
C.60° D.70°
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,OA,OB,OC 都是 ⊙O 的半径,∠AOB =2∠BOC.
求证:∠ACB = 2∠BAC.
A
O
B
C
∴∠ACB=2∠BAC.
证明:
∠AOB=2∠BOC,
∵
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.圆周角的定义
顶点在圆上,并且两边都与圆相交角叫做圆周角.
2.圆周角定理及推论
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角
所对的弧也相等.
推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
