2025年中考数学解答题专题系列:解直角三角形的应用(含解析)
文档属性
| 名称 | 2025年中考数学解答题专题系列:解直角三角形的应用(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 00:00:00 | ||
图片预览




文档简介
/ 让教学更有效 高效备考 | 英语学科
2025年中考数学解答题专题系列:解直角三角形的应用
1.研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的扫描仪采集纪念碑的相关数据.
数据采集:如图,点是纪念碑顶部一点,的长表示点到水平地面的距离.航模从纪念碑前水平地面的点处竖直上升,飞行至距离地面20米的点处时,测得点的仰角;然后沿方向继续飞行,飞行方向与水平线的夹角,当到达点正上方的点处时,测得米;
数据应用:已知图中各点均在同一竖直平面内,,,三点在同一直线上.请根据上述数据,计算纪念碑顶部点到地面的距离的长(结果精确到1米.参考数据:,,,,,.
2.在数学综合实践活动中,次仁和格桑自主设计了“测量家附近的一座小山高度”的探究作业.如图,次仁在A处测得山顶C的仰角为;格桑在B处测得山顶C的仰角为.已知两人所处位置的水平距离米,A处距地面的垂直高度米,B处距地面的垂直高度米,点M,F,N在同一条直线上,求小山的高度.(结果保留根号)
3.如图,为了测量无人机的飞行高度,在水平地面上选择观测点A,B. 无人机悬停在C处,此时在A处测得C的仰角为无人机垂直上升悬停在D处,此时在B 处测得 D的仰角为点A, B, C, D在同一平面内, A, B两点在 的同侧. 求无人机在 C 处时离地面的高度.(参考数据:)
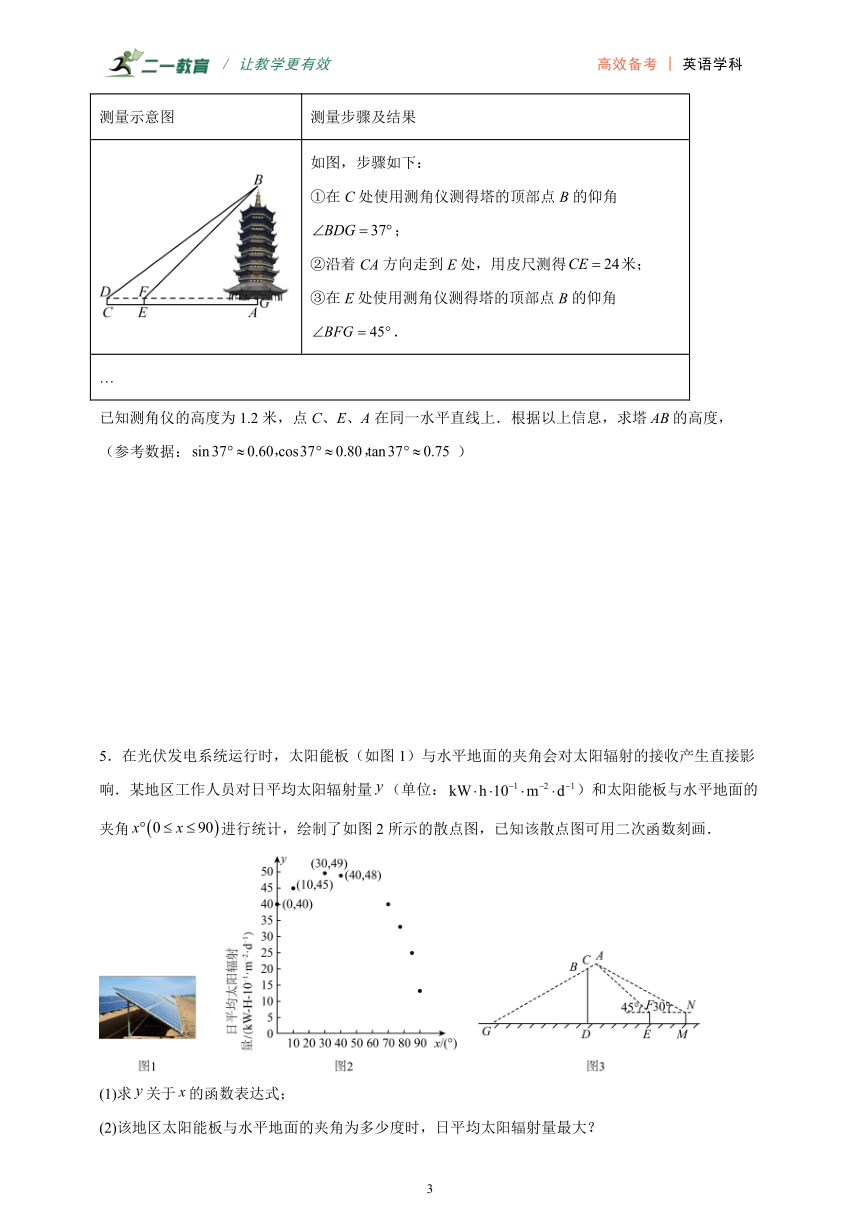
4.双塔是古黄河宿迁景观带的标志性建筑之一,由九层的九龙塔和七层的七凤塔构成.某校数学实践小组开展测量七凤塔高度的实践活动,该小组制定了测量方案,在实地测量后撰写活动报告,报告部分内容如下表:
测量七凤塔高度
测量工具 测角仪、皮尺等 活动形式 以小组为单位
测量示意图 测量步骤及结果
如图,步骤如下: ①在C处使用测角仪测得塔的顶部点B的仰角; ②沿着CA方向走到E处,用皮尺测得米; ③在E处使用测角仪测得塔的顶部点B的仰角.
…
已知测角仪的高度为1.2米,点C、E、A在同一水平直线上.根据以上信息,求塔的高度,
(参考数据:)
5.在光伏发电系统运行时,太阳能板(如图1)与水平地面的夹角会对太阳辐射的接收产生直接影响.某地区工作人员对日平均太阳辐射量(单位:)和太阳能板与水平地面的夹角进行统计,绘制了如图2所示的散点图,已知该散点图可用二次函数刻画.
(1)求关于的函数表达式;
(2)该地区太阳能板与水平地面的夹角为多少度时,日平均太阳辐射量最大?
(3)图3是该地区太阳能板安装后的示意图(此时,太阳能板与水平地面的夹角使得日平均太阳辐射量最大),为太阳能板与水平地面的夹角,为支撑杆.已知,是的中点,.在延长线上选取一点,在两点间选取一点,测得,在两点处分别用测角仪测得太阳能板顶端的仰角为,,该测角仪支架的高为1m.求支撑杆的长.(精确到m,参考数据:,)
6.如图,是一座南北走向的大桥,一辆汽车在笔直的公路上由北向南行驶,在处测得桥头在南偏东方向上,继续行驶米后到达处,测得桥头在南偏东方向上,桥头在南偏东方向上,求大桥的长度.(结果精确到米,参考数据:)
7.如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东方向,且A,B相距海里.一渔船在C处捕鱼,测得C处在灯塔A的北偏东方向、灯塔B的正北方向.
(1)求B,C两处的距离;
(2)该渔船从C处沿北偏东方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东方向,便立即以18海里/小时的速度沿方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:,)
8.如图,一艘海轮位于灯塔的北偏东方向,距离灯塔100海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处.这时,处距离处有多远?(参考数据:,,)
9.如图,甲、乙两艘货轮同时从港出发,分别向,两港运送物资,最后到达港正东方向的港装运新的物资.甲货轮沿港的东南方向航行海里后到达港,再沿北偏东方向航行一定距离到达港.乙货轮沿港的北偏东方向航行一定距离到达港,再沿南偏东方向航行一定距离到达港.(参考数据:,,)
(1)求,两港之间的距离(结果保留小数点后一位);
(2)若甲、乙两艘货轮的速度相同(停靠、两港的时间相同),哪艘货轮先到达港?请通过计算说明.
10.宜宾地标广场位于三江汇合口(如图1,左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C、D,在地标广场上选择两个观测点A、B(点A、B、C、D在同一水平面,且).如图2所示,在点A处测得点C在北偏西方向上,测得点D在北偏东方向上;在B处测得点C在北偏西方向上,测得点D在北偏东方向上,测得米.求长江口的宽度的值(结果精确到1米).(参考数据:,,,,,)
11.某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡的坡度,,在处测得电线塔顶部的仰角为,在处测得电线塔顶部的仰角为.
(1)求点离水平地面的高度.
(2)求电线塔的高度(结果保留根号).
12.风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1)某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点,,,均在同一平面内,).已知斜坡长为20米,斜坡的坡角为,在斜坡顶部处测得风力发电机塔杆顶端点的仰角为,坡底与塔杆底的距离米,求该风力发电机塔杆的高度.
(结果精确到个位;参考数据:,,,)
13.如图,堤坝长为,坡度i为,底端A在地面上,堤坝与对面的山之间有一深沟,山顶D处立有高的铁塔.小明欲测量山高,他在A处看到铁塔顶端C刚好在视线上,又在坝顶B处测得塔底D的仰角为.求堤坝高及山高.(,,,小明身高忽略不计,结果精确到)
14.某中学依山而建,校门A处有一坡角的斜坡,长度为30米,在坡顶B处测得教学楼的楼顶C的仰角,离B点4米远的E处有一个花台,在E处测得C的仰角,的延长线交水平线于点D,求的长(结果保留根号).
15.渔湾是国家“AAAA”级风景区,图1是景区游览的部分示意图.如图2,小卓从九孔桥处出发,沿着坡角为的山坡向上走了到达处的三龙潭瀑布,再沿坡角为的山坡向上走了到达处的二龙潭瀑布.求小卓从处的九孔桥到处的二龙潭瀑布上升的高度为多少米?(结果精确到)
(参考数据:)
16.实验是培养学生创新能力的重要途径.如图是小亮同学安装的化学实验装置,安装要求为试管口略向下倾斜,铁夹应固定在距试管口的三分之一处.现将左侧的实验装置图抽象成右侧示意图,已知试管,试管倾斜角为.
(1)求试管口B与铁杆的水平距离的长度;(结果用含非特殊角的三角函数表示)
(2)实验时,导气管紧靠水槽壁,延长交的延长线于点F,且于点N(点C,D,N,F在一条直线上),经测得:,求线段的长度.(结果用含非特殊角的三角函数表示)
17.如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图2,此时测得点到所在直线的距离,;停止位置示意图如图3,此时测得(点,,在同一直线上,且直线与平面平行,图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变.(参考数据:,,,)
(1)求的长;
(2)求物体上升的高度(结果精确到).
18.小明从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A,B,C,D分别是长方体棱的中点,若光线经真空从矩形对角线交点O处射入,其折射光线恰好从点C处射出.如图②,已知,,求截面的面积.
《2025年中考数学解答题专题系列:解直角三角形的应用》参考答案
1.点A到地面的距离的长约为27米
【分析】本题考查解直角三角形的应用—仰角俯角问题、锐角三角函数,解答本题的关键是明确题意,利用数形结合的思想解答.
延长交于点,根据矩形的性质得到,解直角三角形即可得到结论.
【详解】解:延长交于点,
由题意得,四边形为矩形,
,
在中,,,
,
,
在中,,,
,
,
设米.
,
,
,
解得,
(米);
答:点到地面的距离的长约为27米.
2.米
【分析】本题主要考查了矩形的判定和性质,解直角三角形的应用,证明四边形和四边形为矩形,得出米,米,,,设,则米,解直角三角形得出,,根据米,得出,求出,最后得出答案即可.
【详解】解:根据题意可得:,,
∴四边形和四边形为矩形,
∴米,米,,,
∴(米),
设,则米,
∵,,
∴,
∵,,
∴,
∴,,
∵米,
∴,
解得:,
∴米.
3.
【分析】过点C作于点M, 设, 则,根据仰角,解直角三角形计算即可.
本题考查了仰角解直角三角形,分式方程的应用,熟练掌握解直角三角形的应用是解题的关键.
【详解】解:过点C作于点M, 设, 则,
在中, ,
则,
则;
在中, ,
则
解得:,
经检验,是该分式方程的解.
∴.
答:无人机在C处时离地面.
4.73.2米
【分析】本题考查了解直角三角形的应用仰角俯角问题,熟练掌握解直角三角形的方法是解题的关键.根据题意得到米,米,,,解直角三角形即可得到结论.
【详解】解:由题意得,米,米,,,
在中,,
,
在中,,
,
米,
,
解得,
(米,
答:塔的高度为73.2米.
5.(1)
(2)
(3)
【分析】本题主要考查待定系数法求二次函数解析式以及二次函数的图像和性质,解直角三角形,熟练掌握二次函数的图像和性质是解题的关键.
(1)设关于的函数表达式为,将图中的点代入即可求出答案;
(2)求出二次函数的对称轴,在对称轴处取最值;
(3)延长与过点作的线交于点,令,根据三角函数进行计算,求出即可得到答案.
【详解】(1)解:设关于的函数表达式为,
将代入,
得,
解得,
;
(2)解:根据函数解析式得函数对称轴,
故阳能板与水平地面的夹角为度时,日平均太阳辐射量最大;
(3)解:,
延长与过点作的线交于点,令,
,,
,
,
,
,
,
延长交与点,
,
,
,
,
,
.
6.米
【分析】本题考查了解直角三角形的应用,分别过点作的垂线,垂足分别为,根据题意得出,解求得,,进而求得,根据,即可求解.
【详解】解:如图所示,分别过点作的垂线,垂足分别为,
∴四边形是矩形,
∴,,
依题意,,
∴,
∴,
∴;
在中,,
;
在中,,
∴.
答:大桥的长度约为米.
7.(1)B,C两处的距离为16海里
(2)渔政船的航行时间为小时
【分析】本题考查了解直角三角形的实际应用,解题的关键是正确画出辅助线,构造直角三角形.
(1)根据题意易得,则,再求出(海里),即可解答;
(2)过点D作于点F,设海里,则,,则,求出,进而得出海里,海里,根据勾股定理可得:(海里),即可解答.
【详解】(1)解:过点A作于点E,
∵灯塔B在灯塔A的南偏东方向,C处在灯塔A的北偏东方向、灯塔B的正北方向.
∴,
∴,
∵,
∴,
∵海里,
∴(海里),
∴(海里),
∴B,C两处的距离为16海里.
(2)解:过点D作于点F,
设海里,
∵,
∴,
由(1)可知,海里,
∴海里,
∵,
∴,
∴,
解得:,
∴海里,海里,
根据勾股定理可得:(海里),
∴渔政船的航行时间为(小时),
答:渔政船的航行时间为小时.
8.处距离处有140海里.
【分析】本题考查了解直角三角形的应用方向角问题.过作于,解直角三角形即可得到结论.
【详解】解:过作于,
在中,,海里,
(海里),
(海里),
在中,,
(海里),
(海里),
答:处距离处有140海里.
9.(1),两港之间的距离海里;
(2)甲货轮先到达港.
【分析】()过作于点,由题意可知:,,求出,即可求解;
()通过三角函数求出甲行驶路程为:,乙行驶路程为:,然后比较即可;
本题考查了方位角视角下的解直角三角形,构造直角三角形,熟练掌握锐角三角函数是解题的关键.
【详解】(1)如图,过作于点,
∴,
由题意可知:,,
∴,
∴,
∴,
∴(海里),
∴,两港之间的距离海里;
(2)由()得:,,,
∴,
∴,
由题意得:,,
∴,
∴,(海里),
∴甲行驶路程为:(海里),乙行驶路程为:(海里),
∵,且甲、乙速度相同,
∴甲货轮先到达港.
10.长江口的宽度为米.
【分析】如图,过作于,过作于,过作于,而,可得四边形,都是矩形,由题意可得:,,证明,可得,设,,再利用三角函数建立方程组求解即可.
【详解】解:如图,过作于,过作于,过作于,而,
∴四边形,都是矩形,
∴,,,,
∵由题意可得:,,
∴,,
∵,
∴,
∴,
设,,
∴,即,
,即,
∴,
∴,
∴,
∴,
∴;
∴长江口的宽度为米.
【点睛】本题考查的是解直角三角形的实际应用,矩形的判定于性质,全等三角形的判定与性质,作出合适的辅助线是解本题的关键.
11.(1);
(2)电线塔的高度.
【分析】本题主要考查了解直角三角形的实际应用.
(1)由斜坡的坡度,求得,利用正切函数的定义得到,据此求解即可;
(2)作于点,设,先解得到,解得到米,进而得到方程,解方程即可得到答案.
【详解】(1)解:∵斜坡的坡度,
∴,
∵,
∴,
∵,
∴;
(2)解:作于点,则四边形是矩形,,,
设,
在中,,
∴,
在中,,
在中,,,
∴,
∴,
∴,
∴,
∴
答:电线塔的高度.
12.32m
【分析】本题考查的是矩形的判定与性质,解直角三角形的实际应用,过点作于点,作于点,先求解,,再证明,再利用锐角的正切可得,从而可得答案.
【详解】解:过点作于点,作于点
由题意得:,
在中,
,
,
,
四边形为矩形,
,,
,
在中.
,
答:该风力发电机塔杆的高度为.
13.堤坝高为8米,山高为20米.
【分析】过B作于H,设,,根据勾股定理得到,求得,过B作于F,则,设,解直角三角形即可得到结论.
【详解】解:过B作于H,
∵坡度i为,
∴设,,
∴,
∴,
∴,
过B作于F,
则,
设,
∵.
∴,
∴,
∵坡度i为,
∴,
∴,
∴(米),
∴(米),
答:堤坝高为8米,山高为20米.
【点睛】本题考查了解直角三角形的应用-俯角仰角,解直角三角形的应用-坡角坡度,正确地作出辅助线是解题的关键.
14.的长为米
【分析】作于点,首先根据坡度求出,并通过矩形的判定确定出,然后通过解三角形求出,即可相加得出结论.
【详解】解:如图所示,作于点,则由题意,四边形为矩形,
∵在中,,,,
∴,
∵四边形为矩形,
∴,
由题意,,,,,
∴为等腰直角三角形,,
设,则,
在中,,
∴,即:,
解得:,经检验,是上述方程的解,且符合题意,
∴,
∴,
∴的长为米.
【点睛】本题考查解直角三角形的应用,准确构造出直角三角形并求解是解题关键.
15.
【分析】过点作,垂足为,在中,根据求出,过点作,垂足为,在中,根据求出,进而求解即可.
【详解】过点作,垂足为.
在中,,
∴.
过点作,垂足为.
在中,,
∴.
∵,
∴.
答:从处的九孔桥到处的二龙潭瀑布上升的高度约为.
【点睛】此题考查了解直角三角形的应用一坡度坡角问题,熟练利用锐角三角函数关系是解题关键.
16.(1)
(2)
【分析】本题主要考查了解直角三角形的应用,通过作辅助线构造直角三角形,掌握直角三角形中的边角关系是解题关键.
(1)先求出,再在中,利用余弦的定义求解即可得;
(2)过点作于点,过点作于点,先解直角三角形可得的长,从而可得的长,再判断出是等腰直角三角形,从而可得的长,最后根据求解即可得.
【详解】(1)解:∵,
∴,
由题意可知,,
在中,,
∴,
答:试管口与铁杆的水平距离的长度.
(2)解:如图,过点作于点,过点作于点,
则四边形和四边形都是矩形,
∴,
在中,,,
∴,
∵,
∴,
∴,
∵,,,
∴,
∴是等腰直角三角形,
∴,
∴,
答:线段的长度为.
17.(1)
(2)
【分析】本题考查了解直角三角形的应用,勾股定理,熟练掌握知识点是解题的关键.
(1)解即可求解;
(2)在中,由勾股定理得,,解求得,由题意得,,故,则.
【详解】(1)解:由题意得,,
∵,,
∴在中,由,
得:,
∴,
答:;
(2)解:在中,由勾股定理得,,
在中,,
∴,
∴,
由题意得,,
∴,
∴,
答:物体上升的高度约为.
18.(1);
(2).
【分析】本题主要考查了解直角三角形的应用,勾股定理等知识,
(1)根据,设,则,利用勾股定理求出,进而可得,问题即可得解;
(2)根据折射率与(1)的材料相同,可得折射率为,根据,可得,则有,在中,设,,问题随之得解.
【详解】(1)∵,
∴如图,
设,则,由勾股定理得,,
∴,
又∵,
∴,
∴折射率为:.
(2)根据折射率与(1)的材料相同,可得折射率为,
∵,
∴,
∴.
∵四边形是矩形,点O是中点,
∴,,
又∵,
∴,
在中,设,,
由勾股定理得,,
∴.
又∵,
∴,
∴,
∴,
∴截面的面积为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
2025年中考数学解答题专题系列:解直角三角形的应用
1.研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的扫描仪采集纪念碑的相关数据.
数据采集:如图,点是纪念碑顶部一点,的长表示点到水平地面的距离.航模从纪念碑前水平地面的点处竖直上升,飞行至距离地面20米的点处时,测得点的仰角;然后沿方向继续飞行,飞行方向与水平线的夹角,当到达点正上方的点处时,测得米;
数据应用:已知图中各点均在同一竖直平面内,,,三点在同一直线上.请根据上述数据,计算纪念碑顶部点到地面的距离的长(结果精确到1米.参考数据:,,,,,.
2.在数学综合实践活动中,次仁和格桑自主设计了“测量家附近的一座小山高度”的探究作业.如图,次仁在A处测得山顶C的仰角为;格桑在B处测得山顶C的仰角为.已知两人所处位置的水平距离米,A处距地面的垂直高度米,B处距地面的垂直高度米,点M,F,N在同一条直线上,求小山的高度.(结果保留根号)
3.如图,为了测量无人机的飞行高度,在水平地面上选择观测点A,B. 无人机悬停在C处,此时在A处测得C的仰角为无人机垂直上升悬停在D处,此时在B 处测得 D的仰角为点A, B, C, D在同一平面内, A, B两点在 的同侧. 求无人机在 C 处时离地面的高度.(参考数据:)
4.双塔是古黄河宿迁景观带的标志性建筑之一,由九层的九龙塔和七层的七凤塔构成.某校数学实践小组开展测量七凤塔高度的实践活动,该小组制定了测量方案,在实地测量后撰写活动报告,报告部分内容如下表:
测量七凤塔高度
测量工具 测角仪、皮尺等 活动形式 以小组为单位
测量示意图 测量步骤及结果
如图,步骤如下: ①在C处使用测角仪测得塔的顶部点B的仰角; ②沿着CA方向走到E处,用皮尺测得米; ③在E处使用测角仪测得塔的顶部点B的仰角.
…
已知测角仪的高度为1.2米,点C、E、A在同一水平直线上.根据以上信息,求塔的高度,
(参考数据:)
5.在光伏发电系统运行时,太阳能板(如图1)与水平地面的夹角会对太阳辐射的接收产生直接影响.某地区工作人员对日平均太阳辐射量(单位:)和太阳能板与水平地面的夹角进行统计,绘制了如图2所示的散点图,已知该散点图可用二次函数刻画.
(1)求关于的函数表达式;
(2)该地区太阳能板与水平地面的夹角为多少度时,日平均太阳辐射量最大?
(3)图3是该地区太阳能板安装后的示意图(此时,太阳能板与水平地面的夹角使得日平均太阳辐射量最大),为太阳能板与水平地面的夹角,为支撑杆.已知,是的中点,.在延长线上选取一点,在两点间选取一点,测得,在两点处分别用测角仪测得太阳能板顶端的仰角为,,该测角仪支架的高为1m.求支撑杆的长.(精确到m,参考数据:,)
6.如图,是一座南北走向的大桥,一辆汽车在笔直的公路上由北向南行驶,在处测得桥头在南偏东方向上,继续行驶米后到达处,测得桥头在南偏东方向上,桥头在南偏东方向上,求大桥的长度.(结果精确到米,参考数据:)
7.如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东方向,且A,B相距海里.一渔船在C处捕鱼,测得C处在灯塔A的北偏东方向、灯塔B的正北方向.
(1)求B,C两处的距离;
(2)该渔船从C处沿北偏东方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东方向,便立即以18海里/小时的速度沿方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:,)
8.如图,一艘海轮位于灯塔的北偏东方向,距离灯塔100海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处.这时,处距离处有多远?(参考数据:,,)
9.如图,甲、乙两艘货轮同时从港出发,分别向,两港运送物资,最后到达港正东方向的港装运新的物资.甲货轮沿港的东南方向航行海里后到达港,再沿北偏东方向航行一定距离到达港.乙货轮沿港的北偏东方向航行一定距离到达港,再沿南偏东方向航行一定距离到达港.(参考数据:,,)
(1)求,两港之间的距离(结果保留小数点后一位);
(2)若甲、乙两艘货轮的速度相同(停靠、两港的时间相同),哪艘货轮先到达港?请通过计算说明.
10.宜宾地标广场位于三江汇合口(如图1,左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C、D,在地标广场上选择两个观测点A、B(点A、B、C、D在同一水平面,且).如图2所示,在点A处测得点C在北偏西方向上,测得点D在北偏东方向上;在B处测得点C在北偏西方向上,测得点D在北偏东方向上,测得米.求长江口的宽度的值(结果精确到1米).(参考数据:,,,,,)
11.某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡的坡度,,在处测得电线塔顶部的仰角为,在处测得电线塔顶部的仰角为.
(1)求点离水平地面的高度.
(2)求电线塔的高度(结果保留根号).
12.风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1)某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点,,,均在同一平面内,).已知斜坡长为20米,斜坡的坡角为,在斜坡顶部处测得风力发电机塔杆顶端点的仰角为,坡底与塔杆底的距离米,求该风力发电机塔杆的高度.
(结果精确到个位;参考数据:,,,)
13.如图,堤坝长为,坡度i为,底端A在地面上,堤坝与对面的山之间有一深沟,山顶D处立有高的铁塔.小明欲测量山高,他在A处看到铁塔顶端C刚好在视线上,又在坝顶B处测得塔底D的仰角为.求堤坝高及山高.(,,,小明身高忽略不计,结果精确到)
14.某中学依山而建,校门A处有一坡角的斜坡,长度为30米,在坡顶B处测得教学楼的楼顶C的仰角,离B点4米远的E处有一个花台,在E处测得C的仰角,的延长线交水平线于点D,求的长(结果保留根号).
15.渔湾是国家“AAAA”级风景区,图1是景区游览的部分示意图.如图2,小卓从九孔桥处出发,沿着坡角为的山坡向上走了到达处的三龙潭瀑布,再沿坡角为的山坡向上走了到达处的二龙潭瀑布.求小卓从处的九孔桥到处的二龙潭瀑布上升的高度为多少米?(结果精确到)
(参考数据:)
16.实验是培养学生创新能力的重要途径.如图是小亮同学安装的化学实验装置,安装要求为试管口略向下倾斜,铁夹应固定在距试管口的三分之一处.现将左侧的实验装置图抽象成右侧示意图,已知试管,试管倾斜角为.
(1)求试管口B与铁杆的水平距离的长度;(结果用含非特殊角的三角函数表示)
(2)实验时,导气管紧靠水槽壁,延长交的延长线于点F,且于点N(点C,D,N,F在一条直线上),经测得:,求线段的长度.(结果用含非特殊角的三角函数表示)
17.如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图2,此时测得点到所在直线的距离,;停止位置示意图如图3,此时测得(点,,在同一直线上,且直线与平面平行,图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变.(参考数据:,,,)
(1)求的长;
(2)求物体上升的高度(结果精确到).
18.小明从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A,B,C,D分别是长方体棱的中点,若光线经真空从矩形对角线交点O处射入,其折射光线恰好从点C处射出.如图②,已知,,求截面的面积.
《2025年中考数学解答题专题系列:解直角三角形的应用》参考答案
1.点A到地面的距离的长约为27米
【分析】本题考查解直角三角形的应用—仰角俯角问题、锐角三角函数,解答本题的关键是明确题意,利用数形结合的思想解答.
延长交于点,根据矩形的性质得到,解直角三角形即可得到结论.
【详解】解:延长交于点,
由题意得,四边形为矩形,
,
在中,,,
,
,
在中,,,
,
,
设米.
,
,
,
解得,
(米);
答:点到地面的距离的长约为27米.
2.米
【分析】本题主要考查了矩形的判定和性质,解直角三角形的应用,证明四边形和四边形为矩形,得出米,米,,,设,则米,解直角三角形得出,,根据米,得出,求出,最后得出答案即可.
【详解】解:根据题意可得:,,
∴四边形和四边形为矩形,
∴米,米,,,
∴(米),
设,则米,
∵,,
∴,
∵,,
∴,
∴,,
∵米,
∴,
解得:,
∴米.
3.
【分析】过点C作于点M, 设, 则,根据仰角,解直角三角形计算即可.
本题考查了仰角解直角三角形,分式方程的应用,熟练掌握解直角三角形的应用是解题的关键.
【详解】解:过点C作于点M, 设, 则,
在中, ,
则,
则;
在中, ,
则
解得:,
经检验,是该分式方程的解.
∴.
答:无人机在C处时离地面.
4.73.2米
【分析】本题考查了解直角三角形的应用仰角俯角问题,熟练掌握解直角三角形的方法是解题的关键.根据题意得到米,米,,,解直角三角形即可得到结论.
【详解】解:由题意得,米,米,,,
在中,,
,
在中,,
,
米,
,
解得,
(米,
答:塔的高度为73.2米.
5.(1)
(2)
(3)
【分析】本题主要考查待定系数法求二次函数解析式以及二次函数的图像和性质,解直角三角形,熟练掌握二次函数的图像和性质是解题的关键.
(1)设关于的函数表达式为,将图中的点代入即可求出答案;
(2)求出二次函数的对称轴,在对称轴处取最值;
(3)延长与过点作的线交于点,令,根据三角函数进行计算,求出即可得到答案.
【详解】(1)解:设关于的函数表达式为,
将代入,
得,
解得,
;
(2)解:根据函数解析式得函数对称轴,
故阳能板与水平地面的夹角为度时,日平均太阳辐射量最大;
(3)解:,
延长与过点作的线交于点,令,
,,
,
,
,
,
,
延长交与点,
,
,
,
,
,
.
6.米
【分析】本题考查了解直角三角形的应用,分别过点作的垂线,垂足分别为,根据题意得出,解求得,,进而求得,根据,即可求解.
【详解】解:如图所示,分别过点作的垂线,垂足分别为,
∴四边形是矩形,
∴,,
依题意,,
∴,
∴,
∴;
在中,,
;
在中,,
∴.
答:大桥的长度约为米.
7.(1)B,C两处的距离为16海里
(2)渔政船的航行时间为小时
【分析】本题考查了解直角三角形的实际应用,解题的关键是正确画出辅助线,构造直角三角形.
(1)根据题意易得,则,再求出(海里),即可解答;
(2)过点D作于点F,设海里,则,,则,求出,进而得出海里,海里,根据勾股定理可得:(海里),即可解答.
【详解】(1)解:过点A作于点E,
∵灯塔B在灯塔A的南偏东方向,C处在灯塔A的北偏东方向、灯塔B的正北方向.
∴,
∴,
∵,
∴,
∵海里,
∴(海里),
∴(海里),
∴B,C两处的距离为16海里.
(2)解:过点D作于点F,
设海里,
∵,
∴,
由(1)可知,海里,
∴海里,
∵,
∴,
∴,
解得:,
∴海里,海里,
根据勾股定理可得:(海里),
∴渔政船的航行时间为(小时),
答:渔政船的航行时间为小时.
8.处距离处有140海里.
【分析】本题考查了解直角三角形的应用方向角问题.过作于,解直角三角形即可得到结论.
【详解】解:过作于,
在中,,海里,
(海里),
(海里),
在中,,
(海里),
(海里),
答:处距离处有140海里.
9.(1),两港之间的距离海里;
(2)甲货轮先到达港.
【分析】()过作于点,由题意可知:,,求出,即可求解;
()通过三角函数求出甲行驶路程为:,乙行驶路程为:,然后比较即可;
本题考查了方位角视角下的解直角三角形,构造直角三角形,熟练掌握锐角三角函数是解题的关键.
【详解】(1)如图,过作于点,
∴,
由题意可知:,,
∴,
∴,
∴,
∴(海里),
∴,两港之间的距离海里;
(2)由()得:,,,
∴,
∴,
由题意得:,,
∴,
∴,(海里),
∴甲行驶路程为:(海里),乙行驶路程为:(海里),
∵,且甲、乙速度相同,
∴甲货轮先到达港.
10.长江口的宽度为米.
【分析】如图,过作于,过作于,过作于,而,可得四边形,都是矩形,由题意可得:,,证明,可得,设,,再利用三角函数建立方程组求解即可.
【详解】解:如图,过作于,过作于,过作于,而,
∴四边形,都是矩形,
∴,,,,
∵由题意可得:,,
∴,,
∵,
∴,
∴,
设,,
∴,即,
,即,
∴,
∴,
∴,
∴,
∴;
∴长江口的宽度为米.
【点睛】本题考查的是解直角三角形的实际应用,矩形的判定于性质,全等三角形的判定与性质,作出合适的辅助线是解本题的关键.
11.(1);
(2)电线塔的高度.
【分析】本题主要考查了解直角三角形的实际应用.
(1)由斜坡的坡度,求得,利用正切函数的定义得到,据此求解即可;
(2)作于点,设,先解得到,解得到米,进而得到方程,解方程即可得到答案.
【详解】(1)解:∵斜坡的坡度,
∴,
∵,
∴,
∵,
∴;
(2)解:作于点,则四边形是矩形,,,
设,
在中,,
∴,
在中,,
在中,,,
∴,
∴,
∴,
∴,
∴
答:电线塔的高度.
12.32m
【分析】本题考查的是矩形的判定与性质,解直角三角形的实际应用,过点作于点,作于点,先求解,,再证明,再利用锐角的正切可得,从而可得答案.
【详解】解:过点作于点,作于点
由题意得:,
在中,
,
,
,
四边形为矩形,
,,
,
在中.
,
答:该风力发电机塔杆的高度为.
13.堤坝高为8米,山高为20米.
【分析】过B作于H,设,,根据勾股定理得到,求得,过B作于F,则,设,解直角三角形即可得到结论.
【详解】解:过B作于H,
∵坡度i为,
∴设,,
∴,
∴,
∴,
过B作于F,
则,
设,
∵.
∴,
∴,
∵坡度i为,
∴,
∴,
∴(米),
∴(米),
答:堤坝高为8米,山高为20米.
【点睛】本题考查了解直角三角形的应用-俯角仰角,解直角三角形的应用-坡角坡度,正确地作出辅助线是解题的关键.
14.的长为米
【分析】作于点,首先根据坡度求出,并通过矩形的判定确定出,然后通过解三角形求出,即可相加得出结论.
【详解】解:如图所示,作于点,则由题意,四边形为矩形,
∵在中,,,,
∴,
∵四边形为矩形,
∴,
由题意,,,,,
∴为等腰直角三角形,,
设,则,
在中,,
∴,即:,
解得:,经检验,是上述方程的解,且符合题意,
∴,
∴,
∴的长为米.
【点睛】本题考查解直角三角形的应用,准确构造出直角三角形并求解是解题关键.
15.
【分析】过点作,垂足为,在中,根据求出,过点作,垂足为,在中,根据求出,进而求解即可.
【详解】过点作,垂足为.
在中,,
∴.
过点作,垂足为.
在中,,
∴.
∵,
∴.
答:从处的九孔桥到处的二龙潭瀑布上升的高度约为.
【点睛】此题考查了解直角三角形的应用一坡度坡角问题,熟练利用锐角三角函数关系是解题关键.
16.(1)
(2)
【分析】本题主要考查了解直角三角形的应用,通过作辅助线构造直角三角形,掌握直角三角形中的边角关系是解题关键.
(1)先求出,再在中,利用余弦的定义求解即可得;
(2)过点作于点,过点作于点,先解直角三角形可得的长,从而可得的长,再判断出是等腰直角三角形,从而可得的长,最后根据求解即可得.
【详解】(1)解:∵,
∴,
由题意可知,,
在中,,
∴,
答:试管口与铁杆的水平距离的长度.
(2)解:如图,过点作于点,过点作于点,
则四边形和四边形都是矩形,
∴,
在中,,,
∴,
∵,
∴,
∴,
∵,,,
∴,
∴是等腰直角三角形,
∴,
∴,
答:线段的长度为.
17.(1)
(2)
【分析】本题考查了解直角三角形的应用,勾股定理,熟练掌握知识点是解题的关键.
(1)解即可求解;
(2)在中,由勾股定理得,,解求得,由题意得,,故,则.
【详解】(1)解:由题意得,,
∵,,
∴在中,由,
得:,
∴,
答:;
(2)解:在中,由勾股定理得,,
在中,,
∴,
∴,
由题意得,,
∴,
∴,
答:物体上升的高度约为.
18.(1);
(2).
【分析】本题主要考查了解直角三角形的应用,勾股定理等知识,
(1)根据,设,则,利用勾股定理求出,进而可得,问题即可得解;
(2)根据折射率与(1)的材料相同,可得折射率为,根据,可得,则有,在中,设,,问题随之得解.
【详解】(1)∵,
∴如图,
设,则,由勾股定理得,,
∴,
又∵,
∴,
∴折射率为:.
(2)根据折射率与(1)的材料相同,可得折射率为,
∵,
∴,
∴.
∵四边形是矩形,点O是中点,
∴,,
又∵,
∴,
在中,设,,
由勾股定理得,,
∴.
又∵,
∴,
∴,
∴,
∴截面的面积为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
