2025年中考数学解答题系列:二次根式综合(含解析)
文档属性
| 名称 | 2025年中考数学解答题系列:二次根式综合(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 17:48:46 | ||
图片预览




文档简介
/ 让教学更有效 高效备考 | 英语学科
2025年中考数学解答题系列:二次根式综合
1.我国南宋时期数学家秦九韶(约1202—约1261),曾提出利用三角形的三边求面积的秦九韶公式(其中a,b,c表示三角形的三边长),此公式与古希腊的几何学家海伦(Heron,约公元50年)提出的海伦公式(其中a,b,c表示三角形的三边长,)如出一辙,所以秦九韶公式与海伦公式实质上是同一个公式,所以我们也称为海伦-秦九韶公式.
(1)已知在中,,,,且a,b,c满足.
①______,______,______.
②请你从两个公式中选择一个合适的公式,求出的面积.
(2)如图,在中,,,,请你用海伦-秦九韶公式求的面积.
2.现有两块同样大小的长方形纸片,小星采用如图①所示的方式,在长方形纸片上裁出两块面积分别为和的正方形纸片A,B.
(1)原长方形纸片的周长是_____ (结果化为最简二次根式);
(2)写出图①中阴影部分的长和宽,并求出它的面积;
(3)小红想采用如图②所示的方式,在长方形纸片上裁出面积为的两块正方形纸片,请你判断能否裁出,并说明理由.
3.阅读:古希腊的几何家海伦,在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了一个公式,如果一个三角形的三边长分别为,记,则三角形的面积,此公式称为“海伦公式”.
思考运用,已知李大爷有一块三角形的菜地,如图,测得,你能求出李大爷这块菜地的面积吗?试试看.
4.阅读与思考:阅读下列材料,完成相应的任务:
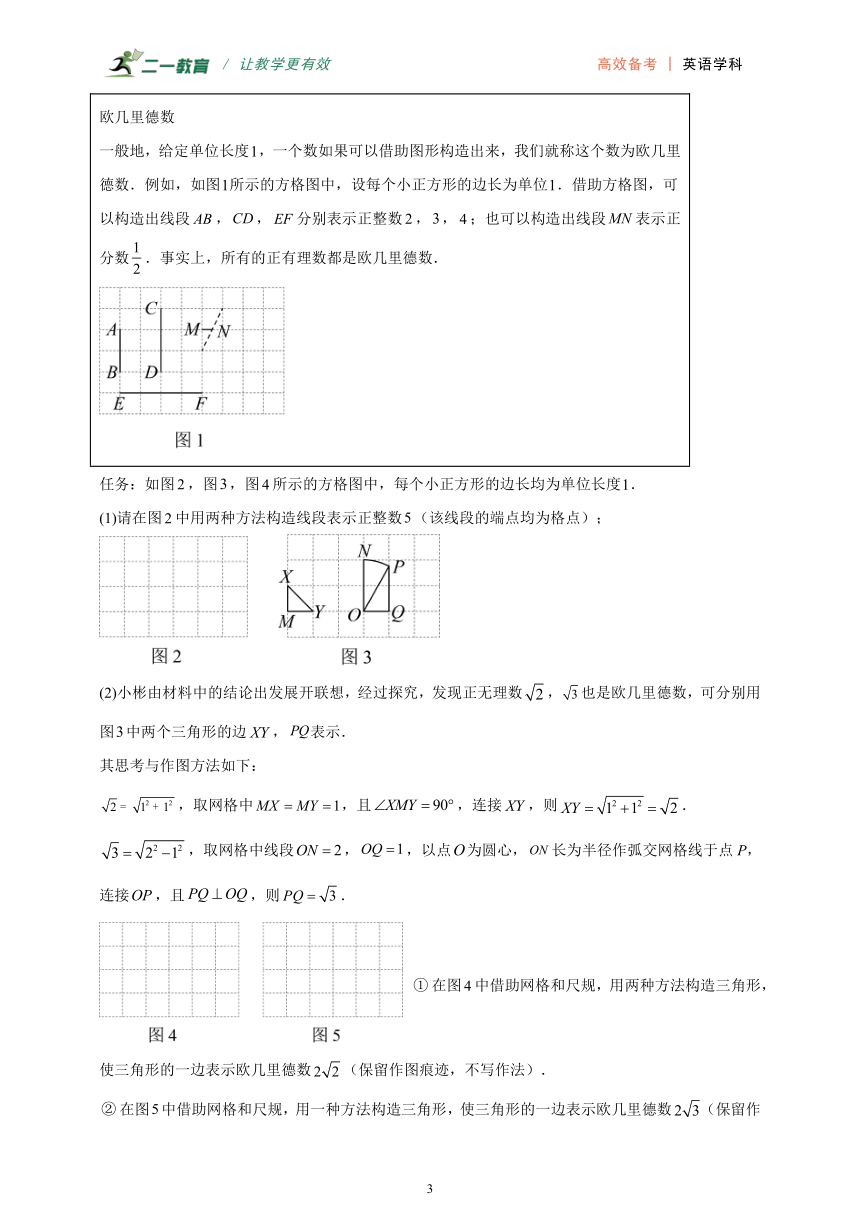
欧几里德数 一般地,给定单位长度,一个数如果可以借助图形构造出来,我们就称这个数为欧几里德数.例如,如图所示的方格图中,设每个小正方形的边长为单位.借助方格图,可以构造出线段,,分别表示正整数,,;也可以构造出线段表示正分数.事实上,所有的正有理数都是欧几里德数.
任务:如图,图,图所示的方格图中,每个小正方形的边长均为单位长度.
(1)请在图中用两种方法构造线段表示正整数(该线段的端点均为格点);
(2)小彬由材料中的结论出发展开联想,经过探究,发现正无理数,也是欧几里德数,可分别用图中两个三角形的边,表示.
其思考与作图方法如下:
,取网格中,且,连接,则.
,取网格中线段,,以点为圆心,长为半径作弧交网格线于点P,连接,且,则.
在图中借助网格和尺规,用两种方法构造三角形,使三角形的一边表示欧几里德数(保留作图痕迹,不写作法).
在图中借助网格和尺规,用一种方法构造三角形,使三角形的一边表示欧几里德数(保留作图痕迹,不写作法).
5.【综合与实践】如图,把图(1)中两个小正方形纸片分别沿对角线剪开,拼成一个面积为的大正方形纸片如图(2).
(1)原小正方形的边长为______ ;
(2)若沿此大正方形边的方向剪出一个长方形,能否使剪出的长方形的长宽之比为,且面积为?若能,试求出剪出的长方形纸片的长宽;若不能,试说明理由
(3)如图(3)是由5个边长为1的小正方形组成的纸片,能否把它剪开并拼成一个大正方形?若能,请画出示意图,并写出边的长度,若不能,请说明理由.
6.如图,某乡村有块形状为长方形的空地,长为,宽为,现要在空地上建休闲广场,中间修建长方形的儿童活动区(图中阴影部分),儿童活动区的长为,宽为.
(1)求长方形的周长.(结果需要化简)
(2)除去儿童活动区,空地的其他地方全部浇筑水泥,求浇筑水泥区的面积.
7.【问题提出】
(1)如图①,在中,(其中),猜测是什么三角形,并说明理由.
【问题探究】
(2)如图②,,点C为射线上一点,且,点D为射线上的动点,当为等腰三角形时,求的长;(结果保留根号)
【问题解决】
(3)如图③,为某植物园的一片绿化区域,且米,米,米,已知在的延长线上,距离A点40米的点D处有一口灌溉水井(灌溉水井的大小忽略不计),管理人员计划沿修一条小路,并在上找一点E,在中种植栀子花,当种植栀子花的区域(为等腰三角形时),直接写出的长.(结果保留根号).
8.综合与实践
问题情境:学校计划利用长和宽分别为和的长方形铁片裁剪焊接成两个无盖的长方体铁箱用于存储备用实验材料,欣欣和畅畅设计了两种不同的裁剪焊接方案.
欣欣的方案:如图1,先将铁片分为左右两个全等的正方形,分得的每一块都在其四个直角处剪掉四个小正方形,再分别沿虚线折起来,得到两个同样大小、且底面为正方形的无盖长方体铁箱.
畅畅的方案:如图2,先将铁片在中间剪掉一块正方形②,再在四个直角处剪掉四个小正方形,最后分别沿着虚线折起来,得到两个同样大小、且底面为长方形的无盖长方体铁箱.
(1)若欣欣的方案中剪掉的小正方形的边长为,求裁剪焊接成的铁箱的底面正方形①的面积.
(2)若畅畅的方案中正方形②的边长为,求裁剪焊接成的一个无盖长方体铁箱的体积.
(3)若这两种方案所制作的无盖长方体铁箱的高都是,则___________的方案中制作的无盖长方体铁箱的体积更大.(填“欣欣”或“畅畅”)
9.某社区计划打造一个休闲区域,有块形状为长方形的空地被规划使用.长为米,宽为米,社区打算在长方形空地中修建两个形状大小相同的长方形花坛来美化环境(即图中阴影部分),每个长方形花坛的长为米,宽为米.
(1)请你求出长方形的周长.(结果化为最简二次根式)
(2)除去修建花坛的地方,其它地方全修建成为步道,步道供居民日常散步等活动.现在要在步道上铺上造价为80元/平方米的地砖,请问要铺完整个步道,购买地砖需要花费多少元?
10.情景:实践小组成员利用两块相同的长方形木板各切割两个正方形木板.
操作:甲组成员的切割方式如图1所示,小正方形①(一边与长方形边重合)的面积为,小正方形②(三边与长方形边重合)的面积为,.
(1)求的长.
探究:乙组成员的切割方式如图2所示,从长方形木板上切下两块完全相同的最大的正方形木板③④.
(2)求剩余部分(阴影)的面积.
11.综合与应用
【阅读材料】小桂和小林在学习了三角形之后,两人对“已知三边长的三角形的面积问题”进行了探究.他们首先各自查找了相关问题的资料.
小桂找到的资料如下:
《数书九章》是我国南宋著名数学家秦九韶的著作,书中记载了:如果一个三角形的三边长分别为a,b,c,则这个三角形的面积公式为:
小林找到的资料如下:
古希腊数学家海伦在他的《测地术》著作中记载了:如果一个三角形的三边长分别为a,b,c,记,则三角形的面积为:
根据以上信息,回答以下问题:
【学以致用】(1)已知一个三角形的三边长分别为3,4,5.
①若利用小林提供的资料求这个三角形的面积,请直接写出p和S的值;
②请利用小桂提供的资料求这个三角形的面积.
【拓展应用】(2)在中,,点M是中点,N是边上的一个三等分点,连接,请求的面积.
12.细心观察下图,认真分析各式,然后解答下列问题:
,(是的面积);
,(是的面积);
,(是的面积);
…
(1)请用含有n(n为正整数)的式子填空:______,______;
(2)在线段,,,…,中,长度为正整数的线段共有______条
(3)求的值;
《2025年中考数学解答题系列:二次根式综合》参考答案
1.(1)①,,3;②的面积为
(2)的面积为
【分析】本题主要考查平方,绝对值,算术平方根的非负性,秦九韶公式与海伦公式,熟练掌握运算法则是解题的关键.
(1)①根据平方,绝对值,算术平方根的非负性得到答案即可;
②选择海伦公式进行计算即可;
(2)根据题目给出的公式进行计算即可.
【详解】(1)解:①,
,
故答案为:,,3;
②;
(2)解:
;
2.(1)
(2)阴影部分的长为,宽为,面积为3
(3)不能截出,见解析
【分析】本题考查了算术平方根的应用以及二次根式的混合运算,正确掌握相关性质内容是解题的关键.
(1)根据正方形面积等于边长的平方,结合面积为,即可计算正方形纸片A的边长,算出正方形纸片B的边长,再得出原长方形纸片的长,宽,即可作答;
(2)先找出图①中阴影部分的长和宽,再结合面积公式列式计算,即可作答.
(3)先计算,则,据此即可作答.
【详解】(1)解:依题意,正方形纸片A的边长为;
则截出的正方形纸片B的边长为,
则原长方形纸片的长为,宽为,
∴,
故答案为:
(2)解:阴影部分的长正方形纸片A的边长,
即阴影部分的长为,
则
∴阴影部分的宽为,
∴阴影部分的面积.
(3)解:不能截出,理由如下:
∵面积为的正方形纸片的边长为,
则,
∴不能在矩形纸片上裁出两块面积是的正方形纸片.
3.李大爷这块菜地的面积为
【分析】本题考查了二次根式的应用,将题目中的已知量代入到海伦公式里面进行计算即可.解题的关键是正确的代入公式并进行计算.
【详解】解:,
.
.
李大爷这块菜地的面积为
4.(1)见解析;
(2)①见解析;②见解析.
【分析】本题考查了作图应用与设计作图,网格与勾股定理,无理数与勾股定理,解题的关键是学会利用勾股定理以及数形结合的思想解决问题.
()利用数形结合的思想解决问题即可;
()利用勾股定理,数形结合的思想解决问题即可;
利用勾股定理,数形结合的思想解决问题即可.
【详解】(1)解:如图,
由网格可知:,,
∴,即为所求;
(2)解:如图,
由网格可知:,,
∴,即为所求;
如图,
∴,,,
∴,即为所求.
5.(1)
(2)能,理由见解析
(3)能,图见解析,
【分析】本题考查了图形的剪拼、正方形的面积、二次根式的实际应用等知识,熟练掌握二次根式的性质是解题的关键.
(1)根据小正方形的面积是大正方形面积的一半可得小正方形的面积,即可解决问题;
(2)设剪出来的长方形长为cm,宽为,根据面积为可得x的值,则长为,即可得出结论;
(3)一共有5个小正方形,那么组成的大正方形的面积为5,边长为,据此画出示意图即可.
【详解】(1)解:小正方形的面积是大正方形面积的一半,
小正方形的面积为(cm2),
设小正方形的边长为a,
则,
∴(舍去负值),
∴小正方形的边长为,
故答案为:;
(2)解:能剪出符合要求的长方形纸片,理由如下:
设剪出来的长方形长为,宽为,
依题意得,
∴或(舍去),
∴长为,
∴能剪出符合要求的长方形纸片;
(3)解:∵一共有5个小正方形,那么组成的大正方形的面积为5,边长为,
画出示意图如图:
6.(1)长方形的周长为米.
(2)浇筑水泥区的面积为平方米.
【分析】本题考查的是二次根式的应用;
(1)由长方形的周长公式列式,再化简计算即可;
(2)由大的长方形的面积减去小的长方形的面积即可;
【详解】(1)解:米,
答:长方形的周长为米.
(2)解:由题意可得:
平方米,
答:浇筑水泥区的面积为平方米.
7.(1)是直角三角形,理由见解析;(2)或或2;(3)米或米或米
【分析】(1)由勾股定理的逆定理可得出结论;
(2)分三种情况,根据等腰三角形的定义和勾股定理讨论求解即可;
(3)先利用勾股定理的逆定理推出是直角三角形,且,再证明为等腰直角三角形,丙利用勾股定理求出的长,接着分三种情况,,根据等腰三角形的定义和勾股定理求解即可.
【详解】解:(1)是直角三角形,理由如下:
在中,,
∴,,,
∴
∴是直角三角形;
(2)①如图,当时,则,
∴,
∴;
②如图,当时,则,
∴,
∴,
∴;
③当满足时,也满足是等腰三角形;
综上所述,当为等腰三角形时,或或2;
(3)∵米,米,米,
∴,,
∴,
∴是直角三角形,且,
又∵米,且点D在延长线上,
∴米,
∴米,
∴为等腰直角三角形,
∴,米,
①当时,则,
∴,
∴,
∵米,
∴米,
∴米,
②当时,则,
∴,
∴米,
∴米,
③当米时,
则米,
综上所述,为等腰三角形时,米或米或米.
【点睛】本题是三角形综合题,考查了等腰三角形的判定与性质,直角三角形的判定与性质,勾股定理及其逆定理,等腰直角三角形的性质,正确进行分类讨论是解题的关键.
8.(1)
(2)
(3)欣欣
【分析】本题考查了二次根式的应用,几何体的展开图,数形结合是解题的关键;
(1)根据图1,根据正方形的面积公式进行计算即可求解;
(2)根据图2,得出盖长方体铁箱的宽为,长为,进而求得体积;
(3)分别求得两个方案中长方体铁箱的体积,比较大小,即可求解.
【详解】(1)解:依题意,
裁剪焊接成的铁箱的底面正方形①的面积为
(2)解:四个直角处的小正方形边长为
无盖长方体铁箱的宽为,长为
裁剪焊接成的一个无盖长方体铁箱的体积为
(3)这两种方案所制作的无盖长方体铁箱的高都是
欣欣的方案中制作的无盖长方体铁箱的高为,则底面正方形①的边长是,
底面积是:
体积为:
畅畅的方案中正方形②的边长为,则制作的无盖长方体铁箱的宽为:
底面积为,
体积为
∵
∴欣欣的方案中制作的无盖长方体铁箱的体积更大.
故答案为:欣欣.
9.(1)米
(2)元
【分析】本题主要考查了二次根式的应用,熟知二次根式的相关计算法则是解题的关键:
(1)根据长方形周长计算公式列式计算即可;
(2)用大长方形面积减去花坛总面积即可求出步道的面积,再乘以地砖每平方米的造价即可得到答案.
【详解】(1)解:米,
答:长方形的周长为米;
(2)解:
元,
答:要铺完整个步道,购买地砖需要花费元.
10.(1)的长为(2)剩余部分(阴影)的面积
【分析】本题主要考查了二次根式混合运算的实际应用,熟练掌握二次根式混合运算的运算顺序和运算法则并能正确根据图形,得出数量关系是解决此题的关键.
(1)根据小正方形的面积,可求出边长,然后计算线段的和差即可得解;
(2)先求出大长方形的长面积,再求出小正方形的面积,然后进行计算即可得解.
【详解】(1)解:∵小正方形①(一边与长方形边重合)的面积为,小正方形②(三边与长方形边重合)的面积为,
∴小正方形①的边长,小正方形②的边长,
∵,
∴,
∴的长为;
(2)解:由(1)知大长方形的长为,宽为,
∴大长方形的面积为,
∵从长方形木板上切下两块完全相同的最大的正方形木板③④,
∴切下两块完全相同的最大的正方形边长为,
∴切下两块完全相同的最大的正方形面积为,
∴剩余部分(阴影)的面积.
11.(1)①,②;(2)或
【分析】本题考查了三角形的中线求面积,二次根式的应用,正确理解题意是解题的关键.
(1)①先求出p,再代入求出面积;②直接代入计算即可;
(2)先利用求出的面积,再由三角形的中线等分面积求出,再由三等分点分类利用共高三角形面积比等于底之比求解.
【详解】解(1)①由题意得,,
∴;
②
;
(2)如图,连接
∵在中,,
∴
∴,
∵点M是中点,N是边上的一个三等分点,
∴,或
∴或,
∴的面积为或.
12.(1)n,
(2)45
(3)18
【分析】考查了新定义的理解,二次根式的化简,关键是理解新定义和有关二次根式的化简运算.
(1)认真阅读新定义,根据已知内容归纳总结即可;
(2)通过分析数据不难发现当边长正好是根号下一个正整数的平方时,出现的就是正整数.分析2025最接近哪个正整数的平方.
(3)代入化简整理求值即可;
【详解】(1)观察所给式子:,,,以此类推,可得.
对于,,,所以(n为正整数).
故答案为:n,.
(2)解:∵,
∴
当时,,
当时,,
当时,,
当时,,
…
当(k为正整数)时,,
∵,,
∴1到2025有45个完全平方数,
∴线段,,,…,中,长度为正整数的线段共有45条.
故答案为:45.
(3)解:∵,,,
∴原式
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
2025年中考数学解答题系列:二次根式综合
1.我国南宋时期数学家秦九韶(约1202—约1261),曾提出利用三角形的三边求面积的秦九韶公式(其中a,b,c表示三角形的三边长),此公式与古希腊的几何学家海伦(Heron,约公元50年)提出的海伦公式(其中a,b,c表示三角形的三边长,)如出一辙,所以秦九韶公式与海伦公式实质上是同一个公式,所以我们也称为海伦-秦九韶公式.
(1)已知在中,,,,且a,b,c满足.
①______,______,______.
②请你从两个公式中选择一个合适的公式,求出的面积.
(2)如图,在中,,,,请你用海伦-秦九韶公式求的面积.
2.现有两块同样大小的长方形纸片,小星采用如图①所示的方式,在长方形纸片上裁出两块面积分别为和的正方形纸片A,B.
(1)原长方形纸片的周长是_____ (结果化为最简二次根式);
(2)写出图①中阴影部分的长和宽,并求出它的面积;
(3)小红想采用如图②所示的方式,在长方形纸片上裁出面积为的两块正方形纸片,请你判断能否裁出,并说明理由.
3.阅读:古希腊的几何家海伦,在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了一个公式,如果一个三角形的三边长分别为,记,则三角形的面积,此公式称为“海伦公式”.
思考运用,已知李大爷有一块三角形的菜地,如图,测得,你能求出李大爷这块菜地的面积吗?试试看.
4.阅读与思考:阅读下列材料,完成相应的任务:
欧几里德数 一般地,给定单位长度,一个数如果可以借助图形构造出来,我们就称这个数为欧几里德数.例如,如图所示的方格图中,设每个小正方形的边长为单位.借助方格图,可以构造出线段,,分别表示正整数,,;也可以构造出线段表示正分数.事实上,所有的正有理数都是欧几里德数.
任务:如图,图,图所示的方格图中,每个小正方形的边长均为单位长度.
(1)请在图中用两种方法构造线段表示正整数(该线段的端点均为格点);
(2)小彬由材料中的结论出发展开联想,经过探究,发现正无理数,也是欧几里德数,可分别用图中两个三角形的边,表示.
其思考与作图方法如下:
,取网格中,且,连接,则.
,取网格中线段,,以点为圆心,长为半径作弧交网格线于点P,连接,且,则.
在图中借助网格和尺规,用两种方法构造三角形,使三角形的一边表示欧几里德数(保留作图痕迹,不写作法).
在图中借助网格和尺规,用一种方法构造三角形,使三角形的一边表示欧几里德数(保留作图痕迹,不写作法).
5.【综合与实践】如图,把图(1)中两个小正方形纸片分别沿对角线剪开,拼成一个面积为的大正方形纸片如图(2).
(1)原小正方形的边长为______ ;
(2)若沿此大正方形边的方向剪出一个长方形,能否使剪出的长方形的长宽之比为,且面积为?若能,试求出剪出的长方形纸片的长宽;若不能,试说明理由
(3)如图(3)是由5个边长为1的小正方形组成的纸片,能否把它剪开并拼成一个大正方形?若能,请画出示意图,并写出边的长度,若不能,请说明理由.
6.如图,某乡村有块形状为长方形的空地,长为,宽为,现要在空地上建休闲广场,中间修建长方形的儿童活动区(图中阴影部分),儿童活动区的长为,宽为.
(1)求长方形的周长.(结果需要化简)
(2)除去儿童活动区,空地的其他地方全部浇筑水泥,求浇筑水泥区的面积.
7.【问题提出】
(1)如图①,在中,(其中),猜测是什么三角形,并说明理由.
【问题探究】
(2)如图②,,点C为射线上一点,且,点D为射线上的动点,当为等腰三角形时,求的长;(结果保留根号)
【问题解决】
(3)如图③,为某植物园的一片绿化区域,且米,米,米,已知在的延长线上,距离A点40米的点D处有一口灌溉水井(灌溉水井的大小忽略不计),管理人员计划沿修一条小路,并在上找一点E,在中种植栀子花,当种植栀子花的区域(为等腰三角形时),直接写出的长.(结果保留根号).
8.综合与实践
问题情境:学校计划利用长和宽分别为和的长方形铁片裁剪焊接成两个无盖的长方体铁箱用于存储备用实验材料,欣欣和畅畅设计了两种不同的裁剪焊接方案.
欣欣的方案:如图1,先将铁片分为左右两个全等的正方形,分得的每一块都在其四个直角处剪掉四个小正方形,再分别沿虚线折起来,得到两个同样大小、且底面为正方形的无盖长方体铁箱.
畅畅的方案:如图2,先将铁片在中间剪掉一块正方形②,再在四个直角处剪掉四个小正方形,最后分别沿着虚线折起来,得到两个同样大小、且底面为长方形的无盖长方体铁箱.
(1)若欣欣的方案中剪掉的小正方形的边长为,求裁剪焊接成的铁箱的底面正方形①的面积.
(2)若畅畅的方案中正方形②的边长为,求裁剪焊接成的一个无盖长方体铁箱的体积.
(3)若这两种方案所制作的无盖长方体铁箱的高都是,则___________的方案中制作的无盖长方体铁箱的体积更大.(填“欣欣”或“畅畅”)
9.某社区计划打造一个休闲区域,有块形状为长方形的空地被规划使用.长为米,宽为米,社区打算在长方形空地中修建两个形状大小相同的长方形花坛来美化环境(即图中阴影部分),每个长方形花坛的长为米,宽为米.
(1)请你求出长方形的周长.(结果化为最简二次根式)
(2)除去修建花坛的地方,其它地方全修建成为步道,步道供居民日常散步等活动.现在要在步道上铺上造价为80元/平方米的地砖,请问要铺完整个步道,购买地砖需要花费多少元?
10.情景:实践小组成员利用两块相同的长方形木板各切割两个正方形木板.
操作:甲组成员的切割方式如图1所示,小正方形①(一边与长方形边重合)的面积为,小正方形②(三边与长方形边重合)的面积为,.
(1)求的长.
探究:乙组成员的切割方式如图2所示,从长方形木板上切下两块完全相同的最大的正方形木板③④.
(2)求剩余部分(阴影)的面积.
11.综合与应用
【阅读材料】小桂和小林在学习了三角形之后,两人对“已知三边长的三角形的面积问题”进行了探究.他们首先各自查找了相关问题的资料.
小桂找到的资料如下:
《数书九章》是我国南宋著名数学家秦九韶的著作,书中记载了:如果一个三角形的三边长分别为a,b,c,则这个三角形的面积公式为:
小林找到的资料如下:
古希腊数学家海伦在他的《测地术》著作中记载了:如果一个三角形的三边长分别为a,b,c,记,则三角形的面积为:
根据以上信息,回答以下问题:
【学以致用】(1)已知一个三角形的三边长分别为3,4,5.
①若利用小林提供的资料求这个三角形的面积,请直接写出p和S的值;
②请利用小桂提供的资料求这个三角形的面积.
【拓展应用】(2)在中,,点M是中点,N是边上的一个三等分点,连接,请求的面积.
12.细心观察下图,认真分析各式,然后解答下列问题:
,(是的面积);
,(是的面积);
,(是的面积);
…
(1)请用含有n(n为正整数)的式子填空:______,______;
(2)在线段,,,…,中,长度为正整数的线段共有______条
(3)求的值;
《2025年中考数学解答题系列:二次根式综合》参考答案
1.(1)①,,3;②的面积为
(2)的面积为
【分析】本题主要考查平方,绝对值,算术平方根的非负性,秦九韶公式与海伦公式,熟练掌握运算法则是解题的关键.
(1)①根据平方,绝对值,算术平方根的非负性得到答案即可;
②选择海伦公式进行计算即可;
(2)根据题目给出的公式进行计算即可.
【详解】(1)解:①,
,
故答案为:,,3;
②;
(2)解:
;
2.(1)
(2)阴影部分的长为,宽为,面积为3
(3)不能截出,见解析
【分析】本题考查了算术平方根的应用以及二次根式的混合运算,正确掌握相关性质内容是解题的关键.
(1)根据正方形面积等于边长的平方,结合面积为,即可计算正方形纸片A的边长,算出正方形纸片B的边长,再得出原长方形纸片的长,宽,即可作答;
(2)先找出图①中阴影部分的长和宽,再结合面积公式列式计算,即可作答.
(3)先计算,则,据此即可作答.
【详解】(1)解:依题意,正方形纸片A的边长为;
则截出的正方形纸片B的边长为,
则原长方形纸片的长为,宽为,
∴,
故答案为:
(2)解:阴影部分的长正方形纸片A的边长,
即阴影部分的长为,
则
∴阴影部分的宽为,
∴阴影部分的面积.
(3)解:不能截出,理由如下:
∵面积为的正方形纸片的边长为,
则,
∴不能在矩形纸片上裁出两块面积是的正方形纸片.
3.李大爷这块菜地的面积为
【分析】本题考查了二次根式的应用,将题目中的已知量代入到海伦公式里面进行计算即可.解题的关键是正确的代入公式并进行计算.
【详解】解:,
.
.
李大爷这块菜地的面积为
4.(1)见解析;
(2)①见解析;②见解析.
【分析】本题考查了作图应用与设计作图,网格与勾股定理,无理数与勾股定理,解题的关键是学会利用勾股定理以及数形结合的思想解决问题.
()利用数形结合的思想解决问题即可;
()利用勾股定理,数形结合的思想解决问题即可;
利用勾股定理,数形结合的思想解决问题即可.
【详解】(1)解:如图,
由网格可知:,,
∴,即为所求;
(2)解:如图,
由网格可知:,,
∴,即为所求;
如图,
∴,,,
∴,即为所求.
5.(1)
(2)能,理由见解析
(3)能,图见解析,
【分析】本题考查了图形的剪拼、正方形的面积、二次根式的实际应用等知识,熟练掌握二次根式的性质是解题的关键.
(1)根据小正方形的面积是大正方形面积的一半可得小正方形的面积,即可解决问题;
(2)设剪出来的长方形长为cm,宽为,根据面积为可得x的值,则长为,即可得出结论;
(3)一共有5个小正方形,那么组成的大正方形的面积为5,边长为,据此画出示意图即可.
【详解】(1)解:小正方形的面积是大正方形面积的一半,
小正方形的面积为(cm2),
设小正方形的边长为a,
则,
∴(舍去负值),
∴小正方形的边长为,
故答案为:;
(2)解:能剪出符合要求的长方形纸片,理由如下:
设剪出来的长方形长为,宽为,
依题意得,
∴或(舍去),
∴长为,
∴能剪出符合要求的长方形纸片;
(3)解:∵一共有5个小正方形,那么组成的大正方形的面积为5,边长为,
画出示意图如图:
6.(1)长方形的周长为米.
(2)浇筑水泥区的面积为平方米.
【分析】本题考查的是二次根式的应用;
(1)由长方形的周长公式列式,再化简计算即可;
(2)由大的长方形的面积减去小的长方形的面积即可;
【详解】(1)解:米,
答:长方形的周长为米.
(2)解:由题意可得:
平方米,
答:浇筑水泥区的面积为平方米.
7.(1)是直角三角形,理由见解析;(2)或或2;(3)米或米或米
【分析】(1)由勾股定理的逆定理可得出结论;
(2)分三种情况,根据等腰三角形的定义和勾股定理讨论求解即可;
(3)先利用勾股定理的逆定理推出是直角三角形,且,再证明为等腰直角三角形,丙利用勾股定理求出的长,接着分三种情况,,根据等腰三角形的定义和勾股定理求解即可.
【详解】解:(1)是直角三角形,理由如下:
在中,,
∴,,,
∴
∴是直角三角形;
(2)①如图,当时,则,
∴,
∴;
②如图,当时,则,
∴,
∴,
∴;
③当满足时,也满足是等腰三角形;
综上所述,当为等腰三角形时,或或2;
(3)∵米,米,米,
∴,,
∴,
∴是直角三角形,且,
又∵米,且点D在延长线上,
∴米,
∴米,
∴为等腰直角三角形,
∴,米,
①当时,则,
∴,
∴,
∵米,
∴米,
∴米,
②当时,则,
∴,
∴米,
∴米,
③当米时,
则米,
综上所述,为等腰三角形时,米或米或米.
【点睛】本题是三角形综合题,考查了等腰三角形的判定与性质,直角三角形的判定与性质,勾股定理及其逆定理,等腰直角三角形的性质,正确进行分类讨论是解题的关键.
8.(1)
(2)
(3)欣欣
【分析】本题考查了二次根式的应用,几何体的展开图,数形结合是解题的关键;
(1)根据图1,根据正方形的面积公式进行计算即可求解;
(2)根据图2,得出盖长方体铁箱的宽为,长为,进而求得体积;
(3)分别求得两个方案中长方体铁箱的体积,比较大小,即可求解.
【详解】(1)解:依题意,
裁剪焊接成的铁箱的底面正方形①的面积为
(2)解:四个直角处的小正方形边长为
无盖长方体铁箱的宽为,长为
裁剪焊接成的一个无盖长方体铁箱的体积为
(3)这两种方案所制作的无盖长方体铁箱的高都是
欣欣的方案中制作的无盖长方体铁箱的高为,则底面正方形①的边长是,
底面积是:
体积为:
畅畅的方案中正方形②的边长为,则制作的无盖长方体铁箱的宽为:
底面积为,
体积为
∵
∴欣欣的方案中制作的无盖长方体铁箱的体积更大.
故答案为:欣欣.
9.(1)米
(2)元
【分析】本题主要考查了二次根式的应用,熟知二次根式的相关计算法则是解题的关键:
(1)根据长方形周长计算公式列式计算即可;
(2)用大长方形面积减去花坛总面积即可求出步道的面积,再乘以地砖每平方米的造价即可得到答案.
【详解】(1)解:米,
答:长方形的周长为米;
(2)解:
元,
答:要铺完整个步道,购买地砖需要花费元.
10.(1)的长为(2)剩余部分(阴影)的面积
【分析】本题主要考查了二次根式混合运算的实际应用,熟练掌握二次根式混合运算的运算顺序和运算法则并能正确根据图形,得出数量关系是解决此题的关键.
(1)根据小正方形的面积,可求出边长,然后计算线段的和差即可得解;
(2)先求出大长方形的长面积,再求出小正方形的面积,然后进行计算即可得解.
【详解】(1)解:∵小正方形①(一边与长方形边重合)的面积为,小正方形②(三边与长方形边重合)的面积为,
∴小正方形①的边长,小正方形②的边长,
∵,
∴,
∴的长为;
(2)解:由(1)知大长方形的长为,宽为,
∴大长方形的面积为,
∵从长方形木板上切下两块完全相同的最大的正方形木板③④,
∴切下两块完全相同的最大的正方形边长为,
∴切下两块完全相同的最大的正方形面积为,
∴剩余部分(阴影)的面积.
11.(1)①,②;(2)或
【分析】本题考查了三角形的中线求面积,二次根式的应用,正确理解题意是解题的关键.
(1)①先求出p,再代入求出面积;②直接代入计算即可;
(2)先利用求出的面积,再由三角形的中线等分面积求出,再由三等分点分类利用共高三角形面积比等于底之比求解.
【详解】解(1)①由题意得,,
∴;
②
;
(2)如图,连接
∵在中,,
∴
∴,
∵点M是中点,N是边上的一个三等分点,
∴,或
∴或,
∴的面积为或.
12.(1)n,
(2)45
(3)18
【分析】考查了新定义的理解,二次根式的化简,关键是理解新定义和有关二次根式的化简运算.
(1)认真阅读新定义,根据已知内容归纳总结即可;
(2)通过分析数据不难发现当边长正好是根号下一个正整数的平方时,出现的就是正整数.分析2025最接近哪个正整数的平方.
(3)代入化简整理求值即可;
【详解】(1)观察所给式子:,,,以此类推,可得.
对于,,,所以(n为正整数).
故答案为:n,.
(2)解:∵,
∴
当时,,
当时,,
当时,,
当时,,
…
当(k为正整数)时,,
∵,,
∴1到2025有45个完全平方数,
∴线段,,,…,中,长度为正整数的线段共有45条.
故答案为:45.
(3)解:∵,,,
∴原式
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
