2025年中考数学解答题系列:锐角三角函数综合(含解析)
文档属性
| 名称 | 2025年中考数学解答题系列:锐角三角函数综合(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 00:00:00 | ||
图片预览

文档简介
/ 让教学更有效 高效备考 | 英语学科
2025年中考数学解答题系列:锐角三角函数综合
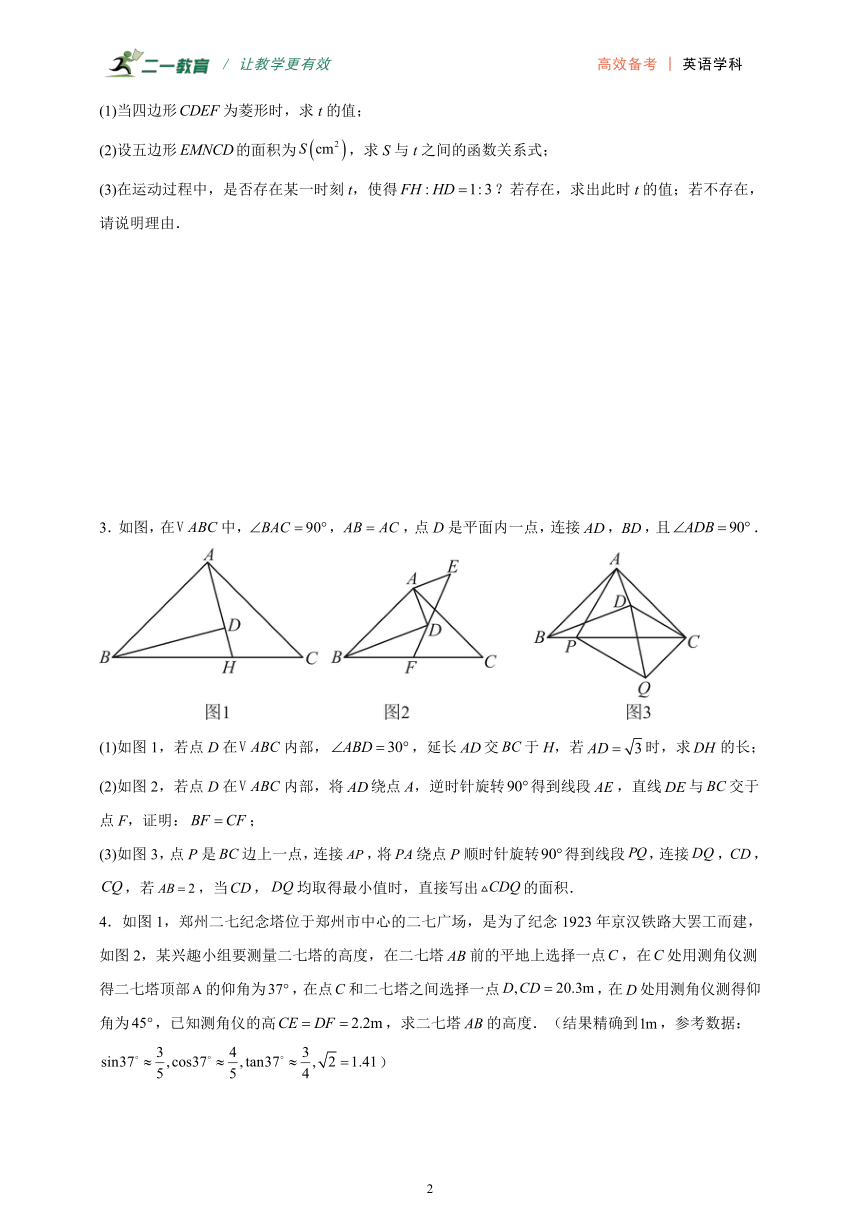
1.小明从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图所示,点,,,分别是长方体棱的中点,若光线经真空从矩形对角线交点处射入,其折射光线恰好从点处射出.如图,已知,,求截面的面积.
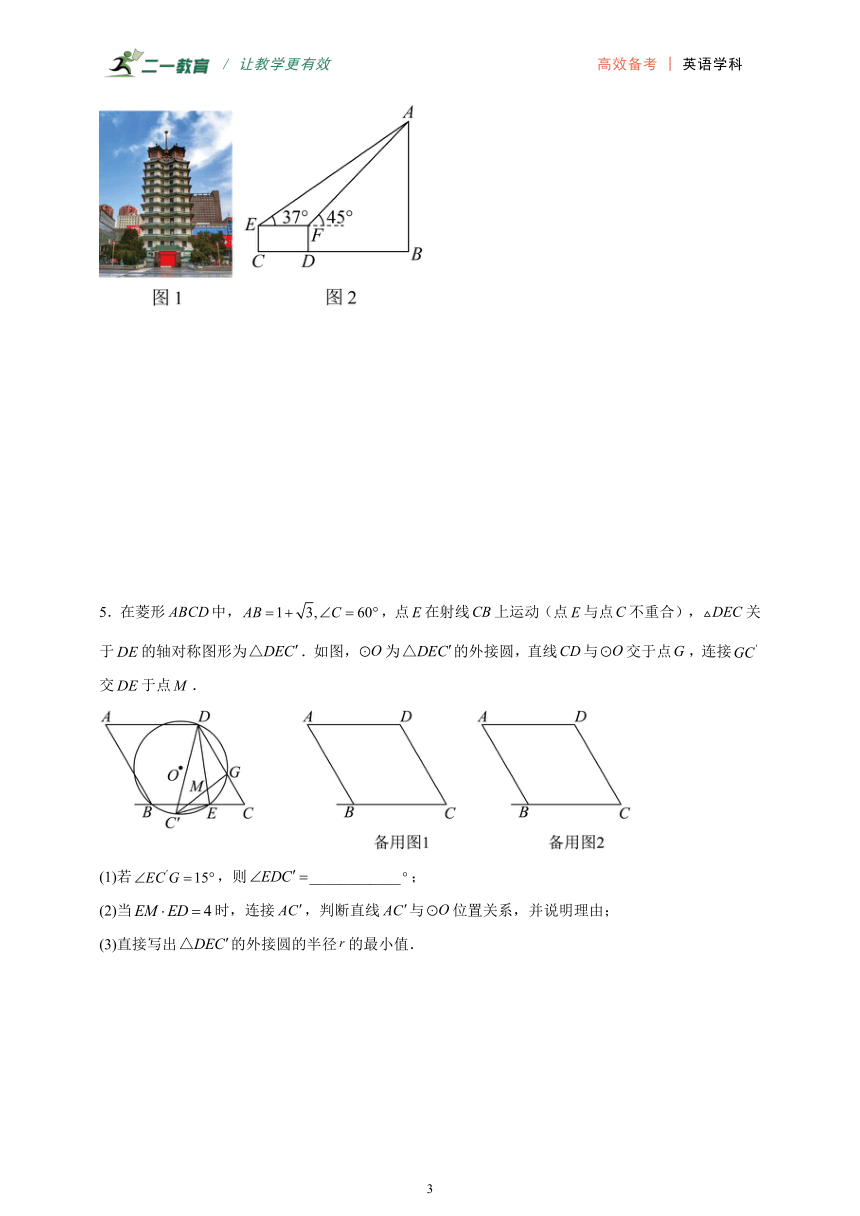
2.如图,在中,,,.动点N从点C出发,沿方向匀速运动,速度为;动点M同时从点D出发,沿DB方向匀速运动,速度为.过点M作,分别交,于点,,与相交于点.设运动时间为,请解答下列问题:
(1)当四边形为菱形时,求t的值;
(2)设五边形的面积为,求S与t之间的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使得?若存在,求出此时t的值;若不存在,请说明理由.
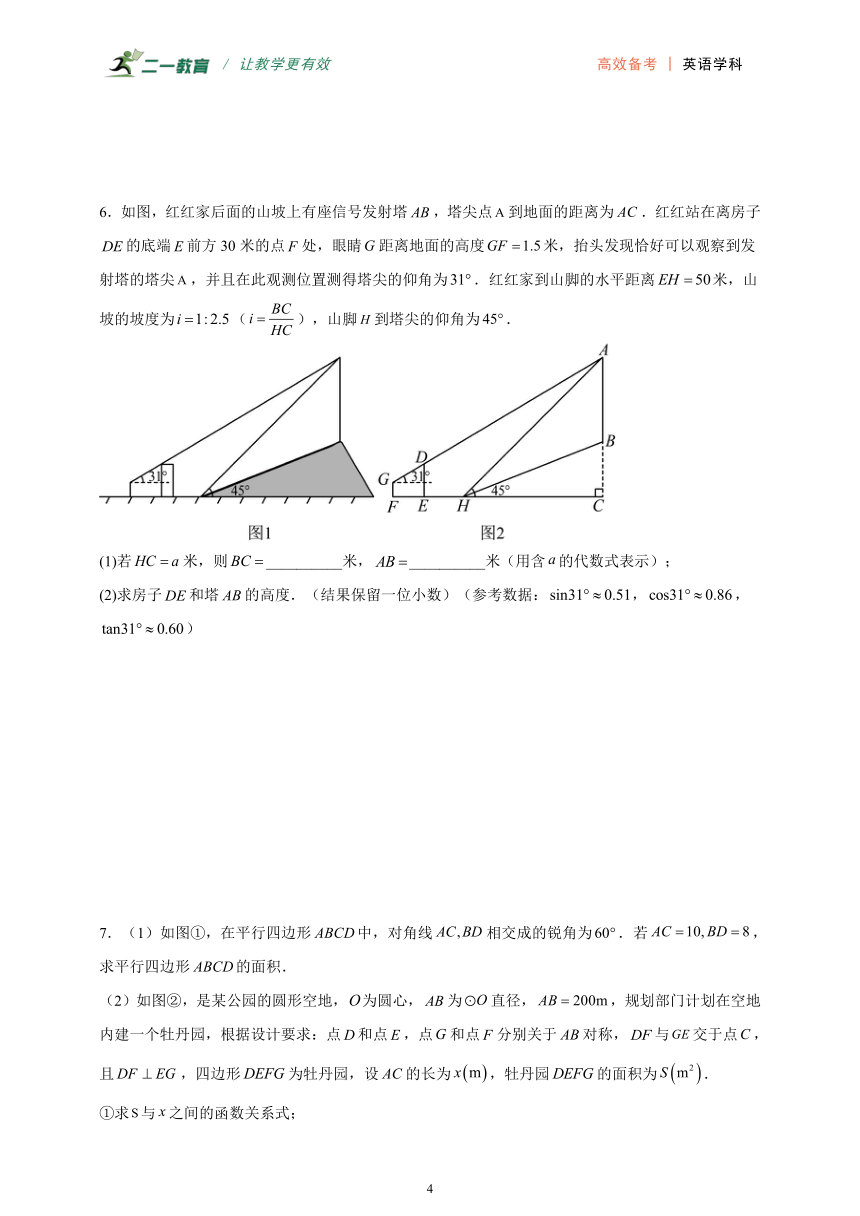
3.如图,在中,,,点D是平面内一点,连接,,且.
(1)如图1,若点D在内部,,延长交于H,若时,求的长;
(2)如图2,若点D在内部,将绕点A,逆时针旋转得到线段,直线与交于点F,证明:;
(3)如图3,点P是边上一点,连接,将绕点P顺时针旋转得到线段,连接,,,若,当,均取得最小值时,直接写出的面积.
4.如图1,郑州二七纪念塔位于郑州市中心的二七广场,是为了纪念1923年京汉铁路大罢工而建,如图2,某兴趣小组要测量二七塔的高度,在二七塔前的平地上选择一点,在处用测角仪测得二七塔顶部的仰角为,在点和二七塔之间选择一点,在处用测角仪测得仰角为,已知测角仪的高,求二七塔的高度.(结果精确到,参考数据:)
5.在菱形中,,点在射线上运动(点与点不重合),关于的轴对称图形为.如图,为的外接圆,直线与交于点,连接交于点.
(1)若,则____________;
(2)当时,连接,判断直线与位置关系,并说明理由;
(3)直接写出的外接圆的半径的最小值.
6.如图,红红家后面的山坡上有座信号发射塔,塔尖点到地面的距离为.红红站在离房子的底端前方30米的点处,眼睛距离地面的高度米,抬头发现恰好可以观察到发射塔的塔尖,并且在此观测位置测得塔尖的仰角为.红红家到山脚的水平距离米,山坡的坡度为(),山脚到塔尖的仰角为.
(1)若米,则__________米,__________米(用含的代数式表示);
(2)求房子和塔的高度.(结果保留一位小数)(参考数据:,,)
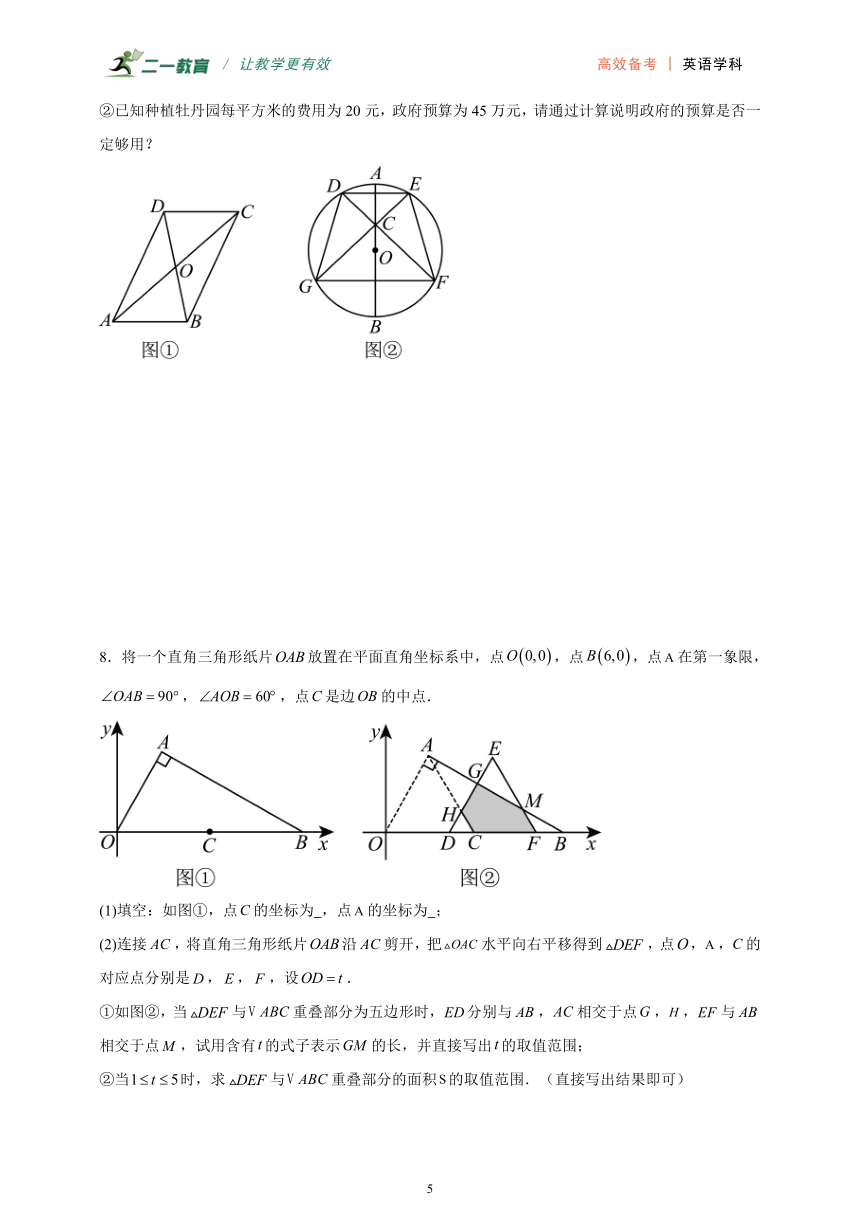
7.(1)如图①,在平行四边形中,对角线相交成的锐角为.若,求平行四边形的面积.
(2)如图②,是某公园的圆形空地,为圆心,为直径,,规划部门计划在空地内建一个牡丹园,根据设计要求:点和点,点和点分别关于对称,与交于点,且,四边形为牡丹园,设的长为,牡丹园的面积为.
①求与之间的函数关系式;
②已知种植牡丹园每平方米的费用为20元,政府预算为45万元,请通过计算说明政府的预算是否一定够用?
8.将一个直角三角形纸片放置在平面直角坐标系中,点,点,点在第一象限,,,点是边的中点.
(1)填空:如图①,点的坐标为 ,点的坐标为 ;
(2)连接,将直角三角形纸片沿剪开,把水平向右平移得到,点,,的对应点分别是,,,设.
①如图②,当与重叠部分为五边形时,分别与,相交于点,,与相交于点,试用含有的式子表示的长,并直接写出的取值范围;
②当时,求与重叠部分的面积的取值范围.(直接写出结果即可)
9.如图,在平面直角坐标系中,正方形的边在轴的正半轴上,顶点,在第一象限内,正比例函数的图象经过点,反比例函数的图象经过点,且与边交于点,连接,已知.
(1)求的值;
(2)观察图象,请直接写出满足的的取值范围;
(3)连接,在线段上取一点,使,过点P作垂直轴,交双曲线于点,请求出线段的长.
10.如图,抛物线与轴交于、两点,与轴交于点,为抛物线的顶点.
(1)求抛物线对应的函数表达式及顶点的坐标;
(2)若四边形为矩形,,点以每秒1个单位长度的速度从点沿向点运动,同时点以每秒2个单位长度的速度从点沿向点运动,一点到达终点,另一点随之停止运动.设运动时间为秒,当以、、为顶点的三角形与相似时,求的值;
(3)抛物线的对称轴与轴交于点,是点关于点的对称点,是轴下方抛物线上的动点.若过点的直线:与抛物线只有一个公共点,且分别与线段、相交于点、,求证:为定值.
11.阅读下列材料,解答问题.
【背景】如图1,李叔家D与水果园E之间隔着一座小土坡,为方便浇水灌溉,从家里铺设的水管到果园,原来经过小土坡铺设的水管()由于风吹日晒,老化损坏,现在李叔准备从土坡下直接埋一条水管(D,B,C,E在同一直线上).
【问题】为了计算新水管的长度,需要测量B,C之间的距离;
要了解水管承受的压力,需要测量土坡的高度.
【工具】一把皮尺和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离;测角仪的功能是在一固定位置测量可以看到的两个地点的夹角大小.
【测量】李叔用皮尺测量出原来土坡两边的长度,,再用测角仪测得.
解答问题:
(1)求的长度;(结果用含a,b,的代数式表示)
(2)若测得,,,求出小土坡的高度.
12.在平面直角坐标系中,抛物线经过点,与直线交于点,两点,点是直线下方抛物线上不与,重合的一动点,过点作的平行线交轴于点,设点的横坐标为.
(1)请直接写出,,的值;
(2)如图,若抛物线的对称轴为直线,点在直线的右侧,与直线交于点,当为的中点时,求的值;
(3)线段的长记为.
①求关于的函数解析式;
②若,结合关于的函数图象,直接写出的取值范围.
《2025年中考数学解答题系列:锐角三角函数综合》参考答案
1.(1)该介质的折射率是;
(2)截面的面积是.
【分析】(1)由特殊角的三角函数值得,与一起代入即可得解;
(2)由(1)中所得的折射率求出,推得,设,,结合勾股定理得出,则,将代入即可得出、,截面的面积即为.
【详解】(1)解:,,
该介质的折射率是;
(2)解:根据折射率与(1)的材料相同,可得折射率为,
,
,
,
依题得,四边形是矩形,点是中点,
,,
由图得,
,
即,
在中,设,,
由勾股定理得,,
,
又,
,
,
截面的面积为:.
【点睛】本题考查的知识点是特殊角的三角函数值、解直角三角形、勾股定理,解题关键是熟练掌握解直角三角形的相关计算.
2.(1),
(2)
(3)
【分析】本题考查了一元一次方程的应用,矩形的判定和性质,菱形的性质,等边三角形的判定和性质,解直角三角形,求函数关系式,角平分线的性质,正确作出辅助线是解题的关键.
(1)当四边形为菱形时,即时,进而由解三角形求出,即可得出结论;
(2)过点作,垂足为,五边形的面积为,利用解三角形把相关线段用表示即可求出;
(3)延长、交于点,根据,,利用相似三角形性质得线段成比例列方程求解即可.
【详解】(1)解:∵在中,
∴,,
又∵,
∴四边形为平行四边形,
∵,
∴,即,
∵在中,
∴,,
∴,
当四边形为菱形时,即时,
,
∴
(2)过点作,垂足为,
依题意得:,,
∵,,,
∴,
,
,
∴,
∵五边形的面积为,
∴,
即
(3)延长、交于点,
∵四边形为平行四边形,∴,,
由(2)得,,
∴,,
,
∴,
∴
∵
∴,,
∴,,
∴,
解并检验得:,,
在运动过程中,时,使得.
3.(1)
(2)见解析
(3)
【分析】(1)作交于,由直角三角形的性质可得,求出,解直角三角形得出,证明为等腰直角三角形,得出,结合,得出,从而可得,即可得解;
(2)连接,延长使得,连接,由旋转的性质可得,,证明,得出,,再证明,得出,,结合对顶角相等得出,从而可得,即可得证;
(3)由等腰直角三角形的性质可得,,由圆周角定理可得,点在以为直径的圆上,取的中点,连接交于,此时最小,为,则,由勾股定理可得,从而求出的最小值为,作于,于,则,,由旋转的性质可得,,证明,得出,,证明为等腰直角三角形,得出,从而推出点在过点且与夹角为的直线上,过点作于,由垂线段最短可得,此时最小,为,证明,由相似三角形的性质求出,,最后由三角形面积公式计算即可得解.
【详解】(1)解:如图,作交于,
,
∵,,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵在中,,,
∴为等腰直角三角形,
∴,
∴,
∴,
∴,
∴;
(2)证明:如图,连接,延长使得,连接,
,
由旋转的性质可得,,
∴,即,,
∵,
∴,
∴,,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,,
∵,
∴,
∴,
∴;
(3)解:∵在中,,,
∴,,
∵,
∴由圆周角定理可得,点在以为直径的圆上,
如图,取的中点,连接交于,此时最小,为,
,
则,
∴,
∴的最小值为,
作于,于,则,,
由旋转的性质可得,,
∵,
∴,
∴,
∴,,
∴,
∴为等腰直角三角形,
∴,
∴点在过点且与夹角为的直线上,
过点作于,
由垂线段最短可得,此时最小,为,
∵,,
∴,
∵,
∴,
∴,即,
∴,,
∴当,均取得最小值时,的面积为.
【点睛】本题考查了全等三角形的判定与性质、相似三角形的判定与性质、圆周角定理、勾股定理、旋转的性质、等腰直角三角形的判定与性质、解直角三角形等知识点,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
4.二七塔的高度约为
【分析】本题主要考查了解直角三角形的应用、矩形的判定与性质等知识点,正确作出辅助线、构造直角三角形成为解题的关键.
如图,延长交于点.易得,.则四边形为矩形,进而得到.在中易得,再在中解直角三角形可得,再结合列方程求解即可.
【详解】解:如图,延长交于点.
由题意可得:,.
∴四边形为矩形,
∴.
设,
在中,,
.
在中,.
,
.解得.
.
答:二七塔的高度约为.
5.(1)15
(2)直线与相切,理由见解析
(3)r的最小值为
【分析】(1)利用轴对称的性质,圆周角定理解答即可得出结论;
(2)过点E作于点H,利用菱形的性质,轴对称的性质和相似三角形的判定与性质求得,利用直角三角形的边角关系定理,等腰直角三角形的判定与性质,圆周角定理得到,则为圆的直径,利用等腰三角形的性质,圆周角定理,三角形的内角和定理,通过计算求得,则,最后利用圆的切线的判定定理解答即可;
(2)利用点的轨迹得到的外接圆为以为弦,所对的圆周角为的圆,则当取得最小值时,的外接圆的半径r取得最小值,过点D作于点E,利用轴对称的性质,菱形的性质,等边三角形的判定与性质得到的长,则结论可求.
【详解】(1)解:∵关于的轴对称图形为,
∴,
∴,
∵,,
∴,
∴;
(2)解:直线与相切,理由:
过点E作于点H,如图,
∵四边形为菱形,
∴,
∵关于的轴对称图形为,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,,
∴,
∴,
∴,
∴,
∴,
∴为圆的直径,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
∵,
∴,
∴,
∴,
∵为圆的直径,
∴直线与相切;
(3)解:的外接圆的半径r的最小值为.
由题意得:,
∴的外接圆为以为弦,弦所对的圆周角为的圆,
∴当取得最小值时,的外接圆的半径r取得最小值,
∵点E在射线上运动,
∴当时,取得最小值,
过点D作于点E,如图,
此时点与点B重合,为的外接圆的直径,
∵,
∴为等边三角形,
∴,
∴的外接圆的半径r的最小值.
【点睛】本题主要考查了圆的有关性质,圆周角定理,圆的切线的判定定理,菱形的性质,等边三角形的判定与性质,轴对称的性质,直角三角形的性质,直角三角形的边角关系定理,相似三角形的判定与性质,等腰直角三角形的判定与性质,熟练掌握轴对称的性质和菱形的性质是解题的关键.
6.(1),
(2)房子的高度为米;塔的高度为米.
【分析】本题考查的是解直角三角形的应用-仰角俯角、坡度坡角问题,掌握仰角俯角、坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
(1)利用,可求得米,在中,利用正切函数的定义求得,进一步计算即可求解;
(2)作于点,交于点,在中,利用正切函数的定义列式得到,求得,在中,利用正切函数的定义列式计算即可求解.
【详解】(1)解:∵米,,
∴,
∴米,
在中,,
∴,
∴,
∴米,
故答案为:,;
(2)解:作于点,交于点,
则四边形和四边形是矩形,
设米,
在中,,
∴,
在矩形中,,,
∴,
在中,,,即,
∴,
解得,
由(1)得米,米,
∵四边形是矩形,,,
在中,,,,∴,
∴米.
答:房子的高度约为米;塔的高度约为米.
7.(1)平行四边形的面积为;(2)①;②政府的预算一定够用,理由见解析.
【分析】1)过点作于点,由题意可知,,根据解直角三角形求出,即可求解;
(2)①在中,,在中,求出 ,在中,求出,再根据三角形面积公式即可求解;
②设种植牧丹园的总费用为元,,即可求解.
【详解】解:(1)如图,过点作于点,由题意可知,,
∵四边形是平行四边形,
∴,
在中,,
∴,
∴平行四边形的面积为;
(2)①如图,连接,过点作,
∵,
∴的半径为,
∴
由题可知点和点,点和点分别关于对称,
∴,,
,即,
∴,
∴,
∵,
∴在中,,
∴,
∵,
∴,
在中,,
,
∴在中,,
,
∵,
∴,
,
,,
,
∵点和点,点和点分别关于对称,
∴,
,
∴;
②设种植牧丹园的总费用为元,
由①可知,
,
∵,
∴当时,取最大值,最大值为,
当时,随的增大而增大,
当时,随的增大而减小,
综上,,
∴政府的预算一定够用.
【点睛】本题考查了平行四边形的性质,解直角三角形,勾股定理,一元二次方程的应用等知识,掌握相关知识是解题的关键.
8.(1),;
(2)①;②.
【分析】(1)由点,得到,根据点是边的中点,得到,从而得出点坐标,连接,过点作于点,证明为等边三角形,求出,即可得出点坐标;
(2)①由平移可知,,,有,得到,再得到,根据解直角三角形可得答案;
②分两种情况:当时,重叠部分为五边形,当时,重叠部分为直角三角形,分别求解即可得出答案.
【详解】(1)解:∵点,
∴,
∵点是边的中点,
∴,
∴点,
如图,连接,过点作于点,
∵,,
∴
∵,
∴为等边三角形,
∴,
∵,
∴,
∴,
∴点,
故答案为:,;
(2)解:①由(1)可知,为等边三角形,
由平移可知,,,有,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
在中,,
∴;
② 当时,重叠部分为五边形,
∴,
由平移可得,,
∴,
∴为等边三角形,
同理,,
在中,
,
,
∵,
∴时,时,,
,
当时,重叠部分为直角三角形,
在中,
∵,
∴,
,
∵,
∴时,时,,
∴综上所述,取值范围为:.
【点睛】本题考查了等边三角形的判定与性质,相似三角形的判定与性质,解直角三角形,平移的性质,勾股定理等知识,掌握相关知识是解题的关键.
9.(1)
(2)
(3)的长为
【分析】本题考查了一次函数与反比例函数的交点问题,解直角三角形,正确的求出函数解析式,利用数形结合的思想进行求解是解题的关键.
(1)先求出点E坐标即可得到的值;
(2)根据图象直接写出不等式解集即可;
(3)先求出解析式,过点作,交于点,则,继而求出的解析式得到点P坐标,最后得到长的即可.
【详解】(1)解:∵四边形是正方形,
∴,
在函数中,当时,,
∴点D的坐标为,
∵点D的坐标为且在反比例函数图象上,
∴,
∴,
∵正方形的边长为3,
∴,
把代入函数中,得,
∴,
∴,
∴;
(2)解:∵在函数中,当时,,
∴由图象可知的x的取值范围为;
(3)解:设直线的解析式为,代入点和得:
,
解得,
∴直线的解析式为,
过点作,交于点,
则,
∴,
∴,
∴,
∵,
∴设直线的解析式为:,把代入得:,
∴直线的解析式为,
∴当时,,
∴,
在反比例函数中,当时,,
∴,
∴.
10.(1),
(2)的值为或
(3)见详解
【分析】本题主要考查了二次函数图象的性质,求二次函数和一次函数的表达式,顶点坐标,三角函数比,相似三角形的性质,勾股定理,一元二次方程根的判别式等知识点,解题的关键是熟练掌握相关性质.
(1)利用待定系数法求二次函数的表达式,利用顶点表达式即可求出顶点坐标;
(2)采用分类讨论,分别当和时,利用相似比列出方程求解即可;
(3)利用勾股定理求得的长,再利用三角函数比求出,根据直线和坐标轴的交点个数得出,利用待定系数法求出直线 对应的函数表达式,最后求的结果即可.
【详解】(1)解: 点 , 在抛物线 上,
解得
抛物线对应的函数表达式为 又 ,
顶点 D 的坐标为 ;
(2)解:由题意得 ,,,,,
①当 时,,即 ,解得 ;
②当 时,,即 ,解得 ;
综上所述,当以 ,,为顶点的三角形与 相似时,的值为 或 ;
(3)解:由题意得 ,,
,
,
由抛物线的对称性易得 ,
,
直线 与抛物线只有一个公共点,
关于 的方程 ,即 有两个相等的实数根,
,
解得 ,
设直线对应的函数表达式为 ,
点 , 在直线 上,
解得
直线 对应的函数表达式为 , 为定值.
11.(1)
(2)
【分析】本题考查了解直角三角形的应用,结合图形构造直角三角形是解题的关键.
(1)过点作交延长线于点,设,在中利用三角函数的定义求出和的长,得出的长,在中利用勾股定理表示出的长,再根据平角的定义得到,即可求解;
(2)过点作于点,结合(1)中的结论,代入数据求出和的长,再利用等面积法得到,求出的长,即可解答.
【详解】(1)解:如图,过点作交延长线于点,则,
设,
在中,,,
,,
,
在中,,
,
,
,即,
,
的长度为.
(2)解:如图,过点作于点,
,,,
,,
,
,
答:小土坡的高度为.
12.(1),,
(2)
(3)①;②的取值范围为或或
【分析】(1)将,两点代入抛物线,求出、的值,令抛物线,即可求解的值;
(2)过点作轴于点,设抛物线的对称轴交轴于点,交轴于点,可证得,得,根据,利用待定系数法求出直线的解析式为,设直线的解析式为,求得,设、,则可得,通过图象得点、在轴的同一侧,即可求解;
(3)①求出,则可得,即可求得关于的函数解析式;②画出函数图象,分析图象即可求解.
【详解】(1)解:抛物线与直线交于点,两点,
将,两点代入抛物线,得:
,解得:,
抛物线,
令,解得:(舍去)或,
点,即.
,,.
(2)解:如图,过点作轴于点,设抛物线的对称轴交轴于点,交轴于点,
,
,
,
点的横坐标为,
,
直线的解析式为,,
设直线的解析式为,
点是抛物线与直线的交点,
,得:,
直线的解析式为,
设,,
,
由图象可得:点、在轴的同一侧,
,解得:,
点在直线的右侧,且,
.
(3)解:①如图,设与轴的交点为点,
直线的解析式为,
直线与轴的交点为,与轴的交点为,
,
,
,
,
.
在中,,
,
.
②点是直线下方抛物线上不与,重合的一动点,且,
画出图象如下:
,
,
,
或,
当时,,
当时,,
点在直线下方,
,
由图象得:若,则的取值范围为或或.
【点睛】本题主要考查了二次函数的图象与性质,利用待定系数法求二次函数的解析式和一次函数的解析式,相似三角形的判定与性质,解二元一次方程组,解一元二次方程等,理解题意、利用参数构建方程是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
2025年中考数学解答题系列:锐角三角函数综合
1.小明从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图所示,点,,,分别是长方体棱的中点,若光线经真空从矩形对角线交点处射入,其折射光线恰好从点处射出.如图,已知,,求截面的面积.
2.如图,在中,,,.动点N从点C出发,沿方向匀速运动,速度为;动点M同时从点D出发,沿DB方向匀速运动,速度为.过点M作,分别交,于点,,与相交于点.设运动时间为,请解答下列问题:
(1)当四边形为菱形时,求t的值;
(2)设五边形的面积为,求S与t之间的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使得?若存在,求出此时t的值;若不存在,请说明理由.
3.如图,在中,,,点D是平面内一点,连接,,且.
(1)如图1,若点D在内部,,延长交于H,若时,求的长;
(2)如图2,若点D在内部,将绕点A,逆时针旋转得到线段,直线与交于点F,证明:;
(3)如图3,点P是边上一点,连接,将绕点P顺时针旋转得到线段,连接,,,若,当,均取得最小值时,直接写出的面积.
4.如图1,郑州二七纪念塔位于郑州市中心的二七广场,是为了纪念1923年京汉铁路大罢工而建,如图2,某兴趣小组要测量二七塔的高度,在二七塔前的平地上选择一点,在处用测角仪测得二七塔顶部的仰角为,在点和二七塔之间选择一点,在处用测角仪测得仰角为,已知测角仪的高,求二七塔的高度.(结果精确到,参考数据:)
5.在菱形中,,点在射线上运动(点与点不重合),关于的轴对称图形为.如图,为的外接圆,直线与交于点,连接交于点.
(1)若,则____________;
(2)当时,连接,判断直线与位置关系,并说明理由;
(3)直接写出的外接圆的半径的最小值.
6.如图,红红家后面的山坡上有座信号发射塔,塔尖点到地面的距离为.红红站在离房子的底端前方30米的点处,眼睛距离地面的高度米,抬头发现恰好可以观察到发射塔的塔尖,并且在此观测位置测得塔尖的仰角为.红红家到山脚的水平距离米,山坡的坡度为(),山脚到塔尖的仰角为.
(1)若米,则__________米,__________米(用含的代数式表示);
(2)求房子和塔的高度.(结果保留一位小数)(参考数据:,,)
7.(1)如图①,在平行四边形中,对角线相交成的锐角为.若,求平行四边形的面积.
(2)如图②,是某公园的圆形空地,为圆心,为直径,,规划部门计划在空地内建一个牡丹园,根据设计要求:点和点,点和点分别关于对称,与交于点,且,四边形为牡丹园,设的长为,牡丹园的面积为.
①求与之间的函数关系式;
②已知种植牡丹园每平方米的费用为20元,政府预算为45万元,请通过计算说明政府的预算是否一定够用?
8.将一个直角三角形纸片放置在平面直角坐标系中,点,点,点在第一象限,,,点是边的中点.
(1)填空:如图①,点的坐标为 ,点的坐标为 ;
(2)连接,将直角三角形纸片沿剪开,把水平向右平移得到,点,,的对应点分别是,,,设.
①如图②,当与重叠部分为五边形时,分别与,相交于点,,与相交于点,试用含有的式子表示的长,并直接写出的取值范围;
②当时,求与重叠部分的面积的取值范围.(直接写出结果即可)
9.如图,在平面直角坐标系中,正方形的边在轴的正半轴上,顶点,在第一象限内,正比例函数的图象经过点,反比例函数的图象经过点,且与边交于点,连接,已知.
(1)求的值;
(2)观察图象,请直接写出满足的的取值范围;
(3)连接,在线段上取一点,使,过点P作垂直轴,交双曲线于点,请求出线段的长.
10.如图,抛物线与轴交于、两点,与轴交于点,为抛物线的顶点.
(1)求抛物线对应的函数表达式及顶点的坐标;
(2)若四边形为矩形,,点以每秒1个单位长度的速度从点沿向点运动,同时点以每秒2个单位长度的速度从点沿向点运动,一点到达终点,另一点随之停止运动.设运动时间为秒,当以、、为顶点的三角形与相似时,求的值;
(3)抛物线的对称轴与轴交于点,是点关于点的对称点,是轴下方抛物线上的动点.若过点的直线:与抛物线只有一个公共点,且分别与线段、相交于点、,求证:为定值.
11.阅读下列材料,解答问题.
【背景】如图1,李叔家D与水果园E之间隔着一座小土坡,为方便浇水灌溉,从家里铺设的水管到果园,原来经过小土坡铺设的水管()由于风吹日晒,老化损坏,现在李叔准备从土坡下直接埋一条水管(D,B,C,E在同一直线上).
【问题】为了计算新水管的长度,需要测量B,C之间的距离;
要了解水管承受的压力,需要测量土坡的高度.
【工具】一把皮尺和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离;测角仪的功能是在一固定位置测量可以看到的两个地点的夹角大小.
【测量】李叔用皮尺测量出原来土坡两边的长度,,再用测角仪测得.
解答问题:
(1)求的长度;(结果用含a,b,的代数式表示)
(2)若测得,,,求出小土坡的高度.
12.在平面直角坐标系中,抛物线经过点,与直线交于点,两点,点是直线下方抛物线上不与,重合的一动点,过点作的平行线交轴于点,设点的横坐标为.
(1)请直接写出,,的值;
(2)如图,若抛物线的对称轴为直线,点在直线的右侧,与直线交于点,当为的中点时,求的值;
(3)线段的长记为.
①求关于的函数解析式;
②若,结合关于的函数图象,直接写出的取值范围.
《2025年中考数学解答题系列:锐角三角函数综合》参考答案
1.(1)该介质的折射率是;
(2)截面的面积是.
【分析】(1)由特殊角的三角函数值得,与一起代入即可得解;
(2)由(1)中所得的折射率求出,推得,设,,结合勾股定理得出,则,将代入即可得出、,截面的面积即为.
【详解】(1)解:,,
该介质的折射率是;
(2)解:根据折射率与(1)的材料相同,可得折射率为,
,
,
,
依题得,四边形是矩形,点是中点,
,,
由图得,
,
即,
在中,设,,
由勾股定理得,,
,
又,
,
,
截面的面积为:.
【点睛】本题考查的知识点是特殊角的三角函数值、解直角三角形、勾股定理,解题关键是熟练掌握解直角三角形的相关计算.
2.(1),
(2)
(3)
【分析】本题考查了一元一次方程的应用,矩形的判定和性质,菱形的性质,等边三角形的判定和性质,解直角三角形,求函数关系式,角平分线的性质,正确作出辅助线是解题的关键.
(1)当四边形为菱形时,即时,进而由解三角形求出,即可得出结论;
(2)过点作,垂足为,五边形的面积为,利用解三角形把相关线段用表示即可求出;
(3)延长、交于点,根据,,利用相似三角形性质得线段成比例列方程求解即可.
【详解】(1)解:∵在中,
∴,,
又∵,
∴四边形为平行四边形,
∵,
∴,即,
∵在中,
∴,,
∴,
当四边形为菱形时,即时,
,
∴
(2)过点作,垂足为,
依题意得:,,
∵,,,
∴,
,
,
∴,
∵五边形的面积为,
∴,
即
(3)延长、交于点,
∵四边形为平行四边形,∴,,
由(2)得,,
∴,,
,
∴,
∴
∵
∴,,
∴,,
∴,
解并检验得:,,
在运动过程中,时,使得.
3.(1)
(2)见解析
(3)
【分析】(1)作交于,由直角三角形的性质可得,求出,解直角三角形得出,证明为等腰直角三角形,得出,结合,得出,从而可得,即可得解;
(2)连接,延长使得,连接,由旋转的性质可得,,证明,得出,,再证明,得出,,结合对顶角相等得出,从而可得,即可得证;
(3)由等腰直角三角形的性质可得,,由圆周角定理可得,点在以为直径的圆上,取的中点,连接交于,此时最小,为,则,由勾股定理可得,从而求出的最小值为,作于,于,则,,由旋转的性质可得,,证明,得出,,证明为等腰直角三角形,得出,从而推出点在过点且与夹角为的直线上,过点作于,由垂线段最短可得,此时最小,为,证明,由相似三角形的性质求出,,最后由三角形面积公式计算即可得解.
【详解】(1)解:如图,作交于,
,
∵,,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵在中,,,
∴为等腰直角三角形,
∴,
∴,
∴,
∴,
∴;
(2)证明:如图,连接,延长使得,连接,
,
由旋转的性质可得,,
∴,即,,
∵,
∴,
∴,,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,,
∵,
∴,
∴,
∴;
(3)解:∵在中,,,
∴,,
∵,
∴由圆周角定理可得,点在以为直径的圆上,
如图,取的中点,连接交于,此时最小,为,
,
则,
∴,
∴的最小值为,
作于,于,则,,
由旋转的性质可得,,
∵,
∴,
∴,
∴,,
∴,
∴为等腰直角三角形,
∴,
∴点在过点且与夹角为的直线上,
过点作于,
由垂线段最短可得,此时最小,为,
∵,,
∴,
∵,
∴,
∴,即,
∴,,
∴当,均取得最小值时,的面积为.
【点睛】本题考查了全等三角形的判定与性质、相似三角形的判定与性质、圆周角定理、勾股定理、旋转的性质、等腰直角三角形的判定与性质、解直角三角形等知识点,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
4.二七塔的高度约为
【分析】本题主要考查了解直角三角形的应用、矩形的判定与性质等知识点,正确作出辅助线、构造直角三角形成为解题的关键.
如图,延长交于点.易得,.则四边形为矩形,进而得到.在中易得,再在中解直角三角形可得,再结合列方程求解即可.
【详解】解:如图,延长交于点.
由题意可得:,.
∴四边形为矩形,
∴.
设,
在中,,
.
在中,.
,
.解得.
.
答:二七塔的高度约为.
5.(1)15
(2)直线与相切,理由见解析
(3)r的最小值为
【分析】(1)利用轴对称的性质,圆周角定理解答即可得出结论;
(2)过点E作于点H,利用菱形的性质,轴对称的性质和相似三角形的判定与性质求得,利用直角三角形的边角关系定理,等腰直角三角形的判定与性质,圆周角定理得到,则为圆的直径,利用等腰三角形的性质,圆周角定理,三角形的内角和定理,通过计算求得,则,最后利用圆的切线的判定定理解答即可;
(2)利用点的轨迹得到的外接圆为以为弦,所对的圆周角为的圆,则当取得最小值时,的外接圆的半径r取得最小值,过点D作于点E,利用轴对称的性质,菱形的性质,等边三角形的判定与性质得到的长,则结论可求.
【详解】(1)解:∵关于的轴对称图形为,
∴,
∴,
∵,,
∴,
∴;
(2)解:直线与相切,理由:
过点E作于点H,如图,
∵四边形为菱形,
∴,
∵关于的轴对称图形为,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,,
∴,
∴,
∴,
∴,
∴,
∴为圆的直径,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
∵,
∴,
∴,
∴,
∵为圆的直径,
∴直线与相切;
(3)解:的外接圆的半径r的最小值为.
由题意得:,
∴的外接圆为以为弦,弦所对的圆周角为的圆,
∴当取得最小值时,的外接圆的半径r取得最小值,
∵点E在射线上运动,
∴当时,取得最小值,
过点D作于点E,如图,
此时点与点B重合,为的外接圆的直径,
∵,
∴为等边三角形,
∴,
∴的外接圆的半径r的最小值.
【点睛】本题主要考查了圆的有关性质,圆周角定理,圆的切线的判定定理,菱形的性质,等边三角形的判定与性质,轴对称的性质,直角三角形的性质,直角三角形的边角关系定理,相似三角形的判定与性质,等腰直角三角形的判定与性质,熟练掌握轴对称的性质和菱形的性质是解题的关键.
6.(1),
(2)房子的高度为米;塔的高度为米.
【分析】本题考查的是解直角三角形的应用-仰角俯角、坡度坡角问题,掌握仰角俯角、坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
(1)利用,可求得米,在中,利用正切函数的定义求得,进一步计算即可求解;
(2)作于点,交于点,在中,利用正切函数的定义列式得到,求得,在中,利用正切函数的定义列式计算即可求解.
【详解】(1)解:∵米,,
∴,
∴米,
在中,,
∴,
∴,
∴米,
故答案为:,;
(2)解:作于点,交于点,
则四边形和四边形是矩形,
设米,
在中,,
∴,
在矩形中,,,
∴,
在中,,,即,
∴,
解得,
由(1)得米,米,
∵四边形是矩形,,,
在中,,,,∴,
∴米.
答:房子的高度约为米;塔的高度约为米.
7.(1)平行四边形的面积为;(2)①;②政府的预算一定够用,理由见解析.
【分析】1)过点作于点,由题意可知,,根据解直角三角形求出,即可求解;
(2)①在中,,在中,求出 ,在中,求出,再根据三角形面积公式即可求解;
②设种植牧丹园的总费用为元,,即可求解.
【详解】解:(1)如图,过点作于点,由题意可知,,
∵四边形是平行四边形,
∴,
在中,,
∴,
∴平行四边形的面积为;
(2)①如图,连接,过点作,
∵,
∴的半径为,
∴
由题可知点和点,点和点分别关于对称,
∴,,
,即,
∴,
∴,
∵,
∴在中,,
∴,
∵,
∴,
在中,,
,
∴在中,,
,
∵,
∴,
,
,,
,
∵点和点,点和点分别关于对称,
∴,
,
∴;
②设种植牧丹园的总费用为元,
由①可知,
,
∵,
∴当时,取最大值,最大值为,
当时,随的增大而增大,
当时,随的增大而减小,
综上,,
∴政府的预算一定够用.
【点睛】本题考查了平行四边形的性质,解直角三角形,勾股定理,一元二次方程的应用等知识,掌握相关知识是解题的关键.
8.(1),;
(2)①;②.
【分析】(1)由点,得到,根据点是边的中点,得到,从而得出点坐标,连接,过点作于点,证明为等边三角形,求出,即可得出点坐标;
(2)①由平移可知,,,有,得到,再得到,根据解直角三角形可得答案;
②分两种情况:当时,重叠部分为五边形,当时,重叠部分为直角三角形,分别求解即可得出答案.
【详解】(1)解:∵点,
∴,
∵点是边的中点,
∴,
∴点,
如图,连接,过点作于点,
∵,,
∴
∵,
∴为等边三角形,
∴,
∵,
∴,
∴,
∴点,
故答案为:,;
(2)解:①由(1)可知,为等边三角形,
由平移可知,,,有,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
在中,,
∴;
② 当时,重叠部分为五边形,
∴,
由平移可得,,
∴,
∴为等边三角形,
同理,,
在中,
,
,
∵,
∴时,时,,
,
当时,重叠部分为直角三角形,
在中,
∵,
∴,
,
∵,
∴时,时,,
∴综上所述,取值范围为:.
【点睛】本题考查了等边三角形的判定与性质,相似三角形的判定与性质,解直角三角形,平移的性质,勾股定理等知识,掌握相关知识是解题的关键.
9.(1)
(2)
(3)的长为
【分析】本题考查了一次函数与反比例函数的交点问题,解直角三角形,正确的求出函数解析式,利用数形结合的思想进行求解是解题的关键.
(1)先求出点E坐标即可得到的值;
(2)根据图象直接写出不等式解集即可;
(3)先求出解析式,过点作,交于点,则,继而求出的解析式得到点P坐标,最后得到长的即可.
【详解】(1)解:∵四边形是正方形,
∴,
在函数中,当时,,
∴点D的坐标为,
∵点D的坐标为且在反比例函数图象上,
∴,
∴,
∵正方形的边长为3,
∴,
把代入函数中,得,
∴,
∴,
∴;
(2)解:∵在函数中,当时,,
∴由图象可知的x的取值范围为;
(3)解:设直线的解析式为,代入点和得:
,
解得,
∴直线的解析式为,
过点作,交于点,
则,
∴,
∴,
∴,
∵,
∴设直线的解析式为:,把代入得:,
∴直线的解析式为,
∴当时,,
∴,
在反比例函数中,当时,,
∴,
∴.
10.(1),
(2)的值为或
(3)见详解
【分析】本题主要考查了二次函数图象的性质,求二次函数和一次函数的表达式,顶点坐标,三角函数比,相似三角形的性质,勾股定理,一元二次方程根的判别式等知识点,解题的关键是熟练掌握相关性质.
(1)利用待定系数法求二次函数的表达式,利用顶点表达式即可求出顶点坐标;
(2)采用分类讨论,分别当和时,利用相似比列出方程求解即可;
(3)利用勾股定理求得的长,再利用三角函数比求出,根据直线和坐标轴的交点个数得出,利用待定系数法求出直线 对应的函数表达式,最后求的结果即可.
【详解】(1)解: 点 , 在抛物线 上,
解得
抛物线对应的函数表达式为 又 ,
顶点 D 的坐标为 ;
(2)解:由题意得 ,,,,,
①当 时,,即 ,解得 ;
②当 时,,即 ,解得 ;
综上所述,当以 ,,为顶点的三角形与 相似时,的值为 或 ;
(3)解:由题意得 ,,
,
,
由抛物线的对称性易得 ,
,
直线 与抛物线只有一个公共点,
关于 的方程 ,即 有两个相等的实数根,
,
解得 ,
设直线对应的函数表达式为 ,
点 , 在直线 上,
解得
直线 对应的函数表达式为 , 为定值.
11.(1)
(2)
【分析】本题考查了解直角三角形的应用,结合图形构造直角三角形是解题的关键.
(1)过点作交延长线于点,设,在中利用三角函数的定义求出和的长,得出的长,在中利用勾股定理表示出的长,再根据平角的定义得到,即可求解;
(2)过点作于点,结合(1)中的结论,代入数据求出和的长,再利用等面积法得到,求出的长,即可解答.
【详解】(1)解:如图,过点作交延长线于点,则,
设,
在中,,,
,,
,
在中,,
,
,
,即,
,
的长度为.
(2)解:如图,过点作于点,
,,,
,,
,
,
答:小土坡的高度为.
12.(1),,
(2)
(3)①;②的取值范围为或或
【分析】(1)将,两点代入抛物线,求出、的值,令抛物线,即可求解的值;
(2)过点作轴于点,设抛物线的对称轴交轴于点,交轴于点,可证得,得,根据,利用待定系数法求出直线的解析式为,设直线的解析式为,求得,设、,则可得,通过图象得点、在轴的同一侧,即可求解;
(3)①求出,则可得,即可求得关于的函数解析式;②画出函数图象,分析图象即可求解.
【详解】(1)解:抛物线与直线交于点,两点,
将,两点代入抛物线,得:
,解得:,
抛物线,
令,解得:(舍去)或,
点,即.
,,.
(2)解:如图,过点作轴于点,设抛物线的对称轴交轴于点,交轴于点,
,
,
,
点的横坐标为,
,
直线的解析式为,,
设直线的解析式为,
点是抛物线与直线的交点,
,得:,
直线的解析式为,
设,,
,
由图象可得:点、在轴的同一侧,
,解得:,
点在直线的右侧,且,
.
(3)解:①如图,设与轴的交点为点,
直线的解析式为,
直线与轴的交点为,与轴的交点为,
,
,
,
,
.
在中,,
,
.
②点是直线下方抛物线上不与,重合的一动点,且,
画出图象如下:
,
,
,
或,
当时,,
当时,,
点在直线下方,
,
由图象得:若,则的取值范围为或或.
【点睛】本题主要考查了二次函数的图象与性质,利用待定系数法求二次函数的解析式和一次函数的解析式,相似三角形的判定与性质,解二元一次方程组,解一元二次方程等,理解题意、利用参数构建方程是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
