2025年中考数学解答题系列:实际问题与二元一次方程组(含解析)
文档属性
| 名称 | 2025年中考数学解答题系列:实际问题与二元一次方程组(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 753.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 17:51:13 | ||
图片预览




文档简介
/ 让教学更有效 高效备考 | 英语学科
2025年中考数学解答题系列:实际问题与二元一次方程组
1.2025年春节档,电影《哪吒之魔童闹海》掀起观影热潮,影片通过粒子水墨技术、动态水墨渲染引擎等技术,将传统水墨画意境融入动画,打造出兼具古典神韵与现代视觉冲击力的场景,形成独特的文化辨识度,向全球展示了“既古老又充满活力的中国形象”. 影片将封神神话中的角色(如哪吒、敖丙)赋予现代价值观,使传统文化符号与当代人民心理形成共振.某文创店果断订购了印有“哪吒”图案和“敖丙”图案的两种书签.经统计,订购30张“哪吒”书签与20张“敖丙”书签,成本共计430元;而订购45张“哪吒”书签和25张“敖丙”书签,则需花费605元.
(1)求“哪吒”、“敖丙”两种书签每张的进价分别是多少元?
(2)该文创店计划购进“哪吒”、“敖丙”两种书签共90张, “哪吒”种书签的购进数量不超过“敖丙”种书签数量,已知“哪吒”、“敖丙”两种书签的销售单价分别为15元和12元,如何规划购买方案,才能使文具店在这批书签全部售出后获得最大利润?最大利润是多少?
2.在农作物不同的生长阶段运用科技手段实现精准施肥,可以提高产量和质量.某农场为种植小麦需要配制复合肥料.小麦在生长过程中需要大量的氮(N)促进叶片生长,适量的磷(P)促进根系发育,以及足够的钾(K)提高果实品质.农场有两种原料可供使用,其氮、磷、钾含量及成本如下表:
原料 氮(N)含量 (千克/吨) 磷(P)含量 (千克/吨) 钾(K)含量 (千克/吨) 成本 (元/吨)
原料A 20 40 30 600
原料B 50 10 40 800
(1)在小麦播种前农场根据土壤检测结果配制底肥,要求肥料中含有240千克氮、120千克磷,求使用A,B两种原料各多少吨?
(2)4月份,小麦进入拔节期,农场根据小麦长势和底肥用量计划配制追肥,要求追肥用量是底肥用量的,且含有不少于100千克钾,请设计出成本最低的配制方案.
3.“周礼伤心凉粉”是安岳的一大美食,它不仅口感鲜美,而且制作工艺独特,传承历史悠久,被誉为四川的传统工艺之一.现有,两类“周礼伤心凉粉”特受顾客喜爱.已知购买2份类和1份类共需38元;购买4份类和3份类共需86元.
(1)分别求出,两类“周礼伤心凉粉”每份的价格;
(2)芮芮家为了招待远道而来的客人,准备购买,两类“周礼伤心凉粉”共20份,且购买的总费用不超过250元,则最多能购买类“周礼伤心凉粉”多少份?
4.年关将至,幸福小区物业决定采购A,B两种型号的灯笼.若购买3个A型灯笼和4个B型灯笼共需要116元;购买6个A型灯笼和5个B型灯笼共需要172元.
(1)求A,B两种型号灯笼的单价;
(2)若需要购买A,B两种型号的灯笼共200个,总费用不超过3000元,至少需要购买A型灯笼多少个?
5.某电脑经销商计划同时购进一批电脑机箱和显示器,若购进电脑机箱5台和显示器4台,共需要资金7000元;若购进电脑机箱2台和显示器5台,共需要资金7900元.
(1)求每台电脑机箱和显示器的进价各是多少元?
(2)该经销商计划购进这两种电脑机箱和显示器共50台,用于购买这两种电脑机箱和显示器的资金不超过36000元.求最多能购进多少台显示器?
6.2025年亚冬会在哈尔滨举办,吉祥物“滨滨”和“妮妮”深受广大游客的喜爱,某专营店计划购进A、B两款纪念品,若购进A款纪念品3件和B款纪念品2件共需150元,若购进A款纪念品1件和B款纪念品4件共需160元.
(1)求A、B两款纪念品每件的进价分别为多少元?
(2)若A款纪念品售价为38元,B款纪念品售价为45元,该专营店计划购进A、B两款纪念品共50件,这两种纪念品全部售出后总获利不低于540元,那么该专营店最多可以购进A款纪念品多少件?
7.2025年第九届亚洲冬季运动会在哈尔滨举办.某经销商发现,与吉祥物“滨滨”和“妮妮”相关的甲、乙两款纪念品深受大家喜爱.已知购买3个甲款纪念品和2个乙款纪念品共需180元;购买5个甲款纪念品比购买3个乙款纪念品多15元.
(1)甲、乙两款纪念品的售价各是多少?
(2)甲款纪念品的进价为20元,乙款纪念品的进价为38元.若该经销商计划购进甲、乙两款纪念品共60个,且乙款纪念品的购买数量不低于甲款纪念品购买数量的2倍,则应如何进货能使得这批纪念品全部售出后所获利润最大,最大利润是多少?
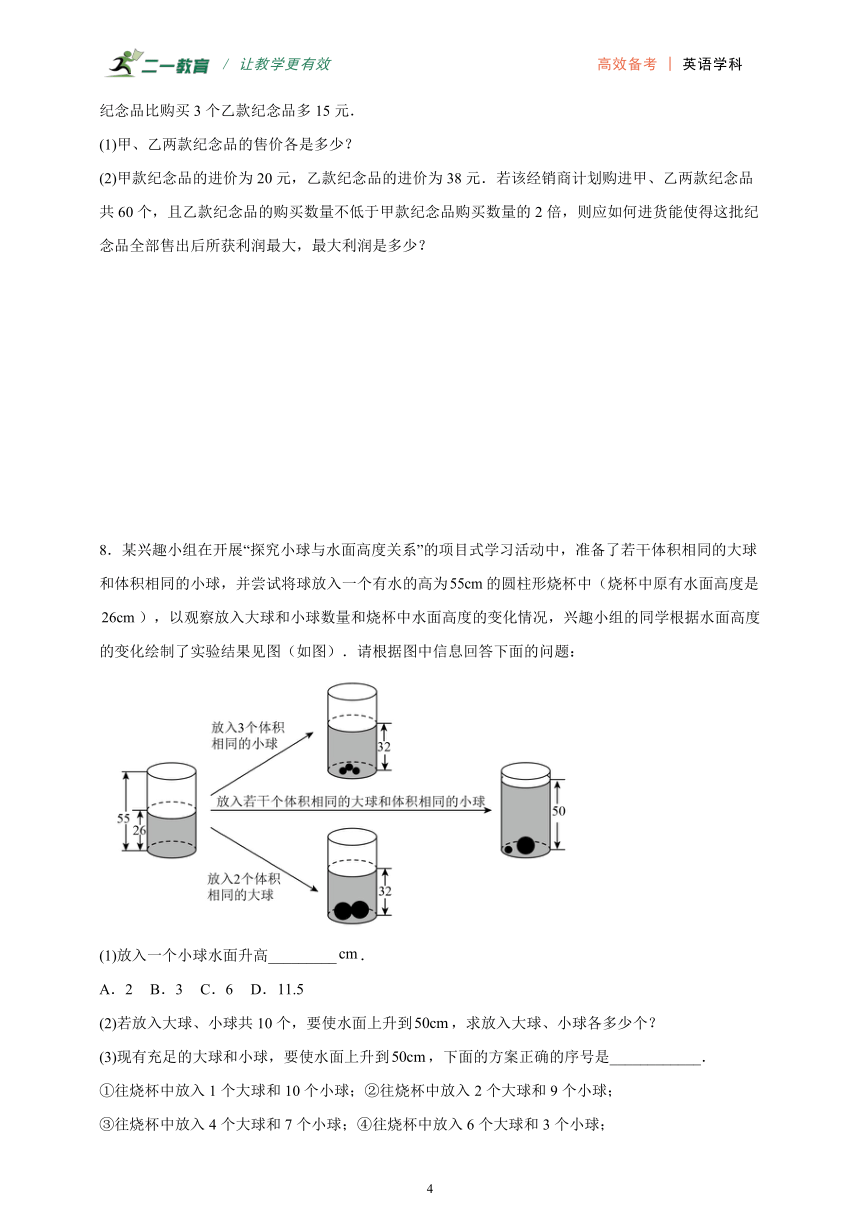
8.某兴趣小组在开展“探究小球与水面高度关系”的项目式学习活动中,准备了若干体积相同的大球和体积相同的小球,并尝试将球放入一个有水的高为的圆柱形烧杯中(烧杯中原有水面高度是),以观察放入大球和小球数量和烧杯中水面高度的变化情况,兴趣小组的同学根据水面高度的变化绘制了实验结果见图(如图).请根据图中信息回答下面的问题:
(1)放入一个小球水面升高_________.
A.2 B.3 C.6 D.
(2)若放入大球、小球共10个,要使水面上升到,求放入大球、小球各多少个?
(3)现有充足的大球和小球,要使水面上升到,下面的方案正确的序号是____________.
①往烧杯中放入1个大球和10个小球;②往烧杯中放入2个大球和9个小球;
③往烧杯中放入4个大球和7个小球;④往烧杯中放入6个大球和3个小球;
⑤往烧杯中放入8个大球.
A.①②④⑤ B.②④⑤ C.①④⑤ D.②③④
9.为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了两种食品作为午餐.这两种食品每包质量均为,营养成分表如下.
(1)若要从这两种食品中摄入热量和蛋白质,应选用两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共8包,要使每份午餐中的蛋白质含量不低于,且热量最低,应如何选用这两种食品?
10.综合与实践
【背景】住尤溪的小颖想给亲朋好友寄送尤溪特产.
【素材】
素材1:她了解到某快递公司的收费标准(单位:元/千克)如下表:
计费单位 收费标准
福建省内 江浙沪地区
首重
续重
素材2:
电子存单1 电子存单2
托寄物:尤溪特产 目的地:福州 计量重量:2千克 件数:1 总费用:12元 托寄物:尤溪特产 目的地:上海 计量重量:5千克 件数:1 总费用:36元
素材3:收费说明
①每件快递按送达地分别计算运费;
②运费计算方式:首重价格+续重×续重运费.首重均为1千克,超过1千克即要续重,续重以1千克为计重单位(不足1千克按1千克计算).
【问题解决】
(1)小颖给在厦门的朋友寄出了千克的尤溪特产,她需要支付快递费多少元?
(2)小颖给在杭州的外婆寄特产快递费花了72元,求这份特产重量的取值范围.
11.佰洋电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是2025年3月前两周的销售情况:
销售时段 销售数量 销售总额
A种型号 B种型号
第一周 3台 5台 18000元
第二周 4台 10台 31000元
(1)求A,B两种型号的净水器的销售单价?
(2)由于前两周两种净水器都销售一空,电器公司第三周采购这两种型号的净水器共30台,恰好花费54000元,求A种型号的净水器采购了多少台?
(3)在(2)的条件下,电器公司第三周开始销售部分刚购进的A型号和B型号净水器,但发现市场将要被新款智能净水器所取代,为扩大销售量,将剩余B种型号净水器按售价的七折进行销售,A种型号净水器原售价不变,当第三周采购的30台净水器都销售一空后统计这30台净水器的利润为6700元,求电器公司第三周采购的30台净水器中,用于打折销售的B种型号净水器为多少个?
12.随着自媒体的盛行,网购及直播带货成为一种趋势,某农产基地准备借助自媒体对某种水果做营销,采用线上及线下两种销售方式,统计销售情况发现,该水果的销售量和总收入如表(总收入销售量单价):
线上销售水果量(单位:) 线下销售水果量(单位:) 总收入(单位:元)
第一批
第二批
(1)求该水果线上、线下的销售单价各是多少元;
(2)若某公司计划从该地采购该水果,因保质期问题,准备采用线上、线下相结合的方式,因实际需要,线下采购该水果量不得少于线上采购该水果量的,请你帮该公司算一算,当线下采购多少水果时最省钱?
《2025年中考数学解答题系列:实际问题与二元一次方程组》参考答案
1.(1)“哪吒”、“敖丙”两种书签每张的进价分别是9、8元
(2)当购进“哪吒”书签40张,“敖丙”书签50张时,获得最大利润,最大利润是440元
【分析】本题主要考查了二元一次方程组的应用,一次函数的实际应用.解决本题的关键是列出利润与购买“哪吒”书签的数量之间的函数关系式,利用一次函数的性质确定购买方案.
(1)设“哪吒”、“敖丙”两种书签每张的进价分别是x、y元,根据两种不同的购买方案所需要的费用列方程组求解即可;
(2)设购进“哪吒”书签m张,“敖丙”书签张,设这批书签全部售出后获利W元,可以得到所获利润与购买“哪吒”书签的数量之间的一次函数关系式,利用一次函数的性质确定购买方案即可.
【详解】(1)解:设“哪吒”、“敖丙”两种书签每张的进价分别是x、y元,
由题意知: ,
解得,
答:“哪吒”、“敖丙”两种书签每张的进价分别是9元,8元.
(2)解:设购进“哪吒”书签m张,“敖丙”书签张,
由题意知:,
解得:,
设这批书签全部售出后获利W元,
则,
∵,
∴W随m的增大而增大,
∴当时,,W有最大值,元.
答:当购进“哪吒”书签40张,“敖丙”书签50张时,获得最大利润,最大利润是440元.
2.(1)使用种原料2吨,种原料4吨
(2)使用种原料2吨,种原枓1吨配制追肥,成本最低
【分析】本题主要考查二元一次方程组,一元一次不等式,一次函数最值的计算,掌握以上知识,正确列式求解是关键.
(1)设使用种原料吨,种原料吨,由数量关系列二元一次方程组求解即可;
(2)设使用种原料吨,则种原料吨,列不等式得,解得,设总成本为元,则,根据一次函数求最值的方法计算即可求解.
【详解】(1)解:设使用种原料吨,种原料吨,
根据题意得,
解得,
答:使用种原料2吨,种原料4吨.
(2)解:追肥用量是底肥用量的,
追肥用量为(吨),
设使用种原料吨,则种原料吨,
要求肥料中含有不少于100千克钾,
,
解得,
设总成本为元,则,
,
随的增大而减小,
当时,最小,
,
答:使用种原料2吨,种原枓1吨配制追肥,成本最低.
3.(1)类“周礼伤心凉粉”每份的价格为元,类“周礼伤心凉粉”每份的价格为元.
(2)最多能购买类“周礼伤心凉粉”12份.
【分析】本题考查了二元一次方程组的实际应用,一元一次不等式的应用,读懂题意,找出等量关系是解题的关键.
(1)设类“周礼伤心凉粉”每份的价格为,类“周礼伤心凉粉”每份的价格为,根据题意列出二元一次方程组,然后解方程即可;
(2)设类“周礼伤心凉粉”购买份,那么类“周礼伤心凉粉”购买份,根据题意列出一元一次不等式,然后解不等式即可.
【详解】(1)解:设类“周礼伤心凉粉”每份的价格为,类“周礼伤心凉粉”每份的价格为.
,解得
答:类“周礼伤心凉粉”每份的价格为元,类“周礼伤心凉粉”每份的价格为元.
(2)解:设类“周礼伤心凉粉”购买份,那么类“周礼伤心凉粉”购买份.
解得
最大为
类“周礼伤心凉粉”最多购买份
答:最多能购买类“周礼伤心凉粉”12份.
4.(1)A,B两种型号灯笼的单价分别为12元和20元
(2)125个
【分析】本题考查了二元一次方程组和一元一次不等式的实际应用,正确理解题意是解题的关键.
(1)设A,B两种型号灯笼的单价分别为元和元,由“购买3个A型灯笼和4个B型灯笼共需要116元;购买6个A型灯笼和5个B型灯笼共需要172元”;
(2)设需要购买A型灯笼个,则需要购买B型灯笼个,由总费用不超过3000元建立不等式求解.
【详解】(1)解:设A,B两种型号灯笼的单价分别为元和元
根据题意列方程组得
解得,
答:A,B两种型号灯笼的单价分别为12元和20元;
(2)解:设需要购买A型灯笼个,则需要购买B型灯笼个
根据题意得
解得
答:至少需要购买A型灯笼125个.
5.(1)每台电脑机箱的进价为200元,每台显示器的进价是1500元
(2)20台
【分析】此题考查了二元一次方程组及一元一次不等式的应用, 根据等量关系列出方程组是解题的关键.
(1)根据题意得出等量关系列出方程组,即可求出电脑机箱和液晶显示器的单价;
(2)根据题意列不等式计算即可求解.
【详解】(1)解:设每台电脑机箱的进价为元,每台显示器的进价是元,
根据题意得:,
解方程组得:,
答:每台电脑机箱的进价为200元,每台显示器的进价是1500元.
(2)解:设购进台显示器,
根据题意得:,
解不等式得:,
答:最多能购进20台显示器.
6.(1)A、B两种工艺品每件的进价分别为28元和33元
(2)该专营店最多购进A种工艺品30件
【分析】本题考查的是二元一次方程组的应用,一元一次不等式的应用,确定相等关系与不等关系是解本题的关键.
(1)设A、B两款纪念品每件的进价分别为x元和y元,再由“若购进A款纪念品3件和B款纪念品2件共需150元,若购进A款纪念品1件和B款纪念品4件共需160元”列方程,再解方程即可;
(2)设该专营店购进A种工艺品a件,由总获利不低于540元,再列不等式,再解不等式即可.
【详解】(1)解:设A、B两款纪念品每件的进价分别为x元和y元,
则,
解得:,
答:A、B两种工艺品每件的进价分别为28元和33元.
(2)解:设该专营店购进A种工艺品a件,
则,
解得:.
答:该专营店最多购进A种工艺品30件.
7.(1)甲款纪念品的售价为元,乙款纪念品的售价为元;
(2)购进甲款个,乙款个时,最大利润为元.
【分析】本题考查了二元一次方程组的应用,一次函数的应用,掌握相关知识是解题的关键.
(1)设甲款纪念品的售价为元,乙款纪念品的售价为元,根据题意列出方程组,求解即可;
(2)设购进甲款个,则乙款为个,利润为元,依题意得,再求出的范围即可求解.
【详解】(1)解:设甲款纪念品的售价为元,乙款纪念品的售价为元,根据题意得:
,
解得:,
答:甲款纪念品的售价为元,乙款纪念品的售价为元;
(2)解:设购进甲款个,则乙款为个,利润为元,依题意得:
,
∵,
∴,
当时,利润最大:元,
答:购进甲款个,乙款个时,最大利润为元.
8.(1)A
(2)放入大球4个、小球各6个.
(3)B
【分析】本题主要考查了一元一次方程、二元一次方程组的应用、有理数的混合运算等知识点,正确求出放入一个小球和大球水面上升的高度是解题的关键.
(1)根据放入3个体积相同的小球水面升高了,据此列式计算即可求解;
(2)根据放入2个体积相同的大球水面升高了,求出放入一个大球水面升高的高度,然后根据意义列二元一次方程组方程组求解即可;
(3)分别求出每一种方案的水面高度即可求解.
【详解】(1)解:由题意可得,放入3个体积相同的小球水面升高了,
∴放入一个小球水面升高.
故选:A.
(2)解:由题意可得,放入2个体积相同的大球水面升高了,
∴放入一个大球水面升高,
设放入大球x个,放入小球y个,
由题意可得:,解得:,
答:放入大球4个、小球各6个.
(3)解:∵,
∴方案①不正确;
∵,
∴方案②正确;
∵,
∴方案③不正确;
∵,
∴方案④正确;
∵,
∴方案⑤正确.
综上,方案正确的是②④⑤.
故选:B.
9.(1)选用A种食品2包,B种食品4包;
(2)选用A种食品6包,B种食品2包.
【分析】本题考查了二元一次方程组的应用,一元一次不等式的应用,一次函数的应用:
(1)设选用A种食品x包,B种食品y包,根据“从这两种食品中摄入热量和蛋白质”列方程组求解即可;
(2)设选用A种食品包,则选用B种食品包,根据“每份午餐中的蛋白质含量不低于”列不等式求得的范围,设总热量为,得到,再利用一次函数的性质求解即可.
【详解】(1)解:设选用A种食品x包,B种食品y包,
根据题意,得
解方程组,得
答:选用A种食品2包,B种食品4包;
(2)解:设选用A种食品包,则选用B种食品包,
根据题意,得.
∴.
设总热量为,则.
∵,
∴w随a的增大而减小.
∴当时,w最小.
∴.
答:选用A种食品6包,B种食品2包.
10.(1)支付快递费16元.
(2)这份特产的重量大于10千克,小于等于11千克.
【分析】本题主要考查了二元一次方程组以及一元一次方程的应用.
(1)根据题意列出关于a,b的二元一次方程组,确定.根据福建省内收费标准计算即可.
(2)设这份特产按千克计费,根据江浙沪地区收费标准列出关于x的一元一次方程,解方程,再结合不足1千克按1千克计算即可得出这份特产重量的取值范围.
【详解】(1)解:由题意可知:
解得.
∵不足1千克按1千克计算,故千克按4千克计算,
即(元).
她需要支付快递费16元.
(2)解:设这份特产按千克计费,
则
解得.
所以这份特产的重量大于10千克,小于等于11千克.
11.(1)A型2500元,B型2100元
(2)10台
(3)10台
【分析】本题考查二元一次方程组与一元一次方程的应用,根据题意正确列方程(组)是解题的关键.
(1)设A种型号的净水器的销售单价为x元,B种型号的净水器的销售单价为y元,根据“第一周A种型号净水器的销售量为3台,B种型号净水器的销售量为5 台,销售总额为18000元;第二周A种型号净水器的销售量为4台,B种型号净水器的销售量为10台,销售总额为31000元”,即可得出关于x, y的二元一次方程组,解之即可得出结论;
(2)设A种型号的净水器采购了m台,则B种型号的净水器采购了台,根据总价单价数量,即可得出关于m的一元一次方程,解之即可得出结论;
(3)设电器公司第三周采购的30台净水器中,用于打折销售的B种型号净水器为n台,则不打折销售的B种型号净水器为台,根据利润销售收入进货成本,即可得出关于n的一元一次方程,解之即可得出结论.
【详解】(1)解:设A种型号的净水器的销售单价为x元,B种型号的净水器的销售单价为y元,
依题意,得,
解得: ,
答:A种型号的净水器的销售单价为2500元,B种型号的净水器的销售单价为2100元.
(2)解:设A种型号的净水器m台,则B种型号的净水器台,
依题意,得:,
解得,
答:A种型号的净水器采购了10台.
(3)解:设电器公司第三周采购的30台净水器中,用于打折销售的B种型号净水器为n台,则不打折销售的B种型号净水器为台,
依题意,得:,
解得:,
答:电器公司第三周采购的30台净水器中,用于打折销售的B种型号净水器为10台.
12.(1)该水果线上的销售单价是元,线下的销售单价是元
(2)当线下采购该水果时最省钱
【分析】本题考查了二元一次方程组的应用、一元一次不等式的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,找出关于的函数关系式.
(1)设该水果线上的销售单价是元,线下的销售单价是元,利用总收入销售单价销售数量,结合第一、二两批该水果的销售量和总收入,可列出关于,的二元一次方程组,解之即可得出结论;
(2)设该公司线上采购该水果,则线下采购该水果,根据线下采购该水果量不得少于线上采购该水果量的,可列出关于的一元一次不等式,解之可得出的取值范围,设该公司采购该水果共花费元,利用总价单价数量,可得出关于的函数关系式,再利用一次函数的性质,即可解决最值问题.
【详解】(1)解:设该水果线上的销售单价是元,线下的销售单价是元,
根据题意得:,
解得:.
答:该水果线上的销售单价是元,线下的销售单价是元;
(2)解:设该公司线上采购该水果,则线下采购该水果,
根据题意得:,
解得:.
设该公司采购该水果共花费元,则,
即,
,
随的增大而减小,
当时,取得最小值.
答:当线下采购该水果时最省钱.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
2025年中考数学解答题系列:实际问题与二元一次方程组
1.2025年春节档,电影《哪吒之魔童闹海》掀起观影热潮,影片通过粒子水墨技术、动态水墨渲染引擎等技术,将传统水墨画意境融入动画,打造出兼具古典神韵与现代视觉冲击力的场景,形成独特的文化辨识度,向全球展示了“既古老又充满活力的中国形象”. 影片将封神神话中的角色(如哪吒、敖丙)赋予现代价值观,使传统文化符号与当代人民心理形成共振.某文创店果断订购了印有“哪吒”图案和“敖丙”图案的两种书签.经统计,订购30张“哪吒”书签与20张“敖丙”书签,成本共计430元;而订购45张“哪吒”书签和25张“敖丙”书签,则需花费605元.
(1)求“哪吒”、“敖丙”两种书签每张的进价分别是多少元?
(2)该文创店计划购进“哪吒”、“敖丙”两种书签共90张, “哪吒”种书签的购进数量不超过“敖丙”种书签数量,已知“哪吒”、“敖丙”两种书签的销售单价分别为15元和12元,如何规划购买方案,才能使文具店在这批书签全部售出后获得最大利润?最大利润是多少?
2.在农作物不同的生长阶段运用科技手段实现精准施肥,可以提高产量和质量.某农场为种植小麦需要配制复合肥料.小麦在生长过程中需要大量的氮(N)促进叶片生长,适量的磷(P)促进根系发育,以及足够的钾(K)提高果实品质.农场有两种原料可供使用,其氮、磷、钾含量及成本如下表:
原料 氮(N)含量 (千克/吨) 磷(P)含量 (千克/吨) 钾(K)含量 (千克/吨) 成本 (元/吨)
原料A 20 40 30 600
原料B 50 10 40 800
(1)在小麦播种前农场根据土壤检测结果配制底肥,要求肥料中含有240千克氮、120千克磷,求使用A,B两种原料各多少吨?
(2)4月份,小麦进入拔节期,农场根据小麦长势和底肥用量计划配制追肥,要求追肥用量是底肥用量的,且含有不少于100千克钾,请设计出成本最低的配制方案.
3.“周礼伤心凉粉”是安岳的一大美食,它不仅口感鲜美,而且制作工艺独特,传承历史悠久,被誉为四川的传统工艺之一.现有,两类“周礼伤心凉粉”特受顾客喜爱.已知购买2份类和1份类共需38元;购买4份类和3份类共需86元.
(1)分别求出,两类“周礼伤心凉粉”每份的价格;
(2)芮芮家为了招待远道而来的客人,准备购买,两类“周礼伤心凉粉”共20份,且购买的总费用不超过250元,则最多能购买类“周礼伤心凉粉”多少份?
4.年关将至,幸福小区物业决定采购A,B两种型号的灯笼.若购买3个A型灯笼和4个B型灯笼共需要116元;购买6个A型灯笼和5个B型灯笼共需要172元.
(1)求A,B两种型号灯笼的单价;
(2)若需要购买A,B两种型号的灯笼共200个,总费用不超过3000元,至少需要购买A型灯笼多少个?
5.某电脑经销商计划同时购进一批电脑机箱和显示器,若购进电脑机箱5台和显示器4台,共需要资金7000元;若购进电脑机箱2台和显示器5台,共需要资金7900元.
(1)求每台电脑机箱和显示器的进价各是多少元?
(2)该经销商计划购进这两种电脑机箱和显示器共50台,用于购买这两种电脑机箱和显示器的资金不超过36000元.求最多能购进多少台显示器?
6.2025年亚冬会在哈尔滨举办,吉祥物“滨滨”和“妮妮”深受广大游客的喜爱,某专营店计划购进A、B两款纪念品,若购进A款纪念品3件和B款纪念品2件共需150元,若购进A款纪念品1件和B款纪念品4件共需160元.
(1)求A、B两款纪念品每件的进价分别为多少元?
(2)若A款纪念品售价为38元,B款纪念品售价为45元,该专营店计划购进A、B两款纪念品共50件,这两种纪念品全部售出后总获利不低于540元,那么该专营店最多可以购进A款纪念品多少件?
7.2025年第九届亚洲冬季运动会在哈尔滨举办.某经销商发现,与吉祥物“滨滨”和“妮妮”相关的甲、乙两款纪念品深受大家喜爱.已知购买3个甲款纪念品和2个乙款纪念品共需180元;购买5个甲款纪念品比购买3个乙款纪念品多15元.
(1)甲、乙两款纪念品的售价各是多少?
(2)甲款纪念品的进价为20元,乙款纪念品的进价为38元.若该经销商计划购进甲、乙两款纪念品共60个,且乙款纪念品的购买数量不低于甲款纪念品购买数量的2倍,则应如何进货能使得这批纪念品全部售出后所获利润最大,最大利润是多少?
8.某兴趣小组在开展“探究小球与水面高度关系”的项目式学习活动中,准备了若干体积相同的大球和体积相同的小球,并尝试将球放入一个有水的高为的圆柱形烧杯中(烧杯中原有水面高度是),以观察放入大球和小球数量和烧杯中水面高度的变化情况,兴趣小组的同学根据水面高度的变化绘制了实验结果见图(如图).请根据图中信息回答下面的问题:
(1)放入一个小球水面升高_________.
A.2 B.3 C.6 D.
(2)若放入大球、小球共10个,要使水面上升到,求放入大球、小球各多少个?
(3)现有充足的大球和小球,要使水面上升到,下面的方案正确的序号是____________.
①往烧杯中放入1个大球和10个小球;②往烧杯中放入2个大球和9个小球;
③往烧杯中放入4个大球和7个小球;④往烧杯中放入6个大球和3个小球;
⑤往烧杯中放入8个大球.
A.①②④⑤ B.②④⑤ C.①④⑤ D.②③④
9.为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了两种食品作为午餐.这两种食品每包质量均为,营养成分表如下.
(1)若要从这两种食品中摄入热量和蛋白质,应选用两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共8包,要使每份午餐中的蛋白质含量不低于,且热量最低,应如何选用这两种食品?
10.综合与实践
【背景】住尤溪的小颖想给亲朋好友寄送尤溪特产.
【素材】
素材1:她了解到某快递公司的收费标准(单位:元/千克)如下表:
计费单位 收费标准
福建省内 江浙沪地区
首重
续重
素材2:
电子存单1 电子存单2
托寄物:尤溪特产 目的地:福州 计量重量:2千克 件数:1 总费用:12元 托寄物:尤溪特产 目的地:上海 计量重量:5千克 件数:1 总费用:36元
素材3:收费说明
①每件快递按送达地分别计算运费;
②运费计算方式:首重价格+续重×续重运费.首重均为1千克,超过1千克即要续重,续重以1千克为计重单位(不足1千克按1千克计算).
【问题解决】
(1)小颖给在厦门的朋友寄出了千克的尤溪特产,她需要支付快递费多少元?
(2)小颖给在杭州的外婆寄特产快递费花了72元,求这份特产重量的取值范围.
11.佰洋电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是2025年3月前两周的销售情况:
销售时段 销售数量 销售总额
A种型号 B种型号
第一周 3台 5台 18000元
第二周 4台 10台 31000元
(1)求A,B两种型号的净水器的销售单价?
(2)由于前两周两种净水器都销售一空,电器公司第三周采购这两种型号的净水器共30台,恰好花费54000元,求A种型号的净水器采购了多少台?
(3)在(2)的条件下,电器公司第三周开始销售部分刚购进的A型号和B型号净水器,但发现市场将要被新款智能净水器所取代,为扩大销售量,将剩余B种型号净水器按售价的七折进行销售,A种型号净水器原售价不变,当第三周采购的30台净水器都销售一空后统计这30台净水器的利润为6700元,求电器公司第三周采购的30台净水器中,用于打折销售的B种型号净水器为多少个?
12.随着自媒体的盛行,网购及直播带货成为一种趋势,某农产基地准备借助自媒体对某种水果做营销,采用线上及线下两种销售方式,统计销售情况发现,该水果的销售量和总收入如表(总收入销售量单价):
线上销售水果量(单位:) 线下销售水果量(单位:) 总收入(单位:元)
第一批
第二批
(1)求该水果线上、线下的销售单价各是多少元;
(2)若某公司计划从该地采购该水果,因保质期问题,准备采用线上、线下相结合的方式,因实际需要,线下采购该水果量不得少于线上采购该水果量的,请你帮该公司算一算,当线下采购多少水果时最省钱?
《2025年中考数学解答题系列:实际问题与二元一次方程组》参考答案
1.(1)“哪吒”、“敖丙”两种书签每张的进价分别是9、8元
(2)当购进“哪吒”书签40张,“敖丙”书签50张时,获得最大利润,最大利润是440元
【分析】本题主要考查了二元一次方程组的应用,一次函数的实际应用.解决本题的关键是列出利润与购买“哪吒”书签的数量之间的函数关系式,利用一次函数的性质确定购买方案.
(1)设“哪吒”、“敖丙”两种书签每张的进价分别是x、y元,根据两种不同的购买方案所需要的费用列方程组求解即可;
(2)设购进“哪吒”书签m张,“敖丙”书签张,设这批书签全部售出后获利W元,可以得到所获利润与购买“哪吒”书签的数量之间的一次函数关系式,利用一次函数的性质确定购买方案即可.
【详解】(1)解:设“哪吒”、“敖丙”两种书签每张的进价分别是x、y元,
由题意知: ,
解得,
答:“哪吒”、“敖丙”两种书签每张的进价分别是9元,8元.
(2)解:设购进“哪吒”书签m张,“敖丙”书签张,
由题意知:,
解得:,
设这批书签全部售出后获利W元,
则,
∵,
∴W随m的增大而增大,
∴当时,,W有最大值,元.
答:当购进“哪吒”书签40张,“敖丙”书签50张时,获得最大利润,最大利润是440元.
2.(1)使用种原料2吨,种原料4吨
(2)使用种原料2吨,种原枓1吨配制追肥,成本最低
【分析】本题主要考查二元一次方程组,一元一次不等式,一次函数最值的计算,掌握以上知识,正确列式求解是关键.
(1)设使用种原料吨,种原料吨,由数量关系列二元一次方程组求解即可;
(2)设使用种原料吨,则种原料吨,列不等式得,解得,设总成本为元,则,根据一次函数求最值的方法计算即可求解.
【详解】(1)解:设使用种原料吨,种原料吨,
根据题意得,
解得,
答:使用种原料2吨,种原料4吨.
(2)解:追肥用量是底肥用量的,
追肥用量为(吨),
设使用种原料吨,则种原料吨,
要求肥料中含有不少于100千克钾,
,
解得,
设总成本为元,则,
,
随的增大而减小,
当时,最小,
,
答:使用种原料2吨,种原枓1吨配制追肥,成本最低.
3.(1)类“周礼伤心凉粉”每份的价格为元,类“周礼伤心凉粉”每份的价格为元.
(2)最多能购买类“周礼伤心凉粉”12份.
【分析】本题考查了二元一次方程组的实际应用,一元一次不等式的应用,读懂题意,找出等量关系是解题的关键.
(1)设类“周礼伤心凉粉”每份的价格为,类“周礼伤心凉粉”每份的价格为,根据题意列出二元一次方程组,然后解方程即可;
(2)设类“周礼伤心凉粉”购买份,那么类“周礼伤心凉粉”购买份,根据题意列出一元一次不等式,然后解不等式即可.
【详解】(1)解:设类“周礼伤心凉粉”每份的价格为,类“周礼伤心凉粉”每份的价格为.
,解得
答:类“周礼伤心凉粉”每份的价格为元,类“周礼伤心凉粉”每份的价格为元.
(2)解:设类“周礼伤心凉粉”购买份,那么类“周礼伤心凉粉”购买份.
解得
最大为
类“周礼伤心凉粉”最多购买份
答:最多能购买类“周礼伤心凉粉”12份.
4.(1)A,B两种型号灯笼的单价分别为12元和20元
(2)125个
【分析】本题考查了二元一次方程组和一元一次不等式的实际应用,正确理解题意是解题的关键.
(1)设A,B两种型号灯笼的单价分别为元和元,由“购买3个A型灯笼和4个B型灯笼共需要116元;购买6个A型灯笼和5个B型灯笼共需要172元”;
(2)设需要购买A型灯笼个,则需要购买B型灯笼个,由总费用不超过3000元建立不等式求解.
【详解】(1)解:设A,B两种型号灯笼的单价分别为元和元
根据题意列方程组得
解得,
答:A,B两种型号灯笼的单价分别为12元和20元;
(2)解:设需要购买A型灯笼个,则需要购买B型灯笼个
根据题意得
解得
答:至少需要购买A型灯笼125个.
5.(1)每台电脑机箱的进价为200元,每台显示器的进价是1500元
(2)20台
【分析】此题考查了二元一次方程组及一元一次不等式的应用, 根据等量关系列出方程组是解题的关键.
(1)根据题意得出等量关系列出方程组,即可求出电脑机箱和液晶显示器的单价;
(2)根据题意列不等式计算即可求解.
【详解】(1)解:设每台电脑机箱的进价为元,每台显示器的进价是元,
根据题意得:,
解方程组得:,
答:每台电脑机箱的进价为200元,每台显示器的进价是1500元.
(2)解:设购进台显示器,
根据题意得:,
解不等式得:,
答:最多能购进20台显示器.
6.(1)A、B两种工艺品每件的进价分别为28元和33元
(2)该专营店最多购进A种工艺品30件
【分析】本题考查的是二元一次方程组的应用,一元一次不等式的应用,确定相等关系与不等关系是解本题的关键.
(1)设A、B两款纪念品每件的进价分别为x元和y元,再由“若购进A款纪念品3件和B款纪念品2件共需150元,若购进A款纪念品1件和B款纪念品4件共需160元”列方程,再解方程即可;
(2)设该专营店购进A种工艺品a件,由总获利不低于540元,再列不等式,再解不等式即可.
【详解】(1)解:设A、B两款纪念品每件的进价分别为x元和y元,
则,
解得:,
答:A、B两种工艺品每件的进价分别为28元和33元.
(2)解:设该专营店购进A种工艺品a件,
则,
解得:.
答:该专营店最多购进A种工艺品30件.
7.(1)甲款纪念品的售价为元,乙款纪念品的售价为元;
(2)购进甲款个,乙款个时,最大利润为元.
【分析】本题考查了二元一次方程组的应用,一次函数的应用,掌握相关知识是解题的关键.
(1)设甲款纪念品的售价为元,乙款纪念品的售价为元,根据题意列出方程组,求解即可;
(2)设购进甲款个,则乙款为个,利润为元,依题意得,再求出的范围即可求解.
【详解】(1)解:设甲款纪念品的售价为元,乙款纪念品的售价为元,根据题意得:
,
解得:,
答:甲款纪念品的售价为元,乙款纪念品的售价为元;
(2)解:设购进甲款个,则乙款为个,利润为元,依题意得:
,
∵,
∴,
当时,利润最大:元,
答:购进甲款个,乙款个时,最大利润为元.
8.(1)A
(2)放入大球4个、小球各6个.
(3)B
【分析】本题主要考查了一元一次方程、二元一次方程组的应用、有理数的混合运算等知识点,正确求出放入一个小球和大球水面上升的高度是解题的关键.
(1)根据放入3个体积相同的小球水面升高了,据此列式计算即可求解;
(2)根据放入2个体积相同的大球水面升高了,求出放入一个大球水面升高的高度,然后根据意义列二元一次方程组方程组求解即可;
(3)分别求出每一种方案的水面高度即可求解.
【详解】(1)解:由题意可得,放入3个体积相同的小球水面升高了,
∴放入一个小球水面升高.
故选:A.
(2)解:由题意可得,放入2个体积相同的大球水面升高了,
∴放入一个大球水面升高,
设放入大球x个,放入小球y个,
由题意可得:,解得:,
答:放入大球4个、小球各6个.
(3)解:∵,
∴方案①不正确;
∵,
∴方案②正确;
∵,
∴方案③不正确;
∵,
∴方案④正确;
∵,
∴方案⑤正确.
综上,方案正确的是②④⑤.
故选:B.
9.(1)选用A种食品2包,B种食品4包;
(2)选用A种食品6包,B种食品2包.
【分析】本题考查了二元一次方程组的应用,一元一次不等式的应用,一次函数的应用:
(1)设选用A种食品x包,B种食品y包,根据“从这两种食品中摄入热量和蛋白质”列方程组求解即可;
(2)设选用A种食品包,则选用B种食品包,根据“每份午餐中的蛋白质含量不低于”列不等式求得的范围,设总热量为,得到,再利用一次函数的性质求解即可.
【详解】(1)解:设选用A种食品x包,B种食品y包,
根据题意,得
解方程组,得
答:选用A种食品2包,B种食品4包;
(2)解:设选用A种食品包,则选用B种食品包,
根据题意,得.
∴.
设总热量为,则.
∵,
∴w随a的增大而减小.
∴当时,w最小.
∴.
答:选用A种食品6包,B种食品2包.
10.(1)支付快递费16元.
(2)这份特产的重量大于10千克,小于等于11千克.
【分析】本题主要考查了二元一次方程组以及一元一次方程的应用.
(1)根据题意列出关于a,b的二元一次方程组,确定.根据福建省内收费标准计算即可.
(2)设这份特产按千克计费,根据江浙沪地区收费标准列出关于x的一元一次方程,解方程,再结合不足1千克按1千克计算即可得出这份特产重量的取值范围.
【详解】(1)解:由题意可知:
解得.
∵不足1千克按1千克计算,故千克按4千克计算,
即(元).
她需要支付快递费16元.
(2)解:设这份特产按千克计费,
则
解得.
所以这份特产的重量大于10千克,小于等于11千克.
11.(1)A型2500元,B型2100元
(2)10台
(3)10台
【分析】本题考查二元一次方程组与一元一次方程的应用,根据题意正确列方程(组)是解题的关键.
(1)设A种型号的净水器的销售单价为x元,B种型号的净水器的销售单价为y元,根据“第一周A种型号净水器的销售量为3台,B种型号净水器的销售量为5 台,销售总额为18000元;第二周A种型号净水器的销售量为4台,B种型号净水器的销售量为10台,销售总额为31000元”,即可得出关于x, y的二元一次方程组,解之即可得出结论;
(2)设A种型号的净水器采购了m台,则B种型号的净水器采购了台,根据总价单价数量,即可得出关于m的一元一次方程,解之即可得出结论;
(3)设电器公司第三周采购的30台净水器中,用于打折销售的B种型号净水器为n台,则不打折销售的B种型号净水器为台,根据利润销售收入进货成本,即可得出关于n的一元一次方程,解之即可得出结论.
【详解】(1)解:设A种型号的净水器的销售单价为x元,B种型号的净水器的销售单价为y元,
依题意,得,
解得: ,
答:A种型号的净水器的销售单价为2500元,B种型号的净水器的销售单价为2100元.
(2)解:设A种型号的净水器m台,则B种型号的净水器台,
依题意,得:,
解得,
答:A种型号的净水器采购了10台.
(3)解:设电器公司第三周采购的30台净水器中,用于打折销售的B种型号净水器为n台,则不打折销售的B种型号净水器为台,
依题意,得:,
解得:,
答:电器公司第三周采购的30台净水器中,用于打折销售的B种型号净水器为10台.
12.(1)该水果线上的销售单价是元,线下的销售单价是元
(2)当线下采购该水果时最省钱
【分析】本题考查了二元一次方程组的应用、一元一次不等式的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,找出关于的函数关系式.
(1)设该水果线上的销售单价是元,线下的销售单价是元,利用总收入销售单价销售数量,结合第一、二两批该水果的销售量和总收入,可列出关于,的二元一次方程组,解之即可得出结论;
(2)设该公司线上采购该水果,则线下采购该水果,根据线下采购该水果量不得少于线上采购该水果量的,可列出关于的一元一次不等式,解之可得出的取值范围,设该公司采购该水果共花费元,利用总价单价数量,可得出关于的函数关系式,再利用一次函数的性质,即可解决最值问题.
【详解】(1)解:设该水果线上的销售单价是元,线下的销售单价是元,
根据题意得:,
解得:.
答:该水果线上的销售单价是元,线下的销售单价是元;
(2)解:设该公司线上采购该水果,则线下采购该水果,
根据题意得:,
解得:.
设该公司采购该水果共花费元,则,
即,
,
随的增大而减小,
当时,取得最小值.
答:当线下采购该水果时最省钱.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
