第十四讲 全等三角形及其实际应用(含解析) 2025年中考数学基础知识分点练
文档属性
| 名称 | 第十四讲 全等三角形及其实际应用(含解析) 2025年中考数学基础知识分点练 |  | |
| 格式 | docx | ||
| 文件大小 | 216.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 18:00:19 | ||
图片预览




文档简介
第十四讲 全等三角形及其实际应用
命题点1 全等三角形的判定与性质
类型一 平移型(7考)
1. 新考法 条件开放(2024盐城)已知:如图,点A,B,C,D在同一条直线上,
若 ,则
请从①CE∥DF;②CE=DF;③∠E=∠F这3个选项中选择一个作为条件(写序号),使结论成立,并说明理由.
2. (2024内江)如图,点A,D,B,E在同一条直线上,
(1)求证:
(2)若 求 的度数.
类型二 轴对称型(122考)
3. (2024安徽)在凸五边形ABCDE中, F是CD的中点.下列条件中,不能推出AF与CD一定垂直的是 ( )
A. ∠ABC=∠AED
C. ∠BCF=∠EDF
4.新考法结合直角坐标系(2024临夏州)如图,在 中,点A 的坐标为(0,1),点B 的坐标为(4.1)点C的坐标为(3,4),点D 在第一象限(不与点C重合),且△ABD与△ABC全等,点D 的坐标是 .
5. (2024乐山)如图,AB是∠CAD的平分线,AC=AD,求证:∠C=∠D.
6. (2024广安)如图,菱形ABCD中,点E,F分别是AB,BC边上的点,BE=BF,求证:∠DEF=∠DFE.
7. (2024苏州)如图,△ABC 中,AB=AC,分别以B,C为圆心,大于 长为半径画弧,两弧交于点D,连接BD,CD,AD,AD与BC交于点E.
(1)求证:△ABD≌△ACD;
(2)若BD=2,∠BDC=120°,求BC的长.
类型三 旋转型(105考)
8. 新考法 条件开放(2024 牡丹江)如图,△ABC中,D是AB上一点,CF∥AB,D,E,F三点共线,请添加一个条件 ,使得AE=CE.(只添一种情况即可)
9. (2024云南)如图,在△ABC和△AED中,AB=AE,∠BAE=∠CAD,AC=AD.
求证:△ABC≌△AED.
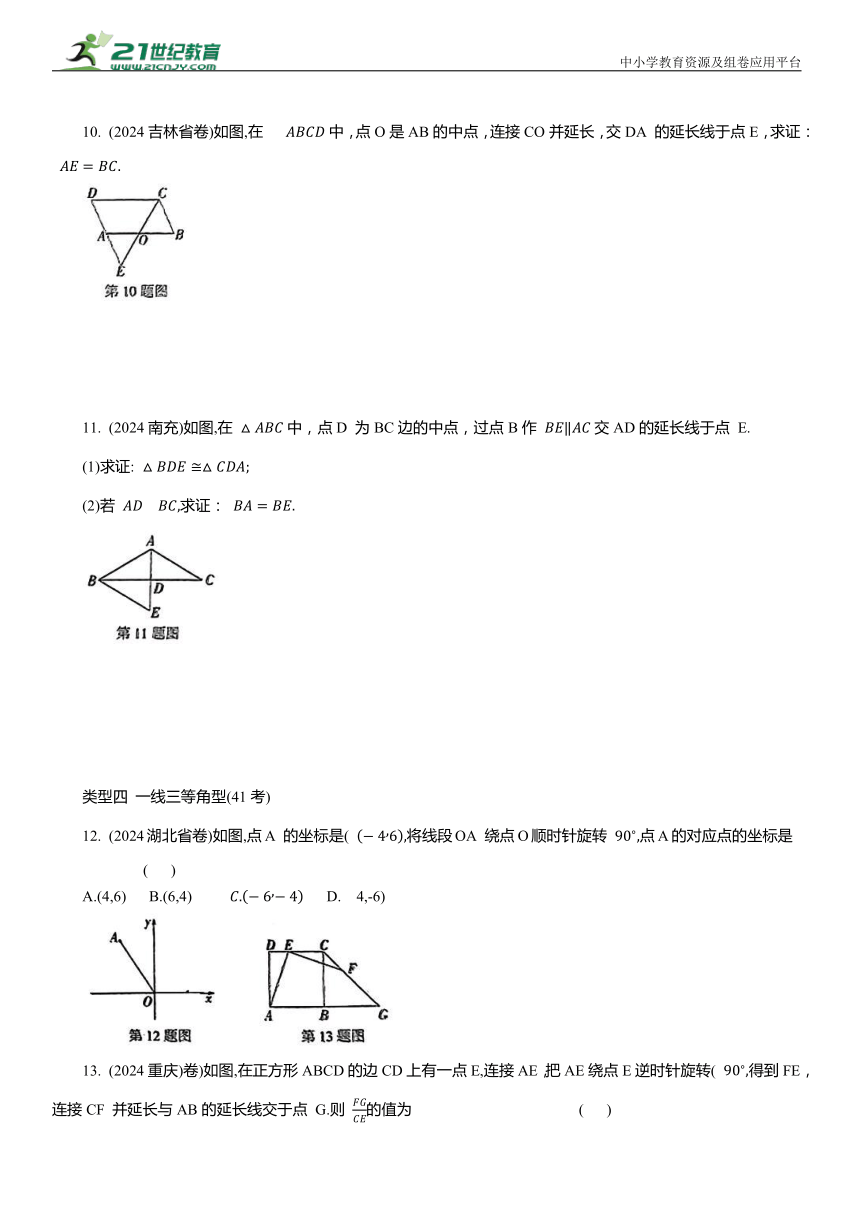
10. (2024吉林省卷)如图,在 中,点O是AB的中点,连接CO并延长,交DA 的延长线于点E,求证:
11. (2024南充)如图,在 中,点D 为BC边的中点,过点B作 交AD的延长线于点 E.
(1)求证:
(2)若 求证:
类型四 一线三等角型(41考)
12. (2024湖北省卷)如图,点A 的坐标是( 将线段OA 绕点O顺时针旋转 点A的对应点的坐标是 ( )
A.(4,6) B.(6,4) D. 4,-6)
13. (2024重庆)卷)如图,在正方形ABCD的边CD上有一点E,连接AE,把AE绕点E逆时针旋转( 得到FE,连接CF 并延长与AB的延长线交于点 G.则 的值为 ( )
中小学教育资源及组卷应用平台
14. (2023通辽)如图,等边三角形ABC的边长为6cm,动点P从点A出发以2cm/s的速度沿AB向点B匀速运动,过点P作 交边AC于点Q,以PQ为边作等边三角形 PQD ,使点A,D 在PQ异侧,当点D落在BC边上时,点P 需移动 s.
15. (2024北京)如图,在正方形ABCD中,点E 在AB上, 于点F, 于点G.若 则 的面积为 .
16. (2024烟台)在等腰直角 中, ,D为直线 BC 上任意一点,连接AD.将线段AD 绕点D 按顺时针方向旋转 得线段 ED,连接BE.
【尝试发现】
(1)如图①,当点D 在线段BC 上时,线段 BE 与 CD的数量关系为 ;
【类比探究】
(2)当点D 在线段BC 的延长线上时,先在图②中补全图形,再探究线段 BE 与 CD 的数量关系并证明;
【联系拓广】
(3)若 请直接写出 的值.
类型五 其他类型(247考)
17.(2024北京)下面是“作一个角使其等于∠AOB”的尺规作图方法.
(1)如图①,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)如图②,作射线( 以点O'为圆心,OC长为半径画弧,交O'A'于点 以点C'为圆心,CD 长为半径画弧,两弧交于点.
(3)过点 D'作射线O'B',则∠A'O'B'=∠AOB.
上述方法通过判定△C'O'D'≌△COD 得到∠A'O'B'=∠AOB,其中判定 的依据是 ( )
A.三边分别相等的两个三角形全等
B.两边及其夹角分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
18. 新考法 新定义(2024遂宁)如图①,△ABC与 满足 我们称这样的两个三角形为“伪全等三角形”.
如图②,在△ABC中,AB=AC,点D,E在线段BC上,且BE=CD,则图中共有“伪全等三角形” ( )
A. 1对 B. 2对 C. 3对 D. 4对
19. (2024成都)如图,△ABC≌△CDE,若∠D=35°,∠ACB=45°,则∠DCE 的度数为 .
20. (2024重庆A卷)如图,在△ABC中,延长AC至点 D,使CD=CA,过点D 作DE∥CB,且DE=DC,连接AE交BC于点 F.若∠CAB=∠CFA,CF=1,则BF= .
命题点2 全等三角形的实际应用(5考)
21.(2024宜宾)宜宾地标广场位于三江汇合口(如图①,左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C,D,在地标广场上选择两个观测点A,B(点A,B,C,D在同一水平面,且 如图②所示,在点A 处测得点 C在北偏西 方向上,测得点 D在北偏东 方向上;在B处测得点 C在北偏西 方向上,测得点D 在北偏东 方向上,测得 米.求长江口的宽度 CD 的值(结果精确到1米).(参考数据: 0.
第十四讲 全等三角形及其实际应用
1. 解:选择①,
理由如下:
∵AE∥BF,
∴∠A=∠FBD,
∵CE∥DF,
∴∠ACE=∠D,
在△AEC和△BFD中,
∴△AEC≌△BFD(AAS),
∴AC=BD,
∴AB=CD.
或选择③,
理由如下:
∵AE∥BF,
∴∠A=∠FBD,
在△AEC和△BFD中,
∴△AEC≌△BFD(ASA),
∴AC=BD,
∴AB=CD.
2. (1)证明:∵AD=BE,
∴AD+DB=BE+DB,即AB=DE,
∵AC=DF,BC=EF,
∴△ABC≌△DEF(SSS);
(2)解:∵△ABC≌△DEF,∠A=55°,
∴∠A=∠FDE=55°,
∵∠E=45°,
∴∠F=180°-∠FDE-∠E=80°.
3. D 【解析】如解图,连接AC,AD,EF,BF,AF,∵AB=AE,BC=DE,∴当∠ABC=∠AED时,△ABC≌△AED(SAS),∴ AC=AD,∵ 点 F 是 CD 的中点,∴ AF⊥CD,∴ 选项 A 不符合题意;∵ AB =AE,∠BAF =∠EAF,AF=AF,∴△ABF≌△AEF(SAS),∴BF=EF,∠AFB=∠AFE,∵ BC =DE,CF = DF,∴ △BCF≌△EDF(SSS), ∴ ∠BFC = ∠EFD, ∴ ∠AFD = CD,∴选项B不符合题意;∵BC=DE,CF=DF,∠BCF=∠EDF,∴△BCF≌△EDF(SAS),∴BF=EF,∠BFC=∠EFD,∵ AB =AE,AF =AF,∴ △ABF≌△AEF(SSS),∴ ∠AFB = ∠AFE,∴ ∠AFD = ∠AFC,∴ .选项C不符合题意;∵选项 D 无法推出 AF 与 CD 一定垂直,∴选项D符合题意.
4. (1,4) 【解析】∵点D 在第一象限(不与点C重合),且△ABD 与△ABC全等,∴△BAD≌△ABC,∴AD=BC,BD=AC,如解图所示,∵A(0,1),B(4,1),C(3,4),由对称性可知D(1,4).
5. 证明:∵AB 是∠CAD 的平分线,
∴∠CAB=∠DAB,
在△ABC和△ABD中,
∴△ABC≌△ABD(SAS),
∴∠C=∠D.
6. 证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠A=∠C,
又∵BE=BF,
∴AB-BE=BC-BF,
∴AE=CF.
在△DAE 和△DCF中,
∴△DAE≌△DCF(SAS),
∴DE=DF,
∴∠DEF=∠DFE.
7. (1)证明:由作图知BD=CD.
在△ABD 和△ACD中.
∴△ABD≌△ACD(SSS);
(2)解:∵△ABD≌△ACD,∠BDC=120°,
∵BD=CD,AB=AC,
∴DA⊥BC,BE=CE,
8. DE=EF 或AD=CF(答案不唯一) 【解析】∵ CF∥AB,∴∠A=∠ECF,∠ADE=∠CFE,∴添加条件 DE=EF,可以使得△ADE≌△CFE(AAS),添加条件AD=CF,可以使得△ADE≌△CFE(ASA),即推出AE=CE.
9. 证明:∵∠BAE=∠CAD,
∴∠BAE+∠CAE=∠CAD+∠CAE,即∠BAC=∠EAD,在△ABC与△AED中,
∴△ABC≌△AED(SAS).
10.证明:∵四边形ABCD 是平行四边形,
∴AD∥BC,
∴DE∥BC,
∴∠OAE=∠B,∠OCB=∠E,
∵点O是AB的中点,
∴OA=OB,
∴△AOE≌△BOC(AAS),
∴AE=BC.
11. 证明:(1)∵D为BC的中点,
∴BD=CD.
∵BE∥AC,
∴∠E=∠DAC,∠DBE=∠C.
在△BDE和△CDA中,
∴△BDE≌△CDA(AAS);
(2)∵△BDE≌△CDA,
∴ED=AD.
∵AD⊥BC,
∴BD垂直平分AE,
∴BA=BE.
12. B 【解析】如解图,线段OA 绕点 O 顺时针旋转90°得到OA',过点A 和点A'分别作x轴的垂线,垂足分别为B,C,∵点A的坐标为(-4,6),∴OB=4,AB=6,∵ 将线段 OA 绕点 O 顺时针旋转 90°得到OA',∴ OA = OA',∠AOA'=90°,∴ ∠AOB = 90°-∠A'OC=∠OA'C,∴△AOB≌△OA'C(AAS),∴A'C=OB=4,OC=AB=6,∴点A'的坐标为(6,4).
13. A 【解析】如解图,过点 F作 DC的垂线交 DC 延长线于点 H,则∠H=90°,由旋转性质可得 EA=EF,∠AEF=90°,∵ 四边形 ABCD 是正方形,∴ ∠D=90°,DC∥AB,DA=DC=BC,设 DA=DC=BC=1,∵∠AEH=∠1+∠AEF =∠2+∠D,∴ ∠1 =∠2,∴△ADE≌△EHF(AAS),∴ DE=HF,AD=EH=1,设DE=HF=x,则CE=DC-DE=1-x,∴CH=EH-EC=1-(1-x)=x,∴HF=CH=x,∵ ∠H=90°,∴ ∠HCF=45°,∴ CF = x,∵ DC∥AB,∴ ∠HCF =∠G=
14.1 【解析】如解图,设点 P 的运动时间为 xs,由题意得AP=2x,BP=AB-AP=6-2x,∵PQ⊥AB,∴∠QPA=90°,∵△PQD 和△ABC都是等边三角形,∴∠A=∠B=∠DPQ = 60°,PQ = PD,∴ ∠BPD = 30°,∴∠PDB=90°,∴△APQ≌△BDP(AAS),∴BD=AP=2x,易得BP=2BD,∴6-2x=4x,解得x=1.∴点 P需移动1s.
15. 【解析】∵ 四边形 ABCD 是正方形,∴ AD=CD,∵ AF⊥DE,CG⊥DE,∴ ∠AFD = ∠DGC =90°,∵ ∠CDG+∠ADF = 90°, ∠CDG+∠DCG =90°,∴ ∠ADF=∠DCG,∴ △DAF≌△CDG,∴ DF=CG=4,由勾股定理得AF=3,∵ ∠DAF+∠FAE=∠FAE+∠FEA=90°,∴ ∠DAF=∠AEF,∴ △DAF∽ 即 AF = DF · EF,∴ EF =
16. 解:(
【解法提示】如解图①,过点 E 作 EM⊥CB,交 CB 的延长线于点 M,由旋转得 AD=DE,∠ADE=90°,∴∠ADC+∠EDM=90°,∵ ∠ACB = 90°,∴ ∠ACD =∠DME, ∠ADC + ∠CAD = 90°, ∴ ∠CAD =∠EDM,∴△ACD≌△DME(AAS),∴CD=EM,AC=DM,∵AC=BC,∴BM=DM-BD=AC-BD=BC-BD=CD,∴BM=EM,∵EM⊥CB,∴BE= EM= CD.
(2)补全图形如解图②,
证明:如解图②,过点 E作EF⊥BC于点 F,
∴ ∠DFE=∠BFE=∠ACD=90°,
由旋转的性质得∠ADE=90°,DE=DA,
∴∠DAC+∠ADC=∠EDF+∠ADC=90°,
∴∠EDF=∠DAC,
∴△DEF≌△ADC(AAS),
∴EF=CD,DF=AC=BC,
∴DF-CF=BC-CF,
∴CD=BF,
∴EF=BF,
∴△BEF为等腰直角三角形,
【解法提示】①当点 D 在 BC 延长线上时,如解图③,过点 E 作 EF⊥CD 于点 F,由(2)知△DEF≌△ADC,∴CD=EF,AC=DF=BC,∵AC=BC=1,CD=2,∴DF=AC=1,EF=CD=2,∴CF=CD-DF=1,在Rt△EFC中 ②当点 D 在 CB 延长线上时,如解图④,过点 E 作 EF⊥CB 交 CB 延长线于点 F,由(2)知△DEF≌△ADC,∴ DF=AC=1,EF=CD=2,在 Rt△EFC中,∵ CF = CD+DF = 3,EF = 2,∴ CE =
17. A 【解析】∵( △C'O'D'≌△COD(SSS).
18. D 【解析】∵AB=AC,∴∠B=∠C,易证得△ABE≌△ACD,∴AE=AD,在△ABD和△ABE中,∠B=∠B,AB=AB,AD=AE,∠BAD≠∠BAE;在△ACE和△ACD中,∠C=∠C,AC=AC,AE=AD,∠CAE≠∠CAD;在△ABD 和△ACD 中,∠B =∠C,AB=AC,AD=AD,∠BAD≠∠CAD;在△ACE 和△ABE 中,∠B=∠C,AE=AE,AC=AB,∠CAE≠∠BAE.综上所述,共有4对“伪全等三角形”.
19. 100° 【解析】∵ △ABC≌△CDE,∠ACB=45°,∴∠CED=∠ACB=45°,∴ ∠DCE=180°-∠D-∠CED=100°.
20. 3 【解析】∵ CD=CA,DE∥CB,CF=1,∴ CF 是△ADE的中位线,∴DE=CD=AC=2CF=2,∴AD=AC+DC=4.∵ DE∥CB,∴ ∠CFA=∠E,∠ACB =∠D,∵∠CAB=∠CFA,∴∠CAB=∠E,∴ △CAB≌△DEA(ASA),∴BC=AD=4,∴BF=BC-CF=3.
21.解:如解图,过点 C作 CH⊥BA交 BA的延长线于点H,过点A作AG⊥CD 于点 G,过点 B作BK⊥CD 于点K,且AB∥CD,
∴四边形AHCG,ABKG都是矩形,
∴GK=AB=100,CG=AH,CH=AG=BK,CH∥AG∥BK,
∵由题意可得:∠CAG=∠DBK=18.17°,∠GAD=∠CBK=21.34°,
∴ ∠ACH = ∠CAG = 18. 17°, ∠BCH = ∠CBK =21.34°,
∵∠AGC=∠BKD=90°,
∴△AGC≌△BKD,
∴CG=DK,
设AH=x,CH=y,
即 x=0.33y,
即x+100
=0.39y,
∴0.33y+100=0.39y,
∴CG=DK=550,
∴ CD=550×2+100=1200(m),
∴长江口的宽度CD约为1 200 m.
解题技巧
通过构造辅助线,在直角三角形中,利用锐角三角函数知识,结合已知数据,得到线段的等量关系式,进而求解.
命题点1 全等三角形的判定与性质
类型一 平移型(7考)
1. 新考法 条件开放(2024盐城)已知:如图,点A,B,C,D在同一条直线上,
若 ,则
请从①CE∥DF;②CE=DF;③∠E=∠F这3个选项中选择一个作为条件(写序号),使结论成立,并说明理由.
2. (2024内江)如图,点A,D,B,E在同一条直线上,
(1)求证:
(2)若 求 的度数.
类型二 轴对称型(122考)
3. (2024安徽)在凸五边形ABCDE中, F是CD的中点.下列条件中,不能推出AF与CD一定垂直的是 ( )
A. ∠ABC=∠AED
C. ∠BCF=∠EDF
4.新考法结合直角坐标系(2024临夏州)如图,在 中,点A 的坐标为(0,1),点B 的坐标为(4.1)点C的坐标为(3,4),点D 在第一象限(不与点C重合),且△ABD与△ABC全等,点D 的坐标是 .
5. (2024乐山)如图,AB是∠CAD的平分线,AC=AD,求证:∠C=∠D.
6. (2024广安)如图,菱形ABCD中,点E,F分别是AB,BC边上的点,BE=BF,求证:∠DEF=∠DFE.
7. (2024苏州)如图,△ABC 中,AB=AC,分别以B,C为圆心,大于 长为半径画弧,两弧交于点D,连接BD,CD,AD,AD与BC交于点E.
(1)求证:△ABD≌△ACD;
(2)若BD=2,∠BDC=120°,求BC的长.
类型三 旋转型(105考)
8. 新考法 条件开放(2024 牡丹江)如图,△ABC中,D是AB上一点,CF∥AB,D,E,F三点共线,请添加一个条件 ,使得AE=CE.(只添一种情况即可)
9. (2024云南)如图,在△ABC和△AED中,AB=AE,∠BAE=∠CAD,AC=AD.
求证:△ABC≌△AED.
10. (2024吉林省卷)如图,在 中,点O是AB的中点,连接CO并延长,交DA 的延长线于点E,求证:
11. (2024南充)如图,在 中,点D 为BC边的中点,过点B作 交AD的延长线于点 E.
(1)求证:
(2)若 求证:
类型四 一线三等角型(41考)
12. (2024湖北省卷)如图,点A 的坐标是( 将线段OA 绕点O顺时针旋转 点A的对应点的坐标是 ( )
A.(4,6) B.(6,4) D. 4,-6)
13. (2024重庆)卷)如图,在正方形ABCD的边CD上有一点E,连接AE,把AE绕点E逆时针旋转( 得到FE,连接CF 并延长与AB的延长线交于点 G.则 的值为 ( )
中小学教育资源及组卷应用平台
14. (2023通辽)如图,等边三角形ABC的边长为6cm,动点P从点A出发以2cm/s的速度沿AB向点B匀速运动,过点P作 交边AC于点Q,以PQ为边作等边三角形 PQD ,使点A,D 在PQ异侧,当点D落在BC边上时,点P 需移动 s.
15. (2024北京)如图,在正方形ABCD中,点E 在AB上, 于点F, 于点G.若 则 的面积为 .
16. (2024烟台)在等腰直角 中, ,D为直线 BC 上任意一点,连接AD.将线段AD 绕点D 按顺时针方向旋转 得线段 ED,连接BE.
【尝试发现】
(1)如图①,当点D 在线段BC 上时,线段 BE 与 CD的数量关系为 ;
【类比探究】
(2)当点D 在线段BC 的延长线上时,先在图②中补全图形,再探究线段 BE 与 CD 的数量关系并证明;
【联系拓广】
(3)若 请直接写出 的值.
类型五 其他类型(247考)
17.(2024北京)下面是“作一个角使其等于∠AOB”的尺规作图方法.
(1)如图①,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)如图②,作射线( 以点O'为圆心,OC长为半径画弧,交O'A'于点 以点C'为圆心,CD 长为半径画弧,两弧交于点.
(3)过点 D'作射线O'B',则∠A'O'B'=∠AOB.
上述方法通过判定△C'O'D'≌△COD 得到∠A'O'B'=∠AOB,其中判定 的依据是 ( )
A.三边分别相等的两个三角形全等
B.两边及其夹角分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
18. 新考法 新定义(2024遂宁)如图①,△ABC与 满足 我们称这样的两个三角形为“伪全等三角形”.
如图②,在△ABC中,AB=AC,点D,E在线段BC上,且BE=CD,则图中共有“伪全等三角形” ( )
A. 1对 B. 2对 C. 3对 D. 4对
19. (2024成都)如图,△ABC≌△CDE,若∠D=35°,∠ACB=45°,则∠DCE 的度数为 .
20. (2024重庆A卷)如图,在△ABC中,延长AC至点 D,使CD=CA,过点D 作DE∥CB,且DE=DC,连接AE交BC于点 F.若∠CAB=∠CFA,CF=1,则BF= .
命题点2 全等三角形的实际应用(5考)
21.(2024宜宾)宜宾地标广场位于三江汇合口(如图①,左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C,D,在地标广场上选择两个观测点A,B(点A,B,C,D在同一水平面,且 如图②所示,在点A 处测得点 C在北偏西 方向上,测得点 D在北偏东 方向上;在B处测得点 C在北偏西 方向上,测得点D 在北偏东 方向上,测得 米.求长江口的宽度 CD 的值(结果精确到1米).(参考数据: 0.
第十四讲 全等三角形及其实际应用
1. 解:选择①,
理由如下:
∵AE∥BF,
∴∠A=∠FBD,
∵CE∥DF,
∴∠ACE=∠D,
在△AEC和△BFD中,
∴△AEC≌△BFD(AAS),
∴AC=BD,
∴AB=CD.
或选择③,
理由如下:
∵AE∥BF,
∴∠A=∠FBD,
在△AEC和△BFD中,
∴△AEC≌△BFD(ASA),
∴AC=BD,
∴AB=CD.
2. (1)证明:∵AD=BE,
∴AD+DB=BE+DB,即AB=DE,
∵AC=DF,BC=EF,
∴△ABC≌△DEF(SSS);
(2)解:∵△ABC≌△DEF,∠A=55°,
∴∠A=∠FDE=55°,
∵∠E=45°,
∴∠F=180°-∠FDE-∠E=80°.
3. D 【解析】如解图,连接AC,AD,EF,BF,AF,∵AB=AE,BC=DE,∴当∠ABC=∠AED时,△ABC≌△AED(SAS),∴ AC=AD,∵ 点 F 是 CD 的中点,∴ AF⊥CD,∴ 选项 A 不符合题意;∵ AB =AE,∠BAF =∠EAF,AF=AF,∴△ABF≌△AEF(SAS),∴BF=EF,∠AFB=∠AFE,∵ BC =DE,CF = DF,∴ △BCF≌△EDF(SSS), ∴ ∠BFC = ∠EFD, ∴ ∠AFD = CD,∴选项B不符合题意;∵BC=DE,CF=DF,∠BCF=∠EDF,∴△BCF≌△EDF(SAS),∴BF=EF,∠BFC=∠EFD,∵ AB =AE,AF =AF,∴ △ABF≌△AEF(SSS),∴ ∠AFB = ∠AFE,∴ ∠AFD = ∠AFC,∴ .选项C不符合题意;∵选项 D 无法推出 AF 与 CD 一定垂直,∴选项D符合题意.
4. (1,4) 【解析】∵点D 在第一象限(不与点C重合),且△ABD 与△ABC全等,∴△BAD≌△ABC,∴AD=BC,BD=AC,如解图所示,∵A(0,1),B(4,1),C(3,4),由对称性可知D(1,4).
5. 证明:∵AB 是∠CAD 的平分线,
∴∠CAB=∠DAB,
在△ABC和△ABD中,
∴△ABC≌△ABD(SAS),
∴∠C=∠D.
6. 证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠A=∠C,
又∵BE=BF,
∴AB-BE=BC-BF,
∴AE=CF.
在△DAE 和△DCF中,
∴△DAE≌△DCF(SAS),
∴DE=DF,
∴∠DEF=∠DFE.
7. (1)证明:由作图知BD=CD.
在△ABD 和△ACD中.
∴△ABD≌△ACD(SSS);
(2)解:∵△ABD≌△ACD,∠BDC=120°,
∵BD=CD,AB=AC,
∴DA⊥BC,BE=CE,
8. DE=EF 或AD=CF(答案不唯一) 【解析】∵ CF∥AB,∴∠A=∠ECF,∠ADE=∠CFE,∴添加条件 DE=EF,可以使得△ADE≌△CFE(AAS),添加条件AD=CF,可以使得△ADE≌△CFE(ASA),即推出AE=CE.
9. 证明:∵∠BAE=∠CAD,
∴∠BAE+∠CAE=∠CAD+∠CAE,即∠BAC=∠EAD,在△ABC与△AED中,
∴△ABC≌△AED(SAS).
10.证明:∵四边形ABCD 是平行四边形,
∴AD∥BC,
∴DE∥BC,
∴∠OAE=∠B,∠OCB=∠E,
∵点O是AB的中点,
∴OA=OB,
∴△AOE≌△BOC(AAS),
∴AE=BC.
11. 证明:(1)∵D为BC的中点,
∴BD=CD.
∵BE∥AC,
∴∠E=∠DAC,∠DBE=∠C.
在△BDE和△CDA中,
∴△BDE≌△CDA(AAS);
(2)∵△BDE≌△CDA,
∴ED=AD.
∵AD⊥BC,
∴BD垂直平分AE,
∴BA=BE.
12. B 【解析】如解图,线段OA 绕点 O 顺时针旋转90°得到OA',过点A 和点A'分别作x轴的垂线,垂足分别为B,C,∵点A的坐标为(-4,6),∴OB=4,AB=6,∵ 将线段 OA 绕点 O 顺时针旋转 90°得到OA',∴ OA = OA',∠AOA'=90°,∴ ∠AOB = 90°-∠A'OC=∠OA'C,∴△AOB≌△OA'C(AAS),∴A'C=OB=4,OC=AB=6,∴点A'的坐标为(6,4).
13. A 【解析】如解图,过点 F作 DC的垂线交 DC 延长线于点 H,则∠H=90°,由旋转性质可得 EA=EF,∠AEF=90°,∵ 四边形 ABCD 是正方形,∴ ∠D=90°,DC∥AB,DA=DC=BC,设 DA=DC=BC=1,∵∠AEH=∠1+∠AEF =∠2+∠D,∴ ∠1 =∠2,∴△ADE≌△EHF(AAS),∴ DE=HF,AD=EH=1,设DE=HF=x,则CE=DC-DE=1-x,∴CH=EH-EC=1-(1-x)=x,∴HF=CH=x,∵ ∠H=90°,∴ ∠HCF=45°,∴ CF = x,∵ DC∥AB,∴ ∠HCF =∠G=
14.1 【解析】如解图,设点 P 的运动时间为 xs,由题意得AP=2x,BP=AB-AP=6-2x,∵PQ⊥AB,∴∠QPA=90°,∵△PQD 和△ABC都是等边三角形,∴∠A=∠B=∠DPQ = 60°,PQ = PD,∴ ∠BPD = 30°,∴∠PDB=90°,∴△APQ≌△BDP(AAS),∴BD=AP=2x,易得BP=2BD,∴6-2x=4x,解得x=1.∴点 P需移动1s.
15. 【解析】∵ 四边形 ABCD 是正方形,∴ AD=CD,∵ AF⊥DE,CG⊥DE,∴ ∠AFD = ∠DGC =90°,∵ ∠CDG+∠ADF = 90°, ∠CDG+∠DCG =90°,∴ ∠ADF=∠DCG,∴ △DAF≌△CDG,∴ DF=CG=4,由勾股定理得AF=3,∵ ∠DAF+∠FAE=∠FAE+∠FEA=90°,∴ ∠DAF=∠AEF,∴ △DAF∽ 即 AF = DF · EF,∴ EF =
16. 解:(
【解法提示】如解图①,过点 E 作 EM⊥CB,交 CB 的延长线于点 M,由旋转得 AD=DE,∠ADE=90°,∴∠ADC+∠EDM=90°,∵ ∠ACB = 90°,∴ ∠ACD =∠DME, ∠ADC + ∠CAD = 90°, ∴ ∠CAD =∠EDM,∴△ACD≌△DME(AAS),∴CD=EM,AC=DM,∵AC=BC,∴BM=DM-BD=AC-BD=BC-BD=CD,∴BM=EM,∵EM⊥CB,∴BE= EM= CD.
(2)补全图形如解图②,
证明:如解图②,过点 E作EF⊥BC于点 F,
∴ ∠DFE=∠BFE=∠ACD=90°,
由旋转的性质得∠ADE=90°,DE=DA,
∴∠DAC+∠ADC=∠EDF+∠ADC=90°,
∴∠EDF=∠DAC,
∴△DEF≌△ADC(AAS),
∴EF=CD,DF=AC=BC,
∴DF-CF=BC-CF,
∴CD=BF,
∴EF=BF,
∴△BEF为等腰直角三角形,
【解法提示】①当点 D 在 BC 延长线上时,如解图③,过点 E 作 EF⊥CD 于点 F,由(2)知△DEF≌△ADC,∴CD=EF,AC=DF=BC,∵AC=BC=1,CD=2,∴DF=AC=1,EF=CD=2,∴CF=CD-DF=1,在Rt△EFC中 ②当点 D 在 CB 延长线上时,如解图④,过点 E 作 EF⊥CB 交 CB 延长线于点 F,由(2)知△DEF≌△ADC,∴ DF=AC=1,EF=CD=2,在 Rt△EFC中,∵ CF = CD+DF = 3,EF = 2,∴ CE =
17. A 【解析】∵( △C'O'D'≌△COD(SSS).
18. D 【解析】∵AB=AC,∴∠B=∠C,易证得△ABE≌△ACD,∴AE=AD,在△ABD和△ABE中,∠B=∠B,AB=AB,AD=AE,∠BAD≠∠BAE;在△ACE和△ACD中,∠C=∠C,AC=AC,AE=AD,∠CAE≠∠CAD;在△ABD 和△ACD 中,∠B =∠C,AB=AC,AD=AD,∠BAD≠∠CAD;在△ACE 和△ABE 中,∠B=∠C,AE=AE,AC=AB,∠CAE≠∠BAE.综上所述,共有4对“伪全等三角形”.
19. 100° 【解析】∵ △ABC≌△CDE,∠ACB=45°,∴∠CED=∠ACB=45°,∴ ∠DCE=180°-∠D-∠CED=100°.
20. 3 【解析】∵ CD=CA,DE∥CB,CF=1,∴ CF 是△ADE的中位线,∴DE=CD=AC=2CF=2,∴AD=AC+DC=4.∵ DE∥CB,∴ ∠CFA=∠E,∠ACB =∠D,∵∠CAB=∠CFA,∴∠CAB=∠E,∴ △CAB≌△DEA(ASA),∴BC=AD=4,∴BF=BC-CF=3.
21.解:如解图,过点 C作 CH⊥BA交 BA的延长线于点H,过点A作AG⊥CD 于点 G,过点 B作BK⊥CD 于点K,且AB∥CD,
∴四边形AHCG,ABKG都是矩形,
∴GK=AB=100,CG=AH,CH=AG=BK,CH∥AG∥BK,
∵由题意可得:∠CAG=∠DBK=18.17°,∠GAD=∠CBK=21.34°,
∴ ∠ACH = ∠CAG = 18. 17°, ∠BCH = ∠CBK =21.34°,
∵∠AGC=∠BKD=90°,
∴△AGC≌△BKD,
∴CG=DK,
设AH=x,CH=y,
即 x=0.33y,
即x+100
=0.39y,
∴0.33y+100=0.39y,
∴CG=DK=550,
∴ CD=550×2+100=1200(m),
∴长江口的宽度CD约为1 200 m.
解题技巧
通过构造辅助线,在直角三角形中,利用锐角三角函数知识,结合已知数据,得到线段的等量关系式,进而求解.
同课章节目录
