第十五讲 相似三角形及其实际应用(含解析) 2025年中考数学基础知识分点练
文档属性
| 名称 | 第十五讲 相似三角形及其实际应用(含解析) 2025年中考数学基础知识分点练 |  | |
| 格式 | docx | ||
| 文件大小 | 235.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 18:01:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十五讲 相似三角形及其实际应用
命题点1 相似三角形的基本性质(37考)
1. (2024内江)已知△ABC与△DEF相似,且相似比为1:3,则 与 的周长之比是 ( )
A. 1:1 B. 1:3 C. 1:6 D. 1:9
2. (2023 重庆 B卷)如图,已知 若AB的长度为6,则DE的长度为 ( )
A. 4 B. 9 C. 12 D. 13.5
命题点2 相似三角形的判定与性质重难
类型一 A 字型(243考)
3. (2024湖南省卷)如图,在△ABC中,点D,E分别为边AB,AC的中点.下列结论中,错误的是 ( )
A. DE∥BC B. △ADE∽△ABC
C. BC=2DE
4. (2023恩施州)如图,在△ABC中,DE∥BC分别交AC,AB 于点D,E,EF∥AC交BC于点F, 则 DE 的长为 ( )
C. 2 D. 3
5. (2023南充)如图,在Rt△ABC中,. 以点A为圆心,适当长为半径画弧,分别交AC,AB 于点M,N,再分别以M,N为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 P,画射线AP与BC交于点D, 垂足为E,则下列结论错误的是 ( )
A. ∠CAD=∠BAD
C. AD=5
6. 新考法 条件开放(2024滨州)如图,在 中,点D,E分别在边AB,AC上.添加一个条件使 ,则这个条件可以是 .(写出一种情况即可)
7. (2023成都)如图,在 中,D是边AB上一点,按以下步骤作图:①以点A为圆心,以适当长为半径作弧,分别交AB,AC于点 M,N;②以点D 为圆心,以AM长为半径作弧,交DB 于点 ③以点 为圆心,以MN长为半径作弧,在 内部交前面的弧于点N';④过点 N'作射线 DN'交 BC 于点 E.若. 与四边形ACED的面积比为4:21,则 的值为 .
8. (2024河北)如图, 的面积为2,AD为BC边上的中线,点A, 是线段( 的五等分点,点A, 是线段 的四等分点,点A 是线段 的中点.
的面积为 ;
的面积为 .
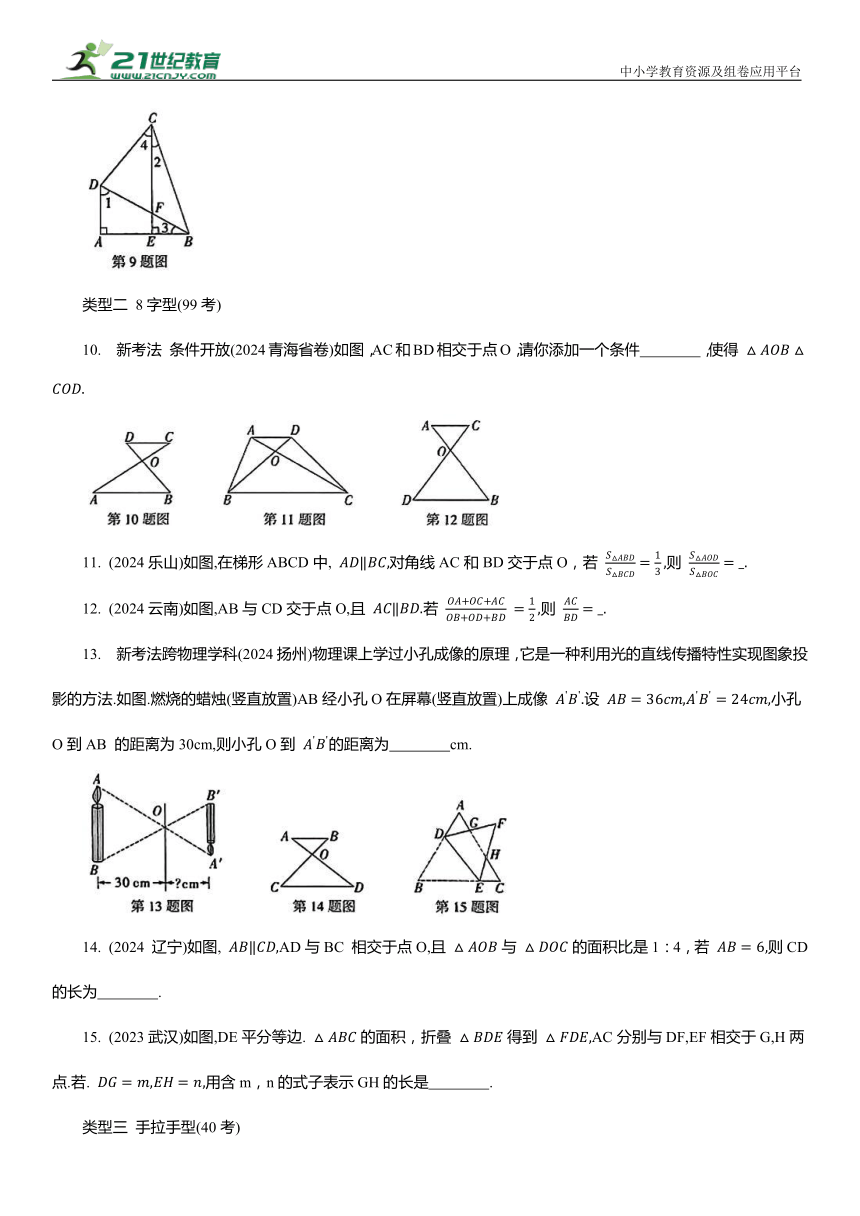
9. (2024甘孜州)如图,在四边形ABCD中, 连接BD,过点C作 垂足为E,CE交BD于点 F,
(1)求证:
(2)若
①请判断线段BC,BD的数量关系,并证明你的结论;
②若 求EF的长.
类型二 8字型(99考)
10. 新考法 条件开放(2024青海省卷)如图,AC和BD相交于点O,请你添加一个条件 ,使得
11. (2024乐山)如图,在梯形ABCD中, 对角线AC和BD交于点O,若 则
12. (2024云南)如图,AB与CD交于点O,且 若 则
13. 新考法跨物理学科(2024扬州)物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图.燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像 设 小孔O到AB 的距离为30cm,则小孔O到 的距离为 cm.
14. (2024 辽宁)如图, AD与BC 相交于点O,且 与 的面积比是1:4,若 则CD的长为 .
15. (2023武汉)如图,DE平分等边. 的面积,折叠 得到 AC分别与DF,EF相交于G,H两点.若. 用含m,n的式子表示GH的长是 .
类型三 手拉手型(40考)
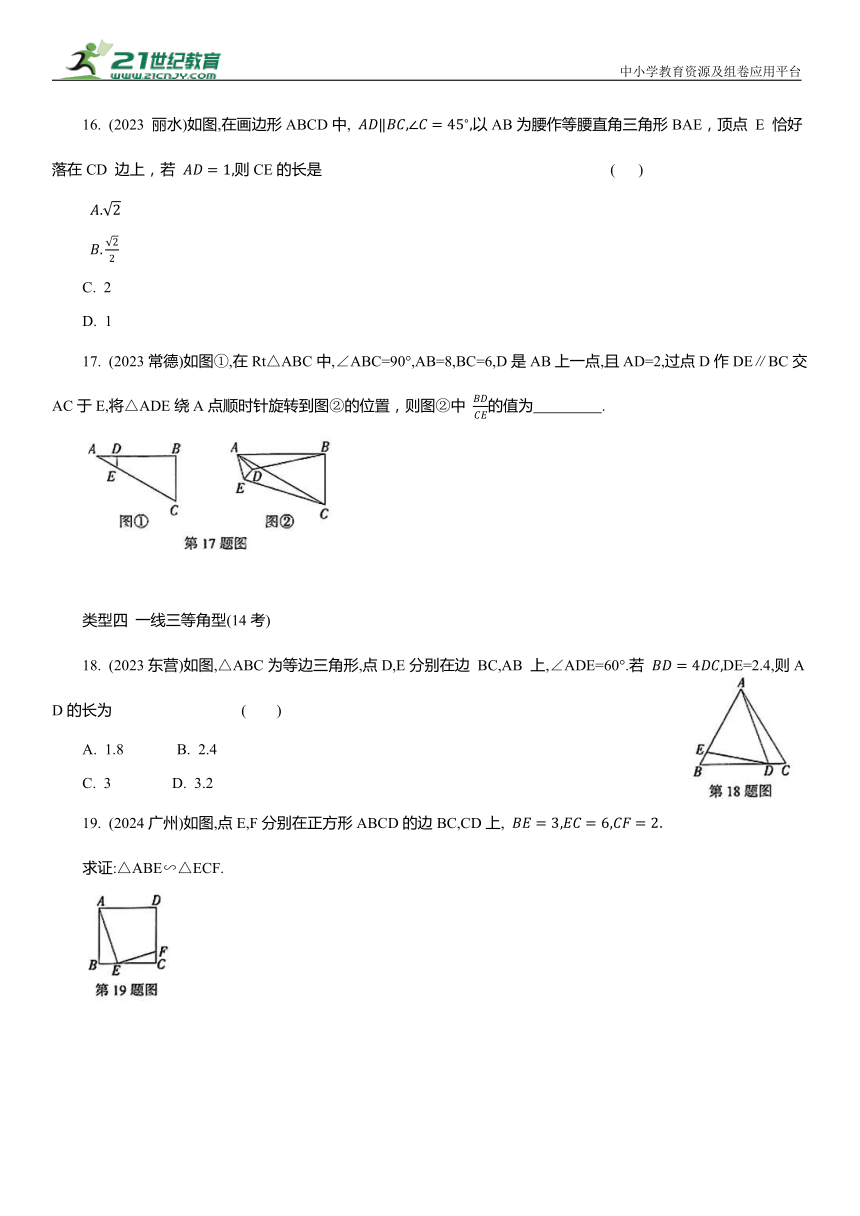
16. (2023 丽水)如图,在画边形ABCD中, 以AB为腰作等腰直角三角形BAE,顶点 E 恰好落在CD 边上,若 则CE的长是 ( )
C. 2
D. 1
17. (2023常德)如图①,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AB上一点,且AD=2,过点D作DE∥BC交AC于E,将△ADE绕A点顺时针旋转到图②的位置,则图②中 的值为 .
类型四 一线三等角型(14考)
18. (2023东营)如图,△ABC为等边三角形,点D,E分别在边 BC,AB 上,∠ADE=60°.若 DE=2.4,则AD的长为 ( )
A. 1.8 B. 2.4
C. 3 D. 3.2
19. (2024广州)如图,点E,F分别在正方形ABCD的边BC,CD上,
求证:△ABE∽△ECF.
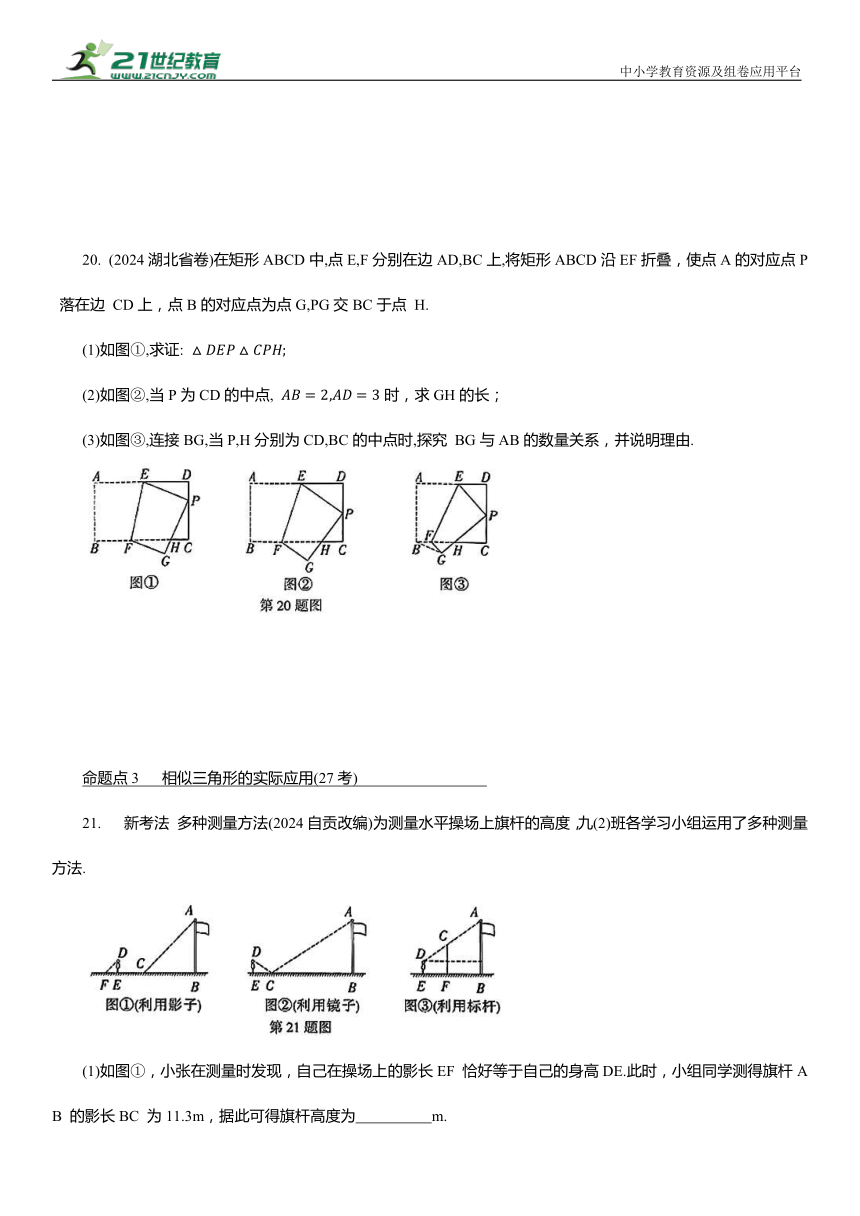
20. (2024湖北省卷)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P 落在边 CD上,点B的对应点为点G,PG交BC于点 H.
(1)如图①,求证:
(2)如图②,当P为CD的中点, 时,求GH的长;
(3)如图③,连接BG,当P,H分别为CD,BC的中点时,探究 BG与AB的数量关系,并说明理由.
命题点3 相似三角形的实际应用(27考)
21. 新考法 多种测量方法(2024自贡改编)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图①,小张在测量时发现,自己在操场上的影长EF 恰好等于自己的身高DE.此时,小组同学测得旗杆AB 的影长BC 为11.3m,据此可得旗杆高度为 m.
(2)如图②,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度 小李到镜面距离 ,镜面到旗杆的距离 16m.求旗杆高度.
(3)小王所在小组采用图③的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高.研学旅行时,他们利用自制工具,成功测量了某广场雕塑的高度.方法如下:
如图④,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图⑤,在支架上端P处,用细线系小重物Q,标高线PQ 始终垂直于水平地面.
如图⑥,在某广场上E 点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高 将观测点D后移24m到 处,采用同样方法,测得( 求雕塑高度(结果精确到1m).
22. 新考法 数学文化(2024连云港)图①是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图②,正八边形游乐城 的边长为 南门O设立在 边的正中央,游乐城南侧有一条东西走向的道路BM, 在BM上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路BC,C处有一座雕塑.在 处测得雕塑在北偏东 方向上,在 处测得雕塑在北偏东 方向上.
(2)求点 到道路BC的距离;
(3)若该小组成员小李出南门O后沿道路MB向东行走、求她离B处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响 (结果精确到0.1km,参考数据:
第十五讲 相似三角形及其实际应用
1. B 【解析】∵ △ABC 与△DEF 相似,且相似比为1:3,∴△ABC与△DEF的周长比为1:3.
2. B 【解析】∵ △ABC∽△EDC,∴AB:DE=AC:EC=2:3,∵AB=6,∴DE=9.
3. D 【解析】∵点 D,E 分别为边 AB,AC 的中点,∴DE∥BC,BC=2DE,故 A,C 选项正确;∵DE∥BC,∴△ADE∽ △ABC, 故 B 选 项正确; ∵ △ADE ∽ 故D选项错误.
4. A 【解析】∵DE∥BC,EF∥AC,∴∠B=∠AED,∠BEF
5. C 【解析】由作图知,AD 是∠CAB 的平分线,∴∠CAD=∠BAD,故A 正确;∵∠C=90°,DE⊥AB,AD平分∠CAB,∴ CD=DE,故 B 正确;∵ AC=6,AB =10,∴在 Rt△ABC中,由勾股定理得BC=8,∵∠B= 又∵ 故C错误,D正确.
6. ∠ADE=∠C(答案不唯一,合理即可) 【解析】∵∠DAE = ∠CAB,∴ 当 ∠ADE = ∠C 时, △ADE ∽△ACB;当∠AED=∠B时,△ADE∽△ACB;当 时,△ADE∽△ACB(答案不唯一,合理即可).
易错点拨
通过添加条件使得△ADE∽△ACB,一定要考虑到,相似符号已经明确给出,说明相似的对应关系已经确定,此时只需找出对应关系,添加条件即可.
7. 【解析】由作图知∠BDE=∠A,∴ DE∥AC,∴△BDE∽△BAC,∵△BDE与四边形ACED 的面积比为4:21,.
8. (1)1;(2)7 【解析】(1)由题意得,AC=AC ,AD=AD ,∠DAC=∠D AC ,∴△DAC≌△D AC ,∴S△D AC (2)如解图,连接D B ,C D ,同理可得 3-8=7.
9. (1)证明:∵CE⊥AB,
∴∠CEB=90°=∠A,
∴∠1+∠3=90°,∠2+∠ABC=90°,
∵∠1=∠ABC,
∴∠2=∠3;
(2)解:①BC=BD,理由如下:
设∠2=∠3=x,
∵∠4=45°,
∴∠BCD=∠CDB,
∴BC=BD;
②∵BD=BC=13,AD=5,
∵BC=BD,∠A=∠CEB,∠2=∠3,
∴△ADB≌△EBC(AAS),
∴BE=AD=5,
∵∠A=∠CEB,∠3=∠3,
∴△EFB∽△ADB,
10. AB∥CD(答案不唯一)
11. 解题思路
分析得△ABD 和△BCD 不同底但等高,可将 转化为 由AD∥BC,得到△ADO∽△CBO,结合相似三角形的性质求解即可.
【解析】∵AD∥BC,∴△ADO∽△CBO,记AD,BC之间的距离为
易错点拨
若高相等,三角形相似,则面积之比等于底边之比;若只有三角形相似,则面积之比等于底边之比的平方.
12. 【解析】∵AC∥BD,∴△AOC∽△BOD,∴ACBD=
13. 20 【解析】由题意可知,△OAB∽△OA'B',相似比为36:24=3:2,由相似三角形的性质知“O到AB的距离”与“O到A'B'的距离”的比等于相似比,设“O到A'B'的距离”为 xcm,则30:x=3:2,解得x=20.
解题技巧
本题为跨物理学科试题,明确小孔成像前后所形成的两个三角形相似,即△OAB∽△OA'B',结合相似三角形的性质求解即可.
14. 12 【解析】∵AB∥CD,∴△AOB∽△DOC,∵△AOB与△DOC的面积比为1:4, CD=2AB=12.
【解析】∵ △ABC是等边三角形,∴∠A=∠B=∠C,∵折叠△BDE 得到△FDE,∴ △BDE≌△FDE,∴S△BDE=S△FDE,∠F=∠B=∠A=∠C,∵DE平分等边△ABC 的面积,∴ 四边形ACED 的面积= ∠FGH, ∠CHE = ∠FHG, ∴ △ADG ∽ △FHG, 解得 或 GH = (舍去),∴GH的长为
16. A 【解析】如解图,连接 BD,∵ AD∥BC,∠C=45°,∴ ∠ADE = 135°,∵ △ABE 为等腰直角三角形,∴∠ABE=45°,∴∠ABE+∠ADE=180°,∴ 四边形ABED 是圆的内接四边形,∵ ∠BEC+∠BED=180°,∠BAD+∠BED=180°,∴ ∠BAD =∠BEC,∵∠ADB = ∠AEB = 45°, ∠C = 45°, ∴ ∠ADB = 即
17. 【解析】题图①中,∵ AB=8,AD=2,BC=6,∠ABC=90°,DE∥BC,∴AC=10,AD∥= ,△ADE∽ 题图②中,由旋转的性质可知,∠DAE = ∠BAC,∴ ∠BAD = ∠CAE,∴
18. C 【解析】∵ △ABC 为等边三角形,∴∠B=∠C=60°,∵∠ADB=∠ADE+∠BDE=∠C+∠DAC,∠ADE=60°,∴∠BDE=∠DAC,∴△ADC∽△DEB,∴ADDE=
19. 证明:∵BE=3,EC=6,
∴BC=9,
∵四边形ABCD是正方形,
∴AB=BC=9,∠B=∠C=90°,
又∵∠B=∠C=90°,
∴ △ABE∽△ECF.
20. (1)
解题思路
根据矩形的性质得∠A=∠D=∠C=90°,由折叠得出∠EPH = ∠A =90°,得出∠DEP =∠CPG,证明△DEP∽△CPH.
证明:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠DPE+∠DEP=90°,
∵∠EPH=∠A=90°,
∴∠DPE+∠CPG=90°,
∴∠DEP=∠CPG,
∴△DEP∽△CPH;
(2)
解题思路
根据矩形的性质以及线段中点,得出DP=CP=1,根据 得出 再结合△DEP∽△CPH,得出 所以
解:∵四边形ABCD是矩形,
∵P 为CD中点,
设EP=AE=x,
∴ED=AD-AE=3-x,
在 Rt△EDP中,
即 解得
由(1)知△DEP∽△CPH,
艮
解得
∵PG=AB=2,
(3)解: 理由如下:
如解图,延长AB,PG交于点 M,连接AP,
∵点E,F分别在边 AD,BC上,将矩形ABCD 沿EF折叠,使点A的对应点 P落在边 CD上,点B 的对应点为G,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴ ∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠C=90°,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
在Rt△PCH 中,
在 Rt△APD中,
∵BG∥AP,
∴△BMG∽△AMP,
解题技巧
由折叠性质得AP⊥EF,BG⊥直线 EF,BG∥AP,∠BAP=∠GPA,△MAP 是等腰三角形,则 MA =MP,∵P为CD中点,H为 BC 中点,∴设 DP=CP=y,BH=CH,∴△MBH≌△PCH(ASA),则 BM=CP, 证明△BMG∽△AMP,则 即可求得BG与AB的数量关系.
21. 审题指导
题干(1):小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE;
信息提取:操场上的影长属于太阳光下的投影,属于平行投影,故△ABC∽△DEF,进而得到旗杆高度等于旗杆的影长;
题干(2):小李站在操场上 E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A;
信息提取:由镜面反射的入射角等于反射角可推出∠DCE=∠ACB,∠ABC=∠DEC=90°.
解:(1)11.3;
【解法提示】由题意得 11. 3m.
(2)如题图②,由题意得DE=1.5m,EC=2m,CB=16m,
根据镜面反射,可知∠ACB=∠DCE,
∵AB⊥BE,DE⊥BE,
∴∠ABC=∠DEC=90°,
∴△ACB∽△DCE,
即
∴AB=12,
∴旗杆高度为12m;
解题技巧
解决由平面镜测高问题的关键是应用入射角等于反射角的原理,即∠ACB = ∠DCE,再由∠ABC =∠DEC,证明△ACB∽△DCE,从而得出线段间的比例关系求解.
(3)
解题思路
分析题干得△DGC∽△DBA,△D'G'C'∽△D'BA 两组相似关系,在已知条件不足的情况下可设所需线段长为 xm,由两组相似比例关系联立方程求解即可.
设BG= xm,
由题意得△DGC∽△DBA,△D'G'C'∽△D'BA,
即
整理得,3.6(1.5+x)=1.8(25.5+x),
解得x=22.5,经检验符合题意,
∴AB=1.8×(1.5+22.5)÷1.5=28.8≈29(m),
∴雕塑高度约为29 m.
22. 解:(1)90,76;
【解法提示】∵正八边形的一个外角的度数为
(2)如解图,过点A 作A D⊥BC于点 D.
在 Rt△CA A 中,
在 Rt△CA D中,.
答:点A 到道路BC的距离约为2.0千米;
解题技巧
求点 A 到 BC 的距离即为求 A D 的长,Rt△CA D中,先利用 Rt△CA A 中锐角三角函数值求出A C的长,从而求得A D的长.
(3)
审题指导
题干:小李出南门O后沿道路MB 向东行走,求她离B处不超过多少千米时,才能确保观察雕塑不会受到游乐城的影响
提取信息:小李出南门O的位置,点A ,点C在一条直线上,此时小李的位置即为小李观察雕塑C不会受到游乐城的影响的临界位置.
解题思路
确保观察不受到游乐城的影响,即可理解为小李的视线不会被游乐城遮挡,即连接CA 并延长交道路BM 于点 E,把题干转化为求 EB 长,先求出 BC 的长,过点 A 作 A F⊥BC 于点 F,再通过证明△CA F∽△CEB,利用相似比求解即可.
如解图,连接CA 并延长交BM 于点 E,延长A A 交BE于点 G,过点A 作A F⊥BC于点 F.
∵正八边形的外角均为45°,
∴在 Rt△A A G中,
又∵
∴EB≈2. 4km.
答:小李离B处不超过2.4km,才能确保观察雕塑不会受到游乐城的影响.
第十五讲 相似三角形及其实际应用
命题点1 相似三角形的基本性质(37考)
1. (2024内江)已知△ABC与△DEF相似,且相似比为1:3,则 与 的周长之比是 ( )
A. 1:1 B. 1:3 C. 1:6 D. 1:9
2. (2023 重庆 B卷)如图,已知 若AB的长度为6,则DE的长度为 ( )
A. 4 B. 9 C. 12 D. 13.5
命题点2 相似三角形的判定与性质重难
类型一 A 字型(243考)
3. (2024湖南省卷)如图,在△ABC中,点D,E分别为边AB,AC的中点.下列结论中,错误的是 ( )
A. DE∥BC B. △ADE∽△ABC
C. BC=2DE
4. (2023恩施州)如图,在△ABC中,DE∥BC分别交AC,AB 于点D,E,EF∥AC交BC于点F, 则 DE 的长为 ( )
C. 2 D. 3
5. (2023南充)如图,在Rt△ABC中,. 以点A为圆心,适当长为半径画弧,分别交AC,AB 于点M,N,再分别以M,N为圆心,大于 的长为半径画弧,两弧在 的内部相交于点 P,画射线AP与BC交于点D, 垂足为E,则下列结论错误的是 ( )
A. ∠CAD=∠BAD
C. AD=5
6. 新考法 条件开放(2024滨州)如图,在 中,点D,E分别在边AB,AC上.添加一个条件使 ,则这个条件可以是 .(写出一种情况即可)
7. (2023成都)如图,在 中,D是边AB上一点,按以下步骤作图:①以点A为圆心,以适当长为半径作弧,分别交AB,AC于点 M,N;②以点D 为圆心,以AM长为半径作弧,交DB 于点 ③以点 为圆心,以MN长为半径作弧,在 内部交前面的弧于点N';④过点 N'作射线 DN'交 BC 于点 E.若. 与四边形ACED的面积比为4:21,则 的值为 .
8. (2024河北)如图, 的面积为2,AD为BC边上的中线,点A, 是线段( 的五等分点,点A, 是线段 的四等分点,点A 是线段 的中点.
的面积为 ;
的面积为 .
9. (2024甘孜州)如图,在四边形ABCD中, 连接BD,过点C作 垂足为E,CE交BD于点 F,
(1)求证:
(2)若
①请判断线段BC,BD的数量关系,并证明你的结论;
②若 求EF的长.
类型二 8字型(99考)
10. 新考法 条件开放(2024青海省卷)如图,AC和BD相交于点O,请你添加一个条件 ,使得
11. (2024乐山)如图,在梯形ABCD中, 对角线AC和BD交于点O,若 则
12. (2024云南)如图,AB与CD交于点O,且 若 则
13. 新考法跨物理学科(2024扬州)物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图.燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像 设 小孔O到AB 的距离为30cm,则小孔O到 的距离为 cm.
14. (2024 辽宁)如图, AD与BC 相交于点O,且 与 的面积比是1:4,若 则CD的长为 .
15. (2023武汉)如图,DE平分等边. 的面积,折叠 得到 AC分别与DF,EF相交于G,H两点.若. 用含m,n的式子表示GH的长是 .
类型三 手拉手型(40考)
16. (2023 丽水)如图,在画边形ABCD中, 以AB为腰作等腰直角三角形BAE,顶点 E 恰好落在CD 边上,若 则CE的长是 ( )
C. 2
D. 1
17. (2023常德)如图①,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AB上一点,且AD=2,过点D作DE∥BC交AC于E,将△ADE绕A点顺时针旋转到图②的位置,则图②中 的值为 .
类型四 一线三等角型(14考)
18. (2023东营)如图,△ABC为等边三角形,点D,E分别在边 BC,AB 上,∠ADE=60°.若 DE=2.4,则AD的长为 ( )
A. 1.8 B. 2.4
C. 3 D. 3.2
19. (2024广州)如图,点E,F分别在正方形ABCD的边BC,CD上,
求证:△ABE∽△ECF.
20. (2024湖北省卷)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P 落在边 CD上,点B的对应点为点G,PG交BC于点 H.
(1)如图①,求证:
(2)如图②,当P为CD的中点, 时,求GH的长;
(3)如图③,连接BG,当P,H分别为CD,BC的中点时,探究 BG与AB的数量关系,并说明理由.
命题点3 相似三角形的实际应用(27考)
21. 新考法 多种测量方法(2024自贡改编)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图①,小张在测量时发现,自己在操场上的影长EF 恰好等于自己的身高DE.此时,小组同学测得旗杆AB 的影长BC 为11.3m,据此可得旗杆高度为 m.
(2)如图②,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度 小李到镜面距离 ,镜面到旗杆的距离 16m.求旗杆高度.
(3)小王所在小组采用图③的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高.研学旅行时,他们利用自制工具,成功测量了某广场雕塑的高度.方法如下:
如图④,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图⑤,在支架上端P处,用细线系小重物Q,标高线PQ 始终垂直于水平地面.
如图⑥,在某广场上E 点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高 将观测点D后移24m到 处,采用同样方法,测得( 求雕塑高度(结果精确到1m).
22. 新考法 数学文化(2024连云港)图①是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图②,正八边形游乐城 的边长为 南门O设立在 边的正中央,游乐城南侧有一条东西走向的道路BM, 在BM上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路BC,C处有一座雕塑.在 处测得雕塑在北偏东 方向上,在 处测得雕塑在北偏东 方向上.
(2)求点 到道路BC的距离;
(3)若该小组成员小李出南门O后沿道路MB向东行走、求她离B处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响 (结果精确到0.1km,参考数据:
第十五讲 相似三角形及其实际应用
1. B 【解析】∵ △ABC 与△DEF 相似,且相似比为1:3,∴△ABC与△DEF的周长比为1:3.
2. B 【解析】∵ △ABC∽△EDC,∴AB:DE=AC:EC=2:3,∵AB=6,∴DE=9.
3. D 【解析】∵点 D,E 分别为边 AB,AC 的中点,∴DE∥BC,BC=2DE,故 A,C 选项正确;∵DE∥BC,∴△ADE∽ △ABC, 故 B 选 项正确; ∵ △ADE ∽ 故D选项错误.
4. A 【解析】∵DE∥BC,EF∥AC,∴∠B=∠AED,∠BEF
5. C 【解析】由作图知,AD 是∠CAB 的平分线,∴∠CAD=∠BAD,故A 正确;∵∠C=90°,DE⊥AB,AD平分∠CAB,∴ CD=DE,故 B 正确;∵ AC=6,AB =10,∴在 Rt△ABC中,由勾股定理得BC=8,∵∠B= 又∵ 故C错误,D正确.
6. ∠ADE=∠C(答案不唯一,合理即可) 【解析】∵∠DAE = ∠CAB,∴ 当 ∠ADE = ∠C 时, △ADE ∽△ACB;当∠AED=∠B时,△ADE∽△ACB;当 时,△ADE∽△ACB(答案不唯一,合理即可).
易错点拨
通过添加条件使得△ADE∽△ACB,一定要考虑到,相似符号已经明确给出,说明相似的对应关系已经确定,此时只需找出对应关系,添加条件即可.
7. 【解析】由作图知∠BDE=∠A,∴ DE∥AC,∴△BDE∽△BAC,∵△BDE与四边形ACED 的面积比为4:21,.
8. (1)1;(2)7 【解析】(1)由题意得,AC=AC ,AD=AD ,∠DAC=∠D AC ,∴△DAC≌△D AC ,∴S△D AC (2)如解图,连接D B ,C D ,同理可得 3-8=7.
9. (1)证明:∵CE⊥AB,
∴∠CEB=90°=∠A,
∴∠1+∠3=90°,∠2+∠ABC=90°,
∵∠1=∠ABC,
∴∠2=∠3;
(2)解:①BC=BD,理由如下:
设∠2=∠3=x,
∵∠4=45°,
∴∠BCD=∠CDB,
∴BC=BD;
②∵BD=BC=13,AD=5,
∵BC=BD,∠A=∠CEB,∠2=∠3,
∴△ADB≌△EBC(AAS),
∴BE=AD=5,
∵∠A=∠CEB,∠3=∠3,
∴△EFB∽△ADB,
10. AB∥CD(答案不唯一)
11. 解题思路
分析得△ABD 和△BCD 不同底但等高,可将 转化为 由AD∥BC,得到△ADO∽△CBO,结合相似三角形的性质求解即可.
【解析】∵AD∥BC,∴△ADO∽△CBO,记AD,BC之间的距离为
易错点拨
若高相等,三角形相似,则面积之比等于底边之比;若只有三角形相似,则面积之比等于底边之比的平方.
12. 【解析】∵AC∥BD,∴△AOC∽△BOD,∴ACBD=
13. 20 【解析】由题意可知,△OAB∽△OA'B',相似比为36:24=3:2,由相似三角形的性质知“O到AB的距离”与“O到A'B'的距离”的比等于相似比,设“O到A'B'的距离”为 xcm,则30:x=3:2,解得x=20.
解题技巧
本题为跨物理学科试题,明确小孔成像前后所形成的两个三角形相似,即△OAB∽△OA'B',结合相似三角形的性质求解即可.
14. 12 【解析】∵AB∥CD,∴△AOB∽△DOC,∵△AOB与△DOC的面积比为1:4, CD=2AB=12.
【解析】∵ △ABC是等边三角形,∴∠A=∠B=∠C,∵折叠△BDE 得到△FDE,∴ △BDE≌△FDE,∴S△BDE=S△FDE,∠F=∠B=∠A=∠C,∵DE平分等边△ABC 的面积,∴ 四边形ACED 的面积= ∠FGH, ∠CHE = ∠FHG, ∴ △ADG ∽ △FHG, 解得 或 GH = (舍去),∴GH的长为
16. A 【解析】如解图,连接 BD,∵ AD∥BC,∠C=45°,∴ ∠ADE = 135°,∵ △ABE 为等腰直角三角形,∴∠ABE=45°,∴∠ABE+∠ADE=180°,∴ 四边形ABED 是圆的内接四边形,∵ ∠BEC+∠BED=180°,∠BAD+∠BED=180°,∴ ∠BAD =∠BEC,∵∠ADB = ∠AEB = 45°, ∠C = 45°, ∴ ∠ADB = 即
17. 【解析】题图①中,∵ AB=8,AD=2,BC=6,∠ABC=90°,DE∥BC,∴AC=10,AD∥= ,△ADE∽ 题图②中,由旋转的性质可知,∠DAE = ∠BAC,∴ ∠BAD = ∠CAE,∴
18. C 【解析】∵ △ABC 为等边三角形,∴∠B=∠C=60°,∵∠ADB=∠ADE+∠BDE=∠C+∠DAC,∠ADE=60°,∴∠BDE=∠DAC,∴△ADC∽△DEB,∴ADDE=
19. 证明:∵BE=3,EC=6,
∴BC=9,
∵四边形ABCD是正方形,
∴AB=BC=9,∠B=∠C=90°,
又∵∠B=∠C=90°,
∴ △ABE∽△ECF.
20. (1)
解题思路
根据矩形的性质得∠A=∠D=∠C=90°,由折叠得出∠EPH = ∠A =90°,得出∠DEP =∠CPG,证明△DEP∽△CPH.
证明:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠DPE+∠DEP=90°,
∵∠EPH=∠A=90°,
∴∠DPE+∠CPG=90°,
∴∠DEP=∠CPG,
∴△DEP∽△CPH;
(2)
解题思路
根据矩形的性质以及线段中点,得出DP=CP=1,根据 得出 再结合△DEP∽△CPH,得出 所以
解:∵四边形ABCD是矩形,
∵P 为CD中点,
设EP=AE=x,
∴ED=AD-AE=3-x,
在 Rt△EDP中,
即 解得
由(1)知△DEP∽△CPH,
艮
解得
∵PG=AB=2,
(3)解: 理由如下:
如解图,延长AB,PG交于点 M,连接AP,
∵点E,F分别在边 AD,BC上,将矩形ABCD 沿EF折叠,使点A的对应点 P落在边 CD上,点B 的对应点为G,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴ ∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠C=90°,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
在Rt△PCH 中,
在 Rt△APD中,
∵BG∥AP,
∴△BMG∽△AMP,
解题技巧
由折叠性质得AP⊥EF,BG⊥直线 EF,BG∥AP,∠BAP=∠GPA,△MAP 是等腰三角形,则 MA =MP,∵P为CD中点,H为 BC 中点,∴设 DP=CP=y,BH=CH,∴△MBH≌△PCH(ASA),则 BM=CP, 证明△BMG∽△AMP,则 即可求得BG与AB的数量关系.
21. 审题指导
题干(1):小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE;
信息提取:操场上的影长属于太阳光下的投影,属于平行投影,故△ABC∽△DEF,进而得到旗杆高度等于旗杆的影长;
题干(2):小李站在操场上 E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A;
信息提取:由镜面反射的入射角等于反射角可推出∠DCE=∠ACB,∠ABC=∠DEC=90°.
解:(1)11.3;
【解法提示】由题意得 11. 3m.
(2)如题图②,由题意得DE=1.5m,EC=2m,CB=16m,
根据镜面反射,可知∠ACB=∠DCE,
∵AB⊥BE,DE⊥BE,
∴∠ABC=∠DEC=90°,
∴△ACB∽△DCE,
即
∴AB=12,
∴旗杆高度为12m;
解题技巧
解决由平面镜测高问题的关键是应用入射角等于反射角的原理,即∠ACB = ∠DCE,再由∠ABC =∠DEC,证明△ACB∽△DCE,从而得出线段间的比例关系求解.
(3)
解题思路
分析题干得△DGC∽△DBA,△D'G'C'∽△D'BA 两组相似关系,在已知条件不足的情况下可设所需线段长为 xm,由两组相似比例关系联立方程求解即可.
设BG= xm,
由题意得△DGC∽△DBA,△D'G'C'∽△D'BA,
即
整理得,3.6(1.5+x)=1.8(25.5+x),
解得x=22.5,经检验符合题意,
∴AB=1.8×(1.5+22.5)÷1.5=28.8≈29(m),
∴雕塑高度约为29 m.
22. 解:(1)90,76;
【解法提示】∵正八边形的一个外角的度数为
(2)如解图,过点A 作A D⊥BC于点 D.
在 Rt△CA A 中,
在 Rt△CA D中,.
答:点A 到道路BC的距离约为2.0千米;
解题技巧
求点 A 到 BC 的距离即为求 A D 的长,Rt△CA D中,先利用 Rt△CA A 中锐角三角函数值求出A C的长,从而求得A D的长.
(3)
审题指导
题干:小李出南门O后沿道路MB 向东行走,求她离B处不超过多少千米时,才能确保观察雕塑不会受到游乐城的影响
提取信息:小李出南门O的位置,点A ,点C在一条直线上,此时小李的位置即为小李观察雕塑C不会受到游乐城的影响的临界位置.
解题思路
确保观察不受到游乐城的影响,即可理解为小李的视线不会被游乐城遮挡,即连接CA 并延长交道路BM 于点 E,把题干转化为求 EB 长,先求出 BC 的长,过点 A 作 A F⊥BC 于点 F,再通过证明△CA F∽△CEB,利用相似比求解即可.
如解图,连接CA 并延长交BM 于点 E,延长A A 交BE于点 G,过点A 作A F⊥BC于点 F.
∵正八边形的外角均为45°,
∴在 Rt△A A G中,
又∵
∴EB≈2. 4km.
答:小李离B处不超过2.4km,才能确保观察雕塑不会受到游乐城的影响.
同课章节目录
