第二讲 整式及其运算(含解析) 2025年中考数学基础知识分点练
文档属性
| 名称 | 第二讲 整式及其运算(含解析) 2025年中考数学基础知识分点练 |  | |
| 格式 | docx | ||
| 文件大小 | 89.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 18:11:17 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二讲 整式及其运算
命题点1 列代数式及代数式求值(86考)
1. (2024广安)下列对代数式-3x的意义表述正确的是 ( )
A. - 3与x的和 B. -3与x的差
C. - 3与x的积 D. - 3与x的商
2. (2024包头)若m,n互为倒数,且满足m+ mn=3,则n的值为 ( )
A. B. C.2 D.4
3. 新考法 传统文化(57考)(2024甘肃省卷)如图①,“燕几”即宴几,是世界上最早的一套组合桌,由北宋进士黄伯思设计.全套“燕几”一共有七张桌子,包括两张长桌、两张中桌和三张小桌,每张桌面的宽都相等.七张桌面分开可组合成不同的图形.如图②给出了《燕几图》中名称为“回文”的桌面拼合方式,若设每张桌面的宽为x尺,长桌的长为y尺,则y与x的关系可以表示为 ( )
A. y=3x B. y=4x C. y=3x+1 D. y=4x+1
4. (2024成都)若m,n为实数,且 则 的值为 .
命题点2 整式的相关概念及运算
类型一 整式的相关概念(14考)
5. (2024广元)如果单项式 与单项式 的和仍是一个单项式,则在平面直角坐标系中点(m,n)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.新考法 结论开放(2024河南)请写出2m 的一个同类项: .
7. (2024泰安)单项式 的次数是 .
类型二 整式的运算(含幂的运算)(641考)
8.(2024烟台)下列计算结果为a 的是 ( )
A. a ·a
9. (2024兰州)计算: ( )
A. a B. - a C. 2a D. - 2a
10. (2024广州)若a≠0,则下列运算正确的是( ).
11.(2024绥化)下列计算中,结果正确的是 ( )
12. (2024河北)若a,b是正整数,且满足则a与b的关系正确的是 ( )
A. a+3=8b B. 3a=8b D. 3a=8+b
13. (2024上海)计算:(a+b)(b-a)= .
14.(2024德阳)若一个多项式加上 结果是 则这个多项式为 .
类型三 乘法公式的应用(9考)
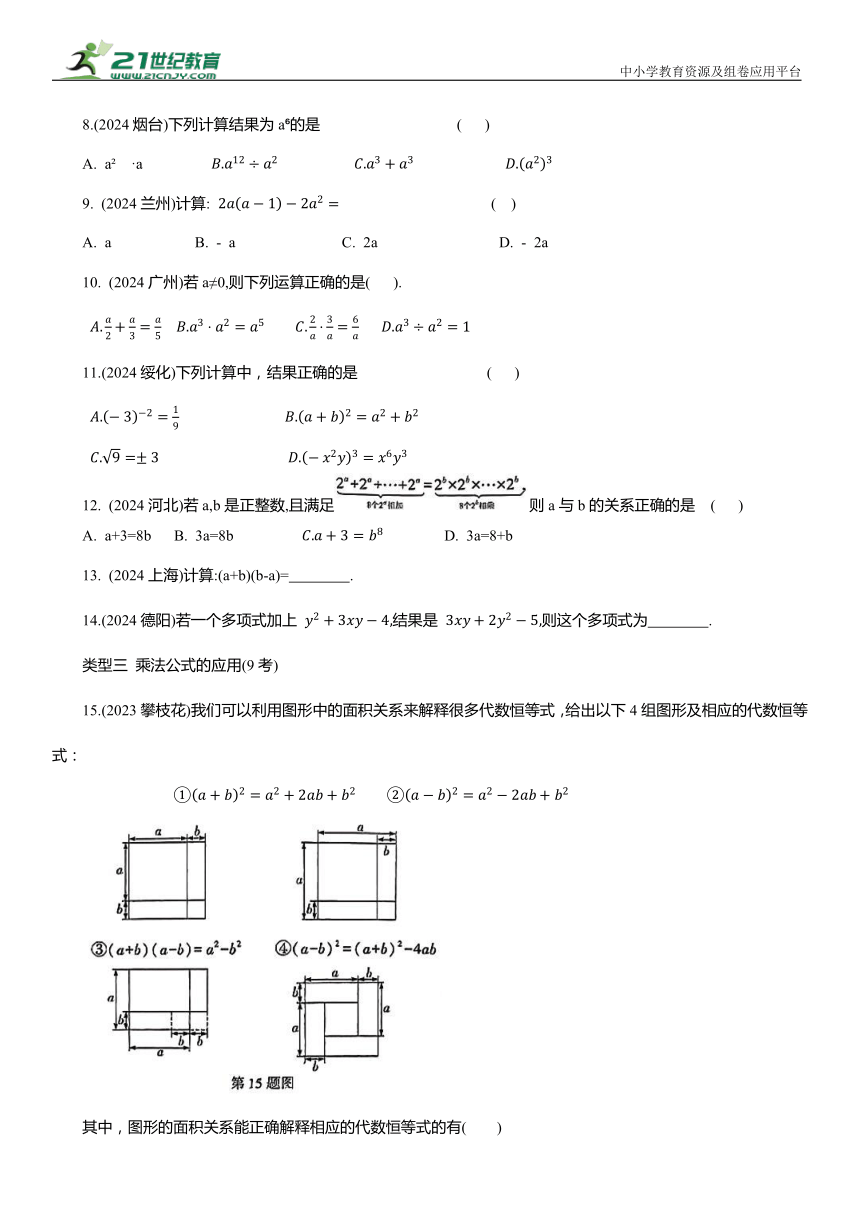
15.(2023攀枝花)我们可以利用图形中的面积关系来解释很多代数恒等式,给出以下4组图形及相应的代数恒等式:
其中,图形的面积关系能正确解释相应的代数恒等式的有( )
A. 1个 B. 2个 C. 3个 D. 4个
类型四 整式的化简及求值(77考)
16. (2024重庆B卷)计算:(
17. (2024赤峰)已知 求代数式 的值.
命题点3 因式分解(146考)
18. (2024陕西)分解因式:
19. (2024甘肃省卷)因式分解:
20. (2024达州)分解因式:
21. (2024威海)因式分解:
命题点4 规律探索题
类型一 数式规律(37考)
22.(2024云南)按一定规律排列的代数式:2x,3x ,4x ,5x ,6x ,…,第n个代数式是 ( )
A. 2x° B. (n-1)x" C. nx'''
23. 新考法 数学文化(98考)(2024扬州)1202年数学家斐波那契在《计算之书》中记载了一列数:1,1,2,3,5, ,这一列数满足:从第三个数开始,每一个数都等于它的前两个数之和.则在这一列数的前2024个数中,奇数的个数为 ( )
A. 676 B. 674 C. 1348 D. 1350
类型二 图形规律(26考)
24. 新考法 跨化学学科(14考)(2024.重庆A卷)烷烃是一类由碳、氢元素组成的有机化合物质,下图是这类物质前四种化合物的分子结构模型图,其中灰球代囊碳原子,白球代表氢原子,第1种如图①有4个氢原子,第2种如图②有6个氢原子,第3种如图③有8个氢原子, 按照这一规律,第10种化合物的分子结构模型中氢原子的个数是 ( )
20 B. 22 C. 24 D. 26
第二讲 整式及其运算
1. C 2. B
3. B 【解析】如解图,两个小桌的宽等于小桌的长,∵小桌的宽为x,∴小桌的长为2x,∵长桌的宽与小桌的宽相等且均为x,∴长桌的长为两个小桌的宽加一个小桌的长,即y=x+x+2x=4x.
4. 1 【解析】 且n-5=0,解得
5. D 6. m(答案不唯一) 7. 3 8. D 9. D
10. B
11. A
12. A 【解析】根据已知得, 即 3=8b.
【解析】
【解析】
15. D 【解析】图形的面积关系能正确解释相应的代数恒等式的有①②③④.
16. 解:原式
=4a-2.
17. 解:原式
当 时,原式
18. a(a-b)
19. 2(x+2)(x-2) 【解析】 (x-2).
20. 3(x-3) 【解析】 3) .
【解析】原式:
22. D 【解析】∵按一定规律排列的代数式:2:2x,3x ,4x ,5x ,6x ,…,∴第n个代数式是(n+1)x".
23. D 【解析】根据“奇数+奇数=偶数”,“奇数+偶数=奇数”,可推断该列数的奇偶性如下:奇,奇,偶,奇,奇,偶,奇,奇,偶,…,∴可发现其奇偶规律为三组一循坏,每个循环里的第一个和第二个数是奇数,第三个数是偶数,∵2024÷3=674……2,∴前2 024个数中奇数的个数为674×2+2=1350.
24. B 【解析】由题图可得,第1种有4个氢原子,即2+2×1=4,第2种有6个氢原子,即2+2×2=6,第3种有8个氢原子,即2+2×3=8,…,∴第10种化合物的分子结构模型中氢原子的个数是2+2×10=22.
类题通法
图形规律探索类解题通法:
首先可将图案标记序号,利用作差法找后一个图案与前一个图案所求图形或元素个数之间的数量关系,若所作差为固定值,则根据固定值可确定每个图案中元素的个数,并进行验证.
第二讲 整式及其运算
命题点1 列代数式及代数式求值(86考)
1. (2024广安)下列对代数式-3x的意义表述正确的是 ( )
A. - 3与x的和 B. -3与x的差
C. - 3与x的积 D. - 3与x的商
2. (2024包头)若m,n互为倒数,且满足m+ mn=3,则n的值为 ( )
A. B. C.2 D.4
3. 新考法 传统文化(57考)(2024甘肃省卷)如图①,“燕几”即宴几,是世界上最早的一套组合桌,由北宋进士黄伯思设计.全套“燕几”一共有七张桌子,包括两张长桌、两张中桌和三张小桌,每张桌面的宽都相等.七张桌面分开可组合成不同的图形.如图②给出了《燕几图》中名称为“回文”的桌面拼合方式,若设每张桌面的宽为x尺,长桌的长为y尺,则y与x的关系可以表示为 ( )
A. y=3x B. y=4x C. y=3x+1 D. y=4x+1
4. (2024成都)若m,n为实数,且 则 的值为 .
命题点2 整式的相关概念及运算
类型一 整式的相关概念(14考)
5. (2024广元)如果单项式 与单项式 的和仍是一个单项式,则在平面直角坐标系中点(m,n)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.新考法 结论开放(2024河南)请写出2m 的一个同类项: .
7. (2024泰安)单项式 的次数是 .
类型二 整式的运算(含幂的运算)(641考)
8.(2024烟台)下列计算结果为a 的是 ( )
A. a ·a
9. (2024兰州)计算: ( )
A. a B. - a C. 2a D. - 2a
10. (2024广州)若a≠0,则下列运算正确的是( ).
11.(2024绥化)下列计算中,结果正确的是 ( )
12. (2024河北)若a,b是正整数,且满足则a与b的关系正确的是 ( )
A. a+3=8b B. 3a=8b D. 3a=8+b
13. (2024上海)计算:(a+b)(b-a)= .
14.(2024德阳)若一个多项式加上 结果是 则这个多项式为 .
类型三 乘法公式的应用(9考)
15.(2023攀枝花)我们可以利用图形中的面积关系来解释很多代数恒等式,给出以下4组图形及相应的代数恒等式:
其中,图形的面积关系能正确解释相应的代数恒等式的有( )
A. 1个 B. 2个 C. 3个 D. 4个
类型四 整式的化简及求值(77考)
16. (2024重庆B卷)计算:(
17. (2024赤峰)已知 求代数式 的值.
命题点3 因式分解(146考)
18. (2024陕西)分解因式:
19. (2024甘肃省卷)因式分解:
20. (2024达州)分解因式:
21. (2024威海)因式分解:
命题点4 规律探索题
类型一 数式规律(37考)
22.(2024云南)按一定规律排列的代数式:2x,3x ,4x ,5x ,6x ,…,第n个代数式是 ( )
A. 2x° B. (n-1)x" C. nx'''
23. 新考法 数学文化(98考)(2024扬州)1202年数学家斐波那契在《计算之书》中记载了一列数:1,1,2,3,5, ,这一列数满足:从第三个数开始,每一个数都等于它的前两个数之和.则在这一列数的前2024个数中,奇数的个数为 ( )
A. 676 B. 674 C. 1348 D. 1350
类型二 图形规律(26考)
24. 新考法 跨化学学科(14考)(2024.重庆A卷)烷烃是一类由碳、氢元素组成的有机化合物质,下图是这类物质前四种化合物的分子结构模型图,其中灰球代囊碳原子,白球代表氢原子,第1种如图①有4个氢原子,第2种如图②有6个氢原子,第3种如图③有8个氢原子, 按照这一规律,第10种化合物的分子结构模型中氢原子的个数是 ( )
20 B. 22 C. 24 D. 26
第二讲 整式及其运算
1. C 2. B
3. B 【解析】如解图,两个小桌的宽等于小桌的长,∵小桌的宽为x,∴小桌的长为2x,∵长桌的宽与小桌的宽相等且均为x,∴长桌的长为两个小桌的宽加一个小桌的长,即y=x+x+2x=4x.
4. 1 【解析】 且n-5=0,解得
5. D 6. m(答案不唯一) 7. 3 8. D 9. D
10. B
11. A
12. A 【解析】根据已知得, 即 3=8b.
【解析】
【解析】
15. D 【解析】图形的面积关系能正确解释相应的代数恒等式的有①②③④.
16. 解:原式
=4a-2.
17. 解:原式
当 时,原式
18. a(a-b)
19. 2(x+2)(x-2) 【解析】 (x-2).
20. 3(x-3) 【解析】 3) .
【解析】原式:
22. D 【解析】∵按一定规律排列的代数式:2:2x,3x ,4x ,5x ,6x ,…,∴第n个代数式是(n+1)x".
23. D 【解析】根据“奇数+奇数=偶数”,“奇数+偶数=奇数”,可推断该列数的奇偶性如下:奇,奇,偶,奇,奇,偶,奇,奇,偶,…,∴可发现其奇偶规律为三组一循坏,每个循环里的第一个和第二个数是奇数,第三个数是偶数,∵2024÷3=674……2,∴前2 024个数中奇数的个数为674×2+2=1350.
24. B 【解析】由题图可得,第1种有4个氢原子,即2+2×1=4,第2种有6个氢原子,即2+2×2=6,第3种有8个氢原子,即2+2×3=8,…,∴第10种化合物的分子结构模型中氢原子的个数是2+2×10=22.
类题通法
图形规律探索类解题通法:
首先可将图案标记序号,利用作差法找后一个图案与前一个图案所求图形或元素个数之间的数量关系,若所作差为固定值,则根据固定值可确定每个图案中元素的个数,并进行验证.
同课章节目录
