2025年山东省济南历下区九年级下学期数学二模考试试题(含答案)
文档属性
| 名称 | 2025年山东省济南历下区九年级下学期数学二模考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 744.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 15:55:16 | ||
图片预览


文档简介
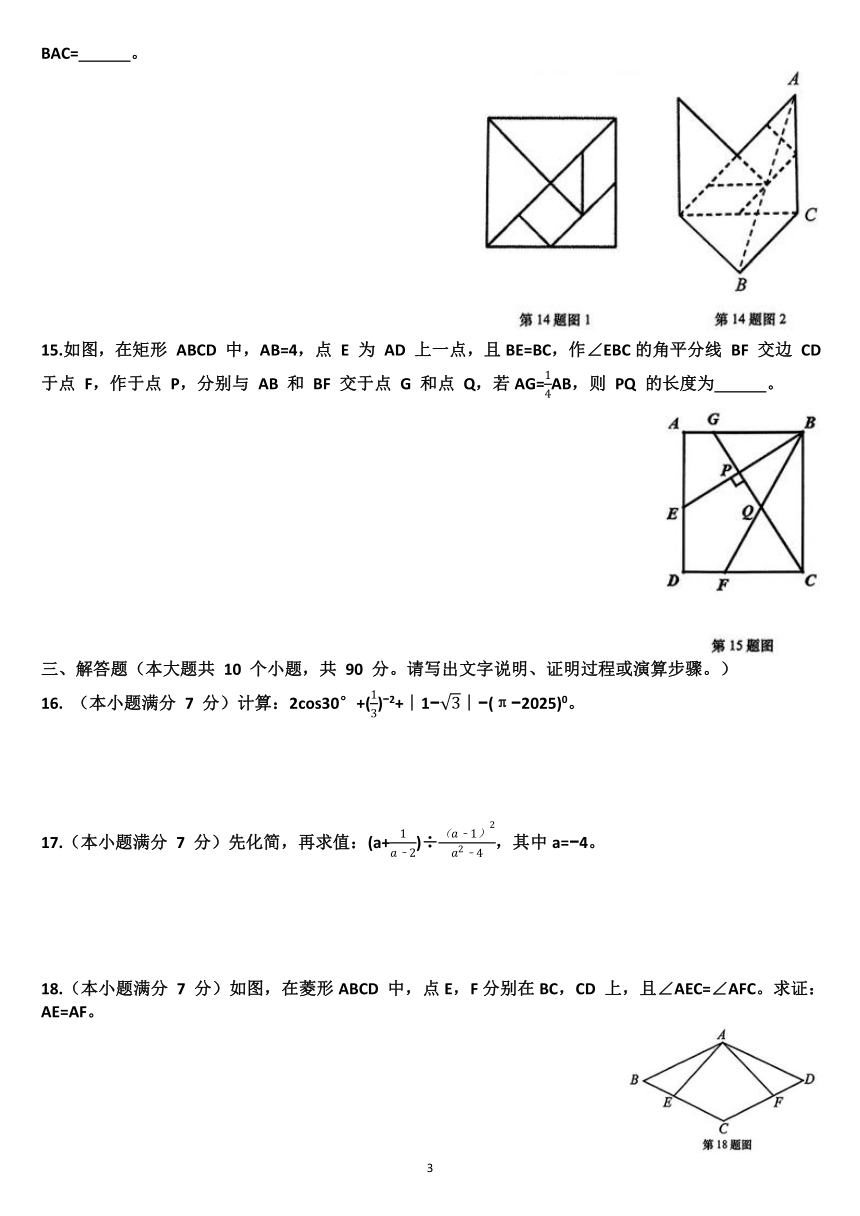
2025 年九年级学业水平第二次模拟考试数学试题(2025.4)
考试时间 120 分钟 满分 150 分
第 Ⅰ 卷(选择题 共 40 分)
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 的绝对值是( )
A. 7 B. -7 C. D.
2.如图是由若干个相同的小正方体搭成的几何体的主视图和左视图,则该几何体可能是( )
3.中国光刻机技术近年来取得显著进展,已量产 28 nm 浸没式 DUV 光刻机,填补国内空白。已知 28 nm = 0.000000028 m。将 0.000000028 用科学记数法表示为( )
A. 28×10 7 B. 2.8×10 8 C. 2.8×10 7 D. 0.28×10 8
4.如图,已知直线 AB 与 CD 交于点 O,OE⊥OC,OF 平分∠BOE。若∠COF = 32°,则∠AOD 的度数为( )
A. 24° B. 26° C. 28° D. 30°
5.花窗是中国古代园林建筑中窗的一种装饰和美化的形式。下列花窗图案中,既是轴对称图形,又是中心对称图形的是( )
6.实数 a,b,c 在数轴上对应点的位置如图所示,下列式子正确的是( )
A. a+c>a+b B. (b a)(b c)>0 C. ac>ab D. c b>c a
7.小亮和爸爸计划乘动车外出旅游。在网上购票时,小亮选定的车厢只剩一排有余座(如图)。若此时 C 座已售出,其余座位由系统随机分配,则小亮和爸爸相邻而坐的概率是( )
A. B. C. D.
8.若关于 x 的一元二次方程2x2 3x m 1=0有实数根,则实数 m 的取值范围是( )
A. m≥ B. m≤ C. m≥ D. m≤
9.如图,将折线O A1 A2 A3 A4绕点A4顺时针旋转 180° 得到一段新的折线A4 A5 A6 A7 A8,再将新的折线绕点A8顺时针旋转 180°…… 以此类推,得到一段连续的折线。则点A2025的坐标为( )
A. (1265, 0) B. (,) C. (1266,) D. (,0)
10.已知点A(x1,y1),B(x2,y2)是二次函数y=x2 bx+c的图象上任意两点,设x2 x1=t,若当 2y1,则 t 的取值范围是( )
A. t< 4或t>7 B. t< 5或t>8 C. t< 5或t>7 D. t< 4或t>8
第 Ⅱ 卷(非选择题 共 110 分)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11. 若二次根式有意义,则实数x 的取值范围是 。
12.如图 1,在边长为 8 cm 的正方形内部有一不规则图案(图中阴影部分),为测算阴影部分面积,小亮利用计算机进行模拟试验,通过计算机在正方形区域随机投放一个点,并记录该点落在阴影上的频率数据,结果如图 2 所示。小亮由此估计阴影部分面积约为 cm2。
13.如图,⊙O的内接正六边形 ABCDEF 的边长为 6,点 P 是弧CD的中点,则弧AP的长为 。
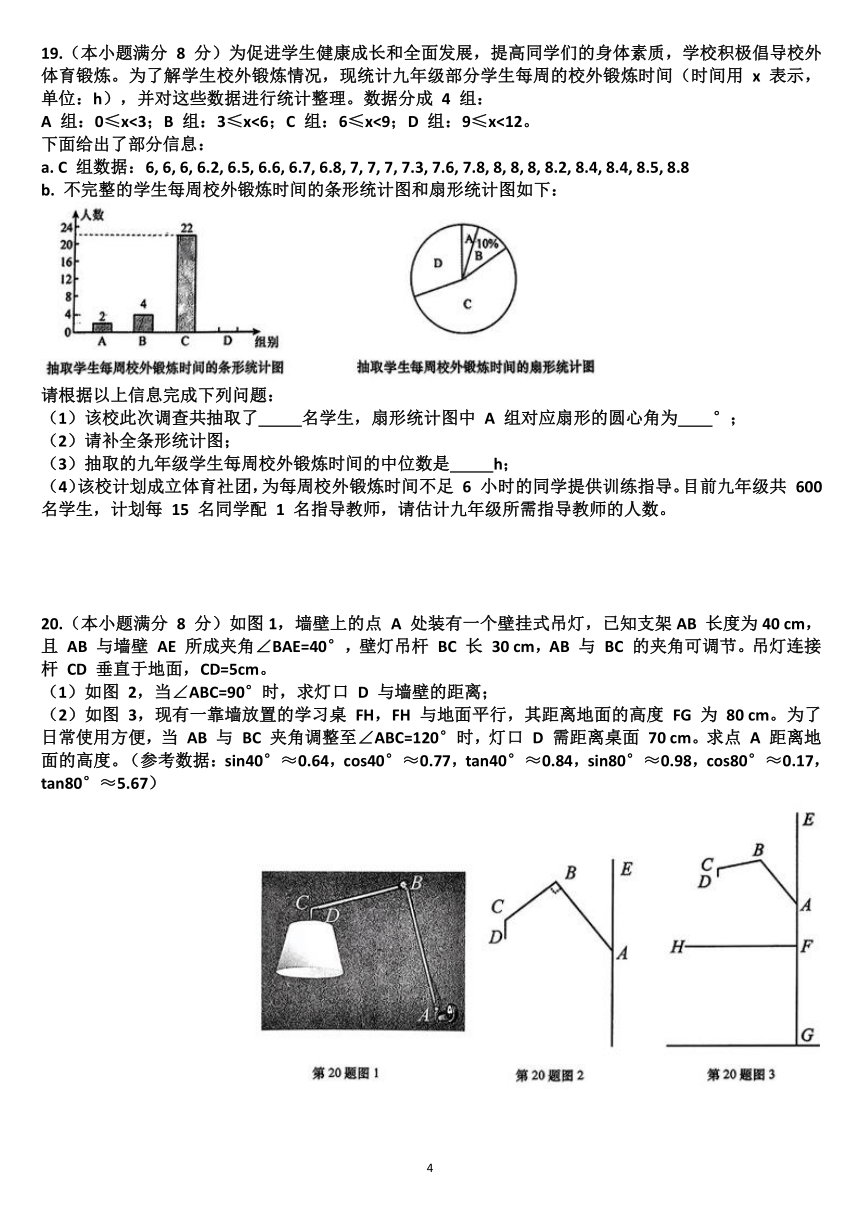
14.七巧板是中国传统数学文化的重要载体,将图 1 所示的七巧板,拼成图 2 所示的图形,则tan∠BAC= 。
15.如图,在矩形 ABCD 中,AB=4,点 E 为 AD 上一点,且BE=BC,作∠EBC的角平分线 BF 交边 CD 于点 F,作于点 P,分别与 AB 和 BF 交于点 G 和点 Q,若AG=AB,则 PQ 的长度为 。
三、解答题(本大题共 10 个小题,共 90 分。请写出文字说明、证明过程或演算步骤。)
16. (本小题满分 7 分)计算:2cos30°+() 2+∣1 ∣ (π 2025)0。
17.(本小题满分 7 分)先化简,再求值:(a+)÷,其中a= 4。
18.(本小题满分 7 分)如图,在菱形ABCD 中,点E,F分别在BC,CD 上,且∠AEC=∠AFC。求证:AE=AF。
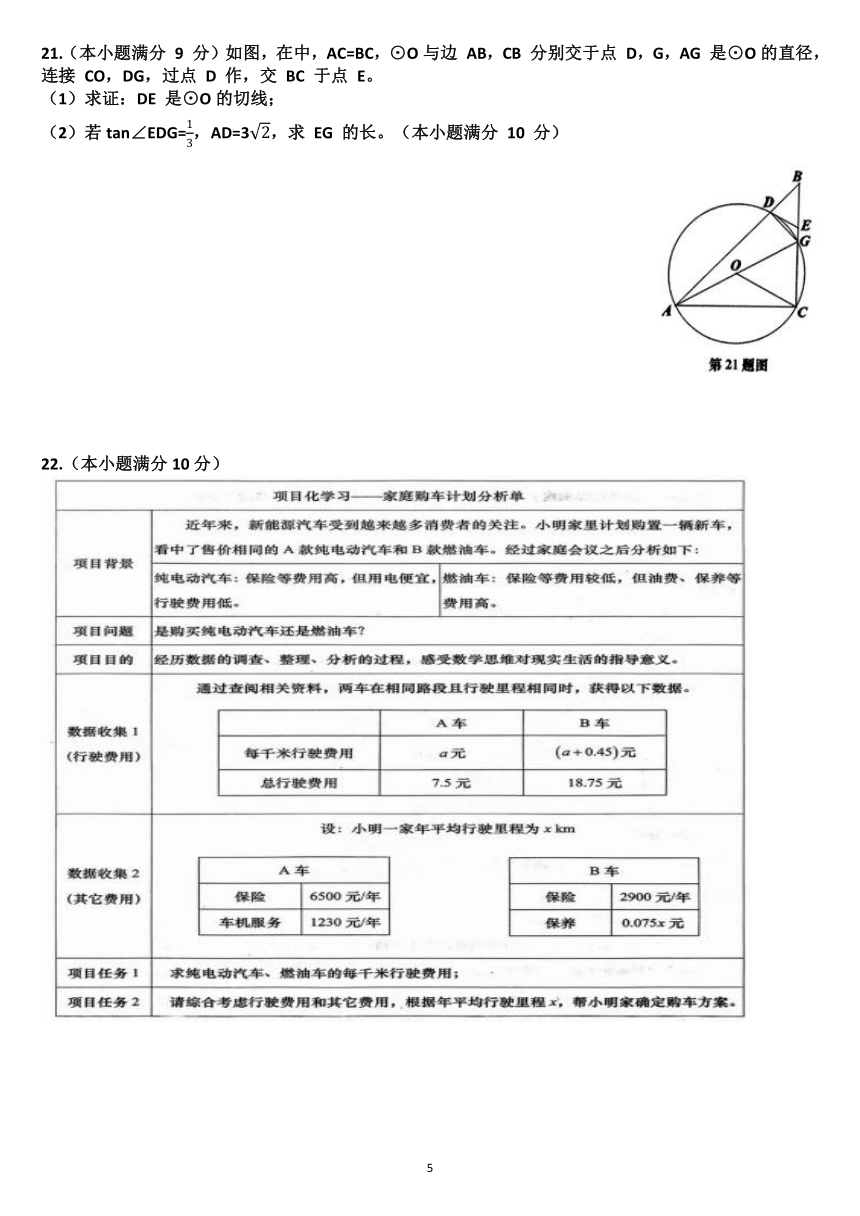
19.(本小题满分 8 分)为促进学生健康成长和全面发展,提高同学们的身体素质,学校积极倡导校外体育锻炼。为了解学生校外锻炼情况,现统计九年级部分学生每周的校外锻炼时间(时间用 x 表示,单位:h),并对这些数据进行统计整理。数据分成 4 组:
A 组:0≤x<3;B 组:3≤x<6;C 组:6≤x<9;D 组:9≤x<12。
下面给出了部分信息:
a. C 组数据:6, 6, 6, 6.2, 6.5, 6.6, 6.7, 6.8, 7, 7, 7, 7.3, 7.6, 7.8, 8, 8, 8, 8.2, 8.4, 8.4, 8.5, 8.8
b. 不完整的学生每周校外锻炼时间的条形统计图和扇形统计图如下:
请根据以上信息完成下列问题:
(1)该校此次调查共抽取了 名学生,扇形统计图中 A 组对应扇形的圆心角为 °;
(2)请补全条形统计图;
(3)抽取的九年级学生每周校外锻炼时间的中位数是 h;
(4)该校计划成立体育社团,为每周校外锻炼时间不足 6 小时的同学提供训练指导。目前九年级共 600 名学生,计划每 15 名同学配 1 名指导教师,请估计九年级所需指导教师的人数。
20.(本小题满分 8 分)如图1,墙壁上的点 A 处装有一个壁挂式吊灯,已知支架AB 长度为40 cm,且 AB 与墙壁 AE 所成夹角∠BAE=40°,壁灯吊杆 BC 长 30 cm,AB 与 BC 的夹角可调节。吊灯连接杆 CD 垂直于地面,CD=5cm。
(1)如图 2,当∠ABC=90°时,求灯口 D 与墙壁的距离;
(2)如图 3,现有一靠墙放置的学习桌 FH,FH 与地面平行,其距离地面的高度 FG 为 80 cm。为了日常使用方便,当 AB 与 BC 夹角调整至∠ABC=120°时,灯口 D 需距离桌面 70 cm。求点 A 距离地面的高度。(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67)
21.(本小题满分 9 分)如图,在中,AC=BC,⊙O与边 AB,CB 分别交于点 D,G,AG 是⊙O的直径,连接 CO,DG,过点 D 作,交 BC 于点 E。
(1)求证:DE 是⊙O的切线;
(2)若tan∠EDG=,AD=3,求 EG 的长。(本小题满分 10 分)
22.(本小题满分10分)
23.(本小题满分10 分)直线y=x+b与双曲线y=(x>0)交于点A(2,3),与y 轴交于点B。
(1)求 k,b 的值;
(2)如图 1,点 C 是直线y=x+b上第一象限内的一点,过点 C 作轴,垂足为点 E,交双曲线于点 D,当=时,求的值;
(3)如图 2,已知点 P 是双曲线上一动点,连接 OA,OP,当∠AOP=∠BAO时,求点 P 的坐标。
24.(本小题满分 12 分)二次函数y=ax2+bx的图象过点A( 4,4),B(,),连接 AB,点 C 是抛物线上一个动点。
(1)求二次函数的表达式;
(2)如图 1,若点C 在 y 轴左侧的抛物线上运动,平移线段 AB,使其一个端点与点 C 重合,另一个端点恰好落在 x 轴上,求点 C 的坐标;
(3)如图 2,若点C 在 y 轴右侧的抛物线上运动,作直线 AC,交 x 轴于点 E,将直线 AC 绕点 A 逆时针旋转45°得直线AG,交y 轴于点F,连接 EF。若EF=FO,直接写出点 C 的坐标。
25.(本小题满分 12 分)在△ABC中,∠A=90°,AB=AC,点 D 在边 AC 上(点 D 不与点 A,点 C 重合),连接 BD 并将 BD 绕点 D 逆时针旋转 90° 得到 DE。
(1)如图 1,连接 CE。
① CE 与 BC 的位置关系为 ,∠ABD与∠CED的数量关系是 ;
②请用等式表示 BC,CD 和 CE 的数量关系,并说明理由;
(2)如图 2,将△ABD沿 BD 翻折,得到△A’BD,连接A’E,若A’E的最小值为 2,求 AB 的长。
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 的绝对值是( C )
A. 7 B. -7 C. D.
2.如图是由若干个相同的小正方体搭成的几何体的主视图和左视图,则该几何体可能是( A )
3.中国光刻机技术近年来取得显著进展,已量产 28 nm 浸没式 DUV 光刻机,填补国内空白。已知 28 nm = 0.000000028 m。将 0.000000028 用科学记数法表示为( B )
A. 28×10 7 B. 2.8×10 8 C. 2.8×10 7 D. 0.28×10 8
4.如图,已知直线 AB 与 CD 交于点 O,OE⊥OC,OF 平分∠BOE。若∠COF = 32°,则∠AOD 的度数为( B )
A. 24° B. 26° C. 28° D. 30°
5.花窗是中国古代园林建筑中窗的一种装饰和美化的形式。下列花窗图案中,既是轴对称图形,又是中心对称图形的是( D )
6.实数 a,b,c 在数轴上对应点的位置如图所示,下列式子正确的是( D )
A. a+c>a+b B. (b a)(b c)>0 C. ac>ab D. c b>c a
7.小亮和爸爸计划乘动车外出旅游。在网上购票时,小亮选定的车厢只剩一排有余座(如图)。若此时 C 座已售出,其余座位由系统随机分配,则小亮和爸爸相邻而坐的概率是( D )
A. B. C. D.
8.若关于 x 的一元二次方程2x2 3x m 1=0有实数根,则实数 m 的取值范围是( A )
A. m≥ B. m≤ C. m≥ D. m≤
9.如图,将折线O A1 A2 A3 A4绕点A4顺时针旋转 180° 得到一段新的折线A4 A5 A6 A7 A8,再将新的折线绕点A8顺时针旋转 180°…… 以此类推,得到一段连续的折线。则点A2025的坐标为( B )
A. (1265, 0) B. (,) C. (1266,) D. (,0)
10.已知点A(x1,y1),B(x2,y2)是二次函数y=x2 bx+c的图象上任意两点,设x2 x1=t,若当 2y1,则 t 的取值范围是( B )
A. t< 4或t>7 B. t< 5或t>8 C. t< 5或t>7 D. t< 4或t>8
第 Ⅱ 卷(非选择题 共 110 分)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11. 若二次根式有意义,则实数x 的取值范围是 x≥3 。
12.如图 1,在边长为 8 cm 的正方形内部有一不规则图案(图中阴影部分),为测算阴影部分面积,小亮利用计算机进行模拟试验,通过计算机在正方形区域随机投放一个点,并记录该点落在阴影上的频率数据,结果如图 2 所示。小亮由此估计阴影部分面积约为 22.4 cm2。
13.如图,⊙O的内接正六边形 ABCDEF 的边长为 6,点 P 是弧CD的中点,则弧AP的长为 5π 。
14.七巧板是中国传统数学文化的重要载体,将图 1 所示的七巧板,拼成图 2 所示的图形,则tan∠BAC= 。
15.如图,在矩形 ABCD 中,AB=4,点 E 为 AD 上一点,且BE=BC,作∠EBC的角平分线 BF 交边 CD 于点 F,作于点 P,分别与 AB 和 BF 交于点 G 和点 Q,若AG=AB,则 PQ 的长度为 。
三、解答题(本大题共 10 个小题,共 90 分。请写出文字说明、证明过程或演算步骤。)
16. (本小题满分 7 分)计算:2cos30°+() 2+∣1 ∣ (π 2025)0。
=+9+﹣1﹣1
=2+7
17.(本小题满分 7 分)先化简,再求值:(a+)÷,其中a= 4。
解原式=×
=a+2
将a=﹣4代入得﹣2
18.(本小题满分 7 分)如图,在菱形ABCD 中,点E,F分别在BC,CD 上,且∠AEC=∠AFC。求证:AE=AF。
证明:∵菱形ABCD
∴∠B=∠D,AB=AD,BC=CD
又∵∠AEC=∠AFC
∴∠AEB=∠AFD
∴△ABE≌△ADF(AAS)
∴AE=AF。
19.(本小题满分 8 分)为促进学生健康成长和全面发展,提高同学们的身体素质,学校积极倡导校外体育锻炼。为了解学生校外锻炼情况,现统计九年级部分学生每周的校外锻炼时间(时间用 x 表示,单位:h),并对这些数据进行统计整理。数据分成 4 组:
A 组:0≤x<3;B 组:3≤x<6;C 组:6≤x<9;D 组:9≤x<12。
下面给出了部分信息:
a. C 组数据:6, 6, 6, 6.2, 6.5, 6.6, 6.7, 6.8, 7, 7, 7, 7.3, 7.6, 7.8, 8, 8, 8, 8.2, 8.4, 8.4, 8.5, 8.8
b. 不完整的学生每周校外锻炼时间的条形统计图和扇形统计图如下:
请根据以上信息完成下列问题:
(1)该校此次调查共抽取了 名学生,扇形统计图中 A 组对应扇形的圆心角为 °;
(2)请补全条形统计图;
(3)抽取的九年级学生每周校外锻炼时间的中位数是 h;
(4)该校计划成立体育社团,为每周校外锻炼时间不足 6 小时的同学提供训练指导。目前九年级共 600 名学生,计划每 15 名同学配 1 名指导教师,请估计九年级所需指导教师的人数。
(1)40,18°
(2)D组12人,图略
(3)7.1
(4)600×÷15=6
20.(本小题满分 8 分)如图1,墙壁上的点 A 处装有一个壁挂式吊灯,已知支架AB 长度为40 cm,且 AB 与墙壁 AE 所成夹角∠BAE=40°,壁灯吊杆 BC 长 30 cm,AB 与 BC 的夹角可调节。吊灯连接杆 CD 垂直于地面,CD=5cm。
(1)如图 2,当∠ABC=90°时,求灯口 D 与墙壁的距离;
(2)如图 3,现有一靠墙放置的学习桌 FH,FH 与地面平行,其距离地面的高度 FG 为 80 cm。为了日常使用方便,当 AB 与 BC 夹角调整至∠ABC=120°时,灯口 D 需距离桌面 70 cm。求点 A 距离地面的高度。(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67)
(1)过B作BM⊥AE于M,过C作CN⊥BM于N
∵在Rt△ABM中,根据正弦和余弦的定义,
sin∠BAE=,cos∠BAE=
已知AB=40cm,sin40 ≈0.64,cos40 ≈0.77
∴BM=ABsin40 ≈40×0.64=25.6cm,AM=ABcos40 ≈40×0.77=30.8cm。
∵∠ABC=90 ,∠ABM+∠MBC=90 ,∠BCN+∠MBC=90
∴∠BCN=∠BAE=40
在Rt△BCN中,sin∠BCN=,已知BC=30cm
∴CN=BCsin40 ≈30×0.64=19.2cm
∴灯口D与墙壁的距离为AM+CN≈30.8+19.2=50cm。
(2)过B作BP⊥AE于P,过C作CQ⊥BP交BP延长线于Q。
在Rt△ABP中,BP=ABsin40 ≈40×0.64=25.6cm,AP=ABcos40 ≈40×0.77=30.8cm。
∵∠ABC=120 ,∠ABP=50
∴∠CBQ=30
在Rt△BCQ中,sin∠CBQ=,cos∠CBQ=
∵BC=30cm
∴CQ=BCsin30 =15cm,BQ=BCcos30 ≈30×≈25.98cm。
∴灯口D距离桌面70cm,桌面距离地面80cm,CD=5cm
∴C到地面的高度为70+80 5=145cm
∴B到地面的高度为145 CQ=145 15=130cm
∴点A距离地面的高度为130+BP≈130+25.6=155.6cm。
21.(本小题满分 9 分)如图,在中,AC=BC,⊙O与边 AB,CB 分别交于点 D,G,AG 是⊙O的直径,连接 CO,DG,过点 D 作,交 BC 于点 E。
(1)求证:DE 是⊙O的切线;
(2)若tan∠EDG=,AD=3,求 EG 的长。(本小题满分 10 分)
(1)证明:连接OD
∵AC=BC,OA=OG
∴CO是△ABC的中线
根据等腰三角形三线合一性质,∴CO⊥AB
∵DE∥CO
∴DE⊥AB
∵OA=OD
∴∠A=∠ODA
∵AC=BC
∴∠A=∠B
∴∠ODA=∠B
∴OD∥BC
∵DE⊥AB,OD∥BC
∴DE⊥OD
∵OD是⊙O的半径
∴DE是⊙O的切线。
(2)解:连接AD,DG
∵AG是⊙O的直径
∴∠ADG=90
∵AC=BC,CO⊥AB
∴D是AB中点。
∵AD=3
∴AB=2AD=6
∵∠EDG+∠BDG=∠BDE=90 ,∠B+∠BDG=90
∴∠EDG=∠B
∵tan∠EDG=
∴tanB=
在Rt△ABD中,AD=3,AB=6
根据勾股定理可得BD=3
∵tanB==
设CO=x,则BO=3x
在Rt△BOC中,根据勾股定理BC2=CO2+BO2
∴BC=x
∵AB=6,D是AB中点,BD=3,且BC=,CD=CO=x
∴BC==x
解得x=3,即CO=3,BO=9
∵∠EDG=∠B,tan∠EDG=
设EG=y,则DE=3y
∵DE∥CO
∴△BDE∽△BOC
则=
BC=3,BE=BG EG,BG=
在Rt△ADG中,tan∠DAG=tanB=,AD=3
∴DG=,AG=2,BG=2
∴=
解得y=1
∴EG=1
22.(本小题满分10分)
项目任务1:设两车行驶里程为s千米。
∵A车每千米行驶费用为a元,总行驶费用7.5元,所以s=;
B车每千米行驶费用为(a+0.45)元,总行驶费用18.75元,所以s=
由于行驶里程相同,则=
解得a=0.3
经检验a=0.3是原方程的根
∴B车每千米行驶费用为0.3+0.45=0.75元。
项目任务 2:
∵A车一年总费用yA=6500+1230+0.3x=7730+0.3x;
B车一年总费用yB=2900+0.075x+0.75x=2900+0.825x。
当yA=yB时,
7730+0.3x=2900+0.825x
解得x=9200
yA>yB时,
7730+0.3x>2900+0.825x
解得x<9200
yA7730+0.3x<2900+0.825x
解得x>9200
∴当x=9200时,购买A车和B车费用相同;当x<9200时,购买B车更划算;当x>9200时,购买A车更划算。
23.(本小题满分10 分)直线y=x+b与双曲线y=(x>0)交于点A(2,3),与y 轴交于点B。
(1)求 k,b 的值;
(2)如图 1,点 C 是直线y=x+b上第一象限内的一点,过点 C 作轴,垂足为点 E,交双曲线于点 D,当=时,求的值;
(3)如图 2,已知点 P 是双曲线上一动点,连接 OA,OP,当∠AOP=∠BAO时,求点 P 的坐标。
(1)将A(2,3)代入y=
得k=3×2=6
将A(2,3)代入y=x+b
得3=+b×2+b
解得b=2
(2)由(1)知直线y=x+b,B(0,2),A(2,3)
∵=
设C点横坐标为m,则C(m,m+2)
根据两点间距离公式得=
且C在第一象限,m>0
解得m=3
∴C(3,),D(3,2)
则=
(3)过A作AH⊥x轴于H,A(2,3),B(0,2),tan∠BAO=
∵∠AOP=∠BAO
∴设P(n,),直线OP的斜率kOP=
∴tan∠AOP=,又tan∠AOP=tan∠BAO=
则=
解得n=3或n= 3(舍去)
∴P(3,2)
24.(本小题满分 12 分)二次函数y=ax2+bx的图象过点A( 4,4),B(,),连接 AB,点 C 是抛物线上一个动点。
(1)求二次函数的表达式;
(2)如图 1,若点C 在 y 轴左侧的抛物线上运动,平移线段 AB,使其一个端点与点 C 重合,另一个端点恰好落在 x 轴上,求点 C 的坐标;
(3)如图 2,若点C 在 y 轴右侧的抛物线上运动,作直线 AC,交 x 轴于点 E,将直线 AC 绕点 A 逆时针旋转45°得直线AG,交y 轴于点F,连接 EF。若EF=FO,直接写出点 C 的坐标。
把A (-4.4), B(,)代入二次函数y=ax2+bx
得
解得
∴二次函数的表达式为 y=x2+3x
(2)设C(a,a2+3a),D(b,0).
①当点 B 与点 C 重合,
∵DC是由 AB 平移所得.则有
解得
将 a =-代入y=x2+3x得y=﹣
∴点C坐标为(-,﹣)
②当点 A 与点 C 重合
则有
解得a1=﹣(舍去),a2=﹣﹣
∴点C(﹣﹣,)
(3)C(,)
25.(本小题满分 12 分)在△ABC中,∠A=90°,AB=AC,点 D 在边 AC 上(点 D 不与点 A,点 C 重合),连接 BD 并将 BD 绕点 D 逆时针旋转 90° 得到 DE。
(1)如图 1,连接 CE。
① CE 与 BC 的位置关系为 ,∠ABD与∠CED的数量关系是 ;
②请用等式表示 BC,CD 和 CE 的数量关系,并说明理由;
(2)如图 2,将△ABD沿 BD 翻折,得到△A’BD,连接A’E,若A’E的最小值为 2,求 AB 的长。
(1)① CE⊥BC;∠ABD=∠CED
过D作DF⊥DC交BC于F
∵∠A=90 ,AB=AC
∴∠ACB=45 ,△DFC为等腰直角三角形,DF=DC
又∵BD=DE,∠BDF=∠EDC
∴△BDF≌△EDC(SAS)。
∴∠DFB=∠DCE=135
故∠BCE=135 45 =90
即CE⊥BC;且∠ABD=∠DEC=∠CED。
②BC=CE+CD
由△BDF≌△EDC
得BF=CE。
又∵△DFC是等腰直角三角形
根据勾股定理
FC=CD
∴BC=BF+FC=CE+CD
(2)AB=2
考试时间 120 分钟 满分 150 分
第 Ⅰ 卷(选择题 共 40 分)
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 的绝对值是( )
A. 7 B. -7 C. D.
2.如图是由若干个相同的小正方体搭成的几何体的主视图和左视图,则该几何体可能是( )
3.中国光刻机技术近年来取得显著进展,已量产 28 nm 浸没式 DUV 光刻机,填补国内空白。已知 28 nm = 0.000000028 m。将 0.000000028 用科学记数法表示为( )
A. 28×10 7 B. 2.8×10 8 C. 2.8×10 7 D. 0.28×10 8
4.如图,已知直线 AB 与 CD 交于点 O,OE⊥OC,OF 平分∠BOE。若∠COF = 32°,则∠AOD 的度数为( )
A. 24° B. 26° C. 28° D. 30°
5.花窗是中国古代园林建筑中窗的一种装饰和美化的形式。下列花窗图案中,既是轴对称图形,又是中心对称图形的是( )
6.实数 a,b,c 在数轴上对应点的位置如图所示,下列式子正确的是( )
A. a+c>a+b B. (b a)(b c)>0 C. ac>ab D. c b>c a
7.小亮和爸爸计划乘动车外出旅游。在网上购票时,小亮选定的车厢只剩一排有余座(如图)。若此时 C 座已售出,其余座位由系统随机分配,则小亮和爸爸相邻而坐的概率是( )
A. B. C. D.
8.若关于 x 的一元二次方程2x2 3x m 1=0有实数根,则实数 m 的取值范围是( )
A. m≥ B. m≤ C. m≥ D. m≤
9.如图,将折线O A1 A2 A3 A4绕点A4顺时针旋转 180° 得到一段新的折线A4 A5 A6 A7 A8,再将新的折线绕点A8顺时针旋转 180°…… 以此类推,得到一段连续的折线。则点A2025的坐标为( )
A. (1265, 0) B. (,) C. (1266,) D. (,0)
10.已知点A(x1,y1),B(x2,y2)是二次函数y=x2 bx+c的图象上任意两点,设x2 x1=t,若当 2
A. t< 4或t>7 B. t< 5或t>8 C. t< 5或t>7 D. t< 4或t>8
第 Ⅱ 卷(非选择题 共 110 分)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11. 若二次根式有意义,则实数x 的取值范围是 。
12.如图 1,在边长为 8 cm 的正方形内部有一不规则图案(图中阴影部分),为测算阴影部分面积,小亮利用计算机进行模拟试验,通过计算机在正方形区域随机投放一个点,并记录该点落在阴影上的频率数据,结果如图 2 所示。小亮由此估计阴影部分面积约为 cm2。
13.如图,⊙O的内接正六边形 ABCDEF 的边长为 6,点 P 是弧CD的中点,则弧AP的长为 。
14.七巧板是中国传统数学文化的重要载体,将图 1 所示的七巧板,拼成图 2 所示的图形,则tan∠BAC= 。
15.如图,在矩形 ABCD 中,AB=4,点 E 为 AD 上一点,且BE=BC,作∠EBC的角平分线 BF 交边 CD 于点 F,作于点 P,分别与 AB 和 BF 交于点 G 和点 Q,若AG=AB,则 PQ 的长度为 。
三、解答题(本大题共 10 个小题,共 90 分。请写出文字说明、证明过程或演算步骤。)
16. (本小题满分 7 分)计算:2cos30°+() 2+∣1 ∣ (π 2025)0。
17.(本小题满分 7 分)先化简,再求值:(a+)÷,其中a= 4。
18.(本小题满分 7 分)如图,在菱形ABCD 中,点E,F分别在BC,CD 上,且∠AEC=∠AFC。求证:AE=AF。
19.(本小题满分 8 分)为促进学生健康成长和全面发展,提高同学们的身体素质,学校积极倡导校外体育锻炼。为了解学生校外锻炼情况,现统计九年级部分学生每周的校外锻炼时间(时间用 x 表示,单位:h),并对这些数据进行统计整理。数据分成 4 组:
A 组:0≤x<3;B 组:3≤x<6;C 组:6≤x<9;D 组:9≤x<12。
下面给出了部分信息:
a. C 组数据:6, 6, 6, 6.2, 6.5, 6.6, 6.7, 6.8, 7, 7, 7, 7.3, 7.6, 7.8, 8, 8, 8, 8.2, 8.4, 8.4, 8.5, 8.8
b. 不完整的学生每周校外锻炼时间的条形统计图和扇形统计图如下:
请根据以上信息完成下列问题:
(1)该校此次调查共抽取了 名学生,扇形统计图中 A 组对应扇形的圆心角为 °;
(2)请补全条形统计图;
(3)抽取的九年级学生每周校外锻炼时间的中位数是 h;
(4)该校计划成立体育社团,为每周校外锻炼时间不足 6 小时的同学提供训练指导。目前九年级共 600 名学生,计划每 15 名同学配 1 名指导教师,请估计九年级所需指导教师的人数。
20.(本小题满分 8 分)如图1,墙壁上的点 A 处装有一个壁挂式吊灯,已知支架AB 长度为40 cm,且 AB 与墙壁 AE 所成夹角∠BAE=40°,壁灯吊杆 BC 长 30 cm,AB 与 BC 的夹角可调节。吊灯连接杆 CD 垂直于地面,CD=5cm。
(1)如图 2,当∠ABC=90°时,求灯口 D 与墙壁的距离;
(2)如图 3,现有一靠墙放置的学习桌 FH,FH 与地面平行,其距离地面的高度 FG 为 80 cm。为了日常使用方便,当 AB 与 BC 夹角调整至∠ABC=120°时,灯口 D 需距离桌面 70 cm。求点 A 距离地面的高度。(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67)
21.(本小题满分 9 分)如图,在中,AC=BC,⊙O与边 AB,CB 分别交于点 D,G,AG 是⊙O的直径,连接 CO,DG,过点 D 作,交 BC 于点 E。
(1)求证:DE 是⊙O的切线;
(2)若tan∠EDG=,AD=3,求 EG 的长。(本小题满分 10 分)
22.(本小题满分10分)
23.(本小题满分10 分)直线y=x+b与双曲线y=(x>0)交于点A(2,3),与y 轴交于点B。
(1)求 k,b 的值;
(2)如图 1,点 C 是直线y=x+b上第一象限内的一点,过点 C 作轴,垂足为点 E,交双曲线于点 D,当=时,求的值;
(3)如图 2,已知点 P 是双曲线上一动点,连接 OA,OP,当∠AOP=∠BAO时,求点 P 的坐标。
24.(本小题满分 12 分)二次函数y=ax2+bx的图象过点A( 4,4),B(,),连接 AB,点 C 是抛物线上一个动点。
(1)求二次函数的表达式;
(2)如图 1,若点C 在 y 轴左侧的抛物线上运动,平移线段 AB,使其一个端点与点 C 重合,另一个端点恰好落在 x 轴上,求点 C 的坐标;
(3)如图 2,若点C 在 y 轴右侧的抛物线上运动,作直线 AC,交 x 轴于点 E,将直线 AC 绕点 A 逆时针旋转45°得直线AG,交y 轴于点F,连接 EF。若EF=FO,直接写出点 C 的坐标。
25.(本小题满分 12 分)在△ABC中,∠A=90°,AB=AC,点 D 在边 AC 上(点 D 不与点 A,点 C 重合),连接 BD 并将 BD 绕点 D 逆时针旋转 90° 得到 DE。
(1)如图 1,连接 CE。
① CE 与 BC 的位置关系为 ,∠ABD与∠CED的数量关系是 ;
②请用等式表示 BC,CD 和 CE 的数量关系,并说明理由;
(2)如图 2,将△ABD沿 BD 翻折,得到△A’BD,连接A’E,若A’E的最小值为 2,求 AB 的长。
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 的绝对值是( C )
A. 7 B. -7 C. D.
2.如图是由若干个相同的小正方体搭成的几何体的主视图和左视图,则该几何体可能是( A )
3.中国光刻机技术近年来取得显著进展,已量产 28 nm 浸没式 DUV 光刻机,填补国内空白。已知 28 nm = 0.000000028 m。将 0.000000028 用科学记数法表示为( B )
A. 28×10 7 B. 2.8×10 8 C. 2.8×10 7 D. 0.28×10 8
4.如图,已知直线 AB 与 CD 交于点 O,OE⊥OC,OF 平分∠BOE。若∠COF = 32°,则∠AOD 的度数为( B )
A. 24° B. 26° C. 28° D. 30°
5.花窗是中国古代园林建筑中窗的一种装饰和美化的形式。下列花窗图案中,既是轴对称图形,又是中心对称图形的是( D )
6.实数 a,b,c 在数轴上对应点的位置如图所示,下列式子正确的是( D )
A. a+c>a+b B. (b a)(b c)>0 C. ac>ab D. c b>c a
7.小亮和爸爸计划乘动车外出旅游。在网上购票时,小亮选定的车厢只剩一排有余座(如图)。若此时 C 座已售出,其余座位由系统随机分配,则小亮和爸爸相邻而坐的概率是( D )
A. B. C. D.
8.若关于 x 的一元二次方程2x2 3x m 1=0有实数根,则实数 m 的取值范围是( A )
A. m≥ B. m≤ C. m≥ D. m≤
9.如图,将折线O A1 A2 A3 A4绕点A4顺时针旋转 180° 得到一段新的折线A4 A5 A6 A7 A8,再将新的折线绕点A8顺时针旋转 180°…… 以此类推,得到一段连续的折线。则点A2025的坐标为( B )
A. (1265, 0) B. (,) C. (1266,) D. (,0)
10.已知点A(x1,y1),B(x2,y2)是二次函数y=x2 bx+c的图象上任意两点,设x2 x1=t,若当 2
A. t< 4或t>7 B. t< 5或t>8 C. t< 5或t>7 D. t< 4或t>8
第 Ⅱ 卷(非选择题 共 110 分)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分。)
11. 若二次根式有意义,则实数x 的取值范围是 x≥3 。
12.如图 1,在边长为 8 cm 的正方形内部有一不规则图案(图中阴影部分),为测算阴影部分面积,小亮利用计算机进行模拟试验,通过计算机在正方形区域随机投放一个点,并记录该点落在阴影上的频率数据,结果如图 2 所示。小亮由此估计阴影部分面积约为 22.4 cm2。
13.如图,⊙O的内接正六边形 ABCDEF 的边长为 6,点 P 是弧CD的中点,则弧AP的长为 5π 。
14.七巧板是中国传统数学文化的重要载体,将图 1 所示的七巧板,拼成图 2 所示的图形,则tan∠BAC= 。
15.如图,在矩形 ABCD 中,AB=4,点 E 为 AD 上一点,且BE=BC,作∠EBC的角平分线 BF 交边 CD 于点 F,作于点 P,分别与 AB 和 BF 交于点 G 和点 Q,若AG=AB,则 PQ 的长度为 。
三、解答题(本大题共 10 个小题,共 90 分。请写出文字说明、证明过程或演算步骤。)
16. (本小题满分 7 分)计算:2cos30°+() 2+∣1 ∣ (π 2025)0。
=+9+﹣1﹣1
=2+7
17.(本小题满分 7 分)先化简,再求值:(a+)÷,其中a= 4。
解原式=×
=a+2
将a=﹣4代入得﹣2
18.(本小题满分 7 分)如图,在菱形ABCD 中,点E,F分别在BC,CD 上,且∠AEC=∠AFC。求证:AE=AF。
证明:∵菱形ABCD
∴∠B=∠D,AB=AD,BC=CD
又∵∠AEC=∠AFC
∴∠AEB=∠AFD
∴△ABE≌△ADF(AAS)
∴AE=AF。
19.(本小题满分 8 分)为促进学生健康成长和全面发展,提高同学们的身体素质,学校积极倡导校外体育锻炼。为了解学生校外锻炼情况,现统计九年级部分学生每周的校外锻炼时间(时间用 x 表示,单位:h),并对这些数据进行统计整理。数据分成 4 组:
A 组:0≤x<3;B 组:3≤x<6;C 组:6≤x<9;D 组:9≤x<12。
下面给出了部分信息:
a. C 组数据:6, 6, 6, 6.2, 6.5, 6.6, 6.7, 6.8, 7, 7, 7, 7.3, 7.6, 7.8, 8, 8, 8, 8.2, 8.4, 8.4, 8.5, 8.8
b. 不完整的学生每周校外锻炼时间的条形统计图和扇形统计图如下:
请根据以上信息完成下列问题:
(1)该校此次调查共抽取了 名学生,扇形统计图中 A 组对应扇形的圆心角为 °;
(2)请补全条形统计图;
(3)抽取的九年级学生每周校外锻炼时间的中位数是 h;
(4)该校计划成立体育社团,为每周校外锻炼时间不足 6 小时的同学提供训练指导。目前九年级共 600 名学生,计划每 15 名同学配 1 名指导教师,请估计九年级所需指导教师的人数。
(1)40,18°
(2)D组12人,图略
(3)7.1
(4)600×÷15=6
20.(本小题满分 8 分)如图1,墙壁上的点 A 处装有一个壁挂式吊灯,已知支架AB 长度为40 cm,且 AB 与墙壁 AE 所成夹角∠BAE=40°,壁灯吊杆 BC 长 30 cm,AB 与 BC 的夹角可调节。吊灯连接杆 CD 垂直于地面,CD=5cm。
(1)如图 2,当∠ABC=90°时,求灯口 D 与墙壁的距离;
(2)如图 3,现有一靠墙放置的学习桌 FH,FH 与地面平行,其距离地面的高度 FG 为 80 cm。为了日常使用方便,当 AB 与 BC 夹角调整至∠ABC=120°时,灯口 D 需距离桌面 70 cm。求点 A 距离地面的高度。(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67)
(1)过B作BM⊥AE于M,过C作CN⊥BM于N
∵在Rt△ABM中,根据正弦和余弦的定义,
sin∠BAE=,cos∠BAE=
已知AB=40cm,sin40 ≈0.64,cos40 ≈0.77
∴BM=ABsin40 ≈40×0.64=25.6cm,AM=ABcos40 ≈40×0.77=30.8cm。
∵∠ABC=90 ,∠ABM+∠MBC=90 ,∠BCN+∠MBC=90
∴∠BCN=∠BAE=40
在Rt△BCN中,sin∠BCN=,已知BC=30cm
∴CN=BCsin40 ≈30×0.64=19.2cm
∴灯口D与墙壁的距离为AM+CN≈30.8+19.2=50cm。
(2)过B作BP⊥AE于P,过C作CQ⊥BP交BP延长线于Q。
在Rt△ABP中,BP=ABsin40 ≈40×0.64=25.6cm,AP=ABcos40 ≈40×0.77=30.8cm。
∵∠ABC=120 ,∠ABP=50
∴∠CBQ=30
在Rt△BCQ中,sin∠CBQ=,cos∠CBQ=
∵BC=30cm
∴CQ=BCsin30 =15cm,BQ=BCcos30 ≈30×≈25.98cm。
∴灯口D距离桌面70cm,桌面距离地面80cm,CD=5cm
∴C到地面的高度为70+80 5=145cm
∴B到地面的高度为145 CQ=145 15=130cm
∴点A距离地面的高度为130+BP≈130+25.6=155.6cm。
21.(本小题满分 9 分)如图,在中,AC=BC,⊙O与边 AB,CB 分别交于点 D,G,AG 是⊙O的直径,连接 CO,DG,过点 D 作,交 BC 于点 E。
(1)求证:DE 是⊙O的切线;
(2)若tan∠EDG=,AD=3,求 EG 的长。(本小题满分 10 分)
(1)证明:连接OD
∵AC=BC,OA=OG
∴CO是△ABC的中线
根据等腰三角形三线合一性质,∴CO⊥AB
∵DE∥CO
∴DE⊥AB
∵OA=OD
∴∠A=∠ODA
∵AC=BC
∴∠A=∠B
∴∠ODA=∠B
∴OD∥BC
∵DE⊥AB,OD∥BC
∴DE⊥OD
∵OD是⊙O的半径
∴DE是⊙O的切线。
(2)解:连接AD,DG
∵AG是⊙O的直径
∴∠ADG=90
∵AC=BC,CO⊥AB
∴D是AB中点。
∵AD=3
∴AB=2AD=6
∵∠EDG+∠BDG=∠BDE=90 ,∠B+∠BDG=90
∴∠EDG=∠B
∵tan∠EDG=
∴tanB=
在Rt△ABD中,AD=3,AB=6
根据勾股定理可得BD=3
∵tanB==
设CO=x,则BO=3x
在Rt△BOC中,根据勾股定理BC2=CO2+BO2
∴BC=x
∵AB=6,D是AB中点,BD=3,且BC=,CD=CO=x
∴BC==x
解得x=3,即CO=3,BO=9
∵∠EDG=∠B,tan∠EDG=
设EG=y,则DE=3y
∵DE∥CO
∴△BDE∽△BOC
则=
BC=3,BE=BG EG,BG=
在Rt△ADG中,tan∠DAG=tanB=,AD=3
∴DG=,AG=2,BG=2
∴=
解得y=1
∴EG=1
22.(本小题满分10分)
项目任务1:设两车行驶里程为s千米。
∵A车每千米行驶费用为a元,总行驶费用7.5元,所以s=;
B车每千米行驶费用为(a+0.45)元,总行驶费用18.75元,所以s=
由于行驶里程相同,则=
解得a=0.3
经检验a=0.3是原方程的根
∴B车每千米行驶费用为0.3+0.45=0.75元。
项目任务 2:
∵A车一年总费用yA=6500+1230+0.3x=7730+0.3x;
B车一年总费用yB=2900+0.075x+0.75x=2900+0.825x。
当yA=yB时,
7730+0.3x=2900+0.825x
解得x=9200
yA>yB时,
7730+0.3x>2900+0.825x
解得x<9200
yA
解得x>9200
∴当x=9200时,购买A车和B车费用相同;当x<9200时,购买B车更划算;当x>9200时,购买A车更划算。
23.(本小题满分10 分)直线y=x+b与双曲线y=(x>0)交于点A(2,3),与y 轴交于点B。
(1)求 k,b 的值;
(2)如图 1,点 C 是直线y=x+b上第一象限内的一点,过点 C 作轴,垂足为点 E,交双曲线于点 D,当=时,求的值;
(3)如图 2,已知点 P 是双曲线上一动点,连接 OA,OP,当∠AOP=∠BAO时,求点 P 的坐标。
(1)将A(2,3)代入y=
得k=3×2=6
将A(2,3)代入y=x+b
得3=+b×2+b
解得b=2
(2)由(1)知直线y=x+b,B(0,2),A(2,3)
∵=
设C点横坐标为m,则C(m,m+2)
根据两点间距离公式得=
且C在第一象限,m>0
解得m=3
∴C(3,),D(3,2)
则=
(3)过A作AH⊥x轴于H,A(2,3),B(0,2),tan∠BAO=
∵∠AOP=∠BAO
∴设P(n,),直线OP的斜率kOP=
∴tan∠AOP=,又tan∠AOP=tan∠BAO=
则=
解得n=3或n= 3(舍去)
∴P(3,2)
24.(本小题满分 12 分)二次函数y=ax2+bx的图象过点A( 4,4),B(,),连接 AB,点 C 是抛物线上一个动点。
(1)求二次函数的表达式;
(2)如图 1,若点C 在 y 轴左侧的抛物线上运动,平移线段 AB,使其一个端点与点 C 重合,另一个端点恰好落在 x 轴上,求点 C 的坐标;
(3)如图 2,若点C 在 y 轴右侧的抛物线上运动,作直线 AC,交 x 轴于点 E,将直线 AC 绕点 A 逆时针旋转45°得直线AG,交y 轴于点F,连接 EF。若EF=FO,直接写出点 C 的坐标。
把A (-4.4), B(,)代入二次函数y=ax2+bx
得
解得
∴二次函数的表达式为 y=x2+3x
(2)设C(a,a2+3a),D(b,0).
①当点 B 与点 C 重合,
∵DC是由 AB 平移所得.则有
解得
将 a =-代入y=x2+3x得y=﹣
∴点C坐标为(-,﹣)
②当点 A 与点 C 重合
则有
解得a1=﹣(舍去),a2=﹣﹣
∴点C(﹣﹣,)
(3)C(,)
25.(本小题满分 12 分)在△ABC中,∠A=90°,AB=AC,点 D 在边 AC 上(点 D 不与点 A,点 C 重合),连接 BD 并将 BD 绕点 D 逆时针旋转 90° 得到 DE。
(1)如图 1,连接 CE。
① CE 与 BC 的位置关系为 ,∠ABD与∠CED的数量关系是 ;
②请用等式表示 BC,CD 和 CE 的数量关系,并说明理由;
(2)如图 2,将△ABD沿 BD 翻折,得到△A’BD,连接A’E,若A’E的最小值为 2,求 AB 的长。
(1)① CE⊥BC;∠ABD=∠CED
过D作DF⊥DC交BC于F
∵∠A=90 ,AB=AC
∴∠ACB=45 ,△DFC为等腰直角三角形,DF=DC
又∵BD=DE,∠BDF=∠EDC
∴△BDF≌△EDC(SAS)。
∴∠DFB=∠DCE=135
故∠BCE=135 45 =90
即CE⊥BC;且∠ABD=∠DEC=∠CED。
②BC=CE+CD
由△BDF≌△EDC
得BF=CE。
又∵△DFC是等腰直角三角形
根据勾股定理
FC=CD
∴BC=BF+FC=CE+CD
(2)AB=2
同课章节目录
