第六讲 平面直角坐标系及函数(含解析) 2025年中考数学基础知识分点练
文档属性
| 名称 | 第六讲 平面直角坐标系及函数(含解析) 2025年中考数学基础知识分点练 |  | |
| 格式 | docx | ||
| 文件大小 | 284.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 18:14:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六讲 平面直角坐标系及函数
命题点1 平面直角坐标系中点的坐标特征(179考)
1. (2024滨州)若点 P(1-2a,a)在第二象限,那么a的取值范围是( )
2.(2024扬州)在平面直角坐标系中,点P(1,2)关于坐标原点的对称点 P'的坐标为 ( )
A. (-1,-2) B. (-1,2) C. (1,-2) D. (1,2)
3.(2024雅安)在平面直角坐标系中,将点 P(1,-1)向右平移2个单位后,得到的点 P 关于x轴的对称点坐标是 ( )
A. (1,1) B. (3,1) C. (3,-1) D. (1,-1)
4.(2024贵州)为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”的坐标分别为 0),(0,0),则“技”所在的象限为 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5. 新考法 新定义(73考)(2024湖南省卷)在平面直角坐标系xOy中,对于点 P(x,y),若x,y均为整数,则称点 P为“整点”,特别地,当 (其中 的值为整数时,称“整点”P为“超整点”.已知点P(2a-4,a+3)在第二象限,下列说法正确的是 ( )
A. a<-3
B.若点 P为“整点”,则点 P的个数为3个
C.若点 P为“超整点”,则点 P 的个数为1个
D.若点P为“超整点”,则点 P到两坐标轴的距离之和大于10
6.(2024江西)在平面直角坐标系中,将点A(1,1)向右平移2个单位长度,再向上平移3个单位长度得到点 B,则点 B 的坐标为 .
7. 新考法结合尺规作图(57考)(2024齐齐哈尔)如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴正半轴于点M,交y轴正半轴于点N,再分别以点M,N为圆心,大于 的长为半径画弧,两弧在第一象限交于点 H,画射线OH,若 则
8. (2024广元)若点Q(x,y)满足 则称点Q 为“美好点”,写出一个“美好点”的坐标 .
命题点2 图形与坐标(12考)
9.(2024临夏州)如图,O是坐标原点,菱形ABOC的顶点B在x轴的负半轴上,顶点C 的坐标为(3,4),则顶点A 的坐标为 ( )
A. (-4,2) C. (-2,4)
10.(2024包头)如图,在平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(1,2),B(3,3),C(5,0),则四边形OABC的面积为 ( )
A. 14 B. 11
C. 10 D. 9
命题点3 函数自变量的取值范围(26考)
11. (2024泸州)函数 的自变量x的取值范围是 .
12. (2024 滨州)若函数 的解析式在实数范围内有意义,则自变量x的取值范围是 .
13. (2024齐齐哈尔)在函数 中,自变量x的取值范围是 .
命题点4 分析、判断函数图象 重难
类型一 实际问题(50考)
14.(2024江西)将常温中的温度计插入一杯( 的热水(恒温)中,温度计的读数 与时间x(min)的关系用图象可近似表示为( )
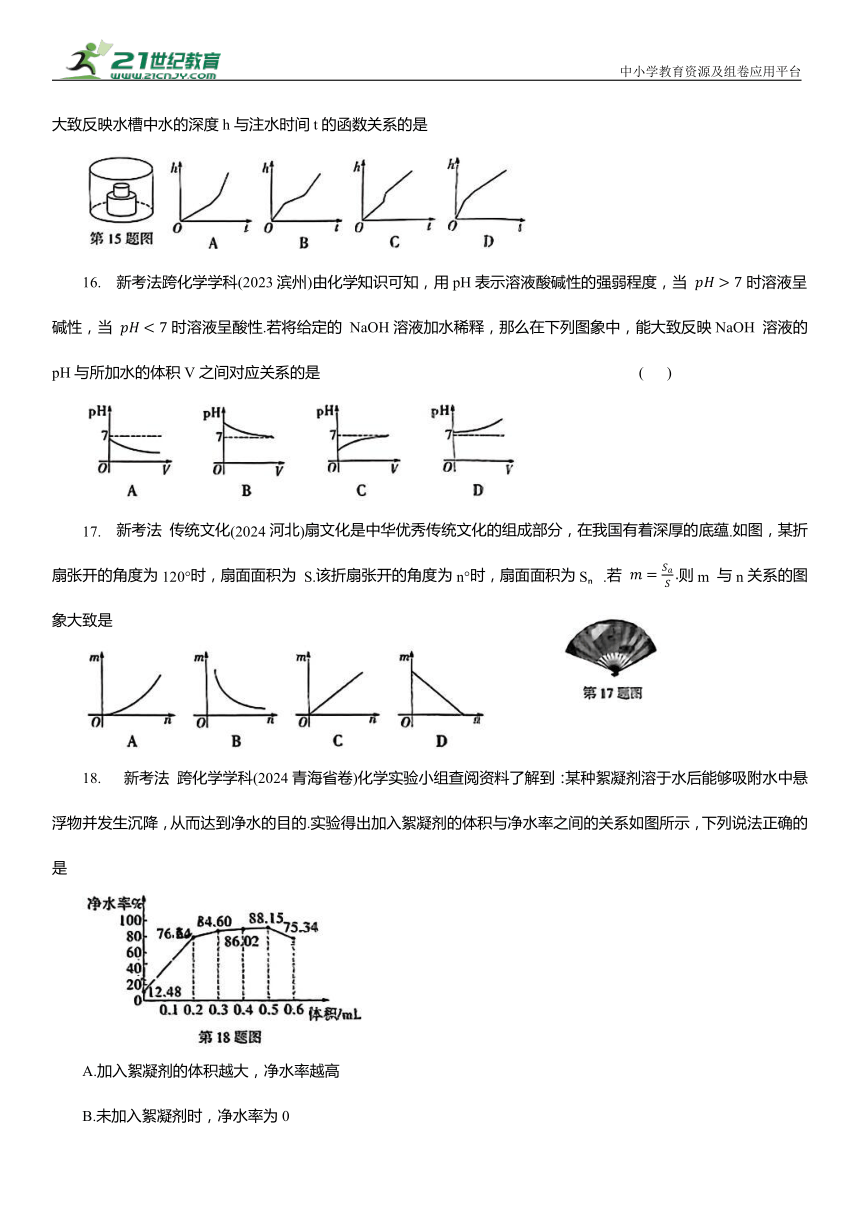
15.(2024武汉)如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反映水槽中水的深度h与注水时间t的函数关系的是
16. 新考法跨化学学科(2023滨州)由化学知识可知,用pH表示溶液酸碱性的强弱程度,当 时溶液呈碱性,当 时溶液呈酸性.若将给定的 NaOH溶液加水稀释,那么在下列图象中,能大致反映NaOH 溶液的pH与所加水的体积V之间对应关系的是 ( )
17. 新考法 传统文化(2024河北)扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为120°时,扇面面积为 S.该折扇张开的角度为n°时,扇面面积为S .若 则m 与n关系的图象大致是
18. 新考法 跨化学学科(2024青海省卷)化学实验小组查阅资料了解到:某种絮凝剂溶于水后能够吸附水中悬浮物并发生沉降,从而达到净水的目的.实验得出加入絮凝剂的体积与净水率之间的关系如图所示,下列说法正确的是
A.加入絮凝剂的体积越大,净水率越高
B.未加入絮凝剂时,净水率为0
C.絮凝剂的体积每增加0.1mL,净水率的增加量相等
D.加入絮凝剂的体积是0.2mL时,净水率达到76.54%
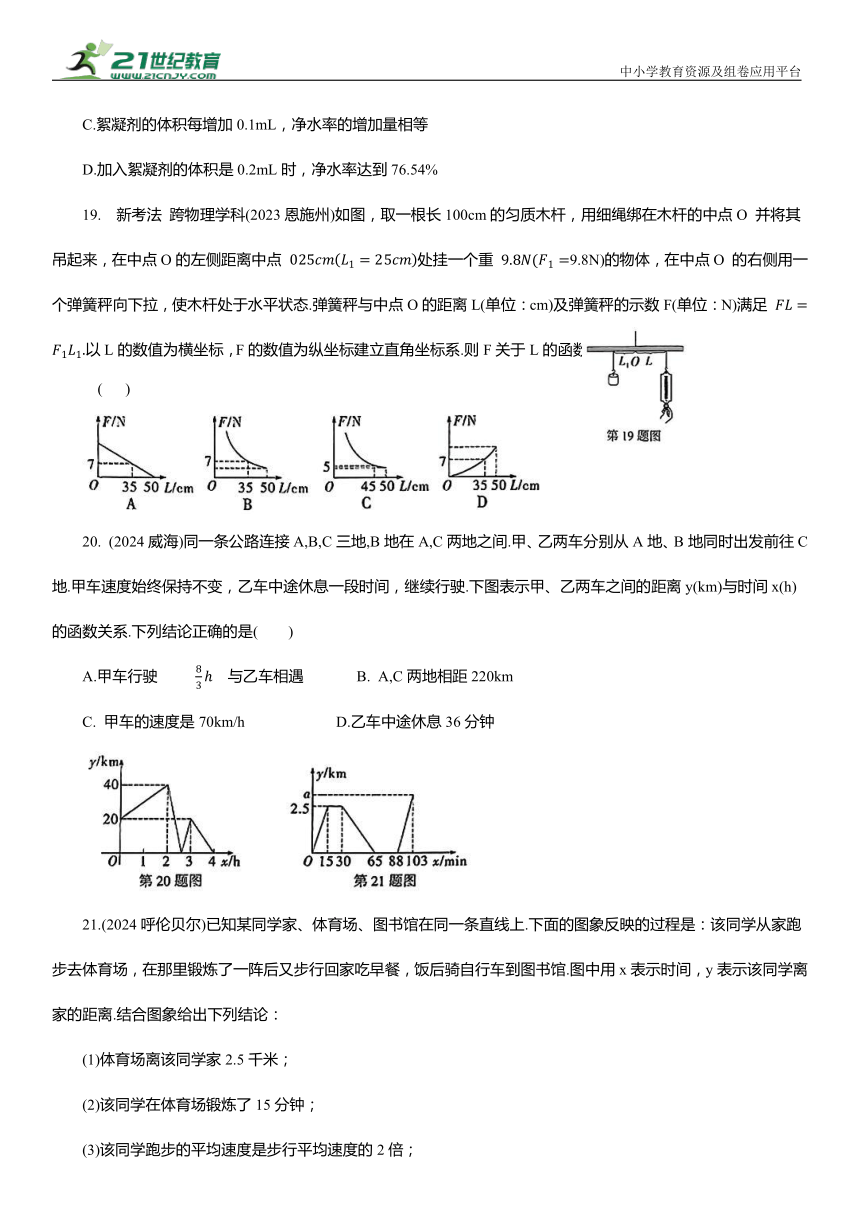
19. 新考法 跨物理学科(2023恩施州)如图,取一根长100cm的匀质木杆,用细绳绑在木杆的中点O 并将其吊起来,在中点O的左侧距离中点 处挂一个重 9.8N)的物体,在中点O 的右侧用一个弹簧秤向下拉,使木杆处于水平状态.弹簧秤与中点O的距离L(单位:cm)及弹簧秤的示数F(单位:N)满足 以L的数值为横坐标,F的数值为纵坐标建立直角坐标系.则F关于L的函数图象大致是 ( )
20. (2024威海)同一条公路连接A,B,C三地,B地在A,C两地之间.甲、乙两车分别从A地、B地同时出发前往C地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.下图表示甲、乙两车之间的距离y(km)与时间x(h)的函数关系.下列结论正确的是( )
A.甲车行驶 与乙车相遇 B. A,C两地相距220km
C. 甲车的速度是70km/h D.乙车中途休息36分钟
21.(2024呼伦贝尔)已知某同学家、体育场、图书馆在同一条直线上.下面的图象反映的过程是:该同学从家跑步去体育场,在那里锻炼了一阵后又步行回家吃早餐,饭后骑自行车到图书馆.图中用x表示时间,y表示该同学离家的距离.结合图象给出下列结论:
(1)体育场离该同学家2.5千米;
(2)该同学在体育场锻炼了15分钟;
(3)该同学跑步的平均速度是步行平均速度的2倍;
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,则a的值是3.75.
其中正确结论的个数是 ( )
A. 1 B. 2 C. 3 D. 4
类型二 几何图形中的动态问题(106考)
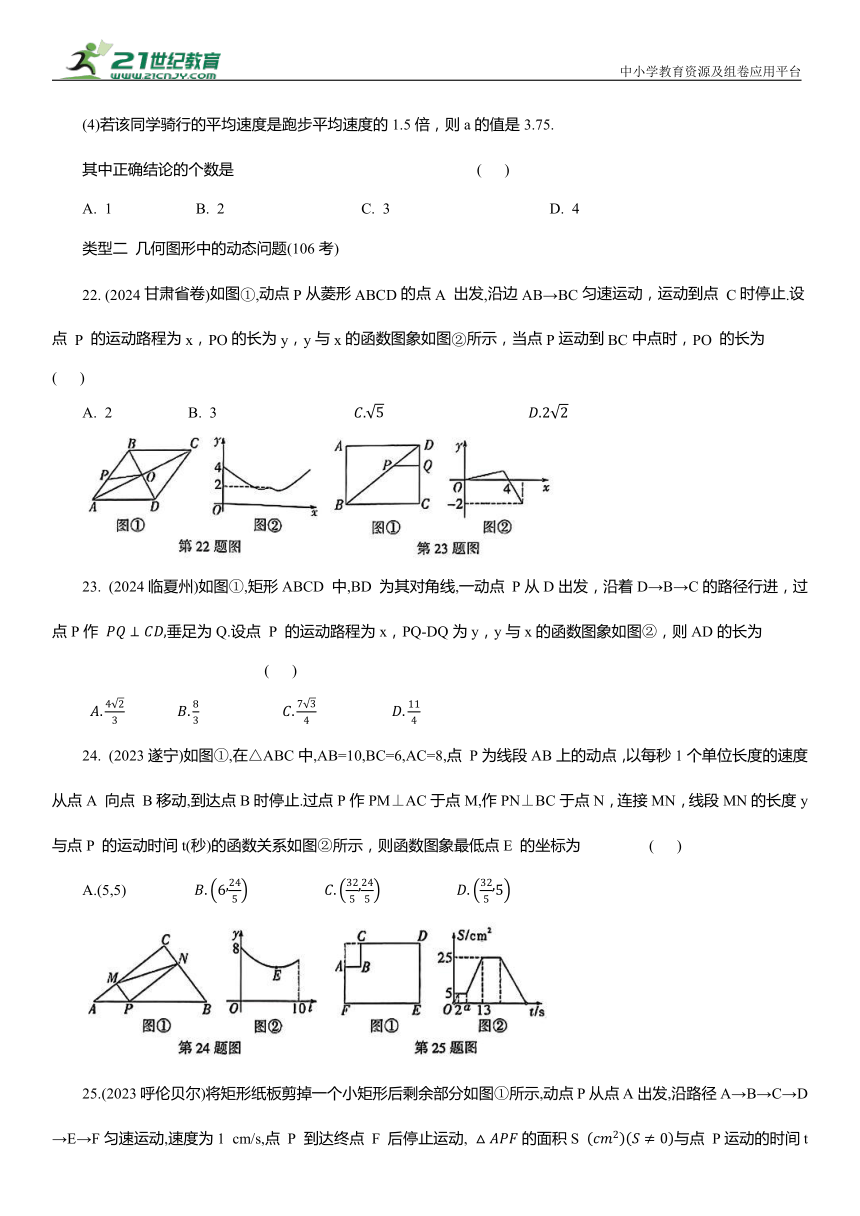
22. (2024甘肃省卷)如图①,动点P从菱形ABCD的点A 出发,沿边AB→BC匀速运动,运动到点 C时停止.设点 P 的运动路程为x,PO的长为y,y与x的函数图象如图②所示,当点P运动到BC中点时,PO 的长为 ( )
A. 2 B. 3
23. (2024临夏州)如图①,矩形ABCD 中,BD 为其对角线,一动点 P从D出发,沿着D→B→C的路径行进,过点P作 垂足为Q.设点 P 的运动路程为x,PQ-DQ为y,y与x的函数图象如图②,则AD的长为 ( )
24. (2023遂宁)如图①,在△ABC中,AB=10,BC=6,AC=8,点 P为线段AB上的动点,以每秒1个单位长度的速度从点A 向点 B移动,到达点B时停止.过点P作PM⊥AC于点M,作PN⊥BC于点N,连接MN,线段MN的长度y与点P 的运动时间t(秒)的函数关系如图②所示,则函数图象最低点E 的坐标为 ( )
A.(5,5)
25.(2023呼伦贝尔)将矩形纸板剪掉一个小矩形后剩余部分如图①所示,动点P从点A出发,沿路径A→B→C→D→E→F匀速运动,速度为1 cm/s,点 P 到达终点 F 后停止运动, 的面积S 与点 P运动的时间t(s)的关系如图②所示,根据图象获取了以下的信息:
①AF=5cm;
③点 P从点 E运动到点 F需要10s;
④矩形纸板裁剪前后周长均为34 cm.
其中正确信息的个数有 ( )
A.4个 B.3个 C.2个 D. 1个
26. (2024齐齐哈尔)如图,在等腰 中, 动点E,F同时从点A 出发,分别沿射线AB 和射线AC的方向匀速运动,且速度大小相同,当点E停止运动时,点F 也随之停止运动,连接EF,以EF为边向下做正方形EFGH,设点 E 运动的路程为 正方形EFGH 和等腰 重合部分的面积为y,下列图象能反映y与x之间函数关系的是 ( )
27. (2024安徽)如图,在 中,∠ABC=90°,AB=4,BC=2,BD是边AC上的高.点E,F分别在边AB,BC上(不与端点重合),且 设 ,四边形DEBF 的面积为y,则y关于x的函数图象为 ( )
28. (2024广元)如图①,在 中, 点P 从点A 出发沿A→C→B以1cm/s的速度匀速运动至点B,图②是点 P运动时, 的面积 随时间x(s)变化的函数图象,则该三角形的斜边AB 的长为( )
A. 5 B. 7
29. (2024烟台)如图,水平放置的矩形ABCD中, 8cm.菱形EFGH的顶点E,G在同一水平线上,点G与AB的中点重合, 现将菱形EFGH以 的速度沿 BC方向匀速运动,当点 E运动到 CD上时停止.在这个运动过程中,菱形 EFGH与矩形ABCD 重叠部分的面积. 与运动时间 t(s)之间的函数关系图象大致是 ( )
第六讲 平面直角坐标系及函数
1. A 【解析】∵点P(1-2a,a)在第二象限 解得
2. A 【解析】点(x,y)关于原点对称的点的坐标为(-x,-y),∴点P(1,2)关于坐标原点的对称点 P'的坐标为(-1,-2).
3. B 【解析】将点 P(1,-1)向右平移2个单位后得到的点 P 坐标为(3,-1),点P (3,-1)关于x轴的对称点坐标为(3,1).
4. A 【解析】根据题意,“新”的坐标为(0,0),其位置是坐标原点,“创”的坐标为(-2,0),其位置在x轴负半轴上,∴以“新”为原点,向右为x轴正方向,向上为y轴正方向建立平面直角坐标系,可得“技”字坐标是(1,1),∴“技”在第一象限.
5. 解题思路
本题以新定义的形式,考查了点到坐标轴的距离,各象限内点的特征等知识,需要先利用各象限内点的特征求出a的取值范围,再进一步结合“整点”,“超整点”的定义判断各选项的正误.
C 【解析】∵ 点 P(2a-4,a+3)在第二象限,∴ 故 A 选项错误;∵点 P(2a-4,a+3)为“整点”, - 36.(3,4) 【解析】将点A向右平移2个单位长度为(3,1),再向上平移3个单位长度为(3,4).
7.2 【解析】根据作图痕迹可得点H在第一象限角平分线上,点H横纵坐标相等且为正数,∴2a-1=a+1,解得a=2.
8. (2,-1)(答案不唯一) 【解析】等式两边同时乘 xy,得x+y=1,令x=2,则y=-1,∴“美好点”的坐标可以为(2,-1).
9. C 【解析】如解图,过点C作CN⊥x轴于点N,过点A作AM⊥x轴于点 M,∵点C的坐标为(3,4),∴ON= ;四边形ABOC是菱形,∴AC=OC=5,AC∥BO,∴四边形AMNC是矩形,∴MN=AC=5,AM=CN=4,∴OM=MN-ON=2,∴点A的坐标为(-2,4).
10. D 【解析】如解图,过点A作AM⊥OC 于点 M,过点B作BN⊥OC于点N,∵O(0,0),A(1,2),B(3,3),C(5,0),∴OM=1,AM=2,ON=BN=3,CO=5,∴MN=ON-OM=2,CN=OC-ON=2,∴四边形OABC的面积为
11. x≥-2 【解析】∵ 在实数范围内有意义,∴x+2≥0,∴x≥-2.
12. x≠1 【解析】∵ 分式 在实数范围内有意义,∴x-1≠0,解得x≠1.
13. x>-3且x≠-2 【解析】由题意可得 解得x>-3且x≠-2.
14. C 【解析】将常温中的温度计插入60℃的热水中,温度计的读数首先会上升,又∵热水恒温,∴温度计的读数上升到60℃后保持不变,故C选项符合题意.
易错点拨
因为热水恒温,所以温度计的读数上升至60℃后便保持不变.
15. D 【解析】下层圆柱底面半径大,水面上升快,上层圆柱底面半径稍小,水面上升稍慢,再往上则水面上升更慢,所以对应图象是第一段比较陡,第二段比第一段缓,第三段比第二段缓.
16. B 【解析】∵ NaOH溶液呈碱性,则pH>7,随着加入水的体积的增加,溶液的浓度越来越低,∴pH的值越来越接近7.
17. C 【解析】由题意得 是关于n的正比例函数.
18. D 【解析】由题图可知加入絮凝剂的体积是0.5mL时,净水率为88.15%,加入絮凝剂的体积是0.6mL时,净水率为75.34%,∵88.15%>75.34%,∴A 选项错误;由题图可知,加入絮凝剂的体积为0时,净水率为12.48%,故B选项错误;由题图可知,加入絮凝剂的体积由 0.2 mL 到0.3 mL 时,净水率增加了84.60%-76.54%=8. 06%,加入絮凝剂的体积由0.3 mL到0.4 mL时,净水率增加了86.02%-84.60%=1.42%,8.06%≠1.42%,∴C 选项错误;由题图可知,加入絮凝剂的体积为0.2mL时,净水率为76.54%,故D选项正确.
19. B 【解析】由题意可得 FL=9.8×25=245,∴图象是反比例函数 位于第一象限的一部分,∵35×7=245,∴B 选项符合题意.
20.解题思路
本题是不同出发地点且同时出发的追及问题,y轴表示甲、乙两车之间的距离,x轴表示时间,所以函数图象的起点就是A,B两地间的距离,再分析函数图象上的每一个拐点所代表的意义及y随x的增大而变化的情况,结合列方程求解.
A 【解析】如解图,可知A,B两地之间的距离为20km,两车行驶了4h,同时到达C地,在1~2h,两车同向运动,在第2 h,即点 D时,两者距离发生改变,此时乙车开始休息,E点的意义是两车相遇,F点意义是乙车休息后再出发,∴乙车休息了1 h,故D 不正确,不符合题意;设甲车的速度为a km/h,1~2h里,乙车的速度为b km/h,根据题意,1~2h甲、乙之间距离增大,则甲车的速度比乙车的速度慢,a21. C 【解析】由图象可知:体育场离该同学家2.5千米,故(1)正确;该同学在体育场锻炼了30-15=15
(分钟),故(2)正确;该同学的跑步速度为2.5÷15= (千米/分钟),步行速度为 千米/分钟),则跑步速度是步行速度的 倍,故(3)错误;若该同学骑行的平均速度是跑步平均速度的1.5倍,则该同学骑行的平均速度为 (千米/分钟),所以 故(4)正确,故选 C.
22. C 【解析】由题图知,当P点从A点运动到B点时,PO 的长度先减小后增大,当P点从B点运动到C点时,PO的长度先减小后增大,当x=0时,PO=AO=4,当点 P 运动到点B时,PO=BO=2,∵四边形ABCD是菱形,∴∠AOB=∠BOC=90°,∴ 在 Rt△AOB 中, ∴ 当点 P运动到BC中点时,PO 的长为
23. B 【解析】由图象得,CD=2,当x=4,y=0,可知点P在BC上,此时点 Q 与点 C 重合,当BD+BP=4时,PQ=CD=2,设BP=a,则BD=4-a,BC=AD=a+2,在Rt△BCD中, 即 2 ,解得
24. C 【解析】如解图,连接PC,∵AB=10,BC=6,AC=8,∴ AB = BC +AC ,∴ ∠ACB=90°,∵ PM⊥AC,PN⊥BC,∴ 四边形 PMCN 为矩形,∴ PC=MN,当PC⊥AB 时,PC 最短,由等积法可知 又∵ tan A= 故函数图象最低点E的坐标为
25. C 【解析】如解图,由题意和图象可得,点P 在AB上运动时S和t的关系在图象上表示为 OM 段,在BC上运动时S和t的关系在图象上表示为MN段,在 CD上运动时 S 和t 的关系在图象上表示为 NG段,在DE上运动时S 和t的关系在图象上表示为GQ段,在EF上运动时S 和t的关系在图象上表示为QY段,当S=5,t=2时,点P运动到点B处,∴AB 解得AF=5,①正确;∵S=25,t=13时,点 P 运动到点 D处,∴此时△APF 底边AF上的高 解得a=5,②错误;∴EF=CD+AB=10(cm),BC=a-2=3(cm),∴DE=AF+BC=8(cm),∵点P的速度为1 cm/s,∴点 P 从点 E运动到点 F需要10s,③正确;∵矩形纸板裁剪前后周长不变,∴矩形纸板周长=2(DE+FE)=36(cm),④错误.故正确信息的个数为2个.
26. A 【解析】当 HG 与 BC 重合时,由题可知AE= 在Rt△EHB中,由勾股定理可得 (负值已舍去),∴当027.A
28. A 【解析】由图象可知,△ABP 面积的最大值为6,由题意可得,当点 P 运动到点C时,△ABP的面积最大 即AC·BC=12,由图象可知,当x=7时,y=0,此时点 P 运动到点 B,∵点 P 的速度为1 cm/s,∴ AC+BC=7,∵ ∠ACB=90°,∴ AB = 25,∴AB=5(负值已舍去).
29.D
解题思路
先求得菱形的面积,再分不同情形讨论,重合部分为三角形,重合部分为五边形,重合部分为菱形,分别求得重叠部分的面积与运动时间的函数关系式,再根据对称性求解.
第六讲 平面直角坐标系及函数
命题点1 平面直角坐标系中点的坐标特征(179考)
1. (2024滨州)若点 P(1-2a,a)在第二象限,那么a的取值范围是( )
2.(2024扬州)在平面直角坐标系中,点P(1,2)关于坐标原点的对称点 P'的坐标为 ( )
A. (-1,-2) B. (-1,2) C. (1,-2) D. (1,2)
3.(2024雅安)在平面直角坐标系中,将点 P(1,-1)向右平移2个单位后,得到的点 P 关于x轴的对称点坐标是 ( )
A. (1,1) B. (3,1) C. (3,-1) D. (1,-1)
4.(2024贵州)为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”的坐标分别为 0),(0,0),则“技”所在的象限为 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5. 新考法 新定义(73考)(2024湖南省卷)在平面直角坐标系xOy中,对于点 P(x,y),若x,y均为整数,则称点 P为“整点”,特别地,当 (其中 的值为整数时,称“整点”P为“超整点”.已知点P(2a-4,a+3)在第二象限,下列说法正确的是 ( )
A. a<-3
B.若点 P为“整点”,则点 P的个数为3个
C.若点 P为“超整点”,则点 P 的个数为1个
D.若点P为“超整点”,则点 P到两坐标轴的距离之和大于10
6.(2024江西)在平面直角坐标系中,将点A(1,1)向右平移2个单位长度,再向上平移3个单位长度得到点 B,则点 B 的坐标为 .
7. 新考法结合尺规作图(57考)(2024齐齐哈尔)如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴正半轴于点M,交y轴正半轴于点N,再分别以点M,N为圆心,大于 的长为半径画弧,两弧在第一象限交于点 H,画射线OH,若 则
8. (2024广元)若点Q(x,y)满足 则称点Q 为“美好点”,写出一个“美好点”的坐标 .
命题点2 图形与坐标(12考)
9.(2024临夏州)如图,O是坐标原点,菱形ABOC的顶点B在x轴的负半轴上,顶点C 的坐标为(3,4),则顶点A 的坐标为 ( )
A. (-4,2) C. (-2,4)
10.(2024包头)如图,在平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(1,2),B(3,3),C(5,0),则四边形OABC的面积为 ( )
A. 14 B. 11
C. 10 D. 9
命题点3 函数自变量的取值范围(26考)
11. (2024泸州)函数 的自变量x的取值范围是 .
12. (2024 滨州)若函数 的解析式在实数范围内有意义,则自变量x的取值范围是 .
13. (2024齐齐哈尔)在函数 中,自变量x的取值范围是 .
命题点4 分析、判断函数图象 重难
类型一 实际问题(50考)
14.(2024江西)将常温中的温度计插入一杯( 的热水(恒温)中,温度计的读数 与时间x(min)的关系用图象可近似表示为( )
15.(2024武汉)如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反映水槽中水的深度h与注水时间t的函数关系的是
16. 新考法跨化学学科(2023滨州)由化学知识可知,用pH表示溶液酸碱性的强弱程度,当 时溶液呈碱性,当 时溶液呈酸性.若将给定的 NaOH溶液加水稀释,那么在下列图象中,能大致反映NaOH 溶液的pH与所加水的体积V之间对应关系的是 ( )
17. 新考法 传统文化(2024河北)扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为120°时,扇面面积为 S.该折扇张开的角度为n°时,扇面面积为S .若 则m 与n关系的图象大致是
18. 新考法 跨化学学科(2024青海省卷)化学实验小组查阅资料了解到:某种絮凝剂溶于水后能够吸附水中悬浮物并发生沉降,从而达到净水的目的.实验得出加入絮凝剂的体积与净水率之间的关系如图所示,下列说法正确的是
A.加入絮凝剂的体积越大,净水率越高
B.未加入絮凝剂时,净水率为0
C.絮凝剂的体积每增加0.1mL,净水率的增加量相等
D.加入絮凝剂的体积是0.2mL时,净水率达到76.54%
19. 新考法 跨物理学科(2023恩施州)如图,取一根长100cm的匀质木杆,用细绳绑在木杆的中点O 并将其吊起来,在中点O的左侧距离中点 处挂一个重 9.8N)的物体,在中点O 的右侧用一个弹簧秤向下拉,使木杆处于水平状态.弹簧秤与中点O的距离L(单位:cm)及弹簧秤的示数F(单位:N)满足 以L的数值为横坐标,F的数值为纵坐标建立直角坐标系.则F关于L的函数图象大致是 ( )
20. (2024威海)同一条公路连接A,B,C三地,B地在A,C两地之间.甲、乙两车分别从A地、B地同时出发前往C地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.下图表示甲、乙两车之间的距离y(km)与时间x(h)的函数关系.下列结论正确的是( )
A.甲车行驶 与乙车相遇 B. A,C两地相距220km
C. 甲车的速度是70km/h D.乙车中途休息36分钟
21.(2024呼伦贝尔)已知某同学家、体育场、图书馆在同一条直线上.下面的图象反映的过程是:该同学从家跑步去体育场,在那里锻炼了一阵后又步行回家吃早餐,饭后骑自行车到图书馆.图中用x表示时间,y表示该同学离家的距离.结合图象给出下列结论:
(1)体育场离该同学家2.5千米;
(2)该同学在体育场锻炼了15分钟;
(3)该同学跑步的平均速度是步行平均速度的2倍;
(4)若该同学骑行的平均速度是跑步平均速度的1.5倍,则a的值是3.75.
其中正确结论的个数是 ( )
A. 1 B. 2 C. 3 D. 4
类型二 几何图形中的动态问题(106考)
22. (2024甘肃省卷)如图①,动点P从菱形ABCD的点A 出发,沿边AB→BC匀速运动,运动到点 C时停止.设点 P 的运动路程为x,PO的长为y,y与x的函数图象如图②所示,当点P运动到BC中点时,PO 的长为 ( )
A. 2 B. 3
23. (2024临夏州)如图①,矩形ABCD 中,BD 为其对角线,一动点 P从D出发,沿着D→B→C的路径行进,过点P作 垂足为Q.设点 P 的运动路程为x,PQ-DQ为y,y与x的函数图象如图②,则AD的长为 ( )
24. (2023遂宁)如图①,在△ABC中,AB=10,BC=6,AC=8,点 P为线段AB上的动点,以每秒1个单位长度的速度从点A 向点 B移动,到达点B时停止.过点P作PM⊥AC于点M,作PN⊥BC于点N,连接MN,线段MN的长度y与点P 的运动时间t(秒)的函数关系如图②所示,则函数图象最低点E 的坐标为 ( )
A.(5,5)
25.(2023呼伦贝尔)将矩形纸板剪掉一个小矩形后剩余部分如图①所示,动点P从点A出发,沿路径A→B→C→D→E→F匀速运动,速度为1 cm/s,点 P 到达终点 F 后停止运动, 的面积S 与点 P运动的时间t(s)的关系如图②所示,根据图象获取了以下的信息:
①AF=5cm;
③点 P从点 E运动到点 F需要10s;
④矩形纸板裁剪前后周长均为34 cm.
其中正确信息的个数有 ( )
A.4个 B.3个 C.2个 D. 1个
26. (2024齐齐哈尔)如图,在等腰 中, 动点E,F同时从点A 出发,分别沿射线AB 和射线AC的方向匀速运动,且速度大小相同,当点E停止运动时,点F 也随之停止运动,连接EF,以EF为边向下做正方形EFGH,设点 E 运动的路程为 正方形EFGH 和等腰 重合部分的面积为y,下列图象能反映y与x之间函数关系的是 ( )
27. (2024安徽)如图,在 中,∠ABC=90°,AB=4,BC=2,BD是边AC上的高.点E,F分别在边AB,BC上(不与端点重合),且 设 ,四边形DEBF 的面积为y,则y关于x的函数图象为 ( )
28. (2024广元)如图①,在 中, 点P 从点A 出发沿A→C→B以1cm/s的速度匀速运动至点B,图②是点 P运动时, 的面积 随时间x(s)变化的函数图象,则该三角形的斜边AB 的长为( )
A. 5 B. 7
29. (2024烟台)如图,水平放置的矩形ABCD中, 8cm.菱形EFGH的顶点E,G在同一水平线上,点G与AB的中点重合, 现将菱形EFGH以 的速度沿 BC方向匀速运动,当点 E运动到 CD上时停止.在这个运动过程中,菱形 EFGH与矩形ABCD 重叠部分的面积. 与运动时间 t(s)之间的函数关系图象大致是 ( )
第六讲 平面直角坐标系及函数
1. A 【解析】∵点P(1-2a,a)在第二象限 解得
2. A 【解析】点(x,y)关于原点对称的点的坐标为(-x,-y),∴点P(1,2)关于坐标原点的对称点 P'的坐标为(-1,-2).
3. B 【解析】将点 P(1,-1)向右平移2个单位后得到的点 P 坐标为(3,-1),点P (3,-1)关于x轴的对称点坐标为(3,1).
4. A 【解析】根据题意,“新”的坐标为(0,0),其位置是坐标原点,“创”的坐标为(-2,0),其位置在x轴负半轴上,∴以“新”为原点,向右为x轴正方向,向上为y轴正方向建立平面直角坐标系,可得“技”字坐标是(1,1),∴“技”在第一象限.
5. 解题思路
本题以新定义的形式,考查了点到坐标轴的距离,各象限内点的特征等知识,需要先利用各象限内点的特征求出a的取值范围,再进一步结合“整点”,“超整点”的定义判断各选项的正误.
C 【解析】∵ 点 P(2a-4,a+3)在第二象限,∴ 故 A 选项错误;∵点 P(2a-4,a+3)为“整点”, - 3
7.2 【解析】根据作图痕迹可得点H在第一象限角平分线上,点H横纵坐标相等且为正数,∴2a-1=a+1,解得a=2.
8. (2,-1)(答案不唯一) 【解析】等式两边同时乘 xy,得x+y=1,令x=2,则y=-1,∴“美好点”的坐标可以为(2,-1).
9. C 【解析】如解图,过点C作CN⊥x轴于点N,过点A作AM⊥x轴于点 M,∵点C的坐标为(3,4),∴ON= ;四边形ABOC是菱形,∴AC=OC=5,AC∥BO,∴四边形AMNC是矩形,∴MN=AC=5,AM=CN=4,∴OM=MN-ON=2,∴点A的坐标为(-2,4).
10. D 【解析】如解图,过点A作AM⊥OC 于点 M,过点B作BN⊥OC于点N,∵O(0,0),A(1,2),B(3,3),C(5,0),∴OM=1,AM=2,ON=BN=3,CO=5,∴MN=ON-OM=2,CN=OC-ON=2,∴四边形OABC的面积为
11. x≥-2 【解析】∵ 在实数范围内有意义,∴x+2≥0,∴x≥-2.
12. x≠1 【解析】∵ 分式 在实数范围内有意义,∴x-1≠0,解得x≠1.
13. x>-3且x≠-2 【解析】由题意可得 解得x>-3且x≠-2.
14. C 【解析】将常温中的温度计插入60℃的热水中,温度计的读数首先会上升,又∵热水恒温,∴温度计的读数上升到60℃后保持不变,故C选项符合题意.
易错点拨
因为热水恒温,所以温度计的读数上升至60℃后便保持不变.
15. D 【解析】下层圆柱底面半径大,水面上升快,上层圆柱底面半径稍小,水面上升稍慢,再往上则水面上升更慢,所以对应图象是第一段比较陡,第二段比第一段缓,第三段比第二段缓.
16. B 【解析】∵ NaOH溶液呈碱性,则pH>7,随着加入水的体积的增加,溶液的浓度越来越低,∴pH的值越来越接近7.
17. C 【解析】由题意得 是关于n的正比例函数.
18. D 【解析】由题图可知加入絮凝剂的体积是0.5mL时,净水率为88.15%,加入絮凝剂的体积是0.6mL时,净水率为75.34%,∵88.15%>75.34%,∴A 选项错误;由题图可知,加入絮凝剂的体积为0时,净水率为12.48%,故B选项错误;由题图可知,加入絮凝剂的体积由 0.2 mL 到0.3 mL 时,净水率增加了84.60%-76.54%=8. 06%,加入絮凝剂的体积由0.3 mL到0.4 mL时,净水率增加了86.02%-84.60%=1.42%,8.06%≠1.42%,∴C 选项错误;由题图可知,加入絮凝剂的体积为0.2mL时,净水率为76.54%,故D选项正确.
19. B 【解析】由题意可得 FL=9.8×25=245,∴图象是反比例函数 位于第一象限的一部分,∵35×7=245,∴B 选项符合题意.
20.解题思路
本题是不同出发地点且同时出发的追及问题,y轴表示甲、乙两车之间的距离,x轴表示时间,所以函数图象的起点就是A,B两地间的距离,再分析函数图象上的每一个拐点所代表的意义及y随x的增大而变化的情况,结合列方程求解.
A 【解析】如解图,可知A,B两地之间的距离为20km,两车行驶了4h,同时到达C地,在1~2h,两车同向运动,在第2 h,即点 D时,两者距离发生改变,此时乙车开始休息,E点的意义是两车相遇,F点意义是乙车休息后再出发,∴乙车休息了1 h,故D 不正确,不符合题意;设甲车的速度为a km/h,1~2h里,乙车的速度为b km/h,根据题意,1~2h甲、乙之间距离增大,则甲车的速度比乙车的速度慢,a
(分钟),故(2)正确;该同学的跑步速度为2.5÷15= (千米/分钟),步行速度为 千米/分钟),则跑步速度是步行速度的 倍,故(3)错误;若该同学骑行的平均速度是跑步平均速度的1.5倍,则该同学骑行的平均速度为 (千米/分钟),所以 故(4)正确,故选 C.
22. C 【解析】由题图知,当P点从A点运动到B点时,PO 的长度先减小后增大,当P点从B点运动到C点时,PO的长度先减小后增大,当x=0时,PO=AO=4,当点 P 运动到点B时,PO=BO=2,∵四边形ABCD是菱形,∴∠AOB=∠BOC=90°,∴ 在 Rt△AOB 中, ∴ 当点 P运动到BC中点时,PO 的长为
23. B 【解析】由图象得,CD=2,当x=4,y=0,可知点P在BC上,此时点 Q 与点 C 重合,当BD+BP=4时,PQ=CD=2,设BP=a,则BD=4-a,BC=AD=a+2,在Rt△BCD中, 即 2 ,解得
24. C 【解析】如解图,连接PC,∵AB=10,BC=6,AC=8,∴ AB = BC +AC ,∴ ∠ACB=90°,∵ PM⊥AC,PN⊥BC,∴ 四边形 PMCN 为矩形,∴ PC=MN,当PC⊥AB 时,PC 最短,由等积法可知 又∵ tan A= 故函数图象最低点E的坐标为
25. C 【解析】如解图,由题意和图象可得,点P 在AB上运动时S和t的关系在图象上表示为 OM 段,在BC上运动时S和t的关系在图象上表示为MN段,在 CD上运动时 S 和t 的关系在图象上表示为 NG段,在DE上运动时S 和t的关系在图象上表示为GQ段,在EF上运动时S 和t的关系在图象上表示为QY段,当S=5,t=2时,点P运动到点B处,∴AB 解得AF=5,①正确;∵S=25,t=13时,点 P 运动到点 D处,∴此时△APF 底边AF上的高 解得a=5,②错误;∴EF=CD+AB=10(cm),BC=a-2=3(cm),∴DE=AF+BC=8(cm),∵点P的速度为1 cm/s,∴点 P 从点 E运动到点 F需要10s,③正确;∵矩形纸板裁剪前后周长不变,∴矩形纸板周长=2(DE+FE)=36(cm),④错误.故正确信息的个数为2个.
26. A 【解析】当 HG 与 BC 重合时,由题可知AE= 在Rt△EHB中,由勾股定理可得 (负值已舍去),∴当0
28. A 【解析】由图象可知,△ABP 面积的最大值为6,由题意可得,当点 P 运动到点C时,△ABP的面积最大 即AC·BC=12,由图象可知,当x=7时,y=0,此时点 P 运动到点 B,∵点 P 的速度为1 cm/s,∴ AC+BC=7,∵ ∠ACB=90°,∴ AB = 25,∴AB=5(负值已舍去).
29.D
解题思路
先求得菱形的面积,再分不同情形讨论,重合部分为三角形,重合部分为五边形,重合部分为菱形,分别求得重叠部分的面积与运动时间的函数关系式,再根据对称性求解.
同课章节目录
