第十九讲 圆的基本性质(含解析)2025年中考数学基础知识分点练
文档属性
| 名称 | 第十九讲 圆的基本性质(含解析)2025年中考数学基础知识分点练 |  | |
| 格式 | docx | ||
| 文件大小 | 439.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 21:03:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十九讲 圆的基本性质
命题点1 圆周角定理及其推论有关的计算(41考)
1. (2024湖南省卷)如图,AB,AC为⊙O的两条弦,连接OB,OC,若∠A=45°,则∠BOC的度数为 ( )
A. 60° B. 75° C. 90° D. 135°
2. (2024云南)如图,CD是⊙O的直径,点A,B在⊙O上.若 则∠D= ( )
A. 9° B. 18° C. 36° D. 45°
3. (2024宜宾)如图,△ABC内接于⊙O,BC为⊙O的直径,AD平分∠BAC交⊙O于D,则 的值为 ( )
4. (2024陕西)如图,BC是⊙O 的弦,连接OB,OC,∠A 是 所对的圆周角,则∠A与 的和的度数是 .
5. (2024山东省卷)如图, 是⊙O的内接三角形.若 则
6. (2024连云港)如图,AB 是圆的直径, 的顶点均在AB 上方的圆弧上, 的一边分别经过点A,B,则
7. (2024眉山)如图,△ABC内接于⊙O,点O在AB上,AD平分∠BAC交⊙O于D,连接BD.若AB=10,BD=2 ,则BC的长为 .
命题点2 圆内接四边形(58考)
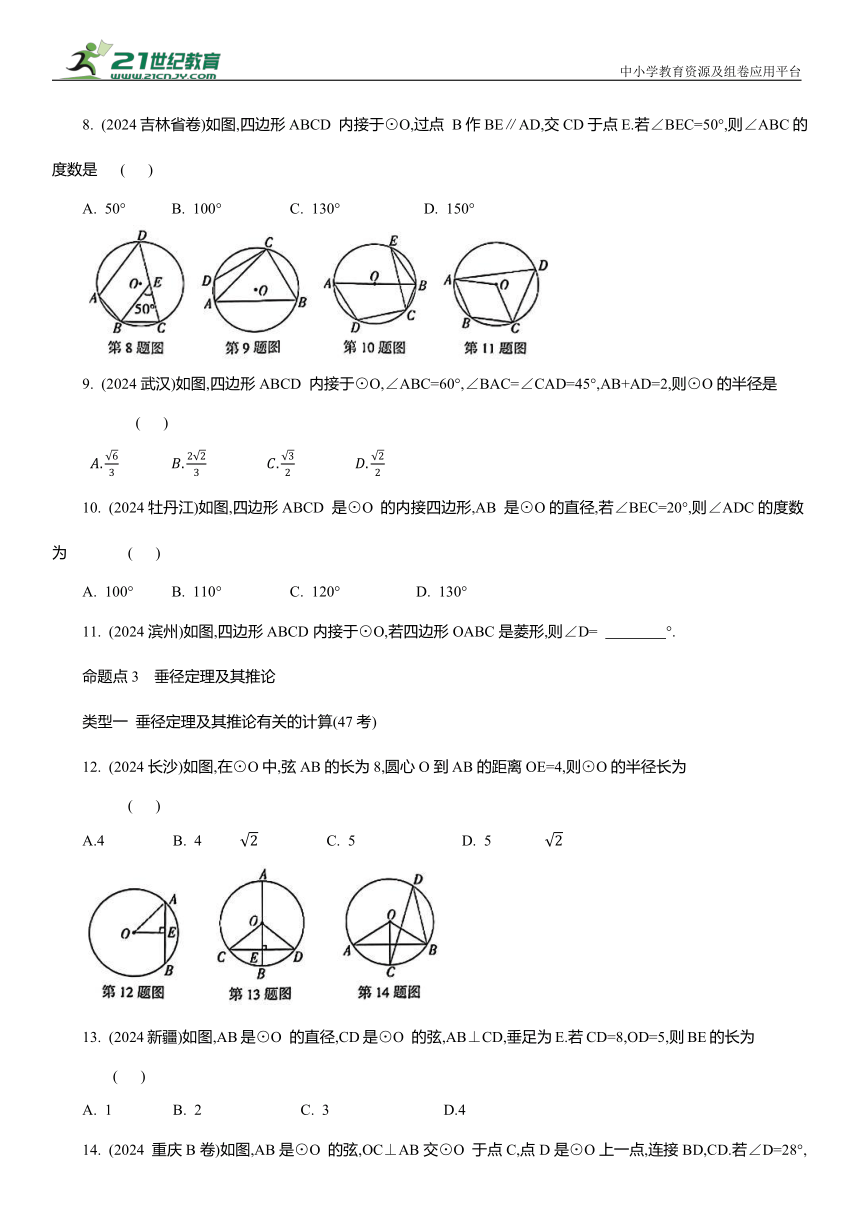
8. (2024吉林省卷)如图,四边形ABCD 内接于⊙O,过点 B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是 ( )
A. 50° B. 100° C. 130° D. 150°
9. (2024武汉)如图,四边形ABCD 内接于⊙O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径是 ( )
10. (2024牡丹江)如图,四边形ABCD 是⊙O 的内接四边形,AB 是⊙O的直径,若∠BEC=20°,则∠ADC的度数为 ( )
A. 100° B. 110° C. 120° D. 130°
11. (2024滨州)如图,四边形ABCD内接于⊙O,若四边形OABC是菱形,则∠D= °.
命题点3 垂径定理及其推论
类型一 垂径定理及其推论有关的计算(47考)
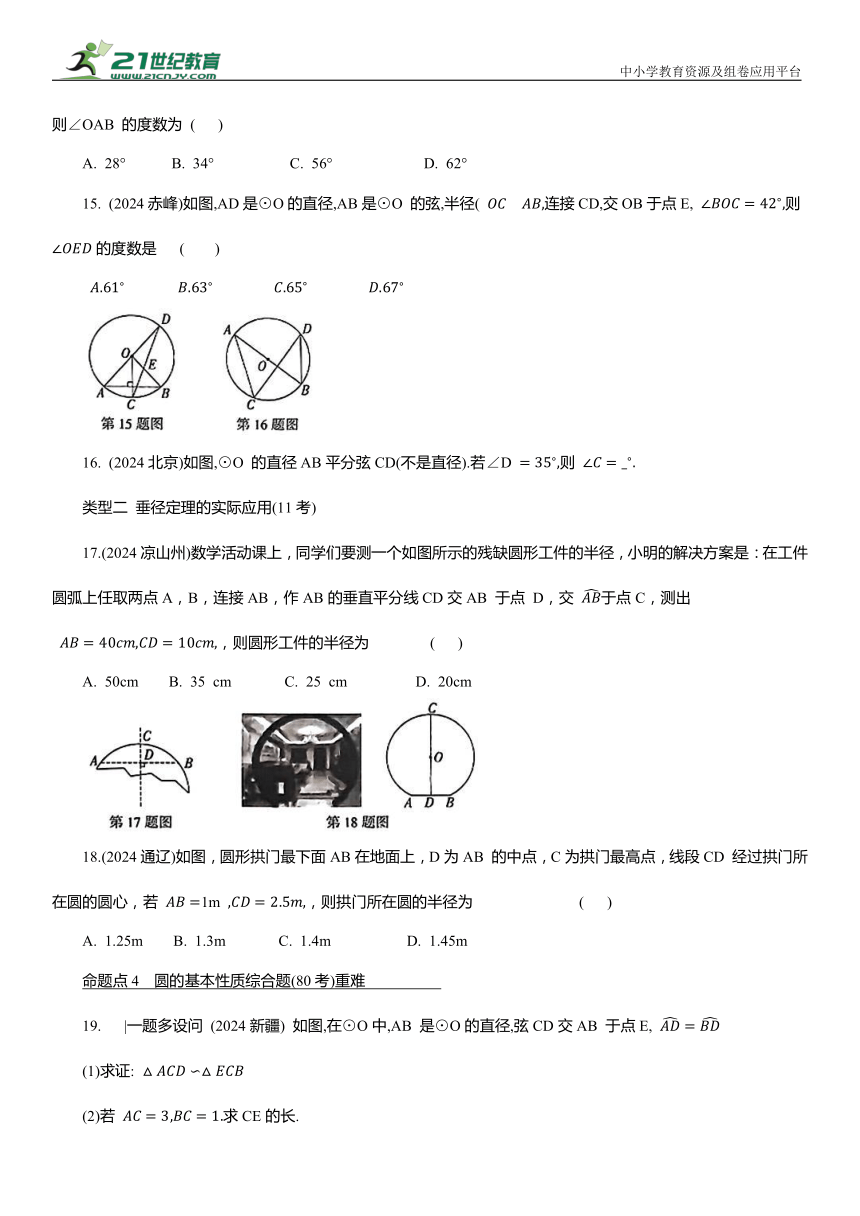
12. (2024长沙)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为 ( )
A.4 B. 4 C. 5 D. 5
13. (2024新疆)如图,AB是⊙O 的直径,CD是⊙O 的弦,AB⊥CD,垂足为E.若CD=8,OD=5,则BE的长为 ( )
A. 1 B. 2 C. 3 D.4
14. (2024 重庆B卷)如图,AB是⊙O 的弦,OC⊥AB交⊙O 于点C,点D是⊙O上一点,连接BD,CD.若∠D=28°,则∠OAB 的度数为 ( )
A. 28° B. 34° C. 56° D. 62°
15. (2024赤峰)如图,AD是⊙O的直径,AB是⊙O 的弦,半径( 连接CD,交OB于点E, 则 的度数是 ( )
16. (2024北京)如图,⊙O 的直径AB平分弦CD(不是直径).若∠D 则
类型二 垂径定理的实际应用(11考)
17.(2024凉山州)数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上任取两点A,B,连接AB,作AB的垂直平分线CD交AB 于点 D,交 于点C,测出 ,则圆形工件的半径为 ( )
A. 50cm B. 35 cm C. 25 cm D. 20cm
18.(2024通辽)如图,圆形拱门最下面AB在地面上,D为AB 的中点,C为拱门最高点,线段CD 经过拱门所在圆的圆心,若 1m ,则拱门所在圆的半径为 ( )
A. 1.25m B. 1.3m C. 1.4m D. 1.45m
命题点4 圆的基本性质综合题(80考)重难
19. |一题多设问 (2024新疆) 如图,在⊙O中,AB 是⊙O的直径,弦CD交AB 于点E,
(1)求证:
(2)若 求CE的长.
新考法 开放性设问(3)在(2)的基础上,下面有两位同学的看法:
请你选择一位同学的说法,并进行计算.
20.(2024安徽)如图,⊙O是 的外接圆,D是直径AB上一点, 的平分线交AB于点 E,交⊙O 于另一点 F,
(1)求证:(
(2)设 垂足为M,若( 求AC的长.
21.(2024苏州)如图, 中, D为AB中点, ⊙O是 的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
新考法 开放性设问(3)下面关于 有三个结论: 你认为哪个正确 请说明理由.
22. (2024包头)如图AB是⊙O的直径,BC,BD是⊙O的两条弦,点C与点D在AB的两侧,E是OB上一点( 连接OC,CE,且
(1)如图①,若 求⊙O 的半径;
(2)如图②,若 求证:BD∥OC.(请用两种证法解答)
23.新考法 结论开放(2023贵州)如图,已知⊙O是等边三角形ABC的外接圆,连接CO并延长交AB于点D,交⊙O 于点E,连接EA,EB.
(1)写出图中一个度数为: 的角: ,图中与 全等的三角形是 ;
(2)求证:
(3)连接OA,OB,判断四边形OAEB 的形状,并说明理由.
24. |一题多设问 (2024成都)如图,在 中, D为斜边AB上一点,以BD为直径作⊙O,交AC于E,F两点,连接BE,BF,DF.
(1)求证:
(2)若 求CF的长和⊙O的直径.
新考法用两种方法解答(3)若点F是弧BD的中点,求证: (请用两种方法解答)
第十九讲 圆的基本性质
1. C 【解析】∠BOC=2∠A=2×45°=90°.
2. B 【解析】如解图,连接OB,∵AC=BC,∴∠BOC=
3. A 【解析】如解图,连接BD,CD,∵BC是⊙O 的直径,∴ ∠BAC = ∠BDC = 90°,∵ AD 平分∠BAC,∴∠BAD=∠CAD=45°,∴BD=CD,∴BD=CD,在四边形 ABDC 中,∠BAC =∠BDC =90°,∴ ∠ACD+∠ABD=180°,将△ADC绕点 D 逆时针旋转到△A'DB,使BD 与 CD 重合,∴ ∠A'BD=∠ACD,∴ ∠A'BD+∠ABD=180°,∴A,B,A'三点共线,∴AB+AC=AB+A'B=AA',由旋转可知∠A'DB=∠ADC,A'D=AD,∴∠A'DA=∠A'DB+∠BDA=∠ADC+∠BDA=∠BDC=90°,∴△A'DA为等腰直角三角形,.
解题技巧
连接BD,CD,构造出圆O的内接四边形,可得∠ACD+∠ABD=180°,由AD平分∠BAC,可知∠BAD=45°,将△ADC绕点D逆时针旋转90°,构造出△A'DB,推出△ADA'为等腰直角三角形,得出AB+AC=AA'是解题的关键.
4. 90° 【解析】如解图,延长 BO 交⊙O 于点A',连接 是⊙O 的直径,∴∠BCA'=
5. 40° 【解析】如解图,连接OB,∵∠ACB=25°,OA∥CB,∴∠AOB=2∠ACB=50°,∠OAC=∠ACB=25°. ∴∠CAB=∠OAB-∠OAC=40°.
6.90 【解析】∵AB 是圆的直径,∴AB 所对的弧是半圆,所对圆心角的度数为180°,∵∠1、∠2、∠3、∠4所对的弧的和为半圆,.
7. 8 【解析】如解图,延长AC,BD交于点 E,∵AB 是⊙O 的直径,∴BD⊥AD,BC⊥AC,∴∠ADB=∠ADE=∠BCE=90°,∵AD平分∠BAC,∴∠BAD=∠EAD,∵AD=AD,∴△BAD≌△EAD(ASA),∴ED=BD=2 ∵在 Rt△ABD 中,AB=10,BD=2 ,∴ ∠CBE,∠BCE=∠ADB=90°,∴△BEC∽△ABD,∴
8. C 【解析】∵BE∥AD,∠BEC=50°,∴∠D=∠BEC=50°,∵ 四边形 ABCD 内接于⊙O,∴∠ABC+∠D=
9. A 【解析】如解图①,延长AB至点E,使BE=AD,连接CE,BD,连接CO并延长交⊙O于点F,连接AF,∵四边形ABCD 内接于⊙O,∴∠ADC+∠ABC=∠ABC+∠CBE=180°,∴∠ADC=∠EBC,∵∠BAC=∠CAD=45°,∴∠CBD=∠CDB=45°,∠DAB=90°,∴BD 是⊙O 的直径,∴∠DCB=90°,∴△DCB是等腰直角三角形,∴DC=BC,∵AD=EB,∴△ADC≌△EBC(SAS),∴∠ACD=∠ECB,AC=EC,∵AB+AD=2,∴AB+BE=AE=2,∵∠DCB=90°,∴∠ACE=90°,∴△ACE 是等腰直角三角形,∴ 60°,∵CF是⊙O的直径,∴ 即⊙O的半径是
如解图②,连接BD,根据题意,得∠DAB=90°,∴BD为⊙O 的直径,∴ ∠DCB=90°,∵ ∠DAC=∠BAC=45°,∴∠DBC=∠BDC=45°,∴ DC=BC,∴ Rt△DCB是等腰直角三角形,过点C分别作 CE⊥AD 交AD的延长线于点 E,CF⊥AB 于点 F,∵AC是∠DAB 的角平分线,∴ CE=CF,∴ Rt△DEC≌Rt△BFC(HL),∴DE=BF,∵AD+AB=AD+AF+BF=2,即AD+DE+AF=AE+AF=2,易得四边形AFCE是正方形,∴AE=AF=CF=1,在Rt△CFB中,∵ ∠FBC=60°,∴FB= ,BC ⊙O的半径是
10. B 【解析】如解图,连接AC,∵AB是⊙O的直径,∴∠ACB = 90°,∵ ∠BEC=20°,∴ ∠CAB =∠BEC=20°,∴∠ABC=90°-∠BAC=70°,∵四边形ABCD 是⊙O 的内接四边形,∴ ∠ADC=180°-∠ABC=110°.
11. 60 【解析】∵四边形ABCD内接于⊙O,∴∠B+∠D=180°,∵四边形 OABC 是菱形,∴∠AOC=∠B,由圆周角定理,得 ∠D+2∠D=180°,解得∠D=60°.
12. B 【解析】∵圆心O到AB 的距离OE=4,∴OE⊥ ∴在 Rt△OAE 中, OA =
13. B 【解析】∵ AB⊥CD,AB 是⊙O 的直径,∴ DE= ∴在 Rt△OED中,由勾股定理得 ∴BE=OB-OE=5-3=2.
14. B 【解析】∵∠D=28°,∴∠BOC=2∠D=56°,∵OC⊥AB,OA=OB,∴∠AOB=2∠BOC=112°,∠OAB=
15. B 【解析】∵ 半径OC⊥AB,∴AC=BC,∴∠AOC=∠BOC=42°,∴ ∠AOB=84°,∵AC=AC,∴∠D= ∠AOC=21°,∴∠OED=∠AOB-∠D=63°.
16. 55 【解析】∵直径AB 平分弦CD(不是直径),∴AB⊥CD,∴∠B=90°-∠D=55°,∴∠C=∠B=55°.
17. C 【解析】如解图,在CD的延长线上取一点 O,使OA=OC,则O为圆心,连接OA,则△OAD为直角三角形, ,结合OA=OC=OD+CD=OD+10,AB=40可得AD=20,OD=OA-10,|即 (OA-10) ,解得OA=25,即圆形工件的半径为25 cm.
18. B 【解析】如解图,连接OA,∵D 为AB的中点,C为拱门最高点,线段CD 经过拱门所在圆的圆心,AB=1m,∴CD⊥AB,AD=BD=0.5m,设拱门所在圆的半径为 rm,∴OA=OC=rm,∵CD=2. 5m ,∴OD= 解得r=1.3,∴拱门所在圆的半径为1.3m.
19. (1)证明:∵
∴∠ACD=∠ECB,
又∵∠ADC=∠EBC,
∴ △ACD∽△ECB;
(2)
解题思路
第一步:由直径所对的圆周角等于 90°知∠ACB=∠ADB=90°,结合 利用勾股定理计算出AB,AD;解:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵AC=3,BC=1,
∴AD=BD,
第二步:由∠BCD=∠ACD,推出E到AC,BC的距离相等,则可利用高相等表示出 S△ACE 与 S△BCE 的比,计算出BE长;
∵∠ACD=∠BCD,
∴E到AC,BC的距离相等,
设E到AC,BC的距离为h,C到AB的距离为m,
第三步:由(1)证明的△ACD∽△ECB,可求出CE的长.
∵△ACD∽△ECB,
I
(3)解:选择小星提出的说法:
如解图①,
∵∠ACB=90°,∠CFA=90°,AC=3,BC=1,
即
由(2)知
选择小红提出的说法:
如解图②,
∵∠ACB=90°,∠AOG=90°,AC=3,BC=1,
∴tan∠BAC=tan∠GAO,即
即
由(2)知
∵O是AB的中点,
在 Rt△AOG 中,由勾股定理得 即
解得 (负值已舍去).
20. (1)证明:∵FA=FE,
∴∠FAE=∠FEA.
∵∠FAE=∠BCE,∠FEA=∠CEB,
∴∠CEB=∠BCE,
∵ CE平分∠ACD,
∴∠ACE=∠DCE.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠BCE+∠ACE=∠CEB+∠DCE=90°,
∴ ∠CDE=180°-∠CEB-∠DCE=180°-90°=90°,即CD⊥AB;
解题技巧
利用FA=FE,求得∠FAE=∠FEA,再利用同弧所对的圆周角相等求得∠FAE=∠BCE,进而求出∠CEB=∠BCE,再利用角平分线的性质以及三角形内角和的关系求出∠CDE,推出CD⊥AB.
(2)解:由(1)知∠BEC=∠BCE,
∴BE=BC,
∵OM=OE=1,AF=EF,FM⊥AB,
∴MA=ME=MO+OE=2,
∴AE=4,
∴OA=OB=AE-OE=3,
∴AB=2OA=6,BC=BE=OB-OE=2.
在△ABC中,AB=6,BC=2,∠ACB=90°,
即AC的长为4
21. 解:(1)∵∠BAC=∠BCD,∠B=∠B,
∴△BAC∽△BCD,
D为AB中点,
∴BC=4;
(2)解题思路
第一步:已知cos∠ADC 的值,构造∠ADC 所在的直角三角形,再利用三角函数求出三角形的边长;
如解图①,过点A 作AE⊥CD 于点 E,连接CO 并延长交⊙O于点F,连接AF,
∵在Rt△AED中,
由(1)知.
解得DE=1,
第二步:由(1)证明△BAC∽△BCD,可列比例式表示出CD,AC之间的关系,然后在第一步构造的直角三角形中,利用勾股定理即可求出CD,AC的值;
∵△BAC∽△BCD,
设CD=x,则AC= x,CE=x-1.
∵在Rt△ACE中,
即 解得 (舍去).
第三步:构造与AC同弧的圆周角,且圆周角经过直径,利用等角的三角函数值相等以及第一,二步求出的长度即可求出半径.
∵CF为⊙O的直径,
∴∠CAF=90°.
∵∠AFC=∠ADC,
即⊙O的半径为
(3)解:我认为 正确.理由如下:
由(1),(2)可知(CD=2,BC=4,BD=2
如解图②,过点 D作DG⊥BC 于点 G,设BG=x,则CG=4-x,
在 Rt△DBG中,由勾股定理可知
在Rt△DCG中,由勾股定理可知
解得
22. (1)解:∵OC=OB,
∵∠BOC=2∠BCE,
即∠OBC+∠BCE=90°,
∴∠OEC=90°,
解得OC=3,
即⊙O的半径为3;
(2)证明:方法一:如解图①,过点O作OF⊥BD于点 F,
∵BD=2OE,
∴OE=BF,
又∵OC=OB,∠OEC=∠BFO=90°,
∴ Rt△CEO≌Rt△OFB(HL),
∴∠COE=∠OBF,
∴BD∥OC;
方法二:如解图②,连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
=2CE,
∴△CEO∽△ADB,
∴∠COE=∠ABD,
∴BD∥OC.
23. (1)解:∠1(或∠2或∠3或∠4),△BCD;
【解法提示】∵CE是⊙O 的直径,△ABC为等边三角形,∴CE垂直且平分线段AB,∴ =30°,又∵AE=AE,BE=BE,∴∠4=∠1=30°,∠3=∠2=30°;∵∠CAD=∠CBD=60°,∠1=∠2,CD=CD,∴△ACD≌△BCD(AAS).
(2)证明:∵⊙O 是等边三角形ABC 的外接圆,CE是⊙O的直径,
∴CE⊥AB,∠CBE=90°,
∴∠ADE=∠CBE=90°,
∵∠3=∠2,
∴△AED∽△CEB;
(3)解:四边形 OAEB 是菱形,理由如下:
∵∠1=30°,∴∠AOE=60°,
∵OA=OE,∴△OAE 是等边三角形,
同理可得△OBE是等边三角形,
∴OA=AE=EB=OB,
∴四边形OAEB 是菱形.
24. (1)证明:∵BD为⊙O的直径,
∵∠CEB=∠BDF,
∴△BCE∽△BFD,
即BC·DF=BF·CE;
解题技巧
当题干中出现求证乘积的等式,一般情况会将乘积的等式化为分式,求证对应的三角形相似.
(2)
解题思路
第一步:由∠A=∠CBF,推出△ABC∽△BFC,得到∠ABC=∠BFC;
解:∵∠A=∠CBF,∠C=∠C,
∴△ABC∽△BFC,
∴∠ABC=∠BFC.
第二步:由tan∠ABC=tan∠BFC,求出AF,BC,CF的值;
解得BC=5,
解得
第三步:由△BCE∽△BFD,有∠CBE=∠FBD,即可得∠A=∠EBA,AE=BE;
由(1)知△BCE∽△BFD,
∴∠CBE=∠FBD,
∴∠CBF=∠EBA,
又∵∠A=∠CBF,
∴∠A=∠EBA,
∴AE=BE.
第四步:在Rt△BCE 和Rt△CBF中,由勾股定理求出EF,BF的长;
设EF=a,则
∵在 Rt△BCE中,
解得 即
∵在Rt△CBF中,
,解得 (负值已舍去).
第五步:由 tan∠CEB=tan∠BDF,求出 DF,再由勾股定理计算出直径BD的长.
∵tan∠CEB=tan∠BDF,
解得
综上所述,CF的长是 ,⊙O 的直径是3
类题通法求线段长的方法:
若题干中作辅助线后有直角三角形存在,常运用勾股定理;2.若题干中含有特殊角(30°,45°,60°等角度)或出现三角函数 sin,cos,tan等时,一般考虑用三角函数解题;3.题干中无直角三角形时,一般考虑利用三角形相似计算线段长度;4.运用等面积公式也可求点到直线的距离.
(3)证明:方法一:∵点F为弧 BD的中点,且 BD为⊙O的直径,
∴∠DFB=90°,∠FBD=∠FDB=45°.
∴∠CEB=∠FDB=45°,
∵ ∠AFD +∠CFB = 90°,∠CFB +∠CBF = 90°,
∴∠AFD=∠CBF,
∴ ∠A+∠CBF=∠A+∠AFD=∠FDB=45°;
方法二:∵ 点 F 为弧 BD 的中点,且 BD 为⊙O 的直径,
∴∠DFB=90°,∠FDB=∠FBD=45°.
∴∠CEB=∠FDB=45°.
由(1)知△BCE∽△BFD,
∴∠CBE=∠FBD=45°,∠CEB=∠FDB=45°,
∴∠DBE=∠CBF,
∴ ∠A+∠CBF=∠A+∠ABE=∠CEB=45°.
第十九讲 圆的基本性质
命题点1 圆周角定理及其推论有关的计算(41考)
1. (2024湖南省卷)如图,AB,AC为⊙O的两条弦,连接OB,OC,若∠A=45°,则∠BOC的度数为 ( )
A. 60° B. 75° C. 90° D. 135°
2. (2024云南)如图,CD是⊙O的直径,点A,B在⊙O上.若 则∠D= ( )
A. 9° B. 18° C. 36° D. 45°
3. (2024宜宾)如图,△ABC内接于⊙O,BC为⊙O的直径,AD平分∠BAC交⊙O于D,则 的值为 ( )
4. (2024陕西)如图,BC是⊙O 的弦,连接OB,OC,∠A 是 所对的圆周角,则∠A与 的和的度数是 .
5. (2024山东省卷)如图, 是⊙O的内接三角形.若 则
6. (2024连云港)如图,AB 是圆的直径, 的顶点均在AB 上方的圆弧上, 的一边分别经过点A,B,则
7. (2024眉山)如图,△ABC内接于⊙O,点O在AB上,AD平分∠BAC交⊙O于D,连接BD.若AB=10,BD=2 ,则BC的长为 .
命题点2 圆内接四边形(58考)
8. (2024吉林省卷)如图,四边形ABCD 内接于⊙O,过点 B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是 ( )
A. 50° B. 100° C. 130° D. 150°
9. (2024武汉)如图,四边形ABCD 内接于⊙O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径是 ( )
10. (2024牡丹江)如图,四边形ABCD 是⊙O 的内接四边形,AB 是⊙O的直径,若∠BEC=20°,则∠ADC的度数为 ( )
A. 100° B. 110° C. 120° D. 130°
11. (2024滨州)如图,四边形ABCD内接于⊙O,若四边形OABC是菱形,则∠D= °.
命题点3 垂径定理及其推论
类型一 垂径定理及其推论有关的计算(47考)
12. (2024长沙)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为 ( )
A.4 B. 4 C. 5 D. 5
13. (2024新疆)如图,AB是⊙O 的直径,CD是⊙O 的弦,AB⊥CD,垂足为E.若CD=8,OD=5,则BE的长为 ( )
A. 1 B. 2 C. 3 D.4
14. (2024 重庆B卷)如图,AB是⊙O 的弦,OC⊥AB交⊙O 于点C,点D是⊙O上一点,连接BD,CD.若∠D=28°,则∠OAB 的度数为 ( )
A. 28° B. 34° C. 56° D. 62°
15. (2024赤峰)如图,AD是⊙O的直径,AB是⊙O 的弦,半径( 连接CD,交OB于点E, 则 的度数是 ( )
16. (2024北京)如图,⊙O 的直径AB平分弦CD(不是直径).若∠D 则
类型二 垂径定理的实际应用(11考)
17.(2024凉山州)数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上任取两点A,B,连接AB,作AB的垂直平分线CD交AB 于点 D,交 于点C,测出 ,则圆形工件的半径为 ( )
A. 50cm B. 35 cm C. 25 cm D. 20cm
18.(2024通辽)如图,圆形拱门最下面AB在地面上,D为AB 的中点,C为拱门最高点,线段CD 经过拱门所在圆的圆心,若 1m ,则拱门所在圆的半径为 ( )
A. 1.25m B. 1.3m C. 1.4m D. 1.45m
命题点4 圆的基本性质综合题(80考)重难
19. |一题多设问 (2024新疆) 如图,在⊙O中,AB 是⊙O的直径,弦CD交AB 于点E,
(1)求证:
(2)若 求CE的长.
新考法 开放性设问(3)在(2)的基础上,下面有两位同学的看法:
请你选择一位同学的说法,并进行计算.
20.(2024安徽)如图,⊙O是 的外接圆,D是直径AB上一点, 的平分线交AB于点 E,交⊙O 于另一点 F,
(1)求证:(
(2)设 垂足为M,若( 求AC的长.
21.(2024苏州)如图, 中, D为AB中点, ⊙O是 的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
新考法 开放性设问(3)下面关于 有三个结论: 你认为哪个正确 请说明理由.
22. (2024包头)如图AB是⊙O的直径,BC,BD是⊙O的两条弦,点C与点D在AB的两侧,E是OB上一点( 连接OC,CE,且
(1)如图①,若 求⊙O 的半径;
(2)如图②,若 求证:BD∥OC.(请用两种证法解答)
23.新考法 结论开放(2023贵州)如图,已知⊙O是等边三角形ABC的外接圆,连接CO并延长交AB于点D,交⊙O 于点E,连接EA,EB.
(1)写出图中一个度数为: 的角: ,图中与 全等的三角形是 ;
(2)求证:
(3)连接OA,OB,判断四边形OAEB 的形状,并说明理由.
24. |一题多设问 (2024成都)如图,在 中, D为斜边AB上一点,以BD为直径作⊙O,交AC于E,F两点,连接BE,BF,DF.
(1)求证:
(2)若 求CF的长和⊙O的直径.
新考法用两种方法解答(3)若点F是弧BD的中点,求证: (请用两种方法解答)
第十九讲 圆的基本性质
1. C 【解析】∠BOC=2∠A=2×45°=90°.
2. B 【解析】如解图,连接OB,∵AC=BC,∴∠BOC=
3. A 【解析】如解图,连接BD,CD,∵BC是⊙O 的直径,∴ ∠BAC = ∠BDC = 90°,∵ AD 平分∠BAC,∴∠BAD=∠CAD=45°,∴BD=CD,∴BD=CD,在四边形 ABDC 中,∠BAC =∠BDC =90°,∴ ∠ACD+∠ABD=180°,将△ADC绕点 D 逆时针旋转到△A'DB,使BD 与 CD 重合,∴ ∠A'BD=∠ACD,∴ ∠A'BD+∠ABD=180°,∴A,B,A'三点共线,∴AB+AC=AB+A'B=AA',由旋转可知∠A'DB=∠ADC,A'D=AD,∴∠A'DA=∠A'DB+∠BDA=∠ADC+∠BDA=∠BDC=90°,∴△A'DA为等腰直角三角形,.
解题技巧
连接BD,CD,构造出圆O的内接四边形,可得∠ACD+∠ABD=180°,由AD平分∠BAC,可知∠BAD=45°,将△ADC绕点D逆时针旋转90°,构造出△A'DB,推出△ADA'为等腰直角三角形,得出AB+AC=AA'是解题的关键.
4. 90° 【解析】如解图,延长 BO 交⊙O 于点A',连接 是⊙O 的直径,∴∠BCA'=
5. 40° 【解析】如解图,连接OB,∵∠ACB=25°,OA∥CB,∴∠AOB=2∠ACB=50°,∠OAC=∠ACB=25°. ∴∠CAB=∠OAB-∠OAC=40°.
6.90 【解析】∵AB 是圆的直径,∴AB 所对的弧是半圆,所对圆心角的度数为180°,∵∠1、∠2、∠3、∠4所对的弧的和为半圆,.
7. 8 【解析】如解图,延长AC,BD交于点 E,∵AB 是⊙O 的直径,∴BD⊥AD,BC⊥AC,∴∠ADB=∠ADE=∠BCE=90°,∵AD平分∠BAC,∴∠BAD=∠EAD,∵AD=AD,∴△BAD≌△EAD(ASA),∴ED=BD=2 ∵在 Rt△ABD 中,AB=10,BD=2 ,∴ ∠CBE,∠BCE=∠ADB=90°,∴△BEC∽△ABD,∴
8. C 【解析】∵BE∥AD,∠BEC=50°,∴∠D=∠BEC=50°,∵ 四边形 ABCD 内接于⊙O,∴∠ABC+∠D=
9. A 【解析】如解图①,延长AB至点E,使BE=AD,连接CE,BD,连接CO并延长交⊙O于点F,连接AF,∵四边形ABCD 内接于⊙O,∴∠ADC+∠ABC=∠ABC+∠CBE=180°,∴∠ADC=∠EBC,∵∠BAC=∠CAD=45°,∴∠CBD=∠CDB=45°,∠DAB=90°,∴BD 是⊙O 的直径,∴∠DCB=90°,∴△DCB是等腰直角三角形,∴DC=BC,∵AD=EB,∴△ADC≌△EBC(SAS),∴∠ACD=∠ECB,AC=EC,∵AB+AD=2,∴AB+BE=AE=2,∵∠DCB=90°,∴∠ACE=90°,∴△ACE 是等腰直角三角形,∴ 60°,∵CF是⊙O的直径,∴ 即⊙O的半径是
如解图②,连接BD,根据题意,得∠DAB=90°,∴BD为⊙O 的直径,∴ ∠DCB=90°,∵ ∠DAC=∠BAC=45°,∴∠DBC=∠BDC=45°,∴ DC=BC,∴ Rt△DCB是等腰直角三角形,过点C分别作 CE⊥AD 交AD的延长线于点 E,CF⊥AB 于点 F,∵AC是∠DAB 的角平分线,∴ CE=CF,∴ Rt△DEC≌Rt△BFC(HL),∴DE=BF,∵AD+AB=AD+AF+BF=2,即AD+DE+AF=AE+AF=2,易得四边形AFCE是正方形,∴AE=AF=CF=1,在Rt△CFB中,∵ ∠FBC=60°,∴FB= ,BC ⊙O的半径是
10. B 【解析】如解图,连接AC,∵AB是⊙O的直径,∴∠ACB = 90°,∵ ∠BEC=20°,∴ ∠CAB =∠BEC=20°,∴∠ABC=90°-∠BAC=70°,∵四边形ABCD 是⊙O 的内接四边形,∴ ∠ADC=180°-∠ABC=110°.
11. 60 【解析】∵四边形ABCD内接于⊙O,∴∠B+∠D=180°,∵四边形 OABC 是菱形,∴∠AOC=∠B,由圆周角定理,得 ∠D+2∠D=180°,解得∠D=60°.
12. B 【解析】∵圆心O到AB 的距离OE=4,∴OE⊥ ∴在 Rt△OAE 中, OA =
13. B 【解析】∵ AB⊥CD,AB 是⊙O 的直径,∴ DE= ∴在 Rt△OED中,由勾股定理得 ∴BE=OB-OE=5-3=2.
14. B 【解析】∵∠D=28°,∴∠BOC=2∠D=56°,∵OC⊥AB,OA=OB,∴∠AOB=2∠BOC=112°,∠OAB=
15. B 【解析】∵ 半径OC⊥AB,∴AC=BC,∴∠AOC=∠BOC=42°,∴ ∠AOB=84°,∵AC=AC,∴∠D= ∠AOC=21°,∴∠OED=∠AOB-∠D=63°.
16. 55 【解析】∵直径AB 平分弦CD(不是直径),∴AB⊥CD,∴∠B=90°-∠D=55°,∴∠C=∠B=55°.
17. C 【解析】如解图,在CD的延长线上取一点 O,使OA=OC,则O为圆心,连接OA,则△OAD为直角三角形, ,结合OA=OC=OD+CD=OD+10,AB=40可得AD=20,OD=OA-10,|即 (OA-10) ,解得OA=25,即圆形工件的半径为25 cm.
18. B 【解析】如解图,连接OA,∵D 为AB的中点,C为拱门最高点,线段CD 经过拱门所在圆的圆心,AB=1m,∴CD⊥AB,AD=BD=0.5m,设拱门所在圆的半径为 rm,∴OA=OC=rm,∵CD=2. 5m ,∴OD= 解得r=1.3,∴拱门所在圆的半径为1.3m.
19. (1)证明:∵
∴∠ACD=∠ECB,
又∵∠ADC=∠EBC,
∴ △ACD∽△ECB;
(2)
解题思路
第一步:由直径所对的圆周角等于 90°知∠ACB=∠ADB=90°,结合 利用勾股定理计算出AB,AD;解:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵AC=3,BC=1,
∴AD=BD,
第二步:由∠BCD=∠ACD,推出E到AC,BC的距离相等,则可利用高相等表示出 S△ACE 与 S△BCE 的比,计算出BE长;
∵∠ACD=∠BCD,
∴E到AC,BC的距离相等,
设E到AC,BC的距离为h,C到AB的距离为m,
第三步:由(1)证明的△ACD∽△ECB,可求出CE的长.
∵△ACD∽△ECB,
I
(3)解:选择小星提出的说法:
如解图①,
∵∠ACB=90°,∠CFA=90°,AC=3,BC=1,
即
由(2)知
选择小红提出的说法:
如解图②,
∵∠ACB=90°,∠AOG=90°,AC=3,BC=1,
∴tan∠BAC=tan∠GAO,即
即
由(2)知
∵O是AB的中点,
在 Rt△AOG 中,由勾股定理得 即
解得 (负值已舍去).
20. (1)证明:∵FA=FE,
∴∠FAE=∠FEA.
∵∠FAE=∠BCE,∠FEA=∠CEB,
∴∠CEB=∠BCE,
∵ CE平分∠ACD,
∴∠ACE=∠DCE.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠BCE+∠ACE=∠CEB+∠DCE=90°,
∴ ∠CDE=180°-∠CEB-∠DCE=180°-90°=90°,即CD⊥AB;
解题技巧
利用FA=FE,求得∠FAE=∠FEA,再利用同弧所对的圆周角相等求得∠FAE=∠BCE,进而求出∠CEB=∠BCE,再利用角平分线的性质以及三角形内角和的关系求出∠CDE,推出CD⊥AB.
(2)解:由(1)知∠BEC=∠BCE,
∴BE=BC,
∵OM=OE=1,AF=EF,FM⊥AB,
∴MA=ME=MO+OE=2,
∴AE=4,
∴OA=OB=AE-OE=3,
∴AB=2OA=6,BC=BE=OB-OE=2.
在△ABC中,AB=6,BC=2,∠ACB=90°,
即AC的长为4
21. 解:(1)∵∠BAC=∠BCD,∠B=∠B,
∴△BAC∽△BCD,
D为AB中点,
∴BC=4;
(2)解题思路
第一步:已知cos∠ADC 的值,构造∠ADC 所在的直角三角形,再利用三角函数求出三角形的边长;
如解图①,过点A 作AE⊥CD 于点 E,连接CO 并延长交⊙O于点F,连接AF,
∵在Rt△AED中,
由(1)知.
解得DE=1,
第二步:由(1)证明△BAC∽△BCD,可列比例式表示出CD,AC之间的关系,然后在第一步构造的直角三角形中,利用勾股定理即可求出CD,AC的值;
∵△BAC∽△BCD,
设CD=x,则AC= x,CE=x-1.
∵在Rt△ACE中,
即 解得 (舍去).
第三步:构造与AC同弧的圆周角,且圆周角经过直径,利用等角的三角函数值相等以及第一,二步求出的长度即可求出半径.
∵CF为⊙O的直径,
∴∠CAF=90°.
∵∠AFC=∠ADC,
即⊙O的半径为
(3)解:我认为 正确.理由如下:
由(1),(2)可知(CD=2,BC=4,BD=2
如解图②,过点 D作DG⊥BC 于点 G,设BG=x,则CG=4-x,
在 Rt△DBG中,由勾股定理可知
在Rt△DCG中,由勾股定理可知
解得
22. (1)解:∵OC=OB,
∵∠BOC=2∠BCE,
即∠OBC+∠BCE=90°,
∴∠OEC=90°,
解得OC=3,
即⊙O的半径为3;
(2)证明:方法一:如解图①,过点O作OF⊥BD于点 F,
∵BD=2OE,
∴OE=BF,
又∵OC=OB,∠OEC=∠BFO=90°,
∴ Rt△CEO≌Rt△OFB(HL),
∴∠COE=∠OBF,
∴BD∥OC;
方法二:如解图②,连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
=2CE,
∴△CEO∽△ADB,
∴∠COE=∠ABD,
∴BD∥OC.
23. (1)解:∠1(或∠2或∠3或∠4),△BCD;
【解法提示】∵CE是⊙O 的直径,△ABC为等边三角形,∴CE垂直且平分线段AB,∴ =30°,又∵AE=AE,BE=BE,∴∠4=∠1=30°,∠3=∠2=30°;∵∠CAD=∠CBD=60°,∠1=∠2,CD=CD,∴△ACD≌△BCD(AAS).
(2)证明:∵⊙O 是等边三角形ABC 的外接圆,CE是⊙O的直径,
∴CE⊥AB,∠CBE=90°,
∴∠ADE=∠CBE=90°,
∵∠3=∠2,
∴△AED∽△CEB;
(3)解:四边形 OAEB 是菱形,理由如下:
∵∠1=30°,∴∠AOE=60°,
∵OA=OE,∴△OAE 是等边三角形,
同理可得△OBE是等边三角形,
∴OA=AE=EB=OB,
∴四边形OAEB 是菱形.
24. (1)证明:∵BD为⊙O的直径,
∵∠CEB=∠BDF,
∴△BCE∽△BFD,
即BC·DF=BF·CE;
解题技巧
当题干中出现求证乘积的等式,一般情况会将乘积的等式化为分式,求证对应的三角形相似.
(2)
解题思路
第一步:由∠A=∠CBF,推出△ABC∽△BFC,得到∠ABC=∠BFC;
解:∵∠A=∠CBF,∠C=∠C,
∴△ABC∽△BFC,
∴∠ABC=∠BFC.
第二步:由tan∠ABC=tan∠BFC,求出AF,BC,CF的值;
解得BC=5,
解得
第三步:由△BCE∽△BFD,有∠CBE=∠FBD,即可得∠A=∠EBA,AE=BE;
由(1)知△BCE∽△BFD,
∴∠CBE=∠FBD,
∴∠CBF=∠EBA,
又∵∠A=∠CBF,
∴∠A=∠EBA,
∴AE=BE.
第四步:在Rt△BCE 和Rt△CBF中,由勾股定理求出EF,BF的长;
设EF=a,则
∵在 Rt△BCE中,
解得 即
∵在Rt△CBF中,
,解得 (负值已舍去).
第五步:由 tan∠CEB=tan∠BDF,求出 DF,再由勾股定理计算出直径BD的长.
∵tan∠CEB=tan∠BDF,
解得
综上所述,CF的长是 ,⊙O 的直径是3
类题通法求线段长的方法:
若题干中作辅助线后有直角三角形存在,常运用勾股定理;2.若题干中含有特殊角(30°,45°,60°等角度)或出现三角函数 sin,cos,tan等时,一般考虑用三角函数解题;3.题干中无直角三角形时,一般考虑利用三角形相似计算线段长度;4.运用等面积公式也可求点到直线的距离.
(3)证明:方法一:∵点F为弧 BD的中点,且 BD为⊙O的直径,
∴∠DFB=90°,∠FBD=∠FDB=45°.
∴∠CEB=∠FDB=45°,
∵ ∠AFD +∠CFB = 90°,∠CFB +∠CBF = 90°,
∴∠AFD=∠CBF,
∴ ∠A+∠CBF=∠A+∠AFD=∠FDB=45°;
方法二:∵ 点 F 为弧 BD 的中点,且 BD 为⊙O 的直径,
∴∠DFB=90°,∠FDB=∠FBD=45°.
∴∠CEB=∠FDB=45°.
由(1)知△BCE∽△BFD,
∴∠CBE=∠FBD=45°,∠CEB=∠FDB=45°,
∴∠DBE=∠CBF,
∴ ∠A+∠CBF=∠A+∠ABE=∠CEB=45°.
同课章节目录
