题型五 新函数图象与性质探究题(含解析)2025年中考数学重难题型分类练
文档属性
| 名称 | 题型五 新函数图象与性质探究题(含解析)2025年中考数学重难题型分类练 |  | |
| 格式 | docx | ||
| 文件大小 | 309.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 21:13:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
题型五 新函数图象与性质探究题
类型一 新函数性质探究
1.(2024吉林省卷)小明利用一次函数和二次函数知识,设计了一个计算程序,其程序框图如图①所示,输入x的值为-2时,输出y的值为1;输入x的值为2时,输出y的值为3;输入x的值为3时,输出y的值为6.
(1)直接写出k,a,b的值;
(2)小明在平面直角坐标系中画出了关于x的函数图象,如图②.
Ⅰ.当y随x的增大而增大时,求x的取值范围;
Ⅱ.若关于x的方程 (t为实数),在( 时无解,求t的取值范围;
Ⅲ.若在函数图象上有点P,Q(P与Q 不重合). P的横坐标为m,Q的横坐标为 .小明对P,Q之间(含P,Q两点)的图象进行研究,当图象对应函数的最大值与最小值均不随m的变化而变化,直接写出m的取值范围.
2. (2023阜新)某中学数学兴趣小组的同学们,对函数y=a|x-b|+c(a,b,c是常数,a≠0)的性质进行了初步探究,部分过程如下,请你将其补充完整.
(1)当a=1,b=c=0时,即y=|x|.当x≥0时,函数化简为y=x;当x<0时,函数化简为y= ;
(2)当a=2,b=1,c=0时,即y=2|x-1|.
①该函数自变量x和函数值y的若干组对应值如下表:
x ... -2 -1 0 1 2 3 4
y 6 m 2 0 2 4 6
其中
②在图①所示的平面直角坐标系内画出函数y=2|x-1|的图象;
(3)当a=-2,b=1,c=2时,即y=-2|x-1|+2.
①当x≥1时,函数化简为y= ,
②在图②所示的平面直角坐标系内画出函数y=-2|x-1|+2的图象;
(4)请写出函数y=a|x-b|+c(a,b,c是常数,a≠0)的一条性质: .(若所列性质多于一条,则仅以第一条为准)
类型二 与几何图形结合的函数性质探究
3. (2024重庆A卷)如图,在 中, 点P为AB上一点, 过点 P 作 交AC于点 Q.点P,Q 的距离为 的周长与 的周长之比为y .
(1)请直接写出, 分别关于x的函数表达式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出函数y ,y 的图象,并分别写 出函数y ,y 的一条性质;
(3)结合函数图象,直接写出 时x的取值范围.(近似值保留小数点后一位,误差不超过0.2)
4.(2023连云港)【问题情境 建构函数】
(1)如图①,在矩形ABCD中, M是CD的中点, 垂足为 E.设 试用含x的代数式表示y.
【由数想形 新知初探】
(2)在上述表达式中,y与x成函数关系,其图象如图②所示.若x取任意实数,此时的函数图象是否具有对称性 若有,请说明理由,并在图②上补全函数图象.
【数形结合 深度探究】
(3)在“x取任意实数”的条件下,对上述函数继续探究,得出以下结论:①函数值y随x的增大而增大;②函数值y的取值范围是 ③存在一条直线与该函数图象有四个交点;④在图象上存在四点A,B,C,D,使得四边形ABCD是平行四边形.其中正确的是 ;(写出所有正确结论的序号)
【抽象回归 拓展总结】
(4)若将(1)中的“AB=4”改成 ,此时y关于x的函数表达式是 ;一般地,当 x取任意实数时,类比一次函数、反比例函数、二次函数的研究过程,探究此类函数的相关性质(直接写出3条即可).
类型三 与实际问题结合的函数性质探究
5.(2024北京)小云有一个圆柱形水杯(记为1号杯).在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来.新水杯(记为2号杯)示意图如下.
当1号杯和2号杯中都有VmL水时,小云分别记录了1号杯的水面高度h (单位:cm)和2号杯的水面高度 (单位:cm),部分数据如下:
V/mL 0 40 100 200 300 400 500
h / cm 0 2.5 5.0 7.5 10.0 12.5
h / cm 0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
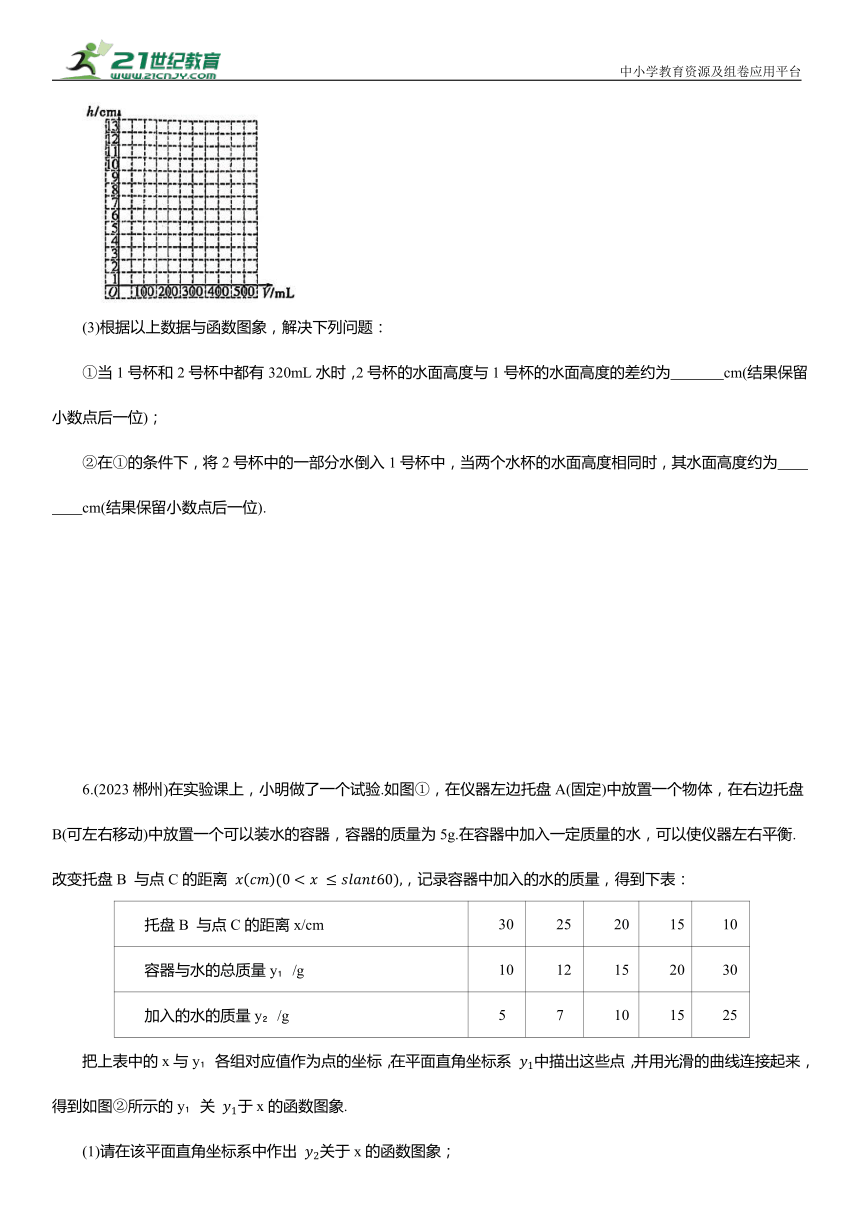
(2)通过分析数据,发现可以用函数刻画 与V,h 与V之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有320mL水时,2号杯的水面高度与1号杯的水面高度的差约为 cm(结果保留小数点后一位);
②在①的条件下,将2号杯中的一部分水倒入1号杯中,当两个水杯的水面高度相同时,其水面高度约为 cm(结果保留小数点后一位).
6.(2023郴州)在实验课上,小明做了一个试验.如图①,在仪器左边托盘A(固定)中放置一个物体,在右边托盘B(可左右移动)中放置一个可以装水的容器,容器的质量为5g.在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘B 与点C的距离 ,记录容器中加入的水的质量,得到下表:
托盘B 与点C的距离x/cm 30 25 20 15 10
容器与水的总质量y /g 10 12 15 20 30
加入的水的质量y /g 5 7 10 15 25
把上表中的x与y 各组对应值作为点的坐标,在平面直角坐标系 中描出这些点,并用光滑的曲线连接起来,得到如图②所示的y 关 于x的函数图象.
(1)请在该平面直角坐标系中作出 关于x的函数图象;
(2)观察函数图象,并结合表中的数据:
①猜测y 与x之间的函数关系,并求y 关于x的函数表达式;
②求 关于x的函数表达式;
③当 时,y 随x的增大而 (填“增大”或“减 小”),y 随x的增大而 (填“增大”或“减小”),y 的图象 可以由y 的图象向 (填“上”或“下”或“左”或“右”)平移 得到;
若在容器中加入的水的质量 满足 求托盘B与点C的距离x(cm)的取值范围.
题型五 新函数图象与性质探究题
1. 解:(1)k的值为1,a的值为1,b的值为-2;
【解法提示】∵x=-2<0,∴将x=-2,y=1代入y= kx+3,得-2k+3=1,解得k=1,∵x=2>0,x=3>0,∴将x=2,y=3 和 x = 3,y = 6 代入 得 解得
(2)Ⅰ.∵k=1,a=1,b=-2,
∴一次函数解析式为y=x+3,二次函数解析式为y=
当:x>0时 的对称轴为直线x=1,图象开口向上,∴x≥1时,y随x的增大而增大;
当x≤0时,y=x+3,k=1>0,
∴x≤0时,y随x的增大而增大,
综上所述,x的取值范围为x≤0或x≥1;
在0∴问题转化为抛物线 与直线y=t在0∵对于 ,当x=1时,y=2,
∴顶点为(1,2),如解图①,
∴当t=2时,抛物线 与直线y=t在0∴当t<2时,抛物线 与直线y=t在0当.
∴当t=11时,抛物线 与直线y=t在0∴当t≥11时,抛物线 与直线y=t在0综上所述,当t<2或t≥11时,抛物线 与直线y=t在0即当t<2或t≥11时,关于x的方程 为实数),在0Ⅲ.-1≤m≤0或1≤m≤2.
【解法提示】∵
∴点 P,Q关于直线 对称,∵图象对应函数的最大值与最小值均不随m的变化而变化,∴当x=1时, ,当x=0时,y最大值=3,当x=2时,y=3,当x=-1时,y=2,∴①当 时,如解图②,由题意得 ②当 时,如解图③,由题意得 综上所述,m的取值范围是-1≤m≤0或1≤m≤2.
2. 解:(1)-x;
【解法提示】y=|x|,当x<0时,函数化简为y=-x.
(2)①4;
【解法提示】当x=-1时,y=2|x-1|=2|-1-1|=4.
②画出函数y=2lx-1|的图象如解图①所示;
(3)①-2x+4;
【解法提示】当x≥1时,函数化简为y=-2(x-1)+2=-2x+4.
②画出函数y=-2|x-1|+2的图象如解图②所示;
(4)当a>0时,函数y=a|x-b|+c的图象有最低点(b,c).(答案不唯一)
3. 解:
(2)画出函数图象如解图;
根据函数图象,函数的性质为:
①当0≤x≤6时,y 随x的增大而增大;
当0②函数y 在自变量的取值范围内,有最大值和最小值.当x=0时,函数取得最小值0;当x=6时,函数取得最大值8;函数y 在自变量的取值范围内,有最小值.当x=6时,函数取得最小值1;(分别写出一条即可)
(3)由函数图象得,当2.1y .
解题技巧
当两个函数比较大小时,先求出交点,再根据图象可知谁大谁就在图象上方,即可求出函数在比大小时的取值范围.
4. 解:(1)在矩形ABCD中,∠ABC=∠C=90°,
∴∠ABE+∠MBC=90°,
∵AE⊥BM,
∴∠AEB=90°,
∴∠BAE+∠ABE=90°,
∴∠AEB=∠C,∠BAE=∠MBC,
∴△ABE∽△BMC,
∵AB=4,M是CD的中点,
在Rt△BMC中,
∴y关于x的函数表达式为
(2)x取任意实数时,对应的函数图象关于原点成中心对称,理由如下:
若P(a,b)为图象上任意一点,则
设P(a,b)关于原点的对称点为Q,则Q(-a,-b),
当x=-a时,
∴Q(-a,-b)也在函数 的图象上,
∴当x取任意实数时,函数 的图象关于原点成中心对称,补全函数图象如解图所示;
(3)①④;
【解法提示】根据函数图象可得,函数值y随x的增大而增大,故①正确;∵在 Rt△AEB 中,AB 为斜边,AE为直角边,∴函数值|y|当k≠0,x取任意实数时,有如下相关性质:当k>0时,图象经过第一、三象限,函数值y随x的增大而增大,y的取值范围为-2k5. 解:(1)1.0;
【解法提示】由题意得,设V与h 的函数关系式为 V= ,由表格数据得100=2.5k,解得k=40,∴V=40h ,∴当lV=40时,
(2)画出函数图象如解图①;
(3)①1.2;②8.8.(答案合理即可)
【解法提示】①当V=320mL时, 由解图②可知高度差CD≈1.2cm;②当 时, ,由解图②可知,此时h 约为8.9cm,∴当两个水杯的水面高度相同时,高度约为8.8cm.(答案合理即可)
6.解:(1)作图如解图所示;
(2)
解题思路
熟练掌握反比例函数的图象特征,可看出y 与x成反比例关系,通过观察y 与y 图象的点的横纵坐标变化,可得出结论.
①y 与x成反比例函数关系,函数表达式为 (0③减小,减小,下;
(3)当y =19时,x=12.5,当 时,x=6,∴6≤x≤12.5.
题型五 新函数图象与性质探究题
类型一 新函数性质探究
1.(2024吉林省卷)小明利用一次函数和二次函数知识,设计了一个计算程序,其程序框图如图①所示,输入x的值为-2时,输出y的值为1;输入x的值为2时,输出y的值为3;输入x的值为3时,输出y的值为6.
(1)直接写出k,a,b的值;
(2)小明在平面直角坐标系中画出了关于x的函数图象,如图②.
Ⅰ.当y随x的增大而增大时,求x的取值范围;
Ⅱ.若关于x的方程 (t为实数),在( 时无解,求t的取值范围;
Ⅲ.若在函数图象上有点P,Q(P与Q 不重合). P的横坐标为m,Q的横坐标为 .小明对P,Q之间(含P,Q两点)的图象进行研究,当图象对应函数的最大值与最小值均不随m的变化而变化,直接写出m的取值范围.
2. (2023阜新)某中学数学兴趣小组的同学们,对函数y=a|x-b|+c(a,b,c是常数,a≠0)的性质进行了初步探究,部分过程如下,请你将其补充完整.
(1)当a=1,b=c=0时,即y=|x|.当x≥0时,函数化简为y=x;当x<0时,函数化简为y= ;
(2)当a=2,b=1,c=0时,即y=2|x-1|.
①该函数自变量x和函数值y的若干组对应值如下表:
x ... -2 -1 0 1 2 3 4
y 6 m 2 0 2 4 6
其中
②在图①所示的平面直角坐标系内画出函数y=2|x-1|的图象;
(3)当a=-2,b=1,c=2时,即y=-2|x-1|+2.
①当x≥1时,函数化简为y= ,
②在图②所示的平面直角坐标系内画出函数y=-2|x-1|+2的图象;
(4)请写出函数y=a|x-b|+c(a,b,c是常数,a≠0)的一条性质: .(若所列性质多于一条,则仅以第一条为准)
类型二 与几何图形结合的函数性质探究
3. (2024重庆A卷)如图,在 中, 点P为AB上一点, 过点 P 作 交AC于点 Q.点P,Q 的距离为 的周长与 的周长之比为y .
(1)请直接写出, 分别关于x的函数表达式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出函数y ,y 的图象,并分别写 出函数y ,y 的一条性质;
(3)结合函数图象,直接写出 时x的取值范围.(近似值保留小数点后一位,误差不超过0.2)
4.(2023连云港)【问题情境 建构函数】
(1)如图①,在矩形ABCD中, M是CD的中点, 垂足为 E.设 试用含x的代数式表示y.
【由数想形 新知初探】
(2)在上述表达式中,y与x成函数关系,其图象如图②所示.若x取任意实数,此时的函数图象是否具有对称性 若有,请说明理由,并在图②上补全函数图象.
【数形结合 深度探究】
(3)在“x取任意实数”的条件下,对上述函数继续探究,得出以下结论:①函数值y随x的增大而增大;②函数值y的取值范围是 ③存在一条直线与该函数图象有四个交点;④在图象上存在四点A,B,C,D,使得四边形ABCD是平行四边形.其中正确的是 ;(写出所有正确结论的序号)
【抽象回归 拓展总结】
(4)若将(1)中的“AB=4”改成 ,此时y关于x的函数表达式是 ;一般地,当 x取任意实数时,类比一次函数、反比例函数、二次函数的研究过程,探究此类函数的相关性质(直接写出3条即可).
类型三 与实际问题结合的函数性质探究
5.(2024北京)小云有一个圆柱形水杯(记为1号杯).在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来.新水杯(记为2号杯)示意图如下.
当1号杯和2号杯中都有VmL水时,小云分别记录了1号杯的水面高度h (单位:cm)和2号杯的水面高度 (单位:cm),部分数据如下:
V/mL 0 40 100 200 300 400 500
h / cm 0 2.5 5.0 7.5 10.0 12.5
h / cm 0 2.8 4.8 7.2 8.9 10.5 11.8
(1)补全表格(结果保留小数点后一位);
(2)通过分析数据,发现可以用函数刻画 与V,h 与V之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有320mL水时,2号杯的水面高度与1号杯的水面高度的差约为 cm(结果保留小数点后一位);
②在①的条件下,将2号杯中的一部分水倒入1号杯中,当两个水杯的水面高度相同时,其水面高度约为 cm(结果保留小数点后一位).
6.(2023郴州)在实验课上,小明做了一个试验.如图①,在仪器左边托盘A(固定)中放置一个物体,在右边托盘B(可左右移动)中放置一个可以装水的容器,容器的质量为5g.在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘B 与点C的距离 ,记录容器中加入的水的质量,得到下表:
托盘B 与点C的距离x/cm 30 25 20 15 10
容器与水的总质量y /g 10 12 15 20 30
加入的水的质量y /g 5 7 10 15 25
把上表中的x与y 各组对应值作为点的坐标,在平面直角坐标系 中描出这些点,并用光滑的曲线连接起来,得到如图②所示的y 关 于x的函数图象.
(1)请在该平面直角坐标系中作出 关于x的函数图象;
(2)观察函数图象,并结合表中的数据:
①猜测y 与x之间的函数关系,并求y 关于x的函数表达式;
②求 关于x的函数表达式;
③当 时,y 随x的增大而 (填“增大”或“减 小”),y 随x的增大而 (填“增大”或“减小”),y 的图象 可以由y 的图象向 (填“上”或“下”或“左”或“右”)平移 得到;
若在容器中加入的水的质量 满足 求托盘B与点C的距离x(cm)的取值范围.
题型五 新函数图象与性质探究题
1. 解:(1)k的值为1,a的值为1,b的值为-2;
【解法提示】∵x=-2<0,∴将x=-2,y=1代入y= kx+3,得-2k+3=1,解得k=1,∵x=2>0,x=3>0,∴将x=2,y=3 和 x = 3,y = 6 代入 得 解得
(2)Ⅰ.∵k=1,a=1,b=-2,
∴一次函数解析式为y=x+3,二次函数解析式为y=
当:x>0时 的对称轴为直线x=1,图象开口向上,∴x≥1时,y随x的增大而增大;
当x≤0时,y=x+3,k=1>0,
∴x≤0时,y随x的增大而增大,
综上所述,x的取值范围为x≤0或x≥1;
在0
∴顶点为(1,2),如解图①,
∴当t=2时,抛物线 与直线y=t在0
∴当t=11时,抛物线 与直线y=t在0
【解法提示】∵
∴点 P,Q关于直线 对称,∵图象对应函数的最大值与最小值均不随m的变化而变化,∴当x=1时, ,当x=0时,y最大值=3,当x=2时,y=3,当x=-1时,y=2,∴①当 时,如解图②,由题意得 ②当 时,如解图③,由题意得 综上所述,m的取值范围是-1≤m≤0或1≤m≤2.
2. 解:(1)-x;
【解法提示】y=|x|,当x<0时,函数化简为y=-x.
(2)①4;
【解法提示】当x=-1时,y=2|x-1|=2|-1-1|=4.
②画出函数y=2lx-1|的图象如解图①所示;
(3)①-2x+4;
【解法提示】当x≥1时,函数化简为y=-2(x-1)+2=-2x+4.
②画出函数y=-2|x-1|+2的图象如解图②所示;
(4)当a>0时,函数y=a|x-b|+c的图象有最低点(b,c).(答案不唯一)
3. 解:
(2)画出函数图象如解图;
根据函数图象,函数的性质为:
①当0≤x≤6时,y 随x的增大而增大;
当0
(3)由函数图象得,当2.1
解题技巧
当两个函数比较大小时,先求出交点,再根据图象可知谁大谁就在图象上方,即可求出函数在比大小时的取值范围.
4. 解:(1)在矩形ABCD中,∠ABC=∠C=90°,
∴∠ABE+∠MBC=90°,
∵AE⊥BM,
∴∠AEB=90°,
∴∠BAE+∠ABE=90°,
∴∠AEB=∠C,∠BAE=∠MBC,
∴△ABE∽△BMC,
∵AB=4,M是CD的中点,
在Rt△BMC中,
∴y关于x的函数表达式为
(2)x取任意实数时,对应的函数图象关于原点成中心对称,理由如下:
若P(a,b)为图象上任意一点,则
设P(a,b)关于原点的对称点为Q,则Q(-a,-b),
当x=-a时,
∴Q(-a,-b)也在函数 的图象上,
∴当x取任意实数时,函数 的图象关于原点成中心对称,补全函数图象如解图所示;
(3)①④;
【解法提示】根据函数图象可得,函数值y随x的增大而增大,故①正确;∵在 Rt△AEB 中,AB 为斜边,AE为直角边,∴函数值|y|
【解法提示】由题意得,设V与h 的函数关系式为 V= ,由表格数据得100=2.5k,解得k=40,∴V=40h ,∴当lV=40时,
(2)画出函数图象如解图①;
(3)①1.2;②8.8.(答案合理即可)
【解法提示】①当V=320mL时, 由解图②可知高度差CD≈1.2cm;②当 时, ,由解图②可知,此时h 约为8.9cm,∴当两个水杯的水面高度相同时,高度约为8.8cm.(答案合理即可)
6.解:(1)作图如解图所示;
(2)
解题思路
熟练掌握反比例函数的图象特征,可看出y 与x成反比例关系,通过观察y 与y 图象的点的横纵坐标变化,可得出结论.
①y 与x成反比例函数关系,函数表达式为 (0
(3)当y =19时,x=12.5,当 时,x=6,∴6≤x≤12.5.
同课章节目录
