题型四 圆的相关证明与计算(含解析)2025年中考数学重难题型分类练
文档属性
| 名称 | 题型四 圆的相关证明与计算(含解析)2025年中考数学重难题型分类练 |  | |
| 格式 | docx | ||
| 文件大小 | 240.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 21:12:17 | ||
图片预览




文档简介
题型四 圆的相关证明与计算
类型一 圆基本性质的证明与计算
1. (2024 浙江)如图,在圆内接四边形ABCD 中, 延长AD至点E,使 ,延长BA 至点 F,连接EF,使
(1)若 CD为直径,求 的度数.
(2)求证:(
2. (2024烟台)如图,AB 是⊙O 的直径, 内接于⊙O,点I为 的内心,连接CI并延长交⊙O 于点D. E是 上任意一点,连接AD,BD,BE,CE.
(1)若 求 的度数;
(2)找出图中所有与DI相等的线段,并证明;
(3)若 求 的周长.
类型二 与切线有关的证明与计算
3. (2024遂宁)如图,AB是⊙O的直径,AC是一条弦,点D 是 的中点, 于点E,交AC于点F,连接DB交AC于点 G.
(1)求证:
(2)延长GD至点M,使. 连接AM.
①求证:AM是⊙O 的切线;
②若 求⊙O 的半径.
4. 新考法 新设问 (2024 云南定心卷)如图, 内接于⊙O,且AB为⊙O的直径,⊙O外的点 D 在射线AC上,过点 D作DE垂直AB的延长线于点E,且BD平分
(1)求证:
(2)若 求AC的长;
(3)过点B作⊙O的切线BF,交AD于点F,是否存在常数k,使 成立 若存在,求常数k的值;若不存在,请说明理由.
5.|一题多设问 (2024 云南)如图,AB是⊙O 的直径.点 D,F是⊙O上异于A,B的点.点C在⊙O外,( 延长BF与CA的延长线交于点M,点N在BA的延长线上, AB·MN.点H在直径AB上, 点E是线段DH的中点.
(1)求 的度数;
(2)求证:直线CM与⊙O 相切;
(3)看一看,想一想,证一证:
以下与线段CE、线段EB、线段CB有关的三个结论:( 你认为哪个正确 请说明理由.
(4)设BC交⊙O 于点G,AG,HD的延长线交于点K,关于线段DK,线段DE有关的两个结论: 你认为哪个正确 请说明理由.
6. (2024福建)如图,在 中, ,以AB为直径的⊙O 交 BC 于点 D, 垂足为E,BE 的延长线交 于点F.
(1)求 的值;
(2)求证:
(3)求证:AD与EF互相平分.
7. (2024河北)已知⊙O 的半径为3,弦 中, 在平面上,先将 和⊙O按图①位置摆放(点B与点N重合,点A在⊙O上,点C在⊙O内),随后移动 使点B 在弦 MN上移动,点A 始终在⊙O 上随之移动.设
(1)当点B与点N重合时,求劣弧 的长;
(2)当 时,如图②,求点 B到OA的距离,并求此时x的值;
(3)设点O到BC的距离为d.
①当点A在劣弧 上,且过点A的切线与AC垂直时,求d的值;
②直接写出d的最小值.
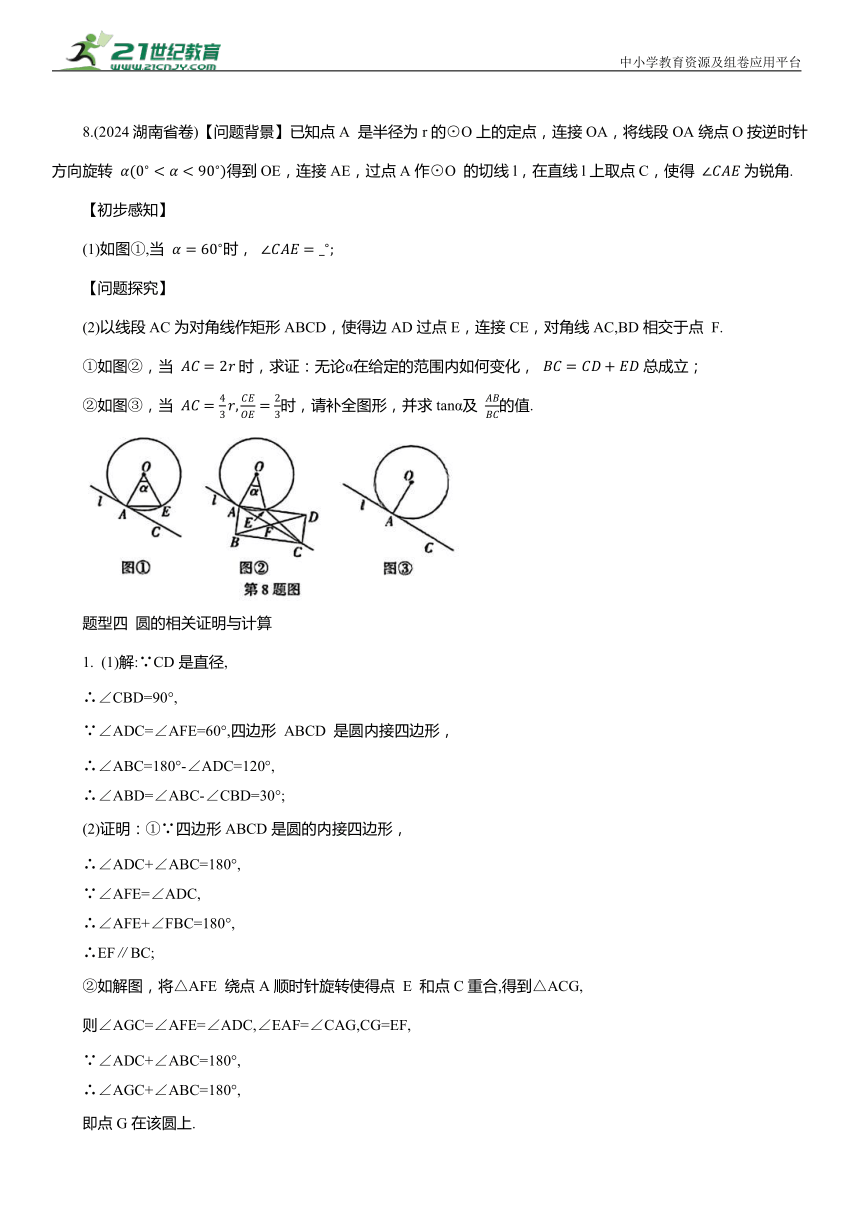
8.(2024湖南省卷)【问题背景】已知点A 是半径为r的⊙O上的定点,连接OA,将线段OA绕点O按逆时针方向旋转 得到OE,连接AE,过点A作⊙O 的切线l,在直线l上取点C,使得 为锐角.
【初步感知】
(1)如图①,当 时,
【问题探究】
(2)以线段AC为对角线作矩形ABCD,使得边AD过点E,连接CE,对角线AC,BD相交于点 F.
①如图②,当 时,求证:无论α在给定的范围内如何变化, 总成立;
②如图③,当 时,请补全图形,并求tanα及 的值.
题型四 圆的相关证明与计算
1. (1)解:∵CD是直径,
∴∠CBD=90°,
∵∠ADC=∠AFE=60°,四边形 ABCD 是圆内接四边形,
∴∠ABC=180°-∠ADC=120°,
∴∠ABD=∠ABC-∠CBD=30°;
(2)证明:①∵四边形ABCD是圆的内接四边形,
∴∠ADC+∠ABC=180°,
∵∠AFE=∠ADC,
∴∠AFE+∠FBC=180°,
∴EF∥BC;
②如解图,将△AFE 绕点A顺时针旋转使得点 E 和点C重合,得到△ACG,
则∠AGC=∠AFE=∠ADC,∠EAF=∠CAG,CG=EF,
∵∠ADC+∠ABC=180°,
∴∠AGC+∠ABC=180°,
即点G在该圆上.
由圆内接四边形性质可知,
∠DAB+∠BCD=180°,
∵∠EAF+∠BAD=180°,
∴∠EAF=∠BCD,
∴∠EAF=∠CAG=∠BCD,
∴BD=CG,
即EF=BD.
2. 解:(1)∵AB是⊙O 的直径,
∴∠ACB=90°,
∵∠ABC=25°,
∴∠BAC=65°,
∵四边形ABEC为⊙O的内接四边形,
∴∠BAC+∠CEB=180°,
(2)
解题思路
根据Ⅰ为△ABC的内心,连接AI,BI,可得到∠DCA=∠DCB,∠BAI=∠CAI,根据同弧所对的圆周角相等得到∠DAB=∠DCB,可推出∠DIA =∠DAI,同理∠DIB=∠DBI,即可得证DA=DI=DB.
DI=DA=DB,
证明:如解图,连接AI,BI,
∵点I为△ABC的内心,
∴CD平分∠ACB,AI平分∠BAC,
∴∠DCA=∠DCB,∠BAI=∠CAI,
∵∠DAB=∠DCB,
∴∠DCA=∠DAB,
∵∠DIA 为△AIC 的外角,
∴∠DIA=∠CAI+∠DCA,
∵∠DAI=∠DAB+∠BAI,
∴∠DIA=∠DAI,
∴DI=DA.
同理可得,∠DIB=∠DBI,
∴DI=DA=DB;
(3)
解题思路
I为 三条角平分线的交点,由角平分线上的点到角两边距离相等,将AC,BC部分长度转化到AB边上去,求出剩余长度与CI的关系,即可求出△ABC的周长.
解:如解图,过点I分别作AC,AB,BC的垂线,垂足分别为F,G,H,
由(2)得,
∴在 Rt△ABD中,
∵点I是△ABC的内心,
∴AI平分∠FAG,
∴∠FAI=∠GAI,
∵∠AFI=∠AGI=90°,
∴△AFI≌△AGI(AAS),
∴AF=AG,
同理,BG=BH,
∵∠ACB=90°,CI平分∠ACB且IF⊥FC,
∴△FIC 为等腰直角三角形,
同理,
∴△ABC 的周长为 AB+AC+BC=2AB+2CF=26+4=30.
3. (1)
解题思路
要证明线段相等,需证明等腰三角形两个底角相等.
证明:如解图,连接AD,
∵D是 的中点,
∴∠ABD=∠CAD,
∵DN⊥AB,AB为⊙O的直径,
中小学教育资源及组卷应用平台
∴∠ADN=∠ABD,
∴∠ADN=∠CAD,
∴AF=DF;
(2)①
解题思路
由AB为直径,推出∠ADB=90°,再结合DM=DG,得到AD是MG的垂直平分线,由等角代换求出∠BAM的值即可证明切线.
证明:如解图,∵AB为⊙O 的直径,
∴∠ADB=90°=∠ADM,
∴∠B+∠BAD=90°,
∵DM=DG,
∴AD是MG的垂直平分线,
∴∠MAD=∠GAD,
∵∠GAD=∠B,
∴∠MAD=∠B,
∴∠MAD+∠BAD=∠B+∠BAD=90°,
∴∠BAM=90°,
∵AB为⊙O的直径,
∴AM是⊙O 的切线;
②
解题思路
由DN⊥AB,推出 DE∥AM,得到△GDF∽△GMA,求出AM值,利用勾股定理求出AD值,再由 即可求出直径AB,进而得到半径长.
解:∵DG=6,
∴DM=DG=6,MG=12,
∵DN⊥AB,∠MAB=90°,
∴DE∥AM,
∴△GDF∽△GMA,
∵DF=5,
∴AM=10,
即
解得
∴⊙O的半径为
4. (1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCD=90°.
∵DE⊥AB,
∴∠AED=90°,
∵BD平分∠ADE,
∴BC=BE;
(2)解:在 Rt△BCD 和 Rt△BED中,
∴Rt△BCD≌Rt△BED(HL),
∴CD=ED=5,
∴AC=AD-CD=13-5=8;
一题多解
在Rt△AED中,∠AED=90°,AD=13,DE=5,
设BC=BE=x,则AB=12-x,
∵∠AED=90°,
又∵∠ACB=90°,
(3)
解题思路
第一步:证明△ACB∽△AED,得到
解:存在常数k=1,使 成立.
理由如下:
∵∠A=∠A,∠ACB=∠AED,
∴△ACB∽△AED,
第二步:由BF为⊙O的切线,得到∠ABF=90°,推出∠A=∠CBF,得到△AED∽△BCF,得到
∵BF为⊙O的切线,
∴∠ABF=90°,
∴∠ABC+∠CBF=90°.
∵∠ABC+∠A=90°,
∴∠CBF=∠A.
∵∠E=∠BCF,
∴△AED∽△BCF,
第三步:将 进行化简,将第一,二步得到的比例式子进行等量代换即可求出k值.
假设
则
∴存在常数k=1,使 成立.
一题多解
存在常数k=1,使 成立.
理由如下:
∵BF切⊙O于点B,
∴BF⊥AB,
∴∠ABC+∠CBF=90°.
∵∠ACB=90°,
∴∠A+∠ABC=90°,
∴∠A=∠CBF,
∵∠ACB=∠BCF=90°,
∵∠AED=90°,∠ABF=90°,
要使 成立,
只需令k=1,
∴存在常数k=1,使 成立.
5.(1)解:∵AB 是⊙O 的直径,点 F 是⊙O 上异于A,B的点,
(2)证明:∵AM·BM=AB·MN,
∴△AMN∽△ABM,
∴∠NAM=∠MAB.
∵∠NAM+∠MAB=180°,
∴∠NAM=∠MAB=90°,
∴OA⊥CM.
∵OA为⊙O的半径,
∴直线 CM 与⊙O 相切;
(3)证明:我认为CE+EB=CB正确,
理由如下:如解图①,连接OC,OD,AD,BD,设OC 交AD于点G,
∵OA=OD,
∴点O 在线段AD 的中垂线上,
∵CA=CD,
∴点C在线段AD的中垂线上,
∴OC⊥AD,
∴∠OGA=90°,
∵AB 是⊙O 的直径,
∴∠ADB=90°,
∴∠OGA=∠ADB,
∴OG∥BD,
∴∠AOC=∠ABD.
∵∠AHD=90°,
∴∠DHB=90°,
∵E为DH的中点,
且
∵∠AOC=∠ABD,
∴tan∠HBE=tan∠ABC,
∴∠HBE=∠ABC,
∴B,E,C三点共线,
∴CE+EB=CB.
一题多解
(3)证明:我认为( 正确,
理由如下:
如解图②,连接OC,OD,过点B作⊙O的切线,交 CD的延长线于点K,设BC与 DH交于点 G,
在△OAC和△ODC中
∴△OAC≌△ODC(SSS),
∴∠OAC=∠ODC.
由(2)知OA⊥CM,
∴∠OAC=∠ODC=90°,
∴OD⊥CD.
∵OD为⊙O的半径,
∴ CK为⊙O 的切线.
∵BK为⊙O的切线,
∴DK=BK,BK⊥AB.
∵DH⊥AB,CA⊥AB,
∴AC∥DH∥BK,
∵CA=CD,
∴GH=GD,
∴点G是线段DH的中点,
∵点E 是线段DH的中点,
∴点G与点E重合.
∴线段 BC 经过点E,
∴CE+EB=CB.
一题多解
(3)证明:我认为CE+EB=CB 正确,理由如下:如解图③,连接OC,OD,
在△OAC和△ODC中
∴△OAC≌△ODC(SSS),
∴∠CDO=∠CAO=90°,
连接BD并延长与AC延长线交于点 P,设 BC与DH交于点G,
∵∠CDO=∠CAO=90°,∠BAC=90°,
∴∠P+∠OBD=90°,∠CDP+∠ODB=90°,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠P=∠CDP,
∴CP=CD,
∵CA=CD,
∴AP=2AC,
∵∠CAO=∠BHD=90°,
∴AP∥HD,
∴△BHG∽△BAC,△BHD∽△BAP,
∵AP=2AC,
∴HD=2HG,即G为HD中点,
又∵E是DH的中点,
∴点G与点E重合,
∴CE+EB=CB.
解题技巧
本题求证CE+BE与CB的数量关系,只需证明CE与BE 共线即可,可用方法一:证明∠HBE=∠ABC或方法二、三:利用三角形相似.
(4)解:我认为DK=2DE正确,理由如下:
如解图④,延长DE 交⊙O 于点 Q,
根据相交弦定理知:
DE·EQ=GE·EB,
又∵AB 为直径,AB⊥DQ,
∴HQ=HD,
∵DE=HE,
∴QE=3DE.
又∵ ∠KGE = 180°-∠AGB = 90°= ∠EHB,∠GEK=∠HEB,
∴△EHB∽△EGK,
∴EH·EK=EG·EB,
∴EK=EQ=3DE.
∴DK=2DE.
6. (1)
解题思路
由∠BAC=90°,且AE⊥OC,利用 即可求解.
解:∵AB=AC,且AB是⊙O的直径,
∴AC=2AO.
∵∠BAC=90°,
∴ 在 Rt△AOC中,
∵AE⊥OC,
∴在 Rt△AOE中,
(2)
解题思路
第一步:利用倍长中线OE,构造与△AEO全等的三角形,求出∠OEB的度数;
证明:如解图①,过点B作BM∥AE,交EO的延长线于点M.
∴∠BAE=∠ABM,∠AEO=∠BMO=90°.
∵AO=BO,
∴△AOE≌△BOM(AAS),
∴AE=BM,OE=OM.
∴BM=2OE=EM,
∴∠MEB=∠MBE=45°,
第二步:由AE⊥OC,推出∠AEB=BEC;
∴∠AEB=∠AEO+∠MEB=135°,
∴ ∠AEB=∠BEC.
第三步:由AB=AC,且∠BAC=90°,推出∠CBA的度数,再由第一步证明的三角形全等,通过等角计算,推出∠BAE=∠CBE 即可得证.
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∴∠ABM=∠CBE,
∴∠BAE=∠CBE,
∴△AEB∽△BEC;
(3)
解题思路
第一步:由AB=AC,∠BAC=90°且∠ADB=90°,推出2BD=BC,由(2)知△AEB∽△BEC,推出△AOE∽△BDE,进而推出AF∥DE;
证明:如解图②,在解图①的基础上,连接DE,DF.
∵AB是⊙O的直径,
∴∠ADB=∠AFB=90°,AB=2AO.
∵AB=AC,∠BAC=90°,
∴BC=2BD,∠DAB=45°.
由(2)知,△AEB∽△BEC,
∴△AOE∽△BDE,
∴∠BED=∠AEO=90°.
∴∠DEF=90°.
∴∠AFB=∠DEF,
∴AF∥DE.
第二步:由(2)知∠AEB 度数,推出∠AEF=∠DFB,进而推出AE∥FD;
由(2)知,∠AEB=135°,
∵∠DFB=∠DAB=45°,
∴∠DFB=∠AEF,
∴AE∥FD,
第三步:由两组对边分别平行推出四边形AEDF是平行四边形,再根据平行四边形的性质进行证明.
∴四边形AEDF 是平行四边形,
∴AD与EF互相平分.
7. 解:(1)如解图①,连接OA,ON,
∵AN=OA=ON=3,
∴△AON是等边三角形,
∴∠AON=60°,
∴劣弧 的长为
(2)
解题思路
第一步:将点B到AO的距离转化成点O到MN的距离是解题的关键,然后利用垂径定理即可求解点B到AO的距离;
如解图②,过点O作OD⊥MN于点D,过点B作BE⊥AO于点 E,连接ON,
则
∵ON=3,
BE=OD=2,
∴点 B到OA的距离为2.
第二步:利用勾股定理求出AE,然后求解x即可.
(3)
解题思路
由勾股定理求出AC,再根据半径求出CO,利用相似三角形即可求出O到BC的距离d.
①过点A的切线与AC垂直时,AC过圆心O,如解图③,过点O作OF⊥BC于点 F,
∵∠ABC=∠OFC=90°,∠ACB=∠OCF,
∴△ABC∽△OFC,
解得
②
【解法提示】如解图④,过点O作OJ⊥BC于点 J,连接OB,在 Rt△OBJ中, .当OB 最小时,即OB⊥MN时,d最小,过点A作AQ⊥BO于点Q,连接OA,∵AB=AO=3,AQ⊥OB,∴BQ= OB=1,∵ d的最小值为
8. (1)解:30;
【解法提示】∵ ∠AOE=α=60°,OA=OE,∴ △OEA 是等边三角形,∴∠OAE=60°,∵ 直线l是⊙O 的切线,
∴∠OAC=90°,∴∠CAE=90°-60°=30°.
(2)
解题思路
由AC=2r,推导得出△OAE≌△FCD,推出AE=CD即可证明.
①证明:∵OA=OE,
∴∠OAE=∠OEA,
∵∠AOE=α,
∴∠OAE+∠OEA+α=180°,
∵∠OAC=90°,
∵四边形ABCD 是矩形,
∵OA=OE=r,
∴OA=FC,OE=FD,
又∵∠AOE=∠CFD,
∴△OAE≌△FCD,
∴AE=CD.
∵BC=AD,AD=AE+DE,
∴ BC=CD+DE;
②解:补全图形如解图①,
过点O作OG⊥AE于点G,过点A作AH⊥OE 于点H,在Rt△AOC中,
∴由勾股定理得,
∴OC=OE+CE,
∴点 E 在线段OC上,
∴在 Rt△AOC中,
∵OG⊥AE,
∴∠OGA=∠OGE=90°,
又∵OA=OE,OG=OG,∴AG=GE,
∴△AOG≌△EOG,
∵OG⊥AE,AH⊥OE,
∴∠EOG+∠OEA=∠EAH+∠OEA=90°,
在 Rt△OAH中,
∴设AH=4m,OH=3m,由勾股定理得,OA=OE=5m,
∴HE=OE-OH=2m,
∴在 Rt△AHE中,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,
由①知
∴在 Rt△ABC中,
一题多解
补全图形如解图②,∵AC 是⊙O 的切线,∴∠OAC= 设OA=3m,则AC OE+CE=5m=OC,即点E在线段OC上,如解图②,过点O作OH⊥AE,垂足为H,则AH=EH,∵∠OHE=90°=∠D,∠OEH=∠CED,∴△OEH∽△CED,∴EHD 设.EH=AH=3a,则DE=2a,∴AD=AH+EH+ED=8a,在 Rt△ACD 中, 64a ,在Rt△CED中,( 解得 负值已舍去),
类型一 圆基本性质的证明与计算
1. (2024 浙江)如图,在圆内接四边形ABCD 中, 延长AD至点E,使 ,延长BA 至点 F,连接EF,使
(1)若 CD为直径,求 的度数.
(2)求证:(
2. (2024烟台)如图,AB 是⊙O 的直径, 内接于⊙O,点I为 的内心,连接CI并延长交⊙O 于点D. E是 上任意一点,连接AD,BD,BE,CE.
(1)若 求 的度数;
(2)找出图中所有与DI相等的线段,并证明;
(3)若 求 的周长.
类型二 与切线有关的证明与计算
3. (2024遂宁)如图,AB是⊙O的直径,AC是一条弦,点D 是 的中点, 于点E,交AC于点F,连接DB交AC于点 G.
(1)求证:
(2)延长GD至点M,使. 连接AM.
①求证:AM是⊙O 的切线;
②若 求⊙O 的半径.
4. 新考法 新设问 (2024 云南定心卷)如图, 内接于⊙O,且AB为⊙O的直径,⊙O外的点 D 在射线AC上,过点 D作DE垂直AB的延长线于点E,且BD平分
(1)求证:
(2)若 求AC的长;
(3)过点B作⊙O的切线BF,交AD于点F,是否存在常数k,使 成立 若存在,求常数k的值;若不存在,请说明理由.
5.|一题多设问 (2024 云南)如图,AB是⊙O 的直径.点 D,F是⊙O上异于A,B的点.点C在⊙O外,( 延长BF与CA的延长线交于点M,点N在BA的延长线上, AB·MN.点H在直径AB上, 点E是线段DH的中点.
(1)求 的度数;
(2)求证:直线CM与⊙O 相切;
(3)看一看,想一想,证一证:
以下与线段CE、线段EB、线段CB有关的三个结论:( 你认为哪个正确 请说明理由.
(4)设BC交⊙O 于点G,AG,HD的延长线交于点K,关于线段DK,线段DE有关的两个结论: 你认为哪个正确 请说明理由.
6. (2024福建)如图,在 中, ,以AB为直径的⊙O 交 BC 于点 D, 垂足为E,BE 的延长线交 于点F.
(1)求 的值;
(2)求证:
(3)求证:AD与EF互相平分.
7. (2024河北)已知⊙O 的半径为3,弦 中, 在平面上,先将 和⊙O按图①位置摆放(点B与点N重合,点A在⊙O上,点C在⊙O内),随后移动 使点B 在弦 MN上移动,点A 始终在⊙O 上随之移动.设
(1)当点B与点N重合时,求劣弧 的长;
(2)当 时,如图②,求点 B到OA的距离,并求此时x的值;
(3)设点O到BC的距离为d.
①当点A在劣弧 上,且过点A的切线与AC垂直时,求d的值;
②直接写出d的最小值.
8.(2024湖南省卷)【问题背景】已知点A 是半径为r的⊙O上的定点,连接OA,将线段OA绕点O按逆时针方向旋转 得到OE,连接AE,过点A作⊙O 的切线l,在直线l上取点C,使得 为锐角.
【初步感知】
(1)如图①,当 时,
【问题探究】
(2)以线段AC为对角线作矩形ABCD,使得边AD过点E,连接CE,对角线AC,BD相交于点 F.
①如图②,当 时,求证:无论α在给定的范围内如何变化, 总成立;
②如图③,当 时,请补全图形,并求tanα及 的值.
题型四 圆的相关证明与计算
1. (1)解:∵CD是直径,
∴∠CBD=90°,
∵∠ADC=∠AFE=60°,四边形 ABCD 是圆内接四边形,
∴∠ABC=180°-∠ADC=120°,
∴∠ABD=∠ABC-∠CBD=30°;
(2)证明:①∵四边形ABCD是圆的内接四边形,
∴∠ADC+∠ABC=180°,
∵∠AFE=∠ADC,
∴∠AFE+∠FBC=180°,
∴EF∥BC;
②如解图,将△AFE 绕点A顺时针旋转使得点 E 和点C重合,得到△ACG,
则∠AGC=∠AFE=∠ADC,∠EAF=∠CAG,CG=EF,
∵∠ADC+∠ABC=180°,
∴∠AGC+∠ABC=180°,
即点G在该圆上.
由圆内接四边形性质可知,
∠DAB+∠BCD=180°,
∵∠EAF+∠BAD=180°,
∴∠EAF=∠BCD,
∴∠EAF=∠CAG=∠BCD,
∴BD=CG,
即EF=BD.
2. 解:(1)∵AB是⊙O 的直径,
∴∠ACB=90°,
∵∠ABC=25°,
∴∠BAC=65°,
∵四边形ABEC为⊙O的内接四边形,
∴∠BAC+∠CEB=180°,
(2)
解题思路
根据Ⅰ为△ABC的内心,连接AI,BI,可得到∠DCA=∠DCB,∠BAI=∠CAI,根据同弧所对的圆周角相等得到∠DAB=∠DCB,可推出∠DIA =∠DAI,同理∠DIB=∠DBI,即可得证DA=DI=DB.
DI=DA=DB,
证明:如解图,连接AI,BI,
∵点I为△ABC的内心,
∴CD平分∠ACB,AI平分∠BAC,
∴∠DCA=∠DCB,∠BAI=∠CAI,
∵∠DAB=∠DCB,
∴∠DCA=∠DAB,
∵∠DIA 为△AIC 的外角,
∴∠DIA=∠CAI+∠DCA,
∵∠DAI=∠DAB+∠BAI,
∴∠DIA=∠DAI,
∴DI=DA.
同理可得,∠DIB=∠DBI,
∴DI=DA=DB;
(3)
解题思路
I为 三条角平分线的交点,由角平分线上的点到角两边距离相等,将AC,BC部分长度转化到AB边上去,求出剩余长度与CI的关系,即可求出△ABC的周长.
解:如解图,过点I分别作AC,AB,BC的垂线,垂足分别为F,G,H,
由(2)得,
∴在 Rt△ABD中,
∵点I是△ABC的内心,
∴AI平分∠FAG,
∴∠FAI=∠GAI,
∵∠AFI=∠AGI=90°,
∴△AFI≌△AGI(AAS),
∴AF=AG,
同理,BG=BH,
∵∠ACB=90°,CI平分∠ACB且IF⊥FC,
∴△FIC 为等腰直角三角形,
同理,
∴△ABC 的周长为 AB+AC+BC=2AB+2CF=26+4=30.
3. (1)
解题思路
要证明线段相等,需证明等腰三角形两个底角相等.
证明:如解图,连接AD,
∵D是 的中点,
∴∠ABD=∠CAD,
∵DN⊥AB,AB为⊙O的直径,
中小学教育资源及组卷应用平台
∴∠ADN=∠ABD,
∴∠ADN=∠CAD,
∴AF=DF;
(2)①
解题思路
由AB为直径,推出∠ADB=90°,再结合DM=DG,得到AD是MG的垂直平分线,由等角代换求出∠BAM的值即可证明切线.
证明:如解图,∵AB为⊙O 的直径,
∴∠ADB=90°=∠ADM,
∴∠B+∠BAD=90°,
∵DM=DG,
∴AD是MG的垂直平分线,
∴∠MAD=∠GAD,
∵∠GAD=∠B,
∴∠MAD=∠B,
∴∠MAD+∠BAD=∠B+∠BAD=90°,
∴∠BAM=90°,
∵AB为⊙O的直径,
∴AM是⊙O 的切线;
②
解题思路
由DN⊥AB,推出 DE∥AM,得到△GDF∽△GMA,求出AM值,利用勾股定理求出AD值,再由 即可求出直径AB,进而得到半径长.
解:∵DG=6,
∴DM=DG=6,MG=12,
∵DN⊥AB,∠MAB=90°,
∴DE∥AM,
∴△GDF∽△GMA,
∵DF=5,
∴AM=10,
即
解得
∴⊙O的半径为
4. (1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCD=90°.
∵DE⊥AB,
∴∠AED=90°,
∵BD平分∠ADE,
∴BC=BE;
(2)解:在 Rt△BCD 和 Rt△BED中,
∴Rt△BCD≌Rt△BED(HL),
∴CD=ED=5,
∴AC=AD-CD=13-5=8;
一题多解
在Rt△AED中,∠AED=90°,AD=13,DE=5,
设BC=BE=x,则AB=12-x,
∵∠AED=90°,
又∵∠ACB=90°,
(3)
解题思路
第一步:证明△ACB∽△AED,得到
解:存在常数k=1,使 成立.
理由如下:
∵∠A=∠A,∠ACB=∠AED,
∴△ACB∽△AED,
第二步:由BF为⊙O的切线,得到∠ABF=90°,推出∠A=∠CBF,得到△AED∽△BCF,得到
∵BF为⊙O的切线,
∴∠ABF=90°,
∴∠ABC+∠CBF=90°.
∵∠ABC+∠A=90°,
∴∠CBF=∠A.
∵∠E=∠BCF,
∴△AED∽△BCF,
第三步:将 进行化简,将第一,二步得到的比例式子进行等量代换即可求出k值.
假设
则
∴存在常数k=1,使 成立.
一题多解
存在常数k=1,使 成立.
理由如下:
∵BF切⊙O于点B,
∴BF⊥AB,
∴∠ABC+∠CBF=90°.
∵∠ACB=90°,
∴∠A+∠ABC=90°,
∴∠A=∠CBF,
∵∠ACB=∠BCF=90°,
∵∠AED=90°,∠ABF=90°,
要使 成立,
只需令k=1,
∴存在常数k=1,使 成立.
5.(1)解:∵AB 是⊙O 的直径,点 F 是⊙O 上异于A,B的点,
(2)证明:∵AM·BM=AB·MN,
∴△AMN∽△ABM,
∴∠NAM=∠MAB.
∵∠NAM+∠MAB=180°,
∴∠NAM=∠MAB=90°,
∴OA⊥CM.
∵OA为⊙O的半径,
∴直线 CM 与⊙O 相切;
(3)证明:我认为CE+EB=CB正确,
理由如下:如解图①,连接OC,OD,AD,BD,设OC 交AD于点G,
∵OA=OD,
∴点O 在线段AD 的中垂线上,
∵CA=CD,
∴点C在线段AD的中垂线上,
∴OC⊥AD,
∴∠OGA=90°,
∵AB 是⊙O 的直径,
∴∠ADB=90°,
∴∠OGA=∠ADB,
∴OG∥BD,
∴∠AOC=∠ABD.
∵∠AHD=90°,
∴∠DHB=90°,
∵E为DH的中点,
且
∵∠AOC=∠ABD,
∴tan∠HBE=tan∠ABC,
∴∠HBE=∠ABC,
∴B,E,C三点共线,
∴CE+EB=CB.
一题多解
(3)证明:我认为( 正确,
理由如下:
如解图②,连接OC,OD,过点B作⊙O的切线,交 CD的延长线于点K,设BC与 DH交于点 G,
在△OAC和△ODC中
∴△OAC≌△ODC(SSS),
∴∠OAC=∠ODC.
由(2)知OA⊥CM,
∴∠OAC=∠ODC=90°,
∴OD⊥CD.
∵OD为⊙O的半径,
∴ CK为⊙O 的切线.
∵BK为⊙O的切线,
∴DK=BK,BK⊥AB.
∵DH⊥AB,CA⊥AB,
∴AC∥DH∥BK,
∵CA=CD,
∴GH=GD,
∴点G是线段DH的中点,
∵点E 是线段DH的中点,
∴点G与点E重合.
∴线段 BC 经过点E,
∴CE+EB=CB.
一题多解
(3)证明:我认为CE+EB=CB 正确,理由如下:如解图③,连接OC,OD,
在△OAC和△ODC中
∴△OAC≌△ODC(SSS),
∴∠CDO=∠CAO=90°,
连接BD并延长与AC延长线交于点 P,设 BC与DH交于点G,
∵∠CDO=∠CAO=90°,∠BAC=90°,
∴∠P+∠OBD=90°,∠CDP+∠ODB=90°,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠P=∠CDP,
∴CP=CD,
∵CA=CD,
∴AP=2AC,
∵∠CAO=∠BHD=90°,
∴AP∥HD,
∴△BHG∽△BAC,△BHD∽△BAP,
∵AP=2AC,
∴HD=2HG,即G为HD中点,
又∵E是DH的中点,
∴点G与点E重合,
∴CE+EB=CB.
解题技巧
本题求证CE+BE与CB的数量关系,只需证明CE与BE 共线即可,可用方法一:证明∠HBE=∠ABC或方法二、三:利用三角形相似.
(4)解:我认为DK=2DE正确,理由如下:
如解图④,延长DE 交⊙O 于点 Q,
根据相交弦定理知:
DE·EQ=GE·EB,
又∵AB 为直径,AB⊥DQ,
∴HQ=HD,
∵DE=HE,
∴QE=3DE.
又∵ ∠KGE = 180°-∠AGB = 90°= ∠EHB,∠GEK=∠HEB,
∴△EHB∽△EGK,
∴EH·EK=EG·EB,
∴EK=EQ=3DE.
∴DK=2DE.
6. (1)
解题思路
由∠BAC=90°,且AE⊥OC,利用 即可求解.
解:∵AB=AC,且AB是⊙O的直径,
∴AC=2AO.
∵∠BAC=90°,
∴ 在 Rt△AOC中,
∵AE⊥OC,
∴在 Rt△AOE中,
(2)
解题思路
第一步:利用倍长中线OE,构造与△AEO全等的三角形,求出∠OEB的度数;
证明:如解图①,过点B作BM∥AE,交EO的延长线于点M.
∴∠BAE=∠ABM,∠AEO=∠BMO=90°.
∵AO=BO,
∴△AOE≌△BOM(AAS),
∴AE=BM,OE=OM.
∴BM=2OE=EM,
∴∠MEB=∠MBE=45°,
第二步:由AE⊥OC,推出∠AEB=BEC;
∴∠AEB=∠AEO+∠MEB=135°,
∴ ∠AEB=∠BEC.
第三步:由AB=AC,且∠BAC=90°,推出∠CBA的度数,再由第一步证明的三角形全等,通过等角计算,推出∠BAE=∠CBE 即可得证.
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∴∠ABM=∠CBE,
∴∠BAE=∠CBE,
∴△AEB∽△BEC;
(3)
解题思路
第一步:由AB=AC,∠BAC=90°且∠ADB=90°,推出2BD=BC,由(2)知△AEB∽△BEC,推出△AOE∽△BDE,进而推出AF∥DE;
证明:如解图②,在解图①的基础上,连接DE,DF.
∵AB是⊙O的直径,
∴∠ADB=∠AFB=90°,AB=2AO.
∵AB=AC,∠BAC=90°,
∴BC=2BD,∠DAB=45°.
由(2)知,△AEB∽△BEC,
∴△AOE∽△BDE,
∴∠BED=∠AEO=90°.
∴∠DEF=90°.
∴∠AFB=∠DEF,
∴AF∥DE.
第二步:由(2)知∠AEB 度数,推出∠AEF=∠DFB,进而推出AE∥FD;
由(2)知,∠AEB=135°,
∵∠DFB=∠DAB=45°,
∴∠DFB=∠AEF,
∴AE∥FD,
第三步:由两组对边分别平行推出四边形AEDF是平行四边形,再根据平行四边形的性质进行证明.
∴四边形AEDF 是平行四边形,
∴AD与EF互相平分.
7. 解:(1)如解图①,连接OA,ON,
∵AN=OA=ON=3,
∴△AON是等边三角形,
∴∠AON=60°,
∴劣弧 的长为
(2)
解题思路
第一步:将点B到AO的距离转化成点O到MN的距离是解题的关键,然后利用垂径定理即可求解点B到AO的距离;
如解图②,过点O作OD⊥MN于点D,过点B作BE⊥AO于点 E,连接ON,
则
∵ON=3,
BE=OD=2,
∴点 B到OA的距离为2.
第二步:利用勾股定理求出AE,然后求解x即可.
(3)
解题思路
由勾股定理求出AC,再根据半径求出CO,利用相似三角形即可求出O到BC的距离d.
①过点A的切线与AC垂直时,AC过圆心O,如解图③,过点O作OF⊥BC于点 F,
∵∠ABC=∠OFC=90°,∠ACB=∠OCF,
∴△ABC∽△OFC,
解得
②
【解法提示】如解图④,过点O作OJ⊥BC于点 J,连接OB,在 Rt△OBJ中, .当OB 最小时,即OB⊥MN时,d最小,过点A作AQ⊥BO于点Q,连接OA,∵AB=AO=3,AQ⊥OB,∴BQ= OB=1,∵ d的最小值为
8. (1)解:30;
【解法提示】∵ ∠AOE=α=60°,OA=OE,∴ △OEA 是等边三角形,∴∠OAE=60°,∵ 直线l是⊙O 的切线,
∴∠OAC=90°,∴∠CAE=90°-60°=30°.
(2)
解题思路
由AC=2r,推导得出△OAE≌△FCD,推出AE=CD即可证明.
①证明:∵OA=OE,
∴∠OAE=∠OEA,
∵∠AOE=α,
∴∠OAE+∠OEA+α=180°,
∵∠OAC=90°,
∵四边形ABCD 是矩形,
∵OA=OE=r,
∴OA=FC,OE=FD,
又∵∠AOE=∠CFD,
∴△OAE≌△FCD,
∴AE=CD.
∵BC=AD,AD=AE+DE,
∴ BC=CD+DE;
②解:补全图形如解图①,
过点O作OG⊥AE于点G,过点A作AH⊥OE 于点H,在Rt△AOC中,
∴由勾股定理得,
∴OC=OE+CE,
∴点 E 在线段OC上,
∴在 Rt△AOC中,
∵OG⊥AE,
∴∠OGA=∠OGE=90°,
又∵OA=OE,OG=OG,∴AG=GE,
∴△AOG≌△EOG,
∵OG⊥AE,AH⊥OE,
∴∠EOG+∠OEA=∠EAH+∠OEA=90°,
在 Rt△OAH中,
∴设AH=4m,OH=3m,由勾股定理得,OA=OE=5m,
∴HE=OE-OH=2m,
∴在 Rt△AHE中,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,
由①知
∴在 Rt△ABC中,
一题多解
补全图形如解图②,∵AC 是⊙O 的切线,∴∠OAC= 设OA=3m,则AC OE+CE=5m=OC,即点E在线段OC上,如解图②,过点O作OH⊥AE,垂足为H,则AH=EH,∵∠OHE=90°=∠D,∠OEH=∠CED,∴△OEH∽△CED,∴EHD 设.EH=AH=3a,则DE=2a,∴AD=AH+EH+ED=8a,在 Rt△ACD 中, 64a ,在Rt△CED中,( 解得 负值已舍去),
同课章节目录
