第十二讲 角、相交线与平行线(含解析)2025年中考数学基础知识分点练
文档属性
| 名称 | 第十二讲 角、相交线与平行线(含解析)2025年中考数学基础知识分点练 |  | |
| 格式 | docx | ||
| 文件大小 | 287.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 21:18:59 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十二讲 角、相交线与平行线
命题点1 直线和线段(7考)
1.(2024吉林省卷)如图,从长春站去往胜利公园,与其它道路相比,走人民大街路程最近,其蕴含的数学道理是 .
命题点2角与角平分线(24考)
2. (2024甘肃省卷)若∠A=55°,则∠A 的补角为 ( )
A. 35° B. 45° C. 115° D. 125°
3. 新考法 真实问题情境(2024广西)如图,2时整,钟表的时针和分针所成的锐角为 ( )
A. 20° B. 40° C. 60° D. 80°
4.(2023临沂)图中用量角器测得∠ABC的度数是 ( )
A. 50° B. 80° C. 130° D. 150°
5.(2024广东省卷)如图,一把直尺、两个含30°的三角尺拼接在一起,则∠ACE的度数为 ( )
A. 120° B. 90° C. 60° D. 30°
6. (2024青海省卷)如图,OC平分 点P在OC上, PD ,则点 P到OA的距离是( )
A. 4 B. 3 C. 2 D. 1
7. (2023乐山)如图,点O 在直线AB上,OD 是 的平分线,若 则 的度数为 .
命题点3 相交线
类型一 相交线求角度(34考)
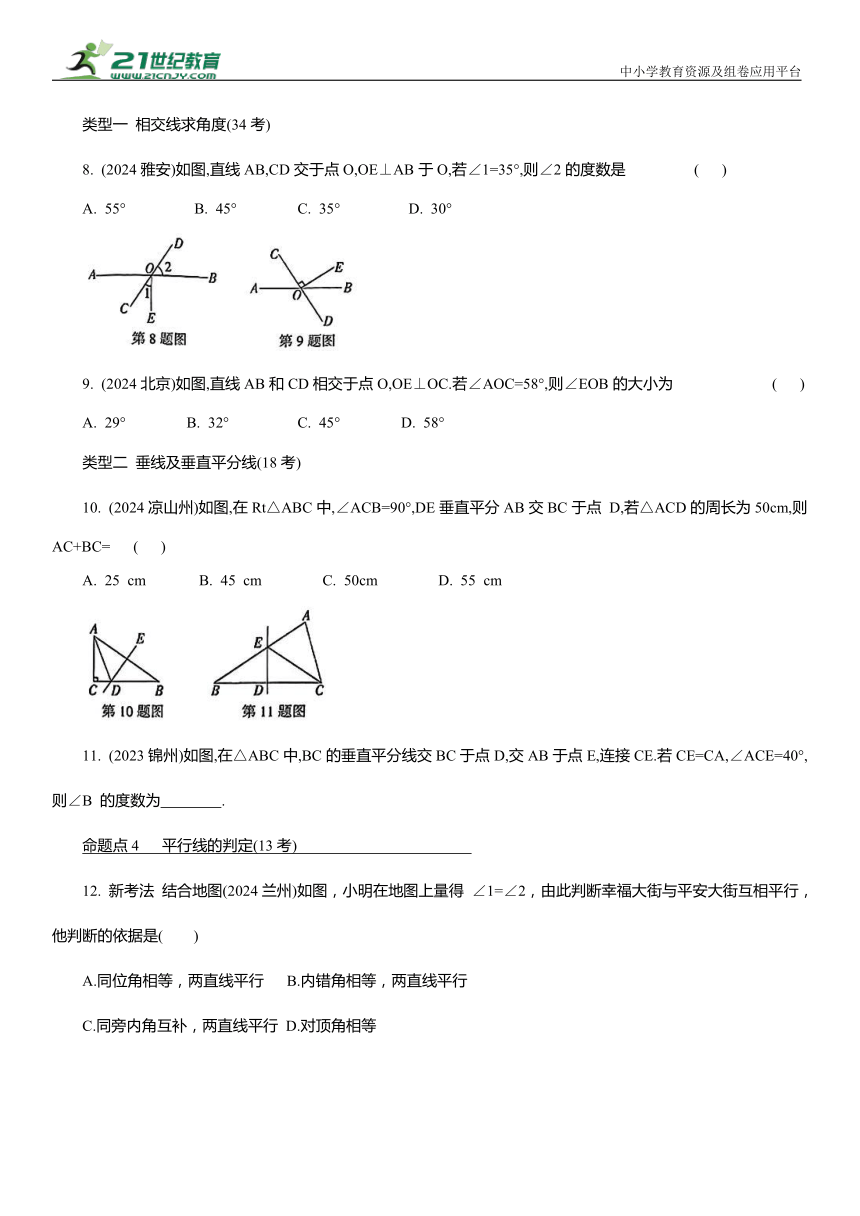
8. (2024雅安)如图,直线AB,CD交于点O,OE⊥AB于O,若∠1=35°,则∠2的度数是 ( )
A. 55° B. 45° C. 35° D. 30°
9. (2024北京)如图,直线AB和CD相交于点O,OE⊥OC.若∠AOC=58°,则∠EOB的大小为 ( )
A. 29° B. 32° C. 45° D. 58°
类型二 垂线及垂直平分线(18考)
10. (2024凉山州)如图,在Rt△ABC中,∠ACB=90°,DE垂直平分AB交BC于点 D,若△ACD的周长为50cm,则AC+BC= ( )
A. 25 cm B. 45 cm C. 50cm D. 55 cm
11. (2023锦州)如图,在△ABC中,BC的垂直平分线交BC于点D,交AB于点E,连接CE.若CE=CA,∠ACE=40°,则∠B 的度数为 .
命题点4 平行线的判定(13考)
12. 新考法 结合地图(2024兰州)如图,小明在地图上量得 ∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.对顶角相等
13.(2023苏州)如图,在正方形网格内,线段PQ 的两个端点都在格点上,网格内另有A,B,C,D四个格点,下面四个结论中,正确的是 ( )
A. 连接AB,则AB∥PQ B. 连接BC、则BC∥PQ
C. 连接BD,则BD⊥PQ D. 连接AD,则AD⊥PQ
命题点5 平行线性质求角度
类型一 直接利用平行线性质求角度(120考)
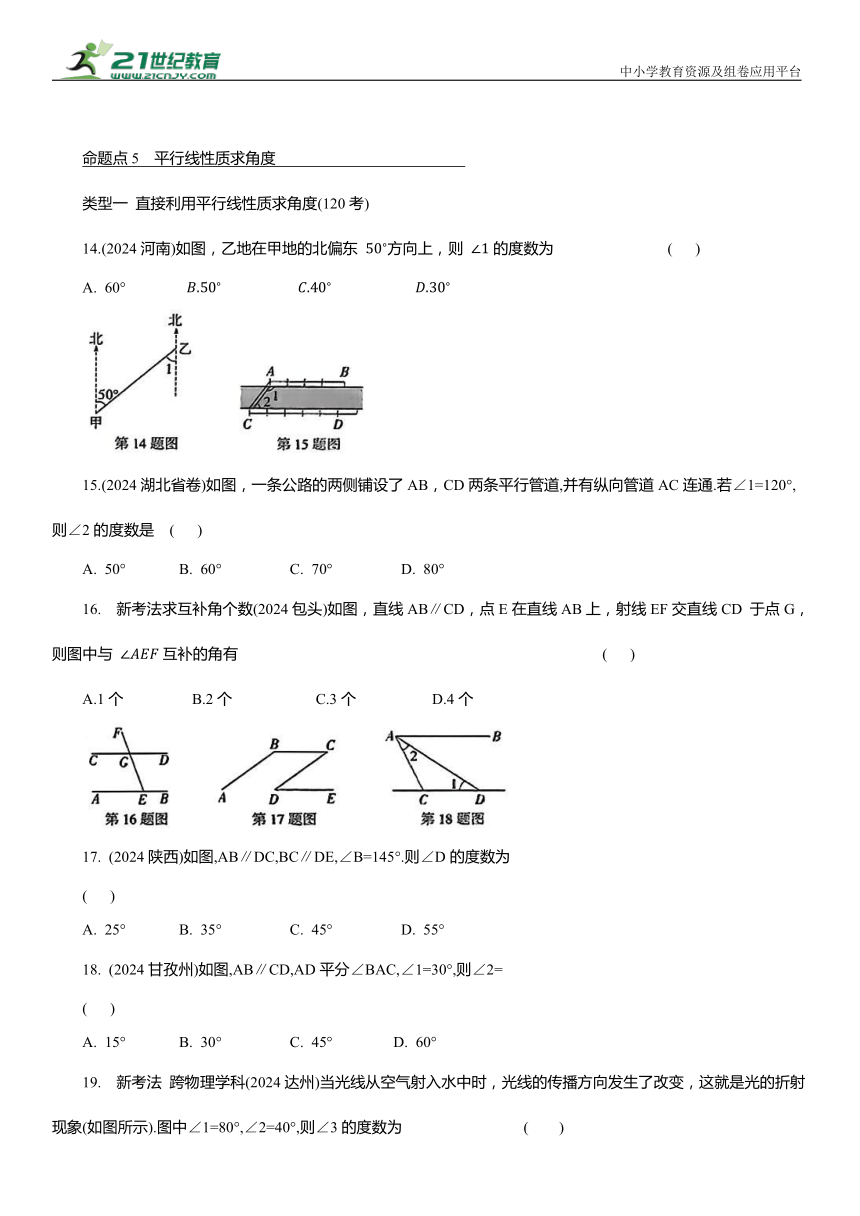
14.(2024河南)如图,乙地在甲地的北偏东 方向上,则 的度数为 ( )
A. 60°
15.(2024湖北省卷)如图,一条公路的两侧铺设了AB,CD两条平行管道,并有纵向管道AC连通.若∠1=120°,则∠2的度数是 ( )
A. 50° B. 60° C. 70° D. 80°
16. 新考法求互补角个数(2024包头)如图,直线AB∥CD,点E在直线AB上,射线EF交直线CD 于点G,则图中与 互补的角有 ( )
A.1个 B.2个 C.3个 D.4个
17. (2024陕西)如图,AB∥DC,BC∥DE,∠B=145°.则∠D的度数为
( )
A. 25° B. 35° C. 45° D. 55°
18. (2024甘孜州)如图,AB∥CD,AD平分∠BAC,∠1=30°,则∠2=
( )
A. 15° B. 30° C. 45° D. 60°
19. 新考法 跨物理学科(2024达州)当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象(如图所示).图中∠1=80°,∠2=40°,则∠3的度数为 ( )
A. 30° B. 40° C. 50° D. 70°
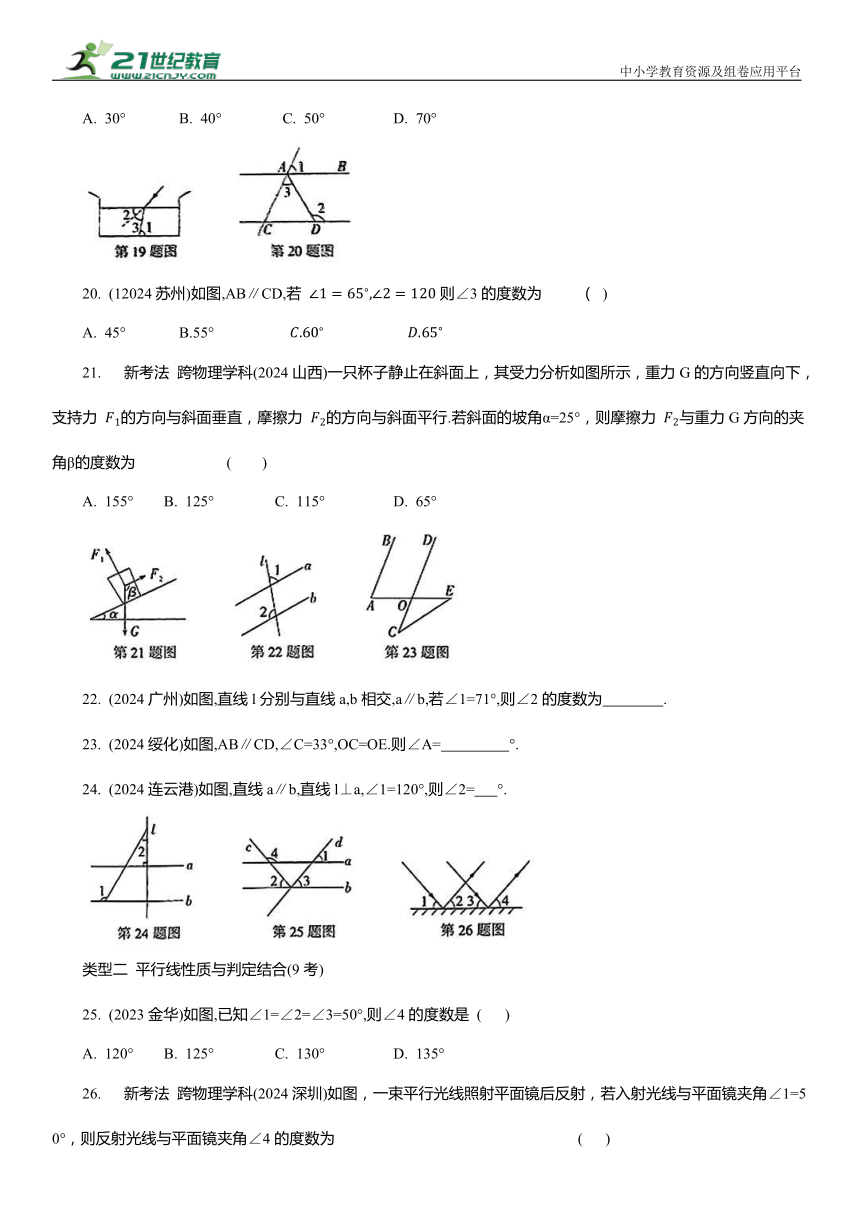
20. (12024苏州)如图,AB∥CD,若 则∠3的度数为 ( )
A. 45° B.55°
21. 新考法 跨物理学科(2024山西)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力 的方向与斜面垂直,摩擦力 的方向与斜面平行.若斜面的坡角α=25°,则摩擦力 与重力G方向的夹角β的度数为 ( )
A. 155° B. 125° C. 115° D. 65°
22. (2024广州)如图,直线l分别与直线a,b相交,a∥b,若∠1=71°,则∠2的度数为 .
23. (2024绥化)如图,AB∥CD,∠C=33°,OC=OE.则∠A= °.
24. (2024连云港)如图,直线a∥b,直线l⊥a,∠1=120°,则∠2= °.
类型二 平行线性质与判定结合(9考)
25. (2023金华)如图,已知∠1=∠2=∠3=50°,则∠4的度数是 ( )
A. 120° B. 125° C. 130° D. 135°
26. 新考法 跨物理学科(2024深圳)如图,一束平行光线照射平面镜后反射,若入射光线与平面镜夹角∠1=50°,则反射光线与平面镜夹角∠4的度数为 ( )
A. 40° B. 50° C. 60° D. 70°
类型三 与直角三角板结合(21考)
27.(2024赤峰)将一副三角尺(厚度不计)按如图所示摆放,使有刻度的两条边互相平行,则图中∠1 的度数为 ( )
A. 100° B. 105° C. 115° D. 120°
28.(2024泸州)把一块含30°角的直角三角板按如图方式放置于两条平行线间,若∠1=45°,则∠2= ( )
A.10° B. 15° C. 20° D. 30°
29.(2024凉山州)一副直角三角板按如图所示的方式摆放,点E 在AB的延长线上,当 时, 的度数为 ( )
A. 10° B. 15°
30.(2024福建)在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD⊥DE)按如图方式摆放,若AB∥CD,则∠1的大小为 ( )
A. 30° B. 45° C. 60° D. 75°
31.(2024齐齐哈尔)将一个含30°角的三角尺和直尺如图放置,若∠1=50°,则∠2的度数是 ( )
A. 30° B. 40° C. 50° D. 60°
32. (2024盐城)小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为 ( )
A. 25° B. 35° C. 45° D. 55°
33.(2024通辽)将三角尺ABC按如图位置摆放,顶点A落在直线 上,顶点B落在直线l 上,若 ,则∠2的度数是
( )
A. 45° B. 35° C. 30° D. 25°
34.(2024滨州)一副三角板 图①摆放,把三角板AOB 绕公共顶点O顺时针旋转至图②,即 时,∠1的大小为 °.
命题点6 平行线分线段成比例(8考)
35.(2023常州)小明按照以下步骤画线段AB的三等分点:
画法 图形
1.以A为端点画一条射线; 2.用圆规在射线上依次截取3 条等长线段AC,CD,DE,连接BE; 3.过点 C,D 分别画BE的平行线,交线段AB 于点M,N,M,N就是线段AB的三等分点.
这一画图过程体现的数学依据是
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
36. (2023北京)如图,直线AD,BC交于点O, 若 OF=1,FD=2,则 的值为 .
命题点7 黄金分割(6考)
37. (2024德阳)宽与长的比是 的矩形叫黄金矩形,黄金矩形给我们以协调的美感,世界各国许多著名建筑为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形ABCD 是黄金矩形( BC),点P是边AD上一点,则满足. 的点P的个数为 ( )
A. 3 B. 2 C. 1 D. 0
38.(2024山西)黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观、已知一条分割线的端点A,B分别在习字格的边 MN,PQ上,且AB∥NP, “晋”字的笔画“、”的位置在AB的黄金分割点 C 处,且 若NP=2cm,则BC的长为 (结果保留根号).
39. 新考法跨音乐学科(2023达州)如图,乐器上的一根弦 80cm,两个端点A,B固定在乐器面板上,支撑点C是靠近点B的黄金分割点,支撑点D 是靠近点A的黄金分割点,则支撑点C,D之间的距离为 cm(结果保留根号)
命题点8 命题(31考)
40.(2924 湖南省卷)下列命题中,正确的是 ( )
A 两点之间,线段最短
B.菱形的对角线相等
正五边形的外角和为
D.直角三角形是轴对称图形
第十二讲 角、相交线与平行线
1.两点之间,线段最短
2. D 【解析】∵∠A=55°,∴∠A的补角为
3. C 【解析】钟表的指针恰好是2点整,时针指向2,分针指向12,所以此时钟表的时针与分针所成的锐角的度数
4. C
5. C 【解析】
6. C 【解析】如解图,过点 P 作 PE⊥OA 于点 E,∵OC平分∠AOB,PD⊥OB,∴由角平分线性质,得 PE=PD=2,∴点 P到OA的距离是2.
7. 20° 【解析】∵ 点 O 在直线AB上,∴∠AOC+∠BOC= 180°,∴ ∠BOC = 180°-∠AOC = 180° - 140°=40°,∵OD为∠BOC 的平分线,∴
8. A 【解析】∵ OE⊥AB,∴ ∠EOB = 90°,∵ ∠1=
9. B 【解析】∵OE⊥OC,∴ ∠COE=90°,∵ ∠AOC=
10. C 【解析】∵DE 垂直平分AB,∴ DA=DB,∵C△ACD=50=AC+CD+DA=AC+CD+DB=AC+BC,∴AC+BC=50cm.
11. 35° 【解析】∵DE 垂直平分BC,∴BE=CE,∴∠B=∠DCE,∵ ∠ACE=40°,CE= CA,∴∠AEC=
12. B 【解析】由题图知∠1与∠2是内错角,∴小明的判断依据为内错角相等,两直线平行.
13. B
14. B 【解析】∵正北方向平行,∴∠1=50°.
15. B 【解析】∵ AB∥CD,∴∠1+∠2=180°,∵∠1=120°,∴∠2=180°-120°=60°.
16. C 【解析】∵ AB∥CD,∴∠AEF+∠CGE=180°,∵∠CGE = ∠DGF,∴ ∠AEF+∠DGF = 180°,又∵∠AEF+∠BEG=180°,∴题图中与∠AEF 互补的角有∠CGE,∠DGF,∠BEG,共3个.
17. B 【解析】∵ AB∥DC,∴ ∠C=180°-∠B=180°-145°=35°.∵BC∥DE,∴∠D=∠C=35°.
18. B 【解析】∵AB∥CD,∴∠BAD=∠1=30°,∵AD 平分∠BAC,∴∠2=∠BAD=30°.
19. B 【解析】依题意,水面与容器底面平行,∴∠1=∠2+∠3.∵ ∠1=80°,∠2=40°,∴ ∠3=∠1-∠2=
20. B 【解析】∵AB∥CD,∴∠ACD=∠1=65°,∵∠2=∠ACD+∠3,∠2=120°,∴∠3=∠2-∠ACD=55°.
21. C 【解析】如解图,作力F 的反向延长线,由题意得它与重力G形成的夹角为α,且与力 F 所在直线垂直,即
22. 109° 【解析】如解图,∵a∥b,∠1=71°,∴∠3=∠1=71°,∴∠2=180°-∠3=109°.
23. 66 【解析】∵ OC=OE,∠C=33°,∴ ∠E=∠C=33°,∴∠DOE=∠E+∠C=66°,∵AB∥CD,∴∠A=∠DOE=66°.
24. 30 【解析】如解图,∵a∥b,∴∠3=∠1=120°,∵l⊥a,∴∠3=∠2+90°,∴∠2=∠3-90°=30°.
25. C 【解析】如解图,∵∠1=∠3=50°,∴a∥b,∴∠5+∠2=180°,∵∠2=50°,∴∠5=130°,∴∠4=∠5=130°.
26. B 【解析】∵入射光线是平行光线,∴∠1=∠3,由反射定律得:∠3=∠4,∴∠4=∠1=50°.
解题技巧
应用反射角等于入射角,是本题的解题关键.
27. B 【解析】如解图所示:由题意得:∠3=∠2=30°,∴∠1=180°-∠3-45°=105°.
28. B 【解析】如解图,∵直角三角板位于两条平行线间且∠1=45°,∴∠3=135°,又∵直角三角板含 30°角,
29. B 【解析】由题意可知,DF∥AB,∴∠DEB=∠FDE=30°,又∵ ∠CBA =∠DEB +∠EDB,∴ ∠EDB =
30. A 【解析】由题可得,点B 处三角尺对应的角为 ∠CDE+∠1=∠ABD=120°,∵CD⊥DE,∴ ∠CDE=
31. B 【解析】如解图,由题意得∠3=∠1=50°,∠5=90°,∠2=∠4,∴∠2=∠4=180°-90°-∠3=90°-50°=40°.
32. B 【解析】如解图,∵对顶角相等,∠1=55°,∴∠ABC=∠1=55°,∵∠BAC=90°,∴ ∠ACB=180°- ·直尺相对的两边平行,∴∠2=∠ACB=35°.
33. B 【解析】如解图,∵l ∥l ∴∠3=∠1=25°,∵在三角板ABC中,∠CAB=60°,∴∠2=∠CAB-∠3=60°-25°=35°.
34. 75 【解析】∵AB∥OD,∴∠BOD=∠B=45°,∴∠1=
35. D 【解析】由步骤2可得 C,D为线段AE的三等分点;步骤3中过点 C,D分别画BE的平行线,由两条直线被一组平行线所截,所得的对应线段成比例,得M,N就是线段AB的三等分点,故选 D.
36. 【解析】∵ /AB ∥EF ∥CD,∴ BEC=AFD=
37. 解题思路
由黄金矩形的定义,得到 设AB=a,BC=b,AP=x,PD=b-x,在 Rt△ABP 和 Rt△PDC中,利用勾股定理得到边的长度,由PB⊥BC,结合勾股定理寻找等量关系求解即可.
D 【解析】如解图,四边形ABCD 是黄金矩形,AB< 设AB=a,BC=b,假设存在点 P,且AP=x,则PD=b-x,在 Rt△ABP 中, 在 Rt△PDC 中, a ,∵ PB⊥PC,∴ BC =BP +PC ,即 整理得 即 方程无解,即点 P 不存在.
【解析】由已知得
39. 80 -160 【解析】由题得,弦AB=80cm,点C是靠近点B的黄金分割点,设 BC=x cm,则AC=(80-x) cm, 解得x=120-40 ,∵点D是靠近点A的黄金分割点,同理得AD=(120-40 ) cm,∴支撑点C,D之间的距离为
40. A 【解析】两点之间,线段最短,A选项正确;菱形的对角线互相垂直,不一定相等,B选项错误;正五边形的外角和为360°,C选项错误;直角三角形不一定是轴对称图形,D选项错误.
第十二讲 角、相交线与平行线
命题点1 直线和线段(7考)
1.(2024吉林省卷)如图,从长春站去往胜利公园,与其它道路相比,走人民大街路程最近,其蕴含的数学道理是 .
命题点2角与角平分线(24考)
2. (2024甘肃省卷)若∠A=55°,则∠A 的补角为 ( )
A. 35° B. 45° C. 115° D. 125°
3. 新考法 真实问题情境(2024广西)如图,2时整,钟表的时针和分针所成的锐角为 ( )
A. 20° B. 40° C. 60° D. 80°
4.(2023临沂)图中用量角器测得∠ABC的度数是 ( )
A. 50° B. 80° C. 130° D. 150°
5.(2024广东省卷)如图,一把直尺、两个含30°的三角尺拼接在一起,则∠ACE的度数为 ( )
A. 120° B. 90° C. 60° D. 30°
6. (2024青海省卷)如图,OC平分 点P在OC上, PD ,则点 P到OA的距离是( )
A. 4 B. 3 C. 2 D. 1
7. (2023乐山)如图,点O 在直线AB上,OD 是 的平分线,若 则 的度数为 .
命题点3 相交线
类型一 相交线求角度(34考)
8. (2024雅安)如图,直线AB,CD交于点O,OE⊥AB于O,若∠1=35°,则∠2的度数是 ( )
A. 55° B. 45° C. 35° D. 30°
9. (2024北京)如图,直线AB和CD相交于点O,OE⊥OC.若∠AOC=58°,则∠EOB的大小为 ( )
A. 29° B. 32° C. 45° D. 58°
类型二 垂线及垂直平分线(18考)
10. (2024凉山州)如图,在Rt△ABC中,∠ACB=90°,DE垂直平分AB交BC于点 D,若△ACD的周长为50cm,则AC+BC= ( )
A. 25 cm B. 45 cm C. 50cm D. 55 cm
11. (2023锦州)如图,在△ABC中,BC的垂直平分线交BC于点D,交AB于点E,连接CE.若CE=CA,∠ACE=40°,则∠B 的度数为 .
命题点4 平行线的判定(13考)
12. 新考法 结合地图(2024兰州)如图,小明在地图上量得 ∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.对顶角相等
13.(2023苏州)如图,在正方形网格内,线段PQ 的两个端点都在格点上,网格内另有A,B,C,D四个格点,下面四个结论中,正确的是 ( )
A. 连接AB,则AB∥PQ B. 连接BC、则BC∥PQ
C. 连接BD,则BD⊥PQ D. 连接AD,则AD⊥PQ
命题点5 平行线性质求角度
类型一 直接利用平行线性质求角度(120考)
14.(2024河南)如图,乙地在甲地的北偏东 方向上,则 的度数为 ( )
A. 60°
15.(2024湖北省卷)如图,一条公路的两侧铺设了AB,CD两条平行管道,并有纵向管道AC连通.若∠1=120°,则∠2的度数是 ( )
A. 50° B. 60° C. 70° D. 80°
16. 新考法求互补角个数(2024包头)如图,直线AB∥CD,点E在直线AB上,射线EF交直线CD 于点G,则图中与 互补的角有 ( )
A.1个 B.2个 C.3个 D.4个
17. (2024陕西)如图,AB∥DC,BC∥DE,∠B=145°.则∠D的度数为
( )
A. 25° B. 35° C. 45° D. 55°
18. (2024甘孜州)如图,AB∥CD,AD平分∠BAC,∠1=30°,则∠2=
( )
A. 15° B. 30° C. 45° D. 60°
19. 新考法 跨物理学科(2024达州)当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象(如图所示).图中∠1=80°,∠2=40°,则∠3的度数为 ( )
A. 30° B. 40° C. 50° D. 70°
20. (12024苏州)如图,AB∥CD,若 则∠3的度数为 ( )
A. 45° B.55°
21. 新考法 跨物理学科(2024山西)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力 的方向与斜面垂直,摩擦力 的方向与斜面平行.若斜面的坡角α=25°,则摩擦力 与重力G方向的夹角β的度数为 ( )
A. 155° B. 125° C. 115° D. 65°
22. (2024广州)如图,直线l分别与直线a,b相交,a∥b,若∠1=71°,则∠2的度数为 .
23. (2024绥化)如图,AB∥CD,∠C=33°,OC=OE.则∠A= °.
24. (2024连云港)如图,直线a∥b,直线l⊥a,∠1=120°,则∠2= °.
类型二 平行线性质与判定结合(9考)
25. (2023金华)如图,已知∠1=∠2=∠3=50°,则∠4的度数是 ( )
A. 120° B. 125° C. 130° D. 135°
26. 新考法 跨物理学科(2024深圳)如图,一束平行光线照射平面镜后反射,若入射光线与平面镜夹角∠1=50°,则反射光线与平面镜夹角∠4的度数为 ( )
A. 40° B. 50° C. 60° D. 70°
类型三 与直角三角板结合(21考)
27.(2024赤峰)将一副三角尺(厚度不计)按如图所示摆放,使有刻度的两条边互相平行,则图中∠1 的度数为 ( )
A. 100° B. 105° C. 115° D. 120°
28.(2024泸州)把一块含30°角的直角三角板按如图方式放置于两条平行线间,若∠1=45°,则∠2= ( )
A.10° B. 15° C. 20° D. 30°
29.(2024凉山州)一副直角三角板按如图所示的方式摆放,点E 在AB的延长线上,当 时, 的度数为 ( )
A. 10° B. 15°
30.(2024福建)在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD⊥DE)按如图方式摆放,若AB∥CD,则∠1的大小为 ( )
A. 30° B. 45° C. 60° D. 75°
31.(2024齐齐哈尔)将一个含30°角的三角尺和直尺如图放置,若∠1=50°,则∠2的度数是 ( )
A. 30° B. 40° C. 50° D. 60°
32. (2024盐城)小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为 ( )
A. 25° B. 35° C. 45° D. 55°
33.(2024通辽)将三角尺ABC按如图位置摆放,顶点A落在直线 上,顶点B落在直线l 上,若 ,则∠2的度数是
( )
A. 45° B. 35° C. 30° D. 25°
34.(2024滨州)一副三角板 图①摆放,把三角板AOB 绕公共顶点O顺时针旋转至图②,即 时,∠1的大小为 °.
命题点6 平行线分线段成比例(8考)
35.(2023常州)小明按照以下步骤画线段AB的三等分点:
画法 图形
1.以A为端点画一条射线; 2.用圆规在射线上依次截取3 条等长线段AC,CD,DE,连接BE; 3.过点 C,D 分别画BE的平行线,交线段AB 于点M,N,M,N就是线段AB的三等分点.
这一画图过程体现的数学依据是
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
36. (2023北京)如图,直线AD,BC交于点O, 若 OF=1,FD=2,则 的值为 .
命题点7 黄金分割(6考)
37. (2024德阳)宽与长的比是 的矩形叫黄金矩形,黄金矩形给我们以协调的美感,世界各国许多著名建筑为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形ABCD 是黄金矩形( BC),点P是边AD上一点,则满足. 的点P的个数为 ( )
A. 3 B. 2 C. 1 D. 0
38.(2024山西)黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观、已知一条分割线的端点A,B分别在习字格的边 MN,PQ上,且AB∥NP, “晋”字的笔画“、”的位置在AB的黄金分割点 C 处,且 若NP=2cm,则BC的长为 (结果保留根号).
39. 新考法跨音乐学科(2023达州)如图,乐器上的一根弦 80cm,两个端点A,B固定在乐器面板上,支撑点C是靠近点B的黄金分割点,支撑点D 是靠近点A的黄金分割点,则支撑点C,D之间的距离为 cm(结果保留根号)
命题点8 命题(31考)
40.(2924 湖南省卷)下列命题中,正确的是 ( )
A 两点之间,线段最短
B.菱形的对角线相等
正五边形的外角和为
D.直角三角形是轴对称图形
第十二讲 角、相交线与平行线
1.两点之间,线段最短
2. D 【解析】∵∠A=55°,∴∠A的补角为
3. C 【解析】钟表的指针恰好是2点整,时针指向2,分针指向12,所以此时钟表的时针与分针所成的锐角的度数
4. C
5. C 【解析】
6. C 【解析】如解图,过点 P 作 PE⊥OA 于点 E,∵OC平分∠AOB,PD⊥OB,∴由角平分线性质,得 PE=PD=2,∴点 P到OA的距离是2.
7. 20° 【解析】∵ 点 O 在直线AB上,∴∠AOC+∠BOC= 180°,∴ ∠BOC = 180°-∠AOC = 180° - 140°=40°,∵OD为∠BOC 的平分线,∴
8. A 【解析】∵ OE⊥AB,∴ ∠EOB = 90°,∵ ∠1=
9. B 【解析】∵OE⊥OC,∴ ∠COE=90°,∵ ∠AOC=
10. C 【解析】∵DE 垂直平分AB,∴ DA=DB,∵C△ACD=50=AC+CD+DA=AC+CD+DB=AC+BC,∴AC+BC=50cm.
11. 35° 【解析】∵DE 垂直平分BC,∴BE=CE,∴∠B=∠DCE,∵ ∠ACE=40°,CE= CA,∴∠AEC=
12. B 【解析】由题图知∠1与∠2是内错角,∴小明的判断依据为内错角相等,两直线平行.
13. B
14. B 【解析】∵正北方向平行,∴∠1=50°.
15. B 【解析】∵ AB∥CD,∴∠1+∠2=180°,∵∠1=120°,∴∠2=180°-120°=60°.
16. C 【解析】∵ AB∥CD,∴∠AEF+∠CGE=180°,∵∠CGE = ∠DGF,∴ ∠AEF+∠DGF = 180°,又∵∠AEF+∠BEG=180°,∴题图中与∠AEF 互补的角有∠CGE,∠DGF,∠BEG,共3个.
17. B 【解析】∵ AB∥DC,∴ ∠C=180°-∠B=180°-145°=35°.∵BC∥DE,∴∠D=∠C=35°.
18. B 【解析】∵AB∥CD,∴∠BAD=∠1=30°,∵AD 平分∠BAC,∴∠2=∠BAD=30°.
19. B 【解析】依题意,水面与容器底面平行,∴∠1=∠2+∠3.∵ ∠1=80°,∠2=40°,∴ ∠3=∠1-∠2=
20. B 【解析】∵AB∥CD,∴∠ACD=∠1=65°,∵∠2=∠ACD+∠3,∠2=120°,∴∠3=∠2-∠ACD=55°.
21. C 【解析】如解图,作力F 的反向延长线,由题意得它与重力G形成的夹角为α,且与力 F 所在直线垂直,即
22. 109° 【解析】如解图,∵a∥b,∠1=71°,∴∠3=∠1=71°,∴∠2=180°-∠3=109°.
23. 66 【解析】∵ OC=OE,∠C=33°,∴ ∠E=∠C=33°,∴∠DOE=∠E+∠C=66°,∵AB∥CD,∴∠A=∠DOE=66°.
24. 30 【解析】如解图,∵a∥b,∴∠3=∠1=120°,∵l⊥a,∴∠3=∠2+90°,∴∠2=∠3-90°=30°.
25. C 【解析】如解图,∵∠1=∠3=50°,∴a∥b,∴∠5+∠2=180°,∵∠2=50°,∴∠5=130°,∴∠4=∠5=130°.
26. B 【解析】∵入射光线是平行光线,∴∠1=∠3,由反射定律得:∠3=∠4,∴∠4=∠1=50°.
解题技巧
应用反射角等于入射角,是本题的解题关键.
27. B 【解析】如解图所示:由题意得:∠3=∠2=30°,∴∠1=180°-∠3-45°=105°.
28. B 【解析】如解图,∵直角三角板位于两条平行线间且∠1=45°,∴∠3=135°,又∵直角三角板含 30°角,
29. B 【解析】由题意可知,DF∥AB,∴∠DEB=∠FDE=30°,又∵ ∠CBA =∠DEB +∠EDB,∴ ∠EDB =
30. A 【解析】由题可得,点B 处三角尺对应的角为 ∠CDE+∠1=∠ABD=120°,∵CD⊥DE,∴ ∠CDE=
31. B 【解析】如解图,由题意得∠3=∠1=50°,∠5=90°,∠2=∠4,∴∠2=∠4=180°-90°-∠3=90°-50°=40°.
32. B 【解析】如解图,∵对顶角相等,∠1=55°,∴∠ABC=∠1=55°,∵∠BAC=90°,∴ ∠ACB=180°- ·直尺相对的两边平行,∴∠2=∠ACB=35°.
33. B 【解析】如解图,∵l ∥l ∴∠3=∠1=25°,∵在三角板ABC中,∠CAB=60°,∴∠2=∠CAB-∠3=60°-25°=35°.
34. 75 【解析】∵AB∥OD,∴∠BOD=∠B=45°,∴∠1=
35. D 【解析】由步骤2可得 C,D为线段AE的三等分点;步骤3中过点 C,D分别画BE的平行线,由两条直线被一组平行线所截,所得的对应线段成比例,得M,N就是线段AB的三等分点,故选 D.
36. 【解析】∵ /AB ∥EF ∥CD,∴ BEC=AFD=
37. 解题思路
由黄金矩形的定义,得到 设AB=a,BC=b,AP=x,PD=b-x,在 Rt△ABP 和 Rt△PDC中,利用勾股定理得到边的长度,由PB⊥BC,结合勾股定理寻找等量关系求解即可.
D 【解析】如解图,四边形ABCD 是黄金矩形,AB< 设AB=a,BC=b,假设存在点 P,且AP=x,则PD=b-x,在 Rt△ABP 中, 在 Rt△PDC 中, a ,∵ PB⊥PC,∴ BC =BP +PC ,即 整理得 即 方程无解,即点 P 不存在.
【解析】由已知得
39. 80 -160 【解析】由题得,弦AB=80cm,点C是靠近点B的黄金分割点,设 BC=x cm,则AC=(80-x) cm, 解得x=120-40 ,∵点D是靠近点A的黄金分割点,同理得AD=(120-40 ) cm,∴支撑点C,D之间的距离为
40. A 【解析】两点之间,线段最短,A选项正确;菱形的对角线互相垂直,不一定相等,B选项错误;正五边形的外角和为360°,C选项错误;直角三角形不一定是轴对称图形,D选项错误.
同课章节目录
