湖南省永州市祁阳市潘市红军学校2025年中考第一次模拟考试数学试卷(含答案)
文档属性
| 名称 | 湖南省永州市祁阳市潘市红军学校2025年中考第一次模拟考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 905.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 19:23:43 | ||
图片预览




文档简介
湖南省祁阳市潘市红军学校2025年中考第一次模拟考试数学试卷
一.选择题(共10小题,满分30分,每小题3分)
1.在﹣(﹣2025),﹣|﹣2025|,0,,﹣20252,﹣202各数中,负数的个数是( )
A.6个 B.5个 C.4个 D.3个
2.“九章三号”是中国科学家构建的光量子计算原型机,它在0.000001s内所处理的最高复杂样本,需要当前最快的超级计算机超过200亿年才能完成.将0.000001用科学记数法表示为( )
A.0.1×10﹣6 B.1×10﹣6 C.0.1×10﹣5 D.1×10﹣5
3.在第46个植树节来临之际,某校师生积极践行“绿水青山就是金山银山”理念,开展以小组为单位的植树活动,七个小组植树情况如下:
第一组 第二组 第三组 第四组 第五组 第六组 第七组
数量(棵) 5 6 5 4 6 5 7
则本组数据的众数与中位数分别为( )
A.5,4 B.5,5 C.6,4 D.6,5
4.当x=﹣1时,下列式子有意义的是( )
A. B. C. D.
5.关于x的一元二次方程方程x2﹣x﹣1=0的根的情况是( )
A.有两个不相等的实数根 B.两个相等的实数根 C.没有实数 D.无法判定
6.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠AOC=40°,则∠CDB的度数是( )
A.100° B.110° C.140° D.160°
7.如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ccosB
第6题图 第7题图 第9题图 第10题图
8.某药店购进A,B两种的口罩,其中A种口罩的单价比B种口罩的单价低0.2元.已知该店主购进A种口罩用了920元,购进B种口罩用了500元,且所购进的A种口罩的数量比B种口罩多20个.设药店购进A种款式的口罩x个,则所列方程正确的是( )
A. B.
C. D.
9.已知点A在反比例函数y第一象限的图象上,B(﹣2,0)、C(2,0)在x轴上,则下列说法中正确的是( )
①满足△ABC面积为4的点A有且只有一个 ②满足△ABC是直角三角形的点A有且只有一个③满足△ABC是等腰三角形的点A有且只有一个④满足△ABC是等边三角形的点A有且只有一个
A.①④ B.①② C.②③ D.③④
10.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,则下列结论:①∠BAD=∠CAD;②若点G为BC的中点,则∠BGD=90°;③连接BE,CE,若∠BAC=40°,则∠BEC=140°;④BD=DE.其中一定正确的个数是( )
A.4 B.3 C.2 D.1
二.填空题(共8小题,满分24分,每小题3分)
11.分解因式:3m2﹣3mn= .
12.计算: .
13.如图,已知AB∥CD,∠1=64°,∠2=33°,则∠B的度数为 .
14.一个扇形的弧长为2π,面积为12π,则这个扇形的半径为 .
15.将二次函数y=2x2﹣1的图象沿y轴向上平移2个单位长度所得图象的解析式为 .
16.小志和小强进行了十次剪刀石头布的对决,已知:①小志出了6次石头,1次剪刀,3次布;②小强出了4次石头,3次剪刀,3次布;③10次对决中没有平局;④你不知道他们的出拳顺序,则这十次对决中小志赢了 次.
17.如图,△ABC是等边三角形,D是线段BC上一点(不与点B,C重合),连接AD,点E,F分别在线段AB,AC的延长线上,且DE=AD,点A与点F关于过点D的某条直线对称,从B运动到C的过程中,△BED周长的变化规律是 .
18.如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(-1,2)、(1,1).抛物线y=ax2+bx+c(a≠0)与x轴交于C、D两点,点C在点D左侧,当顶点在线段AB上移动时,点C横坐标的最小值为-2.在抛物线移动过程中,a-b+c的最小值是 。
第13题图 第17题图 第18题图
三.解答题(共9小题,满分72分)
19.(6分)计算:|2|6÷().
20.(6分)解不等式组.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上分别表示出来;
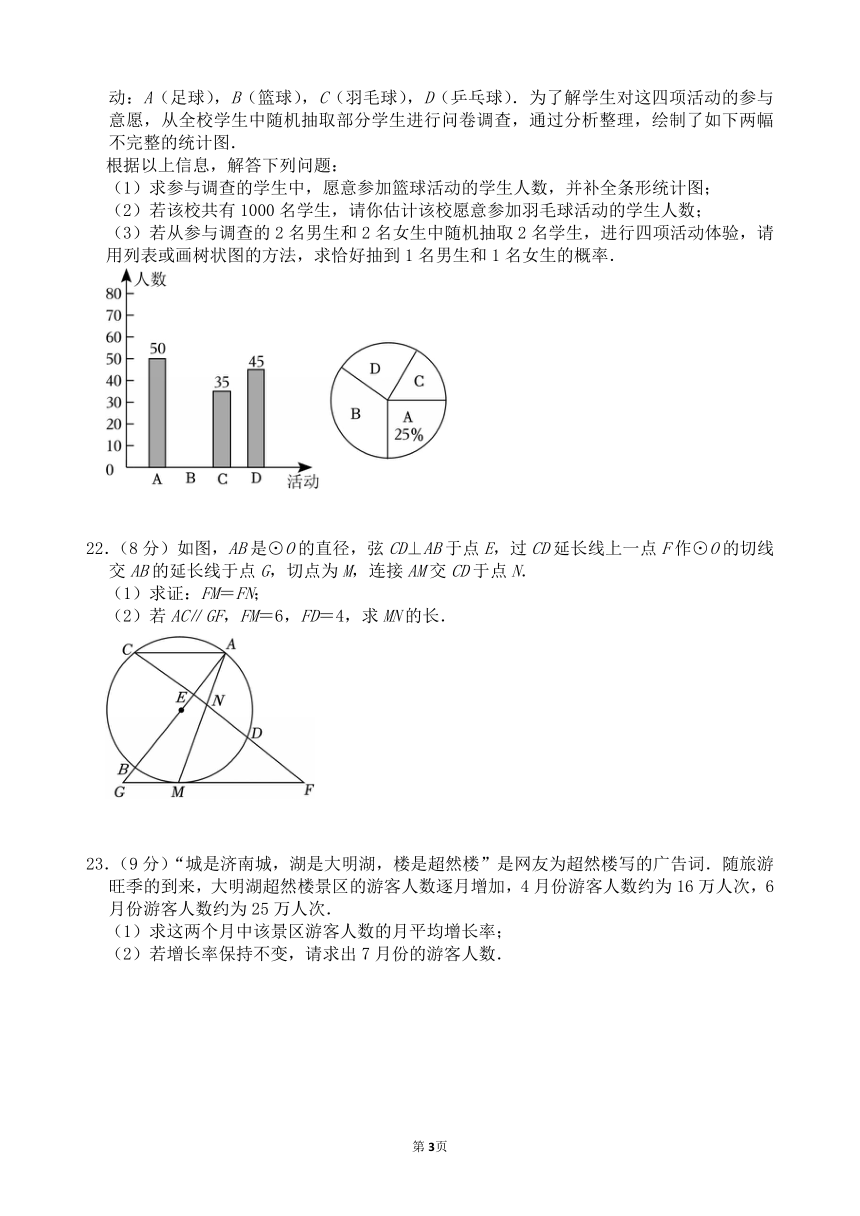
21.(8分)去年7月28日至8月8日在成都举行的世界大学生夏季运动会再次引发了成都市的校园运动热潮.我校在准备体育运动节期间在全校范围内邀请学生参加以下四项活动:A(足球),B(篮球),C(羽毛球),D(乒乓球).为了解学生对这四项活动的参与意愿,从全校学生中随机抽取部分学生进行问卷调查,通过分析整理,绘制了如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)求参与调查的学生中,愿意参加篮球活动的学生人数,并补全条形统计图;
(2)若该校共有1000名学生,请你估计该校愿意参加羽毛球活动的学生人数;
(3)若从参与调查的2名男生和2名女生中随机抽取2名学生,进行四项活动体验,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
22.(8分)如图,AB是⊙O的直径,弦CD⊥AB于点E,过CD延长线上一点F作⊙O的切线交AB的延长线于点G,切点为M,连接AM交CD于点N.
(1)求证:FM=FN;
(2)若AC∥GF,FM=6,FD=4,求MN的长.
23.(9分)“城是济南城,湖是大明湖,楼是超然楼”是网友为超然楼写的广告词.随旅游旺季的到来,大明湖超然楼景区的游客人数逐月增加,4月份游客人数约为16万人次,6月份游客人数约为25万人次.
(1)求这两个月中该景区游客人数的月平均增长率;
(2)若增长率保持不变,请求出7月份的游客人数.
24.(9分)如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:AD∥CE;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
25.(10分)综合与探究:如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.直线l与抛物线交于A,D两点,与y轴交于点E,点D的坐标为(4,﹣3).
(1)请直接写出A,B两点的坐标及直线l的函数表达式;
(2)若点P是抛物线上的点,点P的横坐标为m(m≥0),过点P作PM⊥x轴,垂足为M.PM与直线l交于点N,当点N是线段PM的三等分点时,求点P的坐标.
26.(10分)如图,点C是以AB为直径的半圆O上的动点,连结AC、BC,作圆心O关于AC的对称点O',射线AO′交半圆O于点D,连结OD,CD,O'C,OD与O'C交于点E.
(1)求证:四边形OO′CB为平行四边形.
(2)若,求的值.
(3)当OA=5,O′D=2时,求△O′DC的面积.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C. B. B B A B B C B B
9.解析:设点A(x,),则AC2=(x﹣2)2+( )2,AB2=(x+2)2+()2,BC=4,
①∴S△ABCBC yA44,
∴x=3,
∴满足△ABC面积为4的点A只有一个,故①正确,符合题意;
②∵点A在第一象限,
∴∠C≠90°,
当∠ACB=90°时,AB2=AC2+BC2,
∴(x﹣2)2+()2+42=(x+2)2+()2,
解得:x=2,
∴点A(2,3),
当∠CAB=90°时,AC2+AB2=BC2,
∴(x﹣2)2+()2+(x+2)2+()2=42,无解,舍去,
综上所述,满足△ABC是直角三角形的点A有且只有一个,故②正确,符合题意
③∵点A在第一象限,点B在x轴的负半轴,
∴CA≠AB,
当BC=AC时,
∵当x=2时,y=3,
∴当以点C为圆心BC=4为半径画圆,与反比例函数图象会有两个交点,
同理,当BC=AC时,以点B为圆心BC=4为半径画圆,与反比例函数图象会有两个交点,
故③错误,不符合题意;
④∵点A在第一象限,
∴AC≠AB,
∴△ABC不可能为等边三角形,故④错误,不符合题意;
综上所述,正确的序号有①②,
10.解析:∵点E是△ABC的内心,
∴AD平分∠BAC,
∴∠BAD=∠CAD,故①正确;
设△ABC外接圆圆心为O,连接OD,则OD垂直平分BC,
∵点G为BC的中点,
∴点G为OD与BC的交点,即∠BGD=90°,故②正确;
∵∠BAC=40°,
∴∠ABC+∠ACB=180°﹣∠BAC=140°,
∵点E是△ABC的内心,
∴,,
∴∠BEC=180°﹣(∠EBC+∠ECB)110°,故③错误;
∵∠BAD=∠CAD,
∴,
∴∠DBC=∠BAD,
∵∠DBE=∠DBC+∠EBC,∠DEB=∠BAD+∠ABE,
∴∠DBE=∠DEB,
∴BD=DE,故④正确,
综上,正确的有3个,
11.3m(m﹣n).
12.4.
13.31°.
14.12.
15.y=2x2+1.
16. 6.解析:∵10次对决中没有平局,∴小志6次石头只能对应小强的3次剪刀3次布,
∴这6局中小志赢3局,同理,小志1次剪刀,3次布只能对应小强4次石头,
∴这4局中小志赢3局,∴小志共赢了3+3=6局.
17.周长先变小后变大.解析:由“ASA”可证△BED≌△CDF,由全等三角形的性质可得BD=CF,BE=CD,可得△BED周长=BD+BE+DE=BD+CD+AD=BC+AD,即可求解.
18.-7 解析:解:点C横坐标最小时,顶点在A点,则函数的表达式为:y=a(x+1)2+2,此时点C(-2,0),将点C的坐标代入上式并解得:a=-2,当顶点在B处时,a-b+c值最小,则抛物线的表达式为:y=-2(x-1)2+1,当x=-1时,y1=a-b+c=-7,
19.解:|2|6÷()=9+23+(﹣8)=9+23﹣8
=6.
20.解:(Ⅰ)解不等式①,得x<3;
(Ⅱ)解不等式②,得x≥﹣3;
(Ⅲ)把不等式①和②的解集表示在数轴上如下:
故答案为:(Ⅰ)x<3;(Ⅱ)x≥﹣3.
21.解:(1)参与调查的学生总数为50÷25%=200(人),
∴愿意参加篮球活动的学生人数为200﹣50﹣35﹣45=70(人),
补全条形统计图如下:
(2)(人),
答:估计该校愿意参加羽手球活动的学生人数为175人;
(3)画树状图如下:
可知所有等可能的情况12种,其中抽取的两名学生为1名男生和1名女生共有8种,
∴恰好抽到1名男生和1名女生的概率为.
答:恰好抽到1名男生和1名女生的概率为.
22.(1)证明:连接OM,如图,
∵FM为⊙O的切线,
∴OM⊥FM.
∴∠OMF=90°,
∴∠OMA+∠AMF=90°.
∵CD⊥AB,
∴∠ANE+∠EAN=90°.
∵OA=OM,
∴∠OAN=∠OMA,
∴∠AMF=∠ANE,
∵∠ANE=∠FNM,
∴∠AMF=∠FNM,
∴FM=FN;
(2)解:连接MD,MC,如图,
∵∠DMF=∠MCF,∠F=∠F,
∴△FMD∽△FCM,
∴,
∴,
∴FC=9,
∴CD=FC﹣FD=5,
由(1)知:FM=FN,
∴FN=6,
∴DN=FN﹣FD=2,
∴CN=CD﹣DN=3.
∵AC∥GF,
∴△ACN∽△MFN,
∴.
设AN=k,则MN=2k,
∵∠ACN=∠DMA,∠CNA=∠DNM,
∴△ACN∽△DMN,
∴,
∴,
∵k>0,
∴k.
∴MN=2k=2.
23.解:(1)设这两个月中该景区游客人数的月平均增长率为x,
由题意得:16(1+x)2=25,
解得:x1=0.25=25%,x2=﹣2.25(不合题意,舍去),
答:这两个月中该景区游客人数的月平均增长率为25%;
(2)由题意可知,25(1+25%)=31.25(万人次),
答:7月份的游客人数为31.25万人次.
24.(1)证明:∵E是AB的中点,
∴AE=EB,
∵DF=BF,
∴EF是△ABD的中位线,
∴AD∥CE;
(2)解:∵EF是△ABD的中位线,
∴AD=2EF=2,
∵∠EFB=90°,
∴∠CFB=180°﹣∠EFB=90°,
在Rt△EFB中,tan∠FEB=3,
∴BF=EF tan∠FEB=3,
∵AD∥CE,AF∥CD,
∴四边形ADCF是平行四边形,
∴AD=CF=2,
在Rt△CFB中,BC.
25.解:(1)A(﹣2,0),B(6,0),直线l的函数表达式为;理由如下:
∵抛物线y与x轴交于A,B两点(点A在点B的左侧),
令y=0,得:x﹣3=0,
解得:x1=﹣2,x2=6.
∴A(﹣2,0),B(6,0),
直线l与抛物线交于A,D两点,点D的坐标为(4,﹣3),设直线l的函数表达式为y=kx+b,将点A,点D的坐标代入得:
,
解得:,
直线l的函数表达式为.
(2)如图,
根据题意可知,点P与点N的坐标分别为,.
∴PM,MN,NP,
分两种情况:
①当PM=3MN时,得,
解得:m1=0,m2=﹣2(不合题意,舍去),
当m=0时,,
∴点P的坐标为(0,﹣3);
②当PM=3NP时,得,
解得:m1=3,m2=﹣2(不合题意,舍去),
当m=3时,,
∴点P的坐标为.
∴当点N是线段PM的三等分点时,点P的坐标为(0,﹣3)或.
26.(1)证明:连接OC,如图,
∵圆心O与点O'关于AC对称,
∴AC垂直平分OO′,
∴AO=AO′,
∴∠OAC=O′AC.
∵AB为直径,
∴∠ACB=90°,
∴BC⊥AC,
∵OO′⊥AC,
∴OO′∥BC,
∵OA=OB,
∴OO′平分AC,
∴AC与OO′互相平分,
∴四边形AOCO′为平行四边形,
∴OA=O′C,AB∥O′C.
∵OB=OA,
∴OB=O′C,
∴四边形OO′CB为平行四边形;
(2)解:连接OC,BD,如图,
∵AB为直径,
∴∠ADB=90°
∵,tan∠DAB,
∴,
设BD=3k,则AD=4k,
∴AB5k,
∴OA=OC=OD=OB=2.5k,
由(1)知:AO=AO′,四边形OO′CB为平行四边形,
∴O′C∥OA,O′C=OA=2.5k.
∴△DO′E∽△DAO,
∴,
∴,
∴O′Ek.
∴CE=O′C﹣O′E=2.5kk.
∴.
解法二:连接OC,BD,如图,
∵AB为直径,
∴∠ADB=90°
∵,tan∠DAB,
∴,
设BD=3k,则AD=4k,
∴AB5k,
∴OA=OC=OD=OB=2.5k,
由(1)知:AO=AO′,四边形OO′CB为平行四边形,
∴O′C∥OA,O′C=OA=2.5k.
∴O′D=AD﹣AO′=1.5k.
∴△DO′E∽△OCE,
∴.
(3)解:过点D作DF⊥AB于点F,交O′C于点H,如图,
∵OA=5,O′D=2,
∴AD=7,OD=OA=5,
设OF=x,则AF=5﹣x,
∵DF2=AD2﹣AF2,DF2=OD2﹣OF2,
∴AD2﹣AF2=OD2﹣OF2,
∴72﹣(5﹣x)2=52﹣x2,
∴x,
∴OF,
∴DF,
∴sin∠DAO,
∵O′C∥AB,
∴∠DO′C=∠DAO,
∴sin∠DO′C=sin∠DAO,
∴DH=O′D sin∠DO′C=2,
∴△O′DC的面积5.
当点O′在线段AD的延长线上时,
延长AD,BC交于点N,过点C作CM⊥AN于点M,连接BD,如图,
∵OA=5,圆心O关于AC的对称点O',
∴AO′=AO=5,
∴AD=AO′﹣O′D=3,
∴BD.
由(1)知:四边形OO′CB为平行四边形,
∴O′C∥OB,O′C=OB,
∵OBAB,
∴O′CAB.
∵O′C∥OB,
∴.
∵AB为圆的直径,
∴∠ADB=90,
∴BD⊥AN,
∵CM⊥AN,
∴BD∥CM,
∴,
∴CMBD,
∴△O′DC的面积O′D CM2.
综上,△O′DC的面积为或.
第1页
一.选择题(共10小题,满分30分,每小题3分)
1.在﹣(﹣2025),﹣|﹣2025|,0,,﹣20252,﹣202各数中,负数的个数是( )
A.6个 B.5个 C.4个 D.3个
2.“九章三号”是中国科学家构建的光量子计算原型机,它在0.000001s内所处理的最高复杂样本,需要当前最快的超级计算机超过200亿年才能完成.将0.000001用科学记数法表示为( )
A.0.1×10﹣6 B.1×10﹣6 C.0.1×10﹣5 D.1×10﹣5
3.在第46个植树节来临之际,某校师生积极践行“绿水青山就是金山银山”理念,开展以小组为单位的植树活动,七个小组植树情况如下:
第一组 第二组 第三组 第四组 第五组 第六组 第七组
数量(棵) 5 6 5 4 6 5 7
则本组数据的众数与中位数分别为( )
A.5,4 B.5,5 C.6,4 D.6,5
4.当x=﹣1时,下列式子有意义的是( )
A. B. C. D.
5.关于x的一元二次方程方程x2﹣x﹣1=0的根的情况是( )
A.有两个不相等的实数根 B.两个相等的实数根 C.没有实数 D.无法判定
6.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠AOC=40°,则∠CDB的度数是( )
A.100° B.110° C.140° D.160°
7.如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ccosB
第6题图 第7题图 第9题图 第10题图
8.某药店购进A,B两种的口罩,其中A种口罩的单价比B种口罩的单价低0.2元.已知该店主购进A种口罩用了920元,购进B种口罩用了500元,且所购进的A种口罩的数量比B种口罩多20个.设药店购进A种款式的口罩x个,则所列方程正确的是( )
A. B.
C. D.
9.已知点A在反比例函数y第一象限的图象上,B(﹣2,0)、C(2,0)在x轴上,则下列说法中正确的是( )
①满足△ABC面积为4的点A有且只有一个 ②满足△ABC是直角三角形的点A有且只有一个③满足△ABC是等腰三角形的点A有且只有一个④满足△ABC是等边三角形的点A有且只有一个
A.①④ B.①② C.②③ D.③④
10.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,则下列结论:①∠BAD=∠CAD;②若点G为BC的中点,则∠BGD=90°;③连接BE,CE,若∠BAC=40°,则∠BEC=140°;④BD=DE.其中一定正确的个数是( )
A.4 B.3 C.2 D.1
二.填空题(共8小题,满分24分,每小题3分)
11.分解因式:3m2﹣3mn= .
12.计算: .
13.如图,已知AB∥CD,∠1=64°,∠2=33°,则∠B的度数为 .
14.一个扇形的弧长为2π,面积为12π,则这个扇形的半径为 .
15.将二次函数y=2x2﹣1的图象沿y轴向上平移2个单位长度所得图象的解析式为 .
16.小志和小强进行了十次剪刀石头布的对决,已知:①小志出了6次石头,1次剪刀,3次布;②小强出了4次石头,3次剪刀,3次布;③10次对决中没有平局;④你不知道他们的出拳顺序,则这十次对决中小志赢了 次.
17.如图,△ABC是等边三角形,D是线段BC上一点(不与点B,C重合),连接AD,点E,F分别在线段AB,AC的延长线上,且DE=AD,点A与点F关于过点D的某条直线对称,从B运动到C的过程中,△BED周长的变化规律是 .
18.如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(-1,2)、(1,1).抛物线y=ax2+bx+c(a≠0)与x轴交于C、D两点,点C在点D左侧,当顶点在线段AB上移动时,点C横坐标的最小值为-2.在抛物线移动过程中,a-b+c的最小值是 。
第13题图 第17题图 第18题图
三.解答题(共9小题,满分72分)
19.(6分)计算:|2|6÷().
20.(6分)解不等式组.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上分别表示出来;
21.(8分)去年7月28日至8月8日在成都举行的世界大学生夏季运动会再次引发了成都市的校园运动热潮.我校在准备体育运动节期间在全校范围内邀请学生参加以下四项活动:A(足球),B(篮球),C(羽毛球),D(乒乓球).为了解学生对这四项活动的参与意愿,从全校学生中随机抽取部分学生进行问卷调查,通过分析整理,绘制了如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)求参与调查的学生中,愿意参加篮球活动的学生人数,并补全条形统计图;
(2)若该校共有1000名学生,请你估计该校愿意参加羽毛球活动的学生人数;
(3)若从参与调查的2名男生和2名女生中随机抽取2名学生,进行四项活动体验,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
22.(8分)如图,AB是⊙O的直径,弦CD⊥AB于点E,过CD延长线上一点F作⊙O的切线交AB的延长线于点G,切点为M,连接AM交CD于点N.
(1)求证:FM=FN;
(2)若AC∥GF,FM=6,FD=4,求MN的长.
23.(9分)“城是济南城,湖是大明湖,楼是超然楼”是网友为超然楼写的广告词.随旅游旺季的到来,大明湖超然楼景区的游客人数逐月增加,4月份游客人数约为16万人次,6月份游客人数约为25万人次.
(1)求这两个月中该景区游客人数的月平均增长率;
(2)若增长率保持不变,请求出7月份的游客人数.
24.(9分)如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:AD∥CE;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
25.(10分)综合与探究:如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.直线l与抛物线交于A,D两点,与y轴交于点E,点D的坐标为(4,﹣3).
(1)请直接写出A,B两点的坐标及直线l的函数表达式;
(2)若点P是抛物线上的点,点P的横坐标为m(m≥0),过点P作PM⊥x轴,垂足为M.PM与直线l交于点N,当点N是线段PM的三等分点时,求点P的坐标.
26.(10分)如图,点C是以AB为直径的半圆O上的动点,连结AC、BC,作圆心O关于AC的对称点O',射线AO′交半圆O于点D,连结OD,CD,O'C,OD与O'C交于点E.
(1)求证:四边形OO′CB为平行四边形.
(2)若,求的值.
(3)当OA=5,O′D=2时,求△O′DC的面积.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C. B. B B A B B C B B
9.解析:设点A(x,),则AC2=(x﹣2)2+( )2,AB2=(x+2)2+()2,BC=4,
①∴S△ABCBC yA44,
∴x=3,
∴满足△ABC面积为4的点A只有一个,故①正确,符合题意;
②∵点A在第一象限,
∴∠C≠90°,
当∠ACB=90°时,AB2=AC2+BC2,
∴(x﹣2)2+()2+42=(x+2)2+()2,
解得:x=2,
∴点A(2,3),
当∠CAB=90°时,AC2+AB2=BC2,
∴(x﹣2)2+()2+(x+2)2+()2=42,无解,舍去,
综上所述,满足△ABC是直角三角形的点A有且只有一个,故②正确,符合题意
③∵点A在第一象限,点B在x轴的负半轴,
∴CA≠AB,
当BC=AC时,
∵当x=2时,y=3,
∴当以点C为圆心BC=4为半径画圆,与反比例函数图象会有两个交点,
同理,当BC=AC时,以点B为圆心BC=4为半径画圆,与反比例函数图象会有两个交点,
故③错误,不符合题意;
④∵点A在第一象限,
∴AC≠AB,
∴△ABC不可能为等边三角形,故④错误,不符合题意;
综上所述,正确的序号有①②,
10.解析:∵点E是△ABC的内心,
∴AD平分∠BAC,
∴∠BAD=∠CAD,故①正确;
设△ABC外接圆圆心为O,连接OD,则OD垂直平分BC,
∵点G为BC的中点,
∴点G为OD与BC的交点,即∠BGD=90°,故②正确;
∵∠BAC=40°,
∴∠ABC+∠ACB=180°﹣∠BAC=140°,
∵点E是△ABC的内心,
∴,,
∴∠BEC=180°﹣(∠EBC+∠ECB)110°,故③错误;
∵∠BAD=∠CAD,
∴,
∴∠DBC=∠BAD,
∵∠DBE=∠DBC+∠EBC,∠DEB=∠BAD+∠ABE,
∴∠DBE=∠DEB,
∴BD=DE,故④正确,
综上,正确的有3个,
11.3m(m﹣n).
12.4.
13.31°.
14.12.
15.y=2x2+1.
16. 6.解析:∵10次对决中没有平局,∴小志6次石头只能对应小强的3次剪刀3次布,
∴这6局中小志赢3局,同理,小志1次剪刀,3次布只能对应小强4次石头,
∴这4局中小志赢3局,∴小志共赢了3+3=6局.
17.周长先变小后变大.解析:由“ASA”可证△BED≌△CDF,由全等三角形的性质可得BD=CF,BE=CD,可得△BED周长=BD+BE+DE=BD+CD+AD=BC+AD,即可求解.
18.-7 解析:解:点C横坐标最小时,顶点在A点,则函数的表达式为:y=a(x+1)2+2,此时点C(-2,0),将点C的坐标代入上式并解得:a=-2,当顶点在B处时,a-b+c值最小,则抛物线的表达式为:y=-2(x-1)2+1,当x=-1时,y1=a-b+c=-7,
19.解:|2|6÷()=9+23+(﹣8)=9+23﹣8
=6.
20.解:(Ⅰ)解不等式①,得x<3;
(Ⅱ)解不等式②,得x≥﹣3;
(Ⅲ)把不等式①和②的解集表示在数轴上如下:
故答案为:(Ⅰ)x<3;(Ⅱ)x≥﹣3.
21.解:(1)参与调查的学生总数为50÷25%=200(人),
∴愿意参加篮球活动的学生人数为200﹣50﹣35﹣45=70(人),
补全条形统计图如下:
(2)(人),
答:估计该校愿意参加羽手球活动的学生人数为175人;
(3)画树状图如下:
可知所有等可能的情况12种,其中抽取的两名学生为1名男生和1名女生共有8种,
∴恰好抽到1名男生和1名女生的概率为.
答:恰好抽到1名男生和1名女生的概率为.
22.(1)证明:连接OM,如图,
∵FM为⊙O的切线,
∴OM⊥FM.
∴∠OMF=90°,
∴∠OMA+∠AMF=90°.
∵CD⊥AB,
∴∠ANE+∠EAN=90°.
∵OA=OM,
∴∠OAN=∠OMA,
∴∠AMF=∠ANE,
∵∠ANE=∠FNM,
∴∠AMF=∠FNM,
∴FM=FN;
(2)解:连接MD,MC,如图,
∵∠DMF=∠MCF,∠F=∠F,
∴△FMD∽△FCM,
∴,
∴,
∴FC=9,
∴CD=FC﹣FD=5,
由(1)知:FM=FN,
∴FN=6,
∴DN=FN﹣FD=2,
∴CN=CD﹣DN=3.
∵AC∥GF,
∴△ACN∽△MFN,
∴.
设AN=k,则MN=2k,
∵∠ACN=∠DMA,∠CNA=∠DNM,
∴△ACN∽△DMN,
∴,
∴,
∵k>0,
∴k.
∴MN=2k=2.
23.解:(1)设这两个月中该景区游客人数的月平均增长率为x,
由题意得:16(1+x)2=25,
解得:x1=0.25=25%,x2=﹣2.25(不合题意,舍去),
答:这两个月中该景区游客人数的月平均增长率为25%;
(2)由题意可知,25(1+25%)=31.25(万人次),
答:7月份的游客人数为31.25万人次.
24.(1)证明:∵E是AB的中点,
∴AE=EB,
∵DF=BF,
∴EF是△ABD的中位线,
∴AD∥CE;
(2)解:∵EF是△ABD的中位线,
∴AD=2EF=2,
∵∠EFB=90°,
∴∠CFB=180°﹣∠EFB=90°,
在Rt△EFB中,tan∠FEB=3,
∴BF=EF tan∠FEB=3,
∵AD∥CE,AF∥CD,
∴四边形ADCF是平行四边形,
∴AD=CF=2,
在Rt△CFB中,BC.
25.解:(1)A(﹣2,0),B(6,0),直线l的函数表达式为;理由如下:
∵抛物线y与x轴交于A,B两点(点A在点B的左侧),
令y=0,得:x﹣3=0,
解得:x1=﹣2,x2=6.
∴A(﹣2,0),B(6,0),
直线l与抛物线交于A,D两点,点D的坐标为(4,﹣3),设直线l的函数表达式为y=kx+b,将点A,点D的坐标代入得:
,
解得:,
直线l的函数表达式为.
(2)如图,
根据题意可知,点P与点N的坐标分别为,.
∴PM,MN,NP,
分两种情况:
①当PM=3MN时,得,
解得:m1=0,m2=﹣2(不合题意,舍去),
当m=0时,,
∴点P的坐标为(0,﹣3);
②当PM=3NP时,得,
解得:m1=3,m2=﹣2(不合题意,舍去),
当m=3时,,
∴点P的坐标为.
∴当点N是线段PM的三等分点时,点P的坐标为(0,﹣3)或.
26.(1)证明:连接OC,如图,
∵圆心O与点O'关于AC对称,
∴AC垂直平分OO′,
∴AO=AO′,
∴∠OAC=O′AC.
∵AB为直径,
∴∠ACB=90°,
∴BC⊥AC,
∵OO′⊥AC,
∴OO′∥BC,
∵OA=OB,
∴OO′平分AC,
∴AC与OO′互相平分,
∴四边形AOCO′为平行四边形,
∴OA=O′C,AB∥O′C.
∵OB=OA,
∴OB=O′C,
∴四边形OO′CB为平行四边形;
(2)解:连接OC,BD,如图,
∵AB为直径,
∴∠ADB=90°
∵,tan∠DAB,
∴,
设BD=3k,则AD=4k,
∴AB5k,
∴OA=OC=OD=OB=2.5k,
由(1)知:AO=AO′,四边形OO′CB为平行四边形,
∴O′C∥OA,O′C=OA=2.5k.
∴△DO′E∽△DAO,
∴,
∴,
∴O′Ek.
∴CE=O′C﹣O′E=2.5kk.
∴.
解法二:连接OC,BD,如图,
∵AB为直径,
∴∠ADB=90°
∵,tan∠DAB,
∴,
设BD=3k,则AD=4k,
∴AB5k,
∴OA=OC=OD=OB=2.5k,
由(1)知:AO=AO′,四边形OO′CB为平行四边形,
∴O′C∥OA,O′C=OA=2.5k.
∴O′D=AD﹣AO′=1.5k.
∴△DO′E∽△OCE,
∴.
(3)解:过点D作DF⊥AB于点F,交O′C于点H,如图,
∵OA=5,O′D=2,
∴AD=7,OD=OA=5,
设OF=x,则AF=5﹣x,
∵DF2=AD2﹣AF2,DF2=OD2﹣OF2,
∴AD2﹣AF2=OD2﹣OF2,
∴72﹣(5﹣x)2=52﹣x2,
∴x,
∴OF,
∴DF,
∴sin∠DAO,
∵O′C∥AB,
∴∠DO′C=∠DAO,
∴sin∠DO′C=sin∠DAO,
∴DH=O′D sin∠DO′C=2,
∴△O′DC的面积5.
当点O′在线段AD的延长线上时,
延长AD,BC交于点N,过点C作CM⊥AN于点M,连接BD,如图,
∵OA=5,圆心O关于AC的对称点O',
∴AO′=AO=5,
∴AD=AO′﹣O′D=3,
∴BD.
由(1)知:四边形OO′CB为平行四边形,
∴O′C∥OB,O′C=OB,
∵OBAB,
∴O′CAB.
∵O′C∥OB,
∴.
∵AB为圆的直径,
∴∠ADB=90,
∴BD⊥AN,
∵CM⊥AN,
∴BD∥CM,
∴,
∴CMBD,
∴△O′DC的面积O′D CM2.
综上,△O′DC的面积为或.
第1页
同课章节目录
