华师大版七下(2024版)9.3.1图形的旋转学案
文档属性
| 名称 | 华师大版七下(2024版)9.3.1图形的旋转学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 819.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 14:15:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第9章轴对称、平移与旋转
9.3.1 图形的旋转
学习目标与重难点
学习目标:
1.能结合教材实例说出旋转的定义,明确旋转中心、旋转方向、旋转角度是旋转的三要素;
2.能在简单图形旋转中,准确找出对应点、对应线段、对应角,理解 "图形各点绕旋转中心同步旋转相同角度" 的特性;
3.通过 "观察生活实例→分类比较特征→抽象数学概念" 的探究过程,经历从具体到抽象的概念建构,发展数学抽象与几何直观能力;
4.发现旋转在建筑、艺术、科技中的应用,体会数学对现实世界的抽象概括作用,增强 "用数学眼光观察旋转现象" 的意识.
学习重点: 1. 旋转三要素的理解与表述;
2. 理解 "旋转后图形各元素一一对应" 的特性.
学习难点:排除 "物体大小、颜色、旋转速度" 等非本质因素干扰,抓住 "绕固定点按固定方向转动固定角度" 的核心特征,准确描述旋转三要素.
预习自测
知识链接
1.列举一些生活中的旋转现象.
2.用自己的话说一说什么是旋转.
自学自测
1.如图,点A,B,C,D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为 ( )
A.30° B.45°
C.90° D.135°
2.如图所示,把菱形ABOC(四条边都相等)绕点O顺时针旋转得到菱形DFOE,则下列角中,不是旋转角的为 ( )
A.∠BOF B.∠AOD
C.∠COE D.∠AOF
3.如图,△OAB绕点O按顺时针方向旋转得到△OEF,在这个旋转过程中旋转中心是 ,经过旋转,点A转到 ,点B转到 ,线段OA,OB,AB分别转到 ,∠A的对应角是 ,∠B的对应角是 ,∠AOB的对应角是 .
教学过程
一、创设情境、导入新课
复习旧知:平移的特征是什么?
在日常生活中, 除了物体的平行移动外, 我们还可以看到许多如图9.3.1所示物体的旋转现象.
时钟上秒针的不停转动提醒着人们时间的流逝,大风车的转动给人们带来快乐, 飞速转动的电风扇叶片给人们带来丝丝凉意.
生活中的这些现象有什么共同特点?
注:本章主要研究平面图形在一个平面上的旋转问题.
二、合作交流、新知探究
探究一: 旋转的概念
教材第138页:
如图 9.3.2, 单摆上的小球绕着悬挂点在一个平面上转动, 由位置P转动到位置P′, 像这样的运动叫做旋转(rotation).这一悬挂点叫做小球旋转的旋转中心(centre of rotation).显然, 旋转中心在旋转过程中是保持不动的, 图形的旋转由 、 和 决定.
注意:在旋转过程中,图形的 和 没有改变.
探究二:新知探究
教材第138页:旋转的对应关系
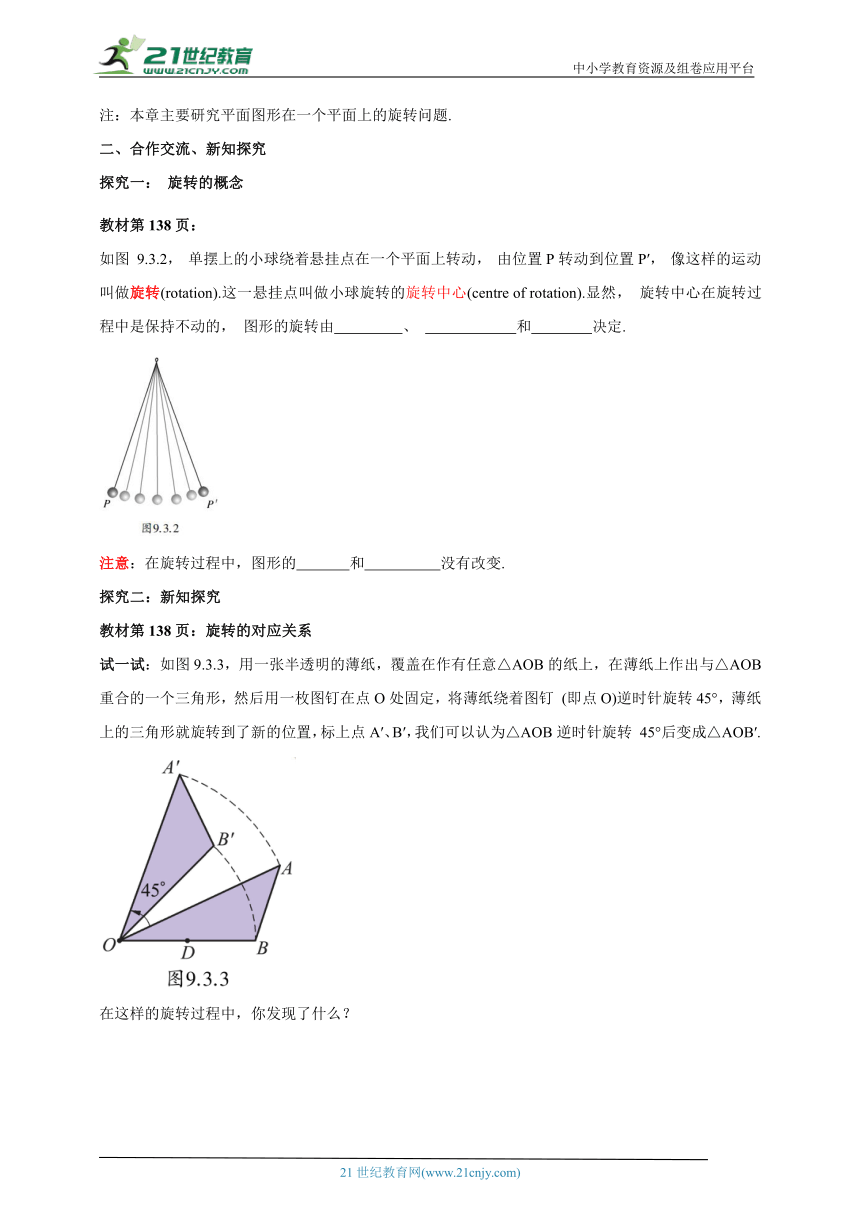
试一试:如图9.3.3,用一张半透明的薄纸,覆盖在作有任意△AOB的纸上,在薄纸上作出与△AOB 重合的一个三角形,然后用一枚图钉在点O处固定,将薄纸绕着图钉 (即点O)逆时针旋转45°,薄纸上的三角形就旋转到了新的位置,标上点A′、B′,我们可以认为△AOB逆时针旋转 45°后变成△AOB′.
在这样的旋转过程中,你发现了什么?
[交流讨论]小组之间交流讨论,完成填空:
从图 9.3.3 中, 可以看到点 A 旋转到点 A′, OA 旋转到 OA′, ∠AOB 旋转到∠A′OB′, 这些分别是互相对应的点、线段和角. 此时:
点B的对应点是点 ;
线段 OB 的对应线段是线段 ;
线段 AB 的对应线段是线段 ;
∠A 的对应角是 ;
∠B 的对应角是 ;
旋转中心是点 ;
旋转的角度是 .
[归纳总结](1)从上面图形中我们可以发现:旋转中心在旋转过程中不动,图形的旋转是由旋转角度和旋转方向决定的.
(2)将一个图形绕某一定点沿某个方向转动一个角度,意味着图形上每个点同时按同一方向旋转相同角度.
探究三:例题讲解
例1 如图 9.3.4, △ABC 是等边三角形, D是边 BC上一点,△ABD经过逆时针旋转后到达△ACE 的位置.
(1) 旋转中心是哪一点
(2) 旋转了多少度
(3) 如果点 M 是 AB 的中点, 那么经过上述旋转后, 点 M 转到了什么位置
例2 如图9.3.5①,点 M 是线段 AB 上一点,将线段 AB 绕着点 M 顺时针方向旋转 90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转 90°呢?
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.下列运动属于旋转的是( )
A.篮球的滚动 B.钟表的钟摆的摆动
C.气球升空的运动 D.一个图形沿某直线对折的过程
2.如图,四边形AOBC绕点O旋转到四边形DOEF的位置,则旋转后点C的对应点是( )
A.点O B.点E C.点D D.点F
3.如图所示,图形①经过________变换得到图形②;图形②经过________变换得到图形③;图形③经过________变换得到图形④.(填“平移”“旋转”或“轴对称”)
选做题:
4.如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的度数为( )
A.42° B.48° C.52° D.58°
5.如图,△ABC沿顺时针方向旋转一个角度后得到△AED,且∠BAD=120°,则旋转中心为________,旋转角度为________.
6.如图,一块等腰直角三角尺ABC在水平桌面上绕点C按顺时针方向旋转到△A′B′C的位置,使A,C,B′三点共线,那么旋转角度为________.
【综合拓展类作业】
7.如图,在正方形ABCD中,△ADE按顺时针方向旋转后与△ABF重合.
(1)旋转中心是点________,旋转了________度;
(2)如果CF=8,CE=4,求四边形AFCE的面积.
总结反思、拓展升华
【课堂总结】
知识点:1.旋转的概念:
在平面内,将一个图形绕某个点沿某个方向转动一定的角度,图形的这种运动就叫做旋转.这个定点叫做旋转中心.
旋转不改变图形的形状和大小.
2.图形在旋转过程中,每一点都绕旋转中心都旋转了相同的角度.旋转只改变图形的位置,不改变图形的大小.
注意事项:旋转的过程中要注意:旋转的角度、旋转中心和旋转的方向;对应点与旋转中心的连线的夹角就是旋转角.
五、【作业布置】
【知识技能类作业】
必做题:
1.用数学的方式理解“当窗理云鬓,对镜帖花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是( )
A.平移和旋转 B.对称和旋转 C.对称和平移 D.旋转和平移
2.如图,在正方形网格中,线段A'B'是线段AB绕某点逆时针旋转角α得到的,点A'与A对应,则角α的大小为( )
A.30° B.60° C.90° D.120°
3.如图,△DBE是等边三角形ABC绕着点B按逆时针旋转30°得到的.
(1)点A、B、C的对应点分别是什么?
(2)线段AB、AC、BC的对应线段分别是什么?
(3)∠A、∠C和∠ABC的对应角分别是什么?
选做题:
4.如图,在正方形ABCD中,点E在BC上,点F在AB上,且∠FDE=45°,△DEC按顺时针转动一个角度后得到△DGA.
(1)图中哪一个点是旋转中心?
(2)旋转了多少度?
(3)指出图中的对应点、对应线段和对应角.
(4)求∠GDF的度数.
【综合拓展类作业】
5.如图,四边形ABCD、四边形EFGH都是边长为1的正方形.
(1)这个图案可以看作是由哪个“基本图案”通过旋转得到的?
(2)请画出旋转中心并指出旋转角.
(3)经过旋转,点A、B、C、D分别移动到什么位置?
答案:
自学测试:
1.C 2.D 3.点O;点E;点F;OE,OF,EF;∠E;∠F;∠EOF
课堂巩固:
1.[答案] B
2.[答案] D
3.[答案] 轴对称 平移 旋转
4.[解析] A ∵在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,
∴∠A′=∠BAC=90°,∠ACA′=48°,
∴∠B′=90°-∠ACA′=42°.
5.[答案] 点A 120°
6.[答案] 135°
7.解:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴△ADE绕点A顺时针旋转90°后与△ABF重合,即旋转中心是点A,旋转了90度.
故答案为A,90.
(2)∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴BF=DE,S△ABF=S△ADE.
∵CF=BC+BF=8,
∴BC+DE=8.
∵CE=CD-DE=BC-DE=4,
∴BC=6,
∴四边形AFCE的面积=S正方形ABCD=62=36.
作业布置:
1.B 2.C
3.(1)点A、B、C的对应点分别是点D、B、E.
(2)线段AB、AC、BC的对应线段分别为线段DB、DE、BE.
(3)∠A、∠C和∠ABC的对应角分别为∠D、∠E和∠DBE.
4.(1)点D是旋转中心.
(2)旋转了90°.
(3)对应点:D对D,G对E,A对C;
对应线段:DG对DE,DA对DC,AG对CE;
对应角:∠CDE对∠ADG,∠CED对∠AGD,∠C对∠DAG.
(4)∠GDF=45°
5.此题答案不唯一.
(1)可看作是由正方形ABCD通过旋转而得到的.
(2)略
(3)点A、B、C、D移动到的位置分别是点F、G、H、E.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第9章轴对称、平移与旋转
9.3.1 图形的旋转
学习目标与重难点
学习目标:
1.能结合教材实例说出旋转的定义,明确旋转中心、旋转方向、旋转角度是旋转的三要素;
2.能在简单图形旋转中,准确找出对应点、对应线段、对应角,理解 "图形各点绕旋转中心同步旋转相同角度" 的特性;
3.通过 "观察生活实例→分类比较特征→抽象数学概念" 的探究过程,经历从具体到抽象的概念建构,发展数学抽象与几何直观能力;
4.发现旋转在建筑、艺术、科技中的应用,体会数学对现实世界的抽象概括作用,增强 "用数学眼光观察旋转现象" 的意识.
学习重点: 1. 旋转三要素的理解与表述;
2. 理解 "旋转后图形各元素一一对应" 的特性.
学习难点:排除 "物体大小、颜色、旋转速度" 等非本质因素干扰,抓住 "绕固定点按固定方向转动固定角度" 的核心特征,准确描述旋转三要素.
预习自测
知识链接
1.列举一些生活中的旋转现象.
2.用自己的话说一说什么是旋转.
自学自测
1.如图,点A,B,C,D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为 ( )
A.30° B.45°
C.90° D.135°
2.如图所示,把菱形ABOC(四条边都相等)绕点O顺时针旋转得到菱形DFOE,则下列角中,不是旋转角的为 ( )
A.∠BOF B.∠AOD
C.∠COE D.∠AOF
3.如图,△OAB绕点O按顺时针方向旋转得到△OEF,在这个旋转过程中旋转中心是 ,经过旋转,点A转到 ,点B转到 ,线段OA,OB,AB分别转到 ,∠A的对应角是 ,∠B的对应角是 ,∠AOB的对应角是 .
教学过程
一、创设情境、导入新课
复习旧知:平移的特征是什么?
在日常生活中, 除了物体的平行移动外, 我们还可以看到许多如图9.3.1所示物体的旋转现象.
时钟上秒针的不停转动提醒着人们时间的流逝,大风车的转动给人们带来快乐, 飞速转动的电风扇叶片给人们带来丝丝凉意.
生活中的这些现象有什么共同特点?
注:本章主要研究平面图形在一个平面上的旋转问题.
二、合作交流、新知探究
探究一: 旋转的概念
教材第138页:
如图 9.3.2, 单摆上的小球绕着悬挂点在一个平面上转动, 由位置P转动到位置P′, 像这样的运动叫做旋转(rotation).这一悬挂点叫做小球旋转的旋转中心(centre of rotation).显然, 旋转中心在旋转过程中是保持不动的, 图形的旋转由 、 和 决定.
注意:在旋转过程中,图形的 和 没有改变.
探究二:新知探究
教材第138页:旋转的对应关系
试一试:如图9.3.3,用一张半透明的薄纸,覆盖在作有任意△AOB的纸上,在薄纸上作出与△AOB 重合的一个三角形,然后用一枚图钉在点O处固定,将薄纸绕着图钉 (即点O)逆时针旋转45°,薄纸上的三角形就旋转到了新的位置,标上点A′、B′,我们可以认为△AOB逆时针旋转 45°后变成△AOB′.
在这样的旋转过程中,你发现了什么?
[交流讨论]小组之间交流讨论,完成填空:
从图 9.3.3 中, 可以看到点 A 旋转到点 A′, OA 旋转到 OA′, ∠AOB 旋转到∠A′OB′, 这些分别是互相对应的点、线段和角. 此时:
点B的对应点是点 ;
线段 OB 的对应线段是线段 ;
线段 AB 的对应线段是线段 ;
∠A 的对应角是 ;
∠B 的对应角是 ;
旋转中心是点 ;
旋转的角度是 .
[归纳总结](1)从上面图形中我们可以发现:旋转中心在旋转过程中不动,图形的旋转是由旋转角度和旋转方向决定的.
(2)将一个图形绕某一定点沿某个方向转动一个角度,意味着图形上每个点同时按同一方向旋转相同角度.
探究三:例题讲解
例1 如图 9.3.4, △ABC 是等边三角形, D是边 BC上一点,△ABD经过逆时针旋转后到达△ACE 的位置.
(1) 旋转中心是哪一点
(2) 旋转了多少度
(3) 如果点 M 是 AB 的中点, 那么经过上述旋转后, 点 M 转到了什么位置
例2 如图9.3.5①,点 M 是线段 AB 上一点,将线段 AB 绕着点 M 顺时针方向旋转 90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转 90°呢?
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.下列运动属于旋转的是( )
A.篮球的滚动 B.钟表的钟摆的摆动
C.气球升空的运动 D.一个图形沿某直线对折的过程
2.如图,四边形AOBC绕点O旋转到四边形DOEF的位置,则旋转后点C的对应点是( )
A.点O B.点E C.点D D.点F
3.如图所示,图形①经过________变换得到图形②;图形②经过________变换得到图形③;图形③经过________变换得到图形④.(填“平移”“旋转”或“轴对称”)
选做题:
4.如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的度数为( )
A.42° B.48° C.52° D.58°
5.如图,△ABC沿顺时针方向旋转一个角度后得到△AED,且∠BAD=120°,则旋转中心为________,旋转角度为________.
6.如图,一块等腰直角三角尺ABC在水平桌面上绕点C按顺时针方向旋转到△A′B′C的位置,使A,C,B′三点共线,那么旋转角度为________.
【综合拓展类作业】
7.如图,在正方形ABCD中,△ADE按顺时针方向旋转后与△ABF重合.
(1)旋转中心是点________,旋转了________度;
(2)如果CF=8,CE=4,求四边形AFCE的面积.
总结反思、拓展升华
【课堂总结】
知识点:1.旋转的概念:
在平面内,将一个图形绕某个点沿某个方向转动一定的角度,图形的这种运动就叫做旋转.这个定点叫做旋转中心.
旋转不改变图形的形状和大小.
2.图形在旋转过程中,每一点都绕旋转中心都旋转了相同的角度.旋转只改变图形的位置,不改变图形的大小.
注意事项:旋转的过程中要注意:旋转的角度、旋转中心和旋转的方向;对应点与旋转中心的连线的夹角就是旋转角.
五、【作业布置】
【知识技能类作业】
必做题:
1.用数学的方式理解“当窗理云鬓,对镜帖花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是( )
A.平移和旋转 B.对称和旋转 C.对称和平移 D.旋转和平移
2.如图,在正方形网格中,线段A'B'是线段AB绕某点逆时针旋转角α得到的,点A'与A对应,则角α的大小为( )
A.30° B.60° C.90° D.120°
3.如图,△DBE是等边三角形ABC绕着点B按逆时针旋转30°得到的.
(1)点A、B、C的对应点分别是什么?
(2)线段AB、AC、BC的对应线段分别是什么?
(3)∠A、∠C和∠ABC的对应角分别是什么?
选做题:
4.如图,在正方形ABCD中,点E在BC上,点F在AB上,且∠FDE=45°,△DEC按顺时针转动一个角度后得到△DGA.
(1)图中哪一个点是旋转中心?
(2)旋转了多少度?
(3)指出图中的对应点、对应线段和对应角.
(4)求∠GDF的度数.
【综合拓展类作业】
5.如图,四边形ABCD、四边形EFGH都是边长为1的正方形.
(1)这个图案可以看作是由哪个“基本图案”通过旋转得到的?
(2)请画出旋转中心并指出旋转角.
(3)经过旋转,点A、B、C、D分别移动到什么位置?
答案:
自学测试:
1.C 2.D 3.点O;点E;点F;OE,OF,EF;∠E;∠F;∠EOF
课堂巩固:
1.[答案] B
2.[答案] D
3.[答案] 轴对称 平移 旋转
4.[解析] A ∵在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,
∴∠A′=∠BAC=90°,∠ACA′=48°,
∴∠B′=90°-∠ACA′=42°.
5.[答案] 点A 120°
6.[答案] 135°
7.解:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴△ADE绕点A顺时针旋转90°后与△ABF重合,即旋转中心是点A,旋转了90度.
故答案为A,90.
(2)∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴BF=DE,S△ABF=S△ADE.
∵CF=BC+BF=8,
∴BC+DE=8.
∵CE=CD-DE=BC-DE=4,
∴BC=6,
∴四边形AFCE的面积=S正方形ABCD=62=36.
作业布置:
1.B 2.C
3.(1)点A、B、C的对应点分别是点D、B、E.
(2)线段AB、AC、BC的对应线段分别为线段DB、DE、BE.
(3)∠A、∠C和∠ABC的对应角分别为∠D、∠E和∠DBE.
4.(1)点D是旋转中心.
(2)旋转了90°.
(3)对应点:D对D,G对E,A对C;
对应线段:DG对DE,DA对DC,AG对CE;
对应角:∠CDE对∠ADG,∠CED对∠AGD,∠C对∠DAG.
(4)∠GDF=45°
5.此题答案不唯一.
(1)可看作是由正方形ABCD通过旋转而得到的.
(2)略
(3)点A、B、C、D移动到的位置分别是点F、G、H、E.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
