华师大版七下(2024版)9.3.1图形的旋转教案
文档属性
| 名称 | 华师大版七下(2024版)9.3.1图形的旋转教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 14:15:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
分课时教学设计
第七课时《9.3.1图形的旋转》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 本课为华师大版七年级下册第九章《图形的旋转》第一课时,聚焦 "旋转概念的建构与三要素理解",是图形变换体系的重要组成部分。教材通过生活实例和数学操作,引导学生从 "物体绕点转动" 的直观感知抽象出 "图形旋转" 的数学概念,明确旋转由旋转中心、旋转方向、旋转角度三要素决定,强调旋转前后图形的对应关系(对应点、对应线段、对应角),为后续学习旋转特征和旋转作图奠定概念基础.
学习者分析 学生已经掌握平移的概念与要素,理解 "图形变换中形状大小不变" 的特性;熟悉教材中列举的旋转现象,能直观判断 "物体绕点转动" 的生活实例;可能混淆 "旋转角度" 与 "旋转路径长度"(如认为 "转动圈数" 等同于旋转角度),或忽略旋转中心的固定性(如误认为旋转中心会移动);在复杂旋转中(如斜向旋转、非 90° 角旋转),难以快速找到对应点及计算旋转角度.
教学目标 1.能结合教材实例说出旋转的定义,明确旋转中心、旋转方向、旋转角度是旋转的三要素; 2.能在简单图形旋转中,准确找出对应点、对应线段、对应角,理解"图形各点绕旋转中心同步旋转相同角度"的特性; 3.通过 "观察生活实例→分类比较特征→抽象数学概念" 的探究过程,经历从具体到抽象的概念建构,发展数学抽象与几何直观能力; 4.发现旋转在建筑、艺术、科技中的应用,体会数学对现实世界的抽象概括作用,增强"用数学眼光观察旋转现象"的意识.
教学重点 1. 旋转三要素的理解与表述; 2. 理解 "旋转后图形各元素一一对应" 的特性.
教学难点 排除 "物体大小、颜色、旋转速度" 等非本质因素干扰,抓住 "绕固定点按固定方向转动固定角度" 的核心特征,准确描述旋转三要素.
学习活动设计
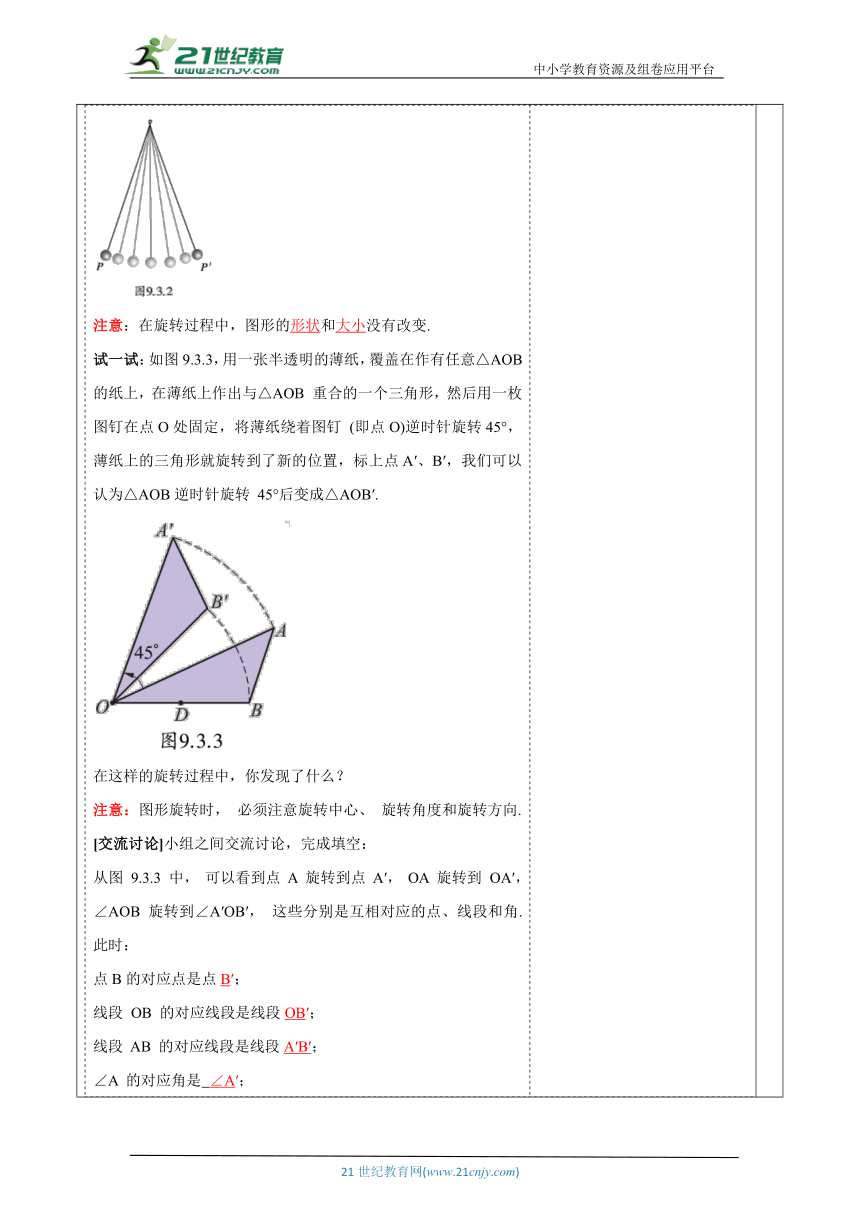
教师活动学生活动环节一:情境导入教师活动1: 复习旧知:平移的特征是什么? (1)平移后的图形与原来的图形的形状与大小不变; (2)平移后的图形与原来的图形的对应线段平行(或共线)且相等; (3)平移后的图形与原来的图形的对应角相等; (4)平移后对应点所连的线段平行(或共线)且相等。 在日常生活中, 除了物体的平行移动外, 我们还可以看到许多如图9.3.1所示物体的旋转现象. 时钟上秒针的不停转动提醒着人们时间的流逝,大风车的转动给人们带来快乐, 飞速转动的电风扇叶片给人们带来丝丝凉意. 生活中的这些现象有什么共同特点? 图形绕某点旋转 注:本章主要研究平面图形在一个平面上的旋转问题.学生活动1: 学生通过已学习的知识经过个人思考、小组合作等方式推导出本课新知.复习上节内容,导入本节图形的旋转。活动意图说明: 从实际出发,从学生已有的生活经验出发. 了解图形的旋转变换的现实用途.通过具体实例认识旋转.环节二:新知探究教师活动2:图形的旋转有关概念 如图 9.3.2, 单摆上的小球绕着悬挂点在一个平面上转动, 由位置P转动到位置P′, 像这样的运动叫做旋转(rotation).这一悬挂点叫做小球旋转的旋转中心(centre of rotation).显然, 旋转中心在旋转过程中是保持不动的, 图形的旋转由旋转中心、 旋转角度和旋转方向决定. 注意:在旋转过程中,图形的形状和大小没有改变. 试一试:如图9.3.3,用一张半透明的薄纸,覆盖在作有任意△AOB的纸上,在薄纸上作出与△AOB 重合的一个三角形,然后用一枚图钉在点O处固定,将薄纸绕着图钉 (即点O)逆时针旋转45°,薄纸上的三角形就旋转到了新的位置,标上点A′、B′,我们可以认为△AOB逆时针旋转 45°后变成△AOB′. 在这样的旋转过程中,你发现了什么? 注意:图形旋转时, 必须注意旋转中心、 旋转角度和旋转方向. [交流讨论]小组之间交流讨论,完成填空: 从图 9.3.3 中, 可以看到点 A 旋转到点 A′, OA 旋转到 OA′, ∠AOB 旋转到∠A′OB′, 这些分别是互相对应的点、线段和角. 此时: 点B的对应点是点B′; 线段 OB 的对应线段是线段OB′; 线段 AB 的对应线段是线段A′B′; ∠A 的对应角是 ∠A′; ∠B 的对应角是 ∠B′; 旋转中心是点O; 旋转的角度是45°. [归纳总结](1)从上面图形中我们可以发现:旋转中心在旋转过程中不动,图形的旋转是由旋转角度和旋转方向决定的. (2)将一个图形绕某一定点沿某个方向转动一个角度,意味着图形上每个点同时按同一方向旋转相同角度.学生活动2: 学生小组合作交流. 学生可小组合作交流,自主探究,得出结论 教师巡视,听取学生的看法、见解,随时参与讨论. 活动意图说明:引导学生建立模型,鼓励学生大胆探索,鼓励学生大胆探索,总结图形的旋转的性质,激发学生探究旋转的本质,加深对旋转的现象的理解.积累解题经验,提高灵活地运用所学知识解决问题的能力.环节三:例题讲解教师活动3: 例1 如图 9.3.4, △ABC 是等边三角形, D是边 BC上一点,△ABD经过逆时针旋转后到达△ACE 的位置. (1) 旋转中心是哪一点 (2) 旋转了多少度 (3) 如果点 M 是 AB 的中点, 那么经过上述旋转后, 点 M 转到了什么位置 解: (1) 旋转中心是点A. (2) 旋转了60°. (3) 点M转到了AC 的中点位置上. 【总结】旋转的过程中要注意:旋转的角度、旋转中心和旋转的方向;对应点与旋转中心的连线的夹角就是旋转角. 例2 如图9.3.5①,点 M 是线段 AB 上一点,将线段 AB 绕着点 M 顺时针方向旋转 90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转 90°呢? 解:如图9.3.5②,顺时针旋转90°,A'B'与AB互相垂直. 如图9.3.5③,逆时针旋转90°,A"B"与AB互相垂直. 注意:线段绕线段上的某一点旋转 90°后与原来位置的线段互相垂直. 图形的旋转在图案设计中也具有广泛应用. 如图 9.3.6 所示的两幅美丽的图案都可以看成是由一个或几个基本图案, 在同一平面上旋转若干次而产生的结果. 学生活动3: 学生观察并回答教师规范解答,教师出示练习题组,巩固例题,学生尝试练习师巡视,个别指导. 活动意图说明: 让学生在一定的数学活动中去体验、感受数学,通过对例题的学习,进一步加深对三角形的概念和三角形分类的理解和掌握.从而更好地理解知识,让学生的认知结构得到不断的完善.
板书设计 9.3.1 图形的旋转 1.旋转的概念: 在平面内,将一个图形绕某个点沿某个方向转动一定的角度,图形的这种运动就叫做旋转.这个定点叫做旋转中心. 旋转不改变图形的形状和大小. 2.图形在旋转过程中,每一点都绕旋转中心都旋转了相同的角度.旋转只改变图形的位置,不改变图形的大小. 例1 例2
课堂练习 【知识技能类作业】 必做题: 1.下列运动属于旋转的是( ) A.篮球的滚动 B.钟表的钟摆的摆动 C.气球升空的运动 D.一个图形沿某直线对折的过程 2.如图,四边形AOBC绕点O旋转到四边形DOEF的位置,则旋转后点C的对应点是( ) A.点O B.点E C.点D D.点F 3.如图所示,图形①经过________变换得到图形②;图形②经过________变换得到图形③;图形③经过________变换得到图形④.(填“平移”“旋转”或“轴对称”) 选做题: 4.如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的度数为( ) A.42° B.48° C.52° D.58° 5.如图,△ABC沿顺时针方向旋转一个角度后得到△AED,且∠BAD=120°,则旋转中心为________,旋转角度为________. 6.如图,一块等腰直角三角尺ABC在水平桌面上绕点C按顺时针方向旋转到△A′B′C的位置,使A,C,B′三点共线,那么旋转角度为________. 【综合拓展类作业】 7.如图,在正方形ABCD中,△ADE按顺时针方向旋转后与△ABF重合. (1)旋转中心是点________,旋转了________度; (2)如果CF=8,CE=4,求四边形AFCE的面积. 1.[答案] B 2.[答案] D 3.[答案] 轴对称 平移 旋转 4.[解析] A ∵在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C, ∴∠A′=∠BAC=90°,∠ACA′=48°, ∴∠B′=90°-∠ACA′=42°. 5.[答案] 点A 120° 6.[答案] 135° 7.解:(1)∵四边形ABCD为正方形, ∴AB=AD,∠BAD=90°, ∴△ADE绕点A顺时针旋转90°后与△ABF重合,即旋转中心是点A,旋转了90度. 故答案为A,90. (2)∵△ADE绕点A顺时针旋转90°后与△ABF重合, ∴BF=DE,S△ABF=S△ADE. ∵CF=BC+BF=8, ∴BC+DE=8. ∵CE=CD-DE=BC-DE=4, ∴BC=6, ∴四边形AFCE的面积=S正方形ABCD=62=36.
作业设计 【知识技能类作业】 必做题: 1.用数学的方式理解“当窗理云鬓,对镜帖花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是( ) A.平移和旋转 B.对称和旋转 C.对称和平移 D.旋转和平移 2.如图,在正方形网格中,线段A'B'是线段AB绕某点逆时针旋转角α得到的,点A'与A对应,则角α的大小为( ) A.30° B.60° C.90° D.120° 3.如图,△DBE是等边三角形ABC绕着点B按逆时针旋转30°得到的. (1)点A、B、C的对应点分别是什么? (2)线段AB、AC、BC的对应线段分别是什么? (3)∠A、∠C和∠ABC的对应角分别是什么? 选做题: 4.如图,在正方形ABCD中,点E在BC上,点F在AB上,且∠FDE=45°,△DEC按顺时针转动一个角度后得到△DGA. (1)图中哪一个点是旋转中心? (2)旋转了多少度? (3)指出图中的对应点、对应线段和对应角. (4)求∠GDF的度数. 【综合拓展类作业】 5.如图,四边形ABCD、四边形EFGH都是边长为1的正方形. (1)这个图案可以看作是由哪个“基本图案”通过旋转得到的? (2)请画出旋转中心并指出旋转角. (3)经过旋转,点A、B、C、D分别移动到什么位置? 1.B 2.C 3.(1)点A、B、C的对应点分别是点D、B、E. (2)线段AB、AC、BC的对应线段分别为线段DB、DE、BE. (3)∠A、∠C和∠ABC的对应角分别为∠D、∠E和∠DBE. 4.(1)点D是旋转中心. (2)旋转了90°. (3)对应点:D对D,G对E,A对C; 对应线段:DG对DE,DA对DC,AG对CE; 对应角:∠CDE对∠ADG,∠CED对∠AGD,∠C对∠DAG. (4)∠GDF=45° 5.此题答案不唯一. (1)可看作是由正方形ABCD通过旋转而得到的. (2)略 (3)点A、B、C、D移动到的位置分别是点F、G、H、E.
教学反思 本节课的学习了旋转的概念,通过本节课的学习要求同学们掌握旋转的概念,知道旋转是由旋转中心、旋转方向及旋转角度决定的并能理解旋转前后的两个图形的对应关系,能正确地找出图形旋转前后的对应点、对应角、对应线段及旋转角.
21世纪教育网(www.21cnjy.com)
分课时教学设计
第七课时《9.3.1图形的旋转》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 本课为华师大版七年级下册第九章《图形的旋转》第一课时,聚焦 "旋转概念的建构与三要素理解",是图形变换体系的重要组成部分。教材通过生活实例和数学操作,引导学生从 "物体绕点转动" 的直观感知抽象出 "图形旋转" 的数学概念,明确旋转由旋转中心、旋转方向、旋转角度三要素决定,强调旋转前后图形的对应关系(对应点、对应线段、对应角),为后续学习旋转特征和旋转作图奠定概念基础.
学习者分析 学生已经掌握平移的概念与要素,理解 "图形变换中形状大小不变" 的特性;熟悉教材中列举的旋转现象,能直观判断 "物体绕点转动" 的生活实例;可能混淆 "旋转角度" 与 "旋转路径长度"(如认为 "转动圈数" 等同于旋转角度),或忽略旋转中心的固定性(如误认为旋转中心会移动);在复杂旋转中(如斜向旋转、非 90° 角旋转),难以快速找到对应点及计算旋转角度.
教学目标 1.能结合教材实例说出旋转的定义,明确旋转中心、旋转方向、旋转角度是旋转的三要素; 2.能在简单图形旋转中,准确找出对应点、对应线段、对应角,理解"图形各点绕旋转中心同步旋转相同角度"的特性; 3.通过 "观察生活实例→分类比较特征→抽象数学概念" 的探究过程,经历从具体到抽象的概念建构,发展数学抽象与几何直观能力; 4.发现旋转在建筑、艺术、科技中的应用,体会数学对现实世界的抽象概括作用,增强"用数学眼光观察旋转现象"的意识.
教学重点 1. 旋转三要素的理解与表述; 2. 理解 "旋转后图形各元素一一对应" 的特性.
教学难点 排除 "物体大小、颜色、旋转速度" 等非本质因素干扰,抓住 "绕固定点按固定方向转动固定角度" 的核心特征,准确描述旋转三要素.
学习活动设计
教师活动学生活动环节一:情境导入教师活动1: 复习旧知:平移的特征是什么? (1)平移后的图形与原来的图形的形状与大小不变; (2)平移后的图形与原来的图形的对应线段平行(或共线)且相等; (3)平移后的图形与原来的图形的对应角相等; (4)平移后对应点所连的线段平行(或共线)且相等。 在日常生活中, 除了物体的平行移动外, 我们还可以看到许多如图9.3.1所示物体的旋转现象. 时钟上秒针的不停转动提醒着人们时间的流逝,大风车的转动给人们带来快乐, 飞速转动的电风扇叶片给人们带来丝丝凉意. 生活中的这些现象有什么共同特点? 图形绕某点旋转 注:本章主要研究平面图形在一个平面上的旋转问题.学生活动1: 学生通过已学习的知识经过个人思考、小组合作等方式推导出本课新知.复习上节内容,导入本节图形的旋转。活动意图说明: 从实际出发,从学生已有的生活经验出发. 了解图形的旋转变换的现实用途.通过具体实例认识旋转.环节二:新知探究教师活动2:图形的旋转有关概念 如图 9.3.2, 单摆上的小球绕着悬挂点在一个平面上转动, 由位置P转动到位置P′, 像这样的运动叫做旋转(rotation).这一悬挂点叫做小球旋转的旋转中心(centre of rotation).显然, 旋转中心在旋转过程中是保持不动的, 图形的旋转由旋转中心、 旋转角度和旋转方向决定. 注意:在旋转过程中,图形的形状和大小没有改变. 试一试:如图9.3.3,用一张半透明的薄纸,覆盖在作有任意△AOB的纸上,在薄纸上作出与△AOB 重合的一个三角形,然后用一枚图钉在点O处固定,将薄纸绕着图钉 (即点O)逆时针旋转45°,薄纸上的三角形就旋转到了新的位置,标上点A′、B′,我们可以认为△AOB逆时针旋转 45°后变成△AOB′. 在这样的旋转过程中,你发现了什么? 注意:图形旋转时, 必须注意旋转中心、 旋转角度和旋转方向. [交流讨论]小组之间交流讨论,完成填空: 从图 9.3.3 中, 可以看到点 A 旋转到点 A′, OA 旋转到 OA′, ∠AOB 旋转到∠A′OB′, 这些分别是互相对应的点、线段和角. 此时: 点B的对应点是点B′; 线段 OB 的对应线段是线段OB′; 线段 AB 的对应线段是线段A′B′; ∠A 的对应角是 ∠A′; ∠B 的对应角是 ∠B′; 旋转中心是点O; 旋转的角度是45°. [归纳总结](1)从上面图形中我们可以发现:旋转中心在旋转过程中不动,图形的旋转是由旋转角度和旋转方向决定的. (2)将一个图形绕某一定点沿某个方向转动一个角度,意味着图形上每个点同时按同一方向旋转相同角度.学生活动2: 学生小组合作交流. 学生可小组合作交流,自主探究,得出结论 教师巡视,听取学生的看法、见解,随时参与讨论. 活动意图说明:引导学生建立模型,鼓励学生大胆探索,鼓励学生大胆探索,总结图形的旋转的性质,激发学生探究旋转的本质,加深对旋转的现象的理解.积累解题经验,提高灵活地运用所学知识解决问题的能力.环节三:例题讲解教师活动3: 例1 如图 9.3.4, △ABC 是等边三角形, D是边 BC上一点,△ABD经过逆时针旋转后到达△ACE 的位置. (1) 旋转中心是哪一点 (2) 旋转了多少度 (3) 如果点 M 是 AB 的中点, 那么经过上述旋转后, 点 M 转到了什么位置 解: (1) 旋转中心是点A. (2) 旋转了60°. (3) 点M转到了AC 的中点位置上. 【总结】旋转的过程中要注意:旋转的角度、旋转中心和旋转的方向;对应点与旋转中心的连线的夹角就是旋转角. 例2 如图9.3.5①,点 M 是线段 AB 上一点,将线段 AB 绕着点 M 顺时针方向旋转 90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转 90°呢? 解:如图9.3.5②,顺时针旋转90°,A'B'与AB互相垂直. 如图9.3.5③,逆时针旋转90°,A"B"与AB互相垂直. 注意:线段绕线段上的某一点旋转 90°后与原来位置的线段互相垂直. 图形的旋转在图案设计中也具有广泛应用. 如图 9.3.6 所示的两幅美丽的图案都可以看成是由一个或几个基本图案, 在同一平面上旋转若干次而产生的结果. 学生活动3: 学生观察并回答教师规范解答,教师出示练习题组,巩固例题,学生尝试练习师巡视,个别指导. 活动意图说明: 让学生在一定的数学活动中去体验、感受数学,通过对例题的学习,进一步加深对三角形的概念和三角形分类的理解和掌握.从而更好地理解知识,让学生的认知结构得到不断的完善.
板书设计 9.3.1 图形的旋转 1.旋转的概念: 在平面内,将一个图形绕某个点沿某个方向转动一定的角度,图形的这种运动就叫做旋转.这个定点叫做旋转中心. 旋转不改变图形的形状和大小. 2.图形在旋转过程中,每一点都绕旋转中心都旋转了相同的角度.旋转只改变图形的位置,不改变图形的大小. 例1 例2
课堂练习 【知识技能类作业】 必做题: 1.下列运动属于旋转的是( ) A.篮球的滚动 B.钟表的钟摆的摆动 C.气球升空的运动 D.一个图形沿某直线对折的过程 2.如图,四边形AOBC绕点O旋转到四边形DOEF的位置,则旋转后点C的对应点是( ) A.点O B.点E C.点D D.点F 3.如图所示,图形①经过________变换得到图形②;图形②经过________变换得到图形③;图形③经过________变换得到图形④.(填“平移”“旋转”或“轴对称”) 选做题: 4.如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的度数为( ) A.42° B.48° C.52° D.58° 5.如图,△ABC沿顺时针方向旋转一个角度后得到△AED,且∠BAD=120°,则旋转中心为________,旋转角度为________. 6.如图,一块等腰直角三角尺ABC在水平桌面上绕点C按顺时针方向旋转到△A′B′C的位置,使A,C,B′三点共线,那么旋转角度为________. 【综合拓展类作业】 7.如图,在正方形ABCD中,△ADE按顺时针方向旋转后与△ABF重合. (1)旋转中心是点________,旋转了________度; (2)如果CF=8,CE=4,求四边形AFCE的面积. 1.[答案] B 2.[答案] D 3.[答案] 轴对称 平移 旋转 4.[解析] A ∵在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C, ∴∠A′=∠BAC=90°,∠ACA′=48°, ∴∠B′=90°-∠ACA′=42°. 5.[答案] 点A 120° 6.[答案] 135° 7.解:(1)∵四边形ABCD为正方形, ∴AB=AD,∠BAD=90°, ∴△ADE绕点A顺时针旋转90°后与△ABF重合,即旋转中心是点A,旋转了90度. 故答案为A,90. (2)∵△ADE绕点A顺时针旋转90°后与△ABF重合, ∴BF=DE,S△ABF=S△ADE. ∵CF=BC+BF=8, ∴BC+DE=8. ∵CE=CD-DE=BC-DE=4, ∴BC=6, ∴四边形AFCE的面积=S正方形ABCD=62=36.
作业设计 【知识技能类作业】 必做题: 1.用数学的方式理解“当窗理云鬓,对镜帖花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是( ) A.平移和旋转 B.对称和旋转 C.对称和平移 D.旋转和平移 2.如图,在正方形网格中,线段A'B'是线段AB绕某点逆时针旋转角α得到的,点A'与A对应,则角α的大小为( ) A.30° B.60° C.90° D.120° 3.如图,△DBE是等边三角形ABC绕着点B按逆时针旋转30°得到的. (1)点A、B、C的对应点分别是什么? (2)线段AB、AC、BC的对应线段分别是什么? (3)∠A、∠C和∠ABC的对应角分别是什么? 选做题: 4.如图,在正方形ABCD中,点E在BC上,点F在AB上,且∠FDE=45°,△DEC按顺时针转动一个角度后得到△DGA. (1)图中哪一个点是旋转中心? (2)旋转了多少度? (3)指出图中的对应点、对应线段和对应角. (4)求∠GDF的度数. 【综合拓展类作业】 5.如图,四边形ABCD、四边形EFGH都是边长为1的正方形. (1)这个图案可以看作是由哪个“基本图案”通过旋转得到的? (2)请画出旋转中心并指出旋转角. (3)经过旋转,点A、B、C、D分别移动到什么位置? 1.B 2.C 3.(1)点A、B、C的对应点分别是点D、B、E. (2)线段AB、AC、BC的对应线段分别为线段DB、DE、BE. (3)∠A、∠C和∠ABC的对应角分别为∠D、∠E和∠DBE. 4.(1)点D是旋转中心. (2)旋转了90°. (3)对应点:D对D,G对E,A对C; 对应线段:DG对DE,DA对DC,AG对CE; 对应角:∠CDE对∠ADG,∠CED对∠AGD,∠C对∠DAG. (4)∠GDF=45° 5.此题答案不唯一. (1)可看作是由正方形ABCD通过旋转而得到的. (2)略 (3)点A、B、C、D移动到的位置分别是点F、G、H、E.
教学反思 本节课的学习了旋转的概念,通过本节课的学习要求同学们掌握旋转的概念,知道旋转是由旋转中心、旋转方向及旋转角度决定的并能理解旋转前后的两个图形的对应关系,能正确地找出图形旋转前后的对应点、对应角、对应线段及旋转角.
21世纪教育网(www.21cnjy.com)
