2024-2025学年广东省佛山市S6高质量发展联盟高一下学期期中联考数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广东省佛山市S6高质量发展联盟高一下学期期中联考数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 87.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 00:00:00 | ||
图片预览



文档简介
2024-2025学年广东省佛山市S6高质量发展联盟高一下学期期中联考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,则的虚部为( )
A. B. C. D.
2.在边长为的等边三角形中,的值为( )
A. B. C. D.
3.如图,在中,点是的中点,点是的中点,设,,那么( )
A. B. C. D.
4.已知非零空间向量,,且,,,则一定共线的三点是( )
A. ,, B. ,, C. ,, D. ,,
5.在中,角,,的对边分别为,,,若,则的形状为( )
A. 等边三角形 B. 直角三角形 C. 等腰三角形 D. 等腰或直角三角形
6.若,,则( )
A. B.
C. D.
7.在中,已知,,,,边上的两条中线,相交于点,则( )
A. B. C. D.
8.已知函数,对于任意的,都有恒成立,则关于的不等式的解集为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知复数满足,则( )
A. 为纯虚数 B. 对应的点在第四象限
C. D. 和是方程的两个根
10.设是三个非零向量,且相互不共线,则下列说法正确的是( )
A. 若,则
B. 若,则
C. 若,则不与垂直
D. 不与垂直
11.对于函数下列说法正确的是( )
A. 当时,函数在上有且只有一个零点
B. 若函数在单调递增,则的取值范围为
C. 若函数在时取得最小值,在时取得最大值,且,则
D. 将函数图象向左平移个单位得到的图象,若为偶函数,则的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.如图,,两点在河的两岸,在同侧的河岸边选取点,测得,,,则,两点间的距离为
13.将函数图象上所有点的纵坐标伸长为原来的倍,横坐标缩短为原来的,再将所得的图象向右平移个单位长度,得到函数的图象,则 .
14.在中,角,,的对边分别为,,已知,的平分线交于点,且,则的最小值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,满足,,且,的夹角为,
求
当向量与垂直时,求实数的值.
16.本小题分
已知,,且,,求的值.
已知,,且及,求的值.
17.本小题分
如图,在中,,,点在线段上.
若,求的长
若,的面积为,求的长.
18.本小题分
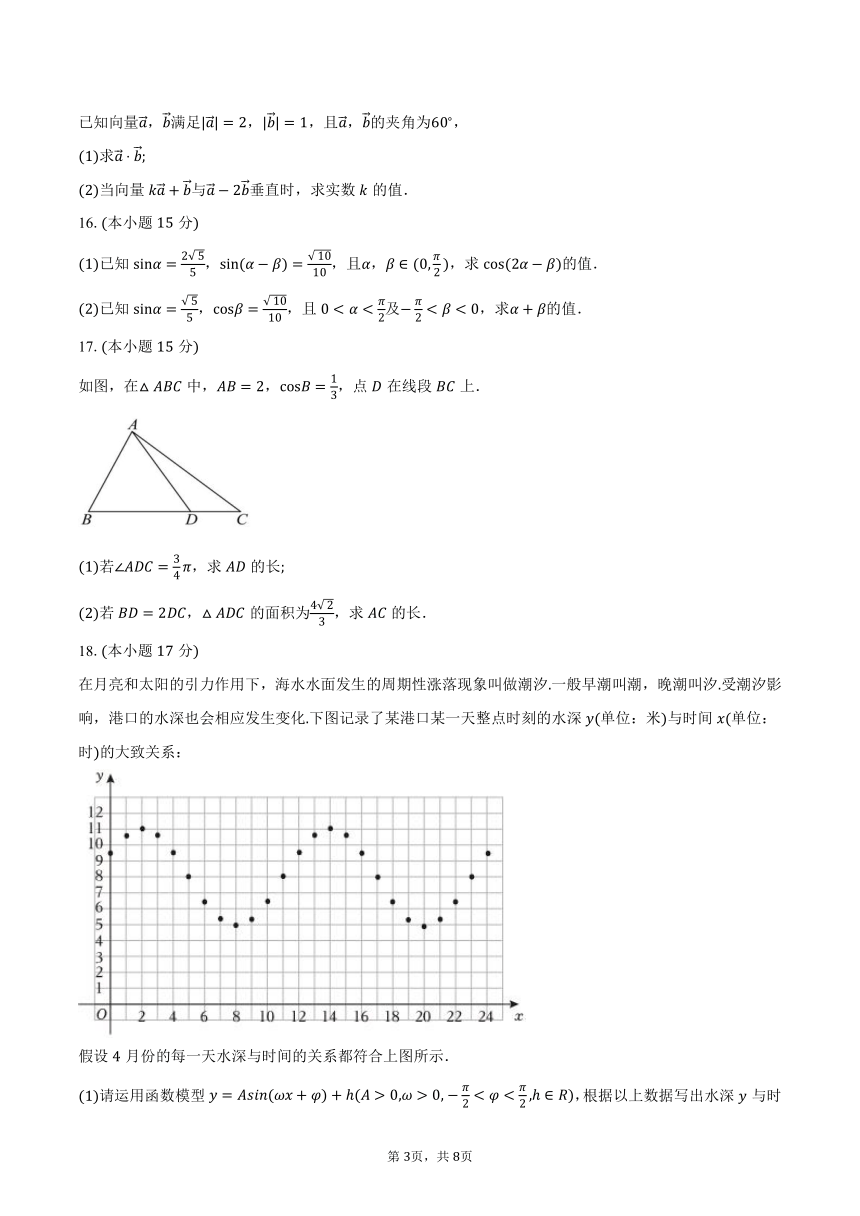
在月亮和太阳的引力作用下,海水水面发生的周期性涨落现象叫做潮汐一般早潮叫潮,晚潮叫汐受潮汐影响,港口的水深也会相应发生变化下图记录了某港口某一天整点时刻的水深单位:米与时间单位:时的大致关系:
假设月份的每一天水深与时间的关系都符合上图所示.
请运用函数模型,根据以上数据写出水深与时间的函数的近似表达式;
根据该港口的安全条例,要求船底与水底的距离必须不小于米,否则该船必须立即离港一艘船满载货物,吃水即船底到水面的距离米,计划明天进港卸货.
求该船可以进港的时间段;
该船今天会到达港口附近,明天点可以及时进港并立即开始卸货,已知卸货时吃水深度以每小时米的速度匀速减少,卸完货后空船吃水米请设计一个卸货方案,在保证严格遵守该港口安全条例的前提下,使该船明天尽早完成卸货不计停靠码头和驶离码头所需时间.
19.本小题分
已知为坐标原点,对于函数,称向量为函数的相伴特征向量,同时称函数为向量的相伴函数.
记向量的相伴函数为,若当且时,求的值;
设,试求函数的相伴特征向量,并求出与同向的单位向量;
已知为函数的相伴特征向量,若在中,,若点为该的外心,求的最大值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由已知得 ,
向量 与 垂直,
,
,
解得 .
16.解:由,可得,
由,可得,则,
,
解:由,可得,
由,则,
,
由于,故.
17.解:在 中, ,
在中,由正弦定理得 ,
又 ,
.
又 .
,
解得: ,
在 中,由余弦定理得 ,
所以 .
18.解:由图象得,则,
又,解得,,
根据一个最高点得,,解得,,
又,则,
函数;
由得,
又,即,即,解得,,
,,
故该船每天可以进港的时间段为时和时;
由题意得,即,解得,
故从点开始卸货到点,此时船已经卸货一半,驶出港口,等到点再次驶入港口进行卸货,直至卸完货.
19.解:根据题意知,
向量的相伴函数为
,
当时,
所以,
又,则,
所以,故;
因为
,
整理得到,
故函数的相伴特征向量,
则与同向的单位向量为
;
由题意得,,
在中,,
,所以,
设外接圆半径为,
根据正弦定理,,故,
所以,
,
,
代入可得,
所以当时,
取得最大值.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,则的虚部为( )
A. B. C. D.
2.在边长为的等边三角形中,的值为( )
A. B. C. D.
3.如图,在中,点是的中点,点是的中点,设,,那么( )
A. B. C. D.
4.已知非零空间向量,,且,,,则一定共线的三点是( )
A. ,, B. ,, C. ,, D. ,,
5.在中,角,,的对边分别为,,,若,则的形状为( )
A. 等边三角形 B. 直角三角形 C. 等腰三角形 D. 等腰或直角三角形
6.若,,则( )
A. B.
C. D.
7.在中,已知,,,,边上的两条中线,相交于点,则( )
A. B. C. D.
8.已知函数,对于任意的,都有恒成立,则关于的不等式的解集为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知复数满足,则( )
A. 为纯虚数 B. 对应的点在第四象限
C. D. 和是方程的两个根
10.设是三个非零向量,且相互不共线,则下列说法正确的是( )
A. 若,则
B. 若,则
C. 若,则不与垂直
D. 不与垂直
11.对于函数下列说法正确的是( )
A. 当时,函数在上有且只有一个零点
B. 若函数在单调递增,则的取值范围为
C. 若函数在时取得最小值,在时取得最大值,且,则
D. 将函数图象向左平移个单位得到的图象,若为偶函数,则的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.如图,,两点在河的两岸,在同侧的河岸边选取点,测得,,,则,两点间的距离为
13.将函数图象上所有点的纵坐标伸长为原来的倍,横坐标缩短为原来的,再将所得的图象向右平移个单位长度,得到函数的图象,则 .
14.在中,角,,的对边分别为,,已知,的平分线交于点,且,则的最小值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,满足,,且,的夹角为,
求
当向量与垂直时,求实数的值.
16.本小题分
已知,,且,,求的值.
已知,,且及,求的值.
17.本小题分
如图,在中,,,点在线段上.
若,求的长
若,的面积为,求的长.
18.本小题分
在月亮和太阳的引力作用下,海水水面发生的周期性涨落现象叫做潮汐一般早潮叫潮,晚潮叫汐受潮汐影响,港口的水深也会相应发生变化下图记录了某港口某一天整点时刻的水深单位:米与时间单位:时的大致关系:
假设月份的每一天水深与时间的关系都符合上图所示.
请运用函数模型,根据以上数据写出水深与时间的函数的近似表达式;
根据该港口的安全条例,要求船底与水底的距离必须不小于米,否则该船必须立即离港一艘船满载货物,吃水即船底到水面的距离米,计划明天进港卸货.
求该船可以进港的时间段;
该船今天会到达港口附近,明天点可以及时进港并立即开始卸货,已知卸货时吃水深度以每小时米的速度匀速减少,卸完货后空船吃水米请设计一个卸货方案,在保证严格遵守该港口安全条例的前提下,使该船明天尽早完成卸货不计停靠码头和驶离码头所需时间.
19.本小题分
已知为坐标原点,对于函数,称向量为函数的相伴特征向量,同时称函数为向量的相伴函数.
记向量的相伴函数为,若当且时,求的值;
设,试求函数的相伴特征向量,并求出与同向的单位向量;
已知为函数的相伴特征向量,若在中,,若点为该的外心,求的最大值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由已知得 ,
向量 与 垂直,
,
,
解得 .
16.解:由,可得,
由,可得,则,
,
解:由,可得,
由,则,
,
由于,故.
17.解:在 中, ,
在中,由正弦定理得 ,
又 ,
.
又 .
,
解得: ,
在 中,由余弦定理得 ,
所以 .
18.解:由图象得,则,
又,解得,,
根据一个最高点得,,解得,,
又,则,
函数;
由得,
又,即,即,解得,,
,,
故该船每天可以进港的时间段为时和时;
由题意得,即,解得,
故从点开始卸货到点,此时船已经卸货一半,驶出港口,等到点再次驶入港口进行卸货,直至卸完货.
19.解:根据题意知,
向量的相伴函数为
,
当时,
所以,
又,则,
所以,故;
因为
,
整理得到,
故函数的相伴特征向量,
则与同向的单位向量为
;
由题意得,,
在中,,
,所以,
设外接圆半径为,
根据正弦定理,,故,
所以,
,
,
代入可得,
所以当时,
取得最大值.
第1页,共1页
同课章节目录
