2025学年四年级数学下册三角形重难点突破练习(含答案)
文档属性
| 名称 | 2025学年四年级数学下册三角形重难点突破练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 21:04:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年小学四年级下册数学三角形重难点突破练习
1. 三角形定义:由3条线段围成(每相邻两条线段的端点相连)的图形。
2. 稳定性与高:三角形具有稳定性,从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高 ,一个三角形有3条高。
3. 三边关系:用于判断三条线段能否构成三角形。
任意两边之和大于第三边,
任意两边之差小于第三边,
即两边之差<第三边<两边之和 。
4. 按角分类
- 锐角三角形:三个角都是锐角的三角形。
- 直角三角形:有一个角是直角的三角形。
- 钝角三角形:有一个角是钝角的三角形。
- 一个三角形中至少有2个锐角,至多有1个直角。
5. 按边分类
- 不等边三角形:三条边都不相等的三角形。
- 等腰三角形:两条边相等的三角形 ,相等的两条边称为这个三角形的腰。
- 等边三角形:三条边都相等的三角形,也叫正三角形 ,它是特殊的等腰三角形,每个内角都是60°。
6. 内角和
- 三角形内角和是180° ,可通过多种方法验证,如剪拼法、折拼法等。
- 四边形可分成两个三角形,内角和是360° 。
7. 多边形内角和公式:(边数 - 2)×180°(必背) ,推导是从一个顶点出发,将多边形分成若干个三角形。
8. 实例分析:三根6厘米小棒摆成的三角形,三边相等是等边三角形,每个角60°,按角分是锐角三角形。
9. 等腰三角形性质:等腰三角形的两个底角相等 ,可通过全等三角形证明。
10. 五边形内角和:根据多边形内角和公式,(5 - 2)×180° = 540° 。
11. 图形拼接:至少用2个完全相同的等腰直角三角形,以斜边重合或直角边重合等方式可拼成正方形。
12. 角的限制:因为三角形内角和180°,直角是90°,钝角大于90°,所以一个三角形中不可能有两个钝(或直)角 。
13. 特殊三角形判断:三角形三个角都相等,每个角是180°÷3 = 60° ,是锐角三角形。
三角形的特性重难点突破
考点归纳:
专项练习
一、单选题
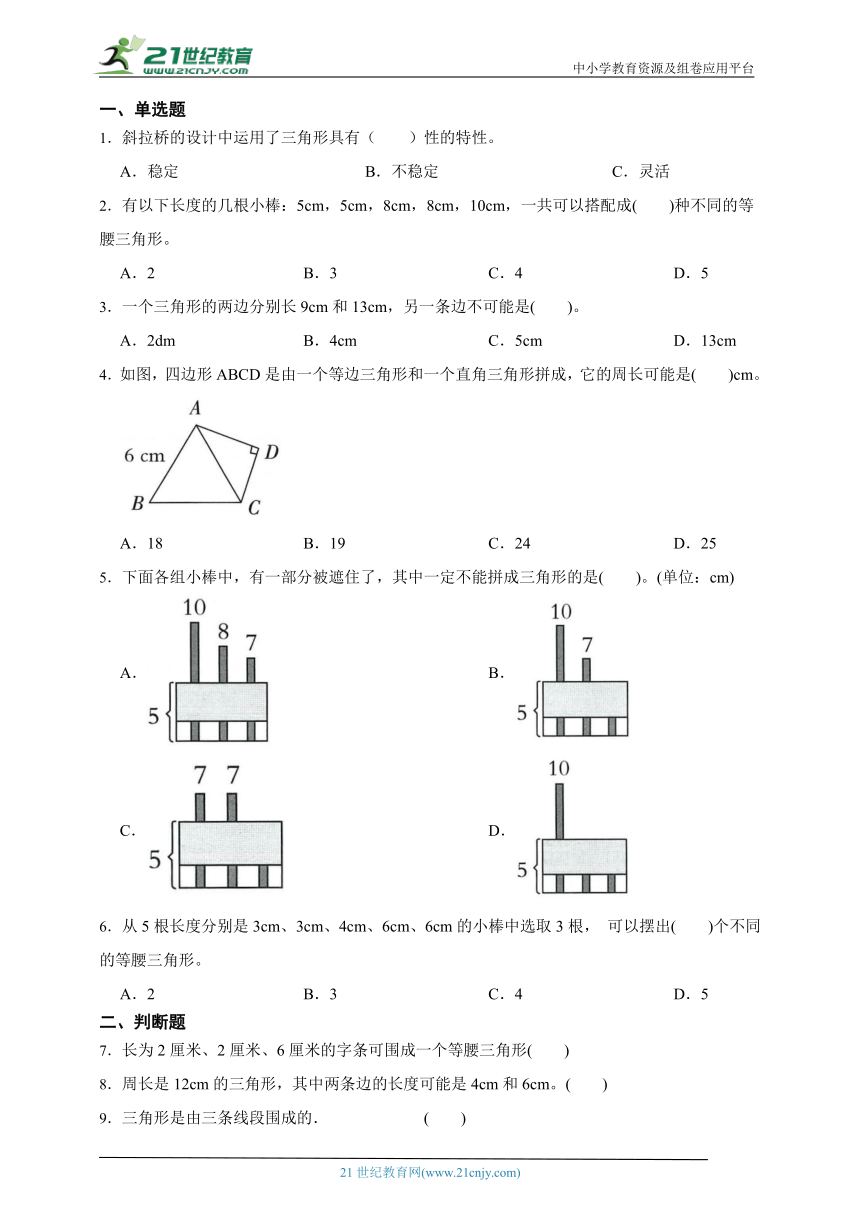
1.斜拉桥的设计中运用了三角形具有( )性的特性。
A.稳定 B.不稳定 C.灵活
2.有以下长度的几根小棒:5cm,5cm,8cm,8cm,10cm,一共可以搭配成( )种不同的等腰三角形。
A.2 B.3 C.4 D.5
3.一个三角形的两边分别长9cm和13cm,另一条边不可能是( )。
A.2dm B.4cm C.5cm D.13cm
4.如图,四边形ABCD是由一个等边三角形和一个直角三角形拼成,它的周长可能是( )cm。
A.18 B.19 C.24 D.25
5.下面各组小棒中,有一部分被遮住了,其中一定不能拼成三角形的是( )。(单位:cm)
A. B.
C. D.
6.从5根长度分别是3cm、3cm、4cm、6cm、6cm的小棒中选取3根, 可以摆出( )个不同的等腰三角形。
A.2 B.3 C.4 D.5
二、判断题
7.长为2厘米、2厘米、6厘米的字条可围成一个等腰三角形( )
8.周长是12cm的三角形,其中两条边的长度可能是4cm和6cm。( )
9.三角形是由三条线段围成的. ( )
10.三角形不一定都具有稳定性。( )
11.在梯形卡纸上一刀剪下一个平行四边形,剩下的部分一定是三角形。( )
三、填空题
12.已知三角形的两条边都是4m,那么它的第三条边最长是 m,最短是 m。(取整米数)
13.为了避免小温长时间低头看书,妈妈给她买了阅读支架,让她抬着头阅读,保护颈椎。如图,书本放在阅读支架上不晃动是运用了三角形具有 的特性。请再列举出两个应用到这个特性的例子: 、 。
14.如图,三角形ABC是 三角形。在三角形ABC中,直角边BC对应的高是 ,BD是 边对应的高。
15.在能拼成三角形的各组小棒后面画“√”,不能的画“×”。
(1)
(2)
(3)
16.如图,小杭从公园门口到荷花池有3 条路可走,走第 条路最近。
理由是: °
17.三角形具有 性,生活中自行车的三角架就是利用了这一特性。
四、计算题
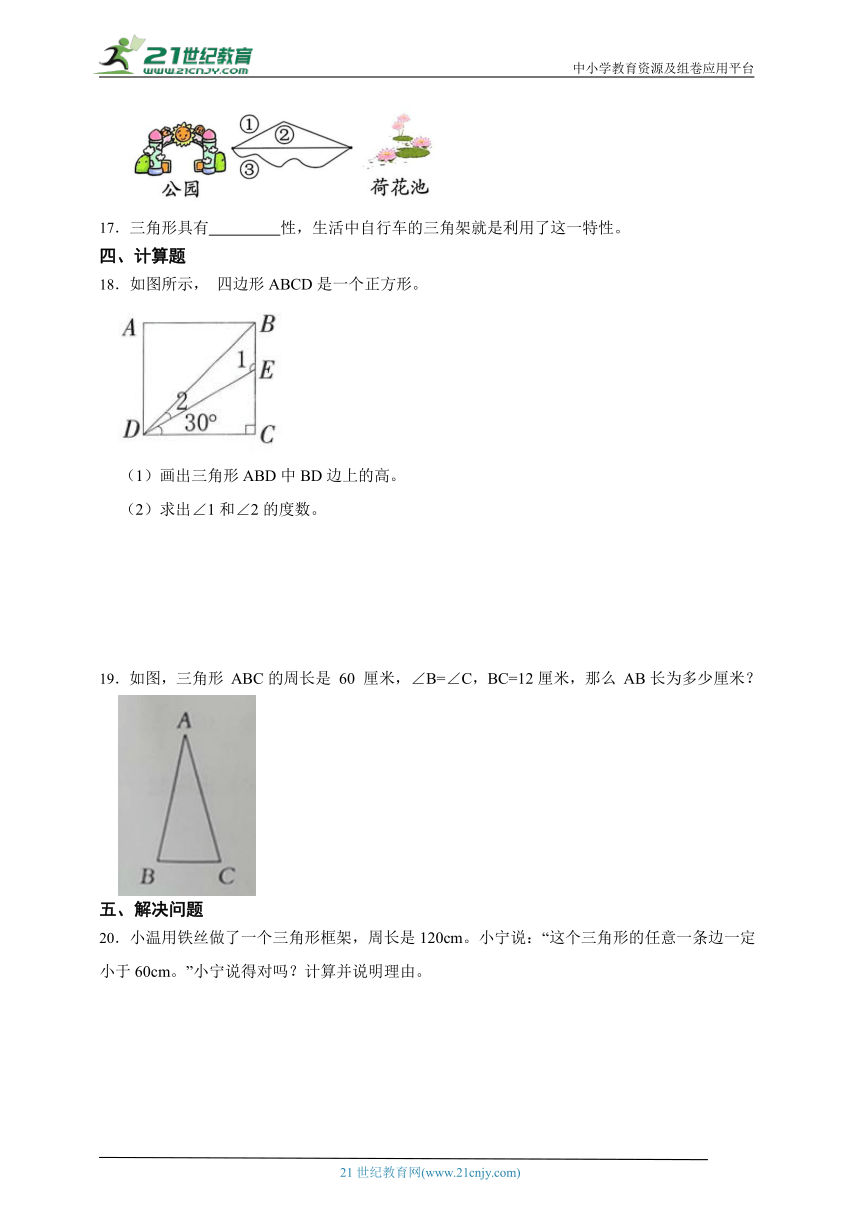
18.如图所示, 四边形ABCD是一个正方形。
(1)画出三角形ABD中BD边上的高。
(2)求出∠1和∠2的度数。
19.如图,三角形 ABC的周长是 60 厘米,∠B=∠C,BC=12厘米,那么 AB长为多少厘米?
五、解决问题
20.小温用铁丝做了一个三角形框架,周长是120cm。小宁说:“这个三角形的任意一条边一定小于60cm。”小宁说得对吗?计算并说明理由。
一个等腰三角形,其中两条边分别长3cm和8cm,这个三角形的周长是多少厘米?
六、综合题
22.
(1)上面三幅图中, 的设计应用了三角形的稳定性。
(2)在三角板中,如果以它的AC边为高,那么对应的底是 边。
(3)一只蜗牛要从A点爬到C点,请你为它设计一条最近的路线,并说明理由。
三角形的分类重难点练习
考点归纳:
专项练习
一、单选题
1.下面被遮住的三角形中,( )一定是锐角三角形。
A. B.
C. D.
2.乐乐有一个等腰三角形风筝,它的顶角是100°,底角是( )。
A.40° B.50° C.30° D.100°
3.三角形可以按角和边的特点进行分类。如果按边的特点分类,下面能表示它们之间关系的是图( )。
A. B.
C. D.
二、判断题
4.长为2厘米、2厘米、6厘米的字条可围成一个等腰三角形( )
5.三条8cm 长的线段可以围成一个三角形。 ( )
6.钝角三角形中两个锐角的和一定大于90°。( )
7. 一个等腰三角形的周长为16cm,其中一条边长为4cm,则该三角形的腰长为4cm或6cm。( )
三、填空题
8.下图是由一个等边三角形 ABD 和一个等腰三角形 ADC组成的大三角形 ABC,∠2= 度。
9.如图的线段表示0°到 ,一个三角形中两个内角度数之和在点A处,这个三角形按角分是 三角形。
10.如图,在方格纸上画三角形,保持三角形的顶点B、C不动,当顶点A向左平移 格时,原三角形变成直角三角形;当顶点A 向右平移 格时,原三角形变成钝角三角形。在两次变化后,三角形BC边上的高的长度 (填“变了”或“不变”)。
11.我国的空间引力波探测“天琴计划”,需要三颗卫星以极高的精度组成周长约为51万千米的等边三角形。组成的这个等边三角形的边长约为 万千米,它的每个内角是 °。
12.如图,三角形ABC是 三角形。在三角形ABC中,直角边BC对应的高是 ,BD是 边对应的高。
四、计算题
13.观察下图,求∠A 和∠B的度数。(单位: cm)
14.在三角形ABC中,∠A=a°,∠B的度数是∠A的2倍。
(1)用式子表示∠C的度数。
当∠A=30°时,求∠C的度数。这是一个什么三角形?
15.四边形ABCD是正方形,三角形CDE是等边三角形,∠AED的度数是多少?
五、解决问题
16.下面是一块三角形玻璃打碎后留下的碎片,你能判断出它原来是什么三角形吗?
17.小棒AC长14cm,小明将小棒从点B 截断,得到两根小棒AB、BC,量得AB长6cm。接着小明把其中一根小棒截成两根,现在一共是3根小棒,可围成一个等腰三角形。
(1)请你在图中用点“D”标出小明第二次截的位置。
(2)小明用3根小棒围成等腰三角形后,量得等腰三角形的顶角是,求这个三角形中一个底角的度数。
18.小阳画了一条线段表示0°到180°,并把它平均分成了四段。
(1)请在线段上标出直角、45°角的相应位置,并注明。
(2)点A 和点 B分别表示三角形ABC中两个角的度数,则这个三角形是( )三角形。请说明你这样判断的理由。
六、解答题
19.猜一猜下面的图形分别是什么三角形。
学完《三角形》这个单元后,小明说:“一个三角形,如果两个内角之和等于第一个内角,那么这个三角形一定是直角三角形。”你认为小明的说法对吗?请说明理由。
21.画一画,说一说。
(1)把下面的三角形分成两个三角形,且分出的两个三角形中有一个是等边三角形。
想一想,(1)中分出的另一个三角形是等腰三角形吗 请说说理由。
22.如下图,等边三角形内有一个等腰三角形,且∠1=∠2,∠3=∠4,那么∠5的度数是多少呢?
七、综合题
23.把下列三角形的序号填在相应的框里。
24.亮亮要做一个钝角三角形的风筝,已经准备好了两根0.8m长的竹条。
(1)第三根竹条长多少米能做成这个风筝 先圈出正确答案,再根据上面的软尺在“③”的后面画出第三根竹条。
0.8m 1.4m 1.6m
如果这个风筝的一个角是,那么另外两个角分别是 °和 °。
三角形的内角和重难点练习
考点归纳:
专项练习
1.强强想知道三角形ABC内角和的度数,下面拼法中正确的是( )。
A. B.
C. D.
2.直角三角形的内角和( )锐角三角形的内角和。
A.大于 B.小于 C.等于 D.无法确定
3.在三角形ABC中, ∠A=20°,∠B=40°, 这个三角形是( )。
A.等边三角形 B.钝角三角形 C.锐角三角形 D.直角三角形
4.用两个完全相同的三角形拼成一个大三角形,拼成的这个三角形内角和是( )。
A.90° B.180° C.270° D.360°
5.在一个三角形中,两个角的和小于 90°, 那么这个三角形一定是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
6.下面每组中的三个角可能在同一个三角形内的是( )。
A.55°、 78°、 102° B.80°、 15°、 60°
C.30°、 50°、 100° D.15°、 30°、 45°
7.如图,一张三角形纸片被撕去了一个角,原来这张纸片是( )三角形。
A.等腰 B.等边 C.直角 D.钝角
二、判断题
8.小明画了一个锐角三角形,其中两个角的度数分别是40°和30°.( )
9.一个三角形的最小内角是 48°,则这个三角形一定不是钝角三角形。( )
10.如果一个三角形的最小内角是 , 那么这个三角形一定是锐角三角形。( )
11.当三角形中两个内角的和等于第三个内角时,这是一个直角三角形。( )
三、填空题
12.如图的线段表示0°到 ,一个三角形中两个内角度数之和在点A处,这个三角形按角分是 三角形。
13.如图所示,一张三角形纸片被撕去了一个角,其中∠1=50°,∠2=65°,撕去的这个角是 °。原来这个三角形按角分是 三角形,按边分是 三角形。
14.如下图,∠A=30°,∠B=120°,则∠C= °。如果沿虚线剪下一个三角形,剩下部分图形的内角和是 °。
15.下图是一个等边三角形, 则∠1= °。
我是这样想的: (用算式表示)。
16.梯形的一条对角线把它分成 个三角形,每个三角形的内角和是 °,所以梯形的内角和是 °。
17.等边三角形每一个角都是 °。
四、计算题
18.求下面未知角的度数。
(1)
(3)
五、操作题
19.(1)画出下图三角形指定底边上的高。
(2)上图中∠1= 。
20.
(1)作出BC边上的高。
(2)按角分,这是一个 三角形。
(3)已知∠B=52°, ∠C= °。
(4)两个这样的三角形拼成一个新的三角形,新三角形的内角和是 °。
六、解决问题
21.将下表中的多边形分成三角形,再完成表格,回答问题。
(1)
图形 边数 内角和
( ) 180°×1
( ) 180°×( )
( ) 180°×( )
( ) 180°×( )
(2)我发现了:多边形的内角和等于 。
(3)根据上面的发现,计算出正十二边形的内角和的度数。
(4)一个多边形的内角和是1260°,这是一个几边形?
七、解答题
22.如图,∠1、∠2、∠3是三角形ABC的三个外角。这三个外角的度数之和是多少?
23.爸爸给明明买了一个等腰三角形的风筝。风筝的一个底角是65°,它的顶角是多少度?
24.
三角形的特性重难点答案解析部分
1.【答案】A
【知识点】三角形的稳定性及应用
2.【答案】B
【知识点】三角形的特点;等腰三角形认识及特征
3.【答案】B
【知识点】三角形的特点
4.【答案】B
【知识点】三角形的特点;三角形的周长
5.【答案】D
【知识点】三角形的特点
6.【答案】B
【知识点】三角形的特点
7.【答案】错误
【知识点】三角形的特点;等腰三角形认识及特征
8.【答案】错误
【知识点】三角形的特点;三角形的周长
9.【答案】错误
【知识点】三角形的特点
10.【答案】错误
【知识点】三角形的稳定性及应用
11.【答案】错误
【知识点】三角形的特点;平行四边形的特征及性质;梯形的特征及分类;平面图形的切拼
12.【答案】7;1
【知识点】三角形的特点
13.【答案】稳定性;篮球架;斜拉桥
【知识点】三角形的稳定性及应用
14.【答案】直角;AB;AC
【知识点】三角形高的特点及画法;三角形的分类
15.【答案】(1)×
(2)√
(3)×
【知识点】三角形的特点
16.【答案】②;两点间的所有连线中线段最短
【知识点】三角形的特点
17.【答案】稳定
【知识点】三角形的稳定性及应用
18.【答案】(1)解:
(2)
【知识点】三角形高的特点及画法;三角形的内角和
19.【答案】解:(60-12)÷2
=48÷2
=24(厘米)
答:AB长为24厘米。
【知识点】三角形的特点;三角形的周长
20.【答案】解:120÷2=60(cm)
答:小宁说得对。三角形任意两边的和大于第三边,这个三角形的周长是120cm,所以它的任意一条边一定小于周长的一半,也就是60cm。
【知识点】三角形的特点;三角形的周长
21.【答案】解:3+3<8,腰长3厘米排除
3+8+8=19(cm)
答:这个三角形的周长是19厘米。
【知识点】三角形的特点;三角形的周长
22.【答案】(1)篱笆
(2)BC
(3)答:路线为线段AC,因为两点之间线段最短。
【知识点】两点间的距离及应用;三角形的稳定性及应用
三角形的分类重难点答案解析部分
1.【答案】D
2.【答案】A
3.【答案】C
4.【答案】错误
5.【答案】正确
6.【答案】错误
7.【答案】错误
8.【答案】30
9.【答案】钝角
10.【答案】2;3;不变
11.【答案】17;60
12.【答案】直角;AB;AC
13.【答案】解:由图可知三角形 BCD 是等边三角形,所以∠B=60° ,∠CDB=60°,
所以∠CDA=120°,
所以∠A=(180°-120°)÷2=60°÷2=30°
答:∠A=30°,∠B=60°。
14.【答案】(1)解:∠B=2a°
a+2a=3a°
∠C=180°-3a°
(2)解:180°-30°×3
=180°-90°
=90°
答:∠C的度数90°,这是一个直角三角形。
15.【答案】解:(180°- 90°-60°)÷2
=30°÷2
=15°
16.【答案】解:
答:原来是钝角三角形。
17.【答案】(1)解:
(2)解:(180°-18°)÷2
=162°÷2
=81°
答:这个三角形中一个底角的度数是81°。
18.【答案】(1)解:。
(2)解:这个三角形是锐角三角形。
理由:∠A 和∠B 都是大于 45°的锐角,∠A+∠B>90°; 根据三角形内角和是180°,第三个角的度数小于 90°,也是锐角。所以三角形ABC是锐角三角形。
19.【答案】解:钝角三角形
直角三角形
锐角三角形、直角三角形或钝角三角形。
20.【答案】解:两个内角和是第一个内角,所以内角和180度是第一个内角度数的两倍。
所以180÷2=90(度)
答:小明的说法正确,因为两个内角的和等于第三个内角,那么第三个内角的度数是180度除以2,即90度,所以一定是直角三角形。
21.【答案】(1)解:
(2)解:(1)中分出的另一个三角形是等腰三角形,理由:
∠1=90°-60°=30°,
另一个三角形中有两个角都是30°,这个三角形是等腰三角形。
22.【答案】解:等边三角形的内角都是60°,
因为∠1=∠2,∠3=∠4,所以∠2=30°,∠3=30°
∠5=180°-∠2-∠3=180°-30°-30°=120°
答:∠5=120°。
23.【答案】解:
24.【答案】(1)解:0.8-0.8<三角形第三边的取值范围<0.8+0.8
0<三角形第三边的取值范围<1.6
第三根竹条长0.8米,做成的是锐角三角形,长1.4米,做成的是钝角三角形,长1.6米,做不成三角形;
(2)30;30
三角形的内角和答案解析部分
1.【答案】D
【知识点】三角形的内角和
2.【答案】C
【知识点】三角形的内角和
3.【答案】B
【知识点】三角形的分类;三角形的内角和
4.【答案】B
【知识点】三角形的内角和
5.【答案】C
【知识点】三角形的分类;三角形的内角和
6.【答案】C
【知识点】三角形的内角和
7.【答案】A
【知识点】三角形的分类;三角形的内角和
8.【答案】错误
【知识点】三角形的内角和
9.【答案】正确
【知识点】三角形的分类;三角形的内角和
10.【答案】正确
【知识点】三角形的分类;三角形的内角和
11.【答案】正确
【知识点】三角形的分类;三角形的内角和
12.【答案】钝角
【知识点】三角形的分类;三角形的内角和
13.【答案】65;锐角;等腰
【知识点】角的度量(计算);三角形的分类;等腰三角形认识及特征;三角形的内角和
14.【答案】30;360
【知识点】三角形的内角和;四边形的内角和
15.【答案】30;180°-90°-60°=30°
【知识点】三角形的内角和
16.【答案】2;180;360
【知识点】三角形的内角和;四边形的内角和
17.【答案】60
【知识点】等边三角形认识及特征;三角形的内角和
18.【答案】(1)解:
(2)解:
(3)解:
【知识点】角的度量(计算);三角形的内角和
19.【答案】(1)解:
(2)30
【知识点】三角形高的特点及画法;三角形的内角和
20.【答案】(1)解:。
(2)直角
(3)38
(4)180
【知识点】三角形高的特点及画法;三角形的分类;三角形的内角和
21.【答案】(1)解:
图形 边数 内角和
3 180°×1
4 180°×2
5 180°×3
6 180°×4
(2)180°×(边数-2)
(3)解:180°×(12-2)
=180°×10
=1800°
(4)解:1260°÷180°+2
=7+2
=9(边)
答:这是一个九边形。
【知识点】三角形的内角和;四边形的内角和;多边形的内角和
22.【答案】解:∠1+∠4=180°
∠2+∠5=180°
∠3+∠6=180°
180°×3=540°
因为三角形的内角和是180°,
所以∠1、∠2、∠3三个角的度数和是180°
540°-180°=360°
答:这三个外角的度数之和是360°。
【知识点】平角、周角的特征;三角形的内角和
23.【答案】解:180°-65°-65°=50°
答:它的顶角是50°。
【知识点】三角形的内角和
24.【答案】解:180°-44°-68°=68°
答:被剪掉的这个角是68度。
【知识点】三角形的内角和
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年小学四年级下册数学三角形重难点突破练习
1. 三角形定义:由3条线段围成(每相邻两条线段的端点相连)的图形。
2. 稳定性与高:三角形具有稳定性,从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高 ,一个三角形有3条高。
3. 三边关系:用于判断三条线段能否构成三角形。
任意两边之和大于第三边,
任意两边之差小于第三边,
即两边之差<第三边<两边之和 。
4. 按角分类
- 锐角三角形:三个角都是锐角的三角形。
- 直角三角形:有一个角是直角的三角形。
- 钝角三角形:有一个角是钝角的三角形。
- 一个三角形中至少有2个锐角,至多有1个直角。
5. 按边分类
- 不等边三角形:三条边都不相等的三角形。
- 等腰三角形:两条边相等的三角形 ,相等的两条边称为这个三角形的腰。
- 等边三角形:三条边都相等的三角形,也叫正三角形 ,它是特殊的等腰三角形,每个内角都是60°。
6. 内角和
- 三角形内角和是180° ,可通过多种方法验证,如剪拼法、折拼法等。
- 四边形可分成两个三角形,内角和是360° 。
7. 多边形内角和公式:(边数 - 2)×180°(必背) ,推导是从一个顶点出发,将多边形分成若干个三角形。
8. 实例分析:三根6厘米小棒摆成的三角形,三边相等是等边三角形,每个角60°,按角分是锐角三角形。
9. 等腰三角形性质:等腰三角形的两个底角相等 ,可通过全等三角形证明。
10. 五边形内角和:根据多边形内角和公式,(5 - 2)×180° = 540° 。
11. 图形拼接:至少用2个完全相同的等腰直角三角形,以斜边重合或直角边重合等方式可拼成正方形。
12. 角的限制:因为三角形内角和180°,直角是90°,钝角大于90°,所以一个三角形中不可能有两个钝(或直)角 。
13. 特殊三角形判断:三角形三个角都相等,每个角是180°÷3 = 60° ,是锐角三角形。
三角形的特性重难点突破
考点归纳:
专项练习
一、单选题
1.斜拉桥的设计中运用了三角形具有( )性的特性。
A.稳定 B.不稳定 C.灵活
2.有以下长度的几根小棒:5cm,5cm,8cm,8cm,10cm,一共可以搭配成( )种不同的等腰三角形。
A.2 B.3 C.4 D.5
3.一个三角形的两边分别长9cm和13cm,另一条边不可能是( )。
A.2dm B.4cm C.5cm D.13cm
4.如图,四边形ABCD是由一个等边三角形和一个直角三角形拼成,它的周长可能是( )cm。
A.18 B.19 C.24 D.25
5.下面各组小棒中,有一部分被遮住了,其中一定不能拼成三角形的是( )。(单位:cm)
A. B.
C. D.
6.从5根长度分别是3cm、3cm、4cm、6cm、6cm的小棒中选取3根, 可以摆出( )个不同的等腰三角形。
A.2 B.3 C.4 D.5
二、判断题
7.长为2厘米、2厘米、6厘米的字条可围成一个等腰三角形( )
8.周长是12cm的三角形,其中两条边的长度可能是4cm和6cm。( )
9.三角形是由三条线段围成的. ( )
10.三角形不一定都具有稳定性。( )
11.在梯形卡纸上一刀剪下一个平行四边形,剩下的部分一定是三角形。( )
三、填空题
12.已知三角形的两条边都是4m,那么它的第三条边最长是 m,最短是 m。(取整米数)
13.为了避免小温长时间低头看书,妈妈给她买了阅读支架,让她抬着头阅读,保护颈椎。如图,书本放在阅读支架上不晃动是运用了三角形具有 的特性。请再列举出两个应用到这个特性的例子: 、 。
14.如图,三角形ABC是 三角形。在三角形ABC中,直角边BC对应的高是 ,BD是 边对应的高。
15.在能拼成三角形的各组小棒后面画“√”,不能的画“×”。
(1)
(2)
(3)
16.如图,小杭从公园门口到荷花池有3 条路可走,走第 条路最近。
理由是: °
17.三角形具有 性,生活中自行车的三角架就是利用了这一特性。
四、计算题
18.如图所示, 四边形ABCD是一个正方形。
(1)画出三角形ABD中BD边上的高。
(2)求出∠1和∠2的度数。
19.如图,三角形 ABC的周长是 60 厘米,∠B=∠C,BC=12厘米,那么 AB长为多少厘米?
五、解决问题
20.小温用铁丝做了一个三角形框架,周长是120cm。小宁说:“这个三角形的任意一条边一定小于60cm。”小宁说得对吗?计算并说明理由。
一个等腰三角形,其中两条边分别长3cm和8cm,这个三角形的周长是多少厘米?
六、综合题
22.
(1)上面三幅图中, 的设计应用了三角形的稳定性。
(2)在三角板中,如果以它的AC边为高,那么对应的底是 边。
(3)一只蜗牛要从A点爬到C点,请你为它设计一条最近的路线,并说明理由。
三角形的分类重难点练习
考点归纳:
专项练习
一、单选题
1.下面被遮住的三角形中,( )一定是锐角三角形。
A. B.
C. D.
2.乐乐有一个等腰三角形风筝,它的顶角是100°,底角是( )。
A.40° B.50° C.30° D.100°
3.三角形可以按角和边的特点进行分类。如果按边的特点分类,下面能表示它们之间关系的是图( )。
A. B.
C. D.
二、判断题
4.长为2厘米、2厘米、6厘米的字条可围成一个等腰三角形( )
5.三条8cm 长的线段可以围成一个三角形。 ( )
6.钝角三角形中两个锐角的和一定大于90°。( )
7. 一个等腰三角形的周长为16cm,其中一条边长为4cm,则该三角形的腰长为4cm或6cm。( )
三、填空题
8.下图是由一个等边三角形 ABD 和一个等腰三角形 ADC组成的大三角形 ABC,∠2= 度。
9.如图的线段表示0°到 ,一个三角形中两个内角度数之和在点A处,这个三角形按角分是 三角形。
10.如图,在方格纸上画三角形,保持三角形的顶点B、C不动,当顶点A向左平移 格时,原三角形变成直角三角形;当顶点A 向右平移 格时,原三角形变成钝角三角形。在两次变化后,三角形BC边上的高的长度 (填“变了”或“不变”)。
11.我国的空间引力波探测“天琴计划”,需要三颗卫星以极高的精度组成周长约为51万千米的等边三角形。组成的这个等边三角形的边长约为 万千米,它的每个内角是 °。
12.如图,三角形ABC是 三角形。在三角形ABC中,直角边BC对应的高是 ,BD是 边对应的高。
四、计算题
13.观察下图,求∠A 和∠B的度数。(单位: cm)
14.在三角形ABC中,∠A=a°,∠B的度数是∠A的2倍。
(1)用式子表示∠C的度数。
当∠A=30°时,求∠C的度数。这是一个什么三角形?
15.四边形ABCD是正方形,三角形CDE是等边三角形,∠AED的度数是多少?
五、解决问题
16.下面是一块三角形玻璃打碎后留下的碎片,你能判断出它原来是什么三角形吗?
17.小棒AC长14cm,小明将小棒从点B 截断,得到两根小棒AB、BC,量得AB长6cm。接着小明把其中一根小棒截成两根,现在一共是3根小棒,可围成一个等腰三角形。
(1)请你在图中用点“D”标出小明第二次截的位置。
(2)小明用3根小棒围成等腰三角形后,量得等腰三角形的顶角是,求这个三角形中一个底角的度数。
18.小阳画了一条线段表示0°到180°,并把它平均分成了四段。
(1)请在线段上标出直角、45°角的相应位置,并注明。
(2)点A 和点 B分别表示三角形ABC中两个角的度数,则这个三角形是( )三角形。请说明你这样判断的理由。
六、解答题
19.猜一猜下面的图形分别是什么三角形。
学完《三角形》这个单元后,小明说:“一个三角形,如果两个内角之和等于第一个内角,那么这个三角形一定是直角三角形。”你认为小明的说法对吗?请说明理由。
21.画一画,说一说。
(1)把下面的三角形分成两个三角形,且分出的两个三角形中有一个是等边三角形。
想一想,(1)中分出的另一个三角形是等腰三角形吗 请说说理由。
22.如下图,等边三角形内有一个等腰三角形,且∠1=∠2,∠3=∠4,那么∠5的度数是多少呢?
七、综合题
23.把下列三角形的序号填在相应的框里。
24.亮亮要做一个钝角三角形的风筝,已经准备好了两根0.8m长的竹条。
(1)第三根竹条长多少米能做成这个风筝 先圈出正确答案,再根据上面的软尺在“③”的后面画出第三根竹条。
0.8m 1.4m 1.6m
如果这个风筝的一个角是,那么另外两个角分别是 °和 °。
三角形的内角和重难点练习
考点归纳:
专项练习
1.强强想知道三角形ABC内角和的度数,下面拼法中正确的是( )。
A. B.
C. D.
2.直角三角形的内角和( )锐角三角形的内角和。
A.大于 B.小于 C.等于 D.无法确定
3.在三角形ABC中, ∠A=20°,∠B=40°, 这个三角形是( )。
A.等边三角形 B.钝角三角形 C.锐角三角形 D.直角三角形
4.用两个完全相同的三角形拼成一个大三角形,拼成的这个三角形内角和是( )。
A.90° B.180° C.270° D.360°
5.在一个三角形中,两个角的和小于 90°, 那么这个三角形一定是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
6.下面每组中的三个角可能在同一个三角形内的是( )。
A.55°、 78°、 102° B.80°、 15°、 60°
C.30°、 50°、 100° D.15°、 30°、 45°
7.如图,一张三角形纸片被撕去了一个角,原来这张纸片是( )三角形。
A.等腰 B.等边 C.直角 D.钝角
二、判断题
8.小明画了一个锐角三角形,其中两个角的度数分别是40°和30°.( )
9.一个三角形的最小内角是 48°,则这个三角形一定不是钝角三角形。( )
10.如果一个三角形的最小内角是 , 那么这个三角形一定是锐角三角形。( )
11.当三角形中两个内角的和等于第三个内角时,这是一个直角三角形。( )
三、填空题
12.如图的线段表示0°到 ,一个三角形中两个内角度数之和在点A处,这个三角形按角分是 三角形。
13.如图所示,一张三角形纸片被撕去了一个角,其中∠1=50°,∠2=65°,撕去的这个角是 °。原来这个三角形按角分是 三角形,按边分是 三角形。
14.如下图,∠A=30°,∠B=120°,则∠C= °。如果沿虚线剪下一个三角形,剩下部分图形的内角和是 °。
15.下图是一个等边三角形, 则∠1= °。
我是这样想的: (用算式表示)。
16.梯形的一条对角线把它分成 个三角形,每个三角形的内角和是 °,所以梯形的内角和是 °。
17.等边三角形每一个角都是 °。
四、计算题
18.求下面未知角的度数。
(1)
(3)
五、操作题
19.(1)画出下图三角形指定底边上的高。
(2)上图中∠1= 。
20.
(1)作出BC边上的高。
(2)按角分,这是一个 三角形。
(3)已知∠B=52°, ∠C= °。
(4)两个这样的三角形拼成一个新的三角形,新三角形的内角和是 °。
六、解决问题
21.将下表中的多边形分成三角形,再完成表格,回答问题。
(1)
图形 边数 内角和
( ) 180°×1
( ) 180°×( )
( ) 180°×( )
( ) 180°×( )
(2)我发现了:多边形的内角和等于 。
(3)根据上面的发现,计算出正十二边形的内角和的度数。
(4)一个多边形的内角和是1260°,这是一个几边形?
七、解答题
22.如图,∠1、∠2、∠3是三角形ABC的三个外角。这三个外角的度数之和是多少?
23.爸爸给明明买了一个等腰三角形的风筝。风筝的一个底角是65°,它的顶角是多少度?
24.
三角形的特性重难点答案解析部分
1.【答案】A
【知识点】三角形的稳定性及应用
2.【答案】B
【知识点】三角形的特点;等腰三角形认识及特征
3.【答案】B
【知识点】三角形的特点
4.【答案】B
【知识点】三角形的特点;三角形的周长
5.【答案】D
【知识点】三角形的特点
6.【答案】B
【知识点】三角形的特点
7.【答案】错误
【知识点】三角形的特点;等腰三角形认识及特征
8.【答案】错误
【知识点】三角形的特点;三角形的周长
9.【答案】错误
【知识点】三角形的特点
10.【答案】错误
【知识点】三角形的稳定性及应用
11.【答案】错误
【知识点】三角形的特点;平行四边形的特征及性质;梯形的特征及分类;平面图形的切拼
12.【答案】7;1
【知识点】三角形的特点
13.【答案】稳定性;篮球架;斜拉桥
【知识点】三角形的稳定性及应用
14.【答案】直角;AB;AC
【知识点】三角形高的特点及画法;三角形的分类
15.【答案】(1)×
(2)√
(3)×
【知识点】三角形的特点
16.【答案】②;两点间的所有连线中线段最短
【知识点】三角形的特点
17.【答案】稳定
【知识点】三角形的稳定性及应用
18.【答案】(1)解:
(2)
【知识点】三角形高的特点及画法;三角形的内角和
19.【答案】解:(60-12)÷2
=48÷2
=24(厘米)
答:AB长为24厘米。
【知识点】三角形的特点;三角形的周长
20.【答案】解:120÷2=60(cm)
答:小宁说得对。三角形任意两边的和大于第三边,这个三角形的周长是120cm,所以它的任意一条边一定小于周长的一半,也就是60cm。
【知识点】三角形的特点;三角形的周长
21.【答案】解:3+3<8,腰长3厘米排除
3+8+8=19(cm)
答:这个三角形的周长是19厘米。
【知识点】三角形的特点;三角形的周长
22.【答案】(1)篱笆
(2)BC
(3)答:路线为线段AC,因为两点之间线段最短。
【知识点】两点间的距离及应用;三角形的稳定性及应用
三角形的分类重难点答案解析部分
1.【答案】D
2.【答案】A
3.【答案】C
4.【答案】错误
5.【答案】正确
6.【答案】错误
7.【答案】错误
8.【答案】30
9.【答案】钝角
10.【答案】2;3;不变
11.【答案】17;60
12.【答案】直角;AB;AC
13.【答案】解:由图可知三角形 BCD 是等边三角形,所以∠B=60° ,∠CDB=60°,
所以∠CDA=120°,
所以∠A=(180°-120°)÷2=60°÷2=30°
答:∠A=30°,∠B=60°。
14.【答案】(1)解:∠B=2a°
a+2a=3a°
∠C=180°-3a°
(2)解:180°-30°×3
=180°-90°
=90°
答:∠C的度数90°,这是一个直角三角形。
15.【答案】解:(180°- 90°-60°)÷2
=30°÷2
=15°
16.【答案】解:
答:原来是钝角三角形。
17.【答案】(1)解:
(2)解:(180°-18°)÷2
=162°÷2
=81°
答:这个三角形中一个底角的度数是81°。
18.【答案】(1)解:。
(2)解:这个三角形是锐角三角形。
理由:∠A 和∠B 都是大于 45°的锐角,∠A+∠B>90°; 根据三角形内角和是180°,第三个角的度数小于 90°,也是锐角。所以三角形ABC是锐角三角形。
19.【答案】解:钝角三角形
直角三角形
锐角三角形、直角三角形或钝角三角形。
20.【答案】解:两个内角和是第一个内角,所以内角和180度是第一个内角度数的两倍。
所以180÷2=90(度)
答:小明的说法正确,因为两个内角的和等于第三个内角,那么第三个内角的度数是180度除以2,即90度,所以一定是直角三角形。
21.【答案】(1)解:
(2)解:(1)中分出的另一个三角形是等腰三角形,理由:
∠1=90°-60°=30°,
另一个三角形中有两个角都是30°,这个三角形是等腰三角形。
22.【答案】解:等边三角形的内角都是60°,
因为∠1=∠2,∠3=∠4,所以∠2=30°,∠3=30°
∠5=180°-∠2-∠3=180°-30°-30°=120°
答:∠5=120°。
23.【答案】解:
24.【答案】(1)解:0.8-0.8<三角形第三边的取值范围<0.8+0.8
0<三角形第三边的取值范围<1.6
第三根竹条长0.8米,做成的是锐角三角形,长1.4米,做成的是钝角三角形,长1.6米,做不成三角形;
(2)30;30
三角形的内角和答案解析部分
1.【答案】D
【知识点】三角形的内角和
2.【答案】C
【知识点】三角形的内角和
3.【答案】B
【知识点】三角形的分类;三角形的内角和
4.【答案】B
【知识点】三角形的内角和
5.【答案】C
【知识点】三角形的分类;三角形的内角和
6.【答案】C
【知识点】三角形的内角和
7.【答案】A
【知识点】三角形的分类;三角形的内角和
8.【答案】错误
【知识点】三角形的内角和
9.【答案】正确
【知识点】三角形的分类;三角形的内角和
10.【答案】正确
【知识点】三角形的分类;三角形的内角和
11.【答案】正确
【知识点】三角形的分类;三角形的内角和
12.【答案】钝角
【知识点】三角形的分类;三角形的内角和
13.【答案】65;锐角;等腰
【知识点】角的度量(计算);三角形的分类;等腰三角形认识及特征;三角形的内角和
14.【答案】30;360
【知识点】三角形的内角和;四边形的内角和
15.【答案】30;180°-90°-60°=30°
【知识点】三角形的内角和
16.【答案】2;180;360
【知识点】三角形的内角和;四边形的内角和
17.【答案】60
【知识点】等边三角形认识及特征;三角形的内角和
18.【答案】(1)解:
(2)解:
(3)解:
【知识点】角的度量(计算);三角形的内角和
19.【答案】(1)解:
(2)30
【知识点】三角形高的特点及画法;三角形的内角和
20.【答案】(1)解:。
(2)直角
(3)38
(4)180
【知识点】三角形高的特点及画法;三角形的分类;三角形的内角和
21.【答案】(1)解:
图形 边数 内角和
3 180°×1
4 180°×2
5 180°×3
6 180°×4
(2)180°×(边数-2)
(3)解:180°×(12-2)
=180°×10
=1800°
(4)解:1260°÷180°+2
=7+2
=9(边)
答:这是一个九边形。
【知识点】三角形的内角和;四边形的内角和;多边形的内角和
22.【答案】解:∠1+∠4=180°
∠2+∠5=180°
∠3+∠6=180°
180°×3=540°
因为三角形的内角和是180°,
所以∠1、∠2、∠3三个角的度数和是180°
540°-180°=360°
答:这三个外角的度数之和是360°。
【知识点】平角、周角的特征;三角形的内角和
23.【答案】解:180°-65°-65°=50°
答:它的顶角是50°。
【知识点】三角形的内角和
24.【答案】解:180°-44°-68°=68°
答:被剪掉的这个角是68度。
【知识点】三角形的内角和
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
