江苏省扬州市梅岭集团2024-2025学年八年级下学期4月期中考试数学试题(图片版,无答案)
文档属性
| 名称 | 江苏省扬州市梅岭集团2024-2025学年八年级下学期4月期中考试数学试题(图片版,无答案) | 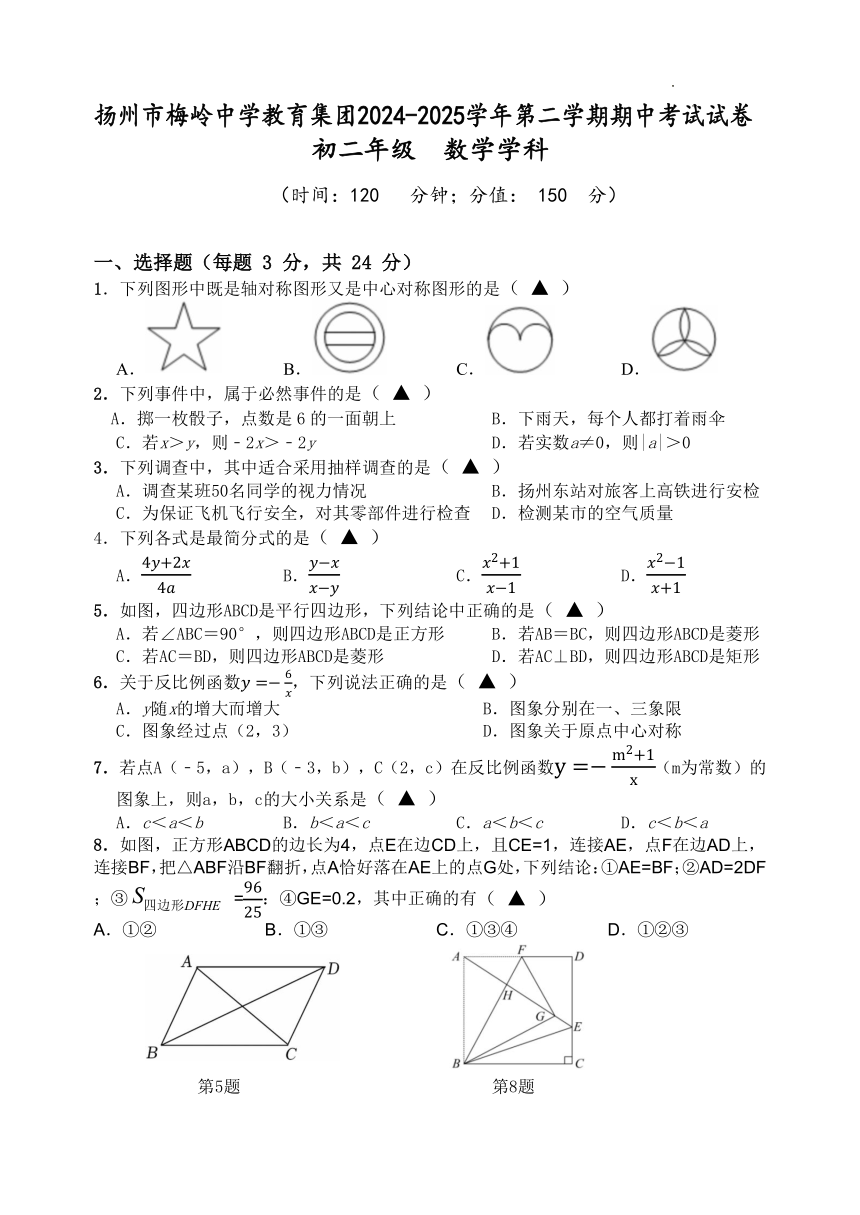 | |
| 格式 | |||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 21:05:20 | ||
图片预览


文档简介
扬州市梅岭中学教育集团2024-2025学年第二学期期中考试试卷
初二年级 数学学科
(时间:120 分钟;分值: 150 分)
一、选择题(每题 3 分,共 24 分)
1.下列图形中既是轴对称图形又是中心对称图形的是( ▲ )
A. B. C. D.
2.下列事件中,属于必然事件的是( ▲ )
A.掷一枚骰子,点数是 6 的一面朝上 B.下雨天,每个人都打着雨伞
C.若x>y,则﹣2x>﹣2y D.若实数a≠0,则|a|>0
3.下列调查中,其中适合采用抽样调查的是( ▲ )
A.调查某班50名同学的视力情况 B.扬州东站对旅客上高铁进行安检
C.为保证飞机飞行安全,对其零部件进行检查 D.检测某市的空气质量
4.下列各式是最简分式的是( ▲ )
4 +2 2+1 2 1
A. B. C. D.
4 1 +1
5.如图,四边形ABCD是平行四边形,下列结论中正确的是( ▲ )
A.若∠ABC=90°,则四边形ABCD是正方形 B.若AB=BC,则四边形ABCD是菱形
C.若AC=BD,则四边形ABCD是菱形 D.若AC⊥BD,则四边形ABCD是矩形
6.关于反比例函数 = 6,下列说法正确的是( ▲ )
A.y随x的增大而增大 B.图象分别在一、三象限
C.图象经过点(2,3) D.图象关于原点中心对称
m2+1
7.若点A(﹣5,a),B(﹣3,b),C(2,c)在反比例函数y = (m为常数)的
x
图象上,则a,b,c的大小关系是( ▲ )
A.c<a<b B.b<a<c C.a<b<c D.c<b<a
8.如图,正方形ABCD的边长为4,点E在边CD上,且CE=1,连接AE,点F在边AD上,
连接BF,把△ABF沿BF翻折,点A恰好落在AE上的点G处,下列结论:①AE=BF;②AD=2DF
;③ S 96四边形DFHE = :④GE=0.2,其中正确的有( ▲ )25
A.①② B.①③ C.①③④ D.①②③
第5题 第8题
(北京)股份有限公司
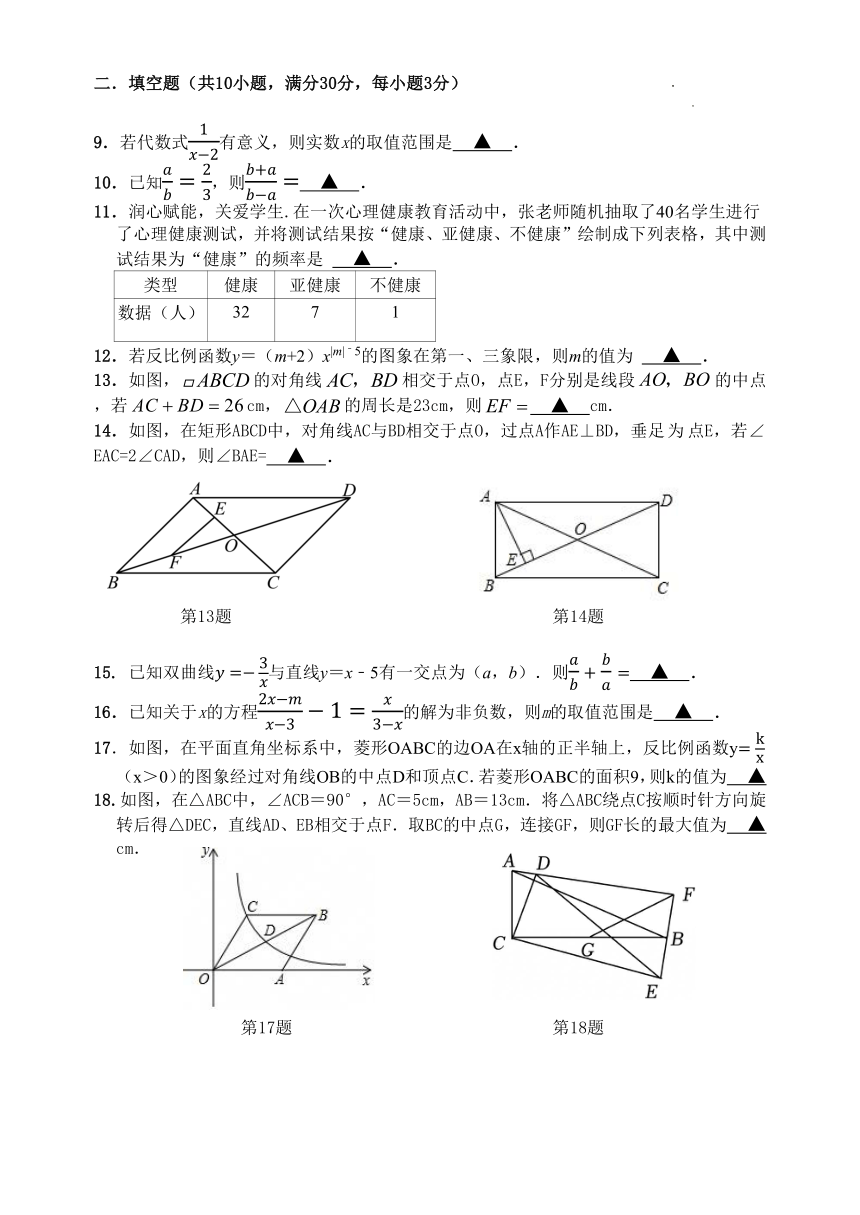
二.填空题(共10小题,满分30分,每小题3分)
1
9.若代数式 有意义,则实数x的取值范围是 ▲ .
2
= 2 + 10.已知 ,则 = ▲ .
3
11.润心赋能,关爱学生.在一次心理健康教育活动中,张老师随机抽取了40名学生进行
了心理健康测试,并将测试结果按“健康、亚健康、不健康”绘制成下列表格,其中测
试结果为“健康”的频率是 ▲ .
类型 健康 亚健康 不健康
数据(人) 32 7 1
﹣
12.若反比例函数y=(m+2)x|m| 5的图象在第一、三象限,则m的值为 ▲ .
13.如图, ABCD的对角线 AC,BD相交于点O,点E,F分别是线段 AO,BO的中点
,若 AC BD 26 cm,△OAB的周长是23cm,则 EF ▲ cm.
14.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠
EAC=2∠CAD,则∠BAE= ▲ .
第13题 第14题
15. 已知双曲线 = 3 与直线y=x﹣5有一交点为(a,b).则 + = ▲ .
2
16.已知关于x的方程 1 = 的解为非负数,则m的取值范围是 ▲ .
3 3
k
17.如图,在平面直角坐标系中,菱形OABC的边OA在x轴的正半轴上,反比例函数y= x
(x>0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积9,则k的值为 ▲
18.如图,在△ABC中,∠ACB=90°,AC=5cm,AB=13cm.将△ABC绕点C按顺时针方向旋
转后得△DEC,直线AD、EB相交于点F.取BC的中点G,连接GF,则GF长的最大值为 ▲
cm.
第17题 第18题
(北京)股份有限公司
三.解答题(共10小题,共96分)
19.(8分)计算.
x 1 a2 a a 1
(1) 2 (2) x 4 2x 4 a2 1 2a a 1
20.(8分)解分式方程:
3 1 1 1
(1) = (2) + 3 =
5 +1 2 2 2
2 4 +4
21.(8分)先化简,再求值: 2 ÷
4
(x ),其中﹣2≤x≤2,取一个合适的整
2
数代入求值.
22.(8分)打造“沸腾校园”,丰富学生的业余生活。学校准备利用大课间时间给同学
们准备以下几种活动:A.跳绳、B.打乒乓球、C.长跑、D.踢足球.随机抽取了八年
级部分同学,调查他们在这四个活动中最感兴趣的一个,并绘制了以下两幅不完整的统
计图,如图所示:
请你根据以上信息.解答下列问题:
(1)本次调查的总人数为 人,C所占的百分比为 .
(2)请补全条形统计图;
(3)本次调查估计该校九年级共有1200名学生中对B打乒乓球最感兴趣的学生人数?
23.(10分)某校为了增强学生对中华优秀传统文化的理解,决定购买一批相关的书籍.
据了解,经典著作的单价比传说故事的单价多8元,用6000元购买经典著作与用4000元购
买传说故事的本数相同,这两类书籍的单价各是多少元?
(北京)股份有限公司
24.(10分)如图,O是矩形ABCD对角线AC的中点,AB=8,BC=16,P是边AD上一动点(不
与A、D重合).
(1)PO的延长线交BC于Q,求证:四边形AQCP是平行四边形;
(2)连接BP、DQ,四边形BPDQ能否成为菱形?若能,请求出此时AP的长;若不能,请
说明理由.
25.(10分)如图,已知一次函数y1=mx+n的图象与x轴、y轴分别交于点A、B,与反比
例函数 2 =
的图象分别交于点C、D,点C坐标为(﹣4,1),点D坐标为(2,a).
(1)求一次函数与反比例函数的表达式;
(2)求△COD的面积;
(3)直接写出当y1≥y2时,自变量x的取值范围.
26.(10分)如图,已知菱形ABCD,请仅用无刻度直尺按要求作图(保留作图痕迹).
(1)如图①,点E,F分别是AD,AB的中点,以EF为边画一矩形;
(2)如图②,点E是对角线AC上的点,∠EDA=15°,∠DAB=60°,以DE为边画一个正
方形.
(北京)股份有限公司
27.(12分)定义:如图1,在平面直角坐标系中,点 P是平面内任意一点(坐标轴上的
点除外),过点 P分别作 x轴、 y轴的垂线,若由点 P、原点O、两个垂足 A、B为顶点的
矩形OAPB的周长与面积的数值相等时,则称点 P是平面直角坐标系中的“美好点”.
【尝试初探】
(1)点C(3,2)______“美好点”(填“是”或“不是”);若点D(4,a)是第一象限内的
一个“美好点”,则a=______;
【深入探究】
(2)①若“美好点”E m,6 m 0 k在双曲线 y (k 0,且 k为常数)上,则 k ______
x
;
②在①的条件下, F 2 n y k, 在双曲线 上,求 S
x △EOF
的值;
【拓展延伸】
(3)我们可以从函数角度研究“美好点”,已知点 P x,y 是第一象限内的“美好点”.
①求 y关于 x的函数表达式;
②在图2的平面直角坐标系中画出函数图像的草图,观察图像可知该图像可由函数______
( x 0)的图像平移得到;
③结合图像研究性质,下列结论正确的选项是______;
A.图象与经过点 2,2 且平行于坐标轴的直线没有交点;
B. y随着 x的增大而减小;
C. y随着 x的增大而增大;
3
D.图像经过点 10, ;
2
④对于图像上任意一点 x,y ,代数式 2 x y 2 是否为定值?如果是,请求出这个定
值,如果不是,请说明理由.
(北京)股份有限公司
28.(12分)数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图①所
示的长方形纸条 ABCD,其中 AD BC 2, AB CD 10.然后在纸条上任意画一条线
段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK .如图②所示:
【基础回顾】
(1)在图②中,若∠1=51°, MKN=______ ;(直接写出答案)
【操作探究】
(2)改变折痕MN位置,请判断△MNK 的形状,请说明理由;
(3)爱动脑筋的小明在研究△MNK 的面积时,发现 KN边上的高始终是个不变的值.根据
这一发现,他很快研究出△KMN 的面积最小值为 2,此时 1的大小可以为______;
【拓展延伸】
(4)小明继续动手操作进行折纸,发现了△MNK 面积存在最大值,请你求出这个最大值.
(北京)股份有限公司
初二年级 数学学科
(时间:120 分钟;分值: 150 分)
一、选择题(每题 3 分,共 24 分)
1.下列图形中既是轴对称图形又是中心对称图形的是( ▲ )
A. B. C. D.
2.下列事件中,属于必然事件的是( ▲ )
A.掷一枚骰子,点数是 6 的一面朝上 B.下雨天,每个人都打着雨伞
C.若x>y,则﹣2x>﹣2y D.若实数a≠0,则|a|>0
3.下列调查中,其中适合采用抽样调查的是( ▲ )
A.调查某班50名同学的视力情况 B.扬州东站对旅客上高铁进行安检
C.为保证飞机飞行安全,对其零部件进行检查 D.检测某市的空气质量
4.下列各式是最简分式的是( ▲ )
4 +2 2+1 2 1
A. B. C. D.
4 1 +1
5.如图,四边形ABCD是平行四边形,下列结论中正确的是( ▲ )
A.若∠ABC=90°,则四边形ABCD是正方形 B.若AB=BC,则四边形ABCD是菱形
C.若AC=BD,则四边形ABCD是菱形 D.若AC⊥BD,则四边形ABCD是矩形
6.关于反比例函数 = 6,下列说法正确的是( ▲ )
A.y随x的增大而增大 B.图象分别在一、三象限
C.图象经过点(2,3) D.图象关于原点中心对称
m2+1
7.若点A(﹣5,a),B(﹣3,b),C(2,c)在反比例函数y = (m为常数)的
x
图象上,则a,b,c的大小关系是( ▲ )
A.c<a<b B.b<a<c C.a<b<c D.c<b<a
8.如图,正方形ABCD的边长为4,点E在边CD上,且CE=1,连接AE,点F在边AD上,
连接BF,把△ABF沿BF翻折,点A恰好落在AE上的点G处,下列结论:①AE=BF;②AD=2DF
;③ S 96四边形DFHE = :④GE=0.2,其中正确的有( ▲ )25
A.①② B.①③ C.①③④ D.①②③
第5题 第8题
(北京)股份有限公司
二.填空题(共10小题,满分30分,每小题3分)
1
9.若代数式 有意义,则实数x的取值范围是 ▲ .
2
= 2 + 10.已知 ,则 = ▲ .
3
11.润心赋能,关爱学生.在一次心理健康教育活动中,张老师随机抽取了40名学生进行
了心理健康测试,并将测试结果按“健康、亚健康、不健康”绘制成下列表格,其中测
试结果为“健康”的频率是 ▲ .
类型 健康 亚健康 不健康
数据(人) 32 7 1
﹣
12.若反比例函数y=(m+2)x|m| 5的图象在第一、三象限,则m的值为 ▲ .
13.如图, ABCD的对角线 AC,BD相交于点O,点E,F分别是线段 AO,BO的中点
,若 AC BD 26 cm,△OAB的周长是23cm,则 EF ▲ cm.
14.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠
EAC=2∠CAD,则∠BAE= ▲ .
第13题 第14题
15. 已知双曲线 = 3 与直线y=x﹣5有一交点为(a,b).则 + = ▲ .
2
16.已知关于x的方程 1 = 的解为非负数,则m的取值范围是 ▲ .
3 3
k
17.如图,在平面直角坐标系中,菱形OABC的边OA在x轴的正半轴上,反比例函数y= x
(x>0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积9,则k的值为 ▲
18.如图,在△ABC中,∠ACB=90°,AC=5cm,AB=13cm.将△ABC绕点C按顺时针方向旋
转后得△DEC,直线AD、EB相交于点F.取BC的中点G,连接GF,则GF长的最大值为 ▲
cm.
第17题 第18题
(北京)股份有限公司
三.解答题(共10小题,共96分)
19.(8分)计算.
x 1 a2 a a 1
(1) 2 (2) x 4 2x 4 a2 1 2a a 1
20.(8分)解分式方程:
3 1 1 1
(1) = (2) + 3 =
5 +1 2 2 2
2 4 +4
21.(8分)先化简,再求值: 2 ÷
4
(x ),其中﹣2≤x≤2,取一个合适的整
2
数代入求值.
22.(8分)打造“沸腾校园”,丰富学生的业余生活。学校准备利用大课间时间给同学
们准备以下几种活动:A.跳绳、B.打乒乓球、C.长跑、D.踢足球.随机抽取了八年
级部分同学,调查他们在这四个活动中最感兴趣的一个,并绘制了以下两幅不完整的统
计图,如图所示:
请你根据以上信息.解答下列问题:
(1)本次调查的总人数为 人,C所占的百分比为 .
(2)请补全条形统计图;
(3)本次调查估计该校九年级共有1200名学生中对B打乒乓球最感兴趣的学生人数?
23.(10分)某校为了增强学生对中华优秀传统文化的理解,决定购买一批相关的书籍.
据了解,经典著作的单价比传说故事的单价多8元,用6000元购买经典著作与用4000元购
买传说故事的本数相同,这两类书籍的单价各是多少元?
(北京)股份有限公司
24.(10分)如图,O是矩形ABCD对角线AC的中点,AB=8,BC=16,P是边AD上一动点(不
与A、D重合).
(1)PO的延长线交BC于Q,求证:四边形AQCP是平行四边形;
(2)连接BP、DQ,四边形BPDQ能否成为菱形?若能,请求出此时AP的长;若不能,请
说明理由.
25.(10分)如图,已知一次函数y1=mx+n的图象与x轴、y轴分别交于点A、B,与反比
例函数 2 =
的图象分别交于点C、D,点C坐标为(﹣4,1),点D坐标为(2,a).
(1)求一次函数与反比例函数的表达式;
(2)求△COD的面积;
(3)直接写出当y1≥y2时,自变量x的取值范围.
26.(10分)如图,已知菱形ABCD,请仅用无刻度直尺按要求作图(保留作图痕迹).
(1)如图①,点E,F分别是AD,AB的中点,以EF为边画一矩形;
(2)如图②,点E是对角线AC上的点,∠EDA=15°,∠DAB=60°,以DE为边画一个正
方形.
(北京)股份有限公司
27.(12分)定义:如图1,在平面直角坐标系中,点 P是平面内任意一点(坐标轴上的
点除外),过点 P分别作 x轴、 y轴的垂线,若由点 P、原点O、两个垂足 A、B为顶点的
矩形OAPB的周长与面积的数值相等时,则称点 P是平面直角坐标系中的“美好点”.
【尝试初探】
(1)点C(3,2)______“美好点”(填“是”或“不是”);若点D(4,a)是第一象限内的
一个“美好点”,则a=______;
【深入探究】
(2)①若“美好点”E m,6 m 0 k在双曲线 y (k 0,且 k为常数)上,则 k ______
x
;
②在①的条件下, F 2 n y k, 在双曲线 上,求 S
x △EOF
的值;
【拓展延伸】
(3)我们可以从函数角度研究“美好点”,已知点 P x,y 是第一象限内的“美好点”.
①求 y关于 x的函数表达式;
②在图2的平面直角坐标系中画出函数图像的草图,观察图像可知该图像可由函数______
( x 0)的图像平移得到;
③结合图像研究性质,下列结论正确的选项是______;
A.图象与经过点 2,2 且平行于坐标轴的直线没有交点;
B. y随着 x的增大而减小;
C. y随着 x的增大而增大;
3
D.图像经过点 10, ;
2
④对于图像上任意一点 x,y ,代数式 2 x y 2 是否为定值?如果是,请求出这个定
值,如果不是,请说明理由.
(北京)股份有限公司
28.(12分)数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图①所
示的长方形纸条 ABCD,其中 AD BC 2, AB CD 10.然后在纸条上任意画一条线
段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK .如图②所示:
【基础回顾】
(1)在图②中,若∠1=51°, MKN=______ ;(直接写出答案)
【操作探究】
(2)改变折痕MN位置,请判断△MNK 的形状,请说明理由;
(3)爱动脑筋的小明在研究△MNK 的面积时,发现 KN边上的高始终是个不变的值.根据
这一发现,他很快研究出△KMN 的面积最小值为 2,此时 1的大小可以为______;
【拓展延伸】
(4)小明继续动手操作进行折纸,发现了△MNK 面积存在最大值,请你求出这个最大值.
(北京)股份有限公司
同课章节目录
