专项1 单项选择2(浙江中考真题+中考模拟) ——2025年中考数学冲刺中考模拟真题速递(浙江专用)第二辑(答案+解析)
文档属性
| 名称 | 专项1 单项选择2(浙江中考真题+中考模拟) ——2025年中考数学冲刺中考模拟真题速递(浙江专用)第二辑(答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 633.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 17:38:05 | ||
图片预览




文档简介
2025年中考数学冲刺中考模拟真题速递(浙江专用)第二辑
专项1 单项选择2(浙江中考真题+中考模拟)
一、选择题
1.(2024·宁海)在中,,,,点是所在平面内一点,则取得最小值时,下列结论正确的是
A.点是三边垂直平分线的交点
B.点是三条内角平分线的交点
C.点是三条高的交点
D.点是三条中线的交点
2.(2025·温州模拟)用科学记数法表示的数5.002×104 的原数是( )
A.5 002 B.500 200 C.50 020 D.500.2
3.(2025·萧山模拟) 的相反数是( )
A. B. C.2023 D.-2023
4.(2024·宁海)如图,截的三条边所得的弦长相等,若,则的度数为
A. B. C. D.
5.(2025·萧山模拟)将抛物线向下平移3个单位,再向右平移3个单位后的解析式为( )
A. B. C. D.
6.(2025·温州模拟) 如图, 这是体育委员对七年级 (5) 班的立定跳远成绩进行全面调查后绘成的统计图, 如果把大于 的成绩视为合格, 再绘制一幅扇形统计图, 那么“不合格”部分对应的圆心角度数是( )
A. B. C. D.
7.(2024·宁海)如图的三条高相交于点,是角平分线,已知,,则图中的等腰三角形共有个.
A.5 B.6 C.7 D.8
8.(2024·宁海)若实数满足,则应满足的条件是
A.或 B.
C. D.
9.(2025·台州模拟)观察下面三行数:
①
②
③
设分别为第①②③行的第个数,则的值为( )
A.0 B. C. D.
10.(2025·台州模拟)如图,,平分,若,则的度数是( )
A. B. C. D.
11.(2024·杭州模拟)在一个不透明的袋子中,装有四个分别标有数字,,0,2的小球,这些小球除数字外其他完全相同.从袋子中随机摸出两个小球,两球上的数字之积恰好是无理数的概率是( )
A. B. C. D.
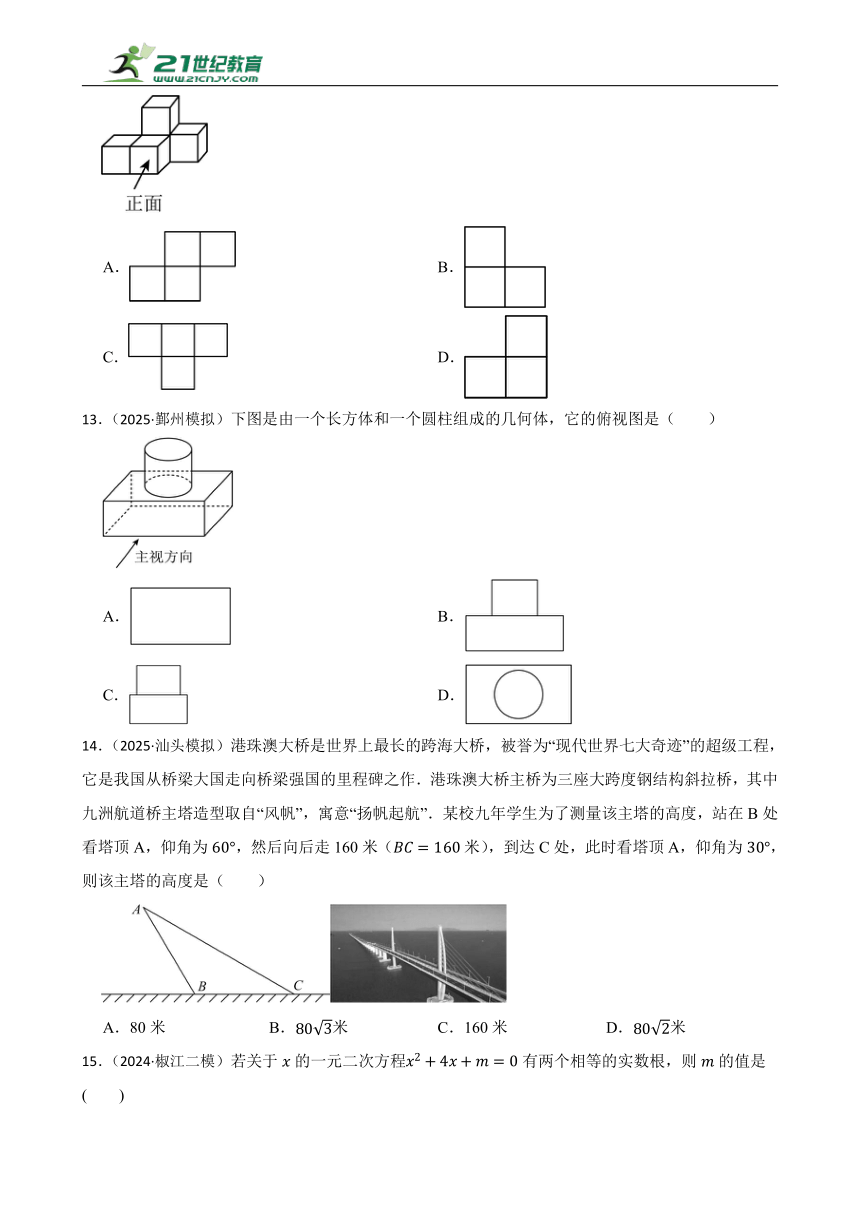
12.(2025·宁波模拟)如图是由5个相同的正方体搭成的几何体,这个几何体的左视图是( )
A. B.
C. D.
13.(2025·鄞州模拟)下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
A. B.
C. D.
14.(2025·汕头模拟)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”.某校九年学生为了测量该主塔的高度,站在B处看塔顶A,仰角为,然后向后走160米(米),到达C处,此时看塔顶A,仰角为,则该主塔的高度是( )
A.80米 B.米 C.160米 D.米
15.(2024·椒江二模)若关于的一元二次方程有两个相等的实数根,则的值是( )
A. B. C. D.
16.(2024·椒江二模)下列收集数据的方式适合抽样调查的是( )
A.旅客进动车站前的安检
B.了解某批次汽车的抗撞击能力
C.了解某班同学的身高情况
D.选出某班短跑最快的同学参加校运动会
17.(2024九下·杭州模拟)如图,在一次夏令营活动中,小亮从位于点的营地出发,沿北偏东方向走了到达地,然后再沿南偏东方向走了若干千米到达地,测得地在地南偏西方向,则,两地的距离为( )
A. B. C. D.
18.(2024九下·西安模拟)如图,是的直径,半径与弦垂直于点,连接.若,,则的长为( )
A. B. C. D.
19.(2025·萧山模拟)据报道,浙江省举全省之力筹办杭州亚运会,共有37600名志愿者参加.其中37600用科学记数法可表示为( )
A. B. C. D.
20.(2025·萧山模拟)如图,是的内接三角形,AD是的直径,若,则图中阴影部分的面积为( )
A. B. C. D.
21.(2025·温州模拟)已知反比例函数的图象经过点,下列说法错误的是( )
A.当时, B.函数图象在第一、三象限
C.随的增大而减小 D.点在此函数的图象上
22.(2025·温州模拟)在平面直角坐标系中,将点 向下平移3个单位长度,所得点的坐标是( )
A.(-1,1) B.(5,1) C.(2,4) D.(2,-2)
23.(2025·温州模拟)已知矩形的周长为56,对角线交点到短边的距离比到长边的距离大4,则该矩形的面积为( )
A.45 B.90 C.140 D.180
24.(2025·温州模拟)已知二次函数y=x2-4x+2,在-1≤x≤3的取值范围内,下列关于该函数的说法中正确的是( )
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值-2
25.(2024九下·安庆模拟)如图,小明想利用“,,”这些条件作.他先作出了和,在用圆规作时,发现点出现和两个位置,那么的长是( )
A. B. C. D.
26.(2025·咸阳模拟)如图,为的直径,C,D为上两点,若,则等于( )
A.35° B.55° C.65° D.70°
27.(2023九下·秀洲模拟)如图,矩形的顶点、分别在反比例函数与的图象上,点、在轴上,,分别交轴于点、F,则阴影部分的面积为( )
A.3 B.5 C.6 D.9
28.(2024九下·浙江模拟)某校九年级进行了3次数学模拟考试,甲、乙、丙三名同学的平均分为及方差如右表所示,那么这三名同学数学成绩最稳定的是( )
甲 乙 丙
91 91 91
6 24 54
A.甲 B.乙 C.丙 D.无法确定
29.(2024九下·宣化模拟)明明和亮亮都在同一直道A、B两地间做匀速往返走锻炼明明的速度小于亮亮的速度忽略掉头等时间明明从A地出发,同时亮亮从B地出发图中的折线段表示从开始到第二次相遇止,两人之间的距离米与行走时间分的函数关系的图象,则
A.明明的速度是80米分 B.第二次相遇时距离B地800米
C.出发25分时两人第一次相遇 D.出发35分时两人相距2000米
30.(2024九下·吉首模拟)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元.问共有多少人?这个物品的价格是多少?设共有个人,则可列方程为( )
A. B. C. D.
31.(2024九下·沭阳模拟)计算的结果是( )
A. B. C. D.
32.(2024九下·浙江模拟)《孙子算经》中有一道题,原文是:今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?意思是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺.问木长多少尺?设木长尺,绳长尺,根据题意列方程组得( )
A. B.
C. D.
33.(2024九下·新昌模拟)如图,一把梯子斜靠在墙上,端点A离地面的高度长为时,.当梯子底端点B沿水平方向向左移动到点,端点A沿墙竖直向上移动到点,设,则的长可以表示为( )
A. B. C. D.
34.(2024·浙江)某班有5位学生参加志愿服务次数为:7,7,8,10,13.则这5位学生志愿服务次数的中位数为( )
A.7 B.8 C.9 D.10
35.(2024·浙江)反比例函数的图象上有,两点.下列正确的选项是( )
A.当时, B.当时,
C.当时, D.当时,
36.(2024·赤峰) 如图, 数轴上点 A, M, B 分别表示数 , 若 , 则下列运算结果一定是正数的是( )
A. B. C.a b D.
37.(2024·浙江)如图,在中,,相交于点,,.过点作的垂线交于点,记长为,长为.当,的值发生变化时,下列代数式的值不变的是( )
A. B. C. D.
38.(2024·浙江)不等式组的解集在数轴上表示为( )
A.
B.
C.
D.
39.(2024·浙江)如图,在平面直角坐标系中,与是位似图形,位似中心为点.若点的对应点为,则点的对应点的坐标为( )
A. B. C. D.
40.(2024·浙江)下列式子运算正确的是( )
A. B. C. D.
41.(2024·浙江)5个相同正方体搭成的几何体主视图为( )
A. B. C. D.
42.(2023·金华)如图,已知,则的度数是( )
A. B. C. D.
43.(2023·湖州)已知某几何体的三视图如图所示,则该几何体可能是( )
A. B. C. D.
44.(2023·台州)下列运算正确的是( ).
A. B.
C. D.
45.(2023·金华)上周双休日,某班8名同学课外阅读的时间如下(单位:时):1,4,2,4,3,3,4,5.这组数据的众数是( )
A.1时 B.2时 C.3时 D.4时
46.(2023·舟山)下面四个数中,比1小的正无理数是( )
A. B. C. D.
47.(2023·杭州)分解因式:( )
A. B.
C. D.
48.(2023·宁波)据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A. B.
C. D.
49.(2023·绍兴)在一个不透明的袋子里装有2个红球和5个白球,它们除颜色外都相同,从中任意摸出1个球,则摸出的球为红球的概率是( )
A. B. C. D.
50.(2023·舟山)已知点均在反比例函数的图象上,则,的大小关系是( )
A. B. C. D.
答案解析部分
1.D
解:过P作 于D, 过P作 于E, 延长CP交AB于M, 延长BP交AC于N, 如图:
∴四边形AEPD是矩形,
设
中,
中,
中,
时, 的值最大,此时
即
即M是AB的中点,同理可得 N为AC中点,
∴P是 三条中线的交点,
故答案为:D.
过P作 于D, 过P作 于E,延长CP交AB于M, 延长BP交AC于N, 设 则 , 当 时, 的值最大,此时 然后根据平行线分线段成比例得到 解出 M是AB的中点,同理可得 N为AC中点, 即P是三条中线的交点.
2.C
解:5.002×104=50020,
故答案为:C.
5.002×104将小数点向右移去4位,即可得出结论.
3.B
解: 的相反数是
故答案为:B.
根据数a的相反数是-a,0的相反数是0解题即可.
4.C
解:过点O作OE⊥AB于E, OD⊥BC于D,OF⊥AC于F,∵∠A=80°,
∴∠ABC+∠ACB=180°-80°= 100°,由题意得, HG= PQ = MN,
∴OD=OE=OF,
∵OE⊥AB, OD⊥BC, OF⊥AC,
∴OB平分∠ABC, OC平分∠ACB,
50°
∴∠BOC =180°-50°=130°,
故答案为:C.
过点O作OE⊥AB于E, OD⊥BC于D, OF⊥AC于F,根据圆心角、弧、弦的关系得到OD=OE=OF,然后得到OB平分∠ABC, OC平分∠ACB,再根据三角形的内角和定理得到解答即可.
5.C
解: 向下平移3个单位后可得 即
再向右平移3个单位后可得 即
故答案为:C.
根据函数图象的平移规律“上加下减,左加右减”求解即可.
6.C
解:.
故答案为:C.
由题意可得“不合格”的人数为8人,再求得“不合格”人数所占百分比,进而得到“不合格”部分对应的圆心角度数.
7.D
解:①∵AD⊥BC, ∠ABC =45°,
∴△ABD是等腰三角形;
②∵CF⊥AB, ∠ABC =45°,
∴△BCF是等腰三角形;
③∵∠ACB=60,
∴∠CBE =90°-60°=30°,
∵CH是角平分线,
∴∠CBI=∠ICB,
∴△BCI是等腰三角形;
④∵∠ACB=60°,
∴∠CAD=90°-60°=30°,
∴∠ACJ=∠CAJ=30°,
∴△ACJ是等腰三角形;
⑤∵∠ACF=60°--45°= 15°,
∴∠CAF=90°--15°=75°,
∴∠AHC=∠ABC+∠BCH =45°+30°=75°,
∴∠CAH=∠CHA=75°,
∴△ACH是等腰三角形;
⑥∵∠GCD=∠DGC =45°,
∴△CDG是等腰三角形;
⑦∵∠GIJ =∠EBC+∠HCB=30°+30°=60°,
∠GJI =∠CJD=90°-30°=60°,
∴∠GIJ =∠GJI=60°,
∴△GIJ是等腰三角形;
⑧△AFG是等腰三角形;
综上分析,图中等腰三角形共有8个:
故答案为:D.
根据等角对等边分别找出等腰三角形即可.
8.C
解:当 时, 则:
当 时, 则:
,
当 时, 则:
,
,
综上所述:若实数x满足则x应满足的条件是,
故答案为:C.
分为, 或 三种情况,分别化简二次根式解题即可.
9.B
10.D
11.B
解:和都是无理数,这四个数乘积为无理数的情况有×2,×2共2种
而任意模出两球的情况有(0,2),(0,),(0,),(,2)(,)(,2)共6种,故P=;
故答案为:B.
列出任意摸出两球的情况和乘积为无理数的情况,即可求出概率.
12.B
解:从左侧看,这个几何体的左视图如下图所示:
故答案为:B.
此题考查了几何体的三视图,根据简单几何体的三视图,左视图是从几何体左侧进行观察,从而直接得到答案.
13.D
解:从上面看下边是一个矩形,矩形的上边是一个圆,
故答案为:D.
利用从上面看得到的几何图形解答即可.
14.B
解:如图,过点A作于点D,
根据题意得:,
∵,
∴,
∴,
∴米,
在中,米.
即该主塔的高度是米.
故答案为:B.
过点A作于点D,利用三角形的外角得到,根据等角对等边求出米,再在中,根据正弦的定义求出长解题.
15.C
解:依题意,,
解得:,
故选:C.
由判别式判断方程的根的情况,当时,一元二次方程有两个相等实数根,据此求出的取值范围即可.
16.B
解:A. 旅客进动车站前的安检,适合全面调查,故该选项不符合题意;
B. 了解某批次汽车的抗撞击能力, 适合抽样调查,故该选项符合题意;
C. 了解某班同学的身高情况, 适合全面调查,故该选项不符合题意;
D. 选出某班短跑最快的同学参加校运动会, 适合全面调查,故该选项不符合题意;
故选:B.
由抽样调查和全面调查的区别,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
17.A
解:如图,由题意可知,,,,,
,
,
,
,
,
,
过点作,垂足为点,
是等腰直角三角形,
设,则,
在中,
,即,
解得:,
在中,
,即,
,
故答案为:.
由方位角补全图形,过B作BE⊥AC于点E,利用二直线平行,内错角相等得∠ACN=∠DAC=15°,∠BAD=∠ABQ=45°,由角的和差得出∠ACB=45°,∠BAC=30°,从而得到△BEC是等腰直角三角形,设BE=CE=xkm,用含x的式子表示出AE,在Rt△AEB中,利用∠BAE的正切函数及特殊锐角三角函数求得x的值;在Rt△BEC中,利用∠BCE的余弦函数及特殊锐角三角函数值求得BC的长.
18.B
解:如图,连接,
∵,,
∴,
设的半径,则,
在中,,
解得,
∵,,
∴,
∵是直径,
∴,
∵是的中位线,
∴,
在中,
,
故答案为:.
根据垂径定理求出的长,设的半径为,在中根据勾股定理得到的值,连接,即可得到,根据中位线求出BE长,再在中运用勾股定理求出即可解题.
19.B
解:.
故答案为:B.
本题考查科学记数法的定义.科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,据此可得:a=3.76,小数点移动了4位,故n=4,进而可选出答案.
20.C
21.C
解:由条件可知
∴函数图象分布在第一、三象限, 当 时,y随x的增大而减小,当 时,y随x的增大而减小,选项B正确;选项C错误;
当 时, 选项A正确;
∴点 )在此函数的图象上,
∴选项D正确,
故答案为: C.
根据反比例函数图象上点的坐标特征以及反比例函数的性质逐一判断即可.
22.D
解:∵在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得到的点的横坐标不变,纵坐标减小3个单位,
∴平移后的的横坐标不变为2,纵坐标为: ,
∴平移后的点的坐标为( ,
故答案为:D.
平面直角坐标系中点的坐标的平移规律为:横坐标左减右加,纵坐标上加下减.
23.D
解:如图,过作,交于,交于,作,交于,交于,
∵四边形是矩形,
∴,
∴,
∴,
∴四边形是矩形,
∴,
同理四边形、四边形,四边形都是矩形,
,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∴,
同理,
设,则,
∵矩形周长是56,
,
解得:,
∴矩形的各边长是.
则该矩形的面积,
故答案为:D.
过作交于,交于,作交于,交于,即可得到四边形、四边形、四边形、四边形是矩形,设,则,利用矩形周长列方程求出x值即可解题.
24.D
解:∵y=x2 4x+2=(x 2)2 2,
∴在 1≤x≤3的取值范围内,当x=2时,有最小值 2,
当x= 1时,有最大值为y=9 2=7.
故答案为:D.
先利用配方法将二次函数的一般式化为顶点式,再利用二次函数的性质分析求解即可.
25.D
解:过点作于点,
∵,,,
∴,
∵,,
∴,
∴
故答案为:D
本题考查30度直角三角形的性质.过点作于点,先利用30度直角三角形的性质可以求出BM=3cm,再利用勾股定理可以求出,再根据可求出的长.
26.B
解:∵为的直径,
∴,
∵,
∴,
∴.
故答案为:B.
根据直径所对的圆周角是直角得∠ACB=90°,由直角三角形的量锐角互余得∠B=55°,进而根据同弧所对的圆周角相等得出∠D=∠B,从而得出答案.
27.B
28.A
29.B
解:第一次相遇两人共走了2800米,第二次相遇两人共走了米,且二者速度不变,,
出发20分时两人第一次相遇,C选项错误;
亮亮的速度为米分,
两人的速度和为米分,
明明的速度为米分,A选项错误;
第二次相遇时距离B地距离为米,B选项正确;
出发35分钟时两人间的距离为米,D选项错误.
故答案为:B.
根据图象提供的信息可得第二次相遇时,两人都行走了60分钟,而第一次相遇是在两人行走35分钟前;由于第一次相遇两人共走了2800米,第二次相遇两人共走了3倍的2800米,且速度不变,从而可得第一次相遇的时间为60分钟的三分之一,据此可判断C选项;当x=35时,出现拐点,显然此时亮亮到达A地,即亮亮用35分钟走了2800米,利用速度=路程÷时间可求出亮亮的速度及两人的速度和,二者做差后可得出明明的速度,据此判断A选项;根据第二次相遇时距离B地的距离=明明的速度×第二次相遇的时间-A、B两地间的距离,据此计算可判断B选项;观察函数图象,可知:出发35分钟时亮亮到达A地,根据出发35分钟时两人间的距离=明明的速度×出发时间,据此计算可判断D选项.
30.A
解:∵ 每人出8元,还盈余3元;每人出7元,则还差4元, 设共有个人,
∴可列方程为,
故答案为:A.
本题考查一元一次方程的实际应用,根据物品的价格是定值,结合" 每人出8元,还盈余3元;每人出7元,则还差4元"列出方程即可.
31.D
32.A
设木长尺,绳长尺,根据题意列方程组得
故答案为:A.
设木长尺,绳长尺,利用“一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺”列二元一次方程组即可.
33.B
解:由题意可知,,
∵,
∴,故,
∵,
∴,
则:,
故选:B.
本题考查锐角三角函数.根据正弦的定义可得:,据此可求出,再利用正弦的定义可得:,利用线段的运算可得:,代入数据可求出答案.
34.B
解:将数从小到大排列为:7,7,8,10,13,处于最中间的数是8,
∴这组数据的中位数是8.
故答案为:B.
求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据;即可求解.
35.A
解:∵k=4>0,
∴在每一个象限内,y随x的增大而减小,切图象分支在第一、三象限,
A、当t<-4时,t+4<0,
∴t<t+4,
∴y2<y1<0,故A符合题意;
B、C、当-4<t<0时,
∴t+4>0,
∴y1<0,y2>0即y1<0<y2,故B、C不符合题意;
D、当t>0时,则t+4>4,
∴t<t+4,
∴0<y2<y1,故D不符合题意;
故答案为:A.
利用反比例函数的性质可证得在每一个象限内,y随x的增大而减小,切图象分支在第一、三象限,由t<-4可得到t+4<0,即可推出t<t+4,由此可得到y1,y2,0的大小关系,可对A作出判断;由-4<t<0,可推出t+4>0,可得到y1<0,y2>0即y1<0<y2,可对B、C作出判断;当t>0时,则t+4>4,可得到t<t+4,由此可推出0<y2<y1,可对D作出判断.
36.A
解:∵ A, M, B 分别表示数 ,且由数轴可知,
∴,,
又∵,
∴,即a+b>0.
故答案为:A.
由数轴可判断数的大小,从而利用数与距离关系表示AM和BM的距离,得出a与b的关系即可.
37.C
解:过点D作DF⊥BC交BC的延长线于点F,
∵四边形ABCD是平行四边形,
∴AB=DC,AD∥BC,
∵AE⊥BC,
∴AE∥DF,∠AEF=90°,
∴四边形AEFD是矩形,
∴AE=DF
在Rt△ABE和Rt△DCF中
∴Rt△ABE≌Rt△DCF(HL),
∴CF=BE=x,
∴EC=BC-BE=y-x,BF=BC+CF=y+x,
∵AE2=AC2-EC2,DF2=BD2-BF2,
∴AC2-EC2=BD2-BF2即4-(y-x)2=()2-(y+x)2,
整理得:xy=2,
∴xy的值不变.
故答案为:C.
过点D作DF⊥BC交BC的延长线于点F,利用平行四边形的性质可证得AB=DC,AD∥BC,再证明四边形AEFD是矩形,利用矩形的性质可证得AE=DF,利用HL可证得Rt△ABE≌Rt△DCF,可推出BE=CF=x,再表示出BF,EC的长,利用勾股定理去证明AC2-EC2=BD2-BF2,可得到关于x,y的方程,解方程求出xy的值,即可求解.
38.A
解:
有①得:2x≥2,
解之:x≥1;
由②得
6-3x>-6,
解之:x<4,
∴不等式组的解集为1≤x<4.
故答案为:A.
分别求出不等式组中的每一个不等式的解集,再确定出不等式组的解集,
39.A
解:∵与是位似图形,位似中心为点.若点的对应点为, 点
∴点B的对应点B'的坐标为(-2×2,4×2)即(-4,8).
故答案为:A.
利用已知条件,可知将点B的横纵坐标都乘以2,可得到点B'的坐标.
40.D
解:A、x3+x2不能合并,故A不符合题意;
B、x3·x2=x5,故B不符合题意;
C、(x3)2=x6,故C不符合题意;
D、x6÷x2=x4,故D符合题意;
故答案为:D.
只有同类项才能合并,可对A作出判断;利用同底数幂相乘,底数不变,指数相加,可对B作出判断;利用幂的乘方法则,可对C作出判断;利用同底数幂相乘,底数不变,指数相减,可对D作出判断.
41.B
解:从几何题的正面看:有三列,三行,第一、二列都有3个小正方形,第三列有1个小正方形,从上到下,最下面一行有3个小正方形.
故答案为:B.
主视图就是从几何题的正面所看到的平面图形,观察已知几何题,可得答案.
42.C
解:如图,
∵∠1=∠3,
∴a∥b,
∴∠2=∠5=50°,
∴∠4=180°-∠5=130°.
故答案为:C.
由同位角相等,两直线平行,得a∥b,由二直线平行,同位角相等,得∠5=∠2=50°,最后根据邻补角定义可求出∠4的度数.
43.D
解:∵此几何体的主视图和左视图是长方形,俯视图是圆,
∴此几何体是圆柱.
故答案为:D.
三个视图中是圆,长方形,可得到此几何体是圆柱体.
44.A
解:A、2(a-1)=2a-2,故此选项计算正确,符合题意;
B、(a+b)2=a2+2ab+b2,故此选项计算错误,不符合题意;
C、3a+2a=5a,故此选项计算错误,不符合题意;
D、(ab)2=a2b2,故此选项计算错误,不符合题意.
故答案为:A.
根据去括号法则(括号前面是负号,去掉括号和负号,括号里的每一项都要变号;括号前面是正号,去掉括号和正号,括号里的每一项都不变号,括号前的数要与括号里的每一项都要相乘),即可判断A选项;由完全平方公式的展开式是一个三项式可判断B选项;整式加法的实质就是合并同类项,所谓同类项就是所含字母相同,而且相同字母的指数也分别相同的项,同类项与字母的顺序没有关系,与系数也没有关系,合并同类项的时候,只需要将系数相加减,字母和字母的指数不变,但不是同类项的一定就不能合并,从而即可判断C选项;由积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘即可判断D选项.
45.D
解: 1,4,2,4,3,3,4,5这组数据中出现次数最多的是4,共出现可三次,
∴这组数据的众数是4时.
故答案为:D.
在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),据此结合题干所给的数据即可得出答案.
46.A
解:、属于正无理数,且()2=<1,>1,
∴比1小的正无理数为.
故答案为:A.
无理数是无限不循环小数,然后利用平方法进行比较即可.
47.A
解:4a2-1=(2a)2-1=(2a-1)(2a+1).
故答案为:A.
直接利用平方差公式分解即可.
48.B
解:380180000000=3.8018×1011.
故答案为:B
根据科学记数法的表示形式为:a×10n,其中1≤|a|<10,此题是绝对值较大的数,因此n=整数数位-1,即可求解.
49.C
解:P( 摸出的球为红球 )=.
故答案为:C.
由概率公式,直接用袋子中红色小球的数量除以袋子中小球的总数量,可得答案.
50.B
解:∵y=,
∴反比例函数的图象位于一、三象限,且在每一象限内,y随x的增大而减小,
∴A(-2,y2)、B(-1,y2)位于第三象限,C(1,y3)位于第一象限.
∵-2<-1,
∴y2故答案为:B.
根据反比例函数的性质可得:其图象位于一、三象限,且在每一象限内,y随x的增大而减小,据此进行比较.
专项1 单项选择2(浙江中考真题+中考模拟)
一、选择题
1.(2024·宁海)在中,,,,点是所在平面内一点,则取得最小值时,下列结论正确的是
A.点是三边垂直平分线的交点
B.点是三条内角平分线的交点
C.点是三条高的交点
D.点是三条中线的交点
2.(2025·温州模拟)用科学记数法表示的数5.002×104 的原数是( )
A.5 002 B.500 200 C.50 020 D.500.2
3.(2025·萧山模拟) 的相反数是( )
A. B. C.2023 D.-2023
4.(2024·宁海)如图,截的三条边所得的弦长相等,若,则的度数为
A. B. C. D.
5.(2025·萧山模拟)将抛物线向下平移3个单位,再向右平移3个单位后的解析式为( )
A. B. C. D.
6.(2025·温州模拟) 如图, 这是体育委员对七年级 (5) 班的立定跳远成绩进行全面调查后绘成的统计图, 如果把大于 的成绩视为合格, 再绘制一幅扇形统计图, 那么“不合格”部分对应的圆心角度数是( )
A. B. C. D.
7.(2024·宁海)如图的三条高相交于点,是角平分线,已知,,则图中的等腰三角形共有个.
A.5 B.6 C.7 D.8
8.(2024·宁海)若实数满足,则应满足的条件是
A.或 B.
C. D.
9.(2025·台州模拟)观察下面三行数:
①
②
③
设分别为第①②③行的第个数,则的值为( )
A.0 B. C. D.
10.(2025·台州模拟)如图,,平分,若,则的度数是( )
A. B. C. D.
11.(2024·杭州模拟)在一个不透明的袋子中,装有四个分别标有数字,,0,2的小球,这些小球除数字外其他完全相同.从袋子中随机摸出两个小球,两球上的数字之积恰好是无理数的概率是( )
A. B. C. D.
12.(2025·宁波模拟)如图是由5个相同的正方体搭成的几何体,这个几何体的左视图是( )
A. B.
C. D.
13.(2025·鄞州模拟)下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
A. B.
C. D.
14.(2025·汕头模拟)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”.某校九年学生为了测量该主塔的高度,站在B处看塔顶A,仰角为,然后向后走160米(米),到达C处,此时看塔顶A,仰角为,则该主塔的高度是( )
A.80米 B.米 C.160米 D.米
15.(2024·椒江二模)若关于的一元二次方程有两个相等的实数根,则的值是( )
A. B. C. D.
16.(2024·椒江二模)下列收集数据的方式适合抽样调查的是( )
A.旅客进动车站前的安检
B.了解某批次汽车的抗撞击能力
C.了解某班同学的身高情况
D.选出某班短跑最快的同学参加校运动会
17.(2024九下·杭州模拟)如图,在一次夏令营活动中,小亮从位于点的营地出发,沿北偏东方向走了到达地,然后再沿南偏东方向走了若干千米到达地,测得地在地南偏西方向,则,两地的距离为( )
A. B. C. D.
18.(2024九下·西安模拟)如图,是的直径,半径与弦垂直于点,连接.若,,则的长为( )
A. B. C. D.
19.(2025·萧山模拟)据报道,浙江省举全省之力筹办杭州亚运会,共有37600名志愿者参加.其中37600用科学记数法可表示为( )
A. B. C. D.
20.(2025·萧山模拟)如图,是的内接三角形,AD是的直径,若,则图中阴影部分的面积为( )
A. B. C. D.
21.(2025·温州模拟)已知反比例函数的图象经过点,下列说法错误的是( )
A.当时, B.函数图象在第一、三象限
C.随的增大而减小 D.点在此函数的图象上
22.(2025·温州模拟)在平面直角坐标系中,将点 向下平移3个单位长度,所得点的坐标是( )
A.(-1,1) B.(5,1) C.(2,4) D.(2,-2)
23.(2025·温州模拟)已知矩形的周长为56,对角线交点到短边的距离比到长边的距离大4,则该矩形的面积为( )
A.45 B.90 C.140 D.180
24.(2025·温州模拟)已知二次函数y=x2-4x+2,在-1≤x≤3的取值范围内,下列关于该函数的说法中正确的是( )
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值-2
25.(2024九下·安庆模拟)如图,小明想利用“,,”这些条件作.他先作出了和,在用圆规作时,发现点出现和两个位置,那么的长是( )
A. B. C. D.
26.(2025·咸阳模拟)如图,为的直径,C,D为上两点,若,则等于( )
A.35° B.55° C.65° D.70°
27.(2023九下·秀洲模拟)如图,矩形的顶点、分别在反比例函数与的图象上,点、在轴上,,分别交轴于点、F,则阴影部分的面积为( )
A.3 B.5 C.6 D.9
28.(2024九下·浙江模拟)某校九年级进行了3次数学模拟考试,甲、乙、丙三名同学的平均分为及方差如右表所示,那么这三名同学数学成绩最稳定的是( )
甲 乙 丙
91 91 91
6 24 54
A.甲 B.乙 C.丙 D.无法确定
29.(2024九下·宣化模拟)明明和亮亮都在同一直道A、B两地间做匀速往返走锻炼明明的速度小于亮亮的速度忽略掉头等时间明明从A地出发,同时亮亮从B地出发图中的折线段表示从开始到第二次相遇止,两人之间的距离米与行走时间分的函数关系的图象,则
A.明明的速度是80米分 B.第二次相遇时距离B地800米
C.出发25分时两人第一次相遇 D.出发35分时两人相距2000米
30.(2024九下·吉首模拟)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元.问共有多少人?这个物品的价格是多少?设共有个人,则可列方程为( )
A. B. C. D.
31.(2024九下·沭阳模拟)计算的结果是( )
A. B. C. D.
32.(2024九下·浙江模拟)《孙子算经》中有一道题,原文是:今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?意思是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺.问木长多少尺?设木长尺,绳长尺,根据题意列方程组得( )
A. B.
C. D.
33.(2024九下·新昌模拟)如图,一把梯子斜靠在墙上,端点A离地面的高度长为时,.当梯子底端点B沿水平方向向左移动到点,端点A沿墙竖直向上移动到点,设,则的长可以表示为( )
A. B. C. D.
34.(2024·浙江)某班有5位学生参加志愿服务次数为:7,7,8,10,13.则这5位学生志愿服务次数的中位数为( )
A.7 B.8 C.9 D.10
35.(2024·浙江)反比例函数的图象上有,两点.下列正确的选项是( )
A.当时, B.当时,
C.当时, D.当时,
36.(2024·赤峰) 如图, 数轴上点 A, M, B 分别表示数 , 若 , 则下列运算结果一定是正数的是( )
A. B. C.a b D.
37.(2024·浙江)如图,在中,,相交于点,,.过点作的垂线交于点,记长为,长为.当,的值发生变化时,下列代数式的值不变的是( )
A. B. C. D.
38.(2024·浙江)不等式组的解集在数轴上表示为( )
A.
B.
C.
D.
39.(2024·浙江)如图,在平面直角坐标系中,与是位似图形,位似中心为点.若点的对应点为,则点的对应点的坐标为( )
A. B. C. D.
40.(2024·浙江)下列式子运算正确的是( )
A. B. C. D.
41.(2024·浙江)5个相同正方体搭成的几何体主视图为( )
A. B. C. D.
42.(2023·金华)如图,已知,则的度数是( )
A. B. C. D.
43.(2023·湖州)已知某几何体的三视图如图所示,则该几何体可能是( )
A. B. C. D.
44.(2023·台州)下列运算正确的是( ).
A. B.
C. D.
45.(2023·金华)上周双休日,某班8名同学课外阅读的时间如下(单位:时):1,4,2,4,3,3,4,5.这组数据的众数是( )
A.1时 B.2时 C.3时 D.4时
46.(2023·舟山)下面四个数中,比1小的正无理数是( )
A. B. C. D.
47.(2023·杭州)分解因式:( )
A. B.
C. D.
48.(2023·宁波)据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A. B.
C. D.
49.(2023·绍兴)在一个不透明的袋子里装有2个红球和5个白球,它们除颜色外都相同,从中任意摸出1个球,则摸出的球为红球的概率是( )
A. B. C. D.
50.(2023·舟山)已知点均在反比例函数的图象上,则,的大小关系是( )
A. B. C. D.
答案解析部分
1.D
解:过P作 于D, 过P作 于E, 延长CP交AB于M, 延长BP交AC于N, 如图:
∴四边形AEPD是矩形,
设
中,
中,
中,
时, 的值最大,此时
即
即M是AB的中点,同理可得 N为AC中点,
∴P是 三条中线的交点,
故答案为:D.
过P作 于D, 过P作 于E,延长CP交AB于M, 延长BP交AC于N, 设 则 , 当 时, 的值最大,此时 然后根据平行线分线段成比例得到 解出 M是AB的中点,同理可得 N为AC中点, 即P是三条中线的交点.
2.C
解:5.002×104=50020,
故答案为:C.
5.002×104将小数点向右移去4位,即可得出结论.
3.B
解: 的相反数是
故答案为:B.
根据数a的相反数是-a,0的相反数是0解题即可.
4.C
解:过点O作OE⊥AB于E, OD⊥BC于D,OF⊥AC于F,∵∠A=80°,
∴∠ABC+∠ACB=180°-80°= 100°,由题意得, HG= PQ = MN,
∴OD=OE=OF,
∵OE⊥AB, OD⊥BC, OF⊥AC,
∴OB平分∠ABC, OC平分∠ACB,
50°
∴∠BOC =180°-50°=130°,
故答案为:C.
过点O作OE⊥AB于E, OD⊥BC于D, OF⊥AC于F,根据圆心角、弧、弦的关系得到OD=OE=OF,然后得到OB平分∠ABC, OC平分∠ACB,再根据三角形的内角和定理得到解答即可.
5.C
解: 向下平移3个单位后可得 即
再向右平移3个单位后可得 即
故答案为:C.
根据函数图象的平移规律“上加下减,左加右减”求解即可.
6.C
解:.
故答案为:C.
由题意可得“不合格”的人数为8人,再求得“不合格”人数所占百分比,进而得到“不合格”部分对应的圆心角度数.
7.D
解:①∵AD⊥BC, ∠ABC =45°,
∴△ABD是等腰三角形;
②∵CF⊥AB, ∠ABC =45°,
∴△BCF是等腰三角形;
③∵∠ACB=60,
∴∠CBE =90°-60°=30°,
∵CH是角平分线,
∴∠CBI=∠ICB,
∴△BCI是等腰三角形;
④∵∠ACB=60°,
∴∠CAD=90°-60°=30°,
∴∠ACJ=∠CAJ=30°,
∴△ACJ是等腰三角形;
⑤∵∠ACF=60°--45°= 15°,
∴∠CAF=90°--15°=75°,
∴∠AHC=∠ABC+∠BCH =45°+30°=75°,
∴∠CAH=∠CHA=75°,
∴△ACH是等腰三角形;
⑥∵∠GCD=∠DGC =45°,
∴△CDG是等腰三角形;
⑦∵∠GIJ =∠EBC+∠HCB=30°+30°=60°,
∠GJI =∠CJD=90°-30°=60°,
∴∠GIJ =∠GJI=60°,
∴△GIJ是等腰三角形;
⑧△AFG是等腰三角形;
综上分析,图中等腰三角形共有8个:
故答案为:D.
根据等角对等边分别找出等腰三角形即可.
8.C
解:当 时, 则:
当 时, 则:
,
当 时, 则:
,
,
综上所述:若实数x满足则x应满足的条件是,
故答案为:C.
分为, 或 三种情况,分别化简二次根式解题即可.
9.B
10.D
11.B
解:和都是无理数,这四个数乘积为无理数的情况有×2,×2共2种
而任意模出两球的情况有(0,2),(0,),(0,),(,2)(,)(,2)共6种,故P=;
故答案为:B.
列出任意摸出两球的情况和乘积为无理数的情况,即可求出概率.
12.B
解:从左侧看,这个几何体的左视图如下图所示:
故答案为:B.
此题考查了几何体的三视图,根据简单几何体的三视图,左视图是从几何体左侧进行观察,从而直接得到答案.
13.D
解:从上面看下边是一个矩形,矩形的上边是一个圆,
故答案为:D.
利用从上面看得到的几何图形解答即可.
14.B
解:如图,过点A作于点D,
根据题意得:,
∵,
∴,
∴,
∴米,
在中,米.
即该主塔的高度是米.
故答案为:B.
过点A作于点D,利用三角形的外角得到,根据等角对等边求出米,再在中,根据正弦的定义求出长解题.
15.C
解:依题意,,
解得:,
故选:C.
由判别式判断方程的根的情况,当时,一元二次方程有两个相等实数根,据此求出的取值范围即可.
16.B
解:A. 旅客进动车站前的安检,适合全面调查,故该选项不符合题意;
B. 了解某批次汽车的抗撞击能力, 适合抽样调查,故该选项符合题意;
C. 了解某班同学的身高情况, 适合全面调查,故该选项不符合题意;
D. 选出某班短跑最快的同学参加校运动会, 适合全面调查,故该选项不符合题意;
故选:B.
由抽样调查和全面调查的区别,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
17.A
解:如图,由题意可知,,,,,
,
,
,
,
,
,
过点作,垂足为点,
是等腰直角三角形,
设,则,
在中,
,即,
解得:,
在中,
,即,
,
故答案为:.
由方位角补全图形,过B作BE⊥AC于点E,利用二直线平行,内错角相等得∠ACN=∠DAC=15°,∠BAD=∠ABQ=45°,由角的和差得出∠ACB=45°,∠BAC=30°,从而得到△BEC是等腰直角三角形,设BE=CE=xkm,用含x的式子表示出AE,在Rt△AEB中,利用∠BAE的正切函数及特殊锐角三角函数求得x的值;在Rt△BEC中,利用∠BCE的余弦函数及特殊锐角三角函数值求得BC的长.
18.B
解:如图,连接,
∵,,
∴,
设的半径,则,
在中,,
解得,
∵,,
∴,
∵是直径,
∴,
∵是的中位线,
∴,
在中,
,
故答案为:.
根据垂径定理求出的长,设的半径为,在中根据勾股定理得到的值,连接,即可得到,根据中位线求出BE长,再在中运用勾股定理求出即可解题.
19.B
解:.
故答案为:B.
本题考查科学记数法的定义.科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,据此可得:a=3.76,小数点移动了4位,故n=4,进而可选出答案.
20.C
21.C
解:由条件可知
∴函数图象分布在第一、三象限, 当 时,y随x的增大而减小,当 时,y随x的增大而减小,选项B正确;选项C错误;
当 时, 选项A正确;
∴点 )在此函数的图象上,
∴选项D正确,
故答案为: C.
根据反比例函数图象上点的坐标特征以及反比例函数的性质逐一判断即可.
22.D
解:∵在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得到的点的横坐标不变,纵坐标减小3个单位,
∴平移后的的横坐标不变为2,纵坐标为: ,
∴平移后的点的坐标为( ,
故答案为:D.
平面直角坐标系中点的坐标的平移规律为:横坐标左减右加,纵坐标上加下减.
23.D
解:如图,过作,交于,交于,作,交于,交于,
∵四边形是矩形,
∴,
∴,
∴,
∴四边形是矩形,
∴,
同理四边形、四边形,四边形都是矩形,
,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∴,
同理,
设,则,
∵矩形周长是56,
,
解得:,
∴矩形的各边长是.
则该矩形的面积,
故答案为:D.
过作交于,交于,作交于,交于,即可得到四边形、四边形、四边形、四边形是矩形,设,则,利用矩形周长列方程求出x值即可解题.
24.D
解:∵y=x2 4x+2=(x 2)2 2,
∴在 1≤x≤3的取值范围内,当x=2时,有最小值 2,
当x= 1时,有最大值为y=9 2=7.
故答案为:D.
先利用配方法将二次函数的一般式化为顶点式,再利用二次函数的性质分析求解即可.
25.D
解:过点作于点,
∵,,,
∴,
∵,,
∴,
∴
故答案为:D
本题考查30度直角三角形的性质.过点作于点,先利用30度直角三角形的性质可以求出BM=3cm,再利用勾股定理可以求出,再根据可求出的长.
26.B
解:∵为的直径,
∴,
∵,
∴,
∴.
故答案为:B.
根据直径所对的圆周角是直角得∠ACB=90°,由直角三角形的量锐角互余得∠B=55°,进而根据同弧所对的圆周角相等得出∠D=∠B,从而得出答案.
27.B
28.A
29.B
解:第一次相遇两人共走了2800米,第二次相遇两人共走了米,且二者速度不变,,
出发20分时两人第一次相遇,C选项错误;
亮亮的速度为米分,
两人的速度和为米分,
明明的速度为米分,A选项错误;
第二次相遇时距离B地距离为米,B选项正确;
出发35分钟时两人间的距离为米,D选项错误.
故答案为:B.
根据图象提供的信息可得第二次相遇时,两人都行走了60分钟,而第一次相遇是在两人行走35分钟前;由于第一次相遇两人共走了2800米,第二次相遇两人共走了3倍的2800米,且速度不变,从而可得第一次相遇的时间为60分钟的三分之一,据此可判断C选项;当x=35时,出现拐点,显然此时亮亮到达A地,即亮亮用35分钟走了2800米,利用速度=路程÷时间可求出亮亮的速度及两人的速度和,二者做差后可得出明明的速度,据此判断A选项;根据第二次相遇时距离B地的距离=明明的速度×第二次相遇的时间-A、B两地间的距离,据此计算可判断B选项;观察函数图象,可知:出发35分钟时亮亮到达A地,根据出发35分钟时两人间的距离=明明的速度×出发时间,据此计算可判断D选项.
30.A
解:∵ 每人出8元,还盈余3元;每人出7元,则还差4元, 设共有个人,
∴可列方程为,
故答案为:A.
本题考查一元一次方程的实际应用,根据物品的价格是定值,结合" 每人出8元,还盈余3元;每人出7元,则还差4元"列出方程即可.
31.D
32.A
设木长尺,绳长尺,根据题意列方程组得
故答案为:A.
设木长尺,绳长尺,利用“一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺”列二元一次方程组即可.
33.B
解:由题意可知,,
∵,
∴,故,
∵,
∴,
则:,
故选:B.
本题考查锐角三角函数.根据正弦的定义可得:,据此可求出,再利用正弦的定义可得:,利用线段的运算可得:,代入数据可求出答案.
34.B
解:将数从小到大排列为:7,7,8,10,13,处于最中间的数是8,
∴这组数据的中位数是8.
故答案为:B.
求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据;即可求解.
35.A
解:∵k=4>0,
∴在每一个象限内,y随x的增大而减小,切图象分支在第一、三象限,
A、当t<-4时,t+4<0,
∴t<t+4,
∴y2<y1<0,故A符合题意;
B、C、当-4<t<0时,
∴t+4>0,
∴y1<0,y2>0即y1<0<y2,故B、C不符合题意;
D、当t>0时,则t+4>4,
∴t<t+4,
∴0<y2<y1,故D不符合题意;
故答案为:A.
利用反比例函数的性质可证得在每一个象限内,y随x的增大而减小,切图象分支在第一、三象限,由t<-4可得到t+4<0,即可推出t<t+4,由此可得到y1,y2,0的大小关系,可对A作出判断;由-4<t<0,可推出t+4>0,可得到y1<0,y2>0即y1<0<y2,可对B、C作出判断;当t>0时,则t+4>4,可得到t<t+4,由此可推出0<y2<y1,可对D作出判断.
36.A
解:∵ A, M, B 分别表示数 ,且由数轴可知,
∴,,
又∵,
∴,即a+b>0.
故答案为:A.
由数轴可判断数的大小,从而利用数与距离关系表示AM和BM的距离,得出a与b的关系即可.
37.C
解:过点D作DF⊥BC交BC的延长线于点F,
∵四边形ABCD是平行四边形,
∴AB=DC,AD∥BC,
∵AE⊥BC,
∴AE∥DF,∠AEF=90°,
∴四边形AEFD是矩形,
∴AE=DF
在Rt△ABE和Rt△DCF中
∴Rt△ABE≌Rt△DCF(HL),
∴CF=BE=x,
∴EC=BC-BE=y-x,BF=BC+CF=y+x,
∵AE2=AC2-EC2,DF2=BD2-BF2,
∴AC2-EC2=BD2-BF2即4-(y-x)2=()2-(y+x)2,
整理得:xy=2,
∴xy的值不变.
故答案为:C.
过点D作DF⊥BC交BC的延长线于点F,利用平行四边形的性质可证得AB=DC,AD∥BC,再证明四边形AEFD是矩形,利用矩形的性质可证得AE=DF,利用HL可证得Rt△ABE≌Rt△DCF,可推出BE=CF=x,再表示出BF,EC的长,利用勾股定理去证明AC2-EC2=BD2-BF2,可得到关于x,y的方程,解方程求出xy的值,即可求解.
38.A
解:
有①得:2x≥2,
解之:x≥1;
由②得
6-3x>-6,
解之:x<4,
∴不等式组的解集为1≤x<4.
故答案为:A.
分别求出不等式组中的每一个不等式的解集,再确定出不等式组的解集,
39.A
解:∵与是位似图形,位似中心为点.若点的对应点为, 点
∴点B的对应点B'的坐标为(-2×2,4×2)即(-4,8).
故答案为:A.
利用已知条件,可知将点B的横纵坐标都乘以2,可得到点B'的坐标.
40.D
解:A、x3+x2不能合并,故A不符合题意;
B、x3·x2=x5,故B不符合题意;
C、(x3)2=x6,故C不符合题意;
D、x6÷x2=x4,故D符合题意;
故答案为:D.
只有同类项才能合并,可对A作出判断;利用同底数幂相乘,底数不变,指数相加,可对B作出判断;利用幂的乘方法则,可对C作出判断;利用同底数幂相乘,底数不变,指数相减,可对D作出判断.
41.B
解:从几何题的正面看:有三列,三行,第一、二列都有3个小正方形,第三列有1个小正方形,从上到下,最下面一行有3个小正方形.
故答案为:B.
主视图就是从几何题的正面所看到的平面图形,观察已知几何题,可得答案.
42.C
解:如图,
∵∠1=∠3,
∴a∥b,
∴∠2=∠5=50°,
∴∠4=180°-∠5=130°.
故答案为:C.
由同位角相等,两直线平行,得a∥b,由二直线平行,同位角相等,得∠5=∠2=50°,最后根据邻补角定义可求出∠4的度数.
43.D
解:∵此几何体的主视图和左视图是长方形,俯视图是圆,
∴此几何体是圆柱.
故答案为:D.
三个视图中是圆,长方形,可得到此几何体是圆柱体.
44.A
解:A、2(a-1)=2a-2,故此选项计算正确,符合题意;
B、(a+b)2=a2+2ab+b2,故此选项计算错误,不符合题意;
C、3a+2a=5a,故此选项计算错误,不符合题意;
D、(ab)2=a2b2,故此选项计算错误,不符合题意.
故答案为:A.
根据去括号法则(括号前面是负号,去掉括号和负号,括号里的每一项都要变号;括号前面是正号,去掉括号和正号,括号里的每一项都不变号,括号前的数要与括号里的每一项都要相乘),即可判断A选项;由完全平方公式的展开式是一个三项式可判断B选项;整式加法的实质就是合并同类项,所谓同类项就是所含字母相同,而且相同字母的指数也分别相同的项,同类项与字母的顺序没有关系,与系数也没有关系,合并同类项的时候,只需要将系数相加减,字母和字母的指数不变,但不是同类项的一定就不能合并,从而即可判断C选项;由积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘即可判断D选项.
45.D
解: 1,4,2,4,3,3,4,5这组数据中出现次数最多的是4,共出现可三次,
∴这组数据的众数是4时.
故答案为:D.
在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),据此结合题干所给的数据即可得出答案.
46.A
解:、属于正无理数,且()2=<1,>1,
∴比1小的正无理数为.
故答案为:A.
无理数是无限不循环小数,然后利用平方法进行比较即可.
47.A
解:4a2-1=(2a)2-1=(2a-1)(2a+1).
故答案为:A.
直接利用平方差公式分解即可.
48.B
解:380180000000=3.8018×1011.
故答案为:B
根据科学记数法的表示形式为:a×10n,其中1≤|a|<10,此题是绝对值较大的数,因此n=整数数位-1,即可求解.
49.C
解:P( 摸出的球为红球 )=.
故答案为:C.
由概率公式,直接用袋子中红色小球的数量除以袋子中小球的总数量,可得答案.
50.B
解:∵y=,
∴反比例函数的图象位于一、三象限,且在每一象限内,y随x的增大而减小,
∴A(-2,y2)、B(-1,y2)位于第三象限,C(1,y3)位于第一象限.
∵-2<-1,
∴y2
根据反比例函数的性质可得:其图象位于一、三象限,且在每一象限内,y随x的增大而减小,据此进行比较.
同课章节目录
