专项1 单项选择3(浙江中考真题+中考模拟) ——2025年中考数学冲刺中考模拟真题速递(浙江专用)第二辑(答案+解析)
文档属性
| 名称 | 专项1 单项选择3(浙江中考真题+中考模拟) ——2025年中考数学冲刺中考模拟真题速递(浙江专用)第二辑(答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 746.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 17:41:06 | ||
图片预览


文档简介
2025年中考数学冲刺中考模拟真题速递(浙江专用)第二辑
专项1 单项选择3(浙江中考真题+中考模拟)
一、选择题
1.(2025九下·宁波模拟)一个不透明的袋中有4个白球,3个黄球和2个红球,这些球除颜色外其余都相同,则从袋中随机摸出一个球是黄球的概率为( )
A. B. C. D.
2.(2024·浙江)在我国古代建筑中经常使用榫卯构件,如图是某种榫卯构件的示意图,其中榫的俯视图是( )
A. B.
C. D.
3.(2025·杭州模拟)如图,的边与相切于点,交于点,延长交于点,连接.若,,,则的长为( )
A.15 B. C. D.12
4.(2024·浙江)下列计算正确的是( )
A. B. C. D.
5.(2024·浙江)一个三位数,其任意两个相邻数字之差的绝对值如果不超过1,则称该三位数为“平稳数”.现在用1,2,3这三个数字随机组成一个无重复数字的三位数中,是“平稳数”的概率为( )
A. B. C. D.
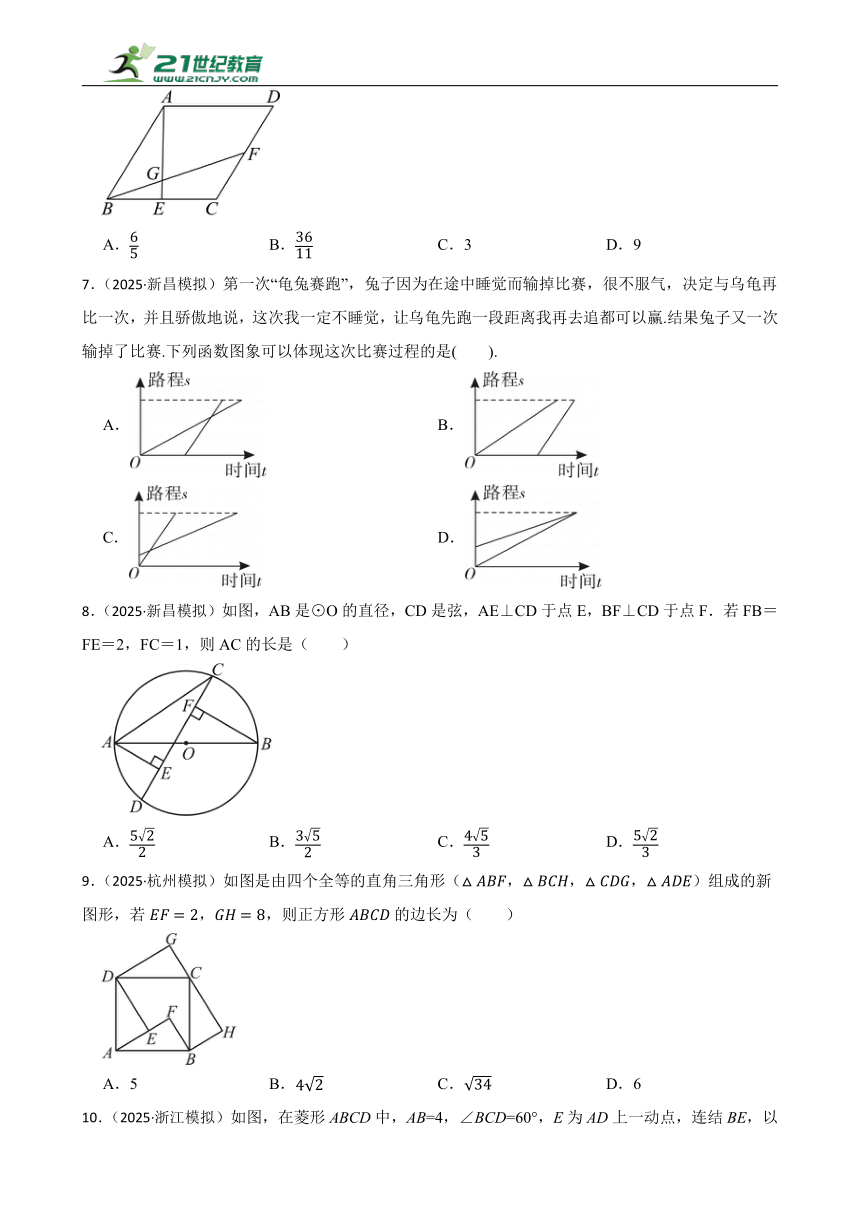
6.(2024·浙江)如图,已知菱形的面积是24,E,F分别是菱形的边的中点,连结与交于点G,则的面积为( )
A. B. C.3 D.9
7.(2025·新昌模拟)第一次“龟兔赛跑”,兔子因为在途中睡觉而输掉比赛,很不服气,决定与乌龟再比一次,并且骄傲地说,这次我一定不睡觉,让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛.下列函数图象可以体现这次比赛过程的是( ).
A. B.
C. D.
8.(2025·新昌模拟)如图,AB是⊙O的直径,CD是弦,AE⊥CD于点E,BF⊥CD于点F.若FB=FE=2,FC=1,则AC的长是( )
A. B. C. D.
9.(2025·杭州模拟)如图是由四个全等的直角三角形(,,,)组成的新图形,若,,则正方形的边长为( )
A.5 B. C. D.6
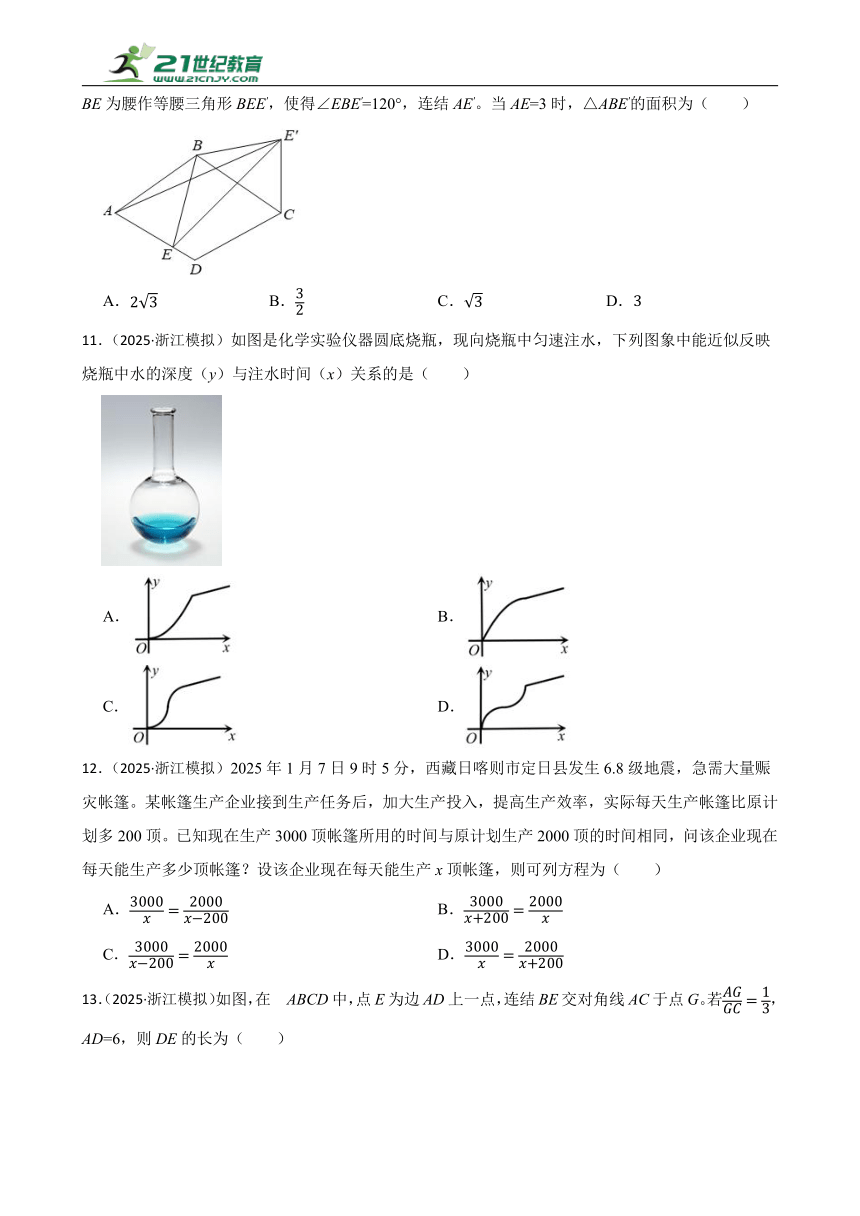
10.(2025·浙江模拟)如图,在菱形ABCD中,AB=4,∠BCD=60°,E为AD上一动点,连结BE,以BE为腰作等腰三角形BEE',使得∠EBE'=120°,连结AE'。当AE=3时,△ABE'的面积为( )
A. B. C. D.
11.(2025·浙江模拟)如图是化学实验仪器圆底烧瓶,现向烧瓶中匀速注水,下列图象中能近似反映烧瓶中水的深度(y)与注水时间(x)关系的是( )
A. B.
C. D.
12.(2025·浙江模拟)2025年1月7日9时5分,西藏日喀则市定日县发生6.8级地震,急需大量赈灾帐篷。某帐篷生产企业接到生产任务后,加大生产投入,提高生产效率,实际每天生产帐篷比原计划多200顶。已知现在生产3000顶帐篷所用的时间与原计划生产2000顶的时间相同,问该企业现在每天能生产多少顶帐篷?设该企业现在每天能生产x顶帐篷,则可列方程为( )
A. B.
C. D.
13.(2025·浙江模拟)如图,在ABCD中,点E为边AD上一点,连结BE交对角线AC于点G。若,AD=6,则DE的长为( )
A. B.4 C. D.5
14.(2025·浙江模拟)下列事件中,属于随机事件的是( )
A.任意画一个四边形,其内角和是360°
B.两张扑克牌,1张是方块,1张是黑桃,从中随机抽取1张扑克牌是红桃
C.掷一枚质地均匀的骰子,六个面上分别刻有1到6的点数,向上一面的点数小于7
D.拨打一个电话号码,电话正被占线中
15.(2025·浙江模拟)下列计算结果为的是( )
A. B. C. D.
16.(2025·浙江模拟)中国是最早使用正负数表示具有相反意义的量的国家。如果把收入20元记作+20元,那么支出10元记作( )
A.-20元 B.+20元 C.-10元 D.+10元
17.(2025九下·东阳模拟)如图,这是由两块完全相同的长方体木块组成的几何体,其左视图为( )
A. B. C. D.
18.(2025·浙江模拟) 已知点 A(x1,y1),B(x1+m,y1+2)两点在反比例函数y=的图象上.则下列判断正确的是( )
A.若k>0,则m<0
B.若k<0,则m可能小于0也可能大于0
C.若k>0,点A,B在同一象限,则m>0
D.若k<0,点A,B在不同象限,则m>0
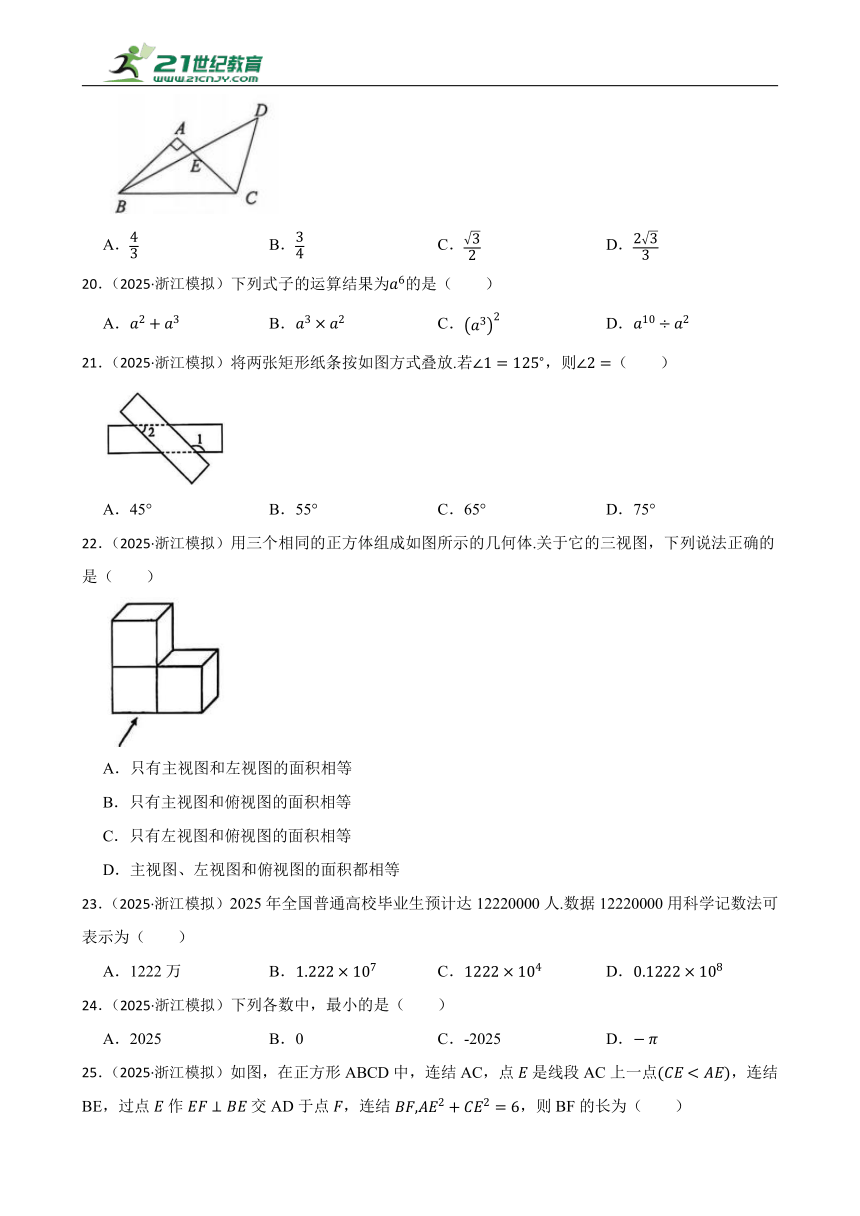
19.(2025·浙江模拟) 如图,在△ABC中,∠BAC=90°,AB=AC,将AC绕着点C按顺时针旋转60°得到CD,连接BD交AC于点E,则S△BEC:S△DEC的值为( )
A. B. C. D.
20.(2025·浙江模拟)下列式子的运算结果为的是( )
A. B. C. D.
21.(2025·浙江模拟)将两张矩形纸条按如图方式叠放.若,则( )
A.45° B.55° C.65° D.75°
22.(2025·浙江模拟)用三个相同的正方体组成如图所示的几何体.关于它的三视图,下列说法正确的是( )
A.只有主视图和左视图的面积相等
B.只有主视图和俯视图的面积相等
C.只有左视图和俯视图的面积相等
D.主视图、左视图和俯视图的面积都相等
23.(2025·浙江模拟)2025年全国普通高校毕业生预计达12220000人.数据12220000用科学记数法可表示为( )
A.1222万 B. C. D.
24.(2025·浙江模拟)下列各数中,最小的是( )
A.2025 B.0 C.-2025 D.
25.(2025·浙江模拟)如图,在正方形ABCD中,连结AC,点是线段AC上一点,连结BE,过点作交AD于点,连结,则BF的长为( )
A. B. C. D.
26.(2025·浙江模拟)已知点都在反比例函数的图象上,且,下列正确的选项是( )
A.若,则 B.若,则
C.若,则 D.若,则
27.(2025·浙江模拟)如图,在中,点在BC边上,,若,,则BC的长为( )
A.10 B. C.8 D.
28.(2025·浙江模拟)我国古代数学专著《九章算术》中有一道关于“分钱”的问题:甲、乙二人有钱若干,若甲给乙10钱,则甲的钱是乙的2倍;若乙给甲5钱,则乙的钱是甲的.若设甲原有x钱,乙原有y钱,则可列方程( )
A. B.
C. D.
29.(2025·浙江模拟)如图,四边形AEFG与四边形ABCD是位似图形,位似比为1:4,则AE:BE=( )
A.1:2 B.1:3 C.1:4 D.1:5
30.(2025·浙江模拟)某小组6名成员的英语口试成绩(满分50分)依次为:45,43,43,47,50,46,这一组数据的中位数是( )
A.43 B.45 C.45.5 D.46
31.(2025·浙江模拟)一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
32.(2025·浙江模拟)如图,几何体是由一个圆锥和一个长方体组成,它的主视图是( )
A. B.
C. D.
33.(2025·浙江模拟)2025年春运期间,铁路杭州站共发送旅客10900000人次.其中10900000用科学记数法可以表示为( )
A.0.109x108 B.10.9×108 C.1.09×108 D.1.09x107
34.(2025·浙江模拟)1月某天,湖州、嘉兴、杭州、温州四地最低气温分别为-4℃,-3℃,-2℃,3℃,其中最低的气温是( )
A.-2℃ B.-3° C.-4℃ D.3℃
35.(2025·浙江模拟)如图,在中,,点是重心,连结AG交BC于点,是边AC上一点,当时,则CF的长为( )
A.1 B. C. D.
36.(2025·浙江模拟)根据国家统计局数据显示,浙江省2024年人均可支配收入52206元,位居全国第三,同比增长4.8%,数据52206用科学记数法表示正确的是( )
A. B.
C. D.
37.(2025九下·洞头模拟)洞头某5天的气温分别为10,10,12,13,15,这5天气温的众数和中位数分别为( )
A.12,10 B.10,12 C.10,13 D.13,15
38.(2025九下·洞头模拟)下列运算正确的是( )
A. B. C. D.
39.(2025九下·洞头模拟)2025年春节假期浙江省累计旅游人数为35673000人次,其中数35673000用科学记数法表示为( )
A. B.
C. D.
40.(2024九下·永昌模拟)不等式组的解集在数轴上表示为( )
A. B.
C. D.
41.(2024九下·临渭模拟)设二次函数是实数,则( )
A.当时,函数的最小值为 B.当时,函数的最小值为
C.当时,函数的最小值为 D.当时,函数的最小值为
42.(2024·杭州模拟)利用尺规作图,过直线AB外一点P作已知直线AB的平行线.下列作法错误的是( )
A. B.
C. D.
43.(2024·杭州模拟)一个不透明的袋子里装有4个红球和2个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )
A. B. C. D.
44.(2025·龙湾模拟)如图,在等腰直角三角形中,,是上一点,,连结接,作,交的垂线于点.连接,交于,若设,在的运动过程中,下列代数式的值不变的是( )
A. B. C. D.
45.(2025·龙湾模拟)如图,在中,,分别以为边向外作正方形和正方形,连结,设,则的值为( )
A. B.2 C. D.
46.(2025·龙湾模拟)如图,,是上的点,,是外的点,和是位似图形,位似中心为点,点,对应点是点,,交于点,若,,则的长为( )
A.3 B.4 C.5 D.6
47.(2025·龙湾模拟)下列四个实数中,最大的数是( )
A. B. C. D.
48.(2025·龙湾模拟)由一个长方体和两个圆柱组合成的凳子如图所示,则它的主视图为( )
A. B.
C. D.
49.(2025九下·洞头模拟)已知两点在反比例函数的图象上,下列判断正确的是( )
A.当时, B.当-时,
C.当时, D.当时,
50.(2025九下·洞头模拟)如图是由四个全等的直角三角形()组成的新图形,若,则正方形ABCD的边长为( )
A.5 B. C. D.6
答案解析部分
1.B
解:由题意得:
不透明袋子里球的总数为4+3+2=9,则从袋中随机摸出一个球是黄球的概率为 ;
故答案为:B.
由袋子中白球、黄球、红球的个数可求得袋子中小球的总数,再根据概率公式可求解.
2.C
3.B
解:连接,如图,
∵是的直径,
∴
∵
∴
在中,,
∵
∴即
∴
在中,;
∵即
∴
∴,
∴
∴,
故答案为:B.
连接,由勾股定理和垂径定理求出,然后根据平行线得到,然后根据相似三角形的对应边成比例解题即可.
4.C
5.B
6.A
7.B
解:A、乌龟比兔子早出发,兔子后出发,先到了,故不符合题意;
B、乌龟比兔子早出发,早到终点,符合题意;
C、乌龟先出发,兔子先到乌龟后到,不符合题意;
D、乌龟先出发,与兔子同时到终点,不符合题意.
故答案为:B.
根据“ 让乌龟先跑一段距离我再去追 ”和“结果兔子又一次输掉了比赛”,可见乌龟早出发到兔子追不上,以此作答.
8.B
9.C
解:由题意得:,
,
,,
设,则,
,
,
,
,
则正方形的边长为,
故答案为:C.
由全等三角形的对应边相等得AF=CH,AE=BF=CG,结合EF=AF-AE=2,CG+CH=GH=8求得AE=BF=3,AF=5,在Rt△ABF中,利用勾股定理即可算出AB的长,从而得到答案.
10.C
解:过E'作E'F⊥CD延长线于点F,延长FE'交AB延长线于点G,作BH⊥CD交于点H,
∵四边形ABCD是菱形,AB=4,∠BCD=60°,
∴AB=BC=CD=AD=4,∠BAD=∠BCD=60°,AB//CD.
∴∠ABC+∠BCD=180°,
∴∠ABC+60°=180°,解得:∠ABC=120°,
∴∠ABC-∠CBE=∠EBE'-∠CBE=120°-∠CBE,
∴∠ABE=∠CBE'.
∵△BEE'是等腰三角形,
∴BE=BE'.
∴△ABE≌△CBE'(SAS).
∴AE=CE'=3,
∴∠E'CD=∠BCE'+∠BCD=120°,
∴∠E'CF=180°-∠E'CD=60°,
∴∠CE'F=180°-∠F-∠E'CF=30°,
∴CF=CE'=,
∴E'F=.
∴∠CBH=180°-∠BHC-∠BCD=30°.
∴CH=BC=2.
∴BH=.
∵AB//CD,E'F⊥CD,
∴GF⊥AB,
∵BH⊥CD,
∴四边形BHFG是矩形,
∴GF=BH=2,
∴E'G=FG-E'F=,
∴ △ABE'的面积为.
故答案为:C.
先根据菱形的性质,利用SAS证明△ABE≌△CBE',再求得∠CE'F,根据含有30度角的直角三角形的性质,求得CF,再利用勾股定理求得E'F,再求得∠CBH,然后利用含有30度角的直角三角形的性质,求得Ch,再利用勾股定理求得BH,接着证明四边形BHFG是矩形,证得GF与E'G,再利用三角形面积公式求解.
11.D
解:化学实验仪器圆底烧瓶,当向烧瓶中匀速注水时,烧瓶中水的深度变化情况会随着注水时间的增加,由急到缓,再由缓到急,到烧瓶颈部时会匀速上升,故D符合.
故答案为:D.
观察烧瓶的形状,再想像加水速度与时间关系,然后作出判断.
12.A
解: 设该企业现在每天能生产x顶帐篷,
则可列方程为:.
故答案为:A.
设该企业现在每天能生产x顶帐篷,根据“ 已知现在生产3000顶帐篷所用的时间与原计划生产2000顶的时间相同 ”列出方程即可.
13.B
解:∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,
∴AE:BC=AG:GC,
∴AE:AD=AG:GC,
又,AD=6,
∴AE:6=1:3,解得AE=2.
∴DE=AD-AE=6-2=4.
故答案为:B.
先根据平行四边形的性质证得AD//BC,再根据平行线分线段成比例,得到比例式求解.
14.D
解:任意画一个四边形,其内角和是360°,这是必然事件,故A不符合;
两张扑克牌,1张是方块,1张是黑桃,从中随机抽取1张扑克牌是红桃,这是不可能事件,故A不符合;
掷一枚质地均匀的骰子,六个面上分别刻有1到6的点数,向上一面的点数小于7,这是必然事件,故B不符合;
拨打一个电话号码,电话正被占线中,这是 随机事件,故D符合.
故答案为:D.
根据事件的种类的意义逐一分析,再作出判断.
15.D
解:中没有同类项,不能合并,故A不符合;
,故B不符合;
,故C不符合;
,故D符合.
故答案为:D.
(1)利用合并同类项法则计算;
(2)利用同底数幂相除法则计算;
(3)利用幂的乘方法则计算;
(4)利用同底数幂相乘法则计算.
16.C
解:收入20元记作+20元,可知收入为正,则支出为负,所以支出10元记作-10元.
故答案为:C.
用正负数表示相反意义的量.
17.D
解:从左面看,左边是一个正方形,右边是一个长方形.
故答案为:D.
左视图就是从几何体的左边所看到的平面图形,据此可得到已知几何体的左视图.
18.B
解:当k>0时,y随x的增大而减小,不知道y1的值在哪个象限,无法判断m<0,故A错误;
当k<0时,点A(x1,y1)与B(x1+m,y1+2)可以在同一象限,也可以不在同一象限,则m可能小于0也可能大于0,故B正确;
当k>0时,点A,B在同一象限,则y随x的增大而减小,所以m<0,故C错误;
当k<0时,点A,B在不同象限,则m<0,故D错误.
故答案为:B.
根据题意,判断当k>0和k<0时,反比例函数y=的增减性,确定m的取值范围.
19.D
解:设AB=2x,如图,连结AD,过点D作DH⊥AC于点H,
∵将AC绕着点C按顺时针旋转60°得到CD,
∴AC=CD,∠ACD=60°,
∴△ACD是等边三角形,
∴AC=AD=CD=2x,AH=CH=x,
∴DH=.
∵,,
∴ S△BEC:S△DEC=:=AB:DH=2x:=.
故答案为:D.
设AB=2x,先证明△ACD是等边三角形,再用x分别表示出AD,AH,再利用勾股定理求出DH,接着根据三角形面积公式,求出 S△BEC:S△DEC.
20.C
解:A:不是同类项,不能合并,不符合题意;
B:,不符合题意;
C:,符合题意;
D:,不符合题意;
故答案为:C.
根据合并同类项、同底数幂的乘法、幂的乘方、同底数幂的除法法则解题即可.
21.B
解:如图,则∠3=180°-∠1=180°-125°=55°,
又∵重叠部分是平行四边形,
∴∠2=∠3=55°,
故答案为:B.
根据邻补角求出∠3的度数,然后根据平行四边形的对角相等解题即可.
22.C
解:依题意,该几何体的三视图,如图所示:
则只有左视图和俯视图的面积相等,
故答案为:C.
根据从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图,可得答案.
23.B
解:
故答案为: B.
本题考查科学记数法的表示方法.科学记数法的表示形式为 的形式,其中 n为整数,表示时关键要正确确定a的值以及n的值.
24.C
解:-2025<<0<2025,
∴最小的数为-2025,
故答案为:C.
根据正数大于零,负数小于零,两个负数比较大小,绝对值大的反而小解题即可.
25.B
解:如图,过点E作GH⊥BC于点H,交AD于点G,
∴∠BHG=90°,
∵四边形ABCD是正方形,
∴∠ACB=∠CAD=45°,∠BAD=∠ABC=90°,
∴四边形ABHG是矩形,△CHE是等腰直角三角形,
∴AG=BH,∠AGH=90°,CH=EH=
∴△AGE是等腰直角三角形,EH2=CE2,
∴BH=AG=GE=,
∴BH2=AE2,
在Rt△BHE中,BE2=BH2+HE2=(AE2+CE2)=3;
∵∠GEF+∠BEH=90°,∠BEH+∠HBE=90°,
∴∠HBE=∠GEF,
在△BHE与△EGF中,∠HBE=∠GEF,BH=GE,∠BHE=∠EGF=90°,
∴△BHE≌△EGF(ASA),
∴BE=EF,
∴BE2=EF2=3,
在Rt△BEF中,.
故答案为:B.
过点E作GH⊥BC于点H,交AD于点G,由正方形性质得∠ACB=∠CAD=45°,∠BAD=∠ABC=90°,则可得四边形ABHG是矩形,△CHE是等腰直角三角形,根据矩形及等腰三角形的性质得AG=BH,∠AGH=90°,CH=EH=,进而可判断出△AGE是等腰直角三角形,则可推出BH=AG=GE=,在Rt△BHE中,利用勾股定理得BE2=(AE2+CE2)=3;由同角的余角相等得∠HBE=∠GEF,从而由ASA判断出△BHE≌△EGF,根据全等三角形的对应边相等得BE=EF,最后在Rt△BEF中,由勾股定理可算出BF的长.
26.D
解:A、∵ 点都在反比例函数的图象上 ,且y3<y1<y2,x3<x2<x1,
∴点A在第三象限,点B、C在第一象限,
∴x3<0,x1>0,x2>0,
∴,故此选项错误,不符合题意;
B、∵ 点都在反比例函数的图象上 ,且y2<y3<y1,x3<x2<x1,
∴点A在第一象限,点B、C在第三象限,
∴x3<0,x1>0,x2<0,
∴,故此选项错误,不符合题意;
C、∵ 点都在反比例函数的图象上 ,且y2<y1<y3,x3<x2<x1,
∴点A、B在第四象限,点C在第二象限,
∴x3<0,x1>0,x2>0,
∴,故此选项错误,不符合题意;
D、∵ 点都在反比例函数的图象上 ,且y1<y3<y2,x3<x2<x1,
∴点A在第四象限,点B、C在第二象限,
∴x3<0,x1>0,x2<0,
∴,故此选项正确,符合题意.
故答案为:D.
反比例函数中,当k>0时,图象的两支分布在第一、三象限,在每一个象限内,y随x的增大而减小;当k<0时,图象的两支分布在第二、四象限,在每一个象限内,y随x的增大而增大,据此结合题干给出的信息,判断出A、B、C三点所在的象限,从而可判断出x1、x2、x3的正负,进而根据有理数乘法法则可判断出x1、x2、x3积的正负.
27.A
解:∵CE⊥AD,AE=DE=2,
∴AD=AE+DE=4,CE是线段AD的垂直平分线,
∴AC=CD=6,
∴∠ADC=∠DAC,
∵∠DAC=2∠B,∠ADC=∠B+∠BAD,
∴∠BAD=∠B,
∴AD=BD=4,
∴BC=BD+CD=10.
故答案为:A.
易得CE是线段AD的垂直平分线,由线段垂直平分线上的点到线段两端点的距离相等可得AC=CD=6,由等边对等角可得∠ADC=∠DAC,进而结合已知及三角形外角的性质推出∠BAD=∠B,由等角对等边得AD=BD=4,结合图形,由BC=BD+CD可求出BC的长.
28.A
解:设甲原有x钱,乙原有y钱,由题意,
得.
故答案为:A.
设甲原有x钱,乙原有y钱,根据“ 甲给乙10钱,则甲的钱是乙的2倍 ”可列方程x-10=2(y+10),根据“ 乙给甲5钱,则乙的钱是甲的 ”可列方程,联立两方程即可.
29.B
解:∵ 四边形AEFG与四边形ABCD是位似图形, 位似比为1:4,
∴AE∶AB=1∶4,
∴AB=4AE,
∴BE=AB-AE=3AE,
∴AE∶BE=1∶3.
故答案为:B.
根据位似比为1∶4可得AB=4AE,则AB=4AE,然后结合图形推出BE=AB-AE=3AE,从而即可求出答案.
30.C
解:将该小组6名成员的英语口试成绩按从低到高依次排列为:43,43,45,46,47,50,
排第3与4位的成绩分别是45与46,
∴这组数据的中位数为:.
故答案为:C.
中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数叫做这组数据的中位数,据此解答即可.
31.A
解:设这个角为x°,则其余角为(90-x)°,由题意,
得2x=90-x,
∴x=30,即这个角的度数为30°.
故答案为:A.
设这个角为x°,由和为90°的两个角互为余角可得则其余角为(90-x)°,再由“ 一个角的余角是它的2倍 ”列出方程,求解即可.
32.B
解:该几何体是由一个圆锥和一个长方体组成,圆锥的主视图是一个等腰三角形,长方体的主视图是一个以长方体的底边长为长,高为宽的长方形,故只有B选项符合题意.
故答案为:B.
主视图,就是从几何体的正面看得到的正投影,能看见的轮廓线画成实线,看不见但又存在的轮廓线画成虚线,据此逐一判断得出答案.
33.D
解:10900000用科学记数法可以表示为: 1.09x107.
故答案为:D.
用科学记数法表示大于10的数,一般表示成a×10n的形式,其中1≤a<10,n等于原数的整数位数减去1,据此解答即可.
34.C
解:∵|-4|=4,|-3|=3,|-2|=2,2<3<4,
∴-4<-3<-2<3,
∴1月某天,湖州、嘉兴、杭州、温州四地最低气温是-4℃.
故答案为:C.
根据正数大于负数,两个负数,绝对值大的反而小,进行解答即可.
35.B
解:连接BG并延长,过点A作AE//BC,交AC于点H,交射线BH于点E,如图:
∴∠E=∠CBH,∠EAH=∠BCH,
∵点G是△ABC的重心,
∴AD是BC边的中线,BH是AC边的中线,
∴,AH=CH,
∴△EAH≌△BCH(AAS)
∴AE=BC=4.
∵AE//BC,
∴.
∵AB=AC,
∴AD⊥BC,
在Rt△ABD中,,
∴.
当GF⊥AD时,
GF//BC,
∴.
∴.
故答案为:B.
连接BG并延长,过点A作AE//BC,交AC于点H,交射线BH于点E,由点是重心可得,AH=CH,证明△EAH≌△BCH,再利用平行线分线段成比例的性质,可证得.利用等腰三角形“三线合一”的性质得AD⊥BC,继而可利用锐角三角函数求得AC长,最后再次利用平行线分线段成比例的性质即可求得FC的长.
36.B
解:52206=5.2206×104,
故答案为:B.
用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|≤9,n为原数的整数位数减1,据此即可求解.
37.B
解:这5天气温的众数是10;中位数是12;
故答案为:B.
本题考查统计应用,众数和中位数的定义.先观察数据可得10出现次数最多,利用众数的定义可求出众数;根据题意可得12排在中间,利用中位数的定义可求出中位数.
38.D
解:A. 与不是同类项,不能合并,故本选项运算错误,不符合题意,A错误;
B. ,故本选项运算错误,不符合题意,B错误;
C. ,故本选项运算错误,不符合题意,C错误;
D. ,本选项运算正确,符合题意,D正确.
故答案为:D.
本题考查合并同类项、同底数幂相乘、幂的乘方、同底数幂除法运算.根据同类项定义可得 与不是同类项,不能合并,据此可判断A选项;根据同底数幂乘法运算法则可得:,据此可判断B选项;根据幂的乘方运算法则可得:,据此可判断C选项;根据同底数幂除法运算法则可得:,据此可判断D选项.
39.D
解:数35673000用科学记数法表示为.
故答案为:D.
本题考查科学记数法表示较大的数的方法.科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同,根据数据可得:a=3.5673.n=7,据此可选出答案.
40.B
解:解不等式,得,
解不等式,得,
∴不等式组的解集为,
在数轴上表示为:
故答案为:B.
分别解出不等式组中两个不等式的解集,根据口诀:同大取大,同小取小,大小小大中间找,大大小小无解了确定出解集,进而根据数轴上表示不等式组的解集的方法“大向右,小向左,实心等于,空心不等”将该不等式组的解集在数轴上表示出来即可.
41.A
解:令y=a(x-m)(x-m-k)中的y=0,
则a(x-m)(x-m-k)=0,
解得x1=m,x2=m+k,
∴该二次函数的对称轴为:,
∵a>0,
∴函数有最低点,即当时,函数有最小值,
当k=2时,函数的最小值y=-a,
当k=4时,函数有最小值y=-4a,
∴只有A选项正确,符合题意.
故答案为:A.
令抛物线中的y=0算出对应的x的值,可得函数与x轴交点的横坐标,进而根据抛物线的对称性可得其对称轴是抛物线与x轴两交点横坐标和的一半求出抛物线的对称轴直线为x=m+k,由于抛物线中二次项的系数大于零,故函数的最小值就是顶点的纵坐标,从而将x=m+k代入抛物线解析式可算出顶点纵坐标,最后再分别代入k的值即可判断.
42.D
解:对于A,根据作图痕迹可知,表示为作一个角等于已知角,此时同位角相等,两直线平行,符合题意;
对于B,此时作∠PAB的角平分线及作等腰PQ=PA,故∠PAQ=∠BAQ=∠PQA,即内错角相等,两直线平行,符合题意;
对于C,以P为圆心PA为半径,交AB于点C、交AP延长线于点D,此时AP=PC=PD,再分别以C和D为圆心作出∠DPC角平分线,
故∠DPC=∠DPQ+∠CPQ=∠PAC+∠PCA,易得∠PAB=∠DPQ,即同位角相等,两直线平行,符合题意;
对于D,以C为圆心,CP为半径作弧交AB于点D,即有CD=CP,再分别以D和P为圆心作出线段DP的垂直平分线交弧于点G,易得PQ=DQ,但无法证明此时PQ=CP,即无法得证菱形,故无法证明平行,不符合题意
故答案为:D.
由作图痕迹结合平行线的判定分析,痕迹为作等角判断A,痕迹为等腰与角平分线角度转换判断B,同理进行角度转换判断C,利用圆的对称性及垂直平分线的性质检验D.
43.D
解: 从袋中任意摸出一个球有6种情况,其中摸出一个球是红色的有4种情况,
∴P=.
故答案为:D.
首先确定从袋中任意摸出一个球共有几种情况,再确定摸出一个球是红色的有几种情况,然后用概率公式求概率即可.
44.D
解:如图所示,过点作于点,
∵等腰直角△ABC中,,
∴,
又∵
∴
∴
∴即
解得:
∴,,都不是定值,故A、B、C选项都不符合题意;
∴是定值,故D选项符合题意.
故答案为:D.
过点A作AG⊥BC于点G,根据等腰直角三角形的性质得AG=CG=4,由同一平面内,垂直于同一直线的两条直线互相平行得AG∥CE,由平行于三角形一边的直线截其它两边的延长线,所截三角形与原三角形相似得△AGF∽△ECF,由相似三角形对应边成比例得出,进而逐项分析判断,即可求解.
45.C
解:如图所示,连接,设交于点,
∵四边形,是正方形,
∴AG⊥CF,AO=OF,∠DAB=∠CAG=45°,
又∵
∴
∴三点共线,
又∵
∴,
∵
∴
∴
故答案为:C.
连AD、AG,设AG与CF交于点O,由正方形对角线互相垂直平分、相等及每条对角线平分一组对角得AG⊥CF,AO=OF及∠DAB=∠CAG=45°,从而证明D、A、G三点共线,利用勾股定理分别算出AD、AO及OF的长,进而根据正切的定义,即可求解.
46.A
解:∵和是位似图形,位似中心为点,
∴,
∵,,
∴,
∴,
∵,
∴,
解得:,
故答案为:A.
利用位似图形对应点到位似中心的距离比等于位似比得出,再结合,,得出,即可求解.
47.D
解:∵3<4,
∴,即
∴,
∴四个实数中最大的是.
故答案为:D.
首先根据被开方数越大,其算术平方根就越大判断出,再根据正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,判断即可.
48.A
解:根据三视图的定义,主视图是从正面看到的图形,
∴它的主视图为:
故答案为:A.
从正面看得到的正投影就是主视图,该几何体从给出的主视方向看,长方体的主视图应该是一个以底面长为长,高为宽的长方形,两个圆柱的主视图应该是以圆柱直径为长,圆柱高为宽的长方形,据此判断即可.
49.A
解:反比例函数的图象位于第一、三象限,在每一个象限内,y随x的增大而减小,
∵,
A.当时,点,点都在第一象限,
∴,A正确;
B.C.当时,,
∴点在第三象限,点在第一象限,
∴,B错误、C错误;
D.当时,,则点,点都在第三象限,
∴,D错误;
故答案为:A.
本题考查反比例函数的图象与性质.根据反比例函数的性质可得:当时,反比例函数的图象位于第一、三象限,在每一个象限内,y随x的增大而减小.当时,点,点都在第一象限,再根据,据此可判断的大小,判断A选项;当时,,点在第三象限,点在第一象限,再根据,据此可判断的大小,判断B选项和C选项;当时,,则点,点都在第三象限,再根据,据此可判断的大小,判断D选项.
50.C
解:由题意得:,
,
,,
设,则,
,
,
,
,
则正方形的边长为,
故答案为:C.
本题考查勾股定理,全等三角形的性质.先利用全等三角形的性质得到,设,则,利用线段的运算可得:,解方程可求出x=3,进而可求得,利用勾股定理可求出AB,进而可求出正方形的边长.
专项1 单项选择3(浙江中考真题+中考模拟)
一、选择题
1.(2025九下·宁波模拟)一个不透明的袋中有4个白球,3个黄球和2个红球,这些球除颜色外其余都相同,则从袋中随机摸出一个球是黄球的概率为( )
A. B. C. D.
2.(2024·浙江)在我国古代建筑中经常使用榫卯构件,如图是某种榫卯构件的示意图,其中榫的俯视图是( )
A. B.
C. D.
3.(2025·杭州模拟)如图,的边与相切于点,交于点,延长交于点,连接.若,,,则的长为( )
A.15 B. C. D.12
4.(2024·浙江)下列计算正确的是( )
A. B. C. D.
5.(2024·浙江)一个三位数,其任意两个相邻数字之差的绝对值如果不超过1,则称该三位数为“平稳数”.现在用1,2,3这三个数字随机组成一个无重复数字的三位数中,是“平稳数”的概率为( )
A. B. C. D.
6.(2024·浙江)如图,已知菱形的面积是24,E,F分别是菱形的边的中点,连结与交于点G,则的面积为( )
A. B. C.3 D.9
7.(2025·新昌模拟)第一次“龟兔赛跑”,兔子因为在途中睡觉而输掉比赛,很不服气,决定与乌龟再比一次,并且骄傲地说,这次我一定不睡觉,让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛.下列函数图象可以体现这次比赛过程的是( ).
A. B.
C. D.
8.(2025·新昌模拟)如图,AB是⊙O的直径,CD是弦,AE⊥CD于点E,BF⊥CD于点F.若FB=FE=2,FC=1,则AC的长是( )
A. B. C. D.
9.(2025·杭州模拟)如图是由四个全等的直角三角形(,,,)组成的新图形,若,,则正方形的边长为( )
A.5 B. C. D.6
10.(2025·浙江模拟)如图,在菱形ABCD中,AB=4,∠BCD=60°,E为AD上一动点,连结BE,以BE为腰作等腰三角形BEE',使得∠EBE'=120°,连结AE'。当AE=3时,△ABE'的面积为( )
A. B. C. D.
11.(2025·浙江模拟)如图是化学实验仪器圆底烧瓶,现向烧瓶中匀速注水,下列图象中能近似反映烧瓶中水的深度(y)与注水时间(x)关系的是( )
A. B.
C. D.
12.(2025·浙江模拟)2025年1月7日9时5分,西藏日喀则市定日县发生6.8级地震,急需大量赈灾帐篷。某帐篷生产企业接到生产任务后,加大生产投入,提高生产效率,实际每天生产帐篷比原计划多200顶。已知现在生产3000顶帐篷所用的时间与原计划生产2000顶的时间相同,问该企业现在每天能生产多少顶帐篷?设该企业现在每天能生产x顶帐篷,则可列方程为( )
A. B.
C. D.
13.(2025·浙江模拟)如图,在ABCD中,点E为边AD上一点,连结BE交对角线AC于点G。若,AD=6,则DE的长为( )
A. B.4 C. D.5
14.(2025·浙江模拟)下列事件中,属于随机事件的是( )
A.任意画一个四边形,其内角和是360°
B.两张扑克牌,1张是方块,1张是黑桃,从中随机抽取1张扑克牌是红桃
C.掷一枚质地均匀的骰子,六个面上分别刻有1到6的点数,向上一面的点数小于7
D.拨打一个电话号码,电话正被占线中
15.(2025·浙江模拟)下列计算结果为的是( )
A. B. C. D.
16.(2025·浙江模拟)中国是最早使用正负数表示具有相反意义的量的国家。如果把收入20元记作+20元,那么支出10元记作( )
A.-20元 B.+20元 C.-10元 D.+10元
17.(2025九下·东阳模拟)如图,这是由两块完全相同的长方体木块组成的几何体,其左视图为( )
A. B. C. D.
18.(2025·浙江模拟) 已知点 A(x1,y1),B(x1+m,y1+2)两点在反比例函数y=的图象上.则下列判断正确的是( )
A.若k>0,则m<0
B.若k<0,则m可能小于0也可能大于0
C.若k>0,点A,B在同一象限,则m>0
D.若k<0,点A,B在不同象限,则m>0
19.(2025·浙江模拟) 如图,在△ABC中,∠BAC=90°,AB=AC,将AC绕着点C按顺时针旋转60°得到CD,连接BD交AC于点E,则S△BEC:S△DEC的值为( )
A. B. C. D.
20.(2025·浙江模拟)下列式子的运算结果为的是( )
A. B. C. D.
21.(2025·浙江模拟)将两张矩形纸条按如图方式叠放.若,则( )
A.45° B.55° C.65° D.75°
22.(2025·浙江模拟)用三个相同的正方体组成如图所示的几何体.关于它的三视图,下列说法正确的是( )
A.只有主视图和左视图的面积相等
B.只有主视图和俯视图的面积相等
C.只有左视图和俯视图的面积相等
D.主视图、左视图和俯视图的面积都相等
23.(2025·浙江模拟)2025年全国普通高校毕业生预计达12220000人.数据12220000用科学记数法可表示为( )
A.1222万 B. C. D.
24.(2025·浙江模拟)下列各数中,最小的是( )
A.2025 B.0 C.-2025 D.
25.(2025·浙江模拟)如图,在正方形ABCD中,连结AC,点是线段AC上一点,连结BE,过点作交AD于点,连结,则BF的长为( )
A. B. C. D.
26.(2025·浙江模拟)已知点都在反比例函数的图象上,且,下列正确的选项是( )
A.若,则 B.若,则
C.若,则 D.若,则
27.(2025·浙江模拟)如图,在中,点在BC边上,,若,,则BC的长为( )
A.10 B. C.8 D.
28.(2025·浙江模拟)我国古代数学专著《九章算术》中有一道关于“分钱”的问题:甲、乙二人有钱若干,若甲给乙10钱,则甲的钱是乙的2倍;若乙给甲5钱,则乙的钱是甲的.若设甲原有x钱,乙原有y钱,则可列方程( )
A. B.
C. D.
29.(2025·浙江模拟)如图,四边形AEFG与四边形ABCD是位似图形,位似比为1:4,则AE:BE=( )
A.1:2 B.1:3 C.1:4 D.1:5
30.(2025·浙江模拟)某小组6名成员的英语口试成绩(满分50分)依次为:45,43,43,47,50,46,这一组数据的中位数是( )
A.43 B.45 C.45.5 D.46
31.(2025·浙江模拟)一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
32.(2025·浙江模拟)如图,几何体是由一个圆锥和一个长方体组成,它的主视图是( )
A. B.
C. D.
33.(2025·浙江模拟)2025年春运期间,铁路杭州站共发送旅客10900000人次.其中10900000用科学记数法可以表示为( )
A.0.109x108 B.10.9×108 C.1.09×108 D.1.09x107
34.(2025·浙江模拟)1月某天,湖州、嘉兴、杭州、温州四地最低气温分别为-4℃,-3℃,-2℃,3℃,其中最低的气温是( )
A.-2℃ B.-3° C.-4℃ D.3℃
35.(2025·浙江模拟)如图,在中,,点是重心,连结AG交BC于点,是边AC上一点,当时,则CF的长为( )
A.1 B. C. D.
36.(2025·浙江模拟)根据国家统计局数据显示,浙江省2024年人均可支配收入52206元,位居全国第三,同比增长4.8%,数据52206用科学记数法表示正确的是( )
A. B.
C. D.
37.(2025九下·洞头模拟)洞头某5天的气温分别为10,10,12,13,15,这5天气温的众数和中位数分别为( )
A.12,10 B.10,12 C.10,13 D.13,15
38.(2025九下·洞头模拟)下列运算正确的是( )
A. B. C. D.
39.(2025九下·洞头模拟)2025年春节假期浙江省累计旅游人数为35673000人次,其中数35673000用科学记数法表示为( )
A. B.
C. D.
40.(2024九下·永昌模拟)不等式组的解集在数轴上表示为( )
A. B.
C. D.
41.(2024九下·临渭模拟)设二次函数是实数,则( )
A.当时,函数的最小值为 B.当时,函数的最小值为
C.当时,函数的最小值为 D.当时,函数的最小值为
42.(2024·杭州模拟)利用尺规作图,过直线AB外一点P作已知直线AB的平行线.下列作法错误的是( )
A. B.
C. D.
43.(2024·杭州模拟)一个不透明的袋子里装有4个红球和2个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )
A. B. C. D.
44.(2025·龙湾模拟)如图,在等腰直角三角形中,,是上一点,,连结接,作,交的垂线于点.连接,交于,若设,在的运动过程中,下列代数式的值不变的是( )
A. B. C. D.
45.(2025·龙湾模拟)如图,在中,,分别以为边向外作正方形和正方形,连结,设,则的值为( )
A. B.2 C. D.
46.(2025·龙湾模拟)如图,,是上的点,,是外的点,和是位似图形,位似中心为点,点,对应点是点,,交于点,若,,则的长为( )
A.3 B.4 C.5 D.6
47.(2025·龙湾模拟)下列四个实数中,最大的数是( )
A. B. C. D.
48.(2025·龙湾模拟)由一个长方体和两个圆柱组合成的凳子如图所示,则它的主视图为( )
A. B.
C. D.
49.(2025九下·洞头模拟)已知两点在反比例函数的图象上,下列判断正确的是( )
A.当时, B.当-时,
C.当时, D.当时,
50.(2025九下·洞头模拟)如图是由四个全等的直角三角形()组成的新图形,若,则正方形ABCD的边长为( )
A.5 B. C. D.6
答案解析部分
1.B
解:由题意得:
不透明袋子里球的总数为4+3+2=9,则从袋中随机摸出一个球是黄球的概率为 ;
故答案为:B.
由袋子中白球、黄球、红球的个数可求得袋子中小球的总数,再根据概率公式可求解.
2.C
3.B
解:连接,如图,
∵是的直径,
∴
∵
∴
在中,,
∵
∴即
∴
在中,;
∵即
∴
∴,
∴
∴,
故答案为:B.
连接,由勾股定理和垂径定理求出,然后根据平行线得到,然后根据相似三角形的对应边成比例解题即可.
4.C
5.B
6.A
7.B
解:A、乌龟比兔子早出发,兔子后出发,先到了,故不符合题意;
B、乌龟比兔子早出发,早到终点,符合题意;
C、乌龟先出发,兔子先到乌龟后到,不符合题意;
D、乌龟先出发,与兔子同时到终点,不符合题意.
故答案为:B.
根据“ 让乌龟先跑一段距离我再去追 ”和“结果兔子又一次输掉了比赛”,可见乌龟早出发到兔子追不上,以此作答.
8.B
9.C
解:由题意得:,
,
,,
设,则,
,
,
,
,
则正方形的边长为,
故答案为:C.
由全等三角形的对应边相等得AF=CH,AE=BF=CG,结合EF=AF-AE=2,CG+CH=GH=8求得AE=BF=3,AF=5,在Rt△ABF中,利用勾股定理即可算出AB的长,从而得到答案.
10.C
解:过E'作E'F⊥CD延长线于点F,延长FE'交AB延长线于点G,作BH⊥CD交于点H,
∵四边形ABCD是菱形,AB=4,∠BCD=60°,
∴AB=BC=CD=AD=4,∠BAD=∠BCD=60°,AB//CD.
∴∠ABC+∠BCD=180°,
∴∠ABC+60°=180°,解得:∠ABC=120°,
∴∠ABC-∠CBE=∠EBE'-∠CBE=120°-∠CBE,
∴∠ABE=∠CBE'.
∵△BEE'是等腰三角形,
∴BE=BE'.
∴△ABE≌△CBE'(SAS).
∴AE=CE'=3,
∴∠E'CD=∠BCE'+∠BCD=120°,
∴∠E'CF=180°-∠E'CD=60°,
∴∠CE'F=180°-∠F-∠E'CF=30°,
∴CF=CE'=,
∴E'F=.
∴∠CBH=180°-∠BHC-∠BCD=30°.
∴CH=BC=2.
∴BH=.
∵AB//CD,E'F⊥CD,
∴GF⊥AB,
∵BH⊥CD,
∴四边形BHFG是矩形,
∴GF=BH=2,
∴E'G=FG-E'F=,
∴ △ABE'的面积为.
故答案为:C.
先根据菱形的性质,利用SAS证明△ABE≌△CBE',再求得∠CE'F,根据含有30度角的直角三角形的性质,求得CF,再利用勾股定理求得E'F,再求得∠CBH,然后利用含有30度角的直角三角形的性质,求得Ch,再利用勾股定理求得BH,接着证明四边形BHFG是矩形,证得GF与E'G,再利用三角形面积公式求解.
11.D
解:化学实验仪器圆底烧瓶,当向烧瓶中匀速注水时,烧瓶中水的深度变化情况会随着注水时间的增加,由急到缓,再由缓到急,到烧瓶颈部时会匀速上升,故D符合.
故答案为:D.
观察烧瓶的形状,再想像加水速度与时间关系,然后作出判断.
12.A
解: 设该企业现在每天能生产x顶帐篷,
则可列方程为:.
故答案为:A.
设该企业现在每天能生产x顶帐篷,根据“ 已知现在生产3000顶帐篷所用的时间与原计划生产2000顶的时间相同 ”列出方程即可.
13.B
解:∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,
∴AE:BC=AG:GC,
∴AE:AD=AG:GC,
又,AD=6,
∴AE:6=1:3,解得AE=2.
∴DE=AD-AE=6-2=4.
故答案为:B.
先根据平行四边形的性质证得AD//BC,再根据平行线分线段成比例,得到比例式求解.
14.D
解:任意画一个四边形,其内角和是360°,这是必然事件,故A不符合;
两张扑克牌,1张是方块,1张是黑桃,从中随机抽取1张扑克牌是红桃,这是不可能事件,故A不符合;
掷一枚质地均匀的骰子,六个面上分别刻有1到6的点数,向上一面的点数小于7,这是必然事件,故B不符合;
拨打一个电话号码,电话正被占线中,这是 随机事件,故D符合.
故答案为:D.
根据事件的种类的意义逐一分析,再作出判断.
15.D
解:中没有同类项,不能合并,故A不符合;
,故B不符合;
,故C不符合;
,故D符合.
故答案为:D.
(1)利用合并同类项法则计算;
(2)利用同底数幂相除法则计算;
(3)利用幂的乘方法则计算;
(4)利用同底数幂相乘法则计算.
16.C
解:收入20元记作+20元,可知收入为正,则支出为负,所以支出10元记作-10元.
故答案为:C.
用正负数表示相反意义的量.
17.D
解:从左面看,左边是一个正方形,右边是一个长方形.
故答案为:D.
左视图就是从几何体的左边所看到的平面图形,据此可得到已知几何体的左视图.
18.B
解:当k>0时,y随x的增大而减小,不知道y1的值在哪个象限,无法判断m<0,故A错误;
当k<0时,点A(x1,y1)与B(x1+m,y1+2)可以在同一象限,也可以不在同一象限,则m可能小于0也可能大于0,故B正确;
当k>0时,点A,B在同一象限,则y随x的增大而减小,所以m<0,故C错误;
当k<0时,点A,B在不同象限,则m<0,故D错误.
故答案为:B.
根据题意,判断当k>0和k<0时,反比例函数y=的增减性,确定m的取值范围.
19.D
解:设AB=2x,如图,连结AD,过点D作DH⊥AC于点H,
∵将AC绕着点C按顺时针旋转60°得到CD,
∴AC=CD,∠ACD=60°,
∴△ACD是等边三角形,
∴AC=AD=CD=2x,AH=CH=x,
∴DH=.
∵,,
∴ S△BEC:S△DEC=:=AB:DH=2x:=.
故答案为:D.
设AB=2x,先证明△ACD是等边三角形,再用x分别表示出AD,AH,再利用勾股定理求出DH,接着根据三角形面积公式,求出 S△BEC:S△DEC.
20.C
解:A:不是同类项,不能合并,不符合题意;
B:,不符合题意;
C:,符合题意;
D:,不符合题意;
故答案为:C.
根据合并同类项、同底数幂的乘法、幂的乘方、同底数幂的除法法则解题即可.
21.B
解:如图,则∠3=180°-∠1=180°-125°=55°,
又∵重叠部分是平行四边形,
∴∠2=∠3=55°,
故答案为:B.
根据邻补角求出∠3的度数,然后根据平行四边形的对角相等解题即可.
22.C
解:依题意,该几何体的三视图,如图所示:
则只有左视图和俯视图的面积相等,
故答案为:C.
根据从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图,可得答案.
23.B
解:
故答案为: B.
本题考查科学记数法的表示方法.科学记数法的表示形式为 的形式,其中 n为整数,表示时关键要正确确定a的值以及n的值.
24.C
解:-2025<<0<2025,
∴最小的数为-2025,
故答案为:C.
根据正数大于零,负数小于零,两个负数比较大小,绝对值大的反而小解题即可.
25.B
解:如图,过点E作GH⊥BC于点H,交AD于点G,
∴∠BHG=90°,
∵四边形ABCD是正方形,
∴∠ACB=∠CAD=45°,∠BAD=∠ABC=90°,
∴四边形ABHG是矩形,△CHE是等腰直角三角形,
∴AG=BH,∠AGH=90°,CH=EH=
∴△AGE是等腰直角三角形,EH2=CE2,
∴BH=AG=GE=,
∴BH2=AE2,
在Rt△BHE中,BE2=BH2+HE2=(AE2+CE2)=3;
∵∠GEF+∠BEH=90°,∠BEH+∠HBE=90°,
∴∠HBE=∠GEF,
在△BHE与△EGF中,∠HBE=∠GEF,BH=GE,∠BHE=∠EGF=90°,
∴△BHE≌△EGF(ASA),
∴BE=EF,
∴BE2=EF2=3,
在Rt△BEF中,.
故答案为:B.
过点E作GH⊥BC于点H,交AD于点G,由正方形性质得∠ACB=∠CAD=45°,∠BAD=∠ABC=90°,则可得四边形ABHG是矩形,△CHE是等腰直角三角形,根据矩形及等腰三角形的性质得AG=BH,∠AGH=90°,CH=EH=,进而可判断出△AGE是等腰直角三角形,则可推出BH=AG=GE=,在Rt△BHE中,利用勾股定理得BE2=(AE2+CE2)=3;由同角的余角相等得∠HBE=∠GEF,从而由ASA判断出△BHE≌△EGF,根据全等三角形的对应边相等得BE=EF,最后在Rt△BEF中,由勾股定理可算出BF的长.
26.D
解:A、∵ 点都在反比例函数的图象上 ,且y3<y1<y2,x3<x2<x1,
∴点A在第三象限,点B、C在第一象限,
∴x3<0,x1>0,x2>0,
∴,故此选项错误,不符合题意;
B、∵ 点都在反比例函数的图象上 ,且y2<y3<y1,x3<x2<x1,
∴点A在第一象限,点B、C在第三象限,
∴x3<0,x1>0,x2<0,
∴,故此选项错误,不符合题意;
C、∵ 点都在反比例函数的图象上 ,且y2<y1<y3,x3<x2<x1,
∴点A、B在第四象限,点C在第二象限,
∴x3<0,x1>0,x2>0,
∴,故此选项错误,不符合题意;
D、∵ 点都在反比例函数的图象上 ,且y1<y3<y2,x3<x2<x1,
∴点A在第四象限,点B、C在第二象限,
∴x3<0,x1>0,x2<0,
∴,故此选项正确,符合题意.
故答案为:D.
反比例函数中,当k>0时,图象的两支分布在第一、三象限,在每一个象限内,y随x的增大而减小;当k<0时,图象的两支分布在第二、四象限,在每一个象限内,y随x的增大而增大,据此结合题干给出的信息,判断出A、B、C三点所在的象限,从而可判断出x1、x2、x3的正负,进而根据有理数乘法法则可判断出x1、x2、x3积的正负.
27.A
解:∵CE⊥AD,AE=DE=2,
∴AD=AE+DE=4,CE是线段AD的垂直平分线,
∴AC=CD=6,
∴∠ADC=∠DAC,
∵∠DAC=2∠B,∠ADC=∠B+∠BAD,
∴∠BAD=∠B,
∴AD=BD=4,
∴BC=BD+CD=10.
故答案为:A.
易得CE是线段AD的垂直平分线,由线段垂直平分线上的点到线段两端点的距离相等可得AC=CD=6,由等边对等角可得∠ADC=∠DAC,进而结合已知及三角形外角的性质推出∠BAD=∠B,由等角对等边得AD=BD=4,结合图形,由BC=BD+CD可求出BC的长.
28.A
解:设甲原有x钱,乙原有y钱,由题意,
得.
故答案为:A.
设甲原有x钱,乙原有y钱,根据“ 甲给乙10钱,则甲的钱是乙的2倍 ”可列方程x-10=2(y+10),根据“ 乙给甲5钱,则乙的钱是甲的 ”可列方程,联立两方程即可.
29.B
解:∵ 四边形AEFG与四边形ABCD是位似图形, 位似比为1:4,
∴AE∶AB=1∶4,
∴AB=4AE,
∴BE=AB-AE=3AE,
∴AE∶BE=1∶3.
故答案为:B.
根据位似比为1∶4可得AB=4AE,则AB=4AE,然后结合图形推出BE=AB-AE=3AE,从而即可求出答案.
30.C
解:将该小组6名成员的英语口试成绩按从低到高依次排列为:43,43,45,46,47,50,
排第3与4位的成绩分别是45与46,
∴这组数据的中位数为:.
故答案为:C.
中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数叫做这组数据的中位数,据此解答即可.
31.A
解:设这个角为x°,则其余角为(90-x)°,由题意,
得2x=90-x,
∴x=30,即这个角的度数为30°.
故答案为:A.
设这个角为x°,由和为90°的两个角互为余角可得则其余角为(90-x)°,再由“ 一个角的余角是它的2倍 ”列出方程,求解即可.
32.B
解:该几何体是由一个圆锥和一个长方体组成,圆锥的主视图是一个等腰三角形,长方体的主视图是一个以长方体的底边长为长,高为宽的长方形,故只有B选项符合题意.
故答案为:B.
主视图,就是从几何体的正面看得到的正投影,能看见的轮廓线画成实线,看不见但又存在的轮廓线画成虚线,据此逐一判断得出答案.
33.D
解:10900000用科学记数法可以表示为: 1.09x107.
故答案为:D.
用科学记数法表示大于10的数,一般表示成a×10n的形式,其中1≤a<10,n等于原数的整数位数减去1,据此解答即可.
34.C
解:∵|-4|=4,|-3|=3,|-2|=2,2<3<4,
∴-4<-3<-2<3,
∴1月某天,湖州、嘉兴、杭州、温州四地最低气温是-4℃.
故答案为:C.
根据正数大于负数,两个负数,绝对值大的反而小,进行解答即可.
35.B
解:连接BG并延长,过点A作AE//BC,交AC于点H,交射线BH于点E,如图:
∴∠E=∠CBH,∠EAH=∠BCH,
∵点G是△ABC的重心,
∴AD是BC边的中线,BH是AC边的中线,
∴,AH=CH,
∴△EAH≌△BCH(AAS)
∴AE=BC=4.
∵AE//BC,
∴.
∵AB=AC,
∴AD⊥BC,
在Rt△ABD中,,
∴.
当GF⊥AD时,
GF//BC,
∴.
∴.
故答案为:B.
连接BG并延长,过点A作AE//BC,交AC于点H,交射线BH于点E,由点是重心可得,AH=CH,证明△EAH≌△BCH,再利用平行线分线段成比例的性质,可证得.利用等腰三角形“三线合一”的性质得AD⊥BC,继而可利用锐角三角函数求得AC长,最后再次利用平行线分线段成比例的性质即可求得FC的长.
36.B
解:52206=5.2206×104,
故答案为:B.
用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|≤9,n为原数的整数位数减1,据此即可求解.
37.B
解:这5天气温的众数是10;中位数是12;
故答案为:B.
本题考查统计应用,众数和中位数的定义.先观察数据可得10出现次数最多,利用众数的定义可求出众数;根据题意可得12排在中间,利用中位数的定义可求出中位数.
38.D
解:A. 与不是同类项,不能合并,故本选项运算错误,不符合题意,A错误;
B. ,故本选项运算错误,不符合题意,B错误;
C. ,故本选项运算错误,不符合题意,C错误;
D. ,本选项运算正确,符合题意,D正确.
故答案为:D.
本题考查合并同类项、同底数幂相乘、幂的乘方、同底数幂除法运算.根据同类项定义可得 与不是同类项,不能合并,据此可判断A选项;根据同底数幂乘法运算法则可得:,据此可判断B选项;根据幂的乘方运算法则可得:,据此可判断C选项;根据同底数幂除法运算法则可得:,据此可判断D选项.
39.D
解:数35673000用科学记数法表示为.
故答案为:D.
本题考查科学记数法表示较大的数的方法.科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同,根据数据可得:a=3.5673.n=7,据此可选出答案.
40.B
解:解不等式,得,
解不等式,得,
∴不等式组的解集为,
在数轴上表示为:
故答案为:B.
分别解出不等式组中两个不等式的解集,根据口诀:同大取大,同小取小,大小小大中间找,大大小小无解了确定出解集,进而根据数轴上表示不等式组的解集的方法“大向右,小向左,实心等于,空心不等”将该不等式组的解集在数轴上表示出来即可.
41.A
解:令y=a(x-m)(x-m-k)中的y=0,
则a(x-m)(x-m-k)=0,
解得x1=m,x2=m+k,
∴该二次函数的对称轴为:,
∵a>0,
∴函数有最低点,即当时,函数有最小值,
当k=2时,函数的最小值y=-a,
当k=4时,函数有最小值y=-4a,
∴只有A选项正确,符合题意.
故答案为:A.
令抛物线中的y=0算出对应的x的值,可得函数与x轴交点的横坐标,进而根据抛物线的对称性可得其对称轴是抛物线与x轴两交点横坐标和的一半求出抛物线的对称轴直线为x=m+k,由于抛物线中二次项的系数大于零,故函数的最小值就是顶点的纵坐标,从而将x=m+k代入抛物线解析式可算出顶点纵坐标,最后再分别代入k的值即可判断.
42.D
解:对于A,根据作图痕迹可知,表示为作一个角等于已知角,此时同位角相等,两直线平行,符合题意;
对于B,此时作∠PAB的角平分线及作等腰PQ=PA,故∠PAQ=∠BAQ=∠PQA,即内错角相等,两直线平行,符合题意;
对于C,以P为圆心PA为半径,交AB于点C、交AP延长线于点D,此时AP=PC=PD,再分别以C和D为圆心作出∠DPC角平分线,
故∠DPC=∠DPQ+∠CPQ=∠PAC+∠PCA,易得∠PAB=∠DPQ,即同位角相等,两直线平行,符合题意;
对于D,以C为圆心,CP为半径作弧交AB于点D,即有CD=CP,再分别以D和P为圆心作出线段DP的垂直平分线交弧于点G,易得PQ=DQ,但无法证明此时PQ=CP,即无法得证菱形,故无法证明平行,不符合题意
故答案为:D.
由作图痕迹结合平行线的判定分析,痕迹为作等角判断A,痕迹为等腰与角平分线角度转换判断B,同理进行角度转换判断C,利用圆的对称性及垂直平分线的性质检验D.
43.D
解: 从袋中任意摸出一个球有6种情况,其中摸出一个球是红色的有4种情况,
∴P=.
故答案为:D.
首先确定从袋中任意摸出一个球共有几种情况,再确定摸出一个球是红色的有几种情况,然后用概率公式求概率即可.
44.D
解:如图所示,过点作于点,
∵等腰直角△ABC中,,
∴,
又∵
∴
∴
∴即
解得:
∴,,都不是定值,故A、B、C选项都不符合题意;
∴是定值,故D选项符合题意.
故答案为:D.
过点A作AG⊥BC于点G,根据等腰直角三角形的性质得AG=CG=4,由同一平面内,垂直于同一直线的两条直线互相平行得AG∥CE,由平行于三角形一边的直线截其它两边的延长线,所截三角形与原三角形相似得△AGF∽△ECF,由相似三角形对应边成比例得出,进而逐项分析判断,即可求解.
45.C
解:如图所示,连接,设交于点,
∵四边形,是正方形,
∴AG⊥CF,AO=OF,∠DAB=∠CAG=45°,
又∵
∴
∴三点共线,
又∵
∴,
∵
∴
∴
故答案为:C.
连AD、AG,设AG与CF交于点O,由正方形对角线互相垂直平分、相等及每条对角线平分一组对角得AG⊥CF,AO=OF及∠DAB=∠CAG=45°,从而证明D、A、G三点共线,利用勾股定理分别算出AD、AO及OF的长,进而根据正切的定义,即可求解.
46.A
解:∵和是位似图形,位似中心为点,
∴,
∵,,
∴,
∴,
∵,
∴,
解得:,
故答案为:A.
利用位似图形对应点到位似中心的距离比等于位似比得出,再结合,,得出,即可求解.
47.D
解:∵3<4,
∴,即
∴,
∴四个实数中最大的是.
故答案为:D.
首先根据被开方数越大,其算术平方根就越大判断出,再根据正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,判断即可.
48.A
解:根据三视图的定义,主视图是从正面看到的图形,
∴它的主视图为:
故答案为:A.
从正面看得到的正投影就是主视图,该几何体从给出的主视方向看,长方体的主视图应该是一个以底面长为长,高为宽的长方形,两个圆柱的主视图应该是以圆柱直径为长,圆柱高为宽的长方形,据此判断即可.
49.A
解:反比例函数的图象位于第一、三象限,在每一个象限内,y随x的增大而减小,
∵,
A.当时,点,点都在第一象限,
∴,A正确;
B.C.当时,,
∴点在第三象限,点在第一象限,
∴,B错误、C错误;
D.当时,,则点,点都在第三象限,
∴,D错误;
故答案为:A.
本题考查反比例函数的图象与性质.根据反比例函数的性质可得:当时,反比例函数的图象位于第一、三象限,在每一个象限内,y随x的增大而减小.当时,点,点都在第一象限,再根据,据此可判断的大小,判断A选项;当时,,点在第三象限,点在第一象限,再根据,据此可判断的大小,判断B选项和C选项;当时,,则点,点都在第三象限,再根据,据此可判断的大小,判断D选项.
50.C
解:由题意得:,
,
,,
设,则,
,
,
,
,
则正方形的边长为,
故答案为:C.
本题考查勾股定理,全等三角形的性质.先利用全等三角形的性质得到,设,则,利用线段的运算可得:,解方程可求出x=3,进而可求得,利用勾股定理可求出AB,进而可求出正方形的边长.
同课章节目录
