专项4 解答题1 (浙江中考真题+中考模拟) ——2025年中考数学冲刺中考模拟真题速递(浙江专用)第二辑(答案+解析)
文档属性
| 名称 | 专项4 解答题1 (浙江中考真题+中考模拟) ——2025年中考数学冲刺中考模拟真题速递(浙江专用)第二辑(答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 944.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 17:52:01 | ||
图片预览




文档简介
2025年中考数学冲刺中考模拟真题速递(浙江专用)第二辑
专项4 解答题1 (浙江中考真题+中考模拟)
一、解答题
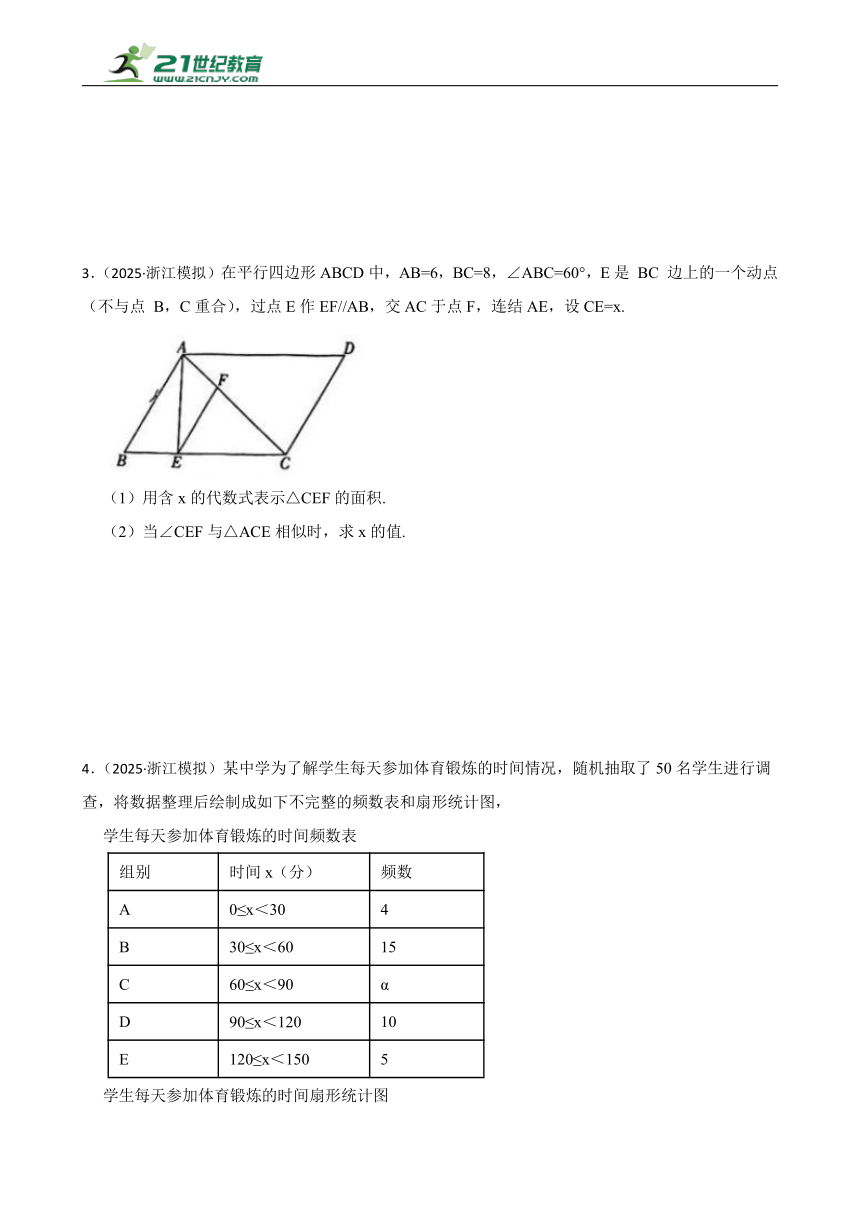
1.(2025·浙江模拟)在Rt∠ABC中,∠ABC=90°,BC>AB.
(1)尺规作图:在BC找一点D,使点D到点A、点C的距离相等(保留作图痕迹,不要求写作法).
(2)在(1)的前提下,若CD=3BD,求 tan∠C的值.
2.(2025·浙江模拟)一条公路上有相距80km的A,B两地,甲、乙、丙三人都在这条公路上匀速行驶.甲从A地出发前往B地,速度为20km/h.甲出发1小时后,乙也从A地出发前往B地,出发半小时后追上了甲,到达B地后停止不动.丙与甲同时出发,从B地前往A地,当丙与甲相遇时,甲与乙相距20 km.设甲行驶的时间为x(h),甲、乙、丙三人离A 地的距离分别为y甲(km),y乙(km),y丙(km),y甲,y乙关于x的函数图象如图所示.
(1)求乙的行驶速度.
(2)求甲与乙相距20km时甲行驶的时间.
(3)丙出发后多少小时与乙相遇?请直接写出答案.
3.(2025·浙江模拟)在平行四边形ABCD中,AB=6,BC=8,∠ABC=60°,E是 BC 边上的一个动点(不与点 B,C重合),过点E作EF//AB,交AC于点F,连结AE,设CE=x.
(1)用含x的代数式表示△CEF的面积.
(2)当∠CEF与△ACE相似时,求x的值.
4.(2025·浙江模拟)某中学为了解学生每天参加体育锻炼的时间情况,随机抽取了50名学生进行调查,将数据整理后绘制成如下不完整的频数表和扇形统计图,
学生每天参加体育锻炼的时间频数表
组别 时间x(分) 频数
A 0≤x<30 4
B 30≤x<60 15
C 60≤x<90 α
D 90≤x<120 10
E 120≤x<150 5
学生每天参加体育锻炼的时间扇形统计图
根据以上信息,解答下列问题:
(1)求a的值及扇形统计图中B组对应的圆心角度数.
(2)已知A组的4名学生中,有2名男生和2名女生,从这4名学生中随机抽取2名学生进行访谈,求恰好抽到一名男生和一名女生的概率。
5.(2025·浙江模拟)小吉购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图如图2,测得底座AB的高为2 cm, ∠ABC=150°,支架长 BC为 18 cm,面板长 DE为24 cm,CD为6 cm(厚度忽略不计).
(1)求支点C离桌面/的高度
(2)当面板DE绕点C转动时,面板与桌面的夹角满足30°<α<60°,当面板与桌面的夹角增大时,点E离桌面1的高度也随之增大,问当面板DE绕点C转动过程中,点E离桌面l最大高度与最小高度的差是多少 (计算结果保留根号)
6.(2024九下·龙湾模拟)已知二次函数.
(1)若函数图象经过点.
①求该二次函数的表达式.
②若将平面内一点向左平移个单位,则与图象上的点重合;若将点A向右平移个单位,则与图象上的点重合,求的值.
(2)设点,是该函数图象上的两点,若,求证:.
7.(2025·浙江模拟)某九年一贯制学校由于学生较多,学校食堂采取错时用餐,初中部每个同学必须在30分钟用好午餐.为了给食堂管理提出合理的建议,小明同学调查了某日11:30下课后15分钟内进入食堂累计人数(人)与经过的时间分钟(为自然数)之间的变化情况,部分数据如下:
经过的时间/分钟 0 1 2 3 4 5 ... 10
累计人数(人) 0 95 180 255 320 375 ... 500
当时与之间的函数关系式.
已知每位同学需排队取餐,食堂开放5个窗口,每个窗口每分钟4个同学取好餐.
(1)根据上述数据,请利用已学知识,求出当时,与之间的函数关系式.
(2)排队人数最多时有多少人
(3)若开始取餐分钟后增设个窗口(受场地限制,窗口总数不能超过10个),以便在11点40分时(第10分钟)正好完成前300位同学的取餐,求的值.
8.(2025·浙江模拟)为了增强学生的安全意识,某校开展了主题为“科学防护·珍爱生命”的安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用表示,共分成四组:,下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82.
八年级10名学生的竞赛成绩在组中的数据是:94,90,94.
八年级抽取的学生竞赛成绩扇形统计图
七、八年级抽取的学生竞赛成绩统计表
年级 七年级 八年级
平均数 92 92
中位数 93
众数 100
方差 52 50.4
根据以上信息,解答下列问题:
(1)直接写出上述图表中的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好?请说明理由(写出一条理由即可).
9.(2025·浙江模拟)如图,在和中,,,,在同一条直线上,.
(1)求证:.
(2)若,,求.
10.(2025·浙江模拟)如图1,小钱家、体育公园、文具店依次在同款练习路上.某日,小钱步行从家出发,先到体育公园锻炼20分钟,再到文具店,用时5分钟购买文具,然后按息路返回家中,小钱往返途中的步行速度不变.设小钱从家出发分钟时,距家米,关于的函数的部分图象如图.2所示。
(1)求小钱的步行速度.
(2)求小钱从文具店回家过程中关于的函数解析式,并补全图象,
(3)当小钱从家出发分钟时,弟弟小塘以和小钱相同的速度减从家中出发,沿相同路线前往文具店.若小钱从文具店返回途中恰好与小塘在体育公园相遇,求t的值;
11.(2025·金华模拟)二次函数的图象经过点,且对称轴为直线.
(1)求这个二次函数的解析式.
(2)图象上的点称为函数的不动点,求这个函数不动点的坐标.
(3)若是二次函数图象上不动点之间的点(包括端点),求的最大值与最小值的差.
12.(2025·金华模拟)如图1,是一台小型输送机,其示意图如图2所示.已知两个支架的端点的距离,传输带与支架所成的角,支架端点离地面的高度,求支架端点离地面的高度.(结果精确到0.1m;参考数据,,).
13.(2025九下·奉化模拟)小江自制了一把水枪(图1),他将水枪固定,在喷水头距离地面1米的位置进行实验.当喷射出的水流与喷水头的水平距离为2米时,水流达到最大高度3米,该水枪喷射出的水流可以近似地看成抛物线,图2为该水枪喷射水流的平面示意图.
(1)求该抛物线的表达式.
(2)在距离喷射头水平距离3米的位置放置一高度为2米的障碍物,试问水流能越过该障碍物吗?
(3)小江通过重新调整喷头处的零件,使水枪喷射出的水流抛物线满足表达式.当时,y的值总大于2,请直接写出a的取值范围.
14.(2025·鄞州模拟)如图,一次函数的图象与反比例函数的图象相交于两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象直接写出时,的取值范围;
(3)过点作直线,交反比例函数图象于点,连结,求的面积.
15.(2025·鄞州模拟)本期开学以来,初2017级开展了轰轰烈烈的体育锻炼,为了解考体育科目训练的效果,九年级学生中随机抽取了部分学生进行了以此中考体育科目测试(把测试结果分为四个等级,A等:优秀;B等:良好;C等:及格;D等:不及格),并将结果汇成了如图1、2所示两幅不同统计图,请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)图1中D等所在的百分比是 ,并把图2条形统计图补充完整;
(3)我校九年级有1800名学生,如果全部参加这次中考体育科目测试,请估计不及格的人数为 ;
16.(2025·绍兴模拟) 一个不透明的口袋中装有若干个红球、 1 个白球、 1 个黑球,这些球除颜色外都相同, 将球摇匀.
(1)从中任意摸出 1 个球, 恰好摸到红球的概率是 , 则红球有 ▲ 个;
(2)在(1)的条件下, 从袋中任意摸出 2 个球, 请用画树状图或列表的方法求摸出的球是一个红球和一个白球的概率.
17.“轻轨飞梭如影重,上天入地驶楼中”,8D魔幻城市重庆吸引了全国各地的游客,而李子坝的“轻轨穿梭”成了游客们争相打卡的热门景点.如图,已知斜坡CD底端C距离轻轨所穿楼栋AB底端A处30米远,斜坡CD长为42米,坡角为,为了方便游客拍照,现需在距斜坡底端C处12米的M处挖去部分坡体修建一个平行于水平线CE的观景平台MN和一条新的坡角为的斜坡DN.
(1)求观景平台MN的长;(结果保留根号)
(2)小育在处测得轻轨所穿楼栋AB顶端的仰角为,点在同一个平面内,点、C、E在同一条直线上,且,求轻轨所穿楼栋AB的高度.
18.(2025九下·温州模拟)已知二次函数的图象经过点.
(1)求二次函数解析式及其对称轴;
(2)将函数图象向上平移个单位长度,图象与轴相交于点A,B(在原点左侧),当时,求的值;
(3)当时,二次函数的最小值为2n,求的值.
19.(2025九下·温州模拟)如图反映的是小温、小州两人从学校出发到S1瓯华站乘车的过程。两人同时从学校步行出发,小温在途中发现有物品遗漏,于是立刻以同样的速度返回学校拿取,在学校停留2分钟后乘出租车赶往瓯华站,结果比小州早3分钟到达瓯华站.
(1)求两人步行的速度;
(2)求出图中出租车行驶时路程与时间的函数解析式;
(3)求学校到瓯华站的路程.
20.(2025九下·温州模拟)某校为了解学生的劳动教育情况,对九年级学生寒假期间“参加家务劳动的时间”进行了抽样调查,并将劳动时间分为如下四组,单位:分钟)进行统计,绘制了如下不完整的统计图.
根据以上信息,解答下列问题:
(1)求出本次抽样的学生人数并补全条形统计图;
(2)已知该校九年级有600名学生,请估计该校九年级学生中参加家务劳动的时间在60到100分钟(含60分钟)的学生有多少人?
(3)若组中有3名女生,其余均是男生,从中随机抽取两名同学交流劳动感受,请用列表法或树状图法,求抽取的两名同学中恰好是一名女生和一名男生的概率.
21.(2025九下·温州模拟)如图,在等边中,点D、E分别是边BC、AC上的点,AD与BE交于点.
(1)求证:;
(2)求的值.
22.(2024·杭州模拟)在平面直角坐标系中,抛物线经过点,.
(1)若,
①求此抛物线的对称轴;
②当时,直接写出的取值范围;
(2)若,点在该抛物线上,且,请比较,的大小,并说明理由.
23.(2025·萧山模拟)【背景】在一次物理实验中,小冉同学用一个固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R,RL之间关系为,通过实验得出如下数据:
R(Ω) … 1 a 3 4 6 …
I(A) … 4 3 2.4 2 b …
(1)a= ,b= .
(2)【探究】根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质.
①在平面直角坐标系中画出对应函数的图象.
②随着自变量的不断增大,函数值的变化趋势是 ▲ .
(3)【拓展】结合(2)中函数图象分析,当0时,的解为 .
24.(2025·金华模拟)二次函数的图象经过点,且对称轴为直线.
(1)求这个二次函数的解析式.
(2)图象上的点称为函数的不动点,求这个函数不动点的坐标.
(3)若是二次函数图象上不动点之间的点(包括端点),求的最大值与最小值的差.
25.(2025·萧山模拟)在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m,n为实数).
(1)求函数图象的对称轴;
(2)若m,n异号,求证:函数y的图象与x轴有两个不同的交点;
(3)已知当x=0,3,4时,对应的函数值分别为p,q,r,若2q<p+r,求证:m<0.
答案解析部分
1.(1)解:如图
(2)解:∵CD=3BD,
∴设BD=x,则CD=3x.
∵DE是AC的中垂线,
∴AD=CD=3x.
∵∠ABC=90°,
∴AB=2x,
(1)作出AC的垂直平分线,它与BC的交点就为点D;
(2)先根据CD与BD的关系,设BD=x,就可以用x表示出CD,再根据垂直平分线的性质,可得AD也可以用x表示,再求出AB,然后求出 tan∠C的值.
2.(1)解:乙的速度为20×(1+0.5)÷0.5=60(km/h).
(2)解:∵甲的速度为20km/h,乙的速度为60km/h,
∴y甲=20x,y乙=60(x-1),
当甲在乙前面20km时,
20x-60(x-1)=20,
解得x=1,
当乙在甲前面20km时,
60(x-1)-20x=20,
解得x=2,
综上所述,甲与乙相距20km时甲行驶的时间为1h或2h.
(3)解:丙与甲同时出发,从B地前往A地,当丙与甲相遇时,甲与乙相距20km,
∴甲与乙相距20km时,甲和丙行驶时间相等,
∴乙与甲相遇时间为1h或2h,
在y甲=20x中,
当x=1时,y甲=20,
当x=2时,y甲=40,
∴y丙过(1,20)或(2,40),
设y丙=kx+b,
当y丙过(1,20)时,
,
解得;
当y丙过(2,40)时,
,
解得;
∴或.
当丙与乙相遇时,
或,
解得或.
(1)根据甲的速度乘以甲出发1小时后,乙用半小时追上,可求出乙的速度;
(2)根据甲、乙的速度,分别求得甲、乙的运动的函数表达式,再分“甲在乙前面20km”、“乙在甲前面20km”两种情况,分别求出所需的时间;
(3)分y丙过(1,20)或(2,40)两种情况,分别求出y丙,当丙与乙相遇时,分别求出x即可.
3.(1)解:过点C作CM⊥AB于点M,
∵BC=8,∠ABC=60°,
∴CM=BCsin∠ABC=4,
∴S△ABC=AB·CM=×6×4=12,
∵EF//lAB,
∴△CEF∽△CBA,
∴,
∴,
解得.
(2)解:过点C作CM⊥AB于点M,
∵BC=8,∠ABC=60°,
∴CM=BCsin∠ABC=4,
BM=BCcos∠ABC=4,
∴AM=AB-BM=2,
∴AC==.
∵△CEF∽△CBA,
∴当△CEF与△ACE相似时,△CBA与△ACE相似,
∵∠ACE=∠BCA,∠AEC>∠B,
∴∠CEA=∠CAB,
∴△CEA∽△CAB,
∴CE:AC=CA:BC,
∴CE:2=2:8,
解得CE=.
即x=.
(1)先利用正弦,求出CM,再利用三角形面积公求得S△ABC,根据EF//AB,可得出△CEF∽△CBA,列出关于的比例式,求出;
(2)先利用正弦求出CM,利用余弦求出BM,再根据AM=AB-BM,求出AM,再△CEF∽△CBA,得出当△CEF与△ACE相似时,△CBA与△ACE相似,可证明△CEA∽△CAB,列出关于CE的比例式,求出CE即可求出x.
4.(1)解:∵A的频数为4,B的频数为15,C的频数为 α,D的频数为10,E的频数为5,共有50名学生,
∴α=50-4-15-10-5=16,
B组对应的圆心角度数为360°×=108°;
(2)解:画树状图:
共有12种等可能的结果,其中恰好抽到一名男生和一名女生的情况数有8种,
∴恰好抽到一名男生和一名女生的概率为.
(1)利用总频数减去其余各频数,求出C组的频数;B组的频数除以总数乘以360度可求得 B组对应的圆心角度数.
(2)画树状图,分别求出总种数与恰好抽到一名男生和一名女生的情况数,再利用概率公式求解.
5.(1)解:如图,过点C作CF⊥l于点F,过点B作BM⊥CF于点M,
∴∠CFA=∠BMC=∠BMF=∠BAF=90°,
∴四边形ABMF是矩形,
∴∠ABM=90°,MF=AB=2,
∵∠ABC=150°,
∴∠MBC=∠ABC-∠ABM=60°,
∵BC=18,
∴CM=BCsin60°=9,
∴CF=CM+MF=2+9,
即支点C离桌面l的高度为2+9cm.
(2)解:如图,过点C作CN//l,过E作EH⊥CN于点H,
∴∠EHC=90,
∵DE=24,CD=2,
∴CE=DE-CD=18,
当∠ECH=30°时,
EH=CEsin30°=9;
当∠ECH=60°时,EH=CEsin60°=9;
∴当面板DE绕点C转动过程中,E离桌面1最大高度与最小 高度的差是 9-9cm.
(1)先证明四边形ABMF是矩形,根据矩形的性质,可得∠ABM=90°,MF=AB=2,再利用角的和差求出∠MBC,然后利用正弦求出CM,再利用线段的和差求出CF即为支点C离桌面l的高度;
(2)分“∠ECH=30°”、“∠ECH=60°”两种情况,分别求出CH,再求出E离桌面1最大高度与最小 高度的差.
6.(1)解:(1)①将代入可得,解得:,
∴该二次函数的表达式为;
②∵将平面内一点向左平移个单位,则与图象上的点重合;若将点A向右平移个单位,则与图象上的点重合,
∴,
∵,
∴抛物线的对称轴为:,
∴,解得:,
∴,
∴.
(2)解:∵设点,是该函数图象上的两点,
∴
∴,,
∴
,
∵,
∴,即.
(1)①利用待定系数法将代入二次函数解析式即可;
②由于B、C两点的纵坐标相同,则B、C两点关于抛物线的对称轴对称,此时可利用抛物线解析式得到对称轴的表达式从而求出的值,再利用二次函数图象上点的坐标特征代入点坐标即可求得n;
(2)由于 与和是定值,则可用含的代数式表示,则可分别用含的代数式表示出与的和,最后再使用配方法即可.
7.(1)解:根据表格数据,当时,设与之间的函数关系式为,
将(0,0),(1,95),(2,180)代入关系式,得,
解得:,
∴当时,与之间的函数关系式为;
(2)解:设排队人数为人,
∵食堂开放5个窗口,每个窗口每分钟4个同学取好餐,
∴每分钟取好餐的同学人数为:5×4=20(个),
当时,,
∴当时,有最大值为320;
当时,,
排队人数最多时有320人;
(3)解:∵开始取餐分钟后增设个窗口,在11点40分时正好完成前300位同学的取餐,
∴,
∴,
都是自然数,
∴,
.
(1)根据题意,可知当时,设与之间的函数关系式为,然后利用待定系数法进行求解即可;
(2)设排队人数为人,根据题意可知每分钟取好餐的同学人数为20人,然后分两种情况讨论:当时,,当时,有最大值为320;当时,,则,据此即可求解;
(3)根据题意列出方程并化简为,由m,x是自然数即可求出m,x的值.
8.(1)解:∵八年级10名学生的竞赛成绩在C组中的数据是:94,90,94,共有3个,
∴,
∴a%=1-10%-20%-30%=40%,
∴a=40,
∵八年级学生竞赛成绩的中位数为第5、6名成绩的平均数,且该成绩在C组中,
∴,
∵七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82,
∴c=99;
(2)解:从方差上看,由于八年级的方差比七年级的方差小,所以八年学生的安全知识竞赛成绩更稳定更好.
(1)先根据八年级学生在C组中的成绩数据,结合扇形统计图求出C组所占百分比,从而求出D组所占百分比,即可得a的值,根据中位数的定义可知八年级学生竞赛成绩的中位数为第5、6名成绩的平均数,结合A,B,C,D所占百分比可知该成绩在C组中,据此可求出b的值,根据众数的定义直接得c的值;
(2)根据方差的意义:方差用来衡量一组数据波动的大小,方差越大,说明数据的波动越大,越不稳定;方差越小,说明数据的波动越小,越稳定,即可求解.
9.(1)证明:∵,
∴,
∵,
∴,
在和中,
∴;
(2)解:由(1)得,
∵,
∴,
∵,
∴.
(1)根据两直线平行,同位角相等得,然后求出,即可证明;
(2)根据全等三角形的性质得,然后利用三角形内角和定理求解即可.
10.(1)解:(米/分),
小钱步行速度为100米/分
(2)解:往返步行速度不变,
返回耗时20分钟,即回到家中为65分钟.
当时,
图象如图所示.
(3)解:由题,小塘从家中到体育公园所需的时间为(分),
得,解得
(1)利用速度=路程÷时间解题即可;
(2)先根据距家的路程=全程-行进路程列出函数关系式,求出时间x的取值范围,补图即可;
(3)根据相遇问题列方程解题即可.
11.(1)解:∵二次函数 的图象经过点(
,且对称轴为直线
解得
∴这个二次函数的解析式为
(2)解:当y=x时, 则
整理得
解得
∴这个函数不动点的坐标是( 和(5,5)
(3)解:
∴抛物线开口向上,顶点为(
∵这个函数不动点的坐标是A(-2,-2), B(5,5),
∴若点P(x,y)是函数图象上的一个动点,当点P在点A,B之间运动时,y的最大值为5,最小值为-11,
∴的最大值与最小值的差为5-(-11)=16
(1)根据待定系数法即可求出答案;
(2)根据为函数的不动点的定义列出方程,求解即可;
(3)根据不动点的坐标以及二次函数的性质求出最小值,然后求差解题.
12.解:过点作于点,可得,在中,,
∴
∴
过点A作于点 F,可得CF长,然后在中根据余弦的定义求BF长解题即可.
13.(1)解:由题意, 抛物线顶点为(2,3),
∴可设该抛物线的表达式为
将点(0,1)代入, 得4
∴该抛物线的表达式为
(2)解:由题意,当 时,
∴水流能越过该障碍物
(3)解:由题意,
∴抛物线的对称轴为直线
①当 即 时,将 代入 得
②当 即 时,将 代入 得
综上所述,a的取值范围为
(1)依据题意,抛物线顶点为(2,3),从而可设该抛物线的表达式为 再将点(0,1)代入, 得 可得 进而可以得解;
(2)依据题意, 当 时,求出y值与2作比较故解题;
(3)依据题意,由 可得抛物线的对称轴为直线 再结合二次函数的性质进行分 和 两种情形讨论计算可以得解.
14.(1)解: 将点A坐标代入反比例函数解析式得,
所以反比例函数解析式为
将点B坐标代入反比例函数解析式得,
所以点B的坐标为(
将A,B两点坐标代入一次函数解析式得,
解得
所以一次函数解析式为
(2)解:由函数图象可知,当 或 时,一次函数的图象在反比例函数图象的上方,即
所以当 x的取值范围是: 或
(3)解:连接AO,令直线AB与x轴的交点为M,
将 代入 得,
所以点M的坐标为(
所以
因为正比例函数图象与反比例函数图象都是中心对
称图形,且坐标原点是对称中心,
所以点B和点C关于点O成中心对称,
所以
所以
(1)先将点A坐标代入反比例函数解析式,求出m,再求出点B坐标,最后用待定系数法求出一次函数解析式即可.
(2)利用数形结合的数学思想即可解决问题.
(3)连接AO,根据反比例函数与正比例函数的对称性,将 的面积转化为 面积的2倍即可解决问题.
15.(1)25
(2)D等级的人数为25﹣4﹣10﹣8=3,
∴D等所在的百分比是×100%=12%
条形统计图补充为:
(3)216
解:(1)本次抽样测试的学生人数为:10÷40%=25(人),
故答案为:25;
(3)1800×=216(人),
故答案为:216.
(1)用B等级的人数除以它所占的百分比即可得到调查的总人数;
(2)用总人数分别减去A、B、C等级的人数得到D等级人数,然后用: 乘以D等级所占的百分比得到D等所在的扇形的圆心角的度数,再补全条形统计图;
(3)利用样本估计总体,用1800乘以D等级所占百分比即可.
16.(1)2
(2)解:树状图如下:
共有12种等可能的结果,其中摸出的球是一个红球和一个白球的结果数为4, 所以摸出的球是一个红球和一个白球的概率为
解:设红球有 x 个,则恰好摸到红球的概率: ,
解得: ,
经检验,x=2为原分式方程的解,
红球有 2 个.
故答案为:2
(1)设袋中红球有x个,根据任意摸出1个球恰好摸到红球的概率是 列出关于x的方程,解之可得答案;
(2)列表得出所有等可能的情况数,找出两次都摸出的球是一个红球和一个白球的情况数,即可求出所求的概率.
17.(1)解:如图,
由题意得,MF⊥DE,FM∥EC,
∴∠DMF=∠DCE=30°,
∵DC=42m,CM=12m,
∴DM=CD-CM=30(m),
在Rt△DFM中,DF=DM=15m,
FM=DF=15(m),
在Rt△DFN中,∠DNF=45°,tan∠DNF=,
∴FN==15(m),
∴MN=FM-FN=(15-15)m,
答:观景平台MN的长为()米
(2)解:如图,
由题意得,FN=EP=15m,EF=AH,FH=EA,
在Rt△DEC中,∠DCE=30°,CD=42m,
∴DE=CD=21m,CE=DE=21m,
∵AC=30m,
∴FH=AE=AC+CE=(30+21)m,
∴NH=FH-FN=30+21-15=(21+15)m,
在Rt△BNH中,∠BNH=30°,
∵tan∠BNH=,
∴BH =NH·tan30°=(21+15)×=(21+5)m,
∵DF=15m,
∴EF=AH=DE-DF=21-15=6(m),
∴AB =BH+AH=(27+5)m.
答:轻轨所穿楼栋AB的高度为米
(1)由题意,由线段的和差DM=CD-CM求出DM的值,在Rt△DFM中,根据锐角三角函数tan∠DNF=求出FN的值,然后由线段的和差MN=FM-FN可求解;
(2)解Rt△DEC可求得CE的值,由线段的和差FH=AE=AC+CE求出FH的值,同理根据NH=FH-FN求出NH的值,在Rt△BNH中,根据锐角三角函数tan∠BNH=求出BH的值,然后由线段的和差AB =BH+AH可求解.
18.(1)解:将代入,得.
,
对称轴为直线
(2)解:函数图象向上平移个单位长度后解析式为
在原点左侧,
设点坐标为,点坐标为
,解得
将代入,得
(3)解:当即时,当时有最小值为2n,
,解得(舍),(舍)
当即时,当时有最小值为,
,解得
综上,
(1)由于抛物线解析中只有一次项系数未知,且知道其图象上一个点的坐标,只需把这个点的坐标代入到函数解析式中即可求出的值,此时再根据抛物线的对称轴公式计算即可;
(2)由于平移不改变抛物线的形状与大小,则沿轴方向平移时,对称轴不变,可根据题意分别设出A、B两点的坐标,再利用对称关系即可求出点A的坐标值,再代入到平移后的抛物线解析式中即可求出的值;
(3)由于抛物线的开口向上,所以二次函数有最小值,此时在对称轴的左边,随的增大而减小;反之,随的增大而增大;因为二次函数 ,即当时,最小值为;所以应当分类讨论,当时,函数最小值为,此时有,解得, ,均与假设不符;当即时,函数最小值为,即时有最小值为,即.
19.(1)解:步行速度(分钟);
(2)解:如图所示
由题可知当时,,所以点;
当时,,所以点;
设函数解析式为,
,解得
(3)解:设学校到瓯华站共米,由题意列方程得:
,解得
答: 学校到瓯华站的路程为
(1)由于小温出发和返回学校的速度相同,则从学校到返回地点用时为10分钟的一半即5分钟,步行路程为325,则速度等于路程除以时间即可;
(2)求出租车的路程与时间的函数解析式,由题意可分别求出A、B两点的坐标,再利用待定系数法联立方程组即可;
(3)求学校到车站的路程,由于相遇后出租车比小州早到3分钟,即在走完剩余路程中,出租车用时比小州少了3分钟,由于小州的速度已知为65,出租车的速度利用函数关系式知为260,剩余路程为总路程减去小州步行16分钟的路程1040,列方程即可求出总路程。
20.(1)解:抽样总人数等于人
C组:50-10-15-5=20人,补全条形图如图
(2)解:人
答: 九年级学生中参加家务劳动的时间在60到100分钟(含60分钟)的学生有420人
(3)解:列表得:共有20种等可能结果,抽取到一男一女有12种结果
女1 女2 女3 男1 男2
女1 / 两女 两女 一男一女 一男一女
女2 两女 / 两女 一男一女 一男一女
女3 两女 两女 / 一男一女 一男一女
男1 一男一女 一男一女 一男一女 / 两男
男2 一男一女 一男一女 一男一女 两男 /
P(一男一女)
(1)观察两个统计图,发现D组人数和在总抽样人数中的占比都知道,则用D组人数除以其占比即可得到总抽样人数,再用抽样总数分别减去A、B、D三组人数即可得出C组人数,补全条形统计图即可;
(2) 要估算该校九年级学生中参加家务劳动的时间在60到100分钟(含60分钟)的学生,先求出满足条件的人数占抽样总数的百分比,再乘以全校总人数即可;
(3)两步试验的概率可通过画树状图或列表格的方法求出,注意画树状图时要不重复不遗漏,列表格时注意每名同学第一次抽到后则第二次不能再抽取,因此对角线栏目上不能填数据.
21.(1)证明:如图
,
又在等边中,
(ASA),
(2)解:,
又
(1)证明BD=CE,可证明这两条边所在的三角形全等,即;由于等边三角形的三边相等,三个内角相等且都是60度,即,还缺少一个条件,此时可借助三角形外角的性质结合已知条件得出,则利用ASA即可证明全等;
(2)求值,观察图形知这两条边分别在和中,由于可证,由相似的性质知化比例式为等积式得,由前面全等的性质可计算.
22.(1)解:①当t=0时,将点A(3,0)代入抛物线解析式得9a+3(a-3)-3=0,得a=1,此时抛物线的解析式为y=x2-2x-3,对称轴为x=1;
②,即有m2-2m-3≧0,即(m+1)(m-3)≧0,
故或解得m≧3或m≦-1;
(2)解:t>0即有9a+3(a-3)-3>0,得a>1,对于抛物线,其对称轴为直线x=<1,即可知抛物线开口向上,且对称轴在直线x=1的左侧,
m>n,m+n>2
当m>n>1时,二次函数在x>1时y随x的增大而增大,p>q;
当m>1,n<1时,注意到m+n>2即有m>2-n,n<1,故2-n>1,故p>q
综上所述,p>q
(1)t=0时直接代入抛物线解析式可得a=1,再分类讨论解不等式;
(2)由题意可得a的范围,同时可知对称轴的位置,再由且 可得p和q的大小关系.
23.(1)2;1.5
(2)解:①根据表格数据描点:,,,,,在平面直角坐标系中画出对应函数的图象如下:
②不断减小
(3)或
(1)根据题意,
故答案为: 2, 1.5;
(2)②由图象可知,随着自变量x的不断增大,函数值y的变化趋势是不断减小,
故答案为:不断减小;
(3)如图:
由函数图象知, 当 或 时,
即当 时,
故答案为: 或
(1)由已知列出方程,即可解得a,b的值;
(2)①描点画出图象即可;
②观察图象可得答案;
(3)同一坐标系内画出图象,观察即可得到答案.
24.(1)
(2)和
(3)16
25.(1)解:∵函数y=m(x+1)2+4n(m≠0,且m,n为实数),
∴函数图象的对称轴为x=-1;
(2)证明:令y=0,则0=m(x+1)2+4n,
即,
∵m,n异号,
∴,
∴一元二次方程有两个不相等的实数根,即函数y的图象与x轴有两个不同的交点;
(3)证明:由题可知p=m+4n,q=16m+4n,r=25m+4n,
∵2q-(p+r)=2(16m+4n)-(m+4n+25m+4n)=6m<0,
∴m<0.
(1)根据抛物线的解析式即可求出抛物线的对称轴;
(2)令y=0,转化为求一元二次方程根的情况,结合题意即可求解;
(3)分别代入求出p、q、r的值,根据不等式,化简即可求解.
专项4 解答题1 (浙江中考真题+中考模拟)
一、解答题
1.(2025·浙江模拟)在Rt∠ABC中,∠ABC=90°,BC>AB.
(1)尺规作图:在BC找一点D,使点D到点A、点C的距离相等(保留作图痕迹,不要求写作法).
(2)在(1)的前提下,若CD=3BD,求 tan∠C的值.
2.(2025·浙江模拟)一条公路上有相距80km的A,B两地,甲、乙、丙三人都在这条公路上匀速行驶.甲从A地出发前往B地,速度为20km/h.甲出发1小时后,乙也从A地出发前往B地,出发半小时后追上了甲,到达B地后停止不动.丙与甲同时出发,从B地前往A地,当丙与甲相遇时,甲与乙相距20 km.设甲行驶的时间为x(h),甲、乙、丙三人离A 地的距离分别为y甲(km),y乙(km),y丙(km),y甲,y乙关于x的函数图象如图所示.
(1)求乙的行驶速度.
(2)求甲与乙相距20km时甲行驶的时间.
(3)丙出发后多少小时与乙相遇?请直接写出答案.
3.(2025·浙江模拟)在平行四边形ABCD中,AB=6,BC=8,∠ABC=60°,E是 BC 边上的一个动点(不与点 B,C重合),过点E作EF//AB,交AC于点F,连结AE,设CE=x.
(1)用含x的代数式表示△CEF的面积.
(2)当∠CEF与△ACE相似时,求x的值.
4.(2025·浙江模拟)某中学为了解学生每天参加体育锻炼的时间情况,随机抽取了50名学生进行调查,将数据整理后绘制成如下不完整的频数表和扇形统计图,
学生每天参加体育锻炼的时间频数表
组别 时间x(分) 频数
A 0≤x<30 4
B 30≤x<60 15
C 60≤x<90 α
D 90≤x<120 10
E 120≤x<150 5
学生每天参加体育锻炼的时间扇形统计图
根据以上信息,解答下列问题:
(1)求a的值及扇形统计图中B组对应的圆心角度数.
(2)已知A组的4名学生中,有2名男生和2名女生,从这4名学生中随机抽取2名学生进行访谈,求恰好抽到一名男生和一名女生的概率。
5.(2025·浙江模拟)小吉购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图如图2,测得底座AB的高为2 cm, ∠ABC=150°,支架长 BC为 18 cm,面板长 DE为24 cm,CD为6 cm(厚度忽略不计).
(1)求支点C离桌面/的高度
(2)当面板DE绕点C转动时,面板与桌面的夹角满足30°<α<60°,当面板与桌面的夹角增大时,点E离桌面1的高度也随之增大,问当面板DE绕点C转动过程中,点E离桌面l最大高度与最小高度的差是多少 (计算结果保留根号)
6.(2024九下·龙湾模拟)已知二次函数.
(1)若函数图象经过点.
①求该二次函数的表达式.
②若将平面内一点向左平移个单位,则与图象上的点重合;若将点A向右平移个单位,则与图象上的点重合,求的值.
(2)设点,是该函数图象上的两点,若,求证:.
7.(2025·浙江模拟)某九年一贯制学校由于学生较多,学校食堂采取错时用餐,初中部每个同学必须在30分钟用好午餐.为了给食堂管理提出合理的建议,小明同学调查了某日11:30下课后15分钟内进入食堂累计人数(人)与经过的时间分钟(为自然数)之间的变化情况,部分数据如下:
经过的时间/分钟 0 1 2 3 4 5 ... 10
累计人数(人) 0 95 180 255 320 375 ... 500
当时与之间的函数关系式.
已知每位同学需排队取餐,食堂开放5个窗口,每个窗口每分钟4个同学取好餐.
(1)根据上述数据,请利用已学知识,求出当时,与之间的函数关系式.
(2)排队人数最多时有多少人
(3)若开始取餐分钟后增设个窗口(受场地限制,窗口总数不能超过10个),以便在11点40分时(第10分钟)正好完成前300位同学的取餐,求的值.
8.(2025·浙江模拟)为了增强学生的安全意识,某校开展了主题为“科学防护·珍爱生命”的安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用表示,共分成四组:,下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82.
八年级10名学生的竞赛成绩在组中的数据是:94,90,94.
八年级抽取的学生竞赛成绩扇形统计图
七、八年级抽取的学生竞赛成绩统计表
年级 七年级 八年级
平均数 92 92
中位数 93
众数 100
方差 52 50.4
根据以上信息,解答下列问题:
(1)直接写出上述图表中的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好?请说明理由(写出一条理由即可).
9.(2025·浙江模拟)如图,在和中,,,,在同一条直线上,.
(1)求证:.
(2)若,,求.
10.(2025·浙江模拟)如图1,小钱家、体育公园、文具店依次在同款练习路上.某日,小钱步行从家出发,先到体育公园锻炼20分钟,再到文具店,用时5分钟购买文具,然后按息路返回家中,小钱往返途中的步行速度不变.设小钱从家出发分钟时,距家米,关于的函数的部分图象如图.2所示。
(1)求小钱的步行速度.
(2)求小钱从文具店回家过程中关于的函数解析式,并补全图象,
(3)当小钱从家出发分钟时,弟弟小塘以和小钱相同的速度减从家中出发,沿相同路线前往文具店.若小钱从文具店返回途中恰好与小塘在体育公园相遇,求t的值;
11.(2025·金华模拟)二次函数的图象经过点,且对称轴为直线.
(1)求这个二次函数的解析式.
(2)图象上的点称为函数的不动点,求这个函数不动点的坐标.
(3)若是二次函数图象上不动点之间的点(包括端点),求的最大值与最小值的差.
12.(2025·金华模拟)如图1,是一台小型输送机,其示意图如图2所示.已知两个支架的端点的距离,传输带与支架所成的角,支架端点离地面的高度,求支架端点离地面的高度.(结果精确到0.1m;参考数据,,).
13.(2025九下·奉化模拟)小江自制了一把水枪(图1),他将水枪固定,在喷水头距离地面1米的位置进行实验.当喷射出的水流与喷水头的水平距离为2米时,水流达到最大高度3米,该水枪喷射出的水流可以近似地看成抛物线,图2为该水枪喷射水流的平面示意图.
(1)求该抛物线的表达式.
(2)在距离喷射头水平距离3米的位置放置一高度为2米的障碍物,试问水流能越过该障碍物吗?
(3)小江通过重新调整喷头处的零件,使水枪喷射出的水流抛物线满足表达式.当时,y的值总大于2,请直接写出a的取值范围.
14.(2025·鄞州模拟)如图,一次函数的图象与反比例函数的图象相交于两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象直接写出时,的取值范围;
(3)过点作直线,交反比例函数图象于点,连结,求的面积.
15.(2025·鄞州模拟)本期开学以来,初2017级开展了轰轰烈烈的体育锻炼,为了解考体育科目训练的效果,九年级学生中随机抽取了部分学生进行了以此中考体育科目测试(把测试结果分为四个等级,A等:优秀;B等:良好;C等:及格;D等:不及格),并将结果汇成了如图1、2所示两幅不同统计图,请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)图1中D等所在的百分比是 ,并把图2条形统计图补充完整;
(3)我校九年级有1800名学生,如果全部参加这次中考体育科目测试,请估计不及格的人数为 ;
16.(2025·绍兴模拟) 一个不透明的口袋中装有若干个红球、 1 个白球、 1 个黑球,这些球除颜色外都相同, 将球摇匀.
(1)从中任意摸出 1 个球, 恰好摸到红球的概率是 , 则红球有 ▲ 个;
(2)在(1)的条件下, 从袋中任意摸出 2 个球, 请用画树状图或列表的方法求摸出的球是一个红球和一个白球的概率.
17.“轻轨飞梭如影重,上天入地驶楼中”,8D魔幻城市重庆吸引了全国各地的游客,而李子坝的“轻轨穿梭”成了游客们争相打卡的热门景点.如图,已知斜坡CD底端C距离轻轨所穿楼栋AB底端A处30米远,斜坡CD长为42米,坡角为,为了方便游客拍照,现需在距斜坡底端C处12米的M处挖去部分坡体修建一个平行于水平线CE的观景平台MN和一条新的坡角为的斜坡DN.
(1)求观景平台MN的长;(结果保留根号)
(2)小育在处测得轻轨所穿楼栋AB顶端的仰角为,点在同一个平面内,点、C、E在同一条直线上,且,求轻轨所穿楼栋AB的高度.
18.(2025九下·温州模拟)已知二次函数的图象经过点.
(1)求二次函数解析式及其对称轴;
(2)将函数图象向上平移个单位长度,图象与轴相交于点A,B(在原点左侧),当时,求的值;
(3)当时,二次函数的最小值为2n,求的值.
19.(2025九下·温州模拟)如图反映的是小温、小州两人从学校出发到S1瓯华站乘车的过程。两人同时从学校步行出发,小温在途中发现有物品遗漏,于是立刻以同样的速度返回学校拿取,在学校停留2分钟后乘出租车赶往瓯华站,结果比小州早3分钟到达瓯华站.
(1)求两人步行的速度;
(2)求出图中出租车行驶时路程与时间的函数解析式;
(3)求学校到瓯华站的路程.
20.(2025九下·温州模拟)某校为了解学生的劳动教育情况,对九年级学生寒假期间“参加家务劳动的时间”进行了抽样调查,并将劳动时间分为如下四组,单位:分钟)进行统计,绘制了如下不完整的统计图.
根据以上信息,解答下列问题:
(1)求出本次抽样的学生人数并补全条形统计图;
(2)已知该校九年级有600名学生,请估计该校九年级学生中参加家务劳动的时间在60到100分钟(含60分钟)的学生有多少人?
(3)若组中有3名女生,其余均是男生,从中随机抽取两名同学交流劳动感受,请用列表法或树状图法,求抽取的两名同学中恰好是一名女生和一名男生的概率.
21.(2025九下·温州模拟)如图,在等边中,点D、E分别是边BC、AC上的点,AD与BE交于点.
(1)求证:;
(2)求的值.
22.(2024·杭州模拟)在平面直角坐标系中,抛物线经过点,.
(1)若,
①求此抛物线的对称轴;
②当时,直接写出的取值范围;
(2)若,点在该抛物线上,且,请比较,的大小,并说明理由.
23.(2025·萧山模拟)【背景】在一次物理实验中,小冉同学用一个固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R,RL之间关系为,通过实验得出如下数据:
R(Ω) … 1 a 3 4 6 …
I(A) … 4 3 2.4 2 b …
(1)a= ,b= .
(2)【探究】根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质.
①在平面直角坐标系中画出对应函数的图象.
②随着自变量的不断增大,函数值的变化趋势是 ▲ .
(3)【拓展】结合(2)中函数图象分析,当0时,的解为 .
24.(2025·金华模拟)二次函数的图象经过点,且对称轴为直线.
(1)求这个二次函数的解析式.
(2)图象上的点称为函数的不动点,求这个函数不动点的坐标.
(3)若是二次函数图象上不动点之间的点(包括端点),求的最大值与最小值的差.
25.(2025·萧山模拟)在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m,n为实数).
(1)求函数图象的对称轴;
(2)若m,n异号,求证:函数y的图象与x轴有两个不同的交点;
(3)已知当x=0,3,4时,对应的函数值分别为p,q,r,若2q<p+r,求证:m<0.
答案解析部分
1.(1)解:如图
(2)解:∵CD=3BD,
∴设BD=x,则CD=3x.
∵DE是AC的中垂线,
∴AD=CD=3x.
∵∠ABC=90°,
∴AB=2x,
(1)作出AC的垂直平分线,它与BC的交点就为点D;
(2)先根据CD与BD的关系,设BD=x,就可以用x表示出CD,再根据垂直平分线的性质,可得AD也可以用x表示,再求出AB,然后求出 tan∠C的值.
2.(1)解:乙的速度为20×(1+0.5)÷0.5=60(km/h).
(2)解:∵甲的速度为20km/h,乙的速度为60km/h,
∴y甲=20x,y乙=60(x-1),
当甲在乙前面20km时,
20x-60(x-1)=20,
解得x=1,
当乙在甲前面20km时,
60(x-1)-20x=20,
解得x=2,
综上所述,甲与乙相距20km时甲行驶的时间为1h或2h.
(3)解:丙与甲同时出发,从B地前往A地,当丙与甲相遇时,甲与乙相距20km,
∴甲与乙相距20km时,甲和丙行驶时间相等,
∴乙与甲相遇时间为1h或2h,
在y甲=20x中,
当x=1时,y甲=20,
当x=2时,y甲=40,
∴y丙过(1,20)或(2,40),
设y丙=kx+b,
当y丙过(1,20)时,
,
解得;
当y丙过(2,40)时,
,
解得;
∴或.
当丙与乙相遇时,
或,
解得或.
(1)根据甲的速度乘以甲出发1小时后,乙用半小时追上,可求出乙的速度;
(2)根据甲、乙的速度,分别求得甲、乙的运动的函数表达式,再分“甲在乙前面20km”、“乙在甲前面20km”两种情况,分别求出所需的时间;
(3)分y丙过(1,20)或(2,40)两种情况,分别求出y丙,当丙与乙相遇时,分别求出x即可.
3.(1)解:过点C作CM⊥AB于点M,
∵BC=8,∠ABC=60°,
∴CM=BCsin∠ABC=4,
∴S△ABC=AB·CM=×6×4=12,
∵EF//lAB,
∴△CEF∽△CBA,
∴,
∴,
解得.
(2)解:过点C作CM⊥AB于点M,
∵BC=8,∠ABC=60°,
∴CM=BCsin∠ABC=4,
BM=BCcos∠ABC=4,
∴AM=AB-BM=2,
∴AC==.
∵△CEF∽△CBA,
∴当△CEF与△ACE相似时,△CBA与△ACE相似,
∵∠ACE=∠BCA,∠AEC>∠B,
∴∠CEA=∠CAB,
∴△CEA∽△CAB,
∴CE:AC=CA:BC,
∴CE:2=2:8,
解得CE=.
即x=.
(1)先利用正弦,求出CM,再利用三角形面积公求得S△ABC,根据EF//AB,可得出△CEF∽△CBA,列出关于的比例式,求出;
(2)先利用正弦求出CM,利用余弦求出BM,再根据AM=AB-BM,求出AM,再△CEF∽△CBA,得出当△CEF与△ACE相似时,△CBA与△ACE相似,可证明△CEA∽△CAB,列出关于CE的比例式,求出CE即可求出x.
4.(1)解:∵A的频数为4,B的频数为15,C的频数为 α,D的频数为10,E的频数为5,共有50名学生,
∴α=50-4-15-10-5=16,
B组对应的圆心角度数为360°×=108°;
(2)解:画树状图:
共有12种等可能的结果,其中恰好抽到一名男生和一名女生的情况数有8种,
∴恰好抽到一名男生和一名女生的概率为.
(1)利用总频数减去其余各频数,求出C组的频数;B组的频数除以总数乘以360度可求得 B组对应的圆心角度数.
(2)画树状图,分别求出总种数与恰好抽到一名男生和一名女生的情况数,再利用概率公式求解.
5.(1)解:如图,过点C作CF⊥l于点F,过点B作BM⊥CF于点M,
∴∠CFA=∠BMC=∠BMF=∠BAF=90°,
∴四边形ABMF是矩形,
∴∠ABM=90°,MF=AB=2,
∵∠ABC=150°,
∴∠MBC=∠ABC-∠ABM=60°,
∵BC=18,
∴CM=BCsin60°=9,
∴CF=CM+MF=2+9,
即支点C离桌面l的高度为2+9cm.
(2)解:如图,过点C作CN//l,过E作EH⊥CN于点H,
∴∠EHC=90,
∵DE=24,CD=2,
∴CE=DE-CD=18,
当∠ECH=30°时,
EH=CEsin30°=9;
当∠ECH=60°时,EH=CEsin60°=9;
∴当面板DE绕点C转动过程中,E离桌面1最大高度与最小 高度的差是 9-9cm.
(1)先证明四边形ABMF是矩形,根据矩形的性质,可得∠ABM=90°,MF=AB=2,再利用角的和差求出∠MBC,然后利用正弦求出CM,再利用线段的和差求出CF即为支点C离桌面l的高度;
(2)分“∠ECH=30°”、“∠ECH=60°”两种情况,分别求出CH,再求出E离桌面1最大高度与最小 高度的差.
6.(1)解:(1)①将代入可得,解得:,
∴该二次函数的表达式为;
②∵将平面内一点向左平移个单位,则与图象上的点重合;若将点A向右平移个单位,则与图象上的点重合,
∴,
∵,
∴抛物线的对称轴为:,
∴,解得:,
∴,
∴.
(2)解:∵设点,是该函数图象上的两点,
∴
∴,,
∴
,
∵,
∴,即.
(1)①利用待定系数法将代入二次函数解析式即可;
②由于B、C两点的纵坐标相同,则B、C两点关于抛物线的对称轴对称,此时可利用抛物线解析式得到对称轴的表达式从而求出的值,再利用二次函数图象上点的坐标特征代入点坐标即可求得n;
(2)由于 与和是定值,则可用含的代数式表示,则可分别用含的代数式表示出与的和,最后再使用配方法即可.
7.(1)解:根据表格数据,当时,设与之间的函数关系式为,
将(0,0),(1,95),(2,180)代入关系式,得,
解得:,
∴当时,与之间的函数关系式为;
(2)解:设排队人数为人,
∵食堂开放5个窗口,每个窗口每分钟4个同学取好餐,
∴每分钟取好餐的同学人数为:5×4=20(个),
当时,,
∴当时,有最大值为320;
当时,,
排队人数最多时有320人;
(3)解:∵开始取餐分钟后增设个窗口,在11点40分时正好完成前300位同学的取餐,
∴,
∴,
都是自然数,
∴,
.
(1)根据题意,可知当时,设与之间的函数关系式为,然后利用待定系数法进行求解即可;
(2)设排队人数为人,根据题意可知每分钟取好餐的同学人数为20人,然后分两种情况讨论:当时,,当时,有最大值为320;当时,,则,据此即可求解;
(3)根据题意列出方程并化简为,由m,x是自然数即可求出m,x的值.
8.(1)解:∵八年级10名学生的竞赛成绩在C组中的数据是:94,90,94,共有3个,
∴,
∴a%=1-10%-20%-30%=40%,
∴a=40,
∵八年级学生竞赛成绩的中位数为第5、6名成绩的平均数,且该成绩在C组中,
∴,
∵七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82,
∴c=99;
(2)解:从方差上看,由于八年级的方差比七年级的方差小,所以八年学生的安全知识竞赛成绩更稳定更好.
(1)先根据八年级学生在C组中的成绩数据,结合扇形统计图求出C组所占百分比,从而求出D组所占百分比,即可得a的值,根据中位数的定义可知八年级学生竞赛成绩的中位数为第5、6名成绩的平均数,结合A,B,C,D所占百分比可知该成绩在C组中,据此可求出b的值,根据众数的定义直接得c的值;
(2)根据方差的意义:方差用来衡量一组数据波动的大小,方差越大,说明数据的波动越大,越不稳定;方差越小,说明数据的波动越小,越稳定,即可求解.
9.(1)证明:∵,
∴,
∵,
∴,
在和中,
∴;
(2)解:由(1)得,
∵,
∴,
∵,
∴.
(1)根据两直线平行,同位角相等得,然后求出,即可证明;
(2)根据全等三角形的性质得,然后利用三角形内角和定理求解即可.
10.(1)解:(米/分),
小钱步行速度为100米/分
(2)解:往返步行速度不变,
返回耗时20分钟,即回到家中为65分钟.
当时,
图象如图所示.
(3)解:由题,小塘从家中到体育公园所需的时间为(分),
得,解得
(1)利用速度=路程÷时间解题即可;
(2)先根据距家的路程=全程-行进路程列出函数关系式,求出时间x的取值范围,补图即可;
(3)根据相遇问题列方程解题即可.
11.(1)解:∵二次函数 的图象经过点(
,且对称轴为直线
解得
∴这个二次函数的解析式为
(2)解:当y=x时, 则
整理得
解得
∴这个函数不动点的坐标是( 和(5,5)
(3)解:
∴抛物线开口向上,顶点为(
∵这个函数不动点的坐标是A(-2,-2), B(5,5),
∴若点P(x,y)是函数图象上的一个动点,当点P在点A,B之间运动时,y的最大值为5,最小值为-11,
∴的最大值与最小值的差为5-(-11)=16
(1)根据待定系数法即可求出答案;
(2)根据为函数的不动点的定义列出方程,求解即可;
(3)根据不动点的坐标以及二次函数的性质求出最小值,然后求差解题.
12.解:过点作于点,可得,在中,,
∴
∴
过点A作于点 F,可得CF长,然后在中根据余弦的定义求BF长解题即可.
13.(1)解:由题意, 抛物线顶点为(2,3),
∴可设该抛物线的表达式为
将点(0,1)代入, 得4
∴该抛物线的表达式为
(2)解:由题意,当 时,
∴水流能越过该障碍物
(3)解:由题意,
∴抛物线的对称轴为直线
①当 即 时,将 代入 得
②当 即 时,将 代入 得
综上所述,a的取值范围为
(1)依据题意,抛物线顶点为(2,3),从而可设该抛物线的表达式为 再将点(0,1)代入, 得 可得 进而可以得解;
(2)依据题意, 当 时,求出y值与2作比较故解题;
(3)依据题意,由 可得抛物线的对称轴为直线 再结合二次函数的性质进行分 和 两种情形讨论计算可以得解.
14.(1)解: 将点A坐标代入反比例函数解析式得,
所以反比例函数解析式为
将点B坐标代入反比例函数解析式得,
所以点B的坐标为(
将A,B两点坐标代入一次函数解析式得,
解得
所以一次函数解析式为
(2)解:由函数图象可知,当 或 时,一次函数的图象在反比例函数图象的上方,即
所以当 x的取值范围是: 或
(3)解:连接AO,令直线AB与x轴的交点为M,
将 代入 得,
所以点M的坐标为(
所以
因为正比例函数图象与反比例函数图象都是中心对
称图形,且坐标原点是对称中心,
所以点B和点C关于点O成中心对称,
所以
所以
(1)先将点A坐标代入反比例函数解析式,求出m,再求出点B坐标,最后用待定系数法求出一次函数解析式即可.
(2)利用数形结合的数学思想即可解决问题.
(3)连接AO,根据反比例函数与正比例函数的对称性,将 的面积转化为 面积的2倍即可解决问题.
15.(1)25
(2)D等级的人数为25﹣4﹣10﹣8=3,
∴D等所在的百分比是×100%=12%
条形统计图补充为:
(3)216
解:(1)本次抽样测试的学生人数为:10÷40%=25(人),
故答案为:25;
(3)1800×=216(人),
故答案为:216.
(1)用B等级的人数除以它所占的百分比即可得到调查的总人数;
(2)用总人数分别减去A、B、C等级的人数得到D等级人数,然后用: 乘以D等级所占的百分比得到D等所在的扇形的圆心角的度数,再补全条形统计图;
(3)利用样本估计总体,用1800乘以D等级所占百分比即可.
16.(1)2
(2)解:树状图如下:
共有12种等可能的结果,其中摸出的球是一个红球和一个白球的结果数为4, 所以摸出的球是一个红球和一个白球的概率为
解:设红球有 x 个,则恰好摸到红球的概率: ,
解得: ,
经检验,x=2为原分式方程的解,
红球有 2 个.
故答案为:2
(1)设袋中红球有x个,根据任意摸出1个球恰好摸到红球的概率是 列出关于x的方程,解之可得答案;
(2)列表得出所有等可能的情况数,找出两次都摸出的球是一个红球和一个白球的情况数,即可求出所求的概率.
17.(1)解:如图,
由题意得,MF⊥DE,FM∥EC,
∴∠DMF=∠DCE=30°,
∵DC=42m,CM=12m,
∴DM=CD-CM=30(m),
在Rt△DFM中,DF=DM=15m,
FM=DF=15(m),
在Rt△DFN中,∠DNF=45°,tan∠DNF=,
∴FN==15(m),
∴MN=FM-FN=(15-15)m,
答:观景平台MN的长为()米
(2)解:如图,
由题意得,FN=EP=15m,EF=AH,FH=EA,
在Rt△DEC中,∠DCE=30°,CD=42m,
∴DE=CD=21m,CE=DE=21m,
∵AC=30m,
∴FH=AE=AC+CE=(30+21)m,
∴NH=FH-FN=30+21-15=(21+15)m,
在Rt△BNH中,∠BNH=30°,
∵tan∠BNH=,
∴BH =NH·tan30°=(21+15)×=(21+5)m,
∵DF=15m,
∴EF=AH=DE-DF=21-15=6(m),
∴AB =BH+AH=(27+5)m.
答:轻轨所穿楼栋AB的高度为米
(1)由题意,由线段的和差DM=CD-CM求出DM的值,在Rt△DFM中,根据锐角三角函数tan∠DNF=求出FN的值,然后由线段的和差MN=FM-FN可求解;
(2)解Rt△DEC可求得CE的值,由线段的和差FH=AE=AC+CE求出FH的值,同理根据NH=FH-FN求出NH的值,在Rt△BNH中,根据锐角三角函数tan∠BNH=求出BH的值,然后由线段的和差AB =BH+AH可求解.
18.(1)解:将代入,得.
,
对称轴为直线
(2)解:函数图象向上平移个单位长度后解析式为
在原点左侧,
设点坐标为,点坐标为
,解得
将代入,得
(3)解:当即时,当时有最小值为2n,
,解得(舍),(舍)
当即时,当时有最小值为,
,解得
综上,
(1)由于抛物线解析中只有一次项系数未知,且知道其图象上一个点的坐标,只需把这个点的坐标代入到函数解析式中即可求出的值,此时再根据抛物线的对称轴公式计算即可;
(2)由于平移不改变抛物线的形状与大小,则沿轴方向平移时,对称轴不变,可根据题意分别设出A、B两点的坐标,再利用对称关系即可求出点A的坐标值,再代入到平移后的抛物线解析式中即可求出的值;
(3)由于抛物线的开口向上,所以二次函数有最小值,此时在对称轴的左边,随的增大而减小;反之,随的增大而增大;因为二次函数 ,即当时,最小值为;所以应当分类讨论,当时,函数最小值为,此时有,解得, ,均与假设不符;当即时,函数最小值为,即时有最小值为,即.
19.(1)解:步行速度(分钟);
(2)解:如图所示
由题可知当时,,所以点;
当时,,所以点;
设函数解析式为,
,解得
(3)解:设学校到瓯华站共米,由题意列方程得:
,解得
答: 学校到瓯华站的路程为
(1)由于小温出发和返回学校的速度相同,则从学校到返回地点用时为10分钟的一半即5分钟,步行路程为325,则速度等于路程除以时间即可;
(2)求出租车的路程与时间的函数解析式,由题意可分别求出A、B两点的坐标,再利用待定系数法联立方程组即可;
(3)求学校到车站的路程,由于相遇后出租车比小州早到3分钟,即在走完剩余路程中,出租车用时比小州少了3分钟,由于小州的速度已知为65,出租车的速度利用函数关系式知为260,剩余路程为总路程减去小州步行16分钟的路程1040,列方程即可求出总路程。
20.(1)解:抽样总人数等于人
C组:50-10-15-5=20人,补全条形图如图
(2)解:人
答: 九年级学生中参加家务劳动的时间在60到100分钟(含60分钟)的学生有420人
(3)解:列表得:共有20种等可能结果,抽取到一男一女有12种结果
女1 女2 女3 男1 男2
女1 / 两女 两女 一男一女 一男一女
女2 两女 / 两女 一男一女 一男一女
女3 两女 两女 / 一男一女 一男一女
男1 一男一女 一男一女 一男一女 / 两男
男2 一男一女 一男一女 一男一女 两男 /
P(一男一女)
(1)观察两个统计图,发现D组人数和在总抽样人数中的占比都知道,则用D组人数除以其占比即可得到总抽样人数,再用抽样总数分别减去A、B、D三组人数即可得出C组人数,补全条形统计图即可;
(2) 要估算该校九年级学生中参加家务劳动的时间在60到100分钟(含60分钟)的学生,先求出满足条件的人数占抽样总数的百分比,再乘以全校总人数即可;
(3)两步试验的概率可通过画树状图或列表格的方法求出,注意画树状图时要不重复不遗漏,列表格时注意每名同学第一次抽到后则第二次不能再抽取,因此对角线栏目上不能填数据.
21.(1)证明:如图
,
又在等边中,
(ASA),
(2)解:,
又
(1)证明BD=CE,可证明这两条边所在的三角形全等,即;由于等边三角形的三边相等,三个内角相等且都是60度,即,还缺少一个条件,此时可借助三角形外角的性质结合已知条件得出,则利用ASA即可证明全等;
(2)求值,观察图形知这两条边分别在和中,由于可证,由相似的性质知化比例式为等积式得,由前面全等的性质可计算.
22.(1)解:①当t=0时,将点A(3,0)代入抛物线解析式得9a+3(a-3)-3=0,得a=1,此时抛物线的解析式为y=x2-2x-3,对称轴为x=1;
②,即有m2-2m-3≧0,即(m+1)(m-3)≧0,
故或解得m≧3或m≦-1;
(2)解:t>0即有9a+3(a-3)-3>0,得a>1,对于抛物线,其对称轴为直线x=<1,即可知抛物线开口向上,且对称轴在直线x=1的左侧,
m>n,m+n>2
当m>n>1时,二次函数在x>1时y随x的增大而增大,p>q;
当m>1,n<1时,注意到m+n>2即有m>2-n,n<1,故2-n>1,故p>q
综上所述,p>q
(1)t=0时直接代入抛物线解析式可得a=1,再分类讨论解不等式;
(2)由题意可得a的范围,同时可知对称轴的位置,再由且 可得p和q的大小关系.
23.(1)2;1.5
(2)解:①根据表格数据描点:,,,,,在平面直角坐标系中画出对应函数的图象如下:
②不断减小
(3)或
(1)根据题意,
故答案为: 2, 1.5;
(2)②由图象可知,随着自变量x的不断增大,函数值y的变化趋势是不断减小,
故答案为:不断减小;
(3)如图:
由函数图象知, 当 或 时,
即当 时,
故答案为: 或
(1)由已知列出方程,即可解得a,b的值;
(2)①描点画出图象即可;
②观察图象可得答案;
(3)同一坐标系内画出图象,观察即可得到答案.
24.(1)
(2)和
(3)16
25.(1)解:∵函数y=m(x+1)2+4n(m≠0,且m,n为实数),
∴函数图象的对称轴为x=-1;
(2)证明:令y=0,则0=m(x+1)2+4n,
即,
∵m,n异号,
∴,
∴一元二次方程有两个不相等的实数根,即函数y的图象与x轴有两个不同的交点;
(3)证明:由题可知p=m+4n,q=16m+4n,r=25m+4n,
∵2q-(p+r)=2(16m+4n)-(m+4n+25m+4n)=6m<0,
∴m<0.
(1)根据抛物线的解析式即可求出抛物线的对称轴;
(2)令y=0,转化为求一元二次方程根的情况,结合题意即可求解;
(3)分别代入求出p、q、r的值,根据不等式,化简即可求解.
同课章节目录
