湖南省祁阳市浯溪二中2024-2025学年下学期第3章《图形与坐标》单元测试卷(含答案) 湘教版数学八年级下册
文档属性
| 名称 | 湖南省祁阳市浯溪二中2024-2025学年下学期第3章《图形与坐标》单元测试卷(含答案) 湘教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 364.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 00:00:00 | ||
图片预览


文档简介
祁阳市浯溪二中2024-2025学年下学期八年级下册数学第3章《图形与坐标》单元测试卷
一.选择题(共10小题,每小题3分,共30分)
1.已知x轴上的点P到原点的距离为5,则点P的坐标为( )
A.(5,0) B.(0,5)或(0,﹣5)
C.(0,5) D.(5,0)或(﹣5,0)
2.在直角坐标系中,点M(﹣2,3)与点N关于x轴对称,则将点M平移到点N的过程可以是( )
A.向上平移6个单位 B.向下平移6个单位
C.向左平移4个单位 D.向右平移4个单位
3.在平面直角坐标系xOy中,长方形ABCD的两条对称轴是坐标轴,邻边长分别为4,6.若点A在第一象限,则点C的坐标是( )
A.(﹣2,﹣3) B.(2,3)
C.(﹣2,﹣3),或(﹣3,﹣2) D.(2,3),或(3,2)
4.若P与A(1,3)关于原点对称,则点P落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知点A在第四象限,且到x轴的距离为2,到y轴的距离为4,则点A的坐标为( )
A.(﹣2,4) B.( 2,﹣4 ) C.(﹣4,﹣2 ) D.( 4,﹣2 )
6.在平面直角坐标系中,若点P(a,b)关于y轴的对称点在第三象限,则( )
A.a>0,b>0 B.a>0,b<0 C.a<0,b>0 D.a<0,b<0
7.在平面直角坐标系中,将点A(n2,1)向右平移(n2+3)个单位长度后得到点B.有四个点M(﹣2n2,1),N(3n2,1),P(n2,n2+4),Q(n2+1,1),一定在线段AB上的是( )
A.点M B.点N C.点P D.点Q
8.如图,在灯塔O处观测到轮船B位于南偏西35°的方向,轮船A在西北方向上,则∠AOB的大小为( )
A.90° B.92° C.96° D.100°
9.在平面直角坐标系中,若A(m+3,﹣1),B(3,1﹣m),且直线AB∥y轴,则m的值是( )
A.0 B.1 C.2 D.3
10.已知点A(a,5)与点B(3,b)关于x轴对称,则a+b的值为( )
A.8 B.﹣8 C.2 D.﹣2
二.填空题(共8小题,每小题3分,共24分)
11.在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,2)的对应点A'的坐标为(﹣2,﹣2),则点B(﹣1,1)的对应点B'的坐标为 。
12.在平面直角坐标系中,点A(﹣3,3),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为 。
13.已知点A(a,1)与点B(﹣4,b)关于原点对称,则a﹣b的值为 。
14.已知点M(a,3)与点N(﹣4,b)关于y轴对称,
(1)2a﹣b= ;
(2)若点P与点M关于原点对称,则PM= .
15.点A在平面直角坐标系第二象限,距离x轴3个单位长度,距离y轴5个单位长度,则点A的坐标是 .
16.如图,网格中的每一个小正方形的边长都为1,△ABC的顶点都在格点上,若点B的坐标为(3,﹣1),点C的坐标为(﹣3,3),CD为△ABC的中线,则点D的坐标为 .
17.点P的坐标是(m,﹣1),且点P关于x轴对称的点的坐标是(﹣3,2n),则m= ,n= .
18.在平面直角坐标系中,三角形OAB的面积为3,点A的坐标为(3,﹣2),点B的坐标为(2m,n﹣1).若线段AB平行于x轴,则nm的值为 .
三.解答题(共8小题,共66分)
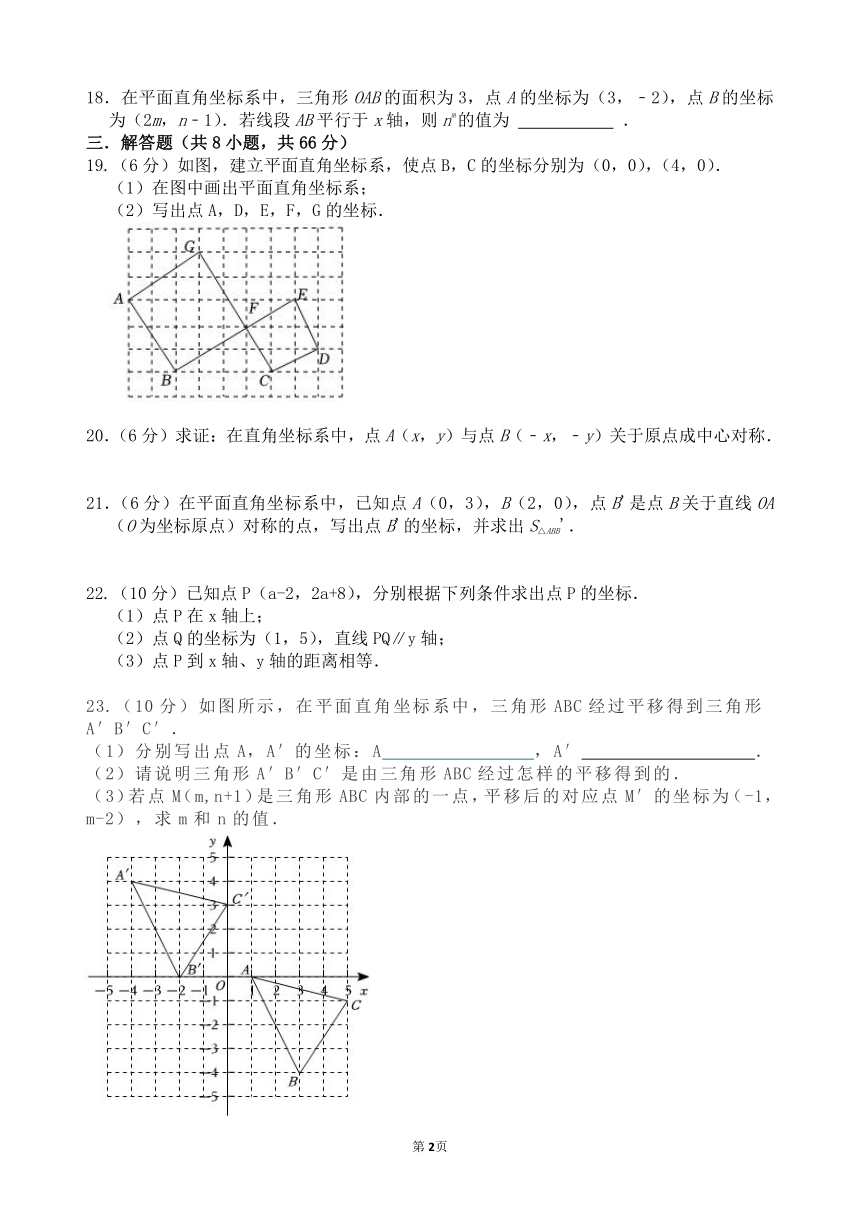
19.(6分)如图,建立平面直角坐标系,使点B,C的坐标分别为(0,0),(4,0).
(1)在图中画出平面直角坐标系;
(2)写出点A,D,E,F,G的坐标.
20.(6分)求证:在直角坐标系中,点A(x,y)与点B(﹣x,﹣y)关于原点成中心对称.
21.(6分)在平面直角坐标系中,已知点A(0,3),B(2,0),点B'是点B关于直线OA(O为坐标原点)对称的点,写出点B'的坐标,并求出S△ABB'.
22.(10分)已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点Q的坐标为(1,5),直线PQ∥y轴;
(3)点P到x轴、y轴的距离相等.
23.(10分)如图所示,在平面直角坐标系中,三角形ABC经过平移得到三角形A′B′C′.
(1)分别写出点A,A′的坐标:A ,A′ .
(2)请说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的.
(3)若点M(m,n+1)是三角形ABC内部的一点,平移后的对应点M′的坐标为(-1,m-2),求m和n的值.
24. (8分)在平面直角坐标系中,已知点A(3,2),B(3,2a+1).
(1)若点B在第四象限且到坐标轴的距离相等,求a的值并写出点B的坐标;
(2)若线段AB=3,求a的值.
25.(10分)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)以点C为原点,方格线为坐标轴建立平面直角坐标系;
(2)画出△ABC关于直线l对称的△A1B1C1;
(3)写出△A1B1C1中B1、C1的坐标:B1 ,C1 ;
(4)求△A1B1C1的面积.
26.(10分)在平面直角坐标系中,A(﹣4,0),C(2,6),连接AC交y轴于点B,∠CAO=45°,过C点作x轴的垂线交x轴于点D.
(1)若点E从点A出发,沿△ADC的边逆时针运动至点C,速度每秒2个单位长度,运动时间为t秒,△ABE的面积为S,请用含t的式子表示S;
(2)如图2,连接BD,当BD向左平移的过程中,y轴上是否存在一点P,使△BDP为等腰直角三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C C D B D D A D
11.(﹣5,﹣3) 12.2,(3,3)13.5 14.(1)5;(2)10.
15.(﹣5,3).
16.(1,﹣1).
17.﹣3;.
18. 1或﹣1.
19.解:(1)建立平面直角坐标系,如图,
(2)A(-2,3),D(6,1),E(5,3),F(3,2),G(1,5).
20.证明:如图,连结AO,BO,作AC⊥x轴,BD⊥x轴,C,D分别为垂足.
∵|x|=|﹣x|,|y|=|﹣y|,
∴CO=DO,AC=BD,
∴Rt△AOC≌Rt△BOD,
∴AO=BO,∠AOC=∠BOD,
∴∠BOD+∠AOD=∠AOC+∠AOD=180°,
即A,O,B在一条直线上,当将点A绕点O旋转180°时,点A与点B重合.
所以点A,B关于原点成中心对称(我们也称为点A,B关于原点对称).
21.解:因为A(0,3),O(0,0),B(2,0),
且点B'是点B关于直线OA对称的点,
所以点B'的坐标为(﹣2,0).
由B(2,0),B'(﹣2,0)得,
BB'=2﹣(﹣2)=4,
又A(0,3),
所以.
22.解:(1)∵点P(a-2,2a+8)在x轴上,∴2a+8=0,解得:a=-4,
故a-2=-4-2=-6,则P(-6,0);
(2)∵点Q的坐标为(1,5),直线PQ∥y轴,∴a-2=1,解得:a=3,
故2a+8=14,则P(1,14);
(3)∵点P到x轴、y轴的距离相等,∴a-2=2a+8或a-2+2a+8=0,解得:a1=-10,a2=-2,
故当a=-10时,a-2=-12,2a+8=-12,则P(-12,-12);故当a=-2时,a-2=-4,2a+8=4,
则P(-4,4).综上所述:P(-12,-12)或(-4,4).
23.解:(1)由所给平面直角坐标系可知,点A的坐标为(1,0),点A′的坐标为(-4,4);
故答案为:(1,0),(-4,4);
(2)因为点A坐标为(1,0),且平移后的对应点A′的坐标为(-4,4),
所以1+(-5)=-4,0+4=4,即△A′B′C′由△ABC向左平移5个单位长度,再向上平移4个单位长度得到;
(3)因为点M(m,n+1)是三角形ABC内部的一点,平移后的对应点M′的坐标为(-1,m-2),所以m+(-5)=-1,n+1+4=m-2,解得m=4,n=-3,故m的值为4,n的值为-3.
24.解:(1)∵点B(3,2a+1)在第四象限且到坐标轴的距离相等,
∴2a+1=-3,∴a=-2,则点B的坐标为(3,-3);
(2)∵线段AB=3,∴2a+1-2=3或2a+1-2=-3,∴a=2或a=-1.
25.解:(1)如图,(2)如图,△A1B1C1为所作;
(3)B1(5,1),C1(2,0);故答案为:(5,1),(2,0);
(4)△A1B1C1的面积=3×41×33×12×4=5.故答案为:5.
26.解:(1)∵∠CAO=45°,A(﹣4,0),C(2,6),∴∠CAO=∠DCA=∠OBA=45°,∴OA=OB=4,AD=CD=6,∴OD=2,如图,当点E在AD上时,
由题意得:AE=2t,∴,如图,当点E在CD上时,
由题意得:DE=2t﹣6,CE=6﹣(2t﹣6)=12﹣2t,
∴,
=18﹣6t+18﹣12+2t,=24﹣4t,
综上可知;
(2)如图,B1P=D1P,∠B1DP1=90°时,
∴∠PB1B=∠D1PO,∴△B1BP≌△POD1(ASA),
∴B1B=PO,BP=OD1,由平移性质可知:B1B=D1D,由(1)得:OD=2,OB=4,
∴B1B=PO=3,∴点P(0,3);
如图,B2P2=B2D2D2,∠P2B2D2=90°时,
由平移性质可知:AD2=OD=2,同理AD2=B2E=2,∴BP2=2,∴OP2=5,∴P2(0,5);
当B3D3=P3D3时,∠P3D3B3=90°,
同理OP3=2,∴P3(0,2),综上可知:点P的坐标为(0,2)或(0,3)或(0,5).
第6页
一.选择题(共10小题,每小题3分,共30分)
1.已知x轴上的点P到原点的距离为5,则点P的坐标为( )
A.(5,0) B.(0,5)或(0,﹣5)
C.(0,5) D.(5,0)或(﹣5,0)
2.在直角坐标系中,点M(﹣2,3)与点N关于x轴对称,则将点M平移到点N的过程可以是( )
A.向上平移6个单位 B.向下平移6个单位
C.向左平移4个单位 D.向右平移4个单位
3.在平面直角坐标系xOy中,长方形ABCD的两条对称轴是坐标轴,邻边长分别为4,6.若点A在第一象限,则点C的坐标是( )
A.(﹣2,﹣3) B.(2,3)
C.(﹣2,﹣3),或(﹣3,﹣2) D.(2,3),或(3,2)
4.若P与A(1,3)关于原点对称,则点P落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知点A在第四象限,且到x轴的距离为2,到y轴的距离为4,则点A的坐标为( )
A.(﹣2,4) B.( 2,﹣4 ) C.(﹣4,﹣2 ) D.( 4,﹣2 )
6.在平面直角坐标系中,若点P(a,b)关于y轴的对称点在第三象限,则( )
A.a>0,b>0 B.a>0,b<0 C.a<0,b>0 D.a<0,b<0
7.在平面直角坐标系中,将点A(n2,1)向右平移(n2+3)个单位长度后得到点B.有四个点M(﹣2n2,1),N(3n2,1),P(n2,n2+4),Q(n2+1,1),一定在线段AB上的是( )
A.点M B.点N C.点P D.点Q
8.如图,在灯塔O处观测到轮船B位于南偏西35°的方向,轮船A在西北方向上,则∠AOB的大小为( )
A.90° B.92° C.96° D.100°
9.在平面直角坐标系中,若A(m+3,﹣1),B(3,1﹣m),且直线AB∥y轴,则m的值是( )
A.0 B.1 C.2 D.3
10.已知点A(a,5)与点B(3,b)关于x轴对称,则a+b的值为( )
A.8 B.﹣8 C.2 D.﹣2
二.填空题(共8小题,每小题3分,共24分)
11.在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,2)的对应点A'的坐标为(﹣2,﹣2),则点B(﹣1,1)的对应点B'的坐标为 。
12.在平面直角坐标系中,点A(﹣3,3),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为 。
13.已知点A(a,1)与点B(﹣4,b)关于原点对称,则a﹣b的值为 。
14.已知点M(a,3)与点N(﹣4,b)关于y轴对称,
(1)2a﹣b= ;
(2)若点P与点M关于原点对称,则PM= .
15.点A在平面直角坐标系第二象限,距离x轴3个单位长度,距离y轴5个单位长度,则点A的坐标是 .
16.如图,网格中的每一个小正方形的边长都为1,△ABC的顶点都在格点上,若点B的坐标为(3,﹣1),点C的坐标为(﹣3,3),CD为△ABC的中线,则点D的坐标为 .
17.点P的坐标是(m,﹣1),且点P关于x轴对称的点的坐标是(﹣3,2n),则m= ,n= .
18.在平面直角坐标系中,三角形OAB的面积为3,点A的坐标为(3,﹣2),点B的坐标为(2m,n﹣1).若线段AB平行于x轴,则nm的值为 .
三.解答题(共8小题,共66分)
19.(6分)如图,建立平面直角坐标系,使点B,C的坐标分别为(0,0),(4,0).
(1)在图中画出平面直角坐标系;
(2)写出点A,D,E,F,G的坐标.
20.(6分)求证:在直角坐标系中,点A(x,y)与点B(﹣x,﹣y)关于原点成中心对称.
21.(6分)在平面直角坐标系中,已知点A(0,3),B(2,0),点B'是点B关于直线OA(O为坐标原点)对称的点,写出点B'的坐标,并求出S△ABB'.
22.(10分)已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点Q的坐标为(1,5),直线PQ∥y轴;
(3)点P到x轴、y轴的距离相等.
23.(10分)如图所示,在平面直角坐标系中,三角形ABC经过平移得到三角形A′B′C′.
(1)分别写出点A,A′的坐标:A ,A′ .
(2)请说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的.
(3)若点M(m,n+1)是三角形ABC内部的一点,平移后的对应点M′的坐标为(-1,m-2),求m和n的值.
24. (8分)在平面直角坐标系中,已知点A(3,2),B(3,2a+1).
(1)若点B在第四象限且到坐标轴的距离相等,求a的值并写出点B的坐标;
(2)若线段AB=3,求a的值.
25.(10分)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)以点C为原点,方格线为坐标轴建立平面直角坐标系;
(2)画出△ABC关于直线l对称的△A1B1C1;
(3)写出△A1B1C1中B1、C1的坐标:B1 ,C1 ;
(4)求△A1B1C1的面积.
26.(10分)在平面直角坐标系中,A(﹣4,0),C(2,6),连接AC交y轴于点B,∠CAO=45°,过C点作x轴的垂线交x轴于点D.
(1)若点E从点A出发,沿△ADC的边逆时针运动至点C,速度每秒2个单位长度,运动时间为t秒,△ABE的面积为S,请用含t的式子表示S;
(2)如图2,连接BD,当BD向左平移的过程中,y轴上是否存在一点P,使△BDP为等腰直角三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C C D B D D A D
11.(﹣5,﹣3) 12.2,(3,3)13.5 14.(1)5;(2)10.
15.(﹣5,3).
16.(1,﹣1).
17.﹣3;.
18. 1或﹣1.
19.解:(1)建立平面直角坐标系,如图,
(2)A(-2,3),D(6,1),E(5,3),F(3,2),G(1,5).
20.证明:如图,连结AO,BO,作AC⊥x轴,BD⊥x轴,C,D分别为垂足.
∵|x|=|﹣x|,|y|=|﹣y|,
∴CO=DO,AC=BD,
∴Rt△AOC≌Rt△BOD,
∴AO=BO,∠AOC=∠BOD,
∴∠BOD+∠AOD=∠AOC+∠AOD=180°,
即A,O,B在一条直线上,当将点A绕点O旋转180°时,点A与点B重合.
所以点A,B关于原点成中心对称(我们也称为点A,B关于原点对称).
21.解:因为A(0,3),O(0,0),B(2,0),
且点B'是点B关于直线OA对称的点,
所以点B'的坐标为(﹣2,0).
由B(2,0),B'(﹣2,0)得,
BB'=2﹣(﹣2)=4,
又A(0,3),
所以.
22.解:(1)∵点P(a-2,2a+8)在x轴上,∴2a+8=0,解得:a=-4,
故a-2=-4-2=-6,则P(-6,0);
(2)∵点Q的坐标为(1,5),直线PQ∥y轴,∴a-2=1,解得:a=3,
故2a+8=14,则P(1,14);
(3)∵点P到x轴、y轴的距离相等,∴a-2=2a+8或a-2+2a+8=0,解得:a1=-10,a2=-2,
故当a=-10时,a-2=-12,2a+8=-12,则P(-12,-12);故当a=-2时,a-2=-4,2a+8=4,
则P(-4,4).综上所述:P(-12,-12)或(-4,4).
23.解:(1)由所给平面直角坐标系可知,点A的坐标为(1,0),点A′的坐标为(-4,4);
故答案为:(1,0),(-4,4);
(2)因为点A坐标为(1,0),且平移后的对应点A′的坐标为(-4,4),
所以1+(-5)=-4,0+4=4,即△A′B′C′由△ABC向左平移5个单位长度,再向上平移4个单位长度得到;
(3)因为点M(m,n+1)是三角形ABC内部的一点,平移后的对应点M′的坐标为(-1,m-2),所以m+(-5)=-1,n+1+4=m-2,解得m=4,n=-3,故m的值为4,n的值为-3.
24.解:(1)∵点B(3,2a+1)在第四象限且到坐标轴的距离相等,
∴2a+1=-3,∴a=-2,则点B的坐标为(3,-3);
(2)∵线段AB=3,∴2a+1-2=3或2a+1-2=-3,∴a=2或a=-1.
25.解:(1)如图,(2)如图,△A1B1C1为所作;
(3)B1(5,1),C1(2,0);故答案为:(5,1),(2,0);
(4)△A1B1C1的面积=3×41×33×12×4=5.故答案为:5.
26.解:(1)∵∠CAO=45°,A(﹣4,0),C(2,6),∴∠CAO=∠DCA=∠OBA=45°,∴OA=OB=4,AD=CD=6,∴OD=2,如图,当点E在AD上时,
由题意得:AE=2t,∴,如图,当点E在CD上时,
由题意得:DE=2t﹣6,CE=6﹣(2t﹣6)=12﹣2t,
∴,
=18﹣6t+18﹣12+2t,=24﹣4t,
综上可知;
(2)如图,B1P=D1P,∠B1DP1=90°时,
∴∠PB1B=∠D1PO,∴△B1BP≌△POD1(ASA),
∴B1B=PO,BP=OD1,由平移性质可知:B1B=D1D,由(1)得:OD=2,OB=4,
∴B1B=PO=3,∴点P(0,3);
如图,B2P2=B2D2D2,∠P2B2D2=90°时,
由平移性质可知:AD2=OD=2,同理AD2=B2E=2,∴BP2=2,∴OP2=5,∴P2(0,5);
当B3D3=P3D3时,∠P3D3B3=90°,
同理OP3=2,∴P3(0,2),综上可知:点P的坐标为(0,2)或(0,3)或(0,5).
第6页
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
