1.3 三角函数的计算 课件(共35张PPT)
文档属性
| 名称 | 1.3 三角函数的计算 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:03:41 | ||
图片预览









文档简介
(共35张PPT)
1.3 三角函数的计算
第一章 直角三角形的边角关系
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示一些生活中与直角三角形相关的图片,如楼梯、斜坡、电线杆的拉线等,并提出问题:在这些生活场景中,我们常常需要知道一些角度或长度的信息,比如楼梯的倾斜程度、斜坡的坡度等,那么如何通过已有的边长信息来获取这些角度信息,或者通过角度来计算边长呢?
引导学生思考,引发学生对直角三角形边角关系的好奇心和探究欲望,从而引出本节课的课题 —— 直角三角形的边角关系。
(二)讲授新课(25 分钟)
锐角三角函数的定义
构建直角三角形模型:在黑板上画出一个 Rt,其中∠C = 90° 。
引入正弦函数:设∠A 为锐角,引导学生观察∠A 的对边 BC 与斜边 AB 的比值,定义 sin= \(\frac{BC}{AB}\),即∠A 的正弦等于∠A 的对边与斜边的比。通过改变∠A 的大小,让学生观察这个比值的变化情况,强调对于一个确定的锐角∠A,其正弦值是固定的。
同理,讲解余弦函数和正切函数的定义:co = \(\frac{AC}{AB}\),∠A 的余弦等于∠A 的邻边与斜边的比;ta = \(\frac{BC}{AC}\),∠A 的正切等于∠A 的对边与邻边的比。
给出多个不同的直角三角形,让学生分别同锐角的正弦、余弦和正切值,加深对定义的理解。
特殊锐角的三角函数值
30° 角的三角函数值:构建一个含 30° 角的直角三角形,设 30° 角所对的直角边为 a,根据直角三角形中 30° 角所对的直角边等于斜边的一半,可得斜边为 2a,再利用勾股定理求出另一条直角边为\(\sqrt{3}a\) 。然后分别计算 sin30° = \(\frac{a}{2a}\) = \(\frac{1}{2}\),cos30° = \(\frac{\sqrt{3}a}{2a}\) = \(\frac{\sqrt{3}}{2}\),tan30° = \(\frac{a}{\sqrt{3}a}\) = \(\frac{\sqrt{3}}{3}\) 。
45° 角的三角函数值:构建一个等腰直角三角形,设直角边为 b,则斜边为\(\sqrt{2}b\) 。计算 sin45° = \(\frac{b}{\sqrt{2}b}\) = \(\frac{\sqrt{2}}{2}\),cos45° = \(\frac{b}{\sqrt{2}b}\) = \(\frac{\sqrt{2}}{2}\),tan45° = \(\frac{b}{b}\) = 1 。
60° 角的三角函数值:利用含 30° 角的直角三角形,因为 60° 角与 30° 角互为余角,根据三角函数的诱导公式或直接计算,可得 sin60° = \(\frac{\sqrt{3}}{2}\),cos60° = \(\frac{1}{2}\),tan60° = \(\sqrt{3}\) 。
制作特殊锐角三角函数值表格,让学生观察表格,总结规律,帮助记忆。
三角函数的应用
举例说明如何运用三角函数解决实际问题,如测量建筑物的高度。已知在离建筑物底部一定距离的地方,测量出观测点到建筑物顶部的仰角以及观测点到建筑物底部的距离,构建直角三角形,选择合适的三角函数(如正切函数)来计算建筑物的高度。
讲解解题的一般步骤:首先根据题意画出直角三角形,明确已知条件和所求问题;然后分析在直角三角形中已知哪些边或角,选择恰当的三角函数关系;最后进行计算求解,并检验答案的合理性。
(三)例题讲解(15 分钟)
例 1:在 Rt中,∠C = 90°,AB = 5,BC = 3,求 sin的值。
分析:根据正弦、余弦和正切函数的定义,先求出 AC 的长度(利用勾股定理 AC = \(\sqrt{AB^{2} - BC^{2}}\) = \(\sqrt{25 - 9}\) = 4),再代入公式计算。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
用科学计算器求任意锐角的三角函数值
1. 求整数度数的锐角的三角函数值
在科学计算器的面板上涉及三角函数的键有
,当我们计算某整数度数的三角函数值时,可先按相应的键,然后从高位向低位按出表示度数的整数,最后按 键,屏幕上就会显示出结果.
知1-讲
感悟新知
2. 求非整数度数的锐角的三角函数值
(1)若度数是用度表示的,则按整数度数的按键步骤操作 即可.
(2)若度数是用度、分、秒表示的,在用科学计算器计算三角函数值时,同样先按 或 或 键,然后依次按 (度) (分) (秒)键,最后按 键,屏幕上就会显示出结果. 若锐角中只有度、秒,则应在
(分)键前补上0 .
感悟新知
知1-练
用计算器求sin 26°,cos 42°,tan 75°,
sin 72°38′25″的值.
例 1
解题秘方:按计算器的使用说明求值.
感悟新知
知1-练
解:求值过程如下表所示.
按键顺序 显示结果
sin 26° sin 26°=0.438 371 146
cos 42° cos 42°=0.743 144 825
tan 75° tan 75°=3.732 050 808
sin 72°38′25″ sin 72°38′25″=
0.954 450 312
知识点
用科学计算器由锐角三角函数值求锐角
知2-讲
感悟新知
2
已知锐角三角函数值求锐角的度数
如果是特殊角(30°,45°或60°角)的三角函数值,可直接写出其相应的角的度数;若不是特殊角的三角函数值,应利用计算器求角的度数. 求角的度数要先按 键,将 转化成它们的第二功能. 当三角函数值为分数时,应先化成小数.
感悟新知
知2-练
根据下列条件求锐角A 的度数:
(1)sin A=0.921 6;
(2)cos A=0.680 7;
(3)tan A=0.189 0.
例2
解题秘方:按计算器的使用说明依次按键.
知2-练
感悟新知
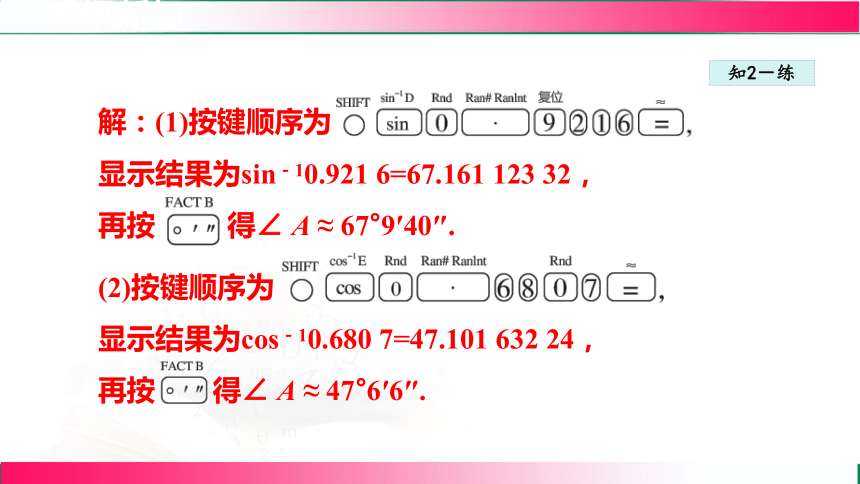
解:(1)按键顺序为
显示结果为sin-10.921 6=67.161 123 32,
再按 得∠ A ≈ 67°9′40″.
(2)按键顺序为
显示结果为cos-10.680 7=47.101 632 24,
再按 得∠ A ≈ 47°6′6″.
知2-练
感悟新知
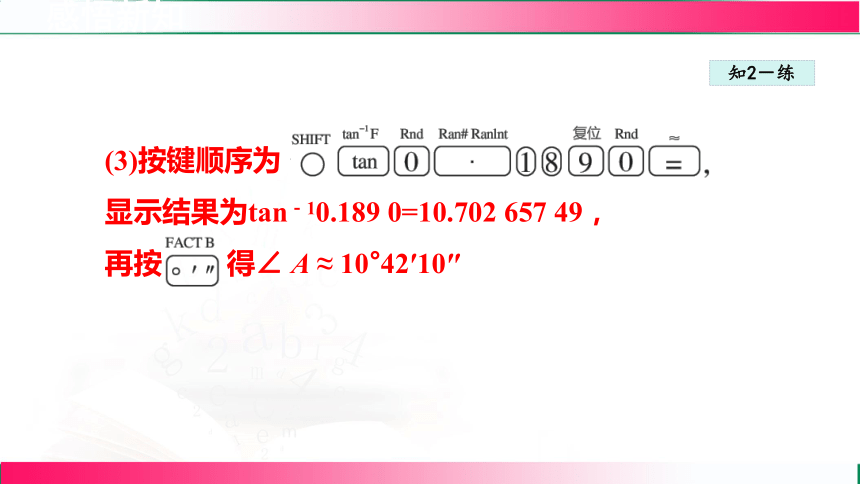
(3)按键顺序为
显示结果为tan-10.189 0=10.702 657 49,
再按 得∠ A ≈ 10°42′10″
知识点
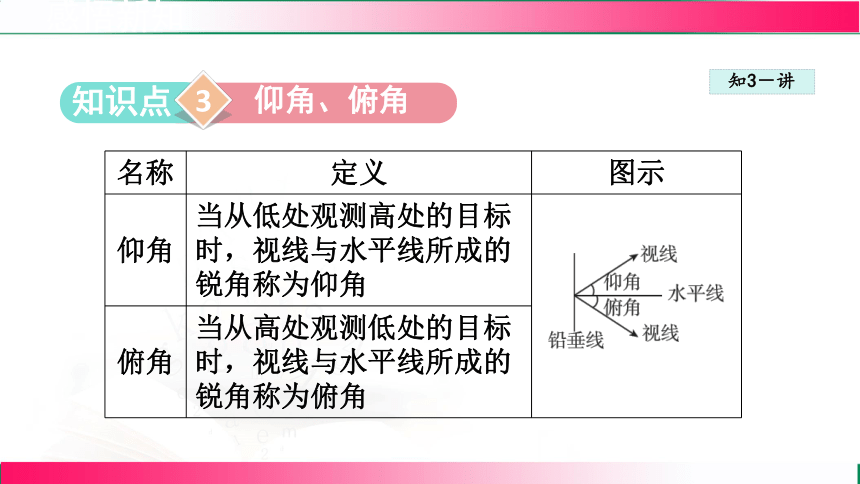
仰角、俯角
知3-讲
感悟新知
3
名称 定义 图示
仰角 当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角
俯角 当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角 感悟新知
知3-练
如图1-3-1,小东在教学楼距地面9 m 高的窗口
C处,测得正前方旗杆顶部A 点的仰角为37°,旗杆底部B 点的俯角为45°. 升旗时,国旗上端在距地面1.95 m处,若国旗随国歌声冉冉升起,并在国歌播放
46 s 结束时到达旗杆顶端,则国旗应以
多大的速度匀速上升?( 参考数据:sin 37 °
≈ 0.60 ,cos 37°≈ 0.80 ,tan 37°≈ 0.75 )
例 3
知3-练
感悟新知
解:如图1-3-1,作CD ⊥ AB 于点D,则BD=9 m.
在Rt△BCD中,BD=9 m,
∠ BCD=45° ,
则BD=CD=9 m.
在Rt△ACD中,CD=9 m,
∠ ACD=37° ,
知3-练
感悟新知
则AD=CD·tan 37°≈ 9×0.75=6.75(m).
所以AB=AD+BD≈ 15.75 m.
因为国旗上升的高度约是15.75-1.95=13.8(m),
整个过程耗时46 s,所以国旗的上升速度约为=0.3(m/s).
因此国旗应以约0.3 m/s 的速度匀速上升.
知3-练
感悟新知
3-1. [中考·新疆] 烽燧即烽火台,是古代军情报警的一种措施,史册记载,夜间举火称“烽”,白天放烟称“燧”.克孜尔尕哈烽燧是古丝绸之路北道上新疆境内时代最早、保存最完好、规模最大的古代烽燧.
知3-练
感悟新知
某数学兴趣小组利用无人机测量该烽燧的高度,如图,无人机飞至距地面高度31.5 米的A处,测得烽燧BC的顶部C处的俯角为50°,测得烽燧BC的底部B处的俯角为65°,试根据提供的数据计算烽燧BC的高度.
(参考数据:sin 50°≈ 0.8,cos 50°≈ 0.6,
tan 50°≈1.2,sin 65°≈0.9,cos 65°≈0.4,
tan 65°≈ 2.1)
知3-练
感悟新知
知3-练
感悟新知
返回
1. 用计算器求sin 70°的值,以下按键顺序正确的是( )
A. B.
C. D.
A
返回
2. 如图,△ABC中,∠ACB=90°,BC=2,AC=3,若用科学计算器求∠A的度数,并以“度、分、秒”为单位表示出这个度数,则下列按键顺序正确的是( )
A.
B.
C.
D.
D
返回
3. [教材P15习题T3] (1)已知cos A=0.785 7,用计算器计算锐角∠A≈________(精确到1′).
(2)已知sin α=0.603 1,用计算器求锐角α≈____________ (精确到1″).
38°13′
37°5′32″
返回
4. 利用计算器计算sin29.5°-cos 58°30′+tan 52°30′≈______. (精确到0.01)
0.81
返回
5. [教材P15习题T5]如图,一个人从山脚下的A点出发,沿山坡小路AB走到山顶B点. 已知坡角为20°,山高BC= 2 km.用科学计算器计算小路AB的长度为__________. (结果精确到0.01 km)
5.85 km
6. 应用计算器填一填,分别比较各个三角函数值的大小,说一说有什么规律:
(1)cos 20°≈________,cos 40°≈________,
cos 60°=________,cos 80°≈________.
规律:
0.939 7
0.766 0
0.5
0.173 6
在锐角范围内,余弦函数值随着角度的增大而减小.
返回
(2)tan 10°≈________,tan 30°≈________,
tan 50°≈________,tan 70°≈________.
规律:
0.176 3
0.577 4
1.191 8
2.747 5
在锐角范围内,正切函数值随着角度的增大而增大.
返回
【答案】C
8. 2024年4月25日,神舟十八号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站. 中国空间站上机械臂的一种工作状态的示意图如图所示,当两臂AC=BC=10 m,两臂夹角∠ACB=100°时,可得A,B两点间的距离为________. (结果精确到0.1 m,
参考数据:sin 50°≈0.766,cos 50°≈
0.643,tan 50°≈1.192)
15.3 m
返回
0.21
返回
10. 如图,在△ABC中,AB=8,AC=9,∠A=48°.求:
(1)AB边上的高(用计算器计算,结果精确到0.01);
(2)∠B的度数(用计算器计算,结果精确到1′).
返回
课堂小结
三角函数的计算
三角函数值
利用仰角、俯角解决问题
任意锐角
计算器
工具
谢谢观看!
1.3 三角函数的计算
第一章 直角三角形的边角关系
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示一些生活中与直角三角形相关的图片,如楼梯、斜坡、电线杆的拉线等,并提出问题:在这些生活场景中,我们常常需要知道一些角度或长度的信息,比如楼梯的倾斜程度、斜坡的坡度等,那么如何通过已有的边长信息来获取这些角度信息,或者通过角度来计算边长呢?
引导学生思考,引发学生对直角三角形边角关系的好奇心和探究欲望,从而引出本节课的课题 —— 直角三角形的边角关系。
(二)讲授新课(25 分钟)
锐角三角函数的定义
构建直角三角形模型:在黑板上画出一个 Rt,其中∠C = 90° 。
引入正弦函数:设∠A 为锐角,引导学生观察∠A 的对边 BC 与斜边 AB 的比值,定义 sin= \(\frac{BC}{AB}\),即∠A 的正弦等于∠A 的对边与斜边的比。通过改变∠A 的大小,让学生观察这个比值的变化情况,强调对于一个确定的锐角∠A,其正弦值是固定的。
同理,讲解余弦函数和正切函数的定义:co = \(\frac{AC}{AB}\),∠A 的余弦等于∠A 的邻边与斜边的比;ta = \(\frac{BC}{AC}\),∠A 的正切等于∠A 的对边与邻边的比。
给出多个不同的直角三角形,让学生分别同锐角的正弦、余弦和正切值,加深对定义的理解。
特殊锐角的三角函数值
30° 角的三角函数值:构建一个含 30° 角的直角三角形,设 30° 角所对的直角边为 a,根据直角三角形中 30° 角所对的直角边等于斜边的一半,可得斜边为 2a,再利用勾股定理求出另一条直角边为\(\sqrt{3}a\) 。然后分别计算 sin30° = \(\frac{a}{2a}\) = \(\frac{1}{2}\),cos30° = \(\frac{\sqrt{3}a}{2a}\) = \(\frac{\sqrt{3}}{2}\),tan30° = \(\frac{a}{\sqrt{3}a}\) = \(\frac{\sqrt{3}}{3}\) 。
45° 角的三角函数值:构建一个等腰直角三角形,设直角边为 b,则斜边为\(\sqrt{2}b\) 。计算 sin45° = \(\frac{b}{\sqrt{2}b}\) = \(\frac{\sqrt{2}}{2}\),cos45° = \(\frac{b}{\sqrt{2}b}\) = \(\frac{\sqrt{2}}{2}\),tan45° = \(\frac{b}{b}\) = 1 。
60° 角的三角函数值:利用含 30° 角的直角三角形,因为 60° 角与 30° 角互为余角,根据三角函数的诱导公式或直接计算,可得 sin60° = \(\frac{\sqrt{3}}{2}\),cos60° = \(\frac{1}{2}\),tan60° = \(\sqrt{3}\) 。
制作特殊锐角三角函数值表格,让学生观察表格,总结规律,帮助记忆。
三角函数的应用
举例说明如何运用三角函数解决实际问题,如测量建筑物的高度。已知在离建筑物底部一定距离的地方,测量出观测点到建筑物顶部的仰角以及观测点到建筑物底部的距离,构建直角三角形,选择合适的三角函数(如正切函数)来计算建筑物的高度。
讲解解题的一般步骤:首先根据题意画出直角三角形,明确已知条件和所求问题;然后分析在直角三角形中已知哪些边或角,选择恰当的三角函数关系;最后进行计算求解,并检验答案的合理性。
(三)例题讲解(15 分钟)
例 1:在 Rt中,∠C = 90°,AB = 5,BC = 3,求 sin的值。
分析:根据正弦、余弦和正切函数的定义,先求出 AC 的长度(利用勾股定理 AC = \(\sqrt{AB^{2} - BC^{2}}\) = \(\sqrt{25 - 9}\) = 4),再代入公式计算。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
用科学计算器求任意锐角的三角函数值
1. 求整数度数的锐角的三角函数值
在科学计算器的面板上涉及三角函数的键有
,当我们计算某整数度数的三角函数值时,可先按相应的键,然后从高位向低位按出表示度数的整数,最后按 键,屏幕上就会显示出结果.
知1-讲
感悟新知
2. 求非整数度数的锐角的三角函数值
(1)若度数是用度表示的,则按整数度数的按键步骤操作 即可.
(2)若度数是用度、分、秒表示的,在用科学计算器计算三角函数值时,同样先按 或 或 键,然后依次按 (度) (分) (秒)键,最后按 键,屏幕上就会显示出结果. 若锐角中只有度、秒,则应在
(分)键前补上0 .
感悟新知
知1-练
用计算器求sin 26°,cos 42°,tan 75°,
sin 72°38′25″的值.
例 1
解题秘方:按计算器的使用说明求值.
感悟新知
知1-练
解:求值过程如下表所示.
按键顺序 显示结果
sin 26° sin 26°=0.438 371 146
cos 42° cos 42°=0.743 144 825
tan 75° tan 75°=3.732 050 808
sin 72°38′25″ sin 72°38′25″=
0.954 450 312
知识点
用科学计算器由锐角三角函数值求锐角
知2-讲
感悟新知
2
已知锐角三角函数值求锐角的度数
如果是特殊角(30°,45°或60°角)的三角函数值,可直接写出其相应的角的度数;若不是特殊角的三角函数值,应利用计算器求角的度数. 求角的度数要先按 键,将 转化成它们的第二功能. 当三角函数值为分数时,应先化成小数.
感悟新知
知2-练
根据下列条件求锐角A 的度数:
(1)sin A=0.921 6;
(2)cos A=0.680 7;
(3)tan A=0.189 0.
例2
解题秘方:按计算器的使用说明依次按键.
知2-练
感悟新知
解:(1)按键顺序为
显示结果为sin-10.921 6=67.161 123 32,
再按 得∠ A ≈ 67°9′40″.
(2)按键顺序为
显示结果为cos-10.680 7=47.101 632 24,
再按 得∠ A ≈ 47°6′6″.
知2-练
感悟新知
(3)按键顺序为
显示结果为tan-10.189 0=10.702 657 49,
再按 得∠ A ≈ 10°42′10″
知识点
仰角、俯角
知3-讲
感悟新知
3
名称 定义 图示
仰角 当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角
俯角 当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角 感悟新知
知3-练
如图1-3-1,小东在教学楼距地面9 m 高的窗口
C处,测得正前方旗杆顶部A 点的仰角为37°,旗杆底部B 点的俯角为45°. 升旗时,国旗上端在距地面1.95 m处,若国旗随国歌声冉冉升起,并在国歌播放
46 s 结束时到达旗杆顶端,则国旗应以
多大的速度匀速上升?( 参考数据:sin 37 °
≈ 0.60 ,cos 37°≈ 0.80 ,tan 37°≈ 0.75 )
例 3
知3-练
感悟新知
解:如图1-3-1,作CD ⊥ AB 于点D,则BD=9 m.
在Rt△BCD中,BD=9 m,
∠ BCD=45° ,
则BD=CD=9 m.
在Rt△ACD中,CD=9 m,
∠ ACD=37° ,
知3-练
感悟新知
则AD=CD·tan 37°≈ 9×0.75=6.75(m).
所以AB=AD+BD≈ 15.75 m.
因为国旗上升的高度约是15.75-1.95=13.8(m),
整个过程耗时46 s,所以国旗的上升速度约为=0.3(m/s).
因此国旗应以约0.3 m/s 的速度匀速上升.
知3-练
感悟新知
3-1. [中考·新疆] 烽燧即烽火台,是古代军情报警的一种措施,史册记载,夜间举火称“烽”,白天放烟称“燧”.克孜尔尕哈烽燧是古丝绸之路北道上新疆境内时代最早、保存最完好、规模最大的古代烽燧.
知3-练
感悟新知
某数学兴趣小组利用无人机测量该烽燧的高度,如图,无人机飞至距地面高度31.5 米的A处,测得烽燧BC的顶部C处的俯角为50°,测得烽燧BC的底部B处的俯角为65°,试根据提供的数据计算烽燧BC的高度.
(参考数据:sin 50°≈ 0.8,cos 50°≈ 0.6,
tan 50°≈1.2,sin 65°≈0.9,cos 65°≈0.4,
tan 65°≈ 2.1)
知3-练
感悟新知
知3-练
感悟新知
返回
1. 用计算器求sin 70°的值,以下按键顺序正确的是( )
A. B.
C. D.
A
返回
2. 如图,△ABC中,∠ACB=90°,BC=2,AC=3,若用科学计算器求∠A的度数,并以“度、分、秒”为单位表示出这个度数,则下列按键顺序正确的是( )
A.
B.
C.
D.
D
返回
3. [教材P15习题T3] (1)已知cos A=0.785 7,用计算器计算锐角∠A≈________(精确到1′).
(2)已知sin α=0.603 1,用计算器求锐角α≈____________ (精确到1″).
38°13′
37°5′32″
返回
4. 利用计算器计算sin29.5°-cos 58°30′+tan 52°30′≈______. (精确到0.01)
0.81
返回
5. [教材P15习题T5]如图,一个人从山脚下的A点出发,沿山坡小路AB走到山顶B点. 已知坡角为20°,山高BC= 2 km.用科学计算器计算小路AB的长度为__________. (结果精确到0.01 km)
5.85 km
6. 应用计算器填一填,分别比较各个三角函数值的大小,说一说有什么规律:
(1)cos 20°≈________,cos 40°≈________,
cos 60°=________,cos 80°≈________.
规律:
0.939 7
0.766 0
0.5
0.173 6
在锐角范围内,余弦函数值随着角度的增大而减小.
返回
(2)tan 10°≈________,tan 30°≈________,
tan 50°≈________,tan 70°≈________.
规律:
0.176 3
0.577 4
1.191 8
2.747 5
在锐角范围内,正切函数值随着角度的增大而增大.
返回
【答案】C
8. 2024年4月25日,神舟十八号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站. 中国空间站上机械臂的一种工作状态的示意图如图所示,当两臂AC=BC=10 m,两臂夹角∠ACB=100°时,可得A,B两点间的距离为________. (结果精确到0.1 m,
参考数据:sin 50°≈0.766,cos 50°≈
0.643,tan 50°≈1.192)
15.3 m
返回
0.21
返回
10. 如图,在△ABC中,AB=8,AC=9,∠A=48°.求:
(1)AB边上的高(用计算器计算,结果精确到0.01);
(2)∠B的度数(用计算器计算,结果精确到1′).
返回
课堂小结
三角函数的计算
三角函数值
利用仰角、俯角解决问题
任意锐角
计算器
工具
谢谢观看!
