1.6 利用三角函数测高 课件(共32张PPT)
文档属性
| 名称 | 1.6 利用三角函数测高 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:08:15 | ||
图片预览








文档简介
(共32张PPT)
1.6 利用三角函数测高
第一章 直角三角形的边角关系
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示一些生活中与直角三角形相关的图片,如楼梯、斜坡、电线杆的拉线等,并提出问题:在这些生活场景中,我们常常需要知道一些角度或长度的信息,比如楼梯的倾斜程度、斜坡的坡度等,那么如何通过已有的边长信息来获取这些角度信息,或者通过角度来计算边长呢?
引导学生思考,引发学生对直角三角形边角关系的好奇心和探究欲望,从而引出本节课的课题 —— 直角三角形的边角关系。
(二)讲授新课(25 分钟)
锐角三角函数的定义
构建直角三角形模型:在黑板上画出一个 Rt,其中∠C = 90° 。
引入正弦函数:设∠A 为锐角,引导学生观察∠A 的对边 BC 与斜边 AB 的比值,定义 sin= \(\frac{BC}{AB}\),即∠A 的正弦等于∠A 的对边与斜边的比。通过改变∠A 的大小,让学生观察这个比值的变化情况,强调对于一个确定的锐角∠A,其正弦值是固定的。
同理,讲解余弦函数和正切函数的定义:co = \(\frac{AC}{AB}\),∠A 的余弦等于∠A 的邻边与斜边的比;ta = \(\frac{BC}{AC}\),∠A 的正切等于∠A 的对边与邻边的比。
给出多个不同的直角三角形,让学生分别同锐角的正弦、余弦和正切值,加深对定义的理解。
特殊锐角的三角函数值
30° 角的三角函数值:构建一个含 30° 角的直角三角形,设 30° 角所对的直角边为 a,根据直角三角形中 30° 角所对的直角边等于斜边的一半,可得斜边为 2a,再利用勾股定理求出另一条直角边为\(\sqrt{3}a\) 。然后分别计算 sin30° = \(\frac{a}{2a}\) = \(\frac{1}{2}\),cos30° = \(\frac{\sqrt{3}a}{2a}\) = \(\frac{\sqrt{3}}{2}\),tan30° = \(\frac{a}{\sqrt{3}a}\) = \(\frac{\sqrt{3}}{3}\) 。
45° 角的三角函数值:构建一个等腰直角三角形,设直角边为 b,则斜边为\(\sqrt{2}b\) 。计算 sin45° = \(\frac{b}{\sqrt{2}b}\) = \(\frac{\sqrt{2}}{2}\),cos45° = \(\frac{b}{\sqrt{2}b}\) = \(\frac{\sqrt{2}}{2}\),tan45° = \(\frac{b}{b}\) = 1 。
60° 角的三角函数值:利用含 30° 角的直角三角形,因为 60° 角与 30° 角互为余角,根据三角函数的诱导公式或直接计算,可得 sin60° = \(\frac{\sqrt{3}}{2}\),cos60° = \(\frac{1}{2}\),tan60° = \(\sqrt{3}\) 。
制作特殊锐角三角函数值表格,让学生观察表格,总结规律,帮助记忆。
三角函数的应用
举例说明如何运用三角函数解决实际问题,如测量建筑物的高度。已知在离建筑物底部一定距离的地方,测量出观测点到建筑物顶部的仰角以及观测点到建筑物底部的距离,构建直角三角形,选择合适的三角函数(如正切函数)来计算建筑物的高度。
讲解解题的一般步骤:首先根据题意画出直角三角形,明确已知条件和所求问题;然后分析在直角三角形中已知哪些边或角,选择恰当的三角函数关系;最后进行计算求解,并检验答案的合理性。
(三)例题讲解(15 分钟)
例 1:在 Rt中,∠C = 90°,AB = 5,BC = 3,求 sin的值。
分析:根据正弦、余弦和正切函数的定义,先求出 AC 的长度(利用勾股定理 AC = \(\sqrt{AB^{2} - BC^{2}}\) = \(\sqrt{25 - 9}\) = 4),再代入公式计算。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
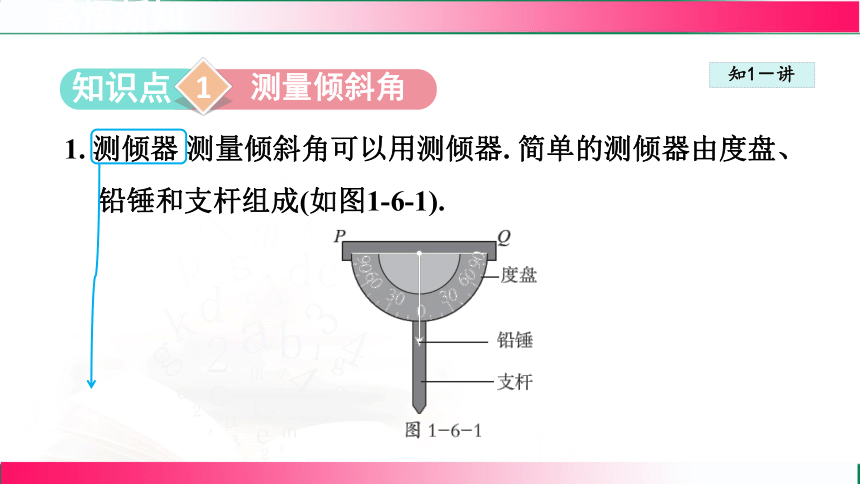
测量倾斜角
1. 测倾器 测量倾斜角可以用测倾器. 简单的测倾器由度盘、铅锤和支杆组成(如图1-6-1).
知1-讲
感悟新知
2. 使用测倾器测量倾斜角的步骤
(1)把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ 在水平位置.
(2)转动度盘,使度盘的直径对准目标,记下此时铅垂线所指的度数.
根据对顶角相等及同角的余角相等可以知道,所测倾斜角(即仰角、俯角)等于铅垂线所指的度数,读出铅垂线所指的度数,即为倾斜角的度数.
感悟新知
知1-练
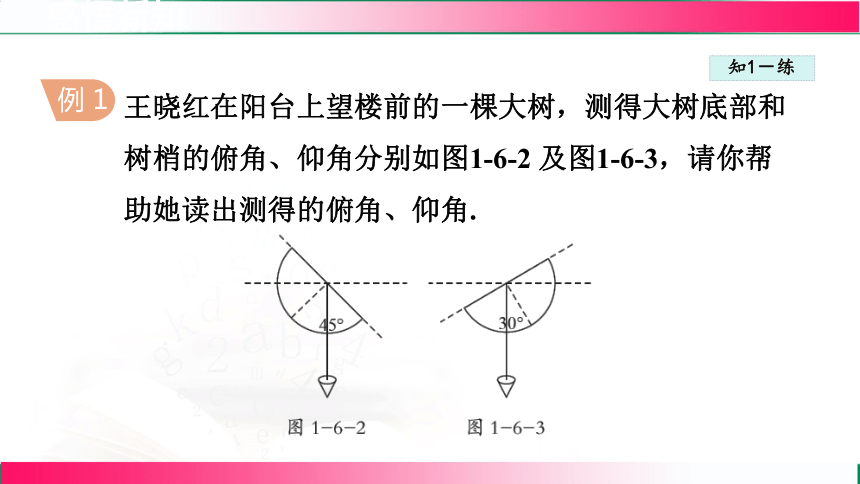
王晓红在阳台上望楼前的一棵大树,测得大树底部和树梢的俯角、仰角分别如图1-6-2 及图1-6-3,请你帮助她读出测得的俯角、仰角.
例 1
感悟新知
知1-练
1-1. 某数学实践活动小组去测量眉山市某标志性建筑物的高CD.如图,在楼前平地A 处测得楼顶C 处的仰角为30°,沿AD 方向前进60 m 到达B 处,测得楼顶C 处的仰角为45°,则∠ ACB=_____ .
15°
知识点
测量底部可以到达的物体的高度
知2-讲
感悟新知
2
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
知2-讲
感悟新知
如图1-6-4,测量MN 高度的步骤如下:
(1)在测点A 处安置测倾器,测得M 的
仰角∠ MCE=α ;
(2)量出测点A 到物体底部N 的水平距离AN=l;
(3)量出测倾器的高度AC=a .
求出MN 的高度MN=ME+EN=ltanα +a.
感悟新知
知2-练
如图1-6-5,李亮用测倾器在点D 处测量旗杆BC 的
高度,测倾器的高度AD=1.21 m,地面上DC=20.04 m,仰角α=28°,请你帮李亮计算一下旗杆BC 有多高(结果精确到0.1 m,参考数据:sin 28°≈
0.469 5,cos 28°≈ 0.882 9,
tan 28°≈ 0.531 7).
例 2
知2-练
感悟新知
解: 如图1-6-5,过点A 作AE ⊥ BC 于点E,由题意,
得AE=DC=20.04 m,EC=AD=1.21 m,
∠ BAE=α =28°.
在Rt△ABE 中,BE=AE·tan α =
20.04×tan 28°≈20.04×0.531 7≈10.66(m).
∴ BC=BE+EC ≈ 10.66+1.21 ≈ 11.9(m).
∴旗杆BC 的高约为11.9 m.
知识点
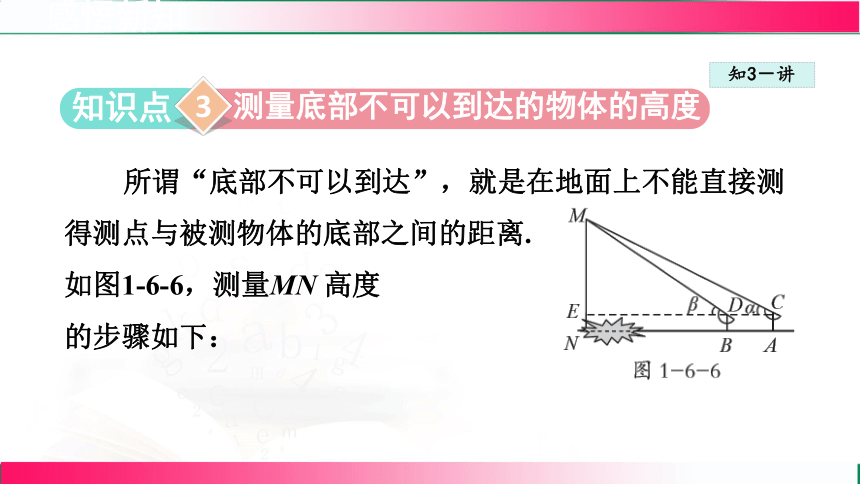
测量底部不可以到达的物体的高度
知3-讲
感悟新知
3
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
如图1-6-6,测量MN 高度
的步骤如下:
知3-讲
感悟新知
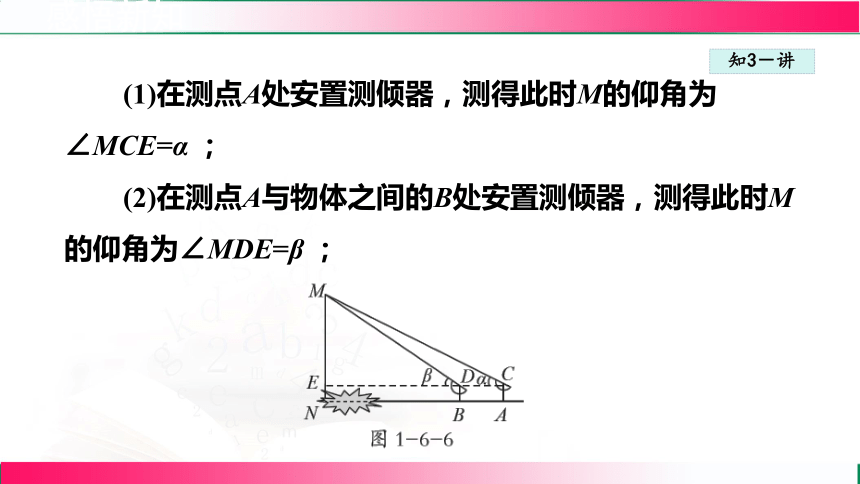
(1)在测点A处安置测倾器,测得此时M的仰角为∠MCE=α ;
(2)在测点A与物体之间的B处安置测倾器,测得此时M的仰角为∠MDE=β ;
知3-讲
感悟新知
(3)量出测倾器的高度AC=BD=a,以及测点A,B 之间的距离AB=b.
借助- = b求出ME,
则MN=ME+EN = +a.
感悟新知
知3-练
[中考·绍兴] 如图1-6-7,从地面上的点A 看一山坡上的电线杆PQ,测得杆顶端点P 的仰角是45°,
向前走6 m 到达点B,测得杆顶端点P
和杆底端点Q 的仰角分别是
60°和30°.
例 3
解题秘方:解几个直角三角形,根据线段之间的和、差关系求出高度.
感悟新知
知3-练
(1)求∠ BPQ 的度数;
解:如图1-6-7,延长PQ 交直线AB 于点E.
(1)在Rt △PBE中,
∵∠PBE=60°,∠PBE=60°,
∴∠BPQ=90°-∠PBE=
90°-60°=30°.
感悟新知
知3-练
(2)求该电线杆PQ 的高度.(结果精确到1 m,参考数据:≈ 1.7,≈ 1 .4 )
解:设PE=x m.
在Rt△APE中,∠PAE=45°,则AE=PE=x m.
在Rt△BPE中,∵∠PBE=60°,tan ∠PBE=,
∴ BE= = PE = x m.
感悟新知
知3-练
∵ AB=AE-BE,∴ x-x=6,解得x=9+3.
∴ PE=(9+3)m,BE= ×(9+3)=3 +3(m).
在Rt△BEQ中,∵∠QBE=30°,tan ∠QBE= ,
∴ QE=BE·tan 30°= ×(3 +3)=3+(m).
∴ PQ=PE-QE=9+ 3-(3+)=6+2 ≈ 9(m).
即该电线杆PQ 的高度约为9 m.
返回
A
2. [2024绥化]如图,用热气球的探测器测一栋楼BC的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,
测得底部点B的俯角为45°,点A与楼BC的
水平距离AD=50m,则这栋楼BC的高度为
___________m(结果保留根号).
返回
3. [2024陕西]如图所示,一座小山顶的水平观景台的海拔高度为1 600 m,小明想利用这个观景台测量对面山顶C点处的海拔高度. 他在该观景台上选定了一点A,在点A处测得C点的仰角∠CAE=42°,再在AE上选一点B,在点B处测得C点的仰角∠CBE=45°,AB=10 m.
求山顶C点处的海拔高度. (小明身高忽略
不计,参考数据:sin 42°≈0.67,
cos 42°≈0.74,tan 42°≈0.90)
【解】如图,过点C作CD⊥AE,交AE的
延长线于点D,设BD=x m,∵AB=10 m,
∴AD=AB+BD=(x+10)m.
在Rt△BCD中,∠CBD=45°,
∴CD=BD·tan 45°=x m.在Rt△ACD中,∠CAE=42°,
∴CD=AD·tan 42°≈0.9(x+10)m.∴x≈0.9(x+10),解得x≈90. ∴CD≈90 m.∵小山顶的水平观景台的海拔高度为1 600 m,∴山顶C点处的海拔高度约为1 600+90=1 690(m).
返回
4. [2024扬州期中]在测量旗杆高度的活动课上,某兴趣小组自制了一个测高仪测量旗杆高度,测高仪ABCD为正方形,AB=30 cm,顶点A处挂了一个铅锤M.如图是测量旗杆高度的示意图,测高仪上的点B,A与旗
杆顶点P在一条直线上,铅垂线AM交CD于
点N.经测量,点A距地面1.8 m,到旗杆
PQ的距离AE=5 m.
(1)若点N与点C重合,则旗杆PQ的高度为________;
(2)若DN=20 cm.求旗杆PQ的高度(结果精确到0.1 m).
6.8 m
【解】由题意可知,∠DAP=∠MAE=∠BAD=90°,
EQ=1.8 m,
则∠PAE+∠DAE=∠DAE+∠DAN=90°,
∴∠PAE=∠DAN.
返回
5. 图①为某大型商场的自动扶梯,图②中的AB为从一楼到二楼的自动扶梯的侧面示意图. 当小明站在扶梯起点的A处时,测得天花板上日光灯C的仰角为37°,此时他的眼睛D与地面MN的距离AD=1.8 m,之后他沿一楼扶梯到达顶端B后又沿BL(BL∥MN)向正前方走了2 m,发现日光灯C刚好在他的正上方.
已知自动扶梯AB的坡度为
1∶2.4,AB=13 m.
(1)求一楼扶梯顶端B到一楼地面的高度;
(2)求日光灯C到一楼地面的高度. (结果保留一位小数,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
【解】如图,过点C作CF⊥MN于
点F,交BL于点G,过点D作DJ⊥
CF于点J,交BE于点H,
∴易得四边形BEFG,四边形ADJF是矩形.
根据题意,得BG=2 m,∠CDJ=37°,AD=1.8 m,
∴EF=BG=2 m,FJ=AD=1.8 m,AF=DJ.
返回
课堂小结
利用三角函数测高
测量物体
的高度
测倾器
工具
底部可
到达
类型
底部不
可到达
谢谢观看!
1.6 利用三角函数测高
第一章 直角三角形的边角关系
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示一些生活中与直角三角形相关的图片,如楼梯、斜坡、电线杆的拉线等,并提出问题:在这些生活场景中,我们常常需要知道一些角度或长度的信息,比如楼梯的倾斜程度、斜坡的坡度等,那么如何通过已有的边长信息来获取这些角度信息,或者通过角度来计算边长呢?
引导学生思考,引发学生对直角三角形边角关系的好奇心和探究欲望,从而引出本节课的课题 —— 直角三角形的边角关系。
(二)讲授新课(25 分钟)
锐角三角函数的定义
构建直角三角形模型:在黑板上画出一个 Rt,其中∠C = 90° 。
引入正弦函数:设∠A 为锐角,引导学生观察∠A 的对边 BC 与斜边 AB 的比值,定义 sin= \(\frac{BC}{AB}\),即∠A 的正弦等于∠A 的对边与斜边的比。通过改变∠A 的大小,让学生观察这个比值的变化情况,强调对于一个确定的锐角∠A,其正弦值是固定的。
同理,讲解余弦函数和正切函数的定义:co = \(\frac{AC}{AB}\),∠A 的余弦等于∠A 的邻边与斜边的比;ta = \(\frac{BC}{AC}\),∠A 的正切等于∠A 的对边与邻边的比。
给出多个不同的直角三角形,让学生分别同锐角的正弦、余弦和正切值,加深对定义的理解。
特殊锐角的三角函数值
30° 角的三角函数值:构建一个含 30° 角的直角三角形,设 30° 角所对的直角边为 a,根据直角三角形中 30° 角所对的直角边等于斜边的一半,可得斜边为 2a,再利用勾股定理求出另一条直角边为\(\sqrt{3}a\) 。然后分别计算 sin30° = \(\frac{a}{2a}\) = \(\frac{1}{2}\),cos30° = \(\frac{\sqrt{3}a}{2a}\) = \(\frac{\sqrt{3}}{2}\),tan30° = \(\frac{a}{\sqrt{3}a}\) = \(\frac{\sqrt{3}}{3}\) 。
45° 角的三角函数值:构建一个等腰直角三角形,设直角边为 b,则斜边为\(\sqrt{2}b\) 。计算 sin45° = \(\frac{b}{\sqrt{2}b}\) = \(\frac{\sqrt{2}}{2}\),cos45° = \(\frac{b}{\sqrt{2}b}\) = \(\frac{\sqrt{2}}{2}\),tan45° = \(\frac{b}{b}\) = 1 。
60° 角的三角函数值:利用含 30° 角的直角三角形,因为 60° 角与 30° 角互为余角,根据三角函数的诱导公式或直接计算,可得 sin60° = \(\frac{\sqrt{3}}{2}\),cos60° = \(\frac{1}{2}\),tan60° = \(\sqrt{3}\) 。
制作特殊锐角三角函数值表格,让学生观察表格,总结规律,帮助记忆。
三角函数的应用
举例说明如何运用三角函数解决实际问题,如测量建筑物的高度。已知在离建筑物底部一定距离的地方,测量出观测点到建筑物顶部的仰角以及观测点到建筑物底部的距离,构建直角三角形,选择合适的三角函数(如正切函数)来计算建筑物的高度。
讲解解题的一般步骤:首先根据题意画出直角三角形,明确已知条件和所求问题;然后分析在直角三角形中已知哪些边或角,选择恰当的三角函数关系;最后进行计算求解,并检验答案的合理性。
(三)例题讲解(15 分钟)
例 1:在 Rt中,∠C = 90°,AB = 5,BC = 3,求 sin的值。
分析:根据正弦、余弦和正切函数的定义,先求出 AC 的长度(利用勾股定理 AC = \(\sqrt{AB^{2} - BC^{2}}\) = \(\sqrt{25 - 9}\) = 4),再代入公式计算。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
测量倾斜角
1. 测倾器 测量倾斜角可以用测倾器. 简单的测倾器由度盘、铅锤和支杆组成(如图1-6-1).
知1-讲
感悟新知
2. 使用测倾器测量倾斜角的步骤
(1)把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ 在水平位置.
(2)转动度盘,使度盘的直径对准目标,记下此时铅垂线所指的度数.
根据对顶角相等及同角的余角相等可以知道,所测倾斜角(即仰角、俯角)等于铅垂线所指的度数,读出铅垂线所指的度数,即为倾斜角的度数.
感悟新知
知1-练
王晓红在阳台上望楼前的一棵大树,测得大树底部和树梢的俯角、仰角分别如图1-6-2 及图1-6-3,请你帮助她读出测得的俯角、仰角.
例 1
感悟新知
知1-练
1-1. 某数学实践活动小组去测量眉山市某标志性建筑物的高CD.如图,在楼前平地A 处测得楼顶C 处的仰角为30°,沿AD 方向前进60 m 到达B 处,测得楼顶C 处的仰角为45°,则∠ ACB=_____ .
15°
知识点
测量底部可以到达的物体的高度
知2-讲
感悟新知
2
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
知2-讲
感悟新知
如图1-6-4,测量MN 高度的步骤如下:
(1)在测点A 处安置测倾器,测得M 的
仰角∠ MCE=α ;
(2)量出测点A 到物体底部N 的水平距离AN=l;
(3)量出测倾器的高度AC=a .
求出MN 的高度MN=ME+EN=ltanα +a.
感悟新知
知2-练
如图1-6-5,李亮用测倾器在点D 处测量旗杆BC 的
高度,测倾器的高度AD=1.21 m,地面上DC=20.04 m,仰角α=28°,请你帮李亮计算一下旗杆BC 有多高(结果精确到0.1 m,参考数据:sin 28°≈
0.469 5,cos 28°≈ 0.882 9,
tan 28°≈ 0.531 7).
例 2
知2-练
感悟新知
解: 如图1-6-5,过点A 作AE ⊥ BC 于点E,由题意,
得AE=DC=20.04 m,EC=AD=1.21 m,
∠ BAE=α =28°.
在Rt△ABE 中,BE=AE·tan α =
20.04×tan 28°≈20.04×0.531 7≈10.66(m).
∴ BC=BE+EC ≈ 10.66+1.21 ≈ 11.9(m).
∴旗杆BC 的高约为11.9 m.
知识点
测量底部不可以到达的物体的高度
知3-讲
感悟新知
3
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
如图1-6-6,测量MN 高度
的步骤如下:
知3-讲
感悟新知
(1)在测点A处安置测倾器,测得此时M的仰角为∠MCE=α ;
(2)在测点A与物体之间的B处安置测倾器,测得此时M的仰角为∠MDE=β ;
知3-讲
感悟新知
(3)量出测倾器的高度AC=BD=a,以及测点A,B 之间的距离AB=b.
借助- = b求出ME,
则MN=ME+EN = +a.
感悟新知
知3-练
[中考·绍兴] 如图1-6-7,从地面上的点A 看一山坡上的电线杆PQ,测得杆顶端点P 的仰角是45°,
向前走6 m 到达点B,测得杆顶端点P
和杆底端点Q 的仰角分别是
60°和30°.
例 3
解题秘方:解几个直角三角形,根据线段之间的和、差关系求出高度.
感悟新知
知3-练
(1)求∠ BPQ 的度数;
解:如图1-6-7,延长PQ 交直线AB 于点E.
(1)在Rt △PBE中,
∵∠PBE=60°,∠PBE=60°,
∴∠BPQ=90°-∠PBE=
90°-60°=30°.
感悟新知
知3-练
(2)求该电线杆PQ 的高度.(结果精确到1 m,参考数据:≈ 1.7,≈ 1 .4 )
解:设PE=x m.
在Rt△APE中,∠PAE=45°,则AE=PE=x m.
在Rt△BPE中,∵∠PBE=60°,tan ∠PBE=,
∴ BE= = PE = x m.
感悟新知
知3-练
∵ AB=AE-BE,∴ x-x=6,解得x=9+3.
∴ PE=(9+3)m,BE= ×(9+3)=3 +3(m).
在Rt△BEQ中,∵∠QBE=30°,tan ∠QBE= ,
∴ QE=BE·tan 30°= ×(3 +3)=3+(m).
∴ PQ=PE-QE=9+ 3-(3+)=6+2 ≈ 9(m).
即该电线杆PQ 的高度约为9 m.
返回
A
2. [2024绥化]如图,用热气球的探测器测一栋楼BC的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,
测得底部点B的俯角为45°,点A与楼BC的
水平距离AD=50m,则这栋楼BC的高度为
___________m(结果保留根号).
返回
3. [2024陕西]如图所示,一座小山顶的水平观景台的海拔高度为1 600 m,小明想利用这个观景台测量对面山顶C点处的海拔高度. 他在该观景台上选定了一点A,在点A处测得C点的仰角∠CAE=42°,再在AE上选一点B,在点B处测得C点的仰角∠CBE=45°,AB=10 m.
求山顶C点处的海拔高度. (小明身高忽略
不计,参考数据:sin 42°≈0.67,
cos 42°≈0.74,tan 42°≈0.90)
【解】如图,过点C作CD⊥AE,交AE的
延长线于点D,设BD=x m,∵AB=10 m,
∴AD=AB+BD=(x+10)m.
在Rt△BCD中,∠CBD=45°,
∴CD=BD·tan 45°=x m.在Rt△ACD中,∠CAE=42°,
∴CD=AD·tan 42°≈0.9(x+10)m.∴x≈0.9(x+10),解得x≈90. ∴CD≈90 m.∵小山顶的水平观景台的海拔高度为1 600 m,∴山顶C点处的海拔高度约为1 600+90=1 690(m).
返回
4. [2024扬州期中]在测量旗杆高度的活动课上,某兴趣小组自制了一个测高仪测量旗杆高度,测高仪ABCD为正方形,AB=30 cm,顶点A处挂了一个铅锤M.如图是测量旗杆高度的示意图,测高仪上的点B,A与旗
杆顶点P在一条直线上,铅垂线AM交CD于
点N.经测量,点A距地面1.8 m,到旗杆
PQ的距离AE=5 m.
(1)若点N与点C重合,则旗杆PQ的高度为________;
(2)若DN=20 cm.求旗杆PQ的高度(结果精确到0.1 m).
6.8 m
【解】由题意可知,∠DAP=∠MAE=∠BAD=90°,
EQ=1.8 m,
则∠PAE+∠DAE=∠DAE+∠DAN=90°,
∴∠PAE=∠DAN.
返回
5. 图①为某大型商场的自动扶梯,图②中的AB为从一楼到二楼的自动扶梯的侧面示意图. 当小明站在扶梯起点的A处时,测得天花板上日光灯C的仰角为37°,此时他的眼睛D与地面MN的距离AD=1.8 m,之后他沿一楼扶梯到达顶端B后又沿BL(BL∥MN)向正前方走了2 m,发现日光灯C刚好在他的正上方.
已知自动扶梯AB的坡度为
1∶2.4,AB=13 m.
(1)求一楼扶梯顶端B到一楼地面的高度;
(2)求日光灯C到一楼地面的高度. (结果保留一位小数,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
【解】如图,过点C作CF⊥MN于
点F,交BL于点G,过点D作DJ⊥
CF于点J,交BE于点H,
∴易得四边形BEFG,四边形ADJF是矩形.
根据题意,得BG=2 m,∠CDJ=37°,AD=1.8 m,
∴EF=BG=2 m,FJ=AD=1.8 m,AF=DJ.
返回
课堂小结
利用三角函数测高
测量物体
的高度
测倾器
工具
底部可
到达
类型
底部不
可到达
谢谢观看!
